Drift-Free Joint Angle Calculation Using Inertial Measurement Units without Magnetometers: An Exploration of Sensor Fusion Methods for the Elbow and Wrist
Abstract
1. Introduction
2. Materials and Methods
2.1. Definitions, Notations, and Joint Angle Calculation Process
2.1.1. Quaternion Definition
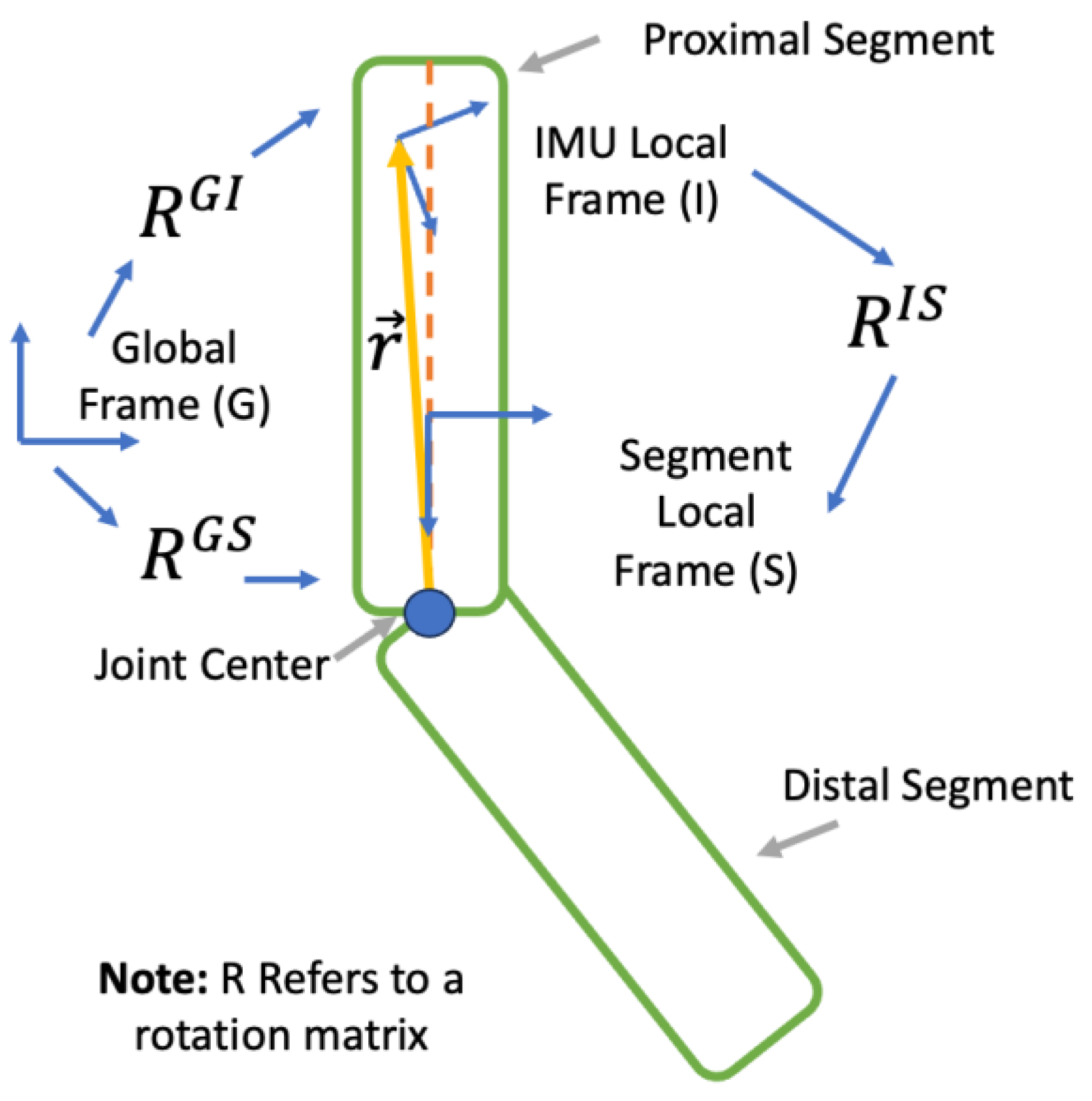
2.1.2. Coordinate Frame Notations and Definitions
2.1.3. Joint Angle Calculation Process
2.2. Sensor Fusion
2.2.1. Multiplicative Extended Kalman Filter
Addition of Rotational Constraint
2.2.2. Rauch–Tung–Striebel Smoother
2.2.3. Maximum a Posteriori
Addition of Rotational Constraint
2.3. IMU-to-Segment Alignment
2.3.1. Translational Alignment
2.3.2. Rotational Alignment
2.4. Data Collection
2.5. Data Analysis
Implementation of Sensor Fusion Algorithms and IMU-to-Segment Alignment
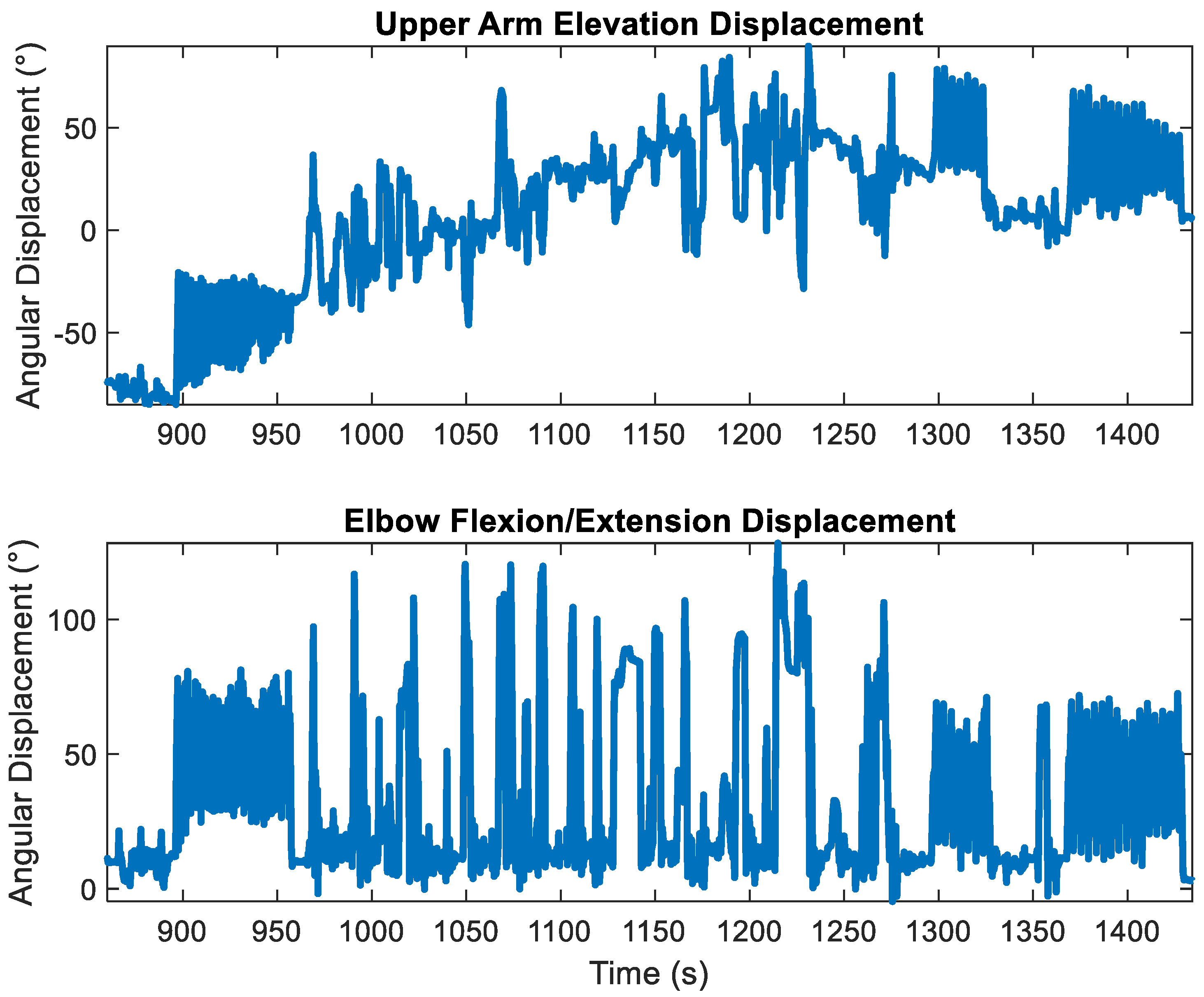
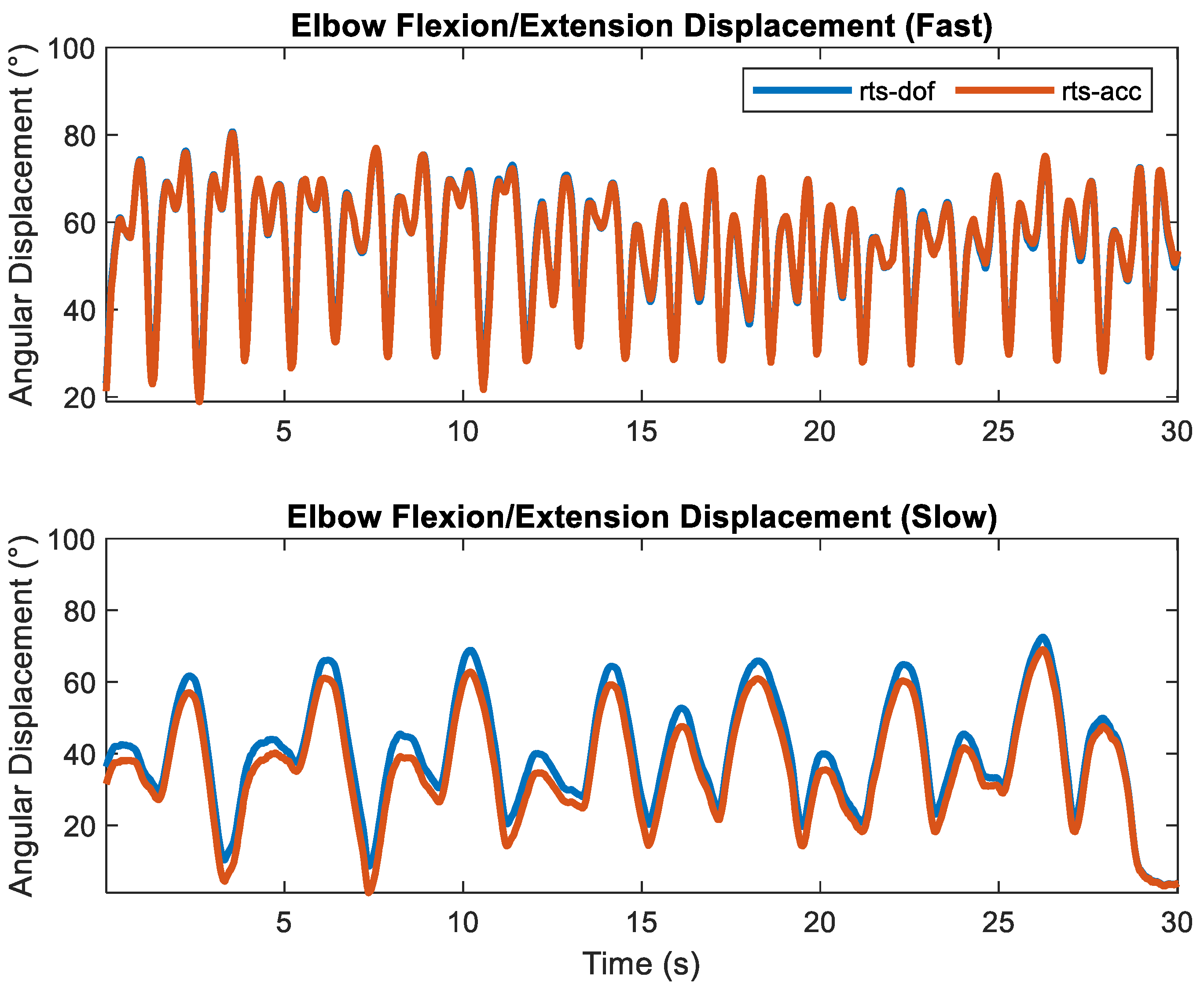
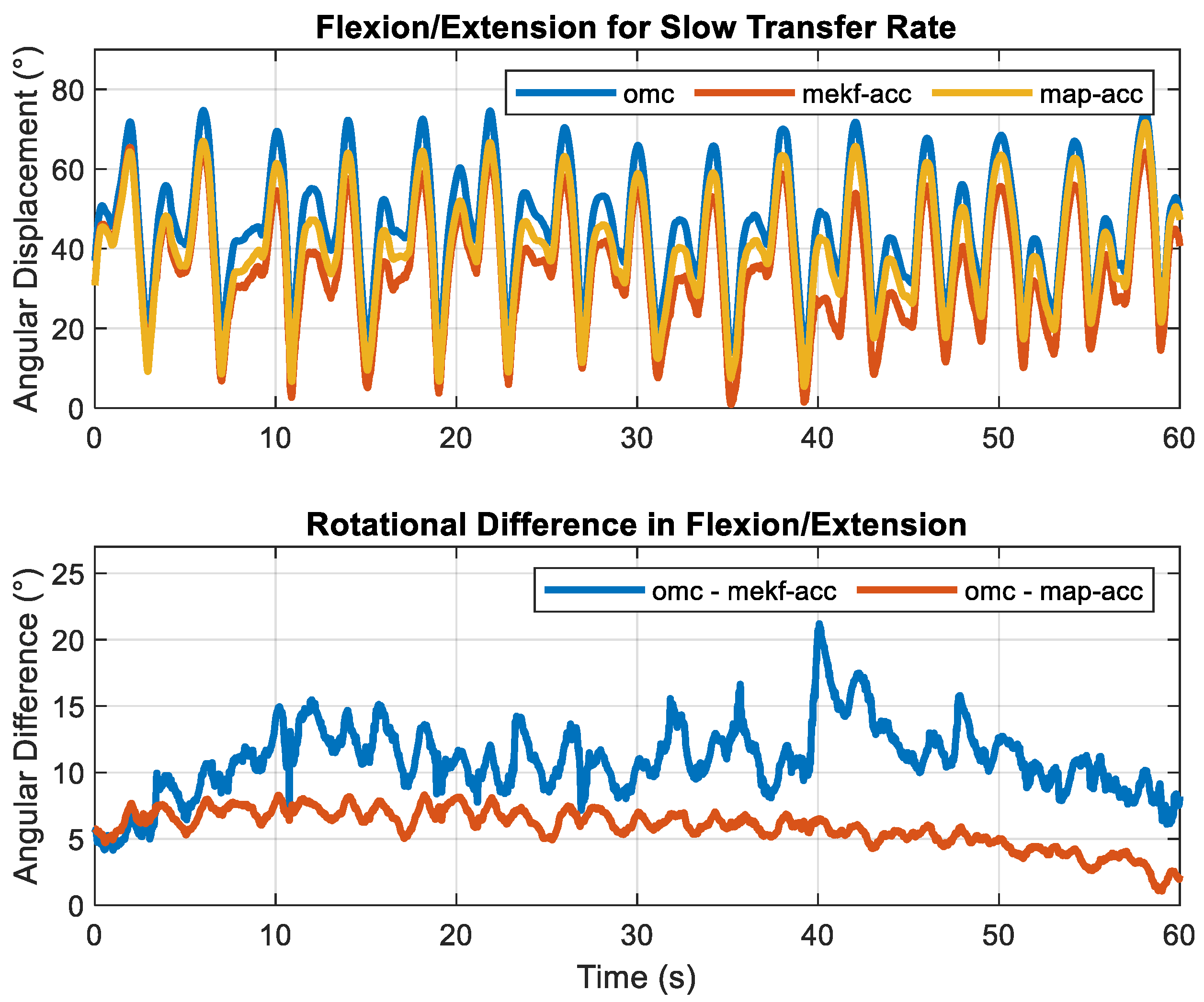
3. Results
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schall, M.C.; Zhang, X.; Chen, H.; Gallagher, S.; Fethke, N.B. Comparing Upper Arm and Trunk Kinematics between Manufacturing Workers Performing Predominantly Cyclic and Non-Cyclic Work Tasks. Appl. Ergon. 2021, 93, 103356. [Google Scholar] [CrossRef] [PubMed]
- Douphrate, D.I.; Fethke, N.B.; Nonnenmann, M.W.; Rosecrance, J.C.; Reynolds, S.J. Full Shift Arm Inclinometry Among Dairy Parlor Workers: A Feasibility Study in a Challenging Work Environment. Appl. Ergon. 2012, 43, 604–613. [Google Scholar] [CrossRef] [PubMed]
- Kersten, J.T.; Fethke, N.B. Radio Frequency Identification to Measure the Duration of Machine-Paced Assembly Tasks: Agreement with Self-Reported Task Duration and Application in Variance Components Analyses of Upper Arm Postures and Movements Recorded over Multiple Days. Appl. Ergon. 2019, 75, 74–82. [Google Scholar] [CrossRef] [PubMed]
- Robert-Lachaine, X.; Larue, C.; Denis, D.; Delisle, A.; Mecheri, H.; Corbeil, P.; Plamondon, A. Feasibility of Quantifying the Physical Exposure of Materials Handlers in the Workplace with Magnetic and Inertial Measurement Units. Ergonomics 2019, 63, 283–292. [Google Scholar] [CrossRef]
- Ji, X.; Littman, A.; Hettiarachchige, R.O.; Piovesan, D. The Effect of Key Anthropometric and Biomechanics Variables Affecting the Lower Back Forces of Healthcare Workers. Sensors 2023, 23, 658. [Google Scholar] [CrossRef]
- Chen, H.; Schall, M.C.; Fethke, N.B. Measuring Upper Arm Elevation Using an Inertial Measurement Unit: An Exploration of Sensor Fusion Algorithms and Gyroscope Models. Appl. Ergon. 2020, 89, 103187. [Google Scholar] [CrossRef]
- Chen, H.; Schall, M.C.; Fethke, N. Effects of Movement Speed and Magnetic Disturbance on the Accuracy of Inertial Measurement Units. Proc. Hum. Factors Ergon. Soc. Annu. Meet. 2017, 61, 1046–1050. [Google Scholar] [CrossRef]
- Bachmann, E.R.; Yun, X.; Peterson, C.W. An Investigation of the Effects of Magnetic Variations on Inertial/Magnetic Orientation Sensors. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation, ICRA 2004, New Orleans, LA, USA, 26 April–1 May 2004; Volume 2, pp. 1115–1122. [Google Scholar]
- Robert-Lachaine, X.; Mecheri, H.; Larue, C.; Plamondon, A. Effect of Local Magnetic Field Disturbances on Inertial Measurement Units Accuracy. Appl. Ergon. 2017, 63, 123–132. [Google Scholar] [CrossRef]
- Ligorio, G.; Bergamini, E.; Truppa, L.; Guaitolini, M.; Raggi, M.; Mannini, A.; Sabatini, A.M.; Vannozzi, G.; Garofalo, P. A Wearable Magnetometer-Free Motion Capture System: Innovative Solutions for Real-World Applications. IEEE Sens. J. 2020, 20, 8844–8857. [Google Scholar] [CrossRef]
- Schiefer, C.; Ellegast, R.P.; Hermanns, I.; Kraus, T.; Ochsmann, E.; Larue, C.; Plamondon, A. Optimization of Inertial Sensor-Based Motion Capturing for Magnetically Distorted Field Applications. J. Biomech. Eng. 2014, 136, 121008. [Google Scholar] [CrossRef]
- Fan, X.; Lind, C.M.; Rhen, I.-M.; Forsman, M. Effects of Sensor Types and Angular Velocity Computational Methods in Field Measurements of Occupational Upper Arm and Trunk Postures and Movements. Sensors 2021, 21, 5527. [Google Scholar] [CrossRef] [PubMed]
- Schall, M.C., Jr.; Fethke, N.B.; Chen, H.; Gerr, F. A Comparison of Instrumentation Methods to Estimate Thoracolumbar Motion in Field-Based Occupational Studies. Appl. Ergon. 2015, 48, 224–231. [Google Scholar] [CrossRef] [PubMed]
- Schall, M.C., Jr.; Fethke, N.B.; Chen, H.; Oyama, S.; Douphrate, D.I. Accuracy and Repeatability of an Inertial Measurement Unit System for Field-Based Occupational Studies. Ergonomics 2016, 59, 591–602. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Schall, M.C.; Fethke, N. Accuracy of Angular Displacements and Velocities from Inertial-Based Inclinometers. Appl. Ergon. 2018, 67, 151–161. [Google Scholar] [CrossRef] [PubMed]
- Sabatini, A.M. Quaternion-Based Extended Kalman Filter for Determining Orientation by Inertial and Magnetic Sensing. IEEE Trans. Biomed. Eng. 2006, 53, 1346–1356. [Google Scholar] [CrossRef] [PubMed]
- Ligorio, G.; Sabatini, A.M. Dealing with Magnetic Disturbances in Human Motion Capture: A Survey of Techniques. Micromachines 2016, 7, 43. [Google Scholar] [CrossRef]
- Roetenberg, D.; Luinge, H.J.; Baten, C.T.M.; Veltink, P.H. Compensation of Magnetic Disturbances Improves Inertial and Magnetic Sensing of Human Body Segment Orientation. IEEE Trans. Neural Syst. Rehabil. Eng. 2005, 13, 395–405. [Google Scholar] [CrossRef] [PubMed]
- Sun, G.; Yang, Y.; Xie, J.; Garrett, M.; Wang, C. Implementing Quaternion Based AHRS on a MEMS Multisensor Hardware Platform. In Proceedings of the International Global Navigation Satellite Systems Society, Gold Coast, Australia, 16 July–18 July 2013. [Google Scholar]
- Renaudin, V.; Combettes, C. Magnetic, Acceleration Fields and Gyroscope Quaternion (MAGYQ)-Based Attitude Estimation with Smartphone Sensors for Indoor Pedestrian Navigation. Sensors 2014, 14, 22864–22890. [Google Scholar] [CrossRef]
- Weygers, I.; Kok, M.; De Vroey, H.; Verbeerst, T.; Versteyhe, M.; Hallez, H.; Claeys, K. Drift-Free Inertial Sensor-Based Joint Kinematics for Long-Term Arbitrary Movements. IEEE Sens. J. 2020, 20, 7969–7979. [Google Scholar] [CrossRef]
- Miezal, M.; Taetz, B.; Bleser, G. On Inertial Body Tracking in the Presence of Model Calibration Errors. Sensors 2016, 16, 1132. [Google Scholar] [CrossRef]
- El-Gohary, M.; McNames, J. Shoulder and Elbow Joint Angle Tracking with Inertial Sensors. IEEE Trans. Biomed. Eng. 2012, 59, 2635–2641. [Google Scholar] [CrossRef] [PubMed]
- El-Gohary, M.; McNames, J. Human Joint Angle Estimation with Inertial Sensors and Validation with A Robot Arm. IEEE Trans. Biomed. Eng. 2015, 62, 1759–1767. [Google Scholar] [CrossRef] [PubMed]
- Teufl, W.; Miezal, M.; Taetz, B.; Fröhlich, M.; Bleser, G.; Teufl, W.; Miezal, M.; Taetz, B.; Fröhlich, M.; Bleser, G. Validity, Test-Retest Reliability and Long-Term Stability of Magnetometer Free Inertial Sensor Based 3D Joint Kinematics. Sensors 2018, 18, 1980. [Google Scholar] [CrossRef] [PubMed]
- Teufl, W.; Miezal, M.; Taetz, B.; Fröhlich, M.; Bleser, G. Validity of Inertial Sensor Based 3D Joint Kinematics of Static and Dynamic Sport and Physiotherapy Specific Movements. PLoS ONE 2019, 14, e0213064. [Google Scholar] [CrossRef]
- Laidig, D.; Müller, P.; Seel, T. Automatic Anatomical Calibration for IMU-Based Elbow Angle Measurement in Disturbed Magnetic Fields. Curr. Dir. Biomed. Eng. 2017, 3, 167–170. [Google Scholar] [CrossRef]
- Luinge, H.J.; Veltink, P.H.; Baten, C.T.M. Ambulatory Measurement of Arm Orientation. J. Biomech. 2007, 40, 78–85. [Google Scholar] [CrossRef]
- Potter, M.V.; Cain, S.M.; Ojeda, L.V.; Gurchiek, R.D.; McGinnis, R.S.; Perkins, N.C. Evaluation of Error-State Kalman Filter Method for Estimating Human Lower-Limb Kinematics during Various Walking Gaits. Sensors 2022, 22, 8398. [Google Scholar] [CrossRef]
- Lee, J.K.; Jeon, T.H. Magnetic Condition-Independent 3D Joint Angle Estimation Using Inertial Sensors and Kinematic Constraints. Sensors 2019, 19, 5522. [Google Scholar] [CrossRef]
- Atrsaei, A.; Salarieh, H.; Alasty, A.; Abediny, M. Human Arm Motion Tracking by Inertial/Magnetic Sensors Using Unscented Kalman Filter and Relative Motion Constraint. J. Intell. Robot. Syst. 2018, 90, 161–170. [Google Scholar] [CrossRef]
- Roetenberg, D.; Luinge, H.J.; Slycke, P. Xsens MVN: Full 6DOF Human Motion Tracking Using Miniature Inertial Sensors. Xsens Motion Technologies BV, Tech. Rep, 1, 1–7. 2009. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=cc2ba84a4d6e06fd85ad434f5b1a8545c1cc993c (accessed on 12 October 2022).
- Kok, M.; Hol, J.D.; Schön, T.B. An Optimization-Based Approach to Human Body Motion Capture Using Inertial Sensors. IFAC Proc. Vol. 2014, 47, 79–85. [Google Scholar] [CrossRef]
- Kortier, H.G.; Sluiter, V.I.; Roetenberg, D.; Veltink, P.H. Assessment of Hand Kinematics Using Inertial and Magnetic Sensors. J. NeuroEng. Rehabil. 2014, 11, 70. [Google Scholar] [CrossRef]
- Lehmann, D.; Laidig, D.; Deimel, R.; Seel, T. Magnetometer-Free Inertial Motion Tracking of Arbitrary Joints with Range of Motion Constraints. arXiv 2020, arXiv:2002.00639. [Google Scholar]
- Yang, H.; Liu, S.; Luo, T.; Liang, H.; Zou, J.; Zhao, L. Research on Human Motion Monitoring Method Based on Multi-Joint Constraint Filter Model. IEEE Sens. J. 2021, 21, 10989–10999. [Google Scholar] [CrossRef]
- Lin, J.F.S.; Kulić, D. Human Pose Recovery Using Wireless Inertial Measurement Units. Physiol. Meas. 2012, 33, 2099. [Google Scholar] [CrossRef]
- Peppoloni, L.; Filippeschi, A.; Ruffaldi, E.; Avizzano, C.A. A Novel 7 Degrees of Freedom Model for Upper Limb Kinematic Reconstruction Based on Wearable Sensors. In Proceedings of the 2013 IEEE 11th International Symposium on Intelligent Systems and Informatics (SISY), Subotica, Serbia, 26–28 September 2013; pp. 105–110. [Google Scholar]
- Bleser, G.; Hendeby, G.; Miezal, M. Using Egocentric Vision to Achieve Robust Inertial Body Tracking under Magnetic Disturbances. In Proceedings of the 2011 10th IEEE International Symposium on Mixed and Augmented Reality, Basel, Switzerland, 26–29 October 2011; pp. 103–109. [Google Scholar]
- Zhang, Z.Q.; Wong, W.C.; Wu, J.K. Ubiquitous Human Upper-Limb Motion Estimation Using Wearable Sensors. IEEE Trans. Inf. Technol. Biomed. 2011, 15, 513–521. [Google Scholar] [CrossRef]
- Zhang, Z.; Wong, W.C.; Wu, J. Wearable Sensors for 3D Upper Limb Motion Modeling and Ubiquitous Estimation. J. Control Theory Appl. 2011, 9, 10–17. [Google Scholar] [CrossRef]
- Ruffaldi, E.; Peppoloni, L.; Filippeschi, A. Sensor Fusion for Complex Articulated Body Tracking Applied in Rowing. Proc. IMechE 2015, 229, 92–102. [Google Scholar] [CrossRef]
- Kok, M.; Schön, T.B. A Fast and Robust Algorithm for Orientation Estimation Using Inertial Sensors. IEEE Signal Process. Lett. 2019, 26, 1673–1677. [Google Scholar] [CrossRef]
- Seel, T.; Ruppin, S. Eliminating the Effect of Magnetic Disturbances on the Inclination Estimates of Inertial Sensors. IFAC-PapersOnLine 2017, 50, 8798–8803. [Google Scholar] [CrossRef]
- Madgwick, S.O.H.; Harrison, A.J.L.; Vaidyanathan, R. Estimation of IMU and MARG Orientation Using a Gradient Descent Algorithm. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011; pp. 1–7. [Google Scholar]
- Remmerswaal, E.; Weygers, I.; Smit, G.; Kok, M. Fast Relative Sensor Orientation Estimation in the Presence of Real-World Disturbances. In Proceedings of the 2021 European Control Conference (ECC), Delft, The Netherlands, 29 June 29–2 July 2021; pp. 411–416. [Google Scholar]
- Ligorio, G.; Sabatini, A.M. A Linear Kalman Filtering-Based Approach for 3D Orientation Estimation from Magnetic/Inertial Sensors. In Proceedings of the 2015 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), San Diego, CA, USA, 14–16 September 2015; pp. 77–82. [Google Scholar]
- Nazarahari, M.; Rouhani, H. 40 Years of Sensor Fusion for Orientation Tracking via Magnetic and Inertial Measurement Units: Methods, Lessons Learned, and Future Challenges. Inf. Fusion 2021, 68, 67–84. [Google Scholar] [CrossRef]
- Särkkä, S. Bayesian Filtering and Smoothing; Cambridge University Press: Cambridge, UK, 2013; ISBN 978-1-107-03065-7. [Google Scholar]
- Yang, Z.; Yan, S.; van Beijnum, B.-J.F.; Li, B.; Veltink, P.H. Improvement of Optical Tracking-Based Orientation Estimation by Fusing Gyroscope Information. IEEE Trans. Instrum. Meas. 2021, 70, 9508913. [Google Scholar] [CrossRef]
- McGrath, T.; Stirling, L. Body-Worn IMU Human Skeletal Pose Estimation Using a Factor Graph-Based Optimization Framework. Sensors 2020, 20, 6887. [Google Scholar] [CrossRef] [PubMed]
- McGrath, T.; Stirling, L. Body-Worn IMU-Based Human Hip and Knee Kinematics Estimation during Treadmill Walking. Sensors 2022, 22, 2544. [Google Scholar] [CrossRef] [PubMed]
- Taetz, B.; Bleser, G.; Miezal, M. Towards Self-Calibrating Inertial Body Motion Capture. In Proceedings of the 2016 19th International Conference on Information Fusion (FUSION), Heidelberg, Germany, 5–8 July 2016; pp. 1751–1759. [Google Scholar]
- Kok, M.; Hol, J.D.; Schon, T.B. Using Inertial Sensors for Position and Orientation Estimation; Foundations and Trends® in Signal Processing: Norwell, MA, USA, 2017; Volume 11, pp. 1–153. [Google Scholar]
- Razavi, H.; Salarieh, H.; Alasty, A. Inertial Motion Capture Accuracy Improvement by Kalman Smoothing and Dynamic Networks. IEEE Sens. J. 2021, 21, 3722–3729. [Google Scholar] [CrossRef]
- Seel, T.; Raisch, J.; Schauer, T. IMU-Based Joint Angle Measurement for Gait Analysis. Sensors 2014, 14, 6891–6909. [Google Scholar] [CrossRef]
- Chen, H.; Schall, M.C.; Fethke, N.B. Gyroscope Vector Magnitude: A Proposed Method for Measuring Angular Velocities. Appl. Ergon. 2023, 109, 103981. [Google Scholar] [CrossRef]
- Dornaika, F.; Horaud, R. Simultaneous Robot-World and Hand-Eye Calibration. IEEE Trans. Robot. Autom. 1998, 14, 617–622. [Google Scholar] [CrossRef]
- Faber, G.S.; Chang, C.-C.; Rizun, P.; Dennerlein, J.T. A Novel Method for Assessing the 3-D Orientation Accuracy of Inertial/Magnetic Sensors. J. Biomech. 2013, 46, 2745–2751. [Google Scholar] [CrossRef]


| mekf-acc | rts-acc | map-acc | mekf-dof | rts-dof | map-dof | |
|---|---|---|---|---|---|---|
| P0 | diag([1, 1, 1]) | diag([1, 1, 1]) | ||||
| (rad/s) | 0.005 | 0.005 | 0.005 | 0.005 | 0.005 | 0.005 |
| 0.01 | 0.02 | 0.04 | 0.05 | 0.05 | 0.05 | |
| - | - | - | 0.01 | 0.02 | 0.04 |
| mekf-acc | rts-acc | map-acc | mekf-dof | rts-dof | map-dof | |
|---|---|---|---|---|---|---|
| P0 | diag([1, 1, 1]) | diag([1, 1, 1]) | ||||
| (rad/s) | 0.005 | 0.005 | 0.005 | 0.005 | 0.005 | 0.005 |
| 0.01 | 0.02 | 0.04 | 0.05 | 0.05 | 0.05 | |
| - | - | - | 0.04 | 0.08 | 0.08 |
| mekf-acc | rts-acc | map-acc | mekf-dof | rts-dof | map-dof | |
|---|---|---|---|---|---|---|
| Slow | ||||||
| Flexion | 7.3(4.4) | 7.0(7.4) | 5.2(3.2) | 6.5(4.4) | 5.2(3.2) | 4.7(2.7) |
| Adduction | 4.5(3.2) | 3.3(2.5) | 3.0(1.8) | 3.8(2.1) | 3.0(2.0) | 2.8(2.0) |
| Rotation | 5.2(3.3) | 4.6(4.1) | 3.8(2.2) | 4.2(2.4) | 3.4(1.8) | 3.2(1.5) |
| Total | 10.2(6.1) | 9.2(8.3) | 7.3(3.9) | 8.8(5.0) | 7.1(3.7) | 6.6(3.4) |
| Medium | ||||||
| Flexion | 3.4(1.6) | 2.3(1.1) | 2.4(1.2) | 3.2(1.5) | 2.4(1.1) | 2.4(1.1) |
| Adduction | 2.5(1.4) | 1.6(0.8) | 1.5(0.7) | 2.0(1.0) | 1.6(0.7) | 1.5(0.6) |
| Rotation | 2.9(1.3) | 1.9(0.7) | 2.0(0.9) | 2.7(1.6) | 2.0(1.0) | 2.0(0.8) |
| Total | 5.3(2.2) | 3.5(1.4) | 3.5(1.4) | 4.8(2.1) | 3.6(1.4) | 3.6(1.3) |
| Fast | ||||||
| Flexion | 2.3(0.5) | 1.2(0.3) | 1.2(0.4) | 1.9(0.6) | 1.2(0.4) | 1.2(0.4) |
| Adduction | 1.9(0.7) | 0.9(0.3) | 1.0(0.3) | 1.4(0.4) | 0.9(0.3) | 1.0(0.3) |
| Rotation | 2.0(0.7) | 1.1(0.3) | 1.2(0.4) | 1.7(0.7) | 1.1(0.3) | 1.2(0.4) |
| Total | 3.7(1.0) | 1.9(0.4) | 2.0(0.5) | 3.0(0.8) | 1.9(0.5) | 2.0(0.5) |
| mekf-acc | rts-acc | map-acc | mekf-dof | rts-dof | map-dof | |
|---|---|---|---|---|---|---|
| Slow | ||||||
| Rotation | 1.8(0.6) | 1.5(0.5) | 1.6(0.5) | 2.5(0.9) | 1.7(0.5) | 1.6(0.5) |
| Flexion | 0.8(0.3) | 0.6(0.2) | 1.0(0.4) | 1.3(0.9) | 0.7(0.3) | 1.0(0.4) |
| Deviation | 2.0(1.3) | 1.4(0.9) | 1.5(0.6) | 3.4(1.6) | 1.7(0.7) | 1.5(0.6) |
| Total | 2.9(1.3) | 2.2(0.9) | 2.4(0.6) | 4.4(1.9) | 2.6(0.8) | 2.5(0.7) |
| Medium | ||||||
| Rotation | 1.5(0.6) | 1.2(0.5) | 1.2(0.5) | 1.5(0.5) | 1.2(0.5) | 1.2(0.5) |
| Flexion | 0.8(0.3) | 0.6(0.2) | 0.8(0.2) | 0.8(0.4) | 0.6(0.2) | 0.8(0.2) |
| Deviation | 1.5(1.0) | 0.8(0.6) | 1.1(0.5) | 1.4(0.7) | 0.8(0.5) | 1.0(0.5) |
| Total | 2.3(1.1) | 1.7(0.7) | 1.8(0.6) | 2.3(0.8) | 1.6(0.5) | 1.8(0.6) |
| Fast | ||||||
| Rotation | 1.4(0.5) | 1.1(0.3) | 1.1(0.4) | 1.2(0.3) | 1.0(0.3) | 1.0(0.4) |
| Flexion | 1.0(0.5) | 0.8(0.2) | 0.8(0.3) | 0.8(0.2) | 0.7(0.2) | 0.8(0.3) |
| Deviation | 1.3(0.6) | 0.7(0.3) | 0.9(0.3) | 1.0(0.4) | 0.6(0.2) | 0.8(0.2) |
| Total | 2.2(0.9) | 1.5(0.4) | 1.6(0.4) | 1.8(0.4) | 1.4(0.3) | 1.6(0.4) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Schall, M.C., Jr.; Martin, S.M.; Fethke, N.B. Drift-Free Joint Angle Calculation Using Inertial Measurement Units without Magnetometers: An Exploration of Sensor Fusion Methods for the Elbow and Wrist. Sensors 2023, 23, 7053. https://doi.org/10.3390/s23167053
Chen H, Schall MC Jr., Martin SM, Fethke NB. Drift-Free Joint Angle Calculation Using Inertial Measurement Units without Magnetometers: An Exploration of Sensor Fusion Methods for the Elbow and Wrist. Sensors. 2023; 23(16):7053. https://doi.org/10.3390/s23167053
Chicago/Turabian StyleChen, Howard, Mark C. Schall, Jr., Scott M. Martin, and Nathan B. Fethke. 2023. "Drift-Free Joint Angle Calculation Using Inertial Measurement Units without Magnetometers: An Exploration of Sensor Fusion Methods for the Elbow and Wrist" Sensors 23, no. 16: 7053. https://doi.org/10.3390/s23167053
APA StyleChen, H., Schall, M. C., Jr., Martin, S. M., & Fethke, N. B. (2023). Drift-Free Joint Angle Calculation Using Inertial Measurement Units without Magnetometers: An Exploration of Sensor Fusion Methods for the Elbow and Wrist. Sensors, 23(16), 7053. https://doi.org/10.3390/s23167053







