Optimization of Magnetoimpedance Effect and Magnetic Properties of Fe-Rich Glass-Coated Microwires by Annealing
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
- A substantial GMI ratio improvement by annealing;
- A remarkable effect of annealing on domain wall dynamics.
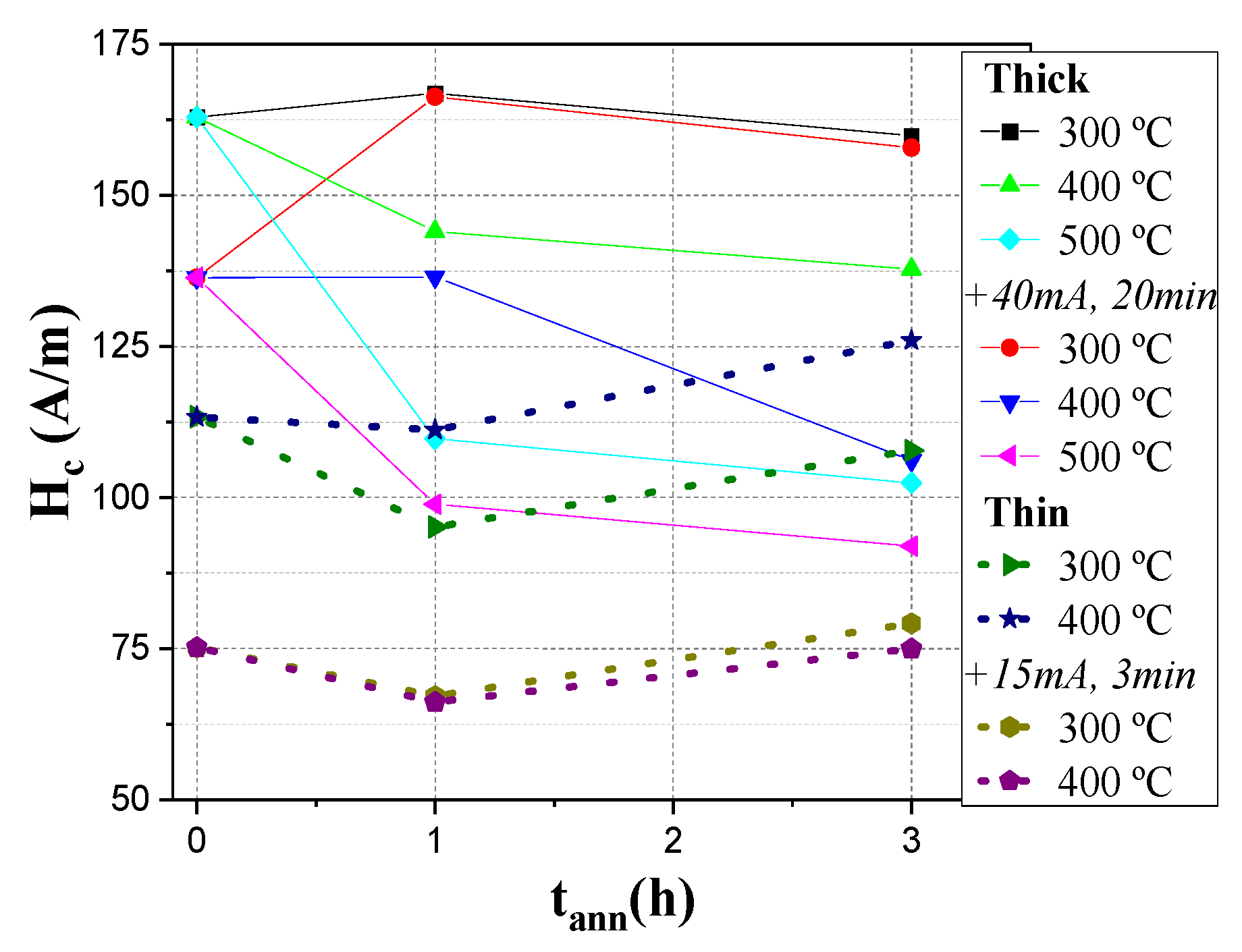
3.1. Hysteresis Loops
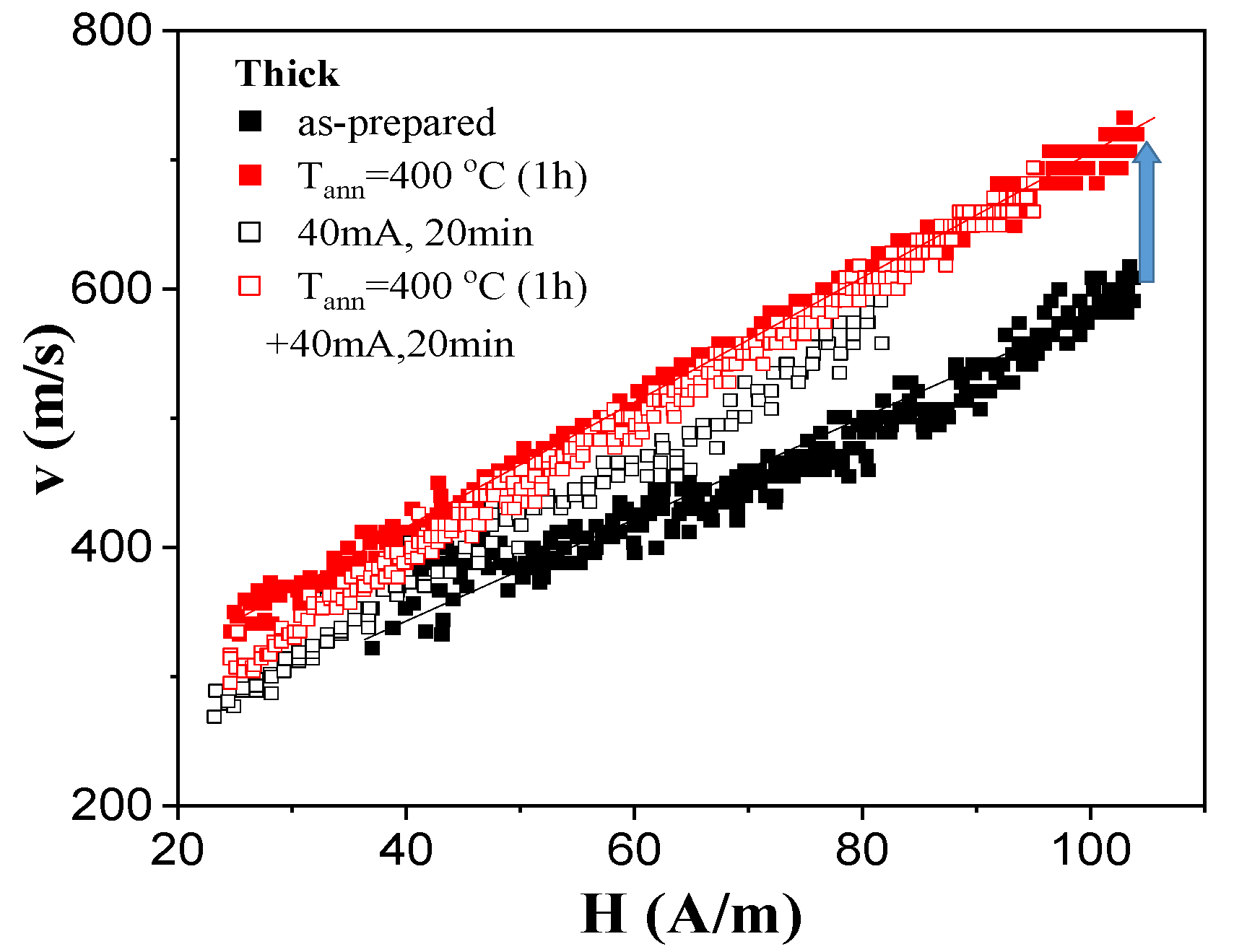
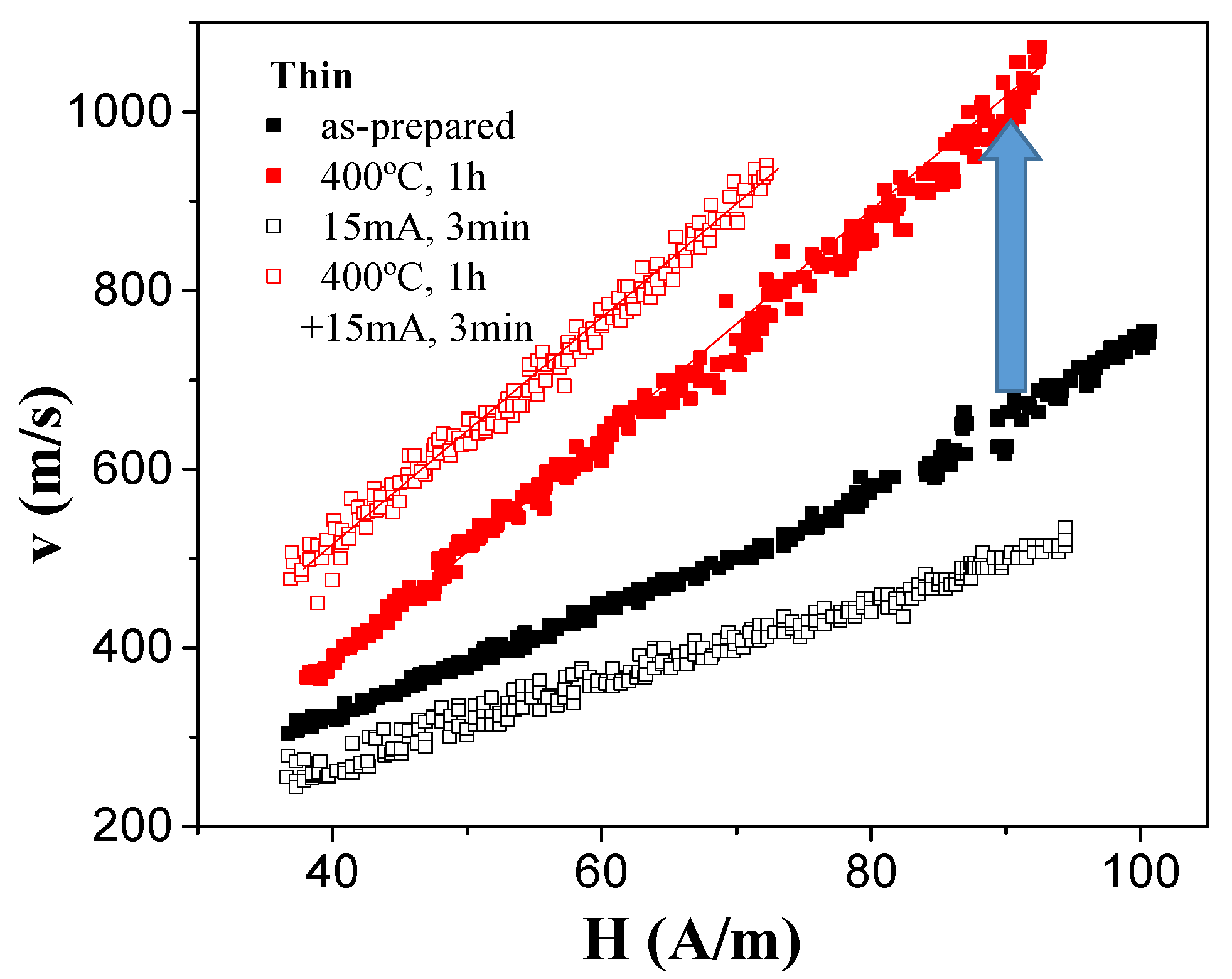
3.2. Domain Wall Dynamics
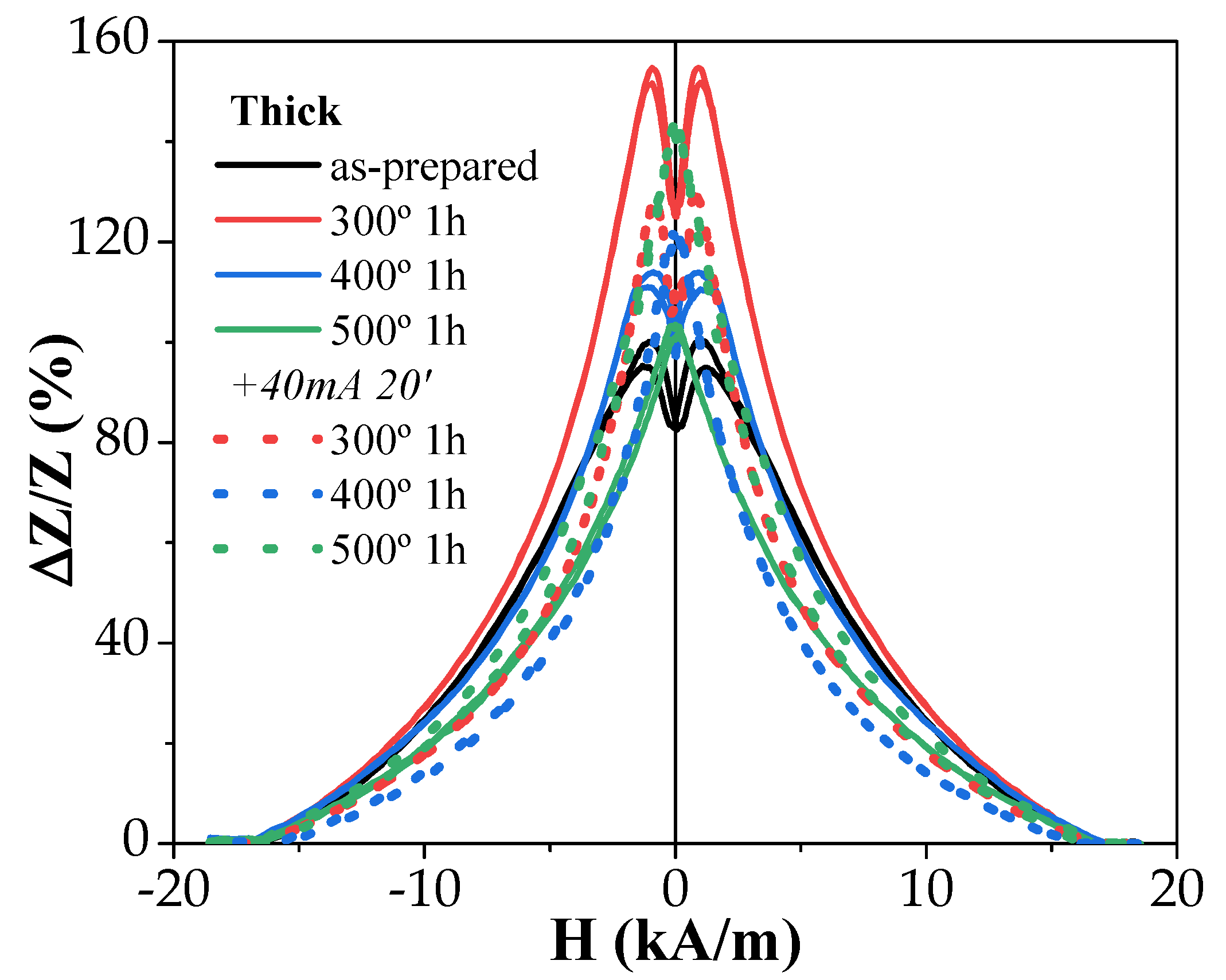
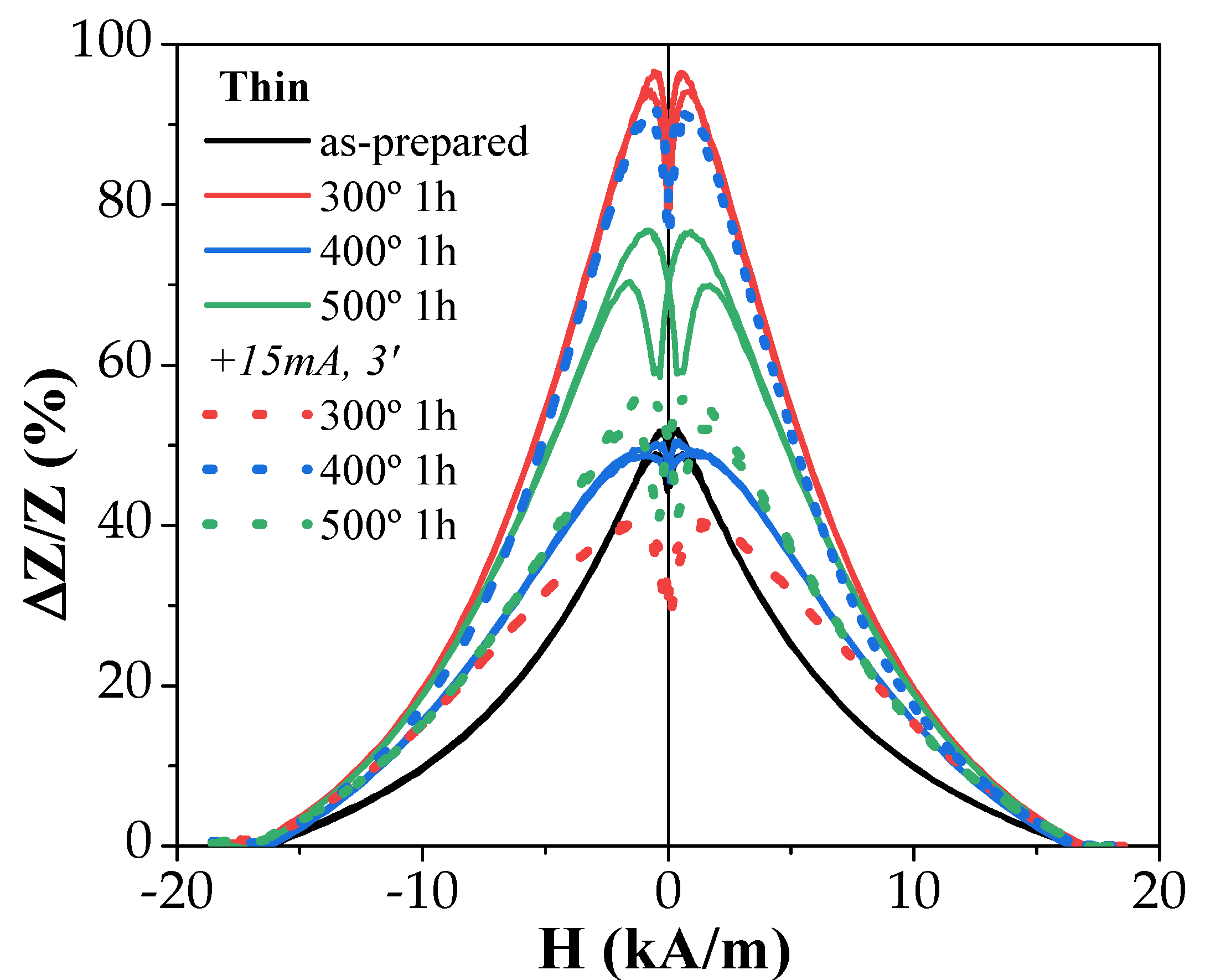
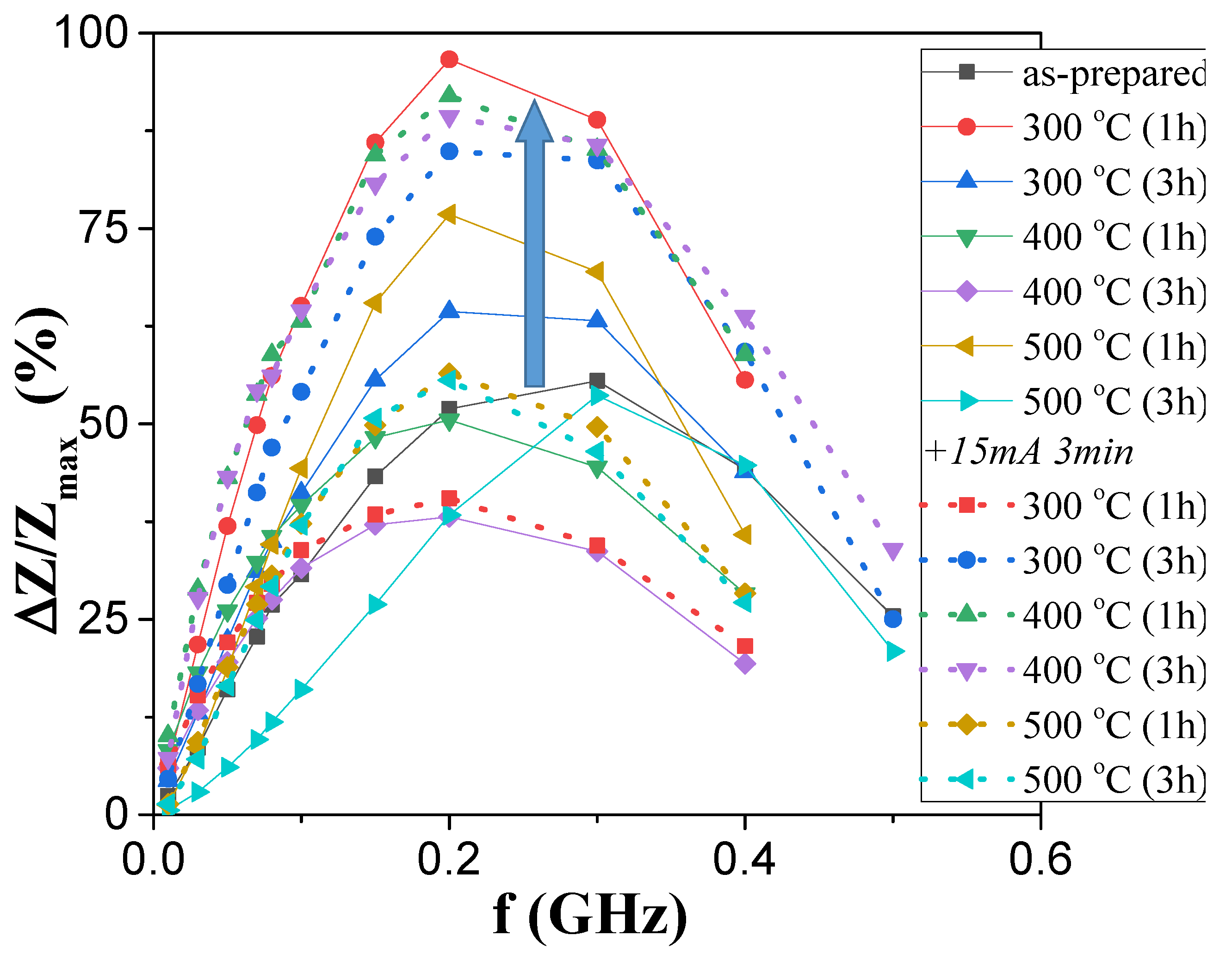
3.3. Giant Magnetoimpedance (GMI) Effect
- (i)
- The GMI ratio of “thick” samples was rather large even in as-prepared samples;
- (ii)
- In both studied samples, for almost all annealing conditions, an increase in ∆Z/Z values was observed after the process;
- (iii)
- Both microwires exhibited a double-peak ∆Z/Z(H) dependence at high enough frequencies. Usually, these double-peak ∆Z/Z(H) dependencies are reported for Co-rich microwires [43,45], while single-peak ∆Z/Z(H) dependencies with ∆Z/Z maximum at H = 0 are predicted for microwires with axial magnetic anisotropy, such as ours (which is confirmed by the hysteresis loops’ character) [50]. Such single-peak ∆Z/Z(H) dependence was observed in “thick” samples annealed at high enough temperatures (see Figure 7).
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ripka, P.; Vertesy, G. Sensors based on soft magnetic materials Panel discussion. J. Magn. Magn. Mater. 2000, 215, 795–799. [Google Scholar] [CrossRef]
- Mohri, K.; Uchiyama, T.; Panina, L.V.; Yamamoto, M.; Bushida, K. Recent Advances of Amorphous Wire CMOS IC Magneto-Impedance Sensors: Innovative High-Performance Micromagnetic Sensor Chip. J. Sens. 2015, 2015, 718069. [Google Scholar] [CrossRef]
- Honkura, Y.; Honkura, S. The Development of ASIC Type GSR Sensor Driven by GHz Pulse Current. Sensors 2020, 20, 1023. [Google Scholar] [CrossRef] [PubMed]
- Uchiyama, T.; Mohri, K.; Nakayama, S. Measurement of Spontaneous Oscillatory Magnetic Field of Guinea-Pig Smooth Muscle Preparation Using Pico-Tesla Resolution Amorphous Wire Magneto-Impedance Sensor. IEEE Trans. Magn. 2011, 47, 3070–3073. [Google Scholar] [CrossRef]
- Zhukov, A.; Cobeño, A.F.; Gonzalez, J.; Blanco, J.M.; Aragoneses, P.; Dominguez, L. Magnetoelastic sensor of level of the liquid based on magnetoelastic properties of Co-rich microwires. Sens. Actuators A Phys. 2000, 81, 129–133. [Google Scholar] [CrossRef]
- Makhnovskiy, D.; Fry, N.; Zhukov, A. On different tag reader architectures for bistable microwires. Sens. Actuators A Phys. 2011, 166, 133–140. [Google Scholar] [CrossRef]
- Zhukova, V.; Corte-Leon, P.; Blanco, J.M.; Ipatov, M.; Gonzalez, J.; Zhukov, A. Electronic Surveillance and Security Applications of Magnetic Microwires. Chemosensors 2021, 9, 100. [Google Scholar] [CrossRef]
- Morón, C.; Cabrera, C.; Morón, A.; García, A.; González, M. Magnetic Sensors Based on Amorphous Ferromagnetic Materials: A Review. Sensors 2015, 15, 28340–28366. [Google Scholar] [CrossRef]
- Hagiwara, M.; Inoue, A.; Masumoto, T. Mechanical properties of Fe–Si–B amorphous wires produced by in-rotating-water spinning method. Metall. Trans. A 1982, 13, 373–382. [Google Scholar] [CrossRef]
- Goto, T.; Nagano, M.; Wehara, N. Mechanical properties of amorphous Fe80P16C3B1 filament produced by glass-coated melt spinning. Trans. JIM 1977, 18, 759–764. [Google Scholar] [CrossRef]
- Zhukova, V.; Cobeño, A.F.; Zhukov, A.; de Arellano Lopez, A.R.; López-Pombero, S.; Blanco, J.M.; Larin, V.; Gonzalez, J. Correlation between magnetic and mechanical properties of devitrified glass-coated Fe71.8Cu1Nb3.1Si15B9.1 microwires. J. Magn. Magn. Mater. 2002, 249, 79–84. [Google Scholar] [CrossRef]
- Masumoto, T.; Hashimoto, K. Corrosion properties of amorphous metals. J. Phys. Colloq. 1980, 41, C8-894–C8-900. [Google Scholar] [CrossRef]
- Chiriac, H.; Ovari, T.-A. Amorphous glass-covered magnetic wires: Preparation, properties, applications. Prog. Mater. Sci. 1996, 40, 333–407. [Google Scholar] [CrossRef]
- Zhukov, A.; Corte-Leon, P.; Gonzalez-Legarreta, L.; Ipatov, M.; Blanco, J.M.; Gonzalez, A.; Zhukova, V. Advanced Functional Magnetic Microwires for Technological Applications. J. Phys. D Appl. Phys. 2022, 55, 253003. [Google Scholar] [CrossRef]
- Baranov, S.A.; Larin, V.S.; Torcunov, A.V. Technology, Preparation and Properties of the Cast Glass-Coated Magnetic Microwires. Crystals 2017, 7, 136. [Google Scholar] [CrossRef]
- Kozejova, D.; Fecova, L.; Klein, P.; Sabol, R.; Hudak, R.; Sulla, I.; Mudronova, D.; Galik, J.; Varga, R. Biomedical Applications of Glass-Coated Microwires. J. Magn. Magn. Mater. 2019, 470, 2–5. [Google Scholar] [CrossRef]
- Mitxelena-Iribarren, O.; Campisi, J.; Martínez de Apellániz, I.; Lizarbe-Sancha, S.; Arana, S.; Zhukova, V.; Mujika, M.; Zhukov, A. Glass-Coated Ferromagnetic Microwire-Induced Magnetic Hyperthermia for in Vitro Cancer Cell Treatment. Mater. Sci. Eng. C 2020, 106, 110261. [Google Scholar] [CrossRef]
- Sabol, R.; Klein, P.; Ryba, T.; Hvizdos, L.; Varga, R.; Rovnak, M.; Sulla, I.; Mudronova, D.; Galik, J.; Polacek, I.; et al. Novel Applications of Bistable Magnetic Microwires. Acta Phys. Pol. A 2017, 131, 1150–1152. [Google Scholar] [CrossRef]
- Allue, A.; Corte-León, P.; Gondra, K.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; Gonzalez, J.; Churyukanova, M.; Taskaev, S.; Zhukov, A. Smart composites with embedded magnetic microwire inclusions allowing non-contact stresses and temperature monitoring. Compos. Part A Appl. Sci. Manuf. 2019, 120, 12–20. [Google Scholar] [CrossRef]
- Ipatov, M.; Aranda, G.R.; Zhukova, V.; Panina, L.V.; González, J.; Zhukov, A. Tunable effective permittivity of composites based on ferromagnetic microwires with high magneto-impedance effect. Appl. Phys. A Mater. Sci. Process. 2011, 103, 693–697. [Google Scholar] [CrossRef]
- Uddin, A.; Estevez, D.; Qin, F.X. From functional units to material design: A review on recent advancement of programmable microwire metacomposites. Compos. Part A Appl. Sci. Manuf. 2022, 153, 106734. [Google Scholar] [CrossRef]
- Corodeanu, S.; Chiriac, H.; Óvári, T.-A. Accurate measurement of domain wall velocity in amorphous microwires, submicron wires, and nanowires. Rev. Sci. Instr. 2011, 82, 094701. [Google Scholar] [CrossRef]
- Corte-Leon, P.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; González, J.; Churyukanova, M.; Taskaev, S.; Zhukov, A. The effect of annealing on magnetic properties of “Thick” microwires. J. Alloys Compd. 2020, 831, 150992. [Google Scholar] [CrossRef]
- Panina, L.V.; Mohri, K. Magneto-impedance effect in amorphous wires. Appl. Phys. Lett. 1994, 65, 1189–1191. [Google Scholar] [CrossRef]
- Beach, R.; Berkowitz, A. Giant magnetic field dependent impedance of amorphous FeCoSiB wire. Appl. Phys. Lett. 1994, 64, 3652–3654. [Google Scholar] [CrossRef]
- Makhotkin, V.E.; Shurukhin, B.P.; Lopatin, V.A.; Marchukov, P.; Levin, Y.K. Magnetic field sensors based on amorphous ribbons. Sens. Actuators A Phys. 1991, 27, 759–762. [Google Scholar] [CrossRef]
- Kronmüller, H. Theory of the coercive field in amorphous ferromagnetic alloys. J. Magn. Magn. Mater. 1981, 24, 159–167. [Google Scholar] [CrossRef]
- Herzer, G. Amorphous and nanocrystalline soft magnets. In Proceedings of the NATO Advanced Study Institute on Magnetic Hysteresis in Novel Materials, Mykonos, Greece, 1–12 July 1996; Hadjipanayis, G.C., Ed.; NATO ASI Series (Series E: Applied Sciences). Kluwer Academic Publishers: Dordrecht, The Netherlands, 1997; Volume 338, pp. 711–730. [Google Scholar]
- Konno, Y.; Mohri, K. Magnetostriction measurements for amorphous wires. IEEE Trans. Magn. 1989, 25, 3623–3625. [Google Scholar] [CrossRef]
- Churyukanova, M.; Semenkova, V.; Kaloshkin, S.; Shuvaeva, E.; Gudoshnikov, S.; Zhukova, V.; Shchetinin, I.; Zhukov, A. Magnetostriction investigation of soft magnetic microwires. Phys. Status Solidi A 2016, 213, 363–367. [Google Scholar] [CrossRef]
- Eggert, R.G. Minerals go critical. Nat. Chem. 2011, 3, 688–691. [Google Scholar] [CrossRef]
- Zhukova, V.; Blanco, J.M.; Ipatov, M.; Gonzalez, J.; Churyukanova, M.; Zhukov, A. Engineering of magnetic softness and giant magnetoimpedance effect in Fe-rich microwires by stress-annealing. Scr. Mater. 2018, 142, 10–14. [Google Scholar] [CrossRef]
- Zhukova, V.; Blanco, J.M.; Ipatov, M.; Churyukanova, M.; Taskaev, S.; Zhukov, A. Tailoring of magnetoimpedance effect and magnetic softness of Fe-rich glass-coated microwires by stress-annealing. Sci. Rep. 2018, 8, 3202. [Google Scholar] [CrossRef]
- Gonzalez, A.; Zhukova, V.; Corte-Leon, P.; Chizhik, A.; Ipatov, M.; Blanco, J.M.; Zhukov, A. Tuning of Magnetoimpedance Effect and Magnetic Properties of Fe-rich Glass-coated Microwires by Joule Heating. Sensors 2022, 22, 1053. [Google Scholar] [CrossRef]
- Corte-Leon, P.; Zhukova, V.; Blanco, J.M.; Ipatov, M.; Taskaev, S.; Churyukanova, M.; Gonzalez, J.; Zhukov, A. Engineering of magnetic properties and magnetoimpedance effect in Fe-rich microwires by reversible and irreversible stress-annealing anisotropy. J. Alloys Compd. 2021, 855, 157460. [Google Scholar] [CrossRef]
- Zhukov, A.; Chichay, K.; Talaat, A.; Rodionova, V.; Blanco, J.M.; Ipatov, M.; Zhukova, V. Manipulation of magnetic properties of glass-coated microwires by annealing. J. Magn. Magn. Mater. 2015, 383, 232–236. [Google Scholar] [CrossRef]
- Vazquez, M.; Chen, D.-X. The magnetization reversal process in amorphous wires. IEEE Trans. Magn. 1995, 31, 1229–1238. [Google Scholar] [CrossRef]
- Mohri, K.; Humphrey, F.B.; Kawashima, K.; Kimura, K.; Muzutani, M. Large Barkhausen and Matteucci Effects in FeCoSiB, FeCrSiB, and FeNiSiB Amorphous Wires. IEEE Trans. Magn. 1990, 26, 1789–1791. [Google Scholar] [CrossRef]
- Zhukova, V.; Zhukov, A.; Blanco, J.M.; Gonzalez, J.; Ponomarev, B.K. Switching field fluctuations in a glass coated Fe-rich amorphous microwire. J. Magn. Magn. Mat. 2002, 249, 131–135. [Google Scholar] [CrossRef]
- Zhukova, V.; Corte-Leon, P.; González-Legarreta, L.; Talaat, A.; Blanco, J.M.; Ipatov, M.; Olivera, J.; Zhukov, A. Review of Domain Wall Dynamics Engineering in Magnetic Microwires. Nanomaterials 2020, 10, 2407. [Google Scholar] [CrossRef]
- Zhang, M.; Qu, G.; Liu, J.; Pang, M.; Wang, X.; Liu, R.; Cao, G.; Ma, G. Enhancement of Magnetic and Tensile Mechanical Performances in Fe-Based Metallic Microwires Induced by Trace Ni-Doping. Materials 2021, 14, 3589. [Google Scholar] [CrossRef]
- Liu, J.; Pang, M.; Cao, G.; Qu, G.; Wang, X.; Zhang, Y.; Liu, R.; Shen, H. Comparative study of tensile properties and magnetic properties for Nb-doped Fe-based wires. J. Mater. Res. Technol. 2020, 9, 12907–12916. [Google Scholar] [CrossRef]
- Gonzalez-Legarreta, L.; Corte-Leon, P.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; Gonzalez, J.; Zhukov, A. Optimization of magnetic properties and GMI effect of Thin Co-rich Microwires for GMI Microsensors. Sensors 2020, 20, 1558. [Google Scholar] [CrossRef]
- Zhukova, V.; Blanco, J.M.; Corte-Leon, P.; Ipatov, M.; Churyukanova, M.; Taskaev, S.; Zhukov, A. Grading the magnetic anisotropy and engineering the domain wall dynamics in Fe-rich microwires by stress-annealing. Acta Mater. 2018, 155, 279–285. [Google Scholar] [CrossRef]
- Zhukov, A.; Ipatov, M.; Talaat, A.; Blanco, J.M.; Churyukanova, M.; Zhukova, V. Studies of High-Frequency Giant Magnetoimpedance Effect in Co-Rich Amorphous Microwires. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Gonzalez, A.; Zhukova, V.; Ipatov, M.; Corte-Leon, P.; Blanco, J.M.; Zhukov, A. Effect of Joule heating on GMI and magnetic properties of Fe-rich glass-coated microwires. AIP Adv. 2022, 12, 035021. [Google Scholar] [CrossRef]
- Zhukov, A.; Rodionova, V.; Ilyn, M.; Aliev, A.M.; Varga, R.; Michalik, S.; Aronin, A.; Abrosimova, G.; Kiselev, A.; Ipatov, M.; et al. Magnetic properties and magnetocaloric effect in Heusler-type glass-coated NiMnGa microwires. J. Alloys Compd. 2013, 575, 73–79. [Google Scholar] [CrossRef]
- Zhukova, V.; Blanco, J.M.; Ipatov, M.; Zhukov, A. Magnetoelastic contribution in domain wall dynamics of amorphous microwires. Phys. B 2012, 407, 1450–1454. [Google Scholar] [CrossRef]
- Varga, R. Magnetization processes in glass-coated microwires with positive magnetostriction. Acta Phys. Slovaca 2012, 62, 411–518. [Google Scholar] [CrossRef]
- Usov, N.A.; Antonov, A.S.; Lagar’kov, A.N. Theory of giant magneto-impedance effect in amorphous wires with different types of magnetic anisotropy. J. Magn. Magn. Mater. 1998, 185, 159–173. [Google Scholar] [CrossRef]
- Zhukova, V.; Blanco, J.M.; Chizhik, A.; Ipatov, M.; Zhukov, A. AC-current-induced magnetization switching in amorphous microwires. Front. Phys. 2018, 13, 137501. [Google Scholar] [CrossRef]
- Corte-León, P.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; Gonzalez, J.; Zhukov, A. Engineering of magnetic properties of Co-rich microwires by joule heating. Intermetallics 2019, 105, 92–98. [Google Scholar] [CrossRef]
- Zhukova, V.; Cobeño, A.F.; Zhukov, A.; Blanco, J.M.; Puerta, S.; Gonzalez, J.; Vázquez, M. Tailoring of magnetic properties of glass coated microwires by current annealing. J. Non-Cryst. Solids. 2001, 287, 31–36. [Google Scholar] [CrossRef]
- Blanco, J.M.; Zhukov, A.; Gonzalez, J. Torsional Stress Impedance and Magneto-impedance in (Co0.95Fe0.05)72.5Si12.5B15 Amorphous Wire with Helical Induced Anisotropy. J. Phys. D Appl. Phys. 1999, 37, 3140–3145. [Google Scholar] [CrossRef]
- Luborsky, F.E.; Walter, J.L. Magnetic Anneal Anisotropy in Amorphous Alloys. IEEE Trans. Magn. 1977, 13, 953–956. [Google Scholar] [CrossRef]
- Becker, J.J. A new mechanism for magnetic annealing in amorphous metals. IEEE Trans. Magn. 1978, 14, 938–940. [Google Scholar] [CrossRef]
- Conca, A.; Papaioannou, E.T.; Klingler, S.; Greser, J.; Sebastian, T.; Leven, B.; Lösch, J.; Hillebrands, B. Annealing influence on the Gilbert damping parameter and the exchange constant of CoFeB thin films. Appl. Phys. Lett. 2014, 104, 182407. [Google Scholar]
- Novak, R.L.; Sinnecker, J.P.; Chiriac, H. Annealing effects on the magnetization reversal and domain wall dynamics in bistable amorphous glass-covered microwires. J. Phys. D Appl. Phys. 2008, 41, 095005. [Google Scholar] [CrossRef]
- Corte-León, P.; Gonzalez-Legarreta, L.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; Churyukanova, M.; Taskaev, S.; Zhukov, A. Controlling the domain wall dynamics in Fe-, Ni- and Co- based magnetic microwires. J. Alloys Compd. 2020, 834, 155170. [Google Scholar] [CrossRef]
- Egami, T. Structural relaxation in amorphous alloys—Compositional short range ordering. Mater. Res. Bull. 1978, 13, 557–562. [Google Scholar] [CrossRef]
- Hernando, A.; Madurga, V.; Núñez de Villavicencio, C.; Vázquez, M. Temperature dependence of the magnetostriction constant of nearly zero magnetostriction amorphous alloys. Appl. Phys. Lett. 1984, 45, 802–804. [Google Scholar] [CrossRef]
- Serebryakov, A.V. Amorphization reactions and glass to crystal transformations in metallic materials. J. Non-Cryst. Solids 1993, 156–158, 594–597. [Google Scholar] [CrossRef]
- Zhukova, V.; Churyukanova, M.; Kaloshkin, S.; Corte-Leon, P.; Ipatov, M.; Zhukov, A. Magnetostriction of amorphous Co-based and Fe-Ni-based magnetic microwires: Effect of stresses and annealing. J. Alloys Compd. 2023, 954, 170122. [Google Scholar] [CrossRef]




| Sample | d (µm) | D (µm) | ρ = d/D | Chemical Composition |
|---|---|---|---|---|
| “Thick” | 47.9 | 53.2 | 0.9 | Fe72B13Si11Nb3Ni1 |
| “Thin” | 15.2 | 17.2 | 0.88 | Fe75B9Si12C4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González, A.; García-Gomez, A.; Zhukova, V.; Corte-Leon, P.; Ipatov, M.; Blanco, J.M.; Gonzalez, J.; Zhukov, A. Optimization of Magnetoimpedance Effect and Magnetic Properties of Fe-Rich Glass-Coated Microwires by Annealing. Sensors 2023, 23, 7481. https://doi.org/10.3390/s23177481
González A, García-Gomez A, Zhukova V, Corte-Leon P, Ipatov M, Blanco JM, Gonzalez J, Zhukov A. Optimization of Magnetoimpedance Effect and Magnetic Properties of Fe-Rich Glass-Coated Microwires by Annealing. Sensors. 2023; 23(17):7481. https://doi.org/10.3390/s23177481
Chicago/Turabian StyleGonzález, Alvaro, Alfonso García-Gomez, Valentina Zhukova, Paula Corte-Leon, Mihail Ipatov, Juan Maria Blanco, Julian Gonzalez, and Arcady Zhukov. 2023. "Optimization of Magnetoimpedance Effect and Magnetic Properties of Fe-Rich Glass-Coated Microwires by Annealing" Sensors 23, no. 17: 7481. https://doi.org/10.3390/s23177481
APA StyleGonzález, A., García-Gomez, A., Zhukova, V., Corte-Leon, P., Ipatov, M., Blanco, J. M., Gonzalez, J., & Zhukov, A. (2023). Optimization of Magnetoimpedance Effect and Magnetic Properties of Fe-Rich Glass-Coated Microwires by Annealing. Sensors, 23(17), 7481. https://doi.org/10.3390/s23177481