Research on an Adaptive Method for the Angle Calibration of Roadside LiDAR Point Clouds
Abstract
:1. Introduction
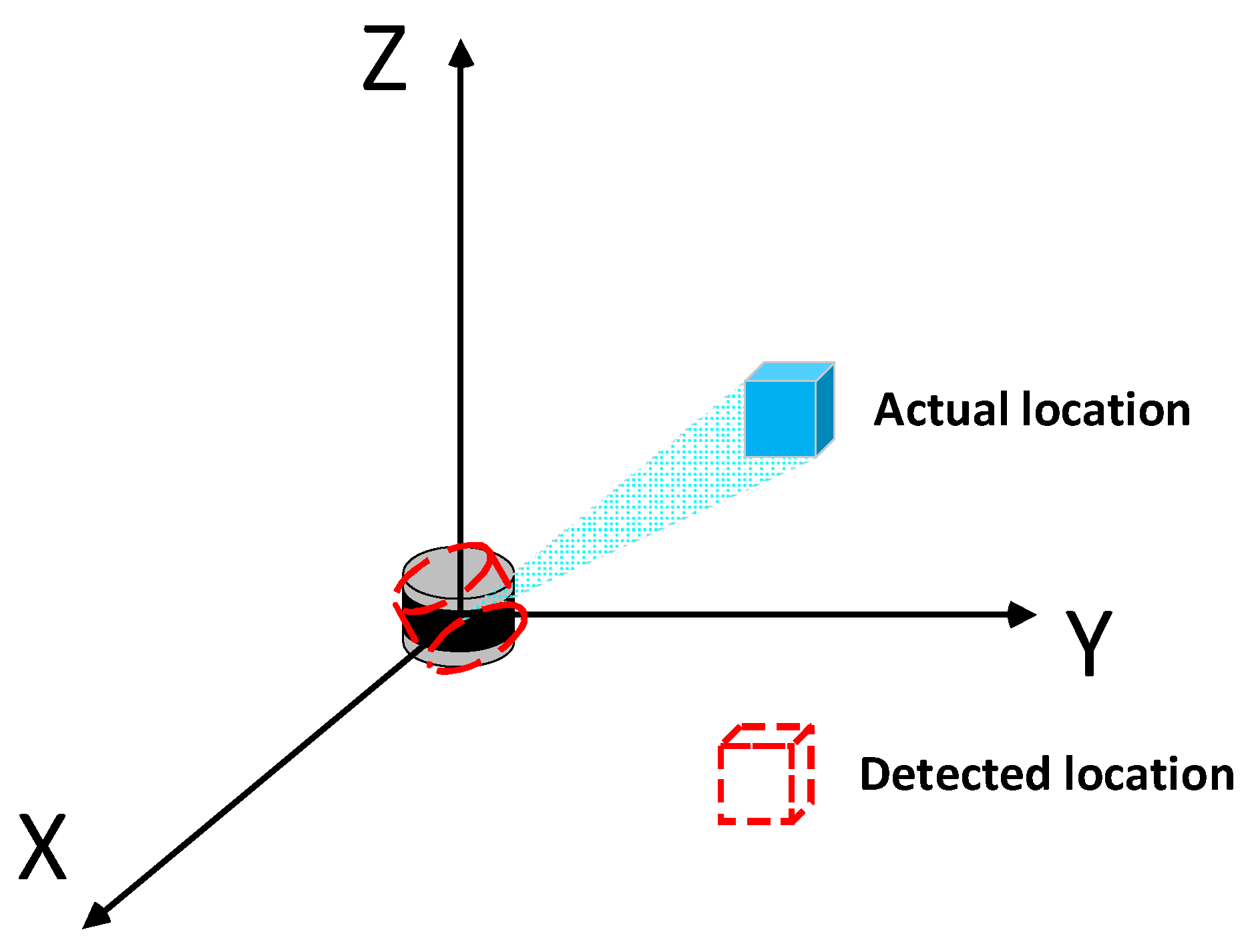
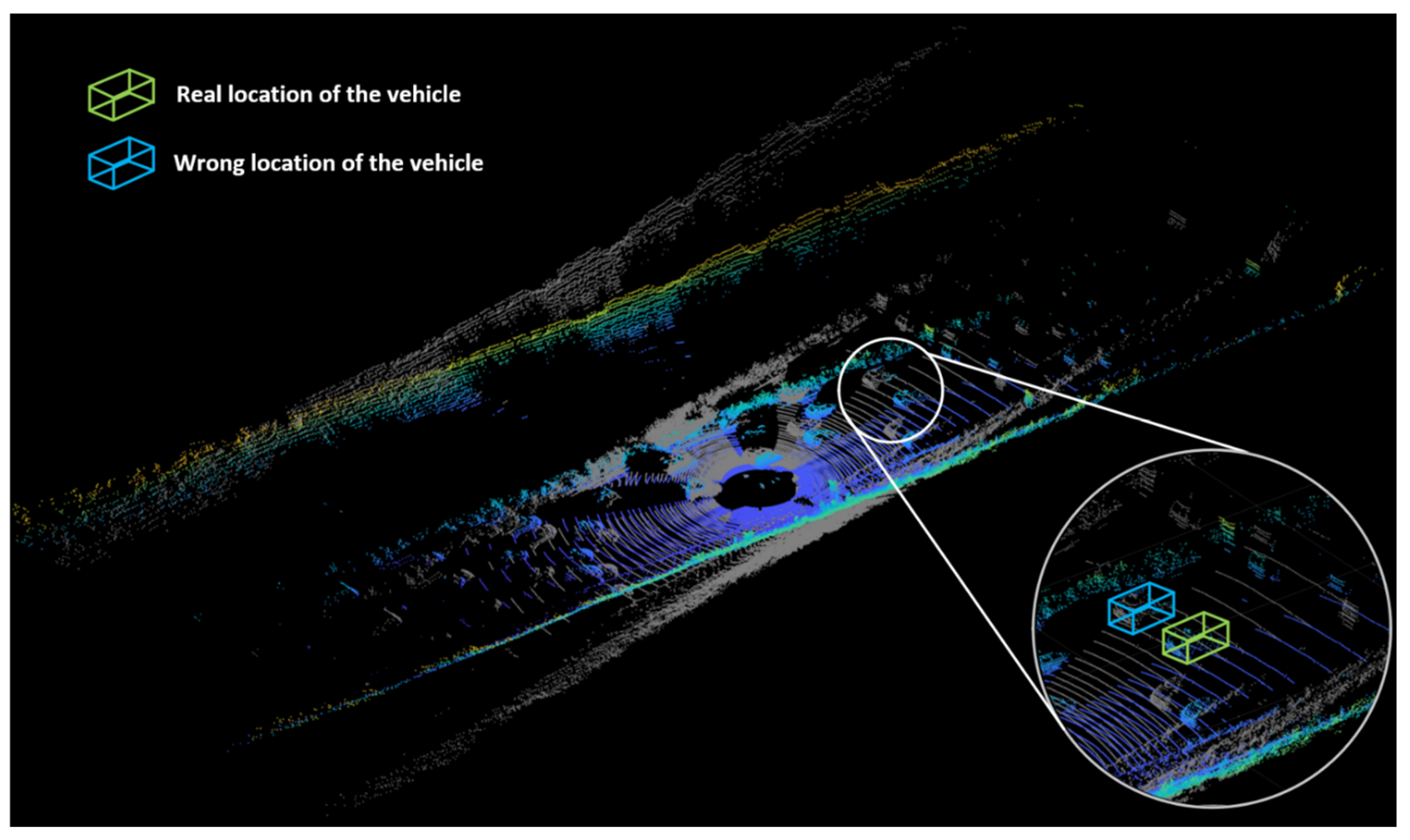
- Positioning deviation: Angle deviations in LiDAR detection can lead to spatial deviations in vehicle positions, resulting in a decrease in the positioning accuracy of vehicle trajectories.
- Trajectory drift: Angle deviations can cause an amplification of the offset error between the LiDAR-perceived vehicle trajectory and the actual trajectory, leading to the presence of trajectory drift.
- Trajectory shape changes: Due to the presence of angle deviations, the perceived shape of the vehicle trajectory may undergo changes, potentially causing errors in determining the vehicle’s driving state and impacting subsequent traffic information processing and analysis.
- Negative impact on multi-sensor fusion perception: Angle deviations in LiDAR can result in inconsistencies between the perceived data and the data obtained from other sensors such as cameras and radars. Such inconsistencies make it challenging to accurately integrate and process data in a multi-sensor fusion perception system, affecting the comprehensive understanding and holistic analysis of traffic situations.
- Adaptive calibration method: This paper proposes a simple and efficient adaptive calibration method to address the accuracy issues of LiDAR sensors in roadside intelligent perception systems. By leveraging the Kalman filter (KF) and the random sample consensus (RANSAC) algorithm, this method ensures real-time calibration without the need for manual intervention.
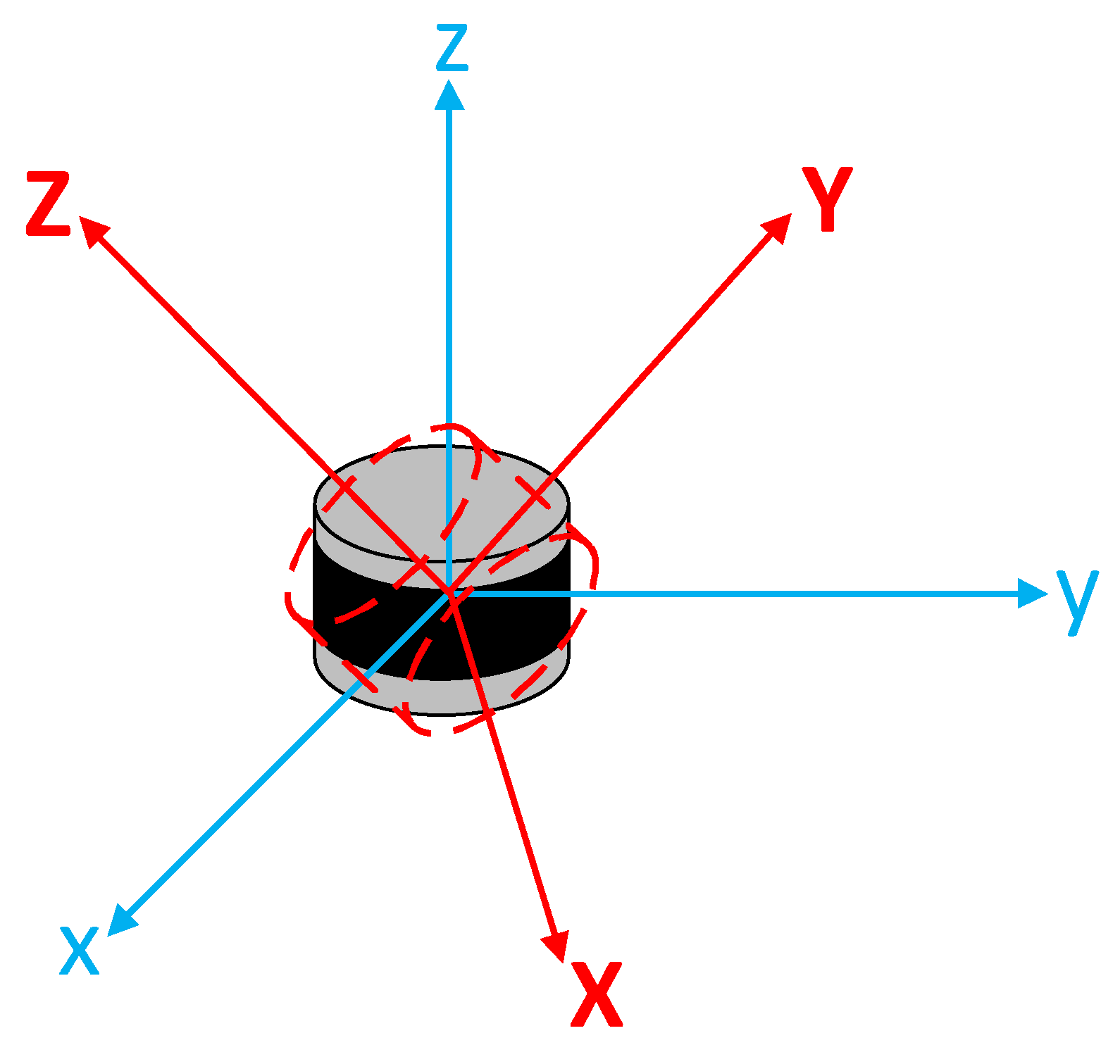
- Ideal coordinate system definition: The method defines an ideal coordinate system based on the road’s forward direction as the X-axis and the intersection line between the vertical plane of the X-axis and the road surface plane as the Y-axis. This ideal coordinate system serves as a reference for calibration, enhancing the precision and stability of the calibration process. Additionally, it provides a universally applicable reference for further multi-sensor fusion perception.
2. The Basic Principles of Point Cloud Calibration Method
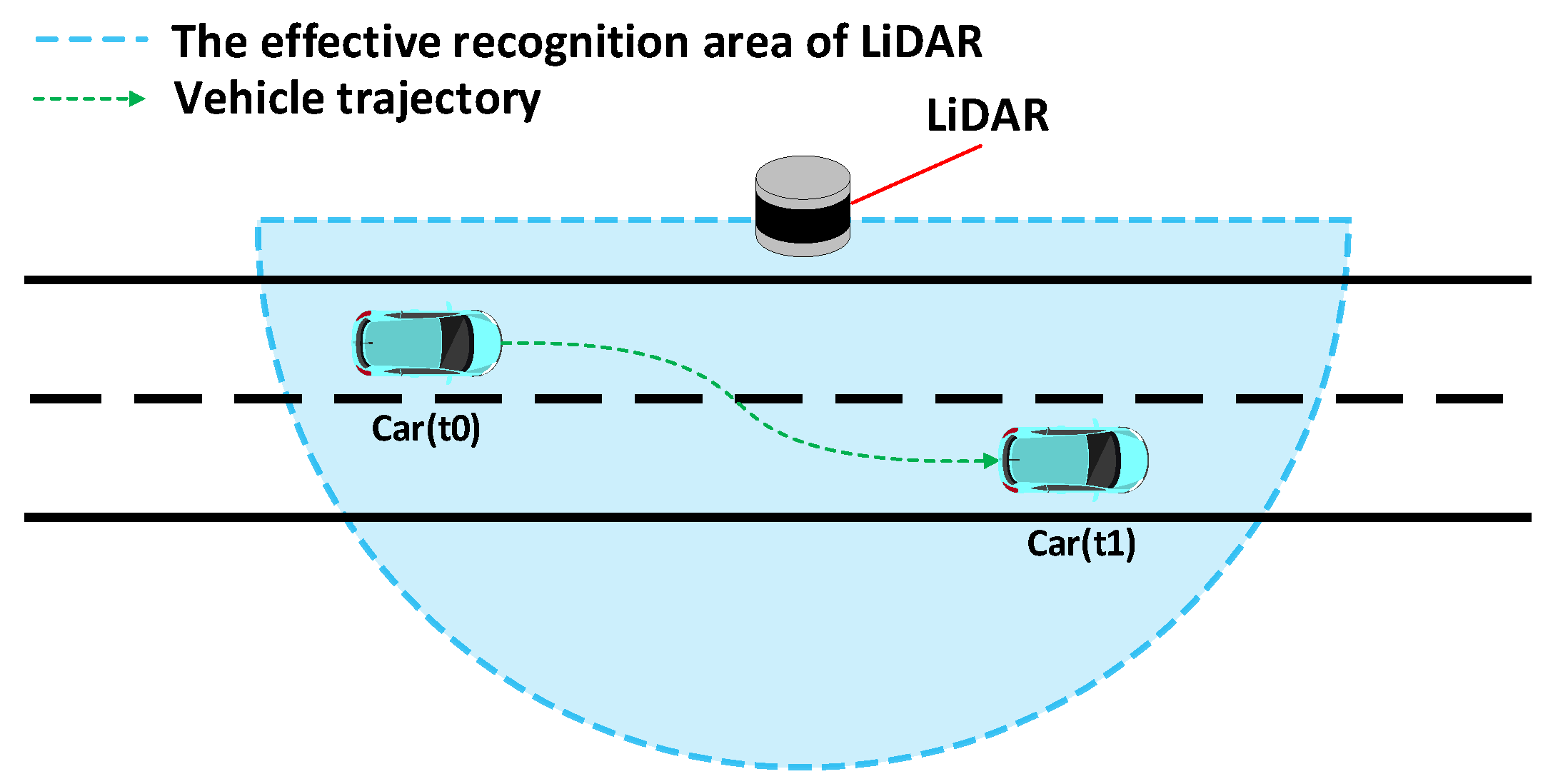
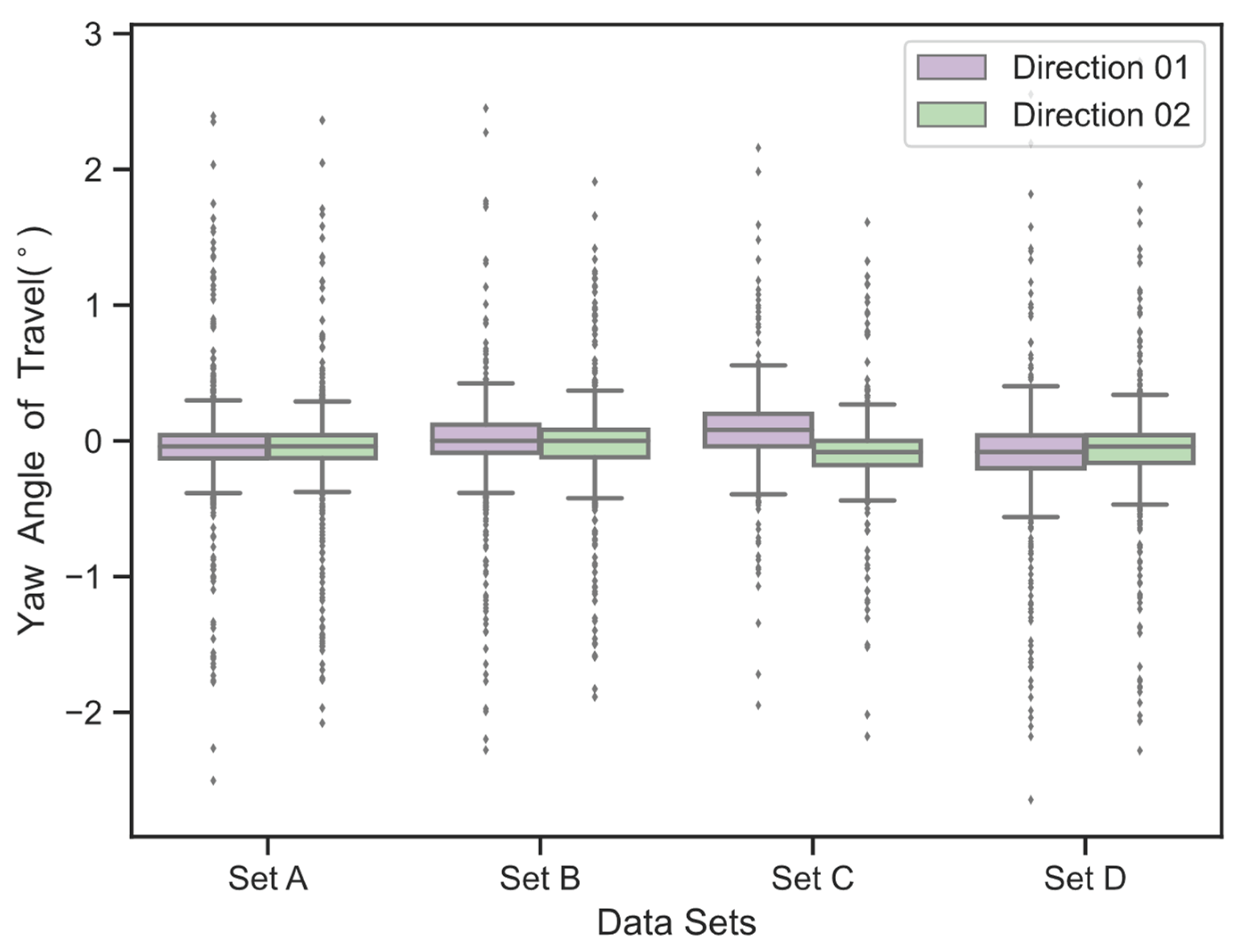
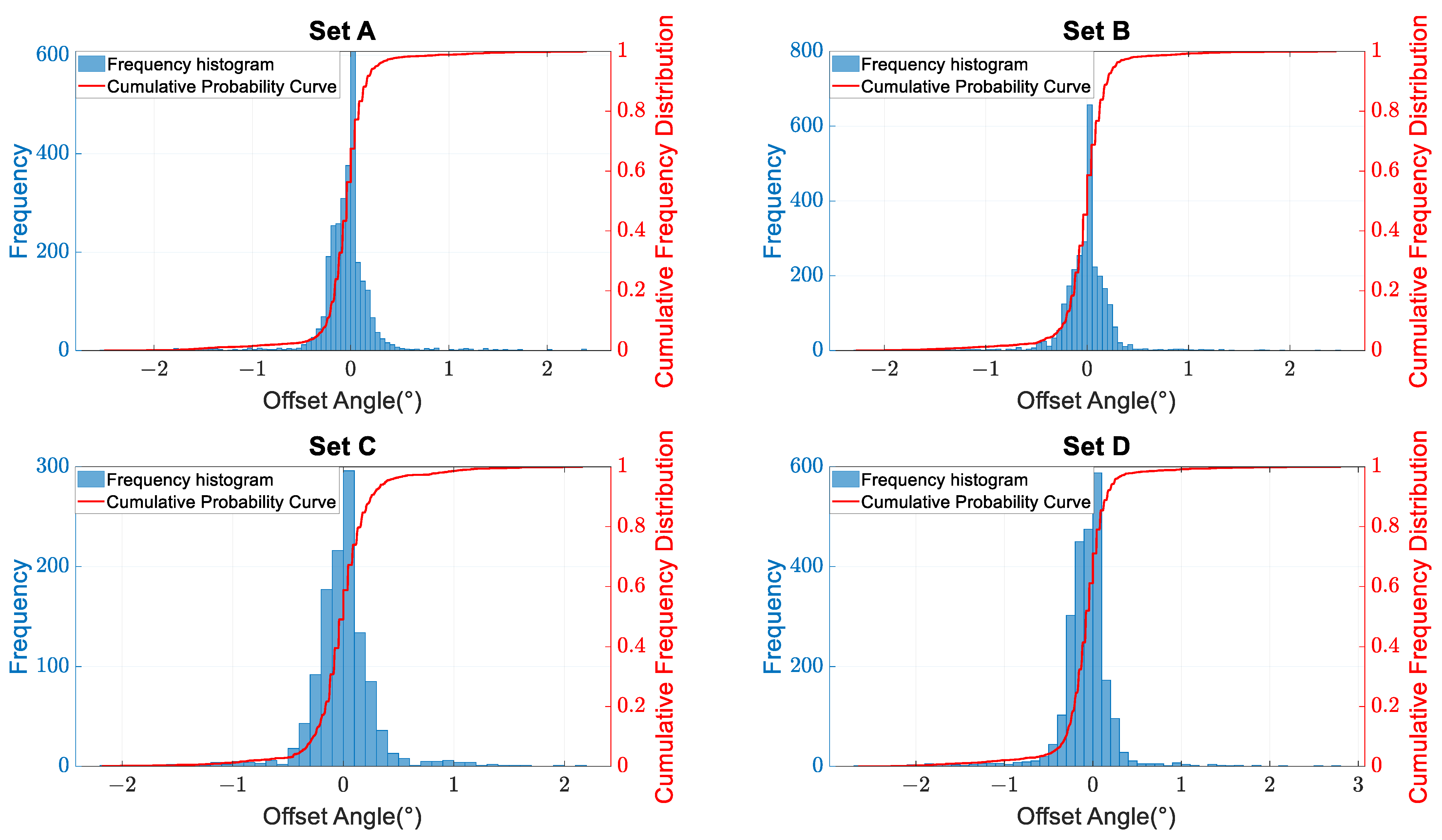
2.1. Statistical Analysis of Vehicle Driving Directions
2.2. Smoothing of Vehicle Trajectories
- Adaptability: The KF demonstrates outstanding adaptability to trajectory smoothing problems in linear systems when the data satisfy the conditions of linearity and Gaussian distribution. Under such conditions, the KF provides accurate and stable estimation results.
- Low computational cost: The KF exhibits relatively low computational complexity. By processing data using a recursive approach, it does not require a substantial amount of computational resources, making it suitable for real-time applications or scenarios with limited computational capacity.
- Optimality: Under the assumptions of linearity and Gaussian distribution, the KF represents the optimal solution for minimum mean square error estimation. This implies that under ideal conditions, it can achieve the best trajectory smoothing effect and deliver the most accurate estimation results.
- Low storage requirement: The KF only necessitates storing the current state and covariance information, without the need to retain historical data. Therefore, it places relatively low demands on storage resources, making it advantageous for applications in resource-constrained environments, such as embedded systems.
2.3. The Principles of Fitting the Ideal Coordinate System
2.3.1. Fitting the X-Axis
- Preprocessing and data preparation: The original data are preprocessed to filter the vehicle trajectory data within the region of interest.
- Calculating the direction of travel vector for each vehicle: Calculate the motion direction vector for each vehicle and record it.
- Statistical analysis of travel direction vectors: Perform statistical analysis on the computed vehicle motion direction vectors to determine the direction of road advancement in the coordinate system.
- Evaluation and validation: Validate the analysis results to determine if there is a significant deviation from the ideal road advancement direction.
2.3.2. Fitting the Y-Axis
- Robustness: RANSAC is capable of handling data sets containing outliers and noise, as it can ignore these abnormal values and produce better fitting results.
- No dependency on initial values: RANSAC does not require initial values or prior information. It obtains an initial fitting model through random sampling, eliminating the need for preliminary estimations.
- Simplicity and efficiency: The basic idea of the RANSAC algorithm is straightforward, making it easy to understand and implement. By randomly selecting samples and iterating to find the best model, it exhibits high computational efficiency in most cases.
- Adjustable parameters: RANSAC allows setting parameters to control the number of samples and the fitting threshold, enabling fine-tuning according to specific problem requirements and achieving improved fitting results.
- Set the maximum number of iterations, .
- Set the distance threshold, , for determining inliers.
- Initialize the parameters for the best-fitting plane: and are set as an empty set, .
- Iterate times:
- a.
- Randomly select the smallest set of points from the input data.
- b.
- Use the selected points to estimate plane parameters (e.g., through least-squares fitting).
- c.
- By calculating the distance between each point and the estimated plane, identify the inliers.
- d.
- Calculate the number of inliers with distances below .
- e.
- If the number of inliers is greater than , update , , and .
- Re-fit the plane using all inliers from step 4(e) to obtain the final estimated plane parameters.
- The final result, A, represents the plane obtained via fitting using the RANSAC algorithm.
- Determine the normal vectors of the two planes: The normal vector of is . The normal vector of plane is .
- Calculate the direction vector of the intersection, :
- Normalize the direction vector of the intersection: The magnitude of the intersection’s direction vector can be calculated using Equation (10):
2.3.3. Fitting the Z-Axis
2.4. Principles of Point Cloud Angle Calibration
2.4.1. Euler Angle
2.4.2. Rotation Matrix
3. Experiments
3.1. Experimental Procedure
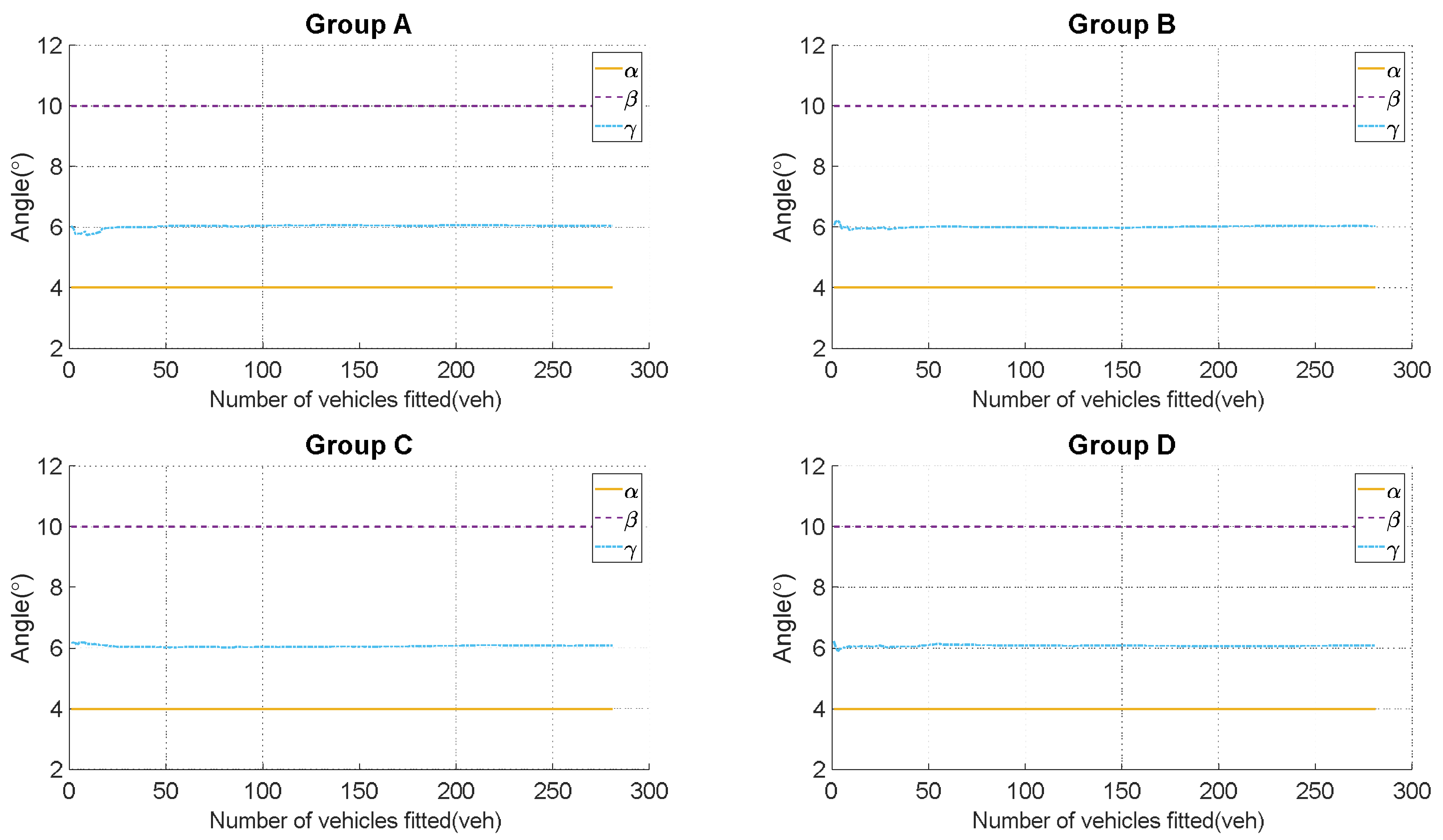
3.2. Experimental Results and Analysis
4. Discussion
- Cost and resource savings: In remote urban areas, embedding the program into the perception system is sufficient to achieve adaptive calibration. Furthermore, it can automatically calibrate the angle deviation of LiDAR periodically, ensuring the perception system maintains high-precision sensing capabilities.
- Applicability to multi-LiDAR systems: In scenarios with a linear layout of the perception area and the presence of multiple LiDAR sensors, relying on known LiDAR deployment positions greatly simplifies the challenges of fusing data from multiple sources, thereby enhancing the accuracy of fused perception results.
- Simplified parameter configuration: As an adaptive calibration method, it requires only the specification of the vehicle trajectory data for fitting, eliminating the need for intricate parameter tuning.
- Cost-effectiveness: It significantly saves human and material resources.
- High safety: It enhances operational safety by eliminating the need for manual intervention by operators at the roadside.
- Non-interference with normal operations: Embedded within the perception system’s program, it does not disrupt the normal sensing functionality of the LiDAR system, accurately capturing vehicle information and trajectory data.
- Adaptation to multi-LiDAR fusion perception: For continuous placement of multiple LiDAR sensors along long straight road sections, this calibration method simplifies the complexity of multi-source data fusion perception by requiring only the determination of LiDAR deployment positions.
- Enhancing trajectory data accuracy: By addressing the issue of angular deviation, this approach contributes to the improved perception accuracy of vehicle trajectory data. Consequently, it establishes a more precise foundational dataset for subsequent applications.
- Initial instability: During the initial operational phase of the system, when vehicles exhibit behaviors like lane changes within the region of interest, the limited quantity of fitted vehicle trajectory data might lead to reduced perception accuracy. However, as the number of fitted vehicle trajectories increases, accuracy gradually improves.
- Real-time impact: In the early stages of system operation, performing the calibration algorithm for almost every perceived vehicle trajectory data point might affect the real-time nature of the perception system, resulting in increased algorithm execution times.
- Applicability to complex road segments: This calibration method performs optimally on straight road segments; however, it might be challenging to find suitable road segments for calibration in complex road scenarios.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Azimjonov, J.; Ozmen, A. Vision-Based Vehicle Tracking on Highway Traffic Using Bounding-Box Features to Extract Statistical Information. Comput. Electr. Eng. 2022, 97, 107560. [Google Scholar] [CrossRef]
- Wang, S.J.; Pi, R.D.; Li, J.; Guo, X.M.; Lu, Y.F.; Li, T.; Tian, Y. Object Tracking Based on the Fusion of Roadside LiDAR and Camera Data. IEEE Trans. Instrum. Meas. 2022, 71, 1–14. [Google Scholar] [CrossRef]
- Sun, P.P.; Sun, C.H.; Wang, R.M.; Zhao, X.M. Object Detection Based on Roadside LiDAR for Cooperative Driving Automation: A Review. Sensors 2022, 22, 9316. [Google Scholar] [CrossRef] [PubMed]
- Lan, X.W.; Wang, C.; Lv, B.; Li, J.; Zhang, M.; Zhang, Z.Y. 3D Point Cloud Stitching for Object Detection with Wide FoV using Roadside LiDAR. Electronics 2023, 12, 703. [Google Scholar] [CrossRef]
- Chang, Y.Z.; Yu, H.Y. Trajectory Prediction Based on Roadside Millimeter Wave Radar and Video Fusion. In Proceedings of the 2021 2nd International Seminar on Artificial Intelligence, Networking and Information Technology (AINIT), Shanghai, China, 15–17 October 2021; pp. 285–288. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, H.Q.; Teng, K.M. A Trajectory Compensation Method Considering the Car-Following Behavior for Data Missing of Millimeter-Wave Radar in Roadside Detection Applications. Sensors 2023, 23, 1515. [Google Scholar] [CrossRef]
- Jung, J.; Tok, A.; Ritchie, S.G. Determining Optimal Sensor Locations under Uncertainty for a Truck Activity Monitoring System on California Freeways. J. Intell. Transp. Syst. 2021, 23, 221–234. [Google Scholar] [CrossRef]
- Du, Y.C.A.; Wang, F.Q.; Zhao, C.; Zhu, Y.F.; Ji, Y.X. Quantifying the Performance and Optimizing the Placement of Roadside Sensors for Cooperative Vehicle-Infrastructure Systems. IET Intell. Transp. Syst. 2022, 16, 908–925. [Google Scholar] [CrossRef]
- Cho, G.; Shinyama, Y.; Nakazato, J.; Maruta, K.; Sakaguchi, K. Object Recognition Network using Continuous Roadside Cameras. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference (VTC2022-SPRING), Helsinki, Finland, 19–22 June 2022. [Google Scholar] [CrossRef]
- Wang, Z.J.; Wu, Y.; Niu, Q.Q. Multi-Sensor Fusion in Automated Driving: A Survey. IEEE Access 2020, 8, 2847–2868. [Google Scholar] [CrossRef]
- Barad, J. Roadside Lidar Helping to Build Smart and Safe Transportation Infrastructure. In Proceedings of the Business of Automated Mobility (BAM) Forum, Virtual, 23–24 June 2021. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision Meets Robotics: The KITTI Dataset. Int. J. Robot. Res. 2013, 32, 1231–1237. [Google Scholar] [CrossRef]
- Park, Y.; Yun, S.; Won, C.S.; Cho, K.; Um, K.; Sim, S. Calibration between Color Camera and 3D LIDAR Instruments with a Polygonal Planar Board. Sensors 2014, 14, 5333. [Google Scholar] [CrossRef]
- Pusztai, Z.; Eichhardt, I.; Hajder, L. Accurate Calibration of Multi-LiDAR-Multi-Camera Systems. Sensors 2018, 18, 2139. [Google Scholar] [CrossRef]
- Zhu, J.; Dong, Y.; Xu, X.; Wang, J.; Wu, J. A Spatiotemporal Registration Method between Roadside Lidar and Camera. In Proceedings of the 2022 International Symposium on Semiconductor and Electronic Technology (ISSET 2022), Fuzhou, China, 12–14 August 2022; p. 012003. [Google Scholar] [CrossRef]
- Wang, Z.; Shen, H.; Du, H.; Zhou, J.; Jin, X. Research on Calibration Method of Extrinsic Parameters of Lidar and Camera Carried by UAV. In Proceedings of the 2022 4th International Conference on Data-driven Optimization of Complex Systems (DOCS), Chengdu, China, 28–30 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Shen, Y.; Addis, D.; Liu, H.; Hussain, F. A LIDAR-Based Tree Canopy Characterization under Simulated Uneven Road Condition: Advance in Tree Orchard Canopy Profile Measurement. J. Sens. 2017, 2017, 8367979. [Google Scholar] [CrossRef]
- Moghadam, P.; Bosse, M.; Zlot, R. Line-Based Extrinsic Calibration of Range and Image Sensors. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 3685–3691. [Google Scholar]
- Taylor, Z.; Nieto, J. Motion-Based Calibration of Multimodal Sensor Extrinsics and Timing Offset Estimation. IEEE Trans. Robot. 2016, 32, 1215–1229. [Google Scholar] [CrossRef]
- Yang, L.; Ma, H.W.; Nie, Z.; Zhang, H.; Wang, Z.Y.; Wang, C.W. 3D LiDAR Point Cloud Registration Based on IMU Preintegration in Coal Mine Roadways. Sensors 2023, 23, 3473. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Yang, F.; Zheng, W.N. A Novel Point Cloud Registration Method Based on ROPNet. Sensors 2023, 23, 993. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.Y.; Zheng, J.Y.; Tao, Y.Y.; Xiao, Y.; Yu, S.M.; Asiri, S.; Li, J.C.; Li, T.S. Traffic Sign Based Point Cloud Data Registration with Roadside LiDARs in Complex Traffic Environments. Electronics 2022, 11, 1559. [Google Scholar] [CrossRef]
- Yue, R.; Xu, H.; Wu, J.Q.; Sun, R.J.; Yuan, C.W. Data Registration with Ground Points for Roadside LiDAR Sensors. Remote Sensing 2019, 11, 1354. [Google Scholar] [CrossRef]
- Zhang, Q.; Bhattarai, N.; Chen, H.; Xu, H.; Liu, H.C. Vehicle Trajectory Tracking Using Adaptive Kalman Filter from Roadside Lidar. J. Transp. Eng. Part A-Syst. 2023, 149, 04023043. [Google Scholar] [CrossRef]
- Krajewski, R.; Bock, J.; Kloeker, L.; Eckstein, L. The highD Dataset: A Drone Dataset of Naturalistic Vehicle Trajectories on German Highways for Validation of Highly Automated Driving Systems. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 2118–2125. [Google Scholar]
- Guo, G.; Zhao, S.J. 3D Multi-Object Tracking with Adaptive Cubature Kalman Filter for Autonomous Driving. IEEE Trans. Intell. Veh. 2023, 8, 512–519. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography–ScienceDirect. Read. Comput. Vis. 1987, 24, 726–740. [Google Scholar] [CrossRef]
- Sarabandi, S.; Thomas, F. Solution Methods to the Nearest Rotation Matrix Problem in Double-Struck Capital R-3: A Comparative Survey. Numer. Linear Algebra Appl. 2023, e2492. [Google Scholar] [CrossRef]
- Zhu, B.; Chen, M.; Li, T. Prescribed Performance-Based Tracking Control for Quadrotor UAV under Input Delays and Input Saturations. Trans. Inst. Meas. Control 2022, 44, 2049–2062. [Google Scholar] [CrossRef]






| Type | Advantages | Disadvantages | Max Working Distance |
|---|---|---|---|
| MMW-Radar |
|
| 5–200 m |
| Camera |
|
| 250 m (Depending on the lens) |
| LiDAR |
|
| 200 m |
| Inductive Sensor |
|
| 100 m |
| The Number of Fitted Vehicles (veh) | The Calculated Results of Angle (°) | The Calculated Results of Angle (°) | The Calculated Results of Angle (°) |
|---|---|---|---|
| 1 | 4.000000 | 10.000000 | 6.030167 |
| 2 | 4.000000 | 10.000000 | 5.969131 |
| 3 | 4.000000 | 10.000000 | 5.780432 |
| 4 | 4.000000 | 10.000000 | 5.779811 |
| 5 | 4.000000 | 10.000000 | 5.790756 |
| 6 | 4.000000 | 10.000000 | 5.782515 |
| 7 | 4.000000 | 10.000000 | 5.812183 |
| 8 | 4.000000 | 10.000000 | 5.861155 |
| 9 | 4.000000 | 10.000000 | 5.730176 |
| 10 | 4.000000 | 10.000000 | 5.753002 |
| 11 | 4.000000 | 10.000000 | 5.760653 |
| 12 | 4.000000 | 10.000000 | 5.774157 |
| 13 | 4.000000 | 10.000000 | 5.778783 |
| 14 | 4.000000 | 10.000000 | 5.798727 |
| 15 | 4.000000 | 10.000000 | 5.820700 |
| 16 | 4.000000 | 10.000000 | 5.846628 |
| 17 | 4.000000 | 10.000000 | 5.960378 |
| 18 | 4.000000 | 10.000000 | 5.953262 |
| 19 | 4.000000 | 10.000000 | 5.962495 |
| 20 | 4.000000 | 10.000000 | 5.968895 |
| 21 | 4.000000 | 10.000000 | 5.978498 |
| 22 | 4.000000 | 10.000000 | 5.979475 |
| 23 | 4.000000 | 10.000000 | 5.982899 |
| 24 | 4.000000 | 10.000000 | 5.988527 |
| 25 | 4.000000 | 10.000000 | 5.992750 |
| 26 | 4.000000 | 10.000000 | 5.992699 |
| 27 | 4.000000 | 10.000000 | 5.992969 |
| 28 | 4.000000 | 10.000000 | 6.002791 |
| 29 | 4.000000 | 10.000000 | 5.999153 |
| 30 | 4.000000 | 10.000000 | 5.997213 |
| ... | ... | ... | ... |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, X.; Hu, J.; Chen, H.; Huang, S.; Hu, H.; Zhang, H. Research on an Adaptive Method for the Angle Calibration of Roadside LiDAR Point Clouds. Sensors 2023, 23, 7542. https://doi.org/10.3390/s23177542
Wen X, Hu J, Chen H, Huang S, Hu H, Zhang H. Research on an Adaptive Method for the Angle Calibration of Roadside LiDAR Point Clouds. Sensors. 2023; 23(17):7542. https://doi.org/10.3390/s23177542
Chicago/Turabian StyleWen, Xin, Jiazun Hu, Haiyu Chen, Shichun Huang, Haonan Hu, and Hui Zhang. 2023. "Research on an Adaptive Method for the Angle Calibration of Roadside LiDAR Point Clouds" Sensors 23, no. 17: 7542. https://doi.org/10.3390/s23177542
APA StyleWen, X., Hu, J., Chen, H., Huang, S., Hu, H., & Zhang, H. (2023). Research on an Adaptive Method for the Angle Calibration of Roadside LiDAR Point Clouds. Sensors, 23(17), 7542. https://doi.org/10.3390/s23177542







