A Deep Learning Model for Correlation Analysis between Electroencephalography Signal and Speech Stimuli
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset
- EEG traces of 19 subjects engaged in 20 trials of an experiment that involved listening to a single audiobook;
- Twenty stimuli files containing the audio of a male speaker reading snippets of a novel and the associated envelope.
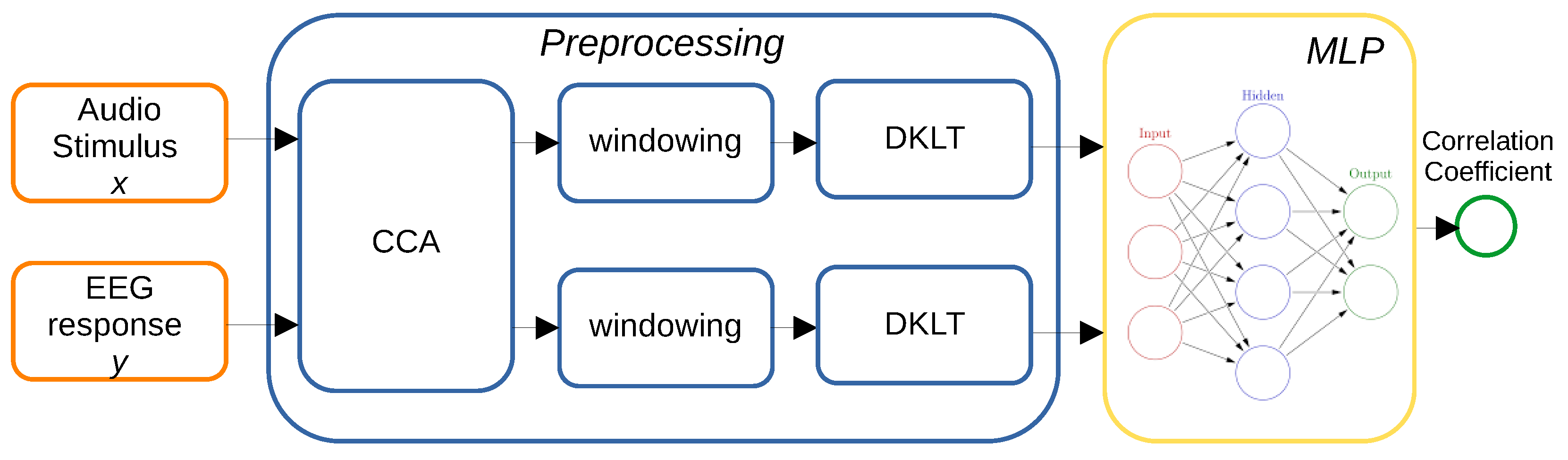
2.2. Proposed Method
2.2.1. Data Preprocessing
2.2.2. CCA
2.2.3. Data Windowing
2.2.4. DKLT
2.2.5. Neural Network
- Input Layer: this layer receives the raw input data. Each neuron in the input layer corresponds to a feature of the input data.
- Hidden Layers: These are one or more layers that come between the input and output layers. Each neuron in a hidden layer takes input from the neurons in the previous layer and applies a linear combination of the inputs followed by a non-linear activation function. The purpose of these hidden layers is to learn complex patterns and relationships within the data.
- Output Layer: This layer produces the final output of the network. The number of neurons in the output layer depends on the specific task.
2.2.6. Loss Function
3. Experimental Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sanei, S.; Chambers, J.A. EEG Signal Processing; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Coles, M.G.; Rugg, M.D. Event-Related Brain Potentials: An Introduction; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Lalor, E.C.; Power, A.J.; Reilly, R.B.; Foxe, J.J. Resolving Precise Temporal Processing Properties of the Auditory System Using Continuous Stimuli. J. Neurophysiol. 2009, 102, 349–359. [Google Scholar] [CrossRef] [PubMed]
- Lalor, E.C.; Foxe, J.J. Neural responses to uninterrupted natural speech can be extracted with precise temporal resolution. Eur. J. Neurosci. 2010, 31, 189–193. [Google Scholar] [CrossRef] [PubMed]
- Power, A.J.; Reilly, R.B.; Lalor, E.C. Comparing linear and quadratic models of the human auditory system using EEG. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 4171–4174. [Google Scholar] [CrossRef]
- de Cheveigné, A.; Wong, D.D.; Di Liberto, G.M.; Hjortkjær, J.; Slaney, M.; Lalor, E. Decoding the auditory brain with canonical component analysis. NeuroImage 2018, 172, 206–216. [Google Scholar] [CrossRef] [PubMed]
- Alickovic, E.; Lunner, T.; Gustafsson, F.; Ljung, L. A tutorial on auditory attention identification methods. Front. Neurosci. 2019, 13, 153. [Google Scholar] [CrossRef] [PubMed]
- Hotelling, H. Relations between two sets of variates. In Breakthroughs in Statistics: Methodology and Distribution; Springer: Berlin/Heidelberg, Germany, 1992; pp. 162–190. [Google Scholar] [CrossRef]
- Thompson, B. Canonical Correlation Analysis: Uses and Interpretation; Number 47; Sage: Newcastle upon Tyne, UK, 1984. [Google Scholar]
- de Cheveigné, A.; Di Liberto, G.M.; Arzounian, D.; Wong, D.D.; Hjortkjær, J.; Fuglsang, S.; Parra, L.C. Multiway canonical correlation analysis of brain data. NeuroImage 2019, 186, 728–740. [Google Scholar] [CrossRef] [PubMed]
- Bharadwaj, S.; Arora, R.; Livescu, K.; Hasegawa-Johnson, M. Multiview acoustic feature learning using articulatory measurements. In Proceedings of the International Workshop on Stat, Machine Learning for Speech Recognition, Kyoto, Japan, 31 March 2012. [Google Scholar]
- Arora, R.; Livescu, K. Kernel CCA for multi-view learning of acoustic features using articulatory measurements. In Proceedings of the Symposium on Machine Learning in Speech and Language Processing, Portland, OR, USA, 14 September 2012. [Google Scholar]
- Arora, R.; Livescu, K. Multi-view CCA-based acoustic features for phonetic recognition across speakers and domains. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 7135–7139. [Google Scholar] [CrossRef]
- Zheng, X.; Chen, W.; Li, M.; Zhang, T.; You, Y.; Jiang, Y. Decoding human brain activity with deep learning. Biomed. Signal Process. Control. 2020, 56, 101730. [Google Scholar] [CrossRef]
- Wang, X.; Liang, X.; Jiang, Z.; Nguchu, B.A.; Zhou, Y.; Wang, Y.; Wang, H.; Li, Y.; Zhu, Y.; Wu, F.; et al. Decoding and mapping task states of the human brain via deep learning. Hum. Brain Mapp. 2020, 41, 1505–1519. [Google Scholar] [CrossRef] [PubMed]
- Stober, S.; Cameron, D.J.; Grahn, J.A. Using Convolutional Neural Networks to Recognize Rhythm Stimuli from Electroencephalography Recordings. In Proceedings of the Advances in Neural Information Processing Systems 27 (NIPS 2014), Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Andrew, G.; Arora, R.; Bilmes, J.; Livescu, K. Deep Canonical Correlation Analysis. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; Dasgupta, S., McAllester, D., Eds.; Proceedings of Machine Learning Research (PMLR): Atlanta, GA, USA, 2013; Volume 28, pp. 1247–1255. [Google Scholar]
- Reddy Katthi, J.; Ganapathy, S. Deep Correlation Analysis for Audio-EEG Decoding. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 2742–2753. [Google Scholar] [CrossRef] [PubMed]
- Katthi, J.R.; Ganapathy, S.; Kothinti, S.; Slaney, M. Deep Canonical Correlation Analysis For Decoding The Auditory Brain. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 3505–3508. [Google Scholar] [CrossRef]
- Data from: Electrophysiological Correlates of Semantic Dissimilarity Reflect the Comprehension of Natural, Narrative Speech. Available online: https://datadryad.org/stash/dataset/doi:10.5061/dryad.070jc(accessed on 24 July 2023).
- Broderick, M.P.; Anderson, A.J.; Di Liberto, G.M.; Crosse, M.J.; Lalor, E.C. Electrophysiological Correlates of Semantic Dissimilarity Reflect the Comprehension of Natural, Narrative Speech. Curr. Biol. 2018, 28, 803–809.e3. [Google Scholar] [CrossRef] [PubMed]
- Pandey, P.; Ahmad, N.; Miyapuram, K.P.; Lomas, D. Predicting Dominant Beat Frequency from Brain Responses While Listening to Music. In Proceedings of the 2021 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Houston, TX, USA, 9–12 December 2021; pp. 3058–3064. [Google Scholar] [CrossRef]
- Kaneshiro, B.; Nguyen, D.T.; Norcia, A.M.; Dmochowski, J.P.; Berger, J. Natural music evokes correlated EEG responses reflecting temporal structure and beat. NeuroImage 2020, 214, 116559. [Google Scholar] [CrossRef] [PubMed]
- Di Liberto, G.; O’Sullivan, J.; Lalor, E. Low-Frequency Cortical Entrainment to Speech Reflects Phoneme-Level Processing. Curr. Biol. 2015, 25, 2457–2465. [Google Scholar] [CrossRef] [PubMed]
- Alessandrini, M.; Biagetti, G.; Crippa, P.; Falaschetti, L.; Luzzi, S.; Turchetti, C. EEG-Based Neurodegenerative Disease Classification using LSTM Neural Networks. In Proceedings of the 2023 IEEE Statistical Signal Processing Workshop (SSP), Hanoi, Vietnam, 2–5 July 2023; pp. 428–432. [Google Scholar] [CrossRef]
- Alessandrini, M.; Biagetti, G.; Crippa, P.; Falaschetti, L.; Luzzi, S.; Turchetti, C. EEG-Based Alzheimer’s Disease Recognition Using Robust-PCA and LSTM Recurrent Neural Network. Sensors 2022, 22, 3696. [Google Scholar] [CrossRef] [PubMed]
- Biagetti, G.; Crippa, P.; Falaschetti, L.; Luzzi, S.; Turchetti, C. Classification of Alzheimer’s Disease from EEG Signal Using Robust-PCA Feature Extraction. Procedia Comput. Sci. 2021, 192, 3114–3122. [Google Scholar] [CrossRef]
- Musci, M.; De Martini, D.; Blago, N.; Facchinetti, T.; Piastra, M. Online Fall Detection Using Recurrent Neural Networks on Smart Wearable Devices. IEEE Trans. Emerg. Top. Comput. 2021, 9, 1276–1289. [Google Scholar] [CrossRef]
- Heinonen, J.; Soman, A.; Reddy Katthi, J.; Ganapathy, S.; Learning and Extraction of Acoustic Patterns (LEAP) Laboratory, Electrical Engineering Department, Indian Institute of Science, Bengaluru, India. Personal communication, 2023.


| Subject | LCCA | Proposed Method |
|---|---|---|
| 1 | 0.020 | 0.338 |
| 2 | 0.032 | 0.223 |
| 3 | 0.027 | 0.218 |
| 4 | 0.034 | 0.386 |
| 5 | 0.031 | 0.432 |
| 6 | 0.046 | 0.436 |
| 7 | 0.026 | 0.207 |
| 8 | 0.029 | 0.352 |
| 9 | 0.030 | 0.318 |
| 10 | 0.049 | 0.432 |
| 11 | 0.032 | 0.332 |
| 12 | 0.038 | 0.398 |
| 13 | 0.031 | 0.222 |
| 14 | 0.038 | 0.441 |
| 15 | 0.047 | 0.306 |
| 16 | 0.032 | 0.197 |
| 17 | 0.038 | 0.352 |
| 18 | 0.039 | 0.235 |
| 19 | 0.037 | 0.365 |
| Overall | 0.035 | 0.326 |
| LCCA | DCCA [18] | Proposed Method | |
|---|---|---|---|
| 0.008 | 0.275 | 0.338 | |
| 0.045 | 0.316 | 0.436 | |
| 0.020 | 0.213 | 0.207 | |
| 0.040 | 0.403 | 0.432 | |
| 0.020 | 0.338 | 0.332 | |
| 0.008 | 0.354 | 0.222 | |
| 0.019 | 0.292 | 0.352 | |
| 0.033 | 0.232 | 0.365 | |
| Overall | 0.024 | 0.303 | 0.335 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alessandrini, M.; Falaschetti, L.; Biagetti, G.; Crippa, P.; Luzzi, S.; Turchetti, C. A Deep Learning Model for Correlation Analysis between Electroencephalography Signal and Speech Stimuli. Sensors 2023, 23, 8039. https://doi.org/10.3390/s23198039
Alessandrini M, Falaschetti L, Biagetti G, Crippa P, Luzzi S, Turchetti C. A Deep Learning Model for Correlation Analysis between Electroencephalography Signal and Speech Stimuli. Sensors. 2023; 23(19):8039. https://doi.org/10.3390/s23198039
Chicago/Turabian StyleAlessandrini, Michele, Laura Falaschetti, Giorgio Biagetti, Paolo Crippa, Simona Luzzi, and Claudio Turchetti. 2023. "A Deep Learning Model for Correlation Analysis between Electroencephalography Signal and Speech Stimuli" Sensors 23, no. 19: 8039. https://doi.org/10.3390/s23198039
APA StyleAlessandrini, M., Falaschetti, L., Biagetti, G., Crippa, P., Luzzi, S., & Turchetti, C. (2023). A Deep Learning Model for Correlation Analysis between Electroencephalography Signal and Speech Stimuli. Sensors, 23(19), 8039. https://doi.org/10.3390/s23198039










