The Use of Deep Learning Methods for Object Height Estimation in High Resolution Satellite Images
Abstract
:1. Introduction
2. Background and Related Works
2.1. Geospatial Data
2.2. Deep Learning for Geospatial Data
2.3. Height Estimation
3. Methodology
3.1. Materials
3.2. Study Area
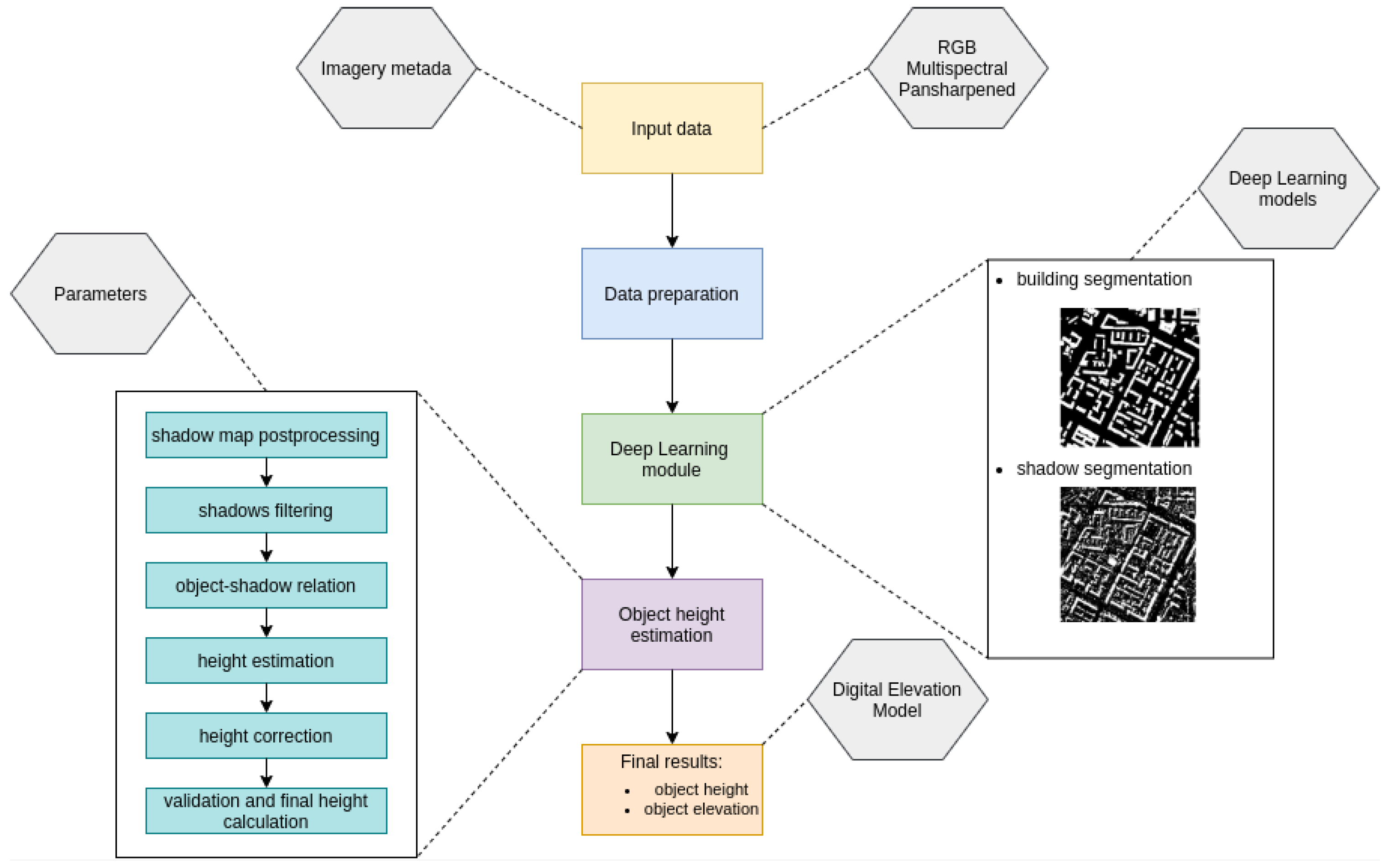
3.3. Pipeline Schema and Algorithm Description
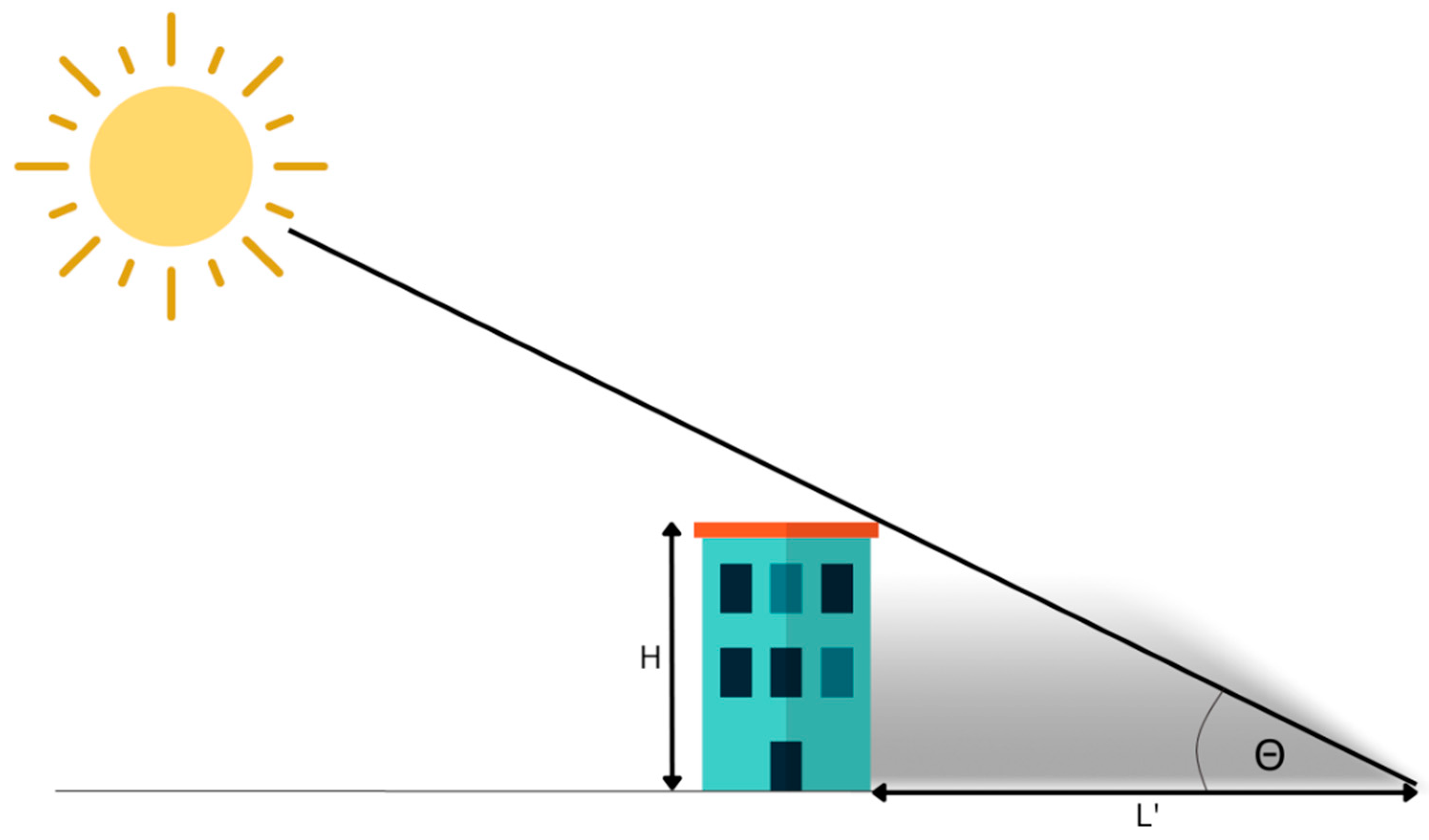
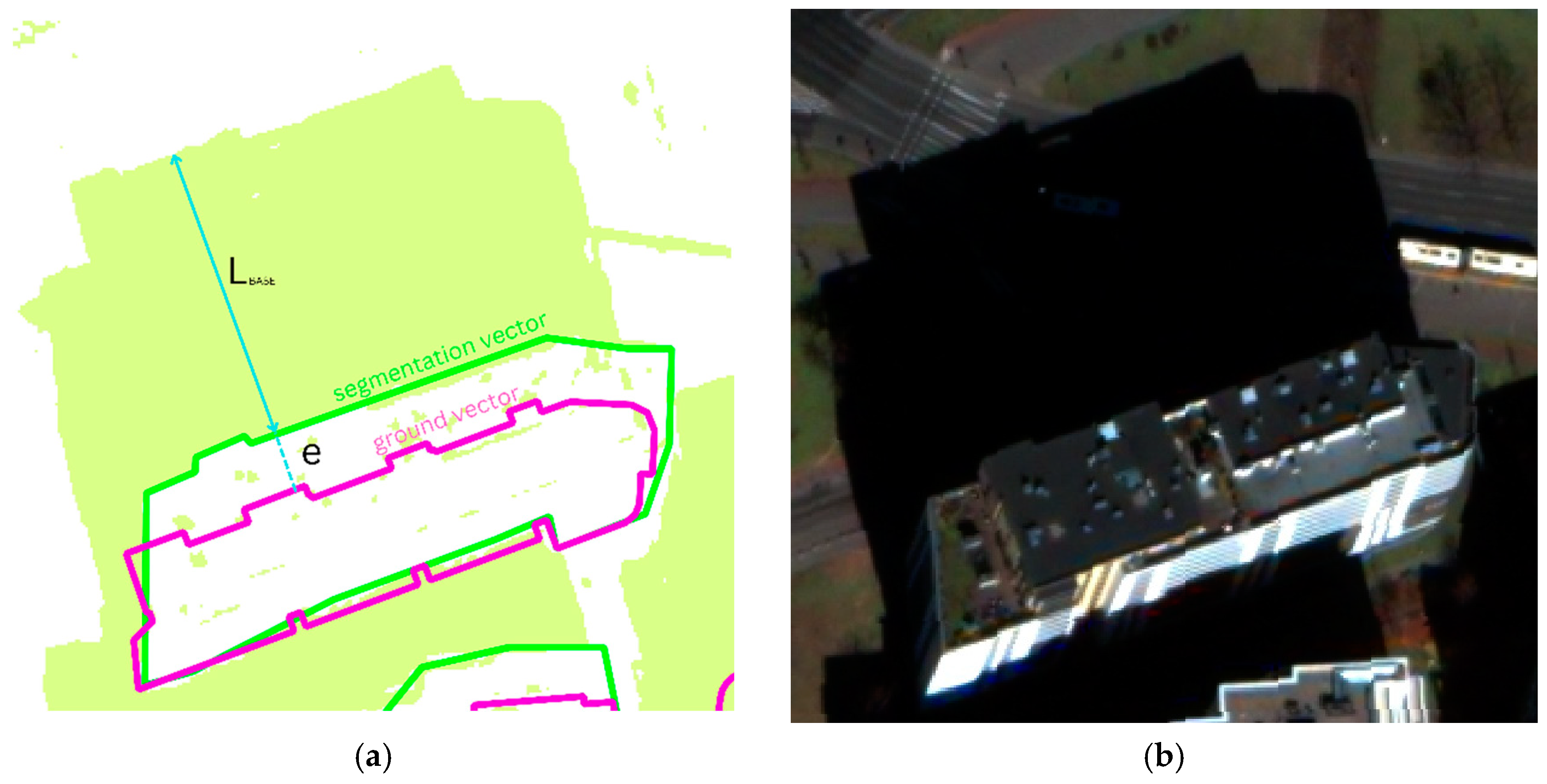
- HBASE—base height of the object;
- LBASE—estimated shadow length based on cutting line;
- e—parameter calculated based on the lengthening or shortening of the cutting line (for vectors on the ground) or calculated in the correction process;
- θ—elevation angle of the sun.
- HBUILDING—total value of the building height;
- HBASE—base height of the object;
- hroof—additional height value from the analysis of objects located on the roof.
- Data Normalization and Unification: The system begins by normalizing and standardizing the input data to ensure consistency and compatibility with the algorithm’s requirements. This step is crucial for accurate processing and analysis.
- Ground Control Points (GCPs): The system utilizes GCPs to match satellite imagery with data from open sources. GCPs help establish spatial references and align different datasets, enabling reliable analysis.
- Tiling: The data are divided into tiles, which are smaller, manageable sections of the overall dataset. Tiling allows for the efficient processing and analysis of large quantities of geospatial data.
- Shadow and Building Segmentation: The system employs segmentation algorithms to detect and distinguish between shadows and buildings in satellite imagery. This enables the identification and measurement of objects above the ground.
- Handling Atypical Objects: The system includes a solution for detecting intermittent and less visible shadows, which helps to accurately identify and analyze atypical objects that might be challenging to detect using conventional methods.
- Height and Geospatial Data Calculation: The system calculates the height, coordinates, and outline of the detected objects using metadata and other relevant information from satellite imagery. This allows for a comprehensive understanding of the identified objects.
- Integration with Database: The system integrates with a database to store and analyze the results of the analysis. This enables the processing of a large volume of obstacles and facilitates data retrieval and querying.
- Data Lake Operation: The system operates based on the principles of a data lake. A data lake is a centralized repository that allows for the storage of structured and unstructured data. It provides a flexible and scalable architecture for data processing and analysis.
4. Results
4.1. Training, Validation and Assessment
4.1.1. Training Process and Results
4.1.2. Height Estimation
4.2. Evaluation
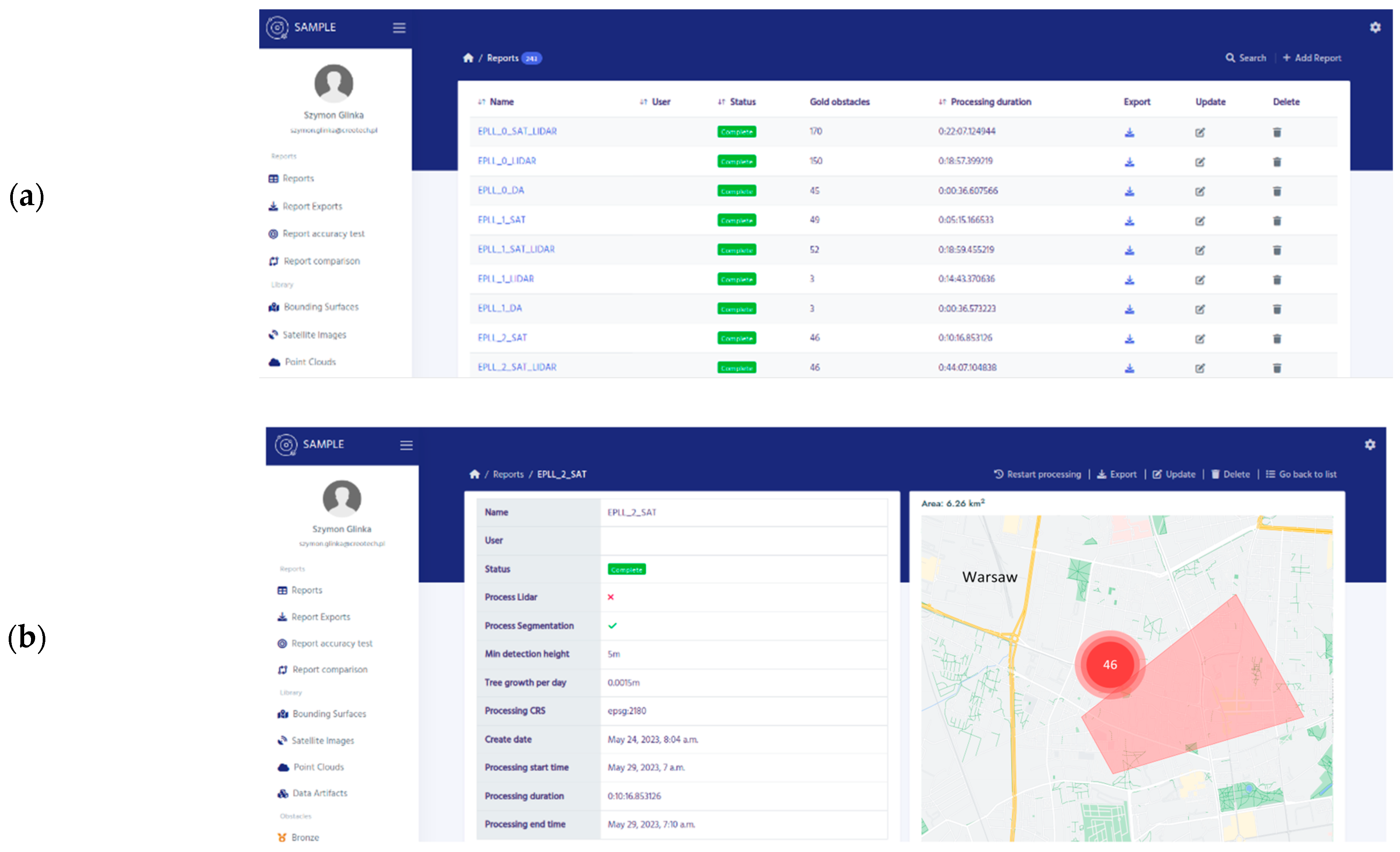
4.3. SAMPLE System
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, D.; Cai, S. A Spatial-Temporal Modeling Approach to Reconstructing Land-Cover Change Trajectories from Multi-Temporal Satellite Imagery. Ann. Assoc. Am. Geogr. 2012, 102, 1329–1347. [Google Scholar] [CrossRef]
- Saadat, H.; Adamowski, J.; Bonnell, R.; Sharifi, F.; Namdar, M.; Ale-Ebrahim, S. Land Use and Land Cover Classification over a Large Area in Iran Based on Single Date Analysis of Satellite Imagery. ISPRS J. Photogramm. Remote Sens. 2011, 66, 608–619. [Google Scholar] [CrossRef]
- Yang, H.; Kong, J.; Hu, H.; Du, Y.; Gao, M.; Chen, F. A Review of Remote Sensing for Water Quality Retrieval: Progress and Challenges. Remote Sens. 2022, 14, 1770. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J. A Survey on Object Detection in Optical Remote Sensing Images. ISPRS J. Photogramm. Remote Sens. 2016, 117, 11–28. [Google Scholar] [CrossRef]
- Nie, X.; Duan, M.; Ding, H.; Hu, B.; Wong, E.K. Attention Mask R-CNN for Ship Detection and Segmentation from Remote Sensing Images. IEEE Access 2020, 8, 9325–9334. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, T.; Ouyang, C. End-to-End Airplane Detection Using Transfer Learning in Remote Sensing Images. Remote Sens. 2018, 10, 139. [Google Scholar] [CrossRef]
- Sishodia, R.P.; Ray, R.L.; Singh, S.K. Applications of Remote Sensing in Precision Agriculture: A Review. Remote Sens. 2020, 12, 3136. [Google Scholar] [CrossRef]
- Li, L.; Zhang, S.; Wu, J. Efficient Object Detection Framework and Hardware Architecture for Remote Sensing Images. Remote Sens. 2019, 11, 2376. [Google Scholar] [CrossRef]
- Asokan, A.; Anitha, J. Change Detection Techniques for Remote Sensing Applications: A Survey. Earth Sci. Inform. 2019, 12, 143–160. [Google Scholar] [CrossRef]
- Patino, J.E.; Duque, J.C. A Review of Regional Science Applications of Satellite Remote Sensing in Urban Settings. Comput. Environ. Urban. Syst. 2013, 37, 1–17. [Google Scholar] [CrossRef]
- Voigt, S.; Kemper, T.; Riedlinger, T.; Kiefl, R.; Scholte, K.; Mehl, H. Satellite Image Analysis for Disaster and Crisis-Management Support. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1520–1528. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep Learning in Remote Sensing Applications: A Meta-Analysis and Review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Liasis, G.; Stavrou, S. Satellite Images Analysis for Shadow Detection and Building Height Estimation. ISPRS J. Photogramm. Remote Sens. 2016, 119, 437–450. [Google Scholar] [CrossRef]
- Lee, T.; Kim, T. Automatic Building Height Extraction by Volumetric Shadow Analysis of Monoscopic Imagery. Int. J. Remote Sens. 2013, 34, 5834–5850. [Google Scholar] [CrossRef]
- Comber, A.; Umezaki, M.; Zhou, R.; Ding, Y.; Li, Y.; Fu, H.; Jiang, H.; Tewkesbury, A. Using Shadows in High-Resolution Imagery to Determine Building Height. Remote Sens. Lett. 2011, 3, 551–556. [Google Scholar] [CrossRef]
- Lee, J.G.; Kang, M. Geospatial Big Data: Challenges and Opportunities. Big Data Res. 2015, 2, 74–81. [Google Scholar] [CrossRef]
- Coetzee, S.; Ivánová, I.; Mitasova, H.; Brovelli, M.A. Open Geospatial Software and Data: A Review of the Current State and A Perspective into the Future. ISPRS Int. J. Geo.-Inf. 2020, 9, 90. [Google Scholar] [CrossRef]
- Satellite Missions Catalogue. Available online: https://www.eoportal.org/satellite-missions (accessed on 21 June 2023).
- Glinka, S.; Owerko, T.; Tomaszkiewicz, K. Using Open Vector-Based Spatial Data to Create Semantic Datasets for Building Segmentation for Raster Data. Remote Sens. 2022, 14, 2745. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep Learning in Environmental Remote Sensing: Achievements and Challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, A.C.; Lo, W.-Y.; et al. Segment Anything. arXiv 2023, arXiv:2304.02643. [Google Scholar]
- Gong, H.; Mu, T.; Li, Q.; Dai, H.; Li, C.; He, Z.; Wang, W.; Han, F.; Tuniyazi, A.; Li, H.; et al. Swin-Transformer-Enabled YOLOv5 with Attention Mechanism for Small Object Detection on Satellite Images. Remote Sens. 2022, 14, 2861. [Google Scholar] [CrossRef]
- Li, J.; Huang, X.; Tu, L.; Zhang, T.; Wang, L. A Review of Building Detection from Very High Resolution Optical Remote Sensing Images. GISci. Remote Sens. 2022, 59, 1199–1225. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, G.; Du, S.; Singh, K.K.; Wu, Z.; Yu, M.; Chen, X.; Zhang, W.; Liu, Y. AGs-UNet: Building Extraction Model for High Resolution Remote Sensing Images Based on Attention Gates U Network. Sensors 2022, 22, 2932. [Google Scholar] [CrossRef]
- Abdollahi, A.; Pradhan, B.; Alamri, A.M. An Ensemble Architecture of Deep Convolutional Segnet and UNet Networks for Building Semantic Segmentation from High-Resolution Aerial Images. Geocarto Int. 2020, 37, 3355–3370. [Google Scholar] [CrossRef]
- Seong, S.; Choi, J. Semantic Segmentation of Urban Buildings Using a High-Resolution Network (HRNet) with Channel and Spatial Attention Gates. Remote Sens. 2021, 13, 3087. [Google Scholar] [CrossRef]
- Abdollahi, A.; Pradhan, B.; Gite, S.; Alamri, A. Building Footprint Extraction from High Resolution Aerial Images Using Generative Adversarial Network (GAN) Architecture. IEEE Access 2020, 8, 209517–209527. [Google Scholar] [CrossRef]
- Wang, L.; Li, R.; Zhang, C.; Fang, S.; Duan, C.; Meng, X.; Atkinson, P.M. UNetFormer: A UNet-like Transformer for Efficient Semantic Segmentation of Remote Sensing Urban Scene Imagery. ISPRS J. Photogramm. Remote Sens. 2022, 190, 196–214. [Google Scholar] [CrossRef]
- Zhou, T.; Fu, H.; Sun, C.; Wang, S. Shadow Detection and Compensation from Remote Sensing Images under Complex Urban Conditions. Remote Sens. 2021, 13, 699. [Google Scholar] [CrossRef]
- Dharani, M.; Sreenivasulu, G. Shadow Detection Using Index-Based Principal Component Analysis of Satellite Images. In Proceedings of the 3rd International Conference on Computing Methodologies and Communication, ICCMC, Erode, India, 27–29 March 2019; pp. 182–187. [Google Scholar] [CrossRef]
- Zhou, G.; Sha, H. Building Shadow Detection on Ghost Images. Remote Sens. 2020, 12, 679. [Google Scholar] [CrossRef]
- Jin, Y.; Xu, W.; Hu, Z.; Jia, H.; Luo, X.; Shao, D. GSCA-UNet: Towards Automatic Shadow Detection in Urban Aerial Imagery with Global-Spatial-Context Attention Module. Remote Sens. 2020, 12, 2864. [Google Scholar] [CrossRef]
- Xie, Y.; Feng, D.; Chen, H.; Liao, Z.; Zhu, J.; Li, C.; Baik, S.W. An Omni-Scale Global–Local Aware Network for Shadow Extraction in Remote Sensing Imagery. ISPRS J. Photogramm. Remote Sens. 2022, 193, 29–44. [Google Scholar] [CrossRef]
- Zhu, Q.; Yang, Y.; Sun, X.; Guo, M. CDANet: Contextual Detail-Aware Network for High-Spatial-Resolution Remote-Sensing Imagery Shadow Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5617415. [Google Scholar] [CrossRef]
- Shettigara, V.K.; Sumerling, G.M. Height determination of extended objects using shadows in SPOT images. Photogramm. Eng. Remote Sens. 1998, 64, 35–43. [Google Scholar]
- Raju, P.L.N.; Chaudhary, H.; Jha, A.K. Shadow Analysis Technique for Extraction of Building Height Using High Resolution Satellite Single Image and Accuracy Assessment. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences—ISPRS Archives, 2014, ISPRS Technical Commission VIII Symposium, Hyderabad, India, 9–12 December 2014; International Society for Photogrammetry and Remote Sensing. Volume 40, pp. 1185–1192. [Google Scholar]
- Karatsiolis, S.; Kamilaris, A.; Cole, I. Article Img2ndsm: Height Estimation from Single Airborne Rgb Images with Deep Learning. Remote Sens. 2021, 13, 2417. [Google Scholar] [CrossRef]
- Amirkolaee, H.A.; Arefi, H. Height Estimation from Single Aerial Images Using a Deep Convolutional Encoder-Decoder Network. ISPRS J. Photogramm. Remote Sens. 2019, 149, 50–66. [Google Scholar] [CrossRef]
- Mou, L.; Xiang Zhu, X. IM2HEIGHT: Height Estimation from Single Monocular Imagery via Fully Residual Convolutional-Deconvolutional Network. arXiv 2017, arXiv:1802.10249. [Google Scholar]
- Panagiotou, E.; Chochlakis, G.; Grammatikopoulos, L.; Charou, E. Generating Elevation Surface from a Single RGB Remotely Sensed Image Using Deep Learning. Remote Sens. 2020, 12, 2002. [Google Scholar] [CrossRef]
- Gao, Q.; Shen, X. StyHighNet: Semi-Supervised Learning Height Estimation from a Single Aerial Image via Unified Style Transferring. Sensors 2021, 21, 2272. [Google Scholar] [CrossRef]
- Zeng, C.; Wang, J.; Zhan, W.; Shi, P.; Gambles, A. An Elevation Difference Model for Building Height Extraction from Stereo-Image-Derived DSMs. Int. J. Remote Sens. 2014, 35, 7614–7630. [Google Scholar] [CrossRef]
- Zhang, C.; Cui, Y.; Zhu, Z.; Jiang, S.; Jiang, W. Building Height Extraction from GF-7 Satellite Images Based on Roof Contour Constrained Stereo Matching. Remote Sens. 2022, 14, 1566. [Google Scholar] [CrossRef]
- Cao, Y.; Huang, X. A Deep Learning Method for Building Height Estimation Using High-Resolution Multi-View Imagery over Urban Areas: A Case Study of 42 Chinese Cities. Remote Sens. Environ. 2021, 264, 112590. [Google Scholar] [CrossRef]
- Recla, M.; Schmitt, M. Deep-Learning-Based Single-Image Height Reconstruction from Very-High-Resolution SAR Intensity Data. ISPRS J. Photogramm. Remote Sens. 2022, 183, 496–509. [Google Scholar] [CrossRef]
- Xue, M.; Li, J.; Luo, Q. A Geometry-Aware Consistent Constraint for Height Estimation from a Single SAR Imagery in Mountain Areas. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Huang, H.; Chen, P.; Xu, X.; Liu, C.; Wang, J.; Liu, C.; Clinton, N.; Gong, P. Estimating Building Height in China from ALOS AW3D30. ISPRS J. Photogramm. Remote Sens. 2022, 185, 146–157. [Google Scholar] [CrossRef]
- Kadhim, N.; Mourshed, M. A Shadow-Overlapping Algorithm for Estimating Building Heights from VHR Satellite Images. IEEE Geosci. Remote Sens. Lett. 2018, 15, 8–12. [Google Scholar] [CrossRef]
- Xie, Y.; Feng, D.; Xiong, S.; Zhu, J.; Liu, Y. Multi-scene Building Height Estimation Method Based on Shadow in High Resolution Imagery. Remote Sens. 2021, 13, 2862. [Google Scholar] [CrossRef]
- Li, B.; Chen, X.; Lin, Z. Building Height Restoration Method of Remote Sensing Images Based on Faster RCNN. In Proceedings of the International Conference on Tools with Artificial Intelligence, ICTAI, Macao, China, 31 October 2022–2 November 2022; pp. 955–959. [Google Scholar] [CrossRef]
- Geoportal.Gov.Pl. Available online: https://mapy.geoportal.gov.pl/imap/Imgp_2.html?gpmap=gp0 (accessed on 22 June 2023).
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Can Semantic Labeling Methods Generalize to Any City? The Inria Aerial Image Labeling Benchmark. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017. [Google Scholar]
- Shao, Y.; Taff, G.N.; Walsh, S.J. Shadow detection and building-height estimation using IKONOS data. Int. J. Remote Sens. 2011, 32, 6929–6944. [Google Scholar] [CrossRef]







| Task | Train | Validation | Test |
|---|---|---|---|
| Building segmentation | 50,000 | 9000 | 4520 |
| Shadow segmentation | 8000 | 1200 | 1200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Glinka, S.; Bajer, J.; Wierzbicki, D.; Karwowska, K.; Kedzierski, M. The Use of Deep Learning Methods for Object Height Estimation in High Resolution Satellite Images. Sensors 2023, 23, 8162. https://doi.org/10.3390/s23198162
Glinka S, Bajer J, Wierzbicki D, Karwowska K, Kedzierski M. The Use of Deep Learning Methods for Object Height Estimation in High Resolution Satellite Images. Sensors. 2023; 23(19):8162. https://doi.org/10.3390/s23198162
Chicago/Turabian StyleGlinka, Szymon, Jarosław Bajer, Damian Wierzbicki, Kinga Karwowska, and Michal Kedzierski. 2023. "The Use of Deep Learning Methods for Object Height Estimation in High Resolution Satellite Images" Sensors 23, no. 19: 8162. https://doi.org/10.3390/s23198162
APA StyleGlinka, S., Bajer, J., Wierzbicki, D., Karwowska, K., & Kedzierski, M. (2023). The Use of Deep Learning Methods for Object Height Estimation in High Resolution Satellite Images. Sensors, 23(19), 8162. https://doi.org/10.3390/s23198162







