Power Line Extraction and Tree Risk Detection Based on Airborne LiDAR
Abstract
:1. Introduction
- (1)
- Although the power line extraction methods based on linear features are mainstream, they rely heavily on geometric constraints and preset parameters, ignore the spatial distribution features of transmission lines, and do not further distinguish differences between aerial ground wires and conductors, which is not conducive to the efficient inspection of transmission lines.
- (2)
- Automated and intelligent tree risk detection methods based on 3D point clouds focus on how to use different heights of spatial segmentation methods, different neighborhood space determination methods, and different point cloud index structures to achieve the rapid point-to-point or point-to-line safety distance calculation. However, they ignore the obvious spatial distribution features of transmission lines and the actual situation, in which the number of tree risk points is small, resulting in a large number of non-essential safety distance calculations and judgments.
- (1)
- The local dimensional feature probability model of a point cloud under the restriction of minimum information entropy is proposed to realize the accurate extraction of power lines, and the method still has good applicability for complex scenarios.
- (2)
- The cloth simulation filtering (CSF) algorithm [48] and region growth method based on the neighborhood sharing degree are used to achieve an accurate distinction between ground wires and conductors.
- (3)
- The candidate area of tree risk points centered on the conductor reconstruction curve based on a catenary-linear equation is constructed, and a safety distance grading calculation strategy is proposed to realize the accurate detection of tree risk points.
2. Methods
2.1. Overall Architecture
2.2. Spatial Distribution Feature Analysis of Transmission Line
- (1)
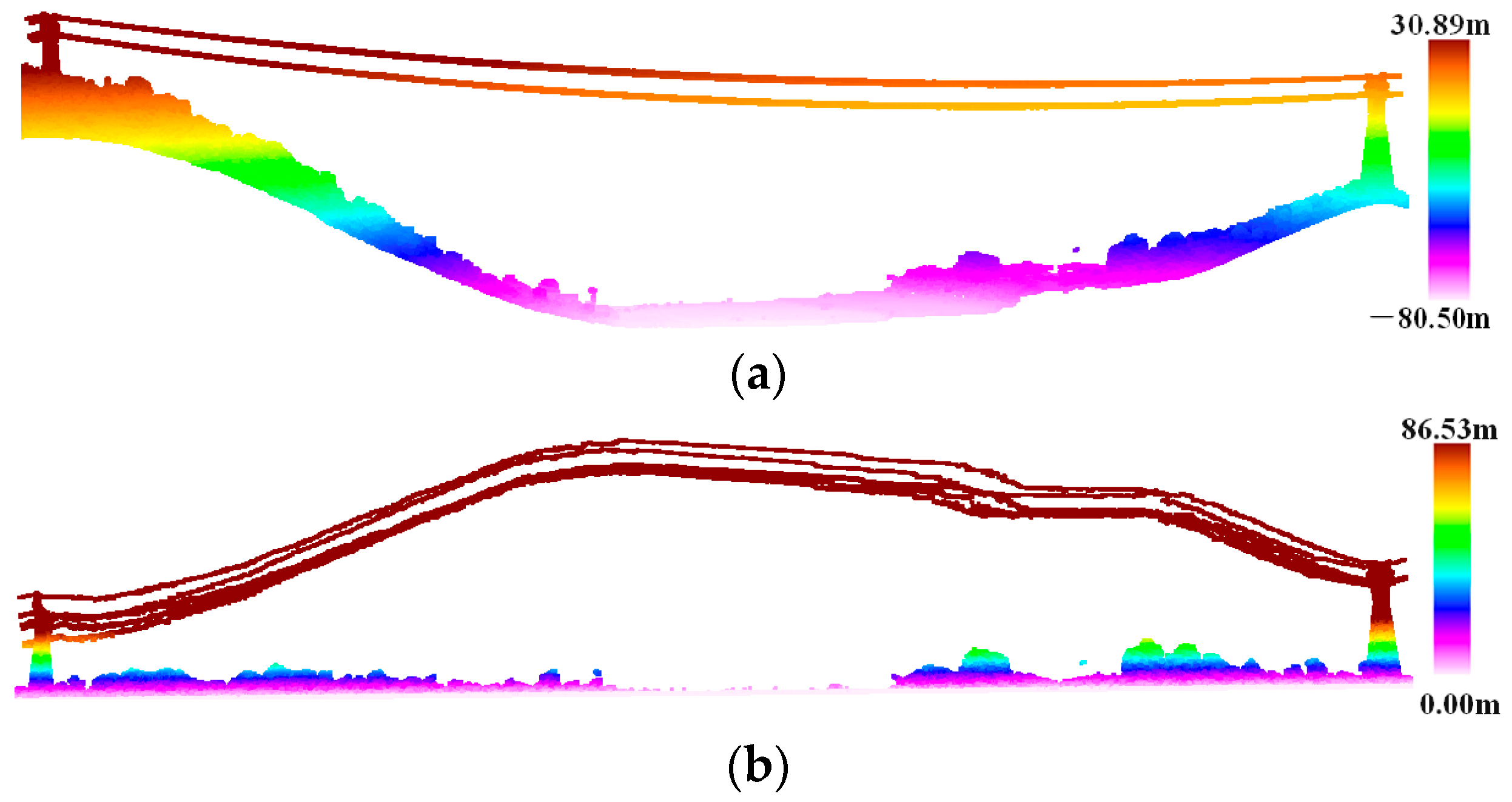
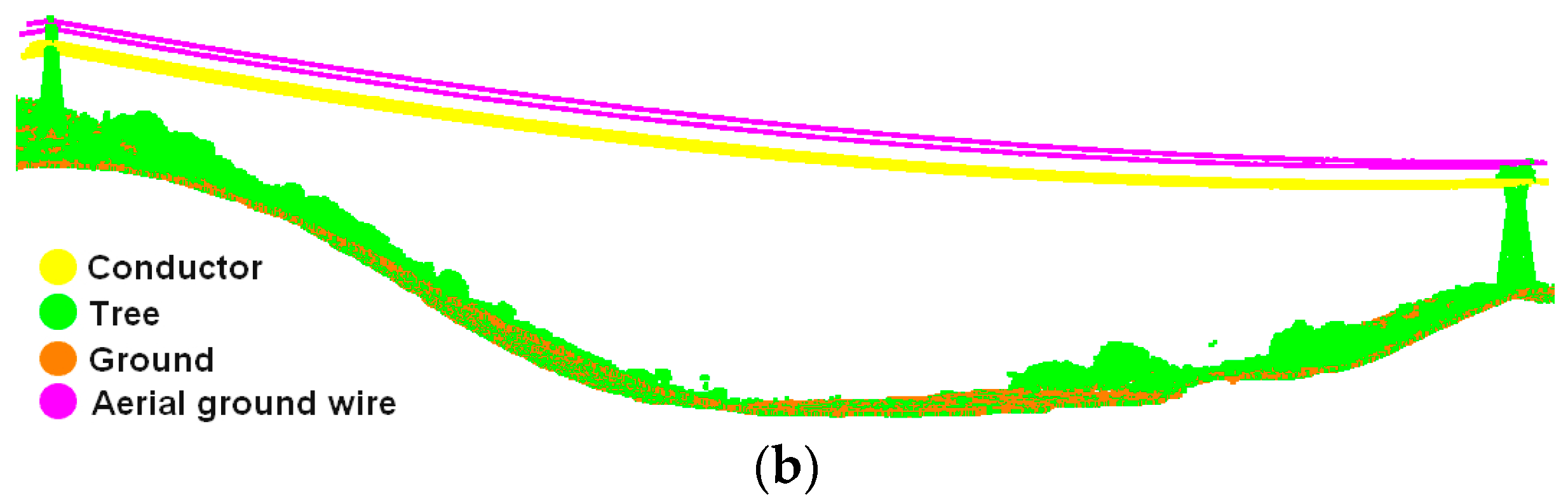
- As shown in Figure 2a, power lines are suspended from the tower in the form of a catenary and the ground wires are above the conductors. The distances between different power lines are kept fixed and distributed approximately in parallel. A single power line is closely connected end to end in the horizontal direction with obvious linear features. However, the vertical distribution of the power line is extremely discontinuous.
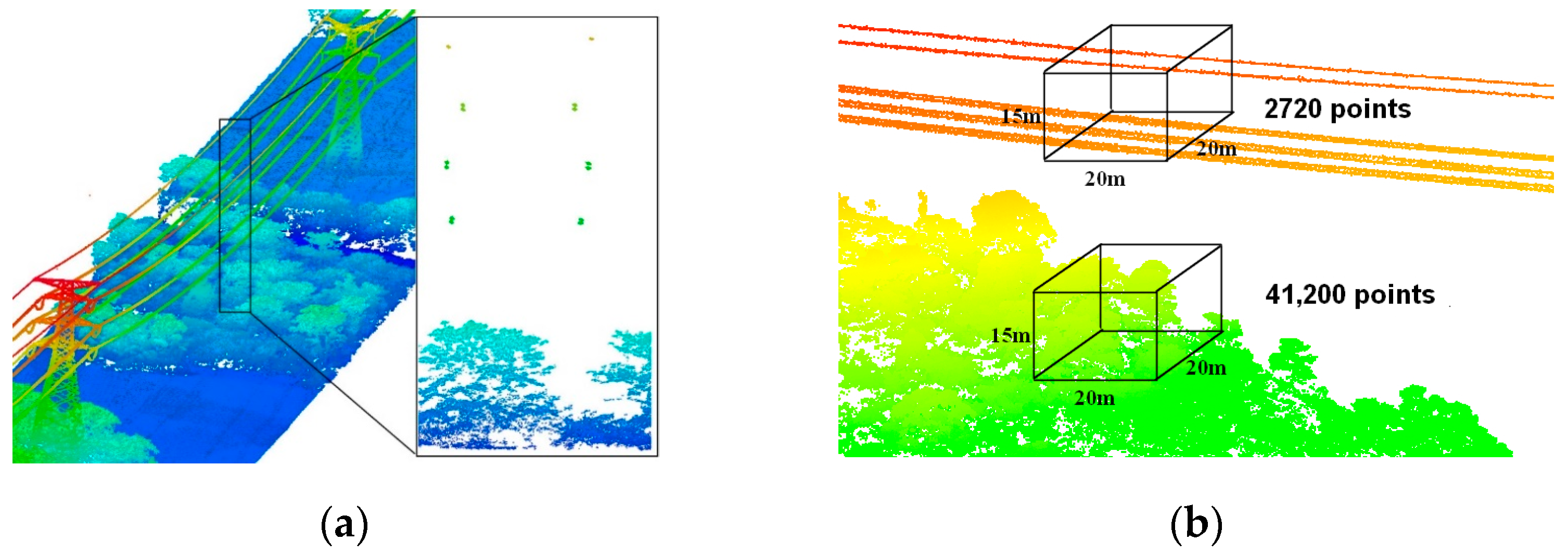
- (2)
- Within the same size area, there are significantly more vegetation points than power line points, which means that when counting some of the indicators related to the point coordinates or numbers, the vegetation points are given more weight. Randomized comparisons of power line point density and vegetation point density are both applicable, as shown in Figure 2b.
2.3. Power Line Extraction
2.3.1. Coarse Extraction of Power Lines Based on Height Difference
- (1)
- In order to ensure the integrity of the transmission line, the original point cloud width is much larger than the transmission line corridor width. Therefore, the point cloud needs to be clipped according to the coordinates of the pylons already known by the State Grid Corporation of China and the specified corridor width, which is generally 100 m. The original point cloud is divided into multiple point clouds that are end to end, each containing two adjacent towers, power lines, and other features, as shown in Figure 3.
- (2)
- In order to eliminate the influence of terrain undulation, facilitate subsequent point elevation statistics, and distinguish ground and non-ground points, an improved progressive TIN densification filtering algorithm is used to obtain the terrain of the transmission line corridor [49]; then, the point cloud is elevation normalized based on the ground point, as shown in Figure 4.
- (3)
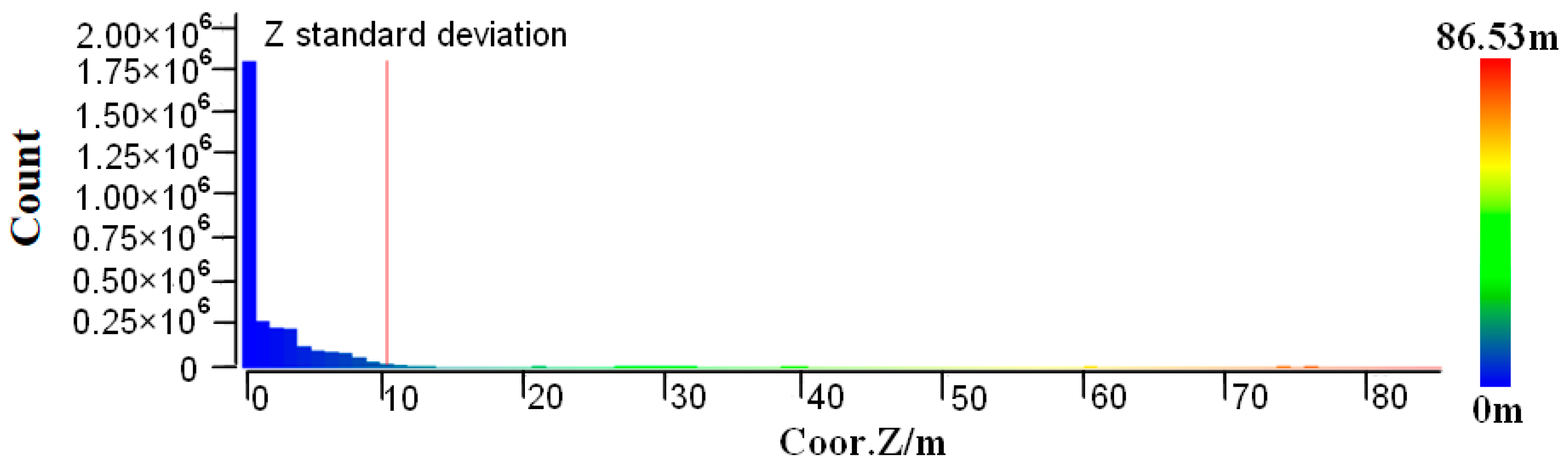
- Starting from the ground, the number of non-ground points corresponding to different elevation ladders is counted with 1 m as the step length. The reason for the 1 m step length is that there is more low vegetation and less medium and high vegetation, and vegetation that is 0–1 m above ground level is considered low vegetation. As shown in Figure 5, the elevation of the points is mainly within 10 m; this predominantly comprises low vegetation close to the ground, with the most points within 0–1 m. However, there are very few points with an elevation greater than 10 m; these are mainly power line points and pylon points.
- (4)
- The Z standard deviation [50] of the non-ground points is calculated using Equation (1).
- (5)
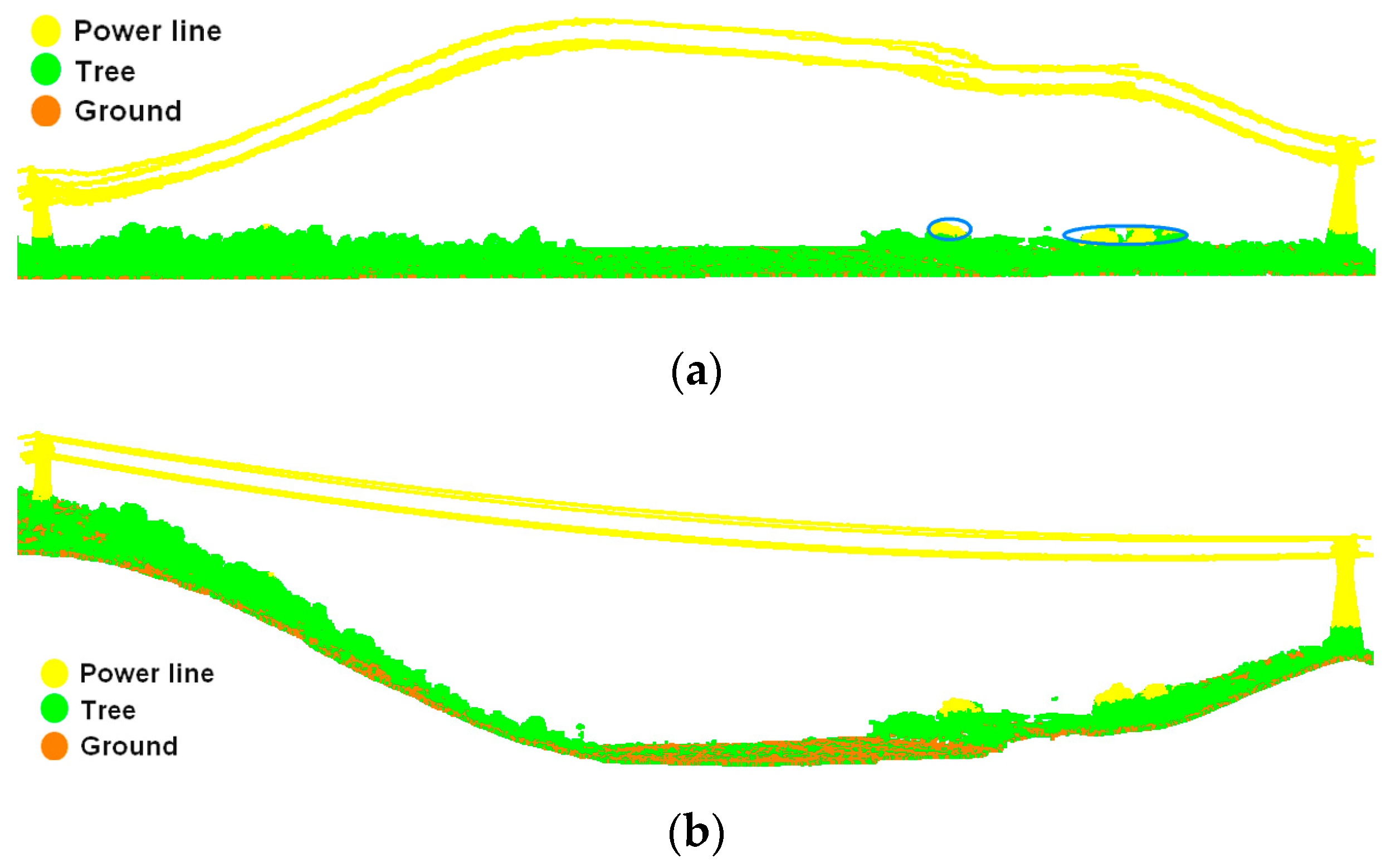
- Points with elevations greater than the Z standard deviation are classified as power line candidate points, and converse situations are classified as vegetation points. The effect of power line coarse extraction is shown in Figure 6; all power line candidate points have been extracted completely and accurately, while a very small number of vegetation canopy points have also been categorized as power lines, such as the points in the blue circle in Figure 6a. This misclassification will be improved in the subsequent power line refined extraction.
- (6)
- Elevation-normalized point clouds are denormalized based on ground points to restore the original elevation of points, as shown in Figure 6b.
2.3.2. Refined Extraction of Power Lines Based on Local Dimensional Features Probability Model
- When , the local feature of the point cloud is one-dimensional linear;
- When , the local feature of the point cloud is two-dimensional planar;
- When , the local feature of the point cloud is three-dimensional spherical.
2.4. Distinction between Aerial Ground Wires and Conductors
2.4.1. Coarse Extraction of Aerial Ground Wires Based on CSF
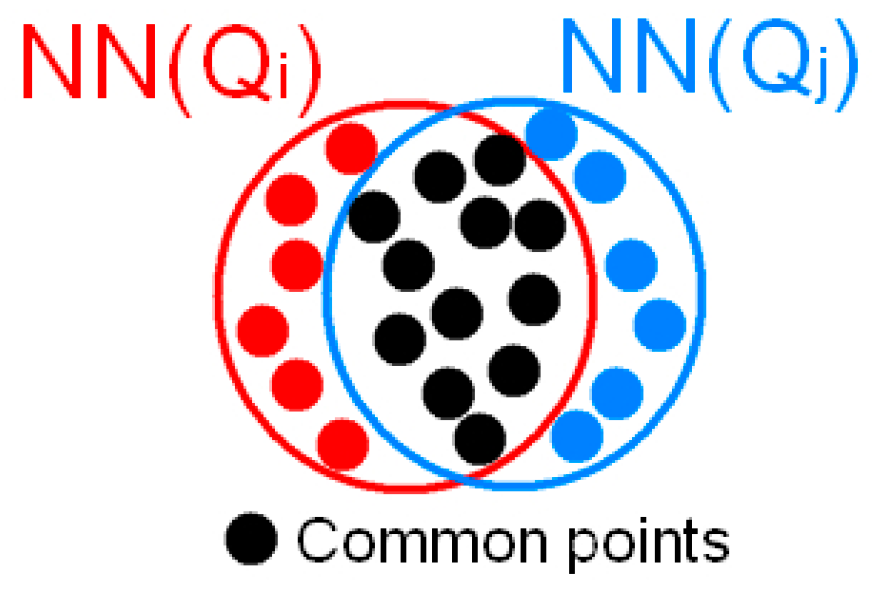
2.4.2. Refined Clustering of Ground Wires Based on Degree of Neighborhood Sharing
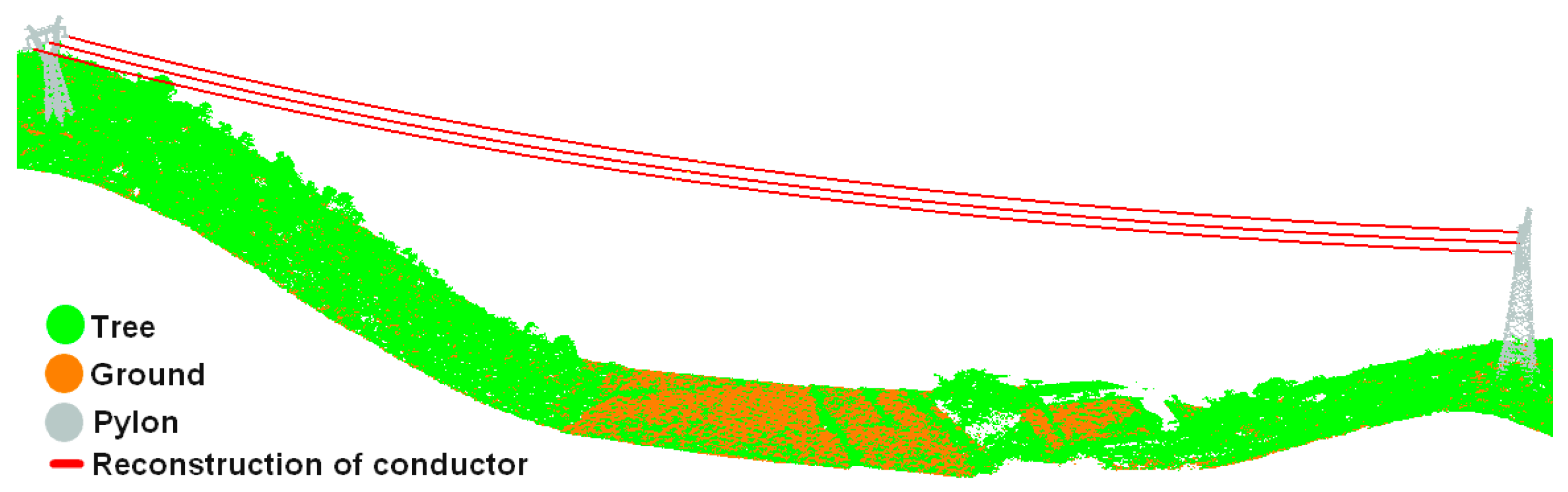
2.5. 3D Reconstruction of Conductors
2.5.1. Linear Equation
2.5.2. Catenary Equation
2.6. Tree Risk Detection
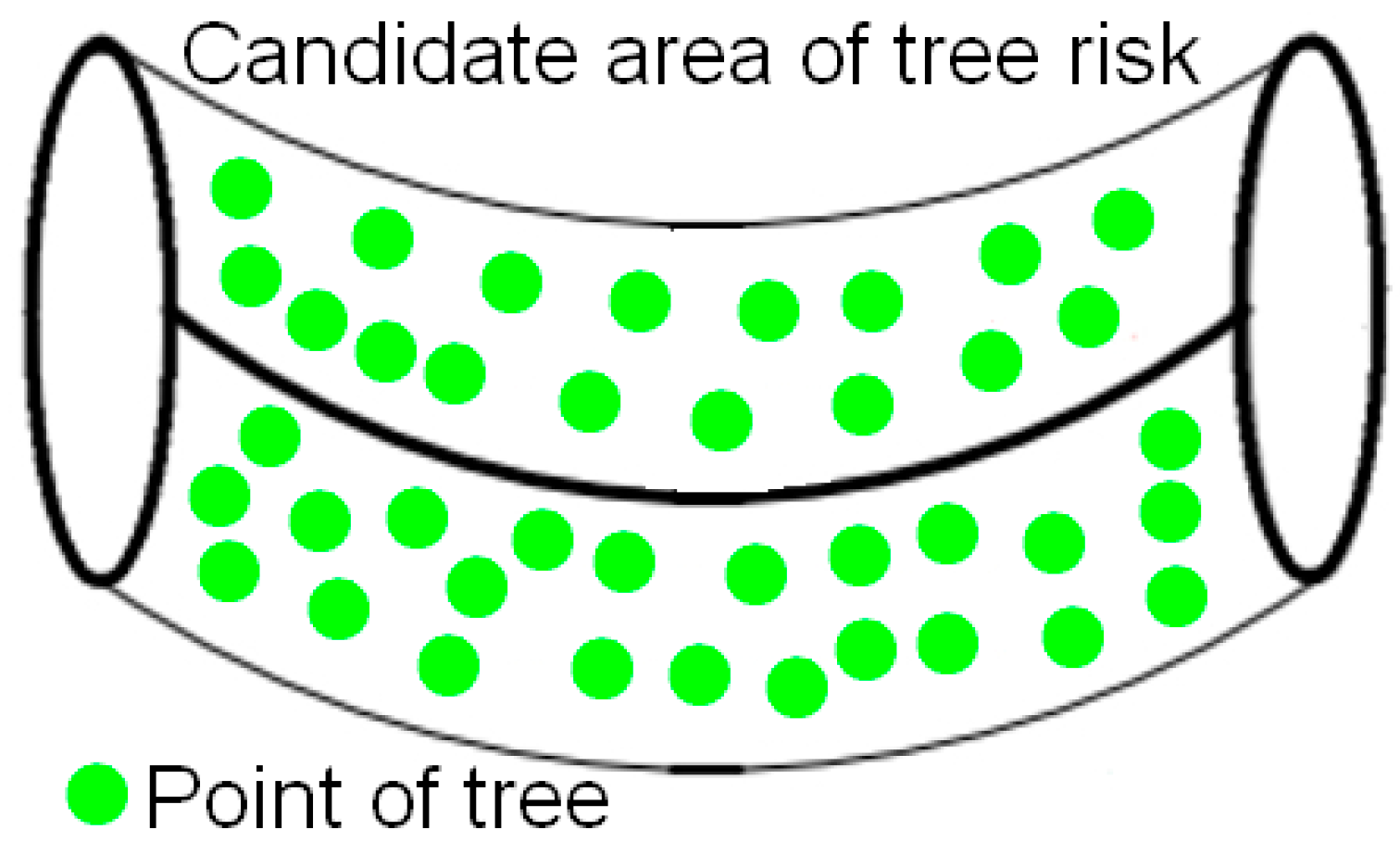
2.6.1. Construction of Tree Risk Candidate Area
2.6.2. Rough Calculation of Safety Distance Based on Grid
2.6.3. Accurate Calculation of Point-to-Point Safety Distance
3. Experiments and Discussion
3.1. Datasets
3.2. Evaluation Methods
3.2.1. Evaluation of the Classification Accuracy of Ground Wires and Conductor Points
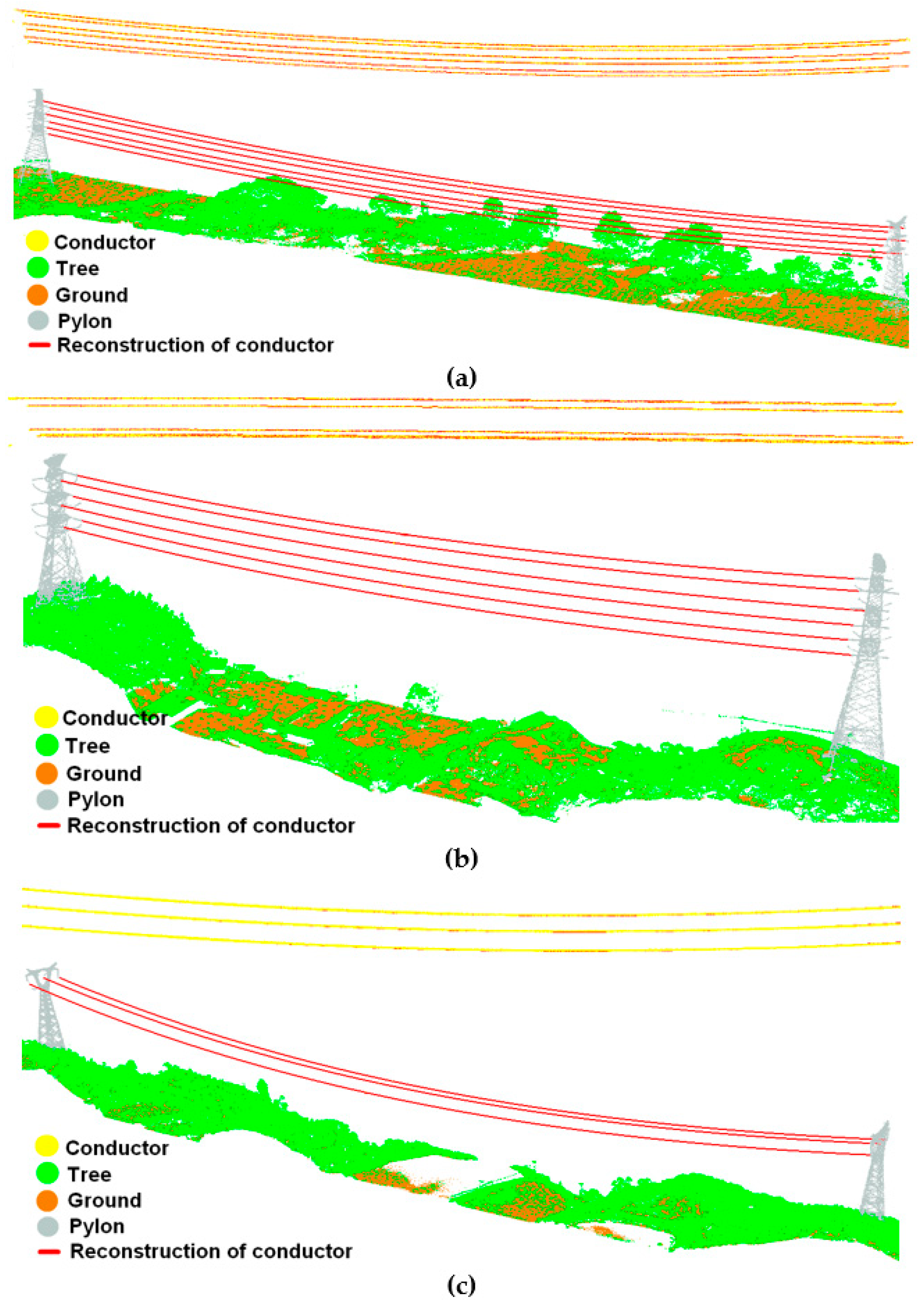
3.2.2. Evaluation of the Spatial Position Accuracy of Conductor 3D Reconstruction
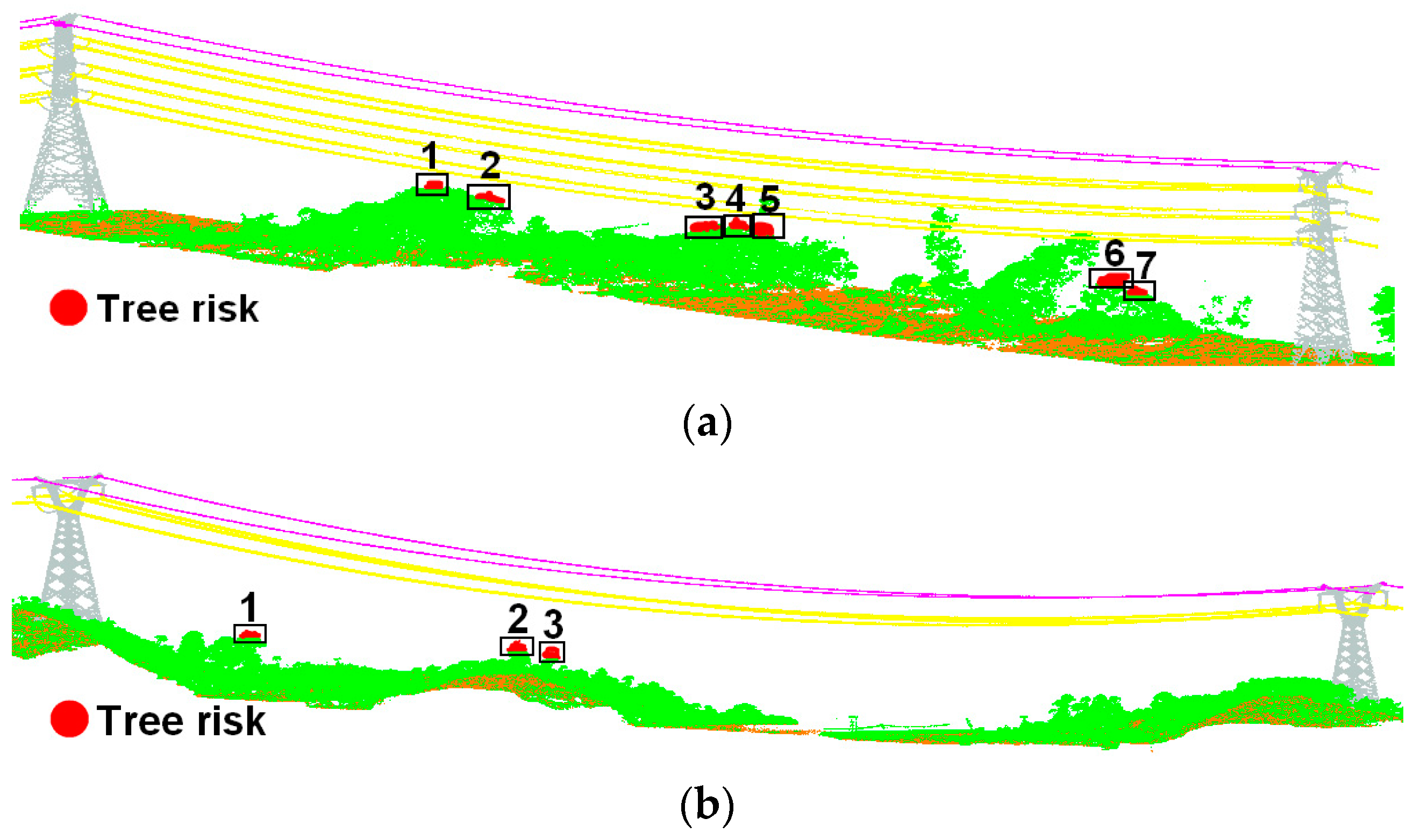
3.2.3. Evaluation Accuracy of Tree Risk Detection
3.3. Experimental Results
3.3.1. The Classification Effect and Accuracy of Ground Wires and Conductor Points
3.3.2. Spatial Position Accuracy of Conductor 3D Reconstruction
3.3.3. The Accuracy of Tree Risk Detection
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Matikainen, L.; Lehtomaki, M.; Ahokas, E.; Hyyppa, J.; Karjalainen, M.; Jaakkola, A.; Kukko, A.; Heinonen, T. Remote Sensing Methods for Power Line Corridor Surveys. ISPRS J. Photogramm. Remote Sens. 2016, 119, 10–31. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, X.; Jiao, Y.J.; Yang, X.; Xu, H.H. Method for Real-time Reconstruction of a Transmission Line Based on the LiDAR Point Cloud Data of a Partial Line Segment. Sustain. Energy Technol. Assess. 2023, 57, 103180. [Google Scholar] [CrossRef]
- Liu, J.X.; Wang, S.; Zhu, Q.Q.; Zhao, C.C.; Zhang, G.B.; Zhao, Z.J.; Lu, X.C. Overhead Transmission Line Condition Assessment Based on Intention Classification and Slot Filling Using Optimized BERT Model. Energy Rep. 2023, 9, 838–846. [Google Scholar] [CrossRef]
- Hao, J.P.; Li, X.G.; Wu, H.; Yang, K.; Zeng, Y.M.; Wang, Y.; Pan, Y.J. Extraction and Analysis of Tree Canopy Height Information in High-voltage Transmission-line Corridors by Using Integrated Optical Remote Sensing and LiDAR. Geod. Geodyn. 2023, 14, 292–303. [Google Scholar] [CrossRef]
- Ahmed, M.F.; Mohanta, J.C.; Nayab Zafar, M. Development of Smart Quadcopter for Autonomous Overhead Power Transmission line Inspection. Mater. Proceeding 2022, 51, 261–268. [Google Scholar] [CrossRef]
- Schofiled, O.B.; Iversen, N.; Ebeid, E. Autonomous Power Line Detection and Tracking System Using UAVs. Microprocess. Microsyst. 2022, 94, 104609. [Google Scholar] [CrossRef]
- Liu, X.Y.; Miao, X.R.; Jiang, H.; Chen, J. Data Analysis in Visual Power line Inspection: An In-depth Review of Deep Learning for Component Detection and Fault Diagnosis. Annu. Rev. Control. 2022, 50, 253–277. [Google Scholar] [CrossRef]
- Wang, Y.J.; Chen, Q.; Liu, L.; Li, X.; Sangaiah, A.K.; Li, K. Systematic Comparison of Power Line Classification Method from ALS and MLS Point Cloud Data. Remote Sens. 2018, 10, 1222. [Google Scholar] [CrossRef]
- Rouseel, J.R.; Achim, A.; Auty, D. Classification of High-voltage Power Line Structures in Low Density ALS Data Acquired Over Broad Non-urban areas. Peerj Comput. Sci. 2021, 7, e672. [Google Scholar] [CrossRef]
- Chen, C.; Yang, B.; Song, S.; Peng, X.; Huang, R. Automatic Clearance Anomaly Detection for Transmission Line Corridors Utilizing UAV-Borne LiDAR Data. Remote Sens. 2018, 10, 613. [Google Scholar] [CrossRef]
- Huang, Y.C.; Du, Y.L.; Shi, W.X. Fast and Accurate Power Line Corridor Survey Using Spatial Line Clustering of Point Cloud. Remote Sens. 2021, 13, 1571. [Google Scholar] [CrossRef]
- Ma, W.F.; Wang, C.; Wang, J.L.; Zhou, J.C.; Ma, Y.Y. Extraction of Power Lines from Laser Point Cloud Based on Residual Clustering Method. Acta Geod. Cartogr. Sin. 2020, 49, 883–892. [Google Scholar]
- Huang, X.F.; Li, N.; Zhang, F.; Wan, W.H. Automatic Power Lines Extraction Method from Airborne LiDAR Point Cloud. Geomat. Inf. Sci. Wuhan Univ. 2015, 40, 1563–1569. [Google Scholar]
- Munir, N.; Awrangieb, M.; Stantic, B. Power Line Extraction and Reconstruction Methods from Laser Scanning Data: A Literature Review. Remote Sens. 2023, 15, 973. [Google Scholar] [CrossRef]
- Azevedo, F.; Dias, A.; Almeida, J.; Oliveira, A.; Ferreira, A.; Santos, T.; Martins, A.; Silva, E. Lidar-based Real-time Detection and Modeling of Power Lines for Unmanned Aerial Vehicles. Sensors 2019, 19, 1812. [Google Scholar] [CrossRef] [PubMed]
- Awrangjeb, M. Extraction of Power Line Pylons and Wires Using Airborne LiDAR Data at Different Height Levels. Remote Sens. 2019, 11, 1798. [Google Scholar] [CrossRef]
- Zou, K.; Jiang, Z. Power Line Extraction Framework Based on Edge Structure and Scene Constraints. Remote Sens. 2022, 14, 4575. [Google Scholar] [CrossRef]
- Lewis, B.; Steven, M.; Tobias, L.; Carl, R. Power Line Detection Using Hough Transform and Line Tracking Techniques. In Proceedings of the 2016 International Conference on Image and Vision Computing New Zealand (IVCNZ), Palmerston North, New Zealand, 21–22 November 2016; pp. 1–6. [Google Scholar]
- Yu, J.; Mu, C.; Feng, Y.M.; Dou, Y.J. Study on Power Line Extraction from Airborne LiDAR Point Cloud Data. Geomat. Inf. Sci. Wuhan. Univ. 2011, 36, 1275–1279. [Google Scholar]
- Guan, H.Y.; Yu, Y.T.; Li, J.; Ji, Z.; Zhang, Q. Extraction of Power-transmission Lines from Vehicle-borne LiDAR Data. Int. J. Remote Sens. 2016, 37, 229–247. [Google Scholar] [CrossRef]
- Chen, D.Q.; Guo, X.H.; Huang, P.; Li, F.H. Safety Distance Analysis of 500Kv Transmission Line Tower UAV Patrol Inspection. IEEE Lett. Electromagn. Compat. Pract. Appl. 2020, 2, 124–128. [Google Scholar] [CrossRef]
- Jung, J.; Che, E.; Olsen, M.J.; Shafer, K.C. Automated and efficient powerline extraction from laser scanning data using a voxel-based subsampling with hierarchical approach. Photogramm. Remote Sens. 2020, 163, 343–361. [Google Scholar] [CrossRef]
- Wang, P.H.; Xi, X.H.; Wang, C.; Xia, S.B. Study on Power Line Fast Extraction Based Airborne LiDAR Data. Sci. Surv. Mapp. 2017, 42, 154–158. [Google Scholar]
- Mclauhlin, R.A. Extracting Transmission Lines from Airborne LiDAR Data. IEEE Geosci. Remote Sens. Lett. 2006, 3, 222–226. [Google Scholar] [CrossRef]
- Liu, Z.J.; Liang, J.; Zhang, J.X. Power Lines Extraction from Airborne LiDAR Data Using Spatial Domain Segmentation. J. Remote Sens. 2014, 18, 61–76. [Google Scholar]
- Liang, C.; Tong, L.; Wang, Y.; Li, M. Extraction of Urban Power Lines from Vehicle-Borne LiDAR Data. Remote Sens. 2014, 6, 3302–3320. [Google Scholar]
- De Geyter, S.; Bassier, M.; Vergauwen, M. Automated training data creation for semantic segmentation of 3D point clouds. Arch.Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 46, 59–67. [Google Scholar]
- Gharineiat, Z.; Tarsha Kurdi, F.; Campbell, G. Review of Automatic Processing of Topography and Surface Feature Identification LiDAR Data Using Machine Learning Techniques. Remote Sens. 2022, 14, 4685. [Google Scholar] [CrossRef]
- Kim, H.B.; Sohn, G. Point-based Classification of Power Line Corridor Scene Using Random Forest. Photogramm. Eng. Remote Sens. 2013, 79, 821–833. [Google Scholar] [CrossRef]
- Fonseca, G.A.; Ferreica, D.D.; Costa, F.B.; Almeida, A.R. Fault Classification in Transmission Lines Using Random Forest and Notch Filter. J. Control Autom. Electr. Syst. 2022, 33, 598–609. [Google Scholar] [CrossRef]
- Guo, B.; Huang, X.; Zhang, F.; Sohn, G. Classification of Airborne Laser Scanning Data Using JointBoost. ISPRS J. Photogramm. Remote Sens. 2015, 100, 71–83. [Google Scholar] [CrossRef]
- Yang, J.; Kang, Z.; Zhou, Y. A Robust Model Fitting-based Method for Transmission Line Extraction from Airborne LiDAR Point Cloud Data. J. Geod. Geoinf. Sci. 2021, 4, 60. [Google Scholar]
- Ni, H.; Lin, X.; Zhang, J. Classification of ALS Point Cloud with Improved Point Cloud Segmentation and Random forests. Remote Sens. 2017, 9, 288. [Google Scholar] [CrossRef]
- Zhou, R.Q.; Xu, Z.H.; Peng, C.G.; Zhang, F.; Jiang, W.S. A JointBoost-based Classification Method of High Voltage Transmission Corridor from Airborne LiDAR Point cloud. Sci. Surv. Mapp. 2019, 44, 21–27. [Google Scholar]
- Liu, Y.X.; Aleksandrov, M.; Zlatanova, S.S.; Zhang, J.J.; Mo, F.; Chen, X.J. Classification of Power Facility Point Clouds from Unmanned Aerial Vehicles Based on Adaboost and Topological Constraints. Sensors 2019, 19, 4717. [Google Scholar] [CrossRef] [PubMed]
- Venkata, P.; Pandya, V.; Vala, K.; Sant, A.V. Support Vector Machine for Fast Fault Detection and Classification in Modern Power Systems Using Quarter Cycle Data. Energy Rep. 2022, 8, 92–98. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, C.S.; Tian, S.W.; Lu, B.L.; Zhang, L.P.; Ning, X.; Bai, X. Deep learning-based 3D Point Cloud Classification: A Systematic Survey and Outlook. Displays 2023, 79, 102456. [Google Scholar] [CrossRef]
- Fang, L.N.; You, Z.L.; Shen, G.X.; Chen, Y.P.; Li, J.R. A Joint Deep Learning Network of Point Clouds and Multiple Views for Roadside Object Classification from Lidar Point Clouds. ISPRS J. Photogramm. Remote Sens. 2022, 193, 115–136. [Google Scholar] [CrossRef]
- Lai, H.B.; Sia, C.W.; Lim, K.H.; Phang, J.T.S. Deep Learning Neural Networks for 3D Point Clouds Shape Classification: A Survey. In Proceedings of the 2022 International Conference on Green Energy, Computing and Sustainable Technology (GECOST), Miri Sarawak, Malaysia, 26–28 October 2022; pp. 394–398. [Google Scholar]
- Yang, J.S.; Huang, Z.J.; Huang, M.C.; Zeng, X.X.; Li, D.; Zhang, Y. Power Line Corridor LiDAR Point Cloud Segmentation Using Convolutional Neural Network. In Proceedings of the Chinese Conference on Pattern Recognition and Computer Vision (PRCV), Xi’an, China, 8–11 November 2019; Volume 11857, pp. 160–171. [Google Scholar]
- Qi, C.R.; Su, H.; Nießner, M.; Dai, A.; Guibas, L.J. Volumetric and Multi-view CNNs for Object Classification on 3D Data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5648–5656. [Google Scholar]
- Zhang, Z.; Hua, B.; Yeung, S. ShellNet: Efficient Point Cloud Convolutional Neural Networks Using Concentric Shells Statistics. In Proceedings of the International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1607–1616. [Google Scholar]
- Walker, M.; Dahle, G.A. Likelihood of Failure of Trees Along Electrical Utility Rights-of-Way: A Literature Review. Arboric. Urban For. 2023, 49, 144–156. [Google Scholar] [CrossRef]
- Guggenmoos, S. Effects of tree mortality on power line security. J. Arboric. 2003, 29, 181–196. [Google Scholar] [CrossRef]
- Walker, M.; Dahle, G.A. Literature Review of Unmanned Aerial Systems and LIDAR with Application to Distribution Utility Vegetation Management. Arboric. Urban For. 2020, 48, 242–257. [Google Scholar] [CrossRef]
- Dihkan, M.; Mus, E. Automatic Detection of Power Transmission Lines and Risky Object Locations Using UAV LiDAR Data. Arab. J. Geosci. 2021, 14, 567. [Google Scholar] [CrossRef]
- Chen, C.; Peng, X.Y.; Song, S.; Wang, K.; Qian, J.J.; Yang, B.S. Safety Distance Diagnosis of Large-Scale Transmission Line Corridor Inspection Based on LiDAR Point Cloud Collected With UAV. Power Syst. Technol. 2017, 41, 76–79. [Google Scholar]
- Zhang, W.M.; Qi, J.B.; Wan, P.; Wang, H.T.; Xie, D.H.; Wang, X.Y.; Yan, G.J. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Zhao, X.Q.; Guo, Q.H.; Su, Y.J.; Xue, B.L. Improved Progressive TIN Densification Filtering Algorithm for Airborne LiDAR Data in Forested Areas. ISPRS J. Photogramm. Remote Sens. 2016, 117, 79–91. [Google Scholar] [CrossRef]
- Rani, P.; Chen, S.M.; Mishra, A.R. Multiple attribute decision making based on MAIRCA, standard deviation-based method, and Pythagorean fuzzy sets. Inf. Sci. 2023, 644, 119274. [Google Scholar] [CrossRef]
- Duan, Y.; Yang, C.C.; Chen, H.; Yan, W.Z.; Li, H.B. Low-complexity Point Cloud Denoising for LiDAR by PCA-based Dimension Reduction. Opt. Commun. 2021, 482, 126567. [Google Scholar] [CrossRef]
- Guan, H.; Gordon, R. A projection access order for speedy convergence of ART (algebraic reconstruction technique): A multilevel scheme for computed tomography. Phys. Med. Biol. 1994, 39, 2005–2022. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, J.; Denis, F.; Coeurjolly, D.; Dupont, F.; Trassoudaine, L.; Checchin, P. Robust Normal Vector Estimation in 3D Point Clouds through Iterative Principal Component Analysis. ISPRS J. Photogramm. Remote Sens. 2020, 163, 18–35. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Li, W.; Luo, Z.P.; Xiao, Z.L.; Chen, Y.P.; Wang, C. A CGN-based Method for Extracting Power Lines and Pylons from Airborne LiDAR Data. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar]
- Miao, Y.L.; Li, S.; Wang, L.Y.; Li, H.; Qiu, R.C.; Zhang, M. A single plant segmentation method of maize point cloud based on Euclidean clustering and K-means clustering. Comput. Electron. Agric. 2023, 210, 107951. [Google Scholar] [CrossRef]
- Khaloo, A.; Lattanzi, D. Robust normal estimation and region growing segmentation of infrastructure 3D point cloud models. Adv. Eng. Inform. 2017, 34, 1–16. [Google Scholar] [CrossRef]
- Chen, H.; Liang, M.; Liu, W.Q.; Wang, W.N.; Liu, P.X.P. An Approach to Boundary Detection for 3D Point Clouds Based on DBSCAN Clustering. Pattern Recognit. 2022, 124, 108431. [Google Scholar] [CrossRef]
- Odibat, Z.M.; Shawagfeh, N.T. Generalized Taylor’s Formula. Appl. Math. Comput. 2007, 186, 286–293. [Google Scholar] [CrossRef]
- Arjomandi-Lari, M.; Karimi, M. Array auto-calibration using a generalized least-squares method. AEU Int. J. Electron. Commun. 2019, 106, 20–31. [Google Scholar] [CrossRef]
- Fränti, P.; Mariescu-Istodor, R. Soft precision and recall. Pattern Recognit. Lett. 2023, 167, 115–121. [Google Scholar] [CrossRef]











| Radius | Information Entropy | Probability of Being One-Dimensional | Probability of Being Two-Dimensional | Probability of Being Three-Dimensional |
|---|---|---|---|---|
| 0.1 m | 1.108 | 0.157 | 0.441 | 0.402 |
| 0.2 m | 0.803 | 0.673 | 0.256 | 0.071 |
| 0.3 m | 0.357 | 0.823 | 0.119 | 0.058 |
| 0.4 m | 0.163 | 0.966 | 0.029 | 0.005 |
| 0.5 m | 0.565 | 0.177 | 0.021 | 0.802 |
| 0.6 m | 0.537 | 0.149 | 0.026 | 0.825 |
| 0.7 m | 0.507 | 0.025 | 0.134 | 0.841 |
| Classification | Count | SD | Maximum | Minimum |
|---|---|---|---|---|
| Power line | 5000 | 0.235° | 4.393° | 0° |
| Pylon | 5000 | 13.061° | 32.415° | 12.337° |
| Vegetation | 5000 | 18.172° | 43.994° | 14.042° |
| Voltage Level | Terrain | Distance | Number of Conductors |
|---|---|---|---|
| 110 kV | flat | 376 m | 6 |
| 220 kV | hill | 227 m | 6 |
| 500 kV | mountain | 591 m | 3 |
| 110 kV | 220 kV | 500 kV | |
|---|---|---|---|
| TP | 63,587 | 89,345 | 159,859 |
| FN | 638 | 785 | 1076 |
| FP | 1009 | 1780 | 2347 |
| Precision | 0.9844 | 0.9805 | 0.9855 |
| Recall | 0.9900 | 0.9912 | 0.9933 |
| F-score | 0.9880 | 0.9858 | 0.9894 |
| 110 kV | 220 kV | 500 kV | |
|---|---|---|---|
| TP | 18,521 | 15,793 | 21,776 |
| FN | 138 | 137 | 142 |
| FP | 309 | 326 | 334 |
| Precision | 0.9836 | 0.9798 | 0.9849 |
| Recall | 0.9926 | 0.9914 | 0.9935 |
| F-score | 0.9881 | 0.9856 | 0.9892 |
| Voltage Level | RMSE/cm | Emax/cm | Emin/cm |
|---|---|---|---|
| 110 kV | 2.76 | 5.34 | 1.91 |
| 220 kV | 3.35 | 6.52 | 1.74 |
| 500 kV | 3.67 | 7.13 | 2.64 |
| Voltage Level | Consistency of Quantity | Quantities of RVs | Quantities of Tree Risk Points Detected Using Proposed Method | MAE/cm | Efficiency (Point to Point) | Efficiency (Proposed Method) |
|---|---|---|---|---|---|---|
| 110 kV | ✓ | 7 | 7 | 6.47 | 1.769 s | 0.663 s |
| 220 kV | 0 | 0 | 0 | 0 | 1.827 s | 0.729 s |
| 500 kV | ✓ | 3 | 3 | 5.53 | 2.003 s | 0.804 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, S.; Zhang, Z.; Niu, Y.; Li, H.; Zhang, Q. Power Line Extraction and Tree Risk Detection Based on Airborne LiDAR. Sensors 2023, 23, 8233. https://doi.org/10.3390/s23198233
Xi S, Zhang Z, Niu Y, Li H, Zhang Q. Power Line Extraction and Tree Risk Detection Based on Airborne LiDAR. Sensors. 2023; 23(19):8233. https://doi.org/10.3390/s23198233
Chicago/Turabian StyleXi, Siyuan, Zhaojiang Zhang, Yufen Niu, Huirong Li, and Qiang Zhang. 2023. "Power Line Extraction and Tree Risk Detection Based on Airborne LiDAR" Sensors 23, no. 19: 8233. https://doi.org/10.3390/s23198233
APA StyleXi, S., Zhang, Z., Niu, Y., Li, H., & Zhang, Q. (2023). Power Line Extraction and Tree Risk Detection Based on Airborne LiDAR. Sensors, 23(19), 8233. https://doi.org/10.3390/s23198233






