Sensitivity of Model-Based Predictions of Post-TKA Kinematic Behavior to Residual Errors in Ultrasound-Based Knee Collateral Ligament Strain Assessment
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Data Collection
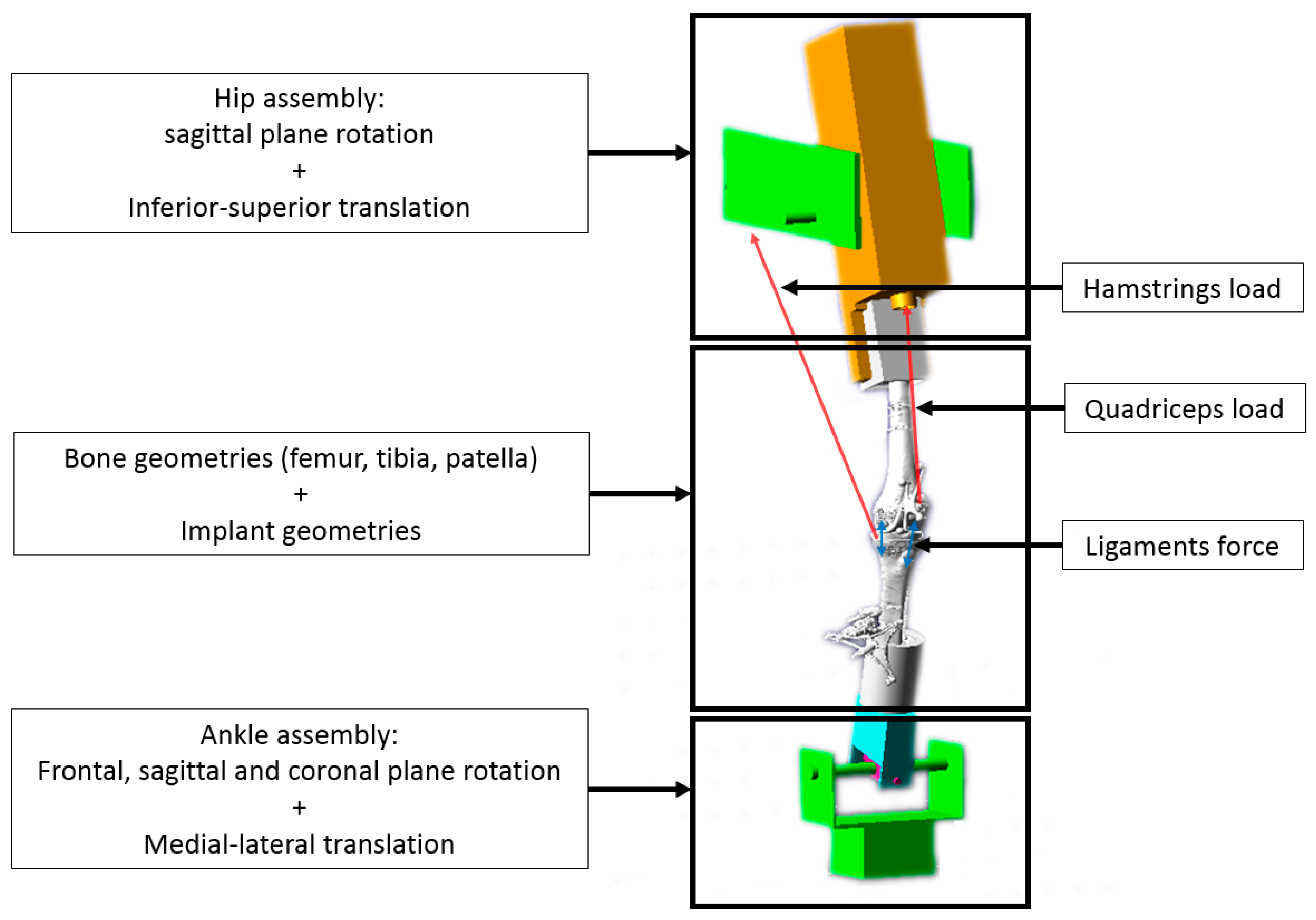
2.2. Computer Modelling
2.3. Sensitivity Analysis
2.4. Statistics
3. Results
3.1. Validity of Computer Simulations
3.2. Sensitivity Analyses
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pabinger, C.; Lothaller, H.; Geissler, A. Utilization rates of knee-arthroplasty in OECD countries. Osteoarthr. Cartil. 2015, 23, 1664–1673. [Google Scholar] [CrossRef] [PubMed]
- McCalden, R.W.; Robert, C.E.; Howard, J.L.; Naudie, D.D.; McAuley, J.P.; MacDonald, S.J. Comparison of outcomes and survivorship between patients of different age groups following TKA. J. Arthroplast. 2013, 28, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Sharkey, P.F.; Lichstein, P.M.; Shen, C.; Tokarski, A.T.; Parvizi, J. Why Are Total Knee Arthroplasties Failing Today—Has Anything Changed After 10 Years? J. Arthroplast. 2014, 29, 1774–1778. [Google Scholar] [CrossRef] [PubMed]
- Le, D.H.; Goodman, S.B.; Maloney, W.J.; Huddleston, J.I. Current modes of failure in TKA: Infection, instability, and stiffness predominate. Clin. Orthop. Relat. Res. 2014, 472, 2197–2200. [Google Scholar] [CrossRef] [PubMed]
- Gustke, K.A.; Golladay, G.J.; Roche, M.W.; Jerry, G.J.; Elson, L.C.; Anderson, C.R. Increased satisfaction after total knee replacement using sensor-guided technology. Bone Jt. J. 2014, 96, 1333–1338. [Google Scholar] [CrossRef]
- Shalhoub, S.; Lawrence, J.M.; Keggi, J.M.; Randall, A.L.; DeClaire, J.H.; Plaskos, C. Imageless, robotic-assisted total knee arthroplasty combined with a robotic tensioning system can help predict and achieve accurate postoperative ligament balance. Arthroplast. Today 2019, 5, 334–340. [Google Scholar] [CrossRef]
- Matsuda, S.; Lustig, S.; van der Merwe, W. (Eds.) Soft Tissue Balancing in Total Knee Arthroplasty; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Callaghan, J.J. The Adult Knee; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2003. [Google Scholar]
- Bendjaballah, M.; Shirazi-Adl, A.; Zukor, D. Finite element analysis of human knee joint in varus-valgus. Clin. Biomech. 1997, 12, 139–148. [Google Scholar] [CrossRef]
- Held, M.B.; Grosso, M.J.; Gazgalis, A.; Sarpong, N.O.; Boddapati, V.; Neuwirth, A.; Geller, J.A. Improved Compartment Balancing Using Robot-Assisted Total Knee Arthroplasty. Arthroplast. Today 2021, 7, 130–134. [Google Scholar] [CrossRef]
- Batailler, C.; Fernandez, A.; Swan, J.; Servien, E.; Haddad, F.S.; Catani, F.; Lustig, S. MAKO CT-based robotic arm-assisted system is a reliable procedure for total knee arthroplasty: A systematic review. Knee Surg. Sports Traumatol. Arthrosc. 2020, 29, 3585–3598. [Google Scholar] [CrossRef]
- Kinney, A.L.; Besier, T.F.; D’Lima, D.D.; Fregly, B.J. Update on Grand Challenge Competition to Predict in Vivo Knee Loads. J. Biomech. Eng. 2013, 135, 021012. [Google Scholar] [CrossRef]
- Fregly, B.J.; Besier, T.F.; Lloyd, D.G.; Delp, S.L.; Banks, S.A.; Pandy, M.G.; D’Lima, D.D. Grand challenge competition to predict in vivo knee loads. J. Orthop. Res. 2012, 30, 503–513. [Google Scholar] [CrossRef] [PubMed]
- Slane, L.C.; Bogaerts, S.; Thelen, D.G.; Scheys, L. Non-uniform deformation of the patellar tendon during passive knee flexion. J. Appl. Biomech. 2017, 34, 14–22. [Google Scholar] [CrossRef] [PubMed]
- Slane, L.C. Achilles Tendon Elasticity and Deformation Patterns in Young and Middle-Aged Adults Evaluated Using Quantitative Ultrasound Approaches. Ph.D. Thesis, University of Wisconsin-Madison, Madison, WI, USA, 2014. [Google Scholar]
- Slane, L.C.; Thelen, D.G. Achilles tendon displacement patterns during passive stretch and eccentric loading are altered in middle-aged adults. Med. Eng. Phys. 2015, 37, 712–716. [Google Scholar] [CrossRef]
- Slane, L.C.; Slane, J.A.; D’Hooge, J.; Scheys, L. The challenges of measuring in vivo knee collateral ligament strains using ultrasound. J. Biomech. 2017, 61, 258–262. [Google Scholar] [CrossRef] [PubMed]
- Gijsbertse, K.; Sprengers, A.; Beidokhti, H.N.; Nillesen, M.; de Korte, C.; Verdonschot, N. Strain imaging of the lateral collateral ligament using high frequency and conventional ultrasound imaging: An ex-vivo comparison. J. Biomech. 2018, 73, 233–237. [Google Scholar] [CrossRef] [PubMed]
- Dandois, F.; Taylan, O.; Bellemans, J.; D’hooge, J.; Vandenneucker, H.; Slane, L.; Scheys, L. Validated Ultrasound Speckle Tracking Method for Measuring Strains of Knee Collateral Ligaments In-Situ during Varus/Valgus Loading. Sensors 2021, 21, 1895. [Google Scholar] [CrossRef]
- Peersman, G.; Taylan, O.; Slane, J.; Vanthienen, B.; Verhaegen, J.; Anthonissen, L.; Van Lenthe, G.H.; Heyse, T.; Scheys, L. Does Unicondylar Knee Arthroplasty Affect Tibial Bone Strain? A Paired Cadaveric Comparison of Fixed- and Mobile-bearing Designs. Clin. Orthop. Relat. Res. 2020, 478, 1990–2000. [Google Scholar] [CrossRef]
- Beckers, L.; Dandois, F.; Ooms, D.; Berger, P.; Van Laere, K.; Scheys, L.; Vandenneucker, H. Assessment of in vivo bone activity patterns in medial mobile-bearing unicompartmental knee arthroplasty. Bone Jt. J. 2022, 104, 34–44. [Google Scholar] [CrossRef]
- Heyse, T.J.; Slane, J.; Peersman, G.; Dirckx, M.; van de Vyver, A.; Dworschak, P.; Fuchs-Winkelmann, S.; Scheys, L. Kinematics of a bicruciate-retaining total knee arthroplasty. Knee Surg. Sports Traumatol. Arthrosc. 2017, 25, 1784–1791. [Google Scholar] [CrossRef]
- Shah, D.S.; Taylan, O.; Verstraete, M.; Berger, P.; Vandenneucker, H.; Scheys, L. Can Intraoperative Intra-Articular Loads Predict Postoperative Knee Joint Laxity Following Total Knee Arthroplasty? A Cadaver Study with Smart Tibial Trays. Sensors 2021, 21, 5078. [Google Scholar] [CrossRef]
- Grood, E.S.; Suntay, W.J. A joint coordinate system for the clinical description of three-dimensional motions: Application to the knee. J. Biomech. Eng. 1983, 105, 136–144. [Google Scholar] [CrossRef] [PubMed]
- Victor, J.; Van Glabbeek, F.; Sloten, J.V.; Parizel, P.M.; Somville, J.; Bellemans, J. An Experimental Model for Kinematic Analysis of the Knee. J. Bone Jt. Surg. 2009, 91, 150–163. [Google Scholar] [CrossRef]
- Müller, J.H.; Razu, S.; Erdemir, A.; Guess, T.M. Prediction of patellofemoral joint kinematics and contact through co-simulation of rigid body dynamics and nonlinear finite element analysis. Comput. Methods Biomech. Biomed. Eng. 2020, 23, 718–733. [Google Scholar] [CrossRef] [PubMed]
- Müller, J.; Zakaria, T.; van der Merwe, W.; D’Angelo, F. Computational modelling of mobile bearing TKA anterior–posterior dislocation. Comput. Methods Biomech. Biomed. Eng. 2015, 19, 549–562. [Google Scholar] [CrossRef] [PubMed]
- Victor, J. A Comparative Study on the Biomechanics of the Native Human Knee Joint and Total Knee Arthroplasty. Ph.D. Thesis, Katholieke Universiteit Leuven, Leuven, Belgium, 2009. [Google Scholar]
- Vanheule, V.; Delport, H.P.; Andersen, M.S.; Scheys, L.; Wirix-Speetjens, R.; Jonkers, I.; Victor, J.; Sloten, J.V. Evaluation of predicted knee function for component malrotation in total knee arthroplasty. Med. Eng. Phys. 2017, 40, 56–64. [Google Scholar] [CrossRef] [PubMed]
- Blankevoort, L.; Huiskes, R. Ligament-bone interaction in a three-dimensional model of the knee. J. Biomech. Eng. 1991, 113, 263–269. [Google Scholar] [CrossRef]
- Blankevoort, L.; Huiskes, R. Validation of a three-dimensional model of the knee. J. Biomech. 1996, 29, 955–961. [Google Scholar] [CrossRef]
- Son, J.; Rymer, W.Z. Relative contribution of altered neuromuscular factors to muscle activation-force relationships following chronic stroke: A simulation study. J. Electromyogr. Kinesiol. 2022, 66, 102680. [Google Scholar] [CrossRef]
- Guess, T.M.; Stylianou, A.P.; Kia, M. Concurrent Prediction of Muscle and Tibiofemoral Contact Forces During Treadmill Gait. J. Biomech. Eng. 2014, 136, 021032. [Google Scholar] [CrossRef]
- Boonen, B.; Schotanus, M.G.M.; Kerens, B.; Hulsmans, F.-J.; Tuinebreijer, W.E.; Kort, N.P. Patient-specific positioning guides for total knee arthroplasty: No significant difference between final component alignment and pre-operative digital plan except for tibial rotation. Knee Surg. Sports Traumatol. Arthrosc. 2015, 25, 2809–2817. [Google Scholar] [CrossRef]
- Taylor, R. Interpretation of the Correlation Coefficient: A Basic Review. J. Diagn. Med. Sonogr. 2016, 6, 35–39. [Google Scholar] [CrossRef]
- Baldwin, M.A.; Clary, C.W.; Fitzpatrick, C.K.; Deacy, J.S.; Maletsky, L.P.; Rullkoetter, P.J. Dynamic finite element knee simulation for evaluation of knee replacement mechanics. J. Biomech. 2012, 45, 474–483. [Google Scholar] [CrossRef] [PubMed]
- LaPrade, R.F.; Tso, A.; Wentorf, F.A. Force Measurements on the Fibular Collateral Ligament, Popliteofibular Ligament, and Popliteus Tendon to Applied Loads. Am. J. Sports Med. 2004, 32, 1695–1701. [Google Scholar] [CrossRef] [PubMed]
- Kaneko, T.; Kono, N.; Mochizuki, Y.; Hada, M.; Toyoda, S.; Musha, Y. Bi-cruciate substituting total knee arthroplasty improved medio-lateral instability in mid-flexion range. J. Orthop. 2017, 14, 201–206. [Google Scholar] [CrossRef]
- Marra, M.A.; Vanheule, V.; Fluit, R.; Koopman, B.H.F.J.M.; Rasmussen, J.; Verdonschot, N.; Andersen, M.S. A Subject-Specific Musculoskeletal Modeling Framework to Predict In Vivo Mechanics of Total Knee Arthroplasty. J. Biomech. Eng. 2015, 137, 020904. [Google Scholar] [CrossRef]
- Kumar, P.; Elfrink, J.; Daniels, J.P.; Aggarwal, A.; Keeney, J.A. Higher Component Malposition Rates with Patient-Specific Cruciate Retaining TKA than Contemporary Posterior Stablisized TKA. J. Knee. Surg. 2021, 34, 1085–1091. [Google Scholar]



| Kinematic Range-of-Motion | Specimen 1 | Specimen 2 |
|---|---|---|
| VV (°) | 5.15 | 10.77 |
| IE (°) | 8.37 | 21.00 |
| AP (mm) | 30.24 | 50.94 |
| ML (mm) | 3.60 | 8.27 |
| IS (mm) | 21.41 | 26.77 |
| α | β | |
|---|---|---|
| Specimen 1 | 85 | 0.05 |
| Specimen 2 | 32.5 | 0.05 |
| Parameter | MCL | LCL | MPFL | LPFL | Patellar Ligament | |
|---|---|---|---|---|---|---|
| Specimen 1 | 0.04 | 0.08 | 0.08 | 0.06 | −0.25 | |
| (N) | 400 | 650 | 6000 | 3000 | 25000 | |
| Specimen 2 | 0.04 | 0.08 | 0.08 | 0.06 | −0.25 | |
| (N) | 700 | 650 | 6000 | 3000 | 20,000 |
| Kinematics | Measure | Specimen 1 | Specimen 2 |
|---|---|---|---|
| FE (°) | RMSE | 0.5 | 3.8 |
| ρ | 1 | 0.99 | |
| VV (°) | RMSE | 0.44 | 2.55 |
| ρ | 0.85 | 0.98 | |
| IE (°) | RMSE | 0.56 | 0.84 |
| ρ | 0.15 | −0.20 | |
| AP (mm) | RMSE | 2.62 | 1.54 |
| ρ | 0.96 | 0.99 | |
| ML (mm) | RMSE | 0.50 | 0.92 |
| ρ | 0 | 0.93 | |
| IS (mm) | RMSE | 2.01 | 1.66 |
| ρ | 0.99 | 0.99 | |
| Ankle load (N) | RMSE | 17.8 (20.23%) | 44 (49.96%) |
| ρ | 0.8 | −0.11 | |
| Quadriceps load (N) | RMSE | 83 (8.00%) | 215 (27.77%) |
| ρ | 0.99 | 0.89 |
| Specimen 1 | Specimen 2 | |
|---|---|---|
| kMCL | 360–440 N | 650–745 N |
| kLCL | 280–1250 N | / |
| Kinematics | Specimen 1 | Specimen 2 | ||||
|---|---|---|---|---|---|---|
| Impact of MCL and LCL stiffness perturbations | ||||||
| kMCL 360 N | kMCL 440 N | kLCL 280 N | kLCL 1250 N | kMCL 650 N | kMCL 745 N | |
| ΔVV (°) | −0.03 ± 0.03 | 0.04 ± 0.03 | −0.01 ± 0.03 | 0.01 ± 0.04 | 0.08 ± 0.07 | −0.06 ± 0.05 |
| ΔIE (°) | 0.26 ± 0.22 | −0.29 ± 0.12 | −0.61 ± 1.06 | 0.73 ± 0.87 | −0.28 ± 0.25 | 0.27 ± 0.18 |
| ΔAP (mm) | −0.02 ± 0.03 | 0 ± 0.30 | −0.1 ± 0.19 | 0.1 ± 0.20 | −0.05 ± 0.02 | 0.03 ± 0.02 |
| ΔML (mm) | −0.02 ± 0.07 | 0.02 ± 0.06 | 0.08 ± 0.14 | −0.07 ± 0.14 | −0.03 ± 0.07 | 0.02 ± 0.07 |
| ΔIS (mm) | 0.02 ± 0.01 | 0.02 ± 0.01 | 0.05 ± 0.03 | −0.02 ± 0.01 | 0.01 ± 0.02 | 0.02 ± 0.02 |
| Impact of implant alignment perturbations | ||||||
| Implant IE − 3.2° | Implant IE + 3.2° | Implant IE − 3.2° | Implant IE + 3.2° | |||
| ΔVV (°) | 0.01 ± 0.10 | −0.02 ± 0.01 | 0.49 ± 0.12 | −0.45 ± 0.12 | ||
| ΔIE (°) | −1.51 ± 0.25 | 1.56 ± 0.22 | −1.86 ± 0.42 | 1.95 ± 0.37 | ||
| ΔAP (mm) | −0.02 ± 0.27 | 0.04 ± 0.17 | −0.27 ± 0.14 | 0.22 ± 0.27 | ||
| ΔML (mm) | 0.70 ± 0.13 | −0.70 ± 0.12 | 0.62 ± 0.12 | −0.61 ± 0.12 | ||
| ΔIS (mm) | −0.06 ± 0.23 | 0.06 ± 0.20 | 0.04 ± 0.14 | 0 ± 0.20 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dandois, F.; Taylan, O.; Müller, J.H.; Scheys, L. Sensitivity of Model-Based Predictions of Post-TKA Kinematic Behavior to Residual Errors in Ultrasound-Based Knee Collateral Ligament Strain Assessment. Sensors 2023, 23, 8268. https://doi.org/10.3390/s23198268
Dandois F, Taylan O, Müller JH, Scheys L. Sensitivity of Model-Based Predictions of Post-TKA Kinematic Behavior to Residual Errors in Ultrasound-Based Knee Collateral Ligament Strain Assessment. Sensors. 2023; 23(19):8268. https://doi.org/10.3390/s23198268
Chicago/Turabian StyleDandois, Félix, Orçun Taylan, Jacobus H. Müller, and Lennart Scheys. 2023. "Sensitivity of Model-Based Predictions of Post-TKA Kinematic Behavior to Residual Errors in Ultrasound-Based Knee Collateral Ligament Strain Assessment" Sensors 23, no. 19: 8268. https://doi.org/10.3390/s23198268
APA StyleDandois, F., Taylan, O., Müller, J. H., & Scheys, L. (2023). Sensitivity of Model-Based Predictions of Post-TKA Kinematic Behavior to Residual Errors in Ultrasound-Based Knee Collateral Ligament Strain Assessment. Sensors, 23(19), 8268. https://doi.org/10.3390/s23198268






