Design, Fabrication, and Characterization of Inkjet-Printed Organic Piezoresistive Tactile Sensor on Flexible Substrate
Abstract
:1. Introduction
1.1. Tactile Sensing for Robotics
1.2. Sensor Requirements and Transduction Types
1.3. Contributions
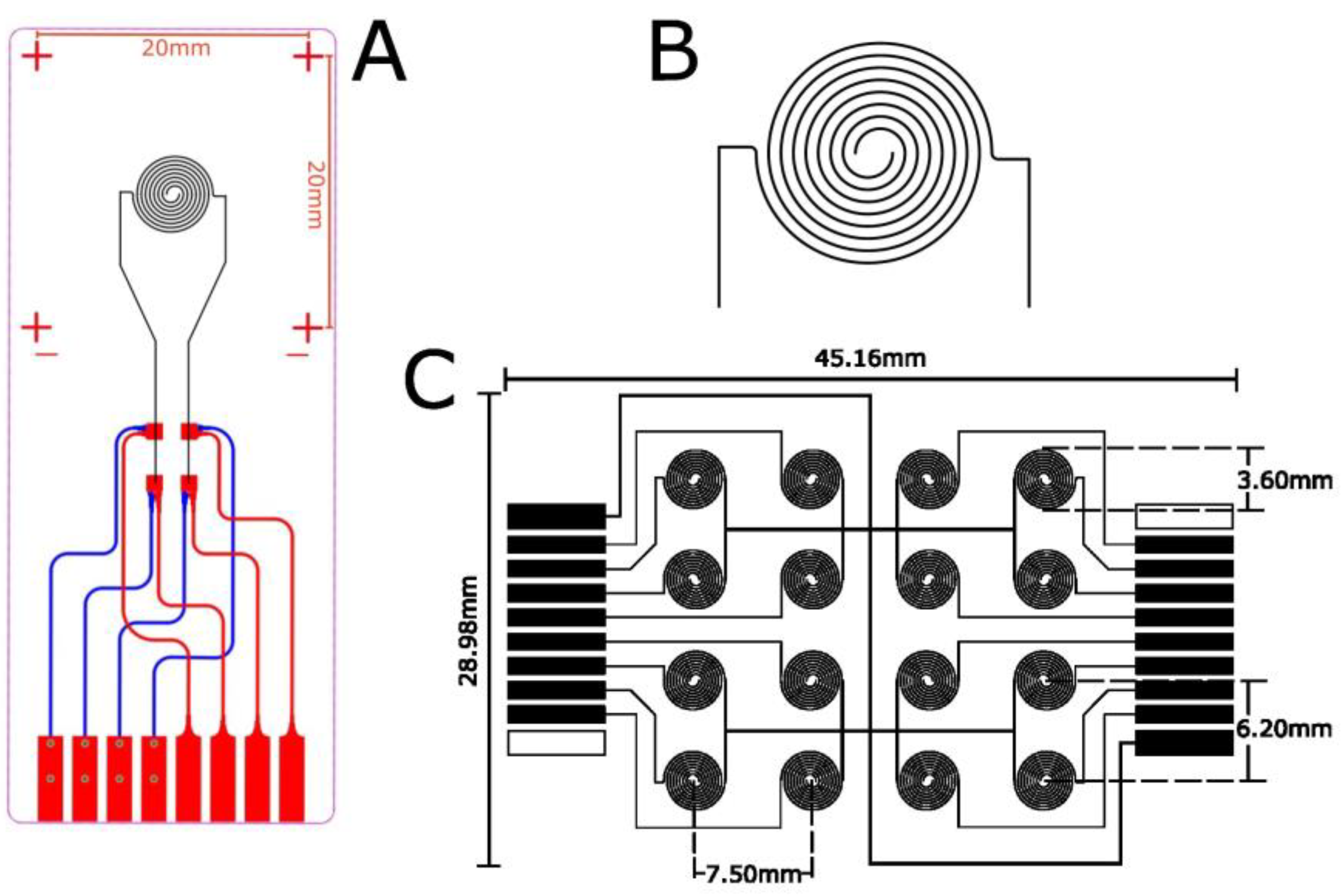
2. Design of Fingerprint Tactile Sensors
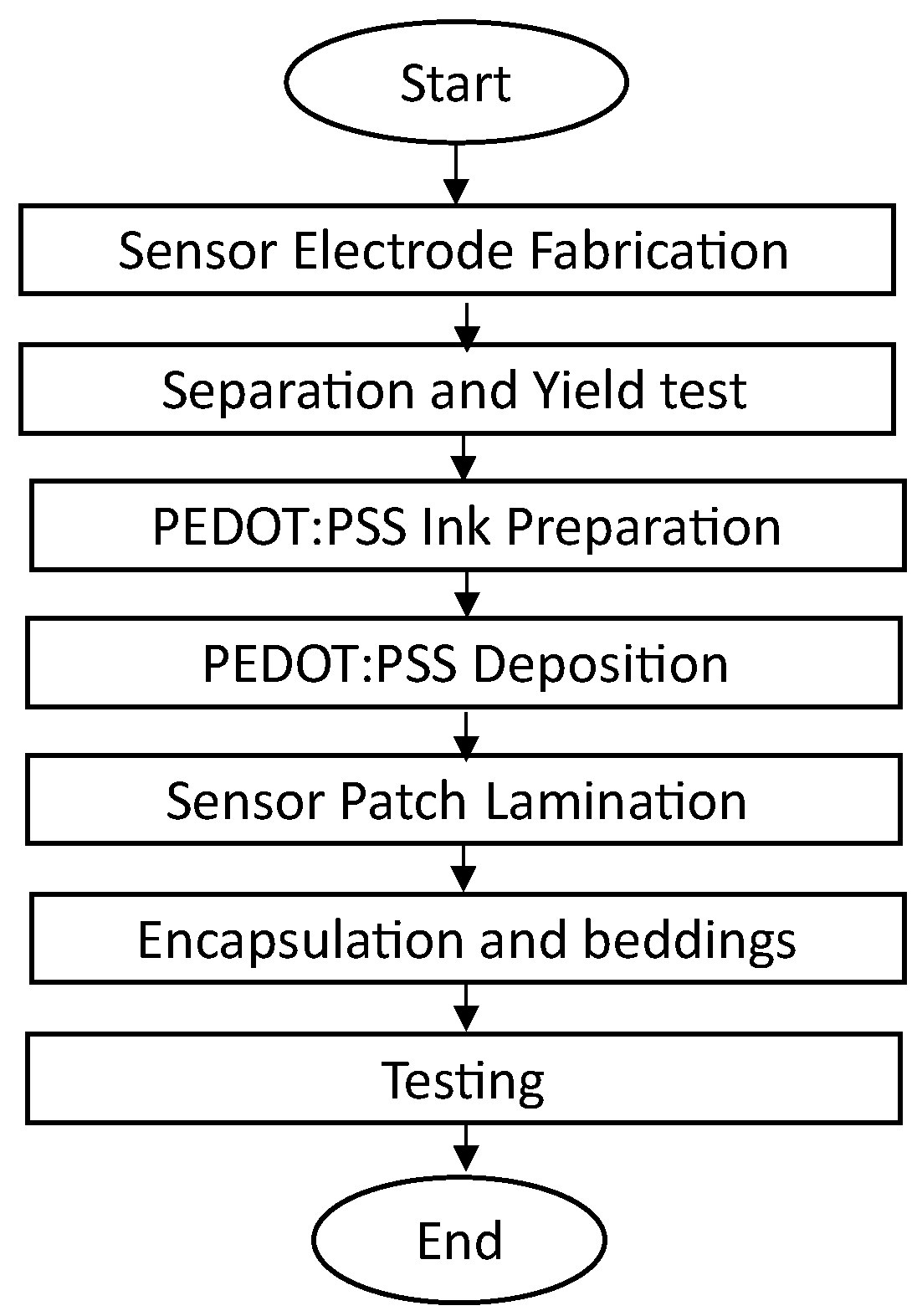
3. Fabrication of Fingerprint Tactile Sensors
3.1. Aerosol Jet Printing System
- -
- The waveform times (open/close/pulse);
- -
- The cycle of the ink-drop dispensing period corresponding to the dispensing frequency, (1–250 Hz);
- -
- The stroke force of ink droplet ejection, expressed in % for which the maximum force equals 100%;
- -
- The deposit height, h (3 mm), which is the distance from the print head nozzle to the substrate;
- -
- The temperature of the ink, (40 °C);
- -
- The air pressure, Pa (20 psi), which is the fluid pressure in the print head valve assembly.
3.2. Tactile Sensor’s Aersol Jet Inkjet Printing Trajectory
3.3. Tactile Sensor Sintering and Plasma Treatment
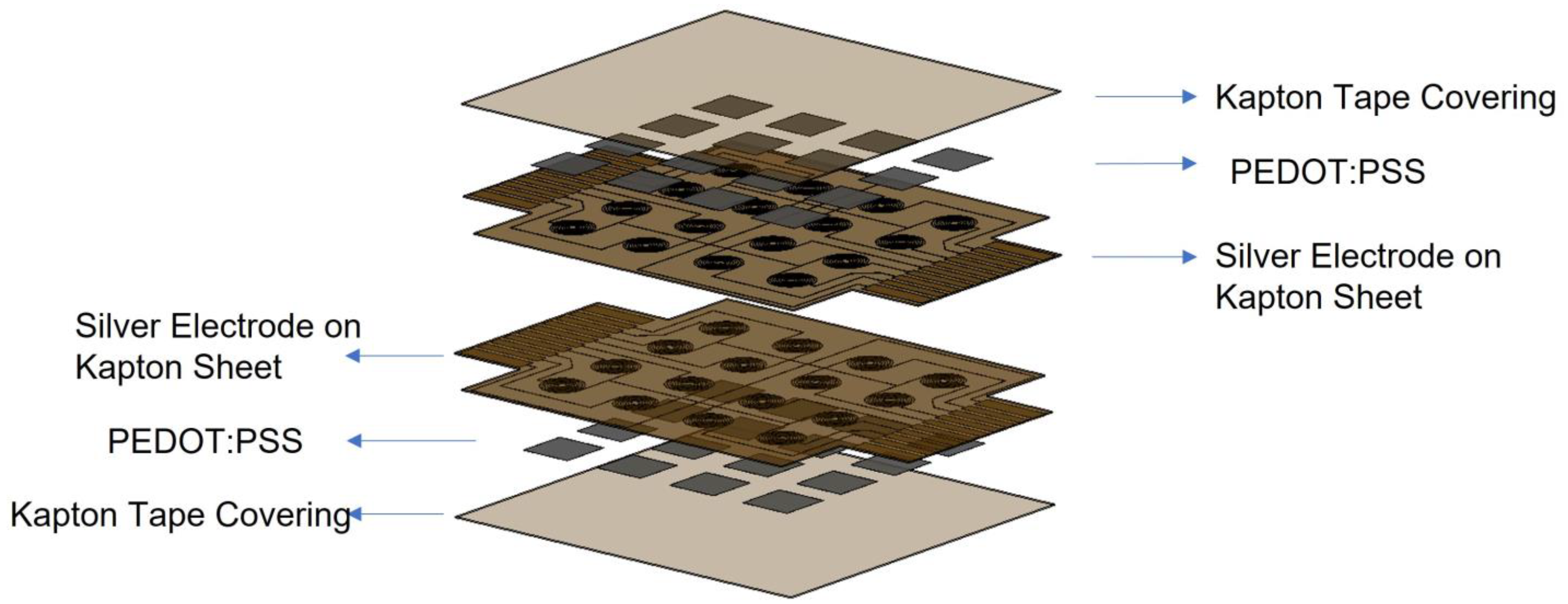
3.4. PEDOT:PSS Deposition
3.5. Sensor Patch Lamination
- 1.
- Placing the completely fabricated sensor patches:
- 2.
- Detaching the sensor patches:
- 3.
- Protecting the sensor electrode connectors:
- 4.
- Protecting the surface with Kapton tape:
- 5.
- Using double-sided tape for alignment:
- 6.
- Aligning the matching pairs:
- 7.
- Applying adhesive spray to the aligned pair:
- 8.
- Smoothing the adhered pair:
- 9.
- Curing and trimming the outline:
- 10.
- Cleaning the laminated paired sensor patch:
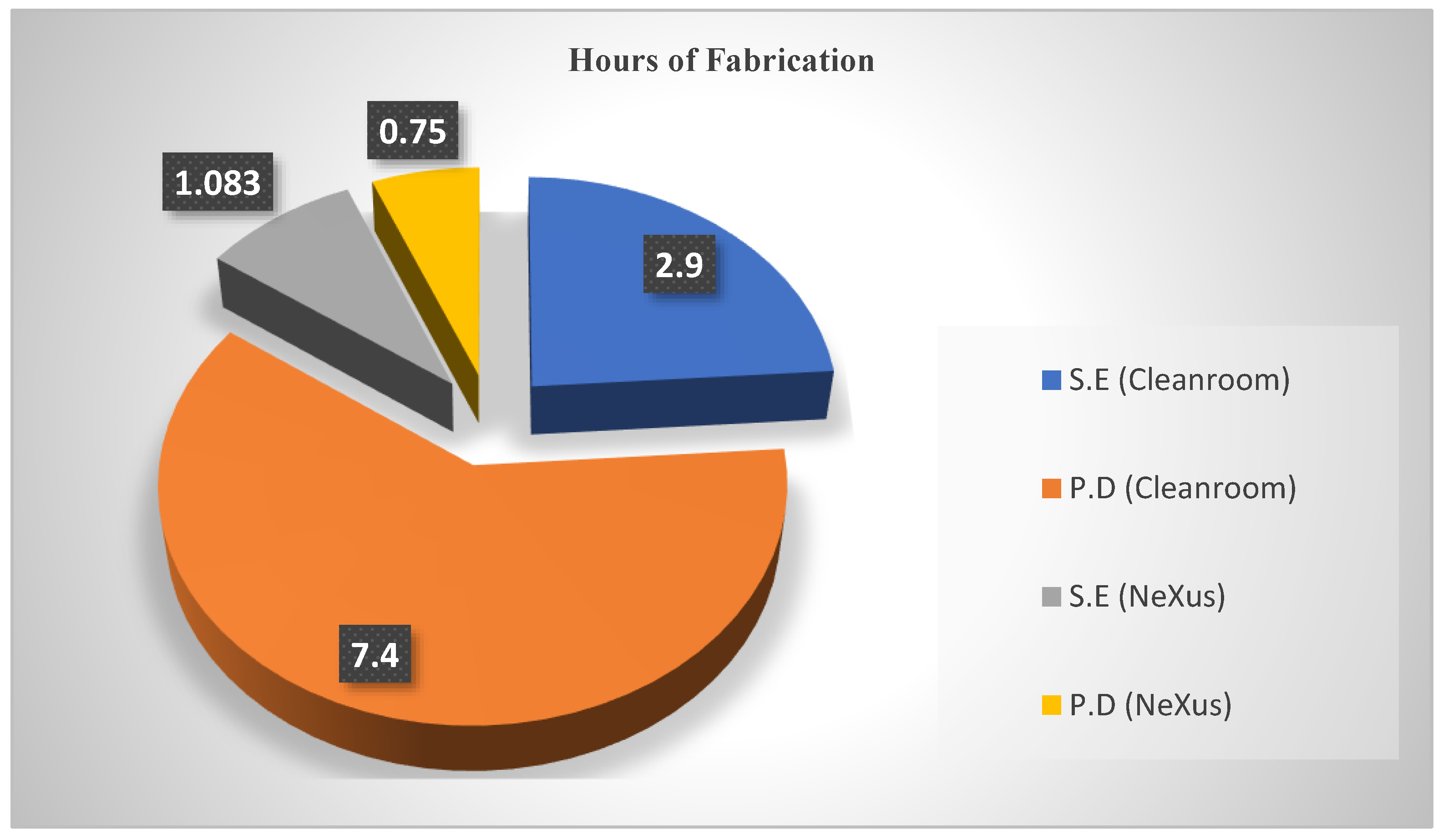
3.6. Fabrication Duration Analysis
- 1.
- Sensor Electrodes
- 2.
- PEDOT:PSS Deposition
4. Experimental Test Setup and Results
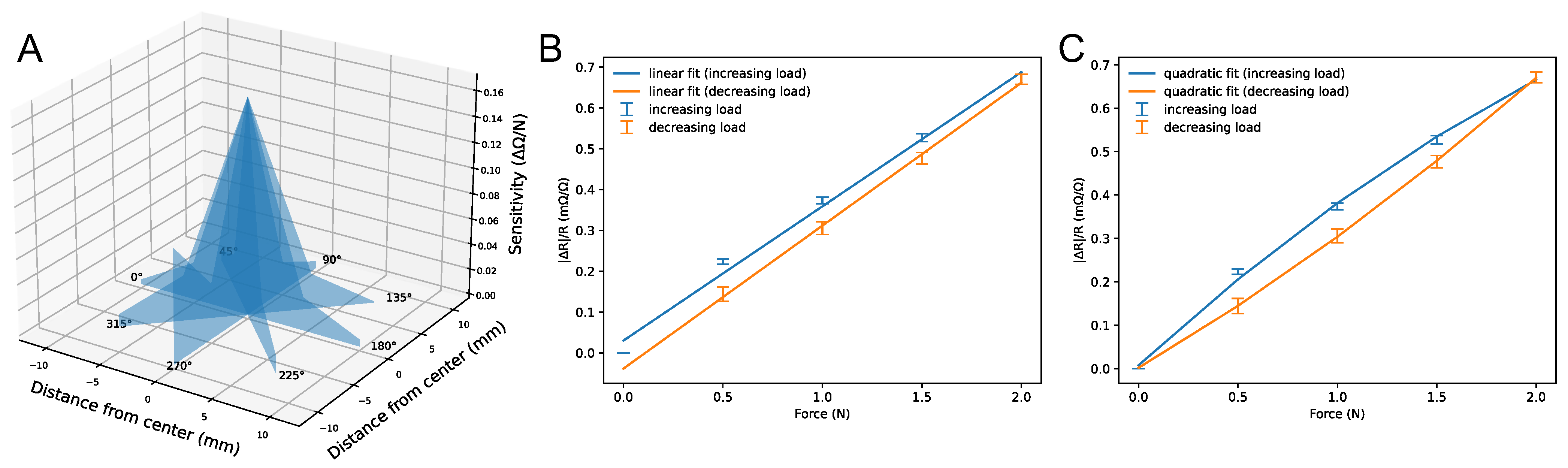
4.1. Spatial Response for a Single Tactel
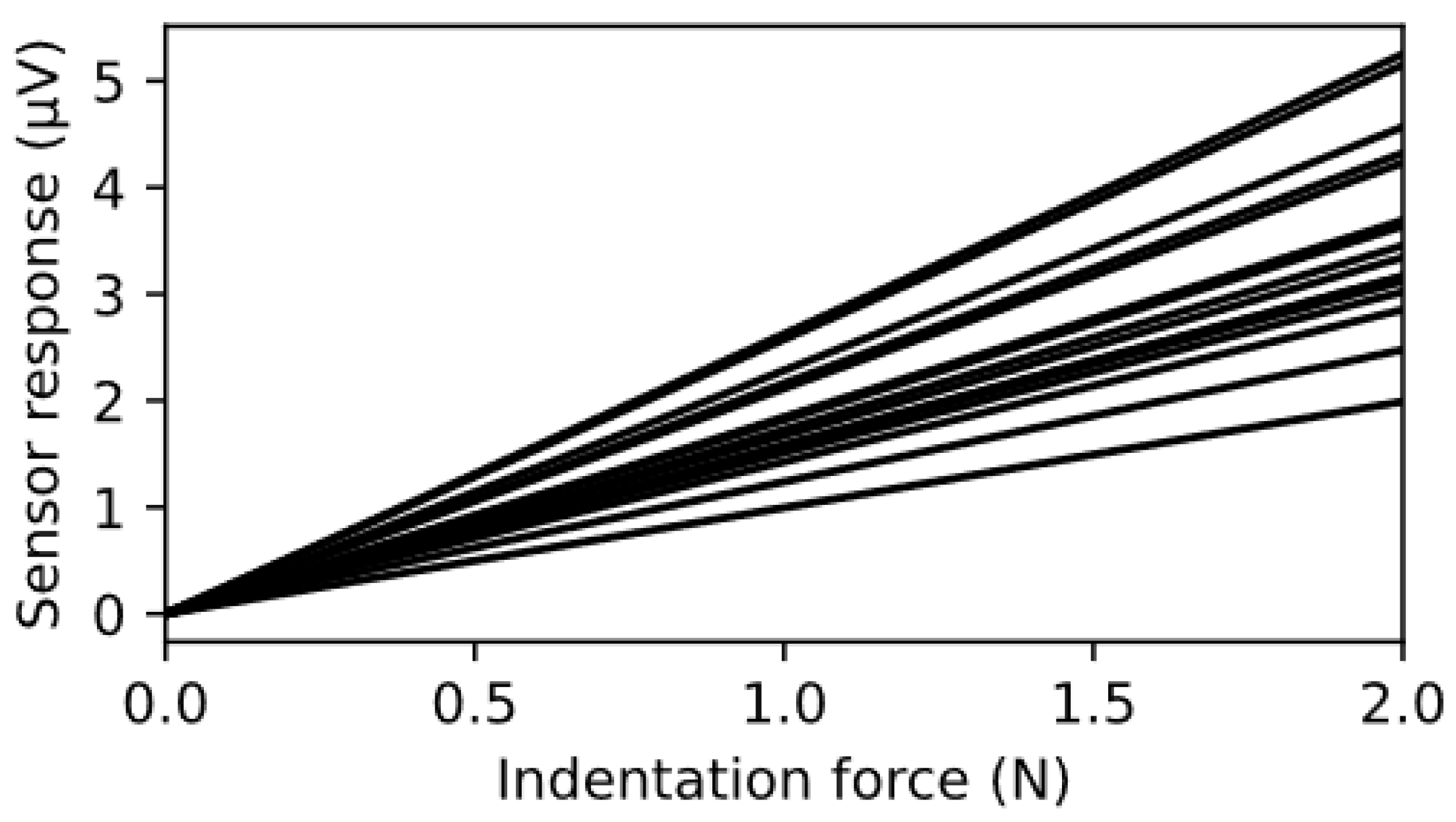
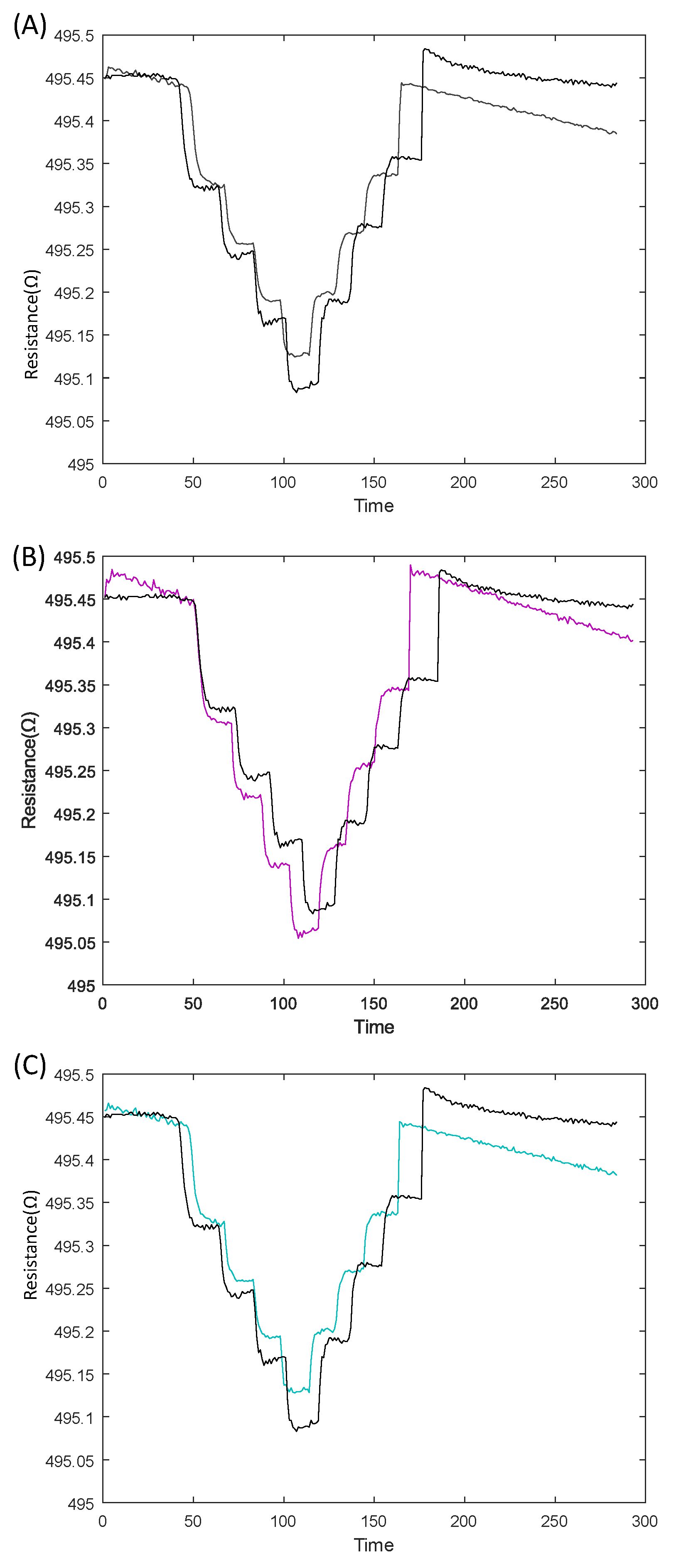
4.2. Repeatability of Sensor Measurements
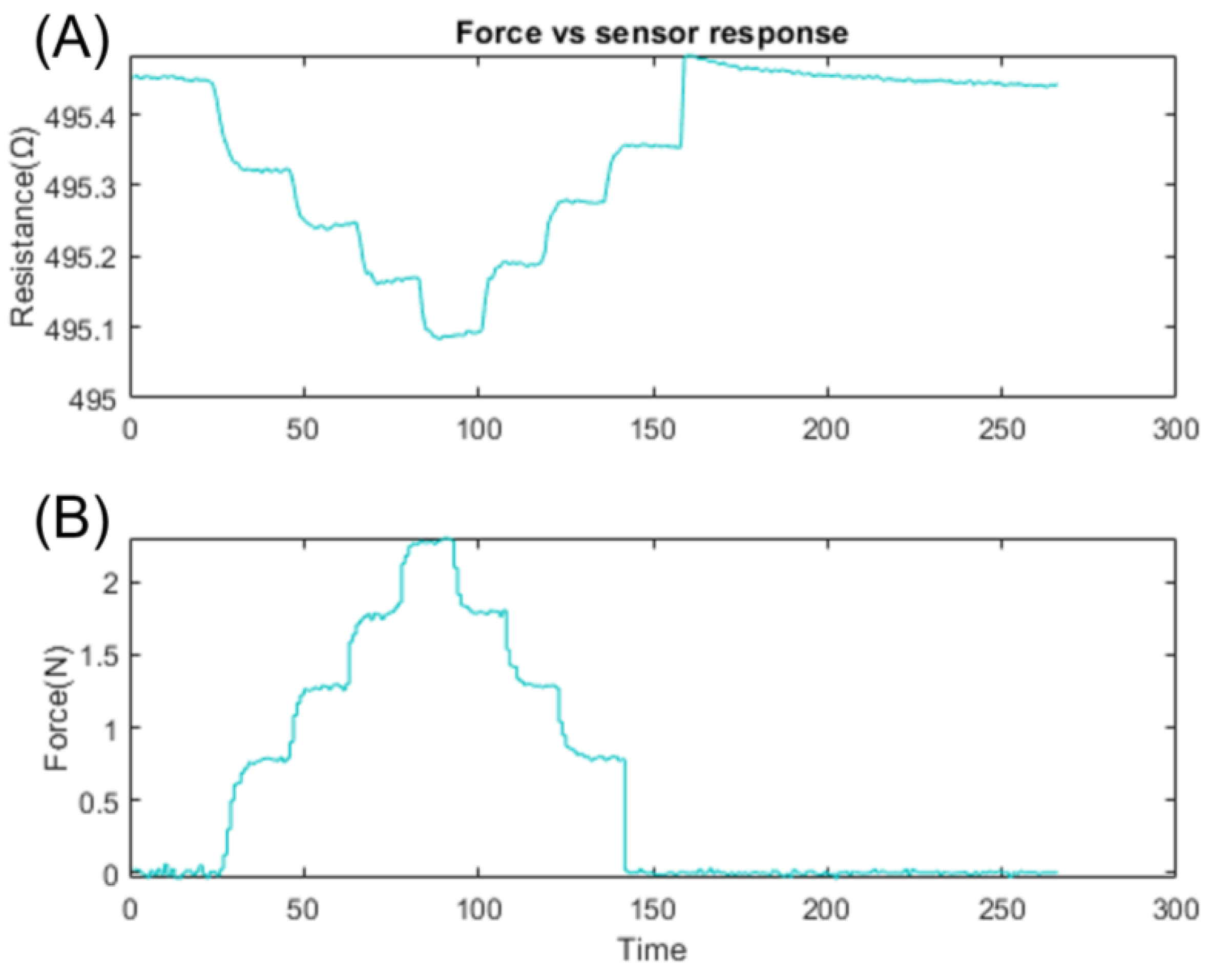
4.3. Resistance and Sensitivity Measurement of Sensor Patch
4.4. Sensor Array Spatial Indentation Results
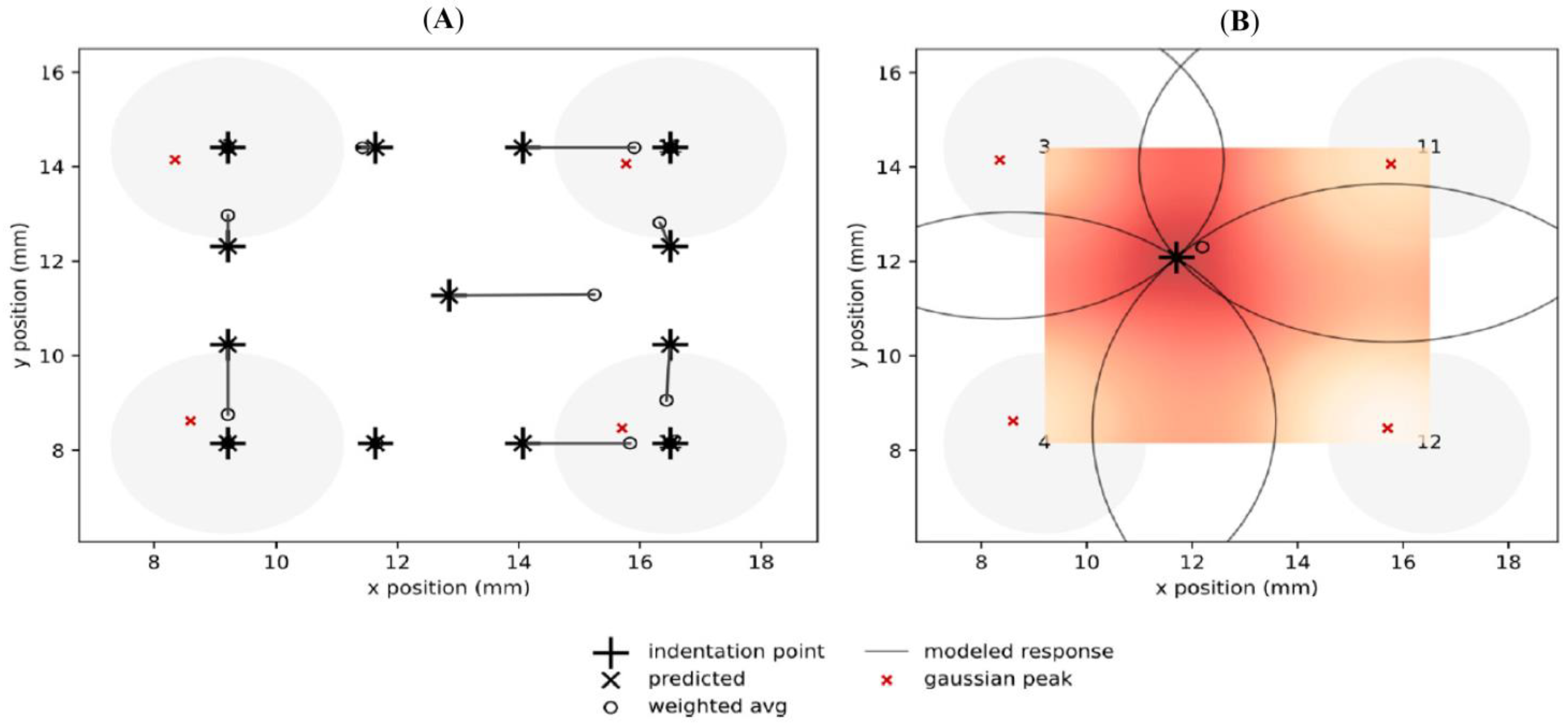
4.5. Spatial Resolution Estimation for Sensor Array
4.5.1. Weighted Averaging Method
4.5.2. Elliptical Intercept Method
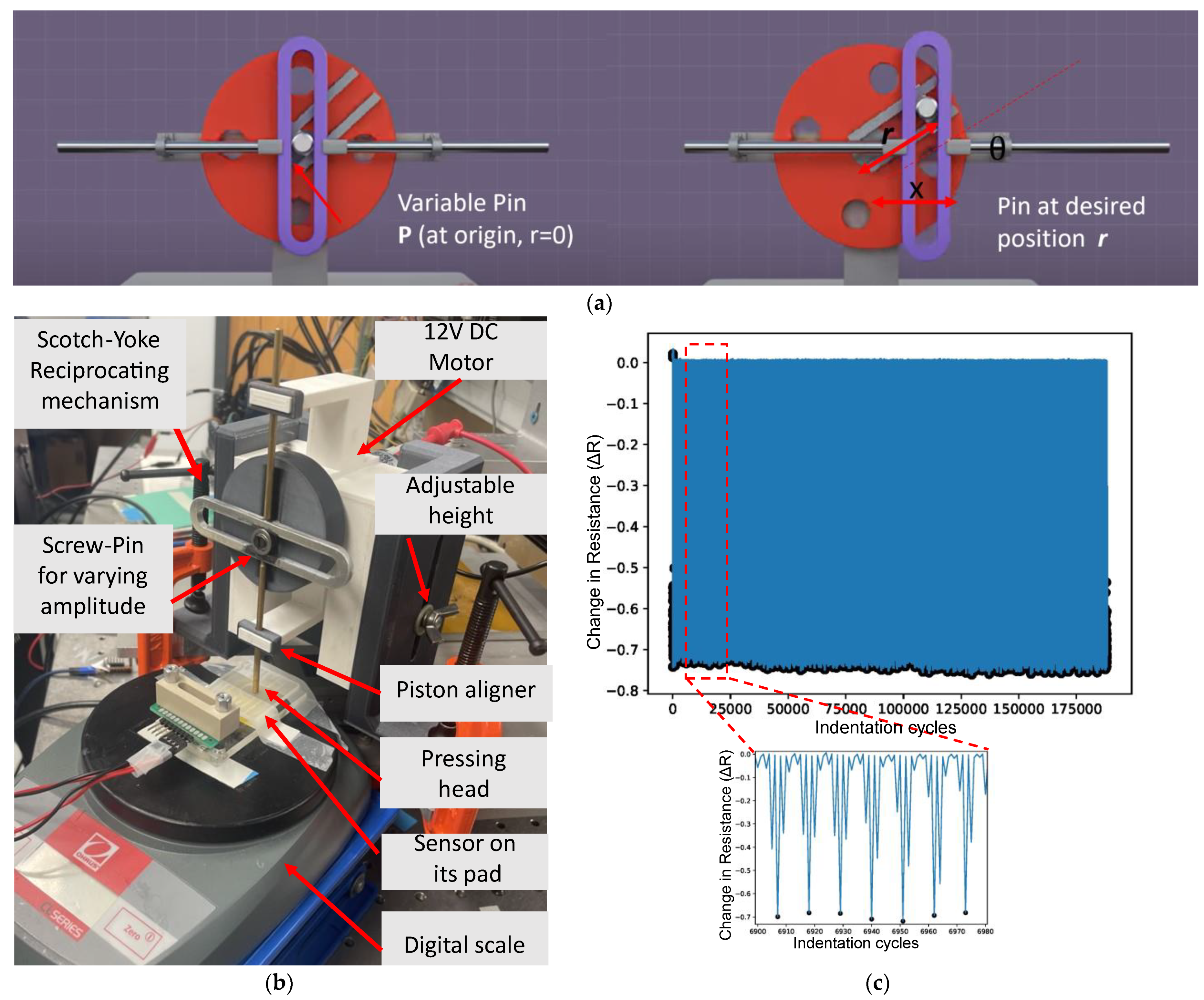
4.6. Dynamic Response Characterization of Tactile Sensors
| K | C | D | ||||||
| −4.116 × | 8.157 × | −1.141 × | 2.05 × | −2.261 × | −2494 | 0.1928 | −0.01798 | −0.09251 |
| −0.133 | −14.9 | 1.485 | −2.828 | −7.695 | ||||
| −0.02731 | −7.206 | −1.572 | −3.067 | 8.4 | ||||
| K | C | D | ||||
| −7.625 × | 4.753 × | −3.617 × | −2712 | 0.1262 | −0.09251 | |
| −0.04459 | −3621 | −3.972 | −0.6717 | |||
| K | C | D | ||
| −1.032 × | −0.0001816 | −2494 | −0.1363 |
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lumelsky, V.; Shur, M.S.; Wagner, S.; Ding, M. Sensitive Skin; World Scientific: Singapore, 2000; Volume 18. [Google Scholar]
- Yang, T.; Xie, D.; Li, Z.; Zhu, H. Recent advances in wearable tactile sensors: Materials, sensing mechanisms, and device performance. Mater. Sci. Eng. R Rep. 2017, 115, 1–37. [Google Scholar] [CrossRef]
- Mandil, W.; Rajendran, V.; Nazari, K.; Ghalamzan-Esfahani, A. Tactile-Sensing Technologies: Trends, Challenges and Outlook in Agri-Food Manipulation. Sensors 2023, 23, 7362. [Google Scholar] [CrossRef] [PubMed]
- Crowder, R. Towards robots that can sense texture by touch. Science 2006, 312, 1479. [Google Scholar] [CrossRef] [PubMed]
- Fukuda, K.; Takeda, Y.; Yoshimura, Y.; Shiwaku, R.; Tran, L.T.; Sekine, T.; Mizukami, M.; Kumaki, D.; Tokito, S. Fully-printed high-performance organic thin-film transistors and circuitry on one-micron-thick polymer films. Nat. Commun. 2014, 5, 4147. [Google Scholar] [CrossRef]
- Tanaka, M.; Okuyama, T.; Sone, M.; Tanahashi, Y.; Chonan, S. Development of an endoscopic tactile sensor using PVDF films. In Nano-Biomedical Engineering 2009; World Scientific: Singapore, 2009; pp. 245–254. [Google Scholar]
- Cannata, G.; Maggiali, M.; Metta, G.; Sandini, G. An embedded artificial skin for humanoid robots. In Proceedings of the 2008 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems, Seoul, Republic of Korea, 20–22 August 2008; pp. 434–438. [Google Scholar]
- Mittendorfer, P.; Yoshida, E.; Moulard, T.; Cheng, G. A general tactile approach for grasping unknown objects with a humanoid robot. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 4747–4752. [Google Scholar]
- Hollinger, A.; Wanderley, M.M. Evaluation of commercial force-sensing resistors. In Proceedings of the International Conference on New Interfaces for Musical Expression, Paris, France, 4–8 June 2006; pp. 4–8. [Google Scholar]
- Wettels, N.; Fishel, J.A.; Su, Z.; Lin, C.H.; Loeb, G.E.; SynTouch, L. Multi-modal synergistic tactile sensing. In Proceedings of the Tactile Sensing in Humanoids—Tactile Sensors and Beyond Workshop, 9th IEEE-RAS International Conference on Humanoid Robots, Paris, France, 7–10 December 2009. [Google Scholar]
- Dahiya, R.S.; Metta, G.; Valle, M.; Sandini, G. Tactile sensing—From humans to humanoids. IEEE Trans. Robot. 2009, 26, 1–20. [Google Scholar] [CrossRef]
- Silvera-Tawil, D.; Rye, D.; Velonaki, M. Artificial skin and tactile sensing for socially interactive robots: A review. Robot. Auton. Syst. 2015, 63, 230–243. [Google Scholar] [CrossRef]
- Raibert, M. An all digital VLSI tactile array sensor. In Proceedings of the 1984 IEEE International Conference on Robotics and Automation, Atlanta, GA, USA, 13–15 March 1984; Volume 1, pp. 314–319. [Google Scholar]
- Takao, H.; Sawada, K.; Ishida, M. Monolithic silicon smart tactile image sensor with integrated strain sensor array on pneumatically swollen single-diaphragm structure. IEEE Trans. Electron Devices 2006, 53, 1250–1259. [Google Scholar] [CrossRef]
- Choi, B.; Choi, H.R.; Kang, S. Development of tactile sensor for detecting contact force and slip. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 2638–2643. [Google Scholar]
- Liu, L.; Zheng, X.; Li, Z. An array tactile sensor with piezoresistive single-crystal silicon diaphragm. Sens. Actuators A Phys. 1993, 35, 193–196. [Google Scholar] [CrossRef]
- Sugiyama, S.; Kawahata, K.; Yoneda, M.; Igarashi, I. Tactile image detection using a 1k-element silicon pressure sensor array. Sens. Actuators A Phys. 1990, 22, 397–400. [Google Scholar] [CrossRef]
- Park, S.; Kim, H.; Vosgueritchian, M.; Cheon, S.; Kim, H.; Koo, J.H.; Kim, T.R.; Lee, S.; Schwartz, G.; Chang, H. Stretchable energy-harvesting tactile electronic skin capable of differentiating multiple mechanical stimuli modes. Adv. Mater. 2014, 26, 7324–7332. [Google Scholar] [CrossRef]
- Mannsfeld, S.C.; Tee, B.C.; Stoltenberg, R.M.; Chen, C.V.; Barman, S.; Muir, B.V.; Sokolov, A.N.; Reese, C.; Bao, Z. Highly sensitive flexible pressure sensors with microstructured rubber dielectric layers. Nat. Mater. 2010, 9, 859–864. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.Y.; Keplinger, C.; Whitesides, G.M.; Suo, Z. Ionic skin. Adv. Mater. 2014, 26, 7608–7614. [Google Scholar] [CrossRef] [PubMed]
- Viry, L.; Levi, A.; Totaro, M.; Mondini, A.; Mattoli, V.; Mazzolai, B.; Beccai, L. Flexible three-axial force sensor for soft and highly sensitive artificial touch. Adv. Mater. 2014, 26, 2659–2664. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, K.; Najafi, K.; Wise, K. A 1024-element high-performance silicon tactile imager. In Technical Digest, International Electron Devices Meeting; IEEE: Piscataway, NJ, USA, 1988; pp. 674–677. [Google Scholar]
- Chu, Z.; Sarro, P.; Middelhoek, S. Silicon three-axial tactile sensor. Sens. Actuators A Phys. 1996, 54, 505–510. [Google Scholar] [CrossRef]
- Gray, B.L.; Fearing, R.S. A surface micromachined microtactile sensor array. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996; Volume 1, pp. 1–6. [Google Scholar]
- De Souza, R.J.; Wise, K.D. A very high density bulk micromachined capacitive tactile imager. In Proceedings of the International Solid State Sensors and Actuators Conference (Transducers’ 97), Chicago, IL, USA, 10–16 June 1997; Volume 2, pp. 1473–1476. [Google Scholar]
- Leineweber, M.; Pelz, G.; Schmidt, M.; Kappert, H.; Zimmer, G. New tactile sensor chip with silicone rubber cover. Sens. Actuators A Phys. 2000, 84, 236–245. [Google Scholar] [CrossRef]
- Kolesar, E.; Dyson, C.; Reston, R.; Fitch, R.; Ford, D.; Nelms, S. Tactile integrated circuit sensor realized with a piezoelectric polymer. In Proceedings of the 1996 Eighth Annual IEEE International Conference on Innovative Systems in Silicon, Austin, TX, USA, 9–11 October 1996; pp. 372–381. [Google Scholar]
- Polla, D.; Chang, W.; Muller, R.; White, R. Integrated zinc oxide-on-silicon tactile-sensor array. In Proceedings of the 1985 International Electron Devices Meeting, Washington, DC, USA, 1–4 December 1985; pp. 133–136. [Google Scholar]
- Nguyen, V.-C.; Oliva-Torres, V.; Bernadet, S.; Rival, G.; Richard, C.; Capsal, J.-F.; Cottinet, P.-J.; Le, M.-Q. Haptic Feedback Device Using 3D-Printed Flexible, Multilayered Piezoelectric Coating for In-Car Touchscreen Interface. Micromachines 2023, 14, 1553. [Google Scholar] [CrossRef]
- Domenici, C.; De Rossi, D. A stress-component-selective tactile sensor array. Sens. Actuators A Phys. 1992, 31, 97–100. [Google Scholar] [CrossRef]
- Sharma, T.; Je, S.-S.; Gill, B.; Zhang, J.X. Patterning piezoelectric thin film PVDF–TrFE based pressure sensor for catheter application. Sens. Actuators A Phys. 2012, 177, 87–92. [Google Scholar] [CrossRef]
- Wu, W.; Wen, X.; Wang, Z.L. Taxel-addressable matrix of vertical-nanowire piezotronic transistors for active and adaptive tactile imaging. Science 2013, 340, 952–957. [Google Scholar] [CrossRef]
- Buchberger, G.; Schwödiauer, R.; Bauer, S. Flexible large area ferroelectret sensors for location sensitive touchpads. Appl. Phys. Lett. 2008, 92, 123511. [Google Scholar] [CrossRef]
- Sun, Q.; Seung, W.; Kim, B.J.; Seo, S.; Kim, S.W.; Cho, J.H. Active matrix electronic skin strain sensor based on piezopotential-powered graphene transistors. Adv. Mater. 2015, 27, 3411–3417. [Google Scholar] [CrossRef]
- Hughes, D.; Lammie, J.; Correll, N. A robotic skin for collision avoidance and affective touch recognition. IEEE Robot. Autom. Lett. 2018, 3, 1386–1393. [Google Scholar] [CrossRef]
- Heo, J.-S.; Chung, J.-H.; Lee, J.-J. Tactile sensor arrays using fiber Bragg grating sensors. Sens. Actuators A Phys. 2006, 126, 312–327. [Google Scholar] [CrossRef]
- Lu, G.; Fu, S.; Zhu, T.; Xu, Y. Research on Finger Pressure Tactile Sensor with Square Hole Structure Based on Fiber Bragg Grating. Sensors 2023, 23, 6897. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Zou, J.; Xing, F.; Zhang, M.; Cao, X.; Wang, N.; Wang, Z.L. From dual-mode triboelectric nanogenerator to smart tactile sensor: A multiplexing design. ACS Nano 2017, 11, 3950–3956. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.L. Triboelectric nanogenerators as new energy technology for self-powered systems and as active mechanical and chemical sensors. ACS Nano 2013, 7, 9533–9557. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Totaro, M.; Beccai, L. Development of Fully Shielded Soft Inductive Tactile Sensors; Center for Micro-BioRobotics, Istituto Italiano di Tecnologia (IIT): Genoa, Italy, 2019. [Google Scholar]
- Olowo, O.O.; Zhang, R.; Yang, Z.; Goulet, B.; Popa, D.O. Organic Piezoresistive Robotic Skin Sensor Fabrication, Integration and Characterization. In Proceedings of the International Manufacturing Science and Engineering Conference, Online, 21–25 June 2021; Volume 85079, p. V002T008A013. [Google Scholar]
- Wei, D.; Zhang, R.; Saadatzi, M.N.; Olowo, O.O.; Popa, D.O. Organic Piezoresistive Pressure Sensitive Robotic Skin for Physical Human-Robot Interaction. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Online, 17–19 August 2020; Volume 83907, p. V001T001A013. [Google Scholar]
- Zhang, R.; Lin, J.-T.; Olowo, O.O.; Goulet, B.P.; Harris, B.; Popa, D.O. SkinCell: A Modular Tactile Sensor Patch for Physical Human–Robot Interaction. IEEE Sens. J. 2022, 23, 2833–2846. [Google Scholar] [CrossRef]
- Olowo, O.; Sherehiy, R.Z.A.; Goulet, B.; Curry, A.; Wei, D.; Yang, Z.; Alqatamin, M.; Popa, D.O. Inkjet Printing of Pedot: Pss Inks for Robotic Skin Sensors. In Proceedings of the ASME 2022 17th International Manufacturing Science and Engineering Conference (MSEC2022) Unpublished, West Lafayette, IN, USA, 27 June–1 July 2022; Volume 80989. [Google Scholar]
- Olowo, O.O.; Zhang, R.; Wei, D.; Ratnayake, D.; Jackson, D.; Popa, D.O. Aerosol Jet Printed Tactile Sensor on Flexible Substrate. In Proceedings of the 2022 IEEE International Conference on Flexible and Printable Sensors and Systems (FLEPS), Vienna, Austria, 10–13 July 2022; pp. 1–4. [Google Scholar]
- Olowo, O.O.; Zhang, R.; Lin, J.-T.; Wei, D.; Sherehiy, A.; Jackson, D.; Ratnayake, D.; Tofangchi, A.; Popa, D.O. Design and Fabrication of an Aerosol Jet Printed Tactile Sensor on Flexible Substrate. IEEE J. Flex. Electron. 2023, 2, 190–200. [Google Scholar] [CrossRef]
- Wei, D.; Zhang, R.; Lin, J.-T.; Ratnayake, D.; Olowo, O.; Nimon, A.; Alqatamin, M.; Sherehiy, A.; Popa, D. Precise Fabrication of Tactile Sensors using a Custom Additive Manufacturing Platform. Res. Sq. Prepr. 2023. [Google Scholar]
- Wei, D.; Zhang, R.; Lin, J.-T.; Ratnayake, D.; Olowo, O.O.; Nimon, A.S.; Alqatamin, M.; Sherehiy, A.; Popa, D.O. Automated Fabrication of Tactile Sensors Using a Custom Additive Manufacturing Platform. In Proceedings of the 2022 International Conference on Manipulation, Automation and Robotics at Small Scales (MARSS), Toronto, ON, Canada, 18–22 July 2022; pp. 1–6. [Google Scholar]
- Wei, D. Design, Evaluation, and Control of Nexus: A Multiscale Additive Manufacturing Platform with Integrated 3D Printing and Robotic Assembly. Ph.D. Thesis, University of Louisville, Louisville, KY, USA, 2022. paper number 3997. [Google Scholar]
- El Zein, A.; Huppé, C.; Cochrane, C. Development of a Flexible Strain Sensor Based on PEDOT:PSS for Thin Film Structures. Sensors 2017, 17, 1337. [Google Scholar] [CrossRef]
- Latessa, G.; Brunetti, F.; Reale, A.; Saggio, G.; Di Carlo, A. Piezoresistive behaviour of flexible PEDOT:PSS based sensors. Sens. Actuators B Chem. 2009, 139, 304–309. [Google Scholar] [CrossRef]
- Ratnayake, D.; Curry, A.; Walsh, K. Demonstrating a new ink material for aerosol printing conductive traces and custom strain gauges on flexible surfaces. In Proceedings of the 2021 IEEE International Conference on Flexible and Printable Sensors and Systems (FLEPS), Manchester, UK, 20–23 June 2021; pp. 1–4. [Google Scholar]
- Baptist, J.R.; Zhang, R.; Wei, D.; Saadatzi, M.N.; Popa, D.O. Fabrication of strain gauge based sensors for tactile skins. In Proceedings of the SPIE Commercial + Scientific Sensing and Imaging, Anaheim, CA, USA, 9–13 April 2017. [Google Scholar]
- Olowo, O.O.; Wei, D.; Ratnayake, D.; Goulet, B.; Curry, A.; Sherehiy, A.; Zhang, R.; Popa, D.O. PEDOT: PSS Polymer Aerosol Jet-printing for Robotic Skin Sensors. In Proceedings of the 2022 IEEE International Conference on Flexible and Printable Sensors and Systems (FLEPS), Vienna, Austria, 10–13 July 2022; pp. 1–4. [Google Scholar]
- Morice, S.; Sherehiy, A.; Wei, D.; Popa, D.O. Characterization of the Direct Write Inkjet Printing Process for Automated Fabrication of PEDOT: PSS Thin Films. In Proceedings of the International Manufacturing Science and Engineering Conference, West Lafayette, IN, USA, 27 June–1 July 2022; Volume 85802, p. V001T001A021. [Google Scholar]
- Saadatzi, M.N.; Baptist, J.R.; Yang, Z.; Popa, D.O. Modeling and fabrication of scalable tactile sensor arrays for flexible robot skins. IEEE Sens. J. 2019, 19, 7632–7643. [Google Scholar] [CrossRef]
- Kane, B.J.; Cutkosky, M.R.; Kovacs, G.T. A traction stress sensor array for use in high-resolution robotic tactile imaging. J. Microelectromech. Syst. 2000, 9, 425–434. [Google Scholar] [CrossRef]
- Feng, W.; Li, P.; Zhang, H.; Sun, K.; Li, W.; Wang, J.; Yang, H.; Li, X. Silicon Micromachined TSVs for Backside Interconnection of Ultra-Small Pressure Sensors. Micromachines 2023, 14, 1448. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.-Y.; Sung, W.-L.; Fang, W. Develop and implement a novel tactile sensor array with stretchable and flexible grid-like spring. In Proceedings of the IEEE SENSORS 2017, Glasgow, UK, 29 October–1 November 2017; pp. 1–3. [Google Scholar]
- Nagelkerke, N.J. A note on a general definition of the coefficient of determination. Biometrika 1991, 78, 691–692. [Google Scholar] [CrossRef]
- Oppenheim, A.V.; Willsky, A.S.; Nawab, S.H.; Ding, J.-J. Signals and Systems; Prentice Hall Upper: Saddle River, NJ, USA, 1997; Volume 2. [Google Scholar]
- Huang, Y.; Jiang, K.; Yi, N. Some weighted averaging methods for gradient recovery. Adv. Appl. Math. Mech. 2012, 4, 131–155. [Google Scholar] [CrossRef]
- Cremer, S.; Saadatzi, M.N.; Wijayasinghe, I.B.; Das, S.K.; Saadatzi, M.H.; Popa, D.O. SkinSim: A Design and Simulation Tool for Robot Skin With Closed-Loop pHRI Controllers. IEEE Trans. Autom. Sci. Eng. 2020, 18, 1302–1314. [Google Scholar] [CrossRef]




| Sheath Flow Rate | 135 sccm | Print Speed | 10 mm/s |
|---|---|---|---|
| Atomizer Flow Rate | 15 sccm | Atomizer Bath Temperature | 27 °C |
| Atomizer Current | 400 mA | Stand-off Distance | 3 mm |
| [Hz] | Stroke | [psi] | [°C] | h [mm] | (μm) | (μm) |
|---|---|---|---|---|---|---|
| 3.3 | 80% | 20 | 40 | 3 | 400 | 10 |
| Number of Sensor | Resistance (Ω) | Number of Sensor | Resistance (Ω) |
|---|---|---|---|
| 1 | 159 | 1 | 184 |
| 2 | 145 | 2 | 169 |
| 3 | 137 | 3 | 160 |
| 4 | 142 | 4 | 165 |
| 5 | 122 | 5 | 148 |
| 6 | 121 | 6 | 152 |
| 7 | 128 | 7 | 158 |
| 8 | 136 | 8 | 167 |
| 1 | 151 | 1 | 151 |
| 2 | 133 | 2 | 145 |
| 3 | 130 | 3 | 135 |
| 4 | 146 | 4 | 134 |
| 5 | 141 | 5 | 120 |
| 6 | 124 | 6 | 117 |
| 7 | 141 | 7 | 115 |
| 8 | 165 | 8 | 124 |
| SkinCell | Height | Offset (mm) | |||||
|---|---|---|---|---|---|---|---|
| 1 | 0.966 | 357 | 8.35 | 14.1 | 2.08 | 1.64 | 0.887 |
| 2 | 0.964 | 384 | 15.8 | 14.1 | 2.19 | 1.72 | 0.804 |
| 3 | 0.978 | 371 | 8.60 | 8.62 | 2.17 | 1.92 | 0.761 |
| 4 | 0.958 | 429 | 15.7 | 8.47 | 2.14 | 1.97 | 0.855 |
| Comparison | Cleanroom Sensors | Fingerprint Sensors |
|---|---|---|
| Fabrication | <10 h | <1 h |
| Yield | Average, 75% | 100% |
| Ease of manufacture/ Fab. Process complexity | Complex | Simplified |
| Substrate Geometry/ Surface Area | Limited by silicon wafer | Custom |
| Reliability (indentation cycles) | >100 | 180,000 |
| Durability | Wearing off terminals (fragile metal electrodes) | Printed electrodes are more resistant to wear |
| Spatial Resolution | N/A | >1 mm |
| Cost | Average (USD 2172) | Average (USD 60) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olowo, O.O.; Harris, B.; Sills, D.; Zhang, R.; Sherehiy, A.; Tofangchi, A.; Wei, D.; Popa, D.O. Design, Fabrication, and Characterization of Inkjet-Printed Organic Piezoresistive Tactile Sensor on Flexible Substrate. Sensors 2023, 23, 8280. https://doi.org/10.3390/s23198280
Olowo OO, Harris B, Sills D, Zhang R, Sherehiy A, Tofangchi A, Wei D, Popa DO. Design, Fabrication, and Characterization of Inkjet-Printed Organic Piezoresistive Tactile Sensor on Flexible Substrate. Sensors. 2023; 23(19):8280. https://doi.org/10.3390/s23198280
Chicago/Turabian StyleOlowo, Olalekan O., Bryan Harris, Daniel Sills, Ruoshi Zhang, Andriy Sherehiy, Alireza Tofangchi, Danming Wei, and Dan O. Popa. 2023. "Design, Fabrication, and Characterization of Inkjet-Printed Organic Piezoresistive Tactile Sensor on Flexible Substrate" Sensors 23, no. 19: 8280. https://doi.org/10.3390/s23198280
APA StyleOlowo, O. O., Harris, B., Sills, D., Zhang, R., Sherehiy, A., Tofangchi, A., Wei, D., & Popa, D. O. (2023). Design, Fabrication, and Characterization of Inkjet-Printed Organic Piezoresistive Tactile Sensor on Flexible Substrate. Sensors, 23(19), 8280. https://doi.org/10.3390/s23198280






