Multi-Robot Task Scheduling with Ant Colony Optimization in Antarctic Environments
Abstract
1. Introduction
- To the best of our knowledge, this is the first approach which solves the multi-robot task scheduling problem in Antarctic environments.
- The performance of the multi-robot task scheduling result was tested and evaluated in both simulated and real Antarctic environments.
- The scheduled paths by the proposed method can improve the efficiency of operating multiple robots by considering the characteristics of robot movement in Antarctic environments.
2. Problem Description
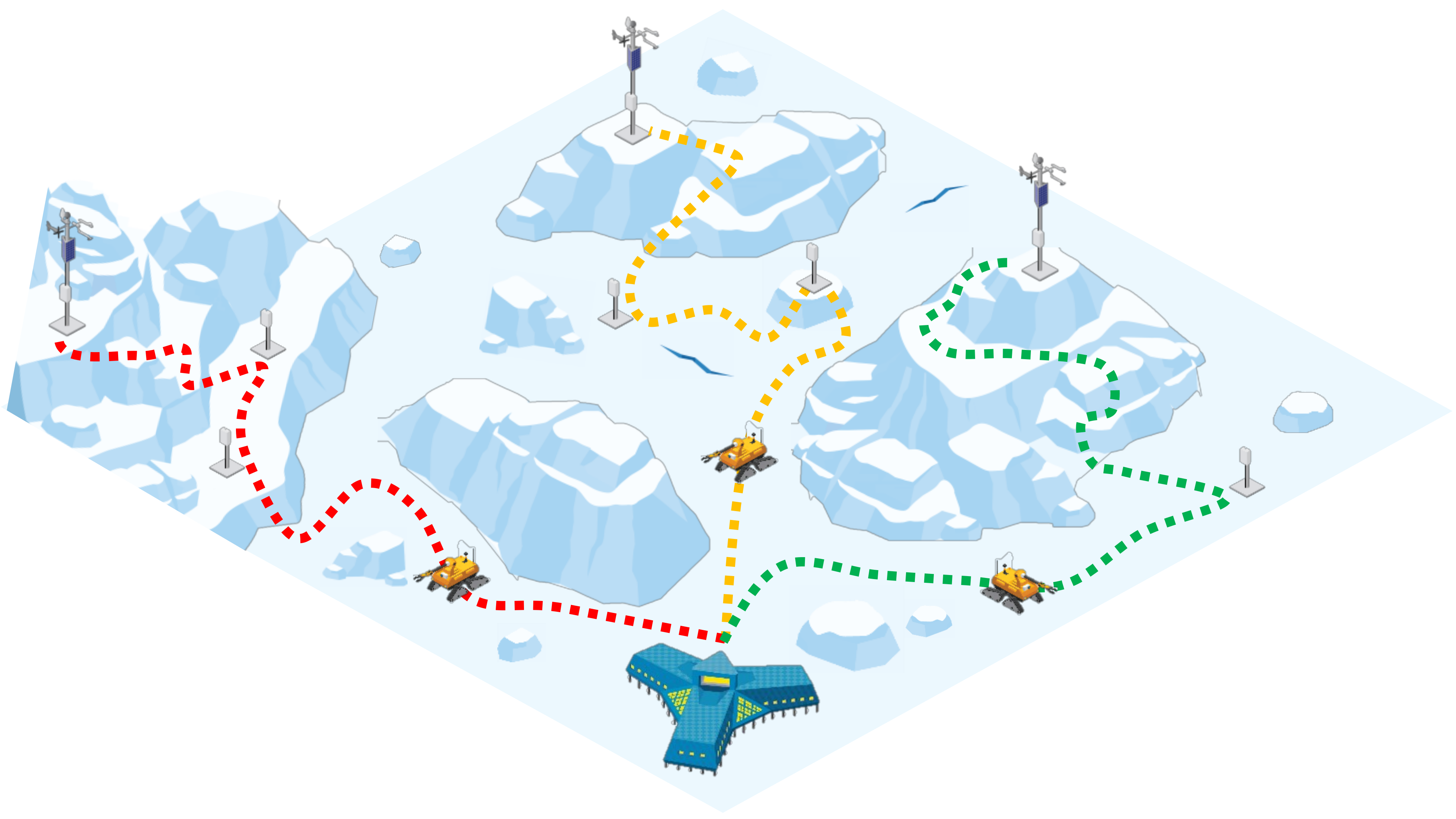
2.1. Antarctic Environments
2.2. Definition of MTSP
2.3. The Problem of Applying the Existing Scheduling Algorithm to Antarctic Environments
- (1)
- Select a starting point for any city and register it as a visiting node.
- (2)
- Move to the unvisited node with the lowest cost and register it as the visited node.
- (3)
- Repeat Step 2 if there is a city that was not visited.
- (1)
- Explore ants.
- (2)
- When the ants finish their search, they leave pheromones in the path of the ant that has the lowest cost.
- (3)
- Repeat as iteration.
- (4)
- After that, the ant that moved to the lowest cost becomes a solution.
3. Proposed Method
3.1. Overview
3.2. Cost Function
3.3. Ant Colony Optimization
| Algorithm 1 Multi-robot scheduling algorithm in Antarctic Environments | |
| 1: | Initialize the multi robot’s tour T |
| 2: | Set number of nodes that the robot will visit N and iteration I |
| 3: | for i N do |
| 4: | for j I do: |
| 5: | for each ant do |
| 6: | Build a solution according to the number of nodes i |
| 7: | Update local pheromone |
| 8: | end for |
| 9: | Update global pheromone |
| 10: | end for |
| 11: | Append best ant’s tour to T |
| 12: | end for |
| 13: | return Multi robot’s tour T |
4. Results
4.1. Results in Simulation Environments
4.2. Results in Real Antarctic Environments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Flood, M.M. The traveling-salesman problem. Oper. Res. 1956, 4, 61–75. [Google Scholar] [CrossRef]
- Croes, G.A. A Method for Solving Traveling-Salesman Problems. Oper. Res. 1958, 6, 791–812. [Google Scholar] [CrossRef]
- Beardwood, J.; Halton, J.H.; Hammersley, J.M. The shortest path through many points. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1959; pp. 299–327. [Google Scholar]
- Matai, R.; Singh, S.P.; Mittal, M.L. Traveling salesman problem: An overview of applications, formulations, and solution approaches. Travel. Salesm. Probl. Theory Appl. 2010, 1. [Google Scholar] [CrossRef]
- Chandra, A.; Naro, A. A Comparative Study of Metaheuristics Methods for Solving Traveling Salesman Problem. Int. J. Inf. Sci. Technol. 2022, 6, 1–7. [Google Scholar]
- Sathya, N.; Muthukumaravel, A. A survey of travelling salesman problem using heuristic search techniques. Int. J. Innov. Res. Comput. Commun. Eng. 2016, 4, 847–851. [Google Scholar]
- Johnson, D.S.; McGeoch, L.A. The traveling salesman problem: A case study in local optimization. Local Search Com-Binatorial Optim. 1997, 1, 215–310. [Google Scholar]
- Golberg, D.E. Genetic algorithms in search, optimization, and machine learning. Addion Wesley 1989, 102, 36. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Al Rahedi, N.T.; Atoum, J. Solving TSP problem using New Operator in Genetic Algorithms. Am. J. Appl. Sci. 2009, 6, 1586–1590. [Google Scholar]
- Dong, X.; Cai, Y. A novel genetic algorithm for large scale colored balanced traveling salesman problem. Futur. Gener. Comput. Syst. 2019, 95, 727–742. [Google Scholar] [CrossRef]
- Gambardella, L.M.; Dorigo, M. Solving symmetric and asymmetric TSPs by ant colonies. In Proceedings of the IEEE International Conference on Evolutionary Computation, Nagoya, Japan, 20–22 May 1996; pp. 622–627. [Google Scholar]
- Dorigo, M.; Gambardella, L. Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Trans. Evol. Comput. 1997, 1, 53–66. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef]
- Dorigo, M.; Gambardella, L.M. Ant colonies for the travelling salesman problem. Biosystems 1997, 43, 73–81. [Google Scholar] [CrossRef]
- Dorigo, M.; Di Caro, G. Ant colony optimization: A new meta-heuristic. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; pp. 1470–1477. [Google Scholar]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Peker, M.; Şen, B.; Kumru, P.Y. An efficient solving of the traveling salesman problem: The ant colony system having parameters optimized by the Taguchi method. Turk. J. Electr. Eng. Comput. Sci. 2013, 21, 2015–2036. [Google Scholar] [CrossRef]
- Gülcü, Ş.; Mahi, M.; Baykan, Ö.K.; Kodaz, H. A parallel cooperative hybrid method based on ant colony optimization and 3-Opt algorithm for solving traveling salesman problem. Soft Comput. 2018, 22, 1669–1685. [Google Scholar] [CrossRef]
- Wang, Y.; Han, Z. Ant colony optimization for traveling salesman problem based on parameters optimization. Appl. Soft Comput. 2021, 107, 107439. [Google Scholar] [CrossRef]
- Bellmore, M.; Hong, S. Transformation of Multisalesman Problem to the Standard Traveling Salesman Problem. J. ACM 1974, 21, 500–504. [Google Scholar] [CrossRef]
- Rao, M.R. Technical Note—A Note on the Multiple Traveling Salesmen Problem. Oper. Res. 1980, 28, 628–632. [Google Scholar] [CrossRef]
- Kara, I.; Bektas, T. Integer linear programming formulations of multiple salesman problems and its variations. Eur. J. Oper. Res. 2006, 174, 1449–1458. [Google Scholar] [CrossRef]
- Venkatesh, P.; Singh, A. Two metaheuristic approaches for the multiple traveling salesperson problem. Appl. Soft Comput. 2015, 26, 74–89. [Google Scholar] [CrossRef]
- Jiang, C.; Wan, Z.; Peng, Z. A new efficient hybrid algorithm for large scale multiple traveling salesman problems. Expert Syst. Appl. 2019, 139, 112867. [Google Scholar] [CrossRef]
- Bektas, T. The multiple traveling salesman problem: An overview of formulations and solution procedures. Omega 2006, 34, 209–219. [Google Scholar] [CrossRef]
- Cheikhrouhou, O.; Khoufi, I. A comprehensive survey on the Multiple Traveling Salesman Problem: Applications, approaches and taxonomy. Comput. Sci. Rev. 2021, 40, 100369. [Google Scholar] [CrossRef]
- Zheng, J.; Hong, Y.; Xu, W.; Li, W.; Chen, Y. An effective iterated two-stage heuristic algorithm for the multiple Traveling Salesmen Problem. Comput. Oper. Res. 2022, 143, 105772. [Google Scholar] [CrossRef]
- Ray, L.E.; Lever, J.H.; Streeter, A.D.; Price, A.D. Design and power management of a solar-powered “cool robot” for polar instrument networks. J. Field Robot. 2007, 24, 581–599. [Google Scholar] [CrossRef]
- Lever, J.H.; Delaney, A.J.; E Ray, L.; Trautmann, E.; Barna, L.A.; Burzynski, A.M. Autonomous GPR Surveys using the Polar Rover Yeti. J. Field Robot. 2012, 30, 194–215. [Google Scholar] [CrossRef]











| Part | Node 20 | Node 30 | Node 40 |
|---|---|---|---|
| Nearest Neighbor | 5476.98 | 6255.67 | 7943.39 |
| Genetic Algorithm | 5729.22 | 6348.65 | 8335.68 |
| Proposed Method | 5584.36 | 5784.93 | 6484.76 |
| Part | Node 10 | Node 20 | Node 30 |
|---|---|---|---|
| Nearest Neighbor | 82.01 km | 99.89 km | 145.67 km |
| Genetic Algorithm | 79.41 km | 93.93 km | 141.36 km |
| Proposed Method | 78.17 km | 82.95 km | 122.78 km |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Lee, H. Multi-Robot Task Scheduling with Ant Colony Optimization in Antarctic Environments. Sensors 2023, 23, 751. https://doi.org/10.3390/s23020751
Kim S, Lee H. Multi-Robot Task Scheduling with Ant Colony Optimization in Antarctic Environments. Sensors. 2023; 23(2):751. https://doi.org/10.3390/s23020751
Chicago/Turabian StyleKim, Seokyoung, and Heoncheol Lee. 2023. "Multi-Robot Task Scheduling with Ant Colony Optimization in Antarctic Environments" Sensors 23, no. 2: 751. https://doi.org/10.3390/s23020751
APA StyleKim, S., & Lee, H. (2023). Multi-Robot Task Scheduling with Ant Colony Optimization in Antarctic Environments. Sensors, 23(2), 751. https://doi.org/10.3390/s23020751






