Research on Two-Round Self-Balancing Robot SLAM Based on the Gmapping Algorithm
Abstract
:1. Introduction
2. Design of a Self-Balancing Mobile System for the Inspection Robot
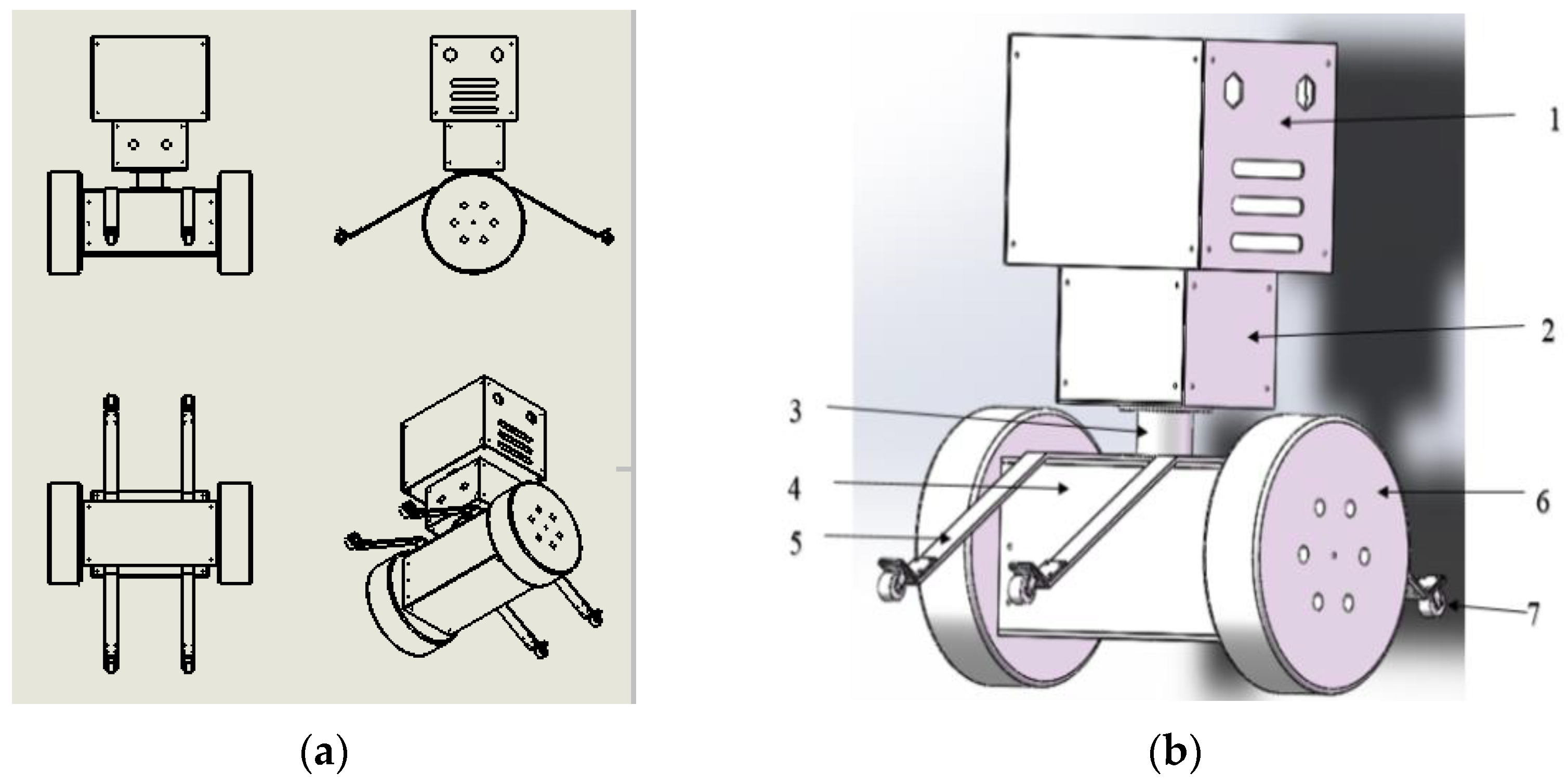
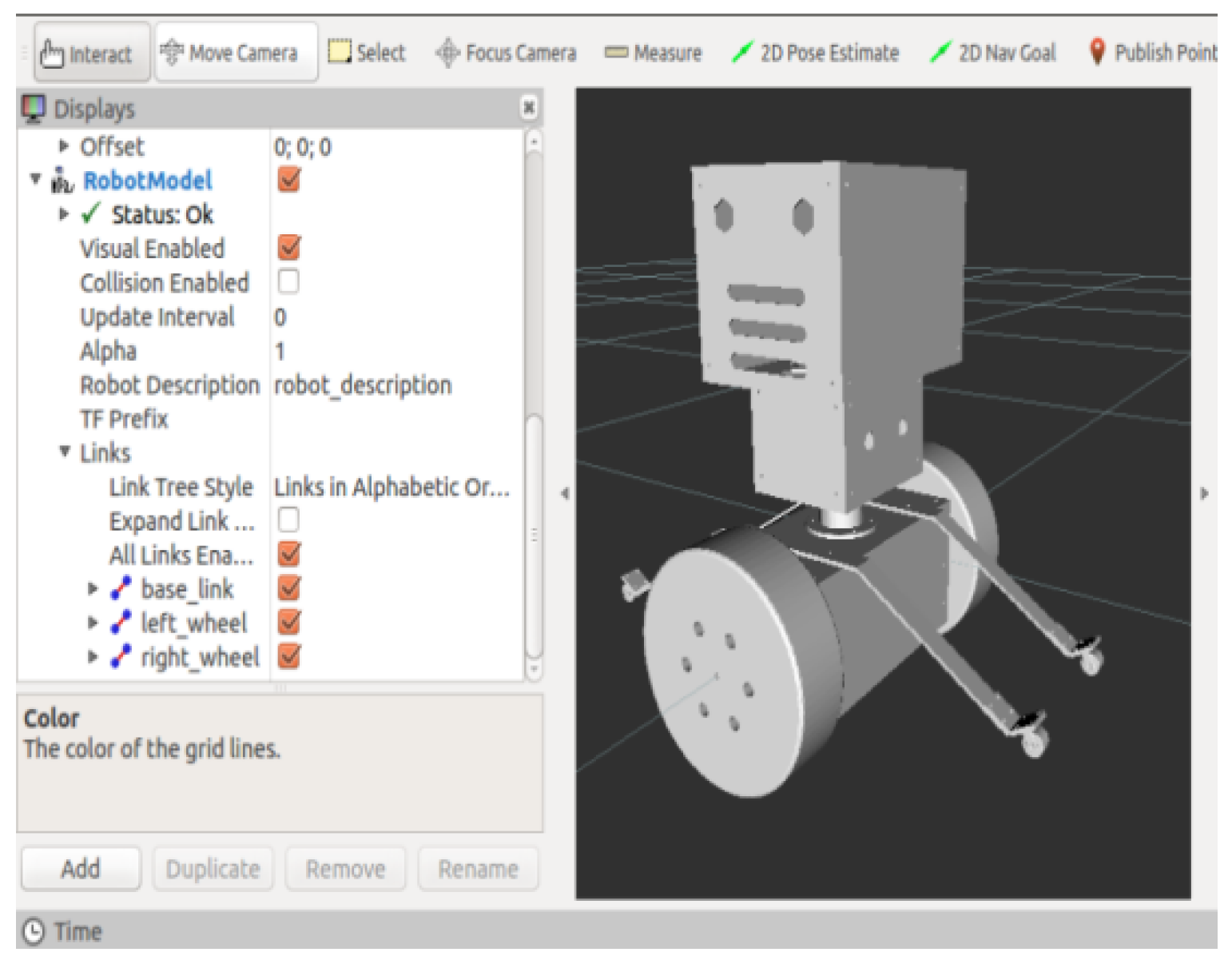
2.1. Overall Mechanical Structure Design of the Inspection Robot
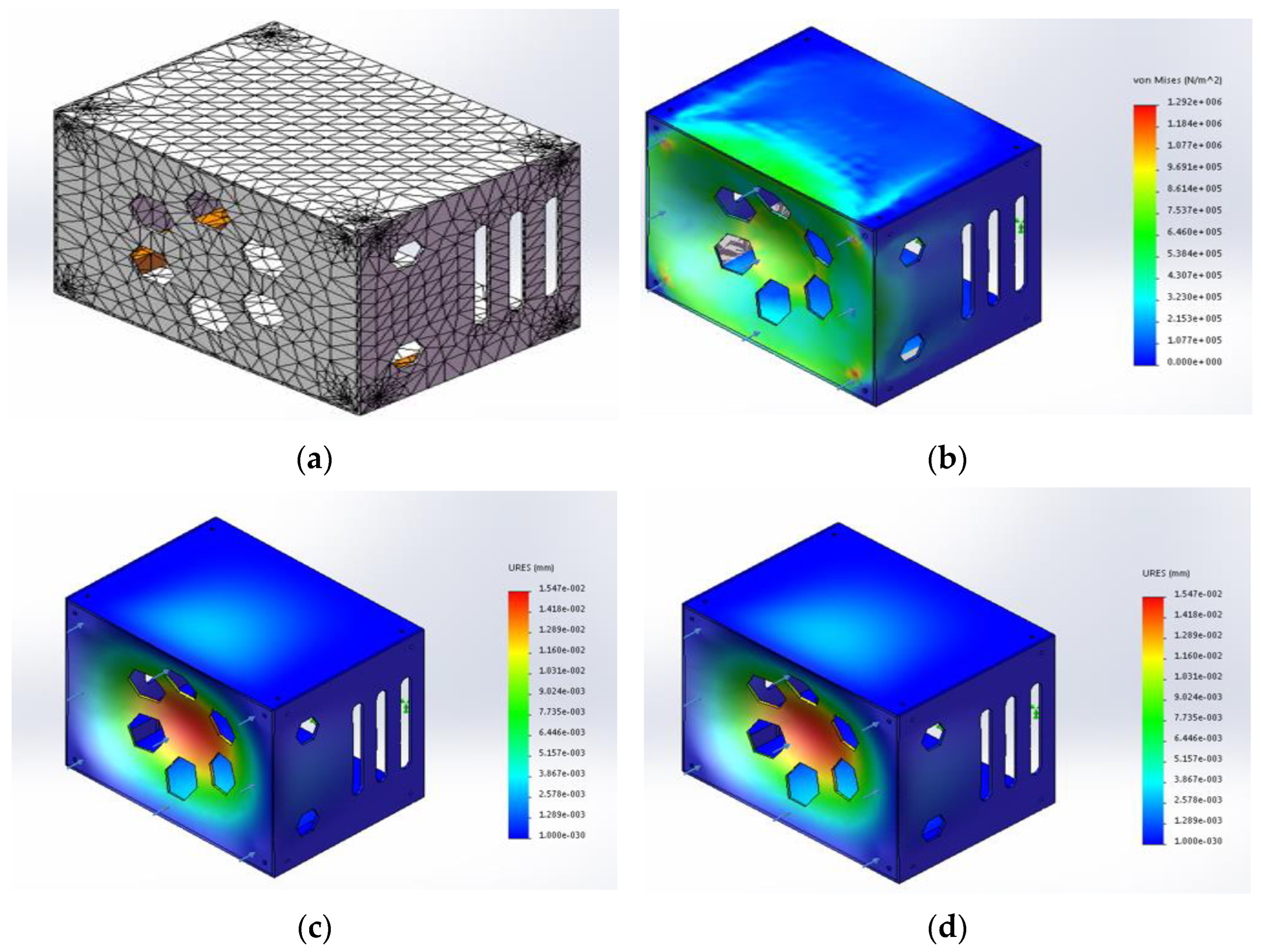
2.2. Statics Analysis of Two-Wheel Self-Balancing Mechanical Structures
2.2.1. Force Analysis of Head Structure of Two-Wheel Self-Balancing Robot
2.2.2. Force Analysis of Bottom Structure of Two-Wheel Self-Balancing Robot
3. Modeling and Analysis of the Two-Wheel Self-Balancing Robot System
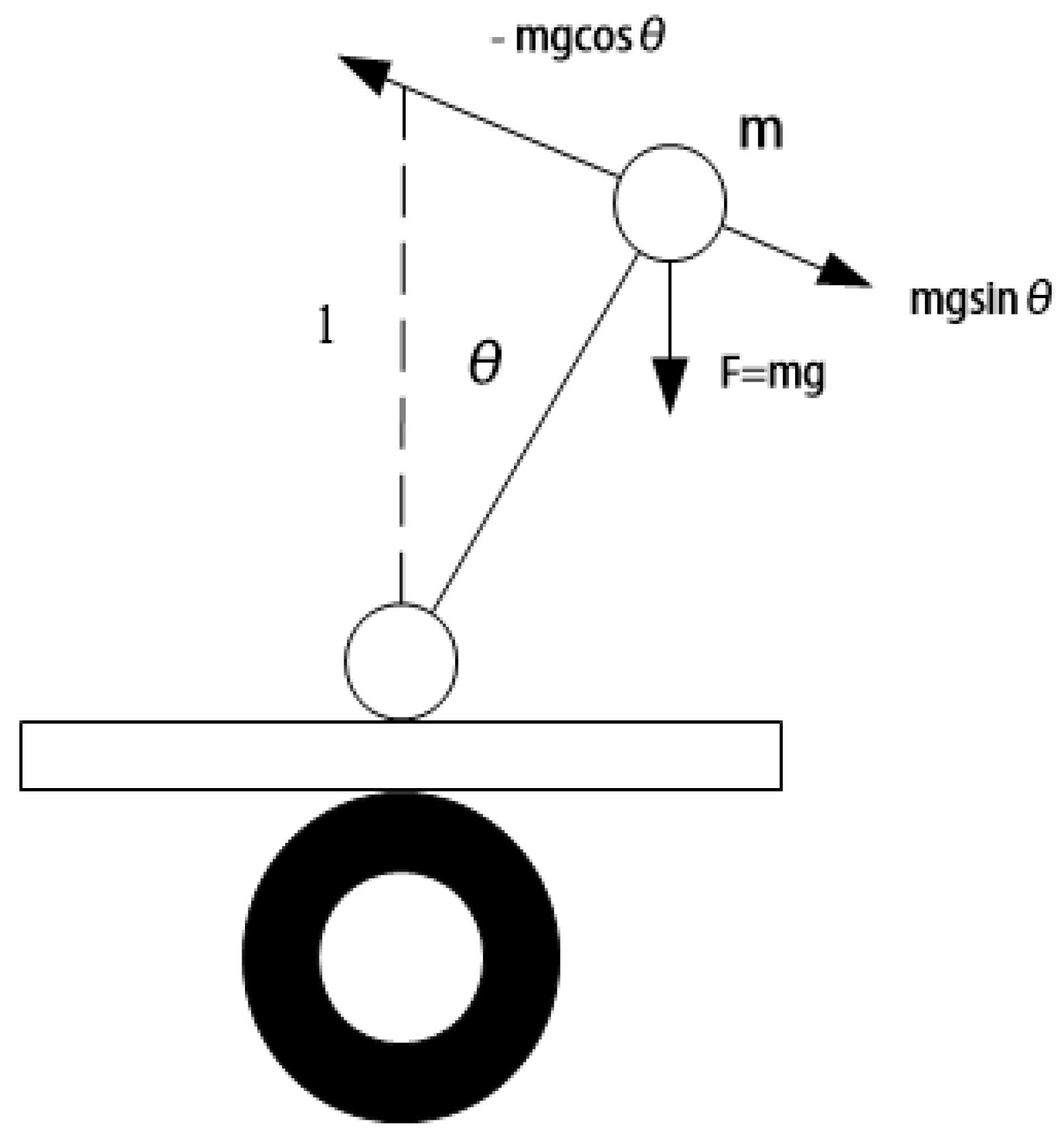
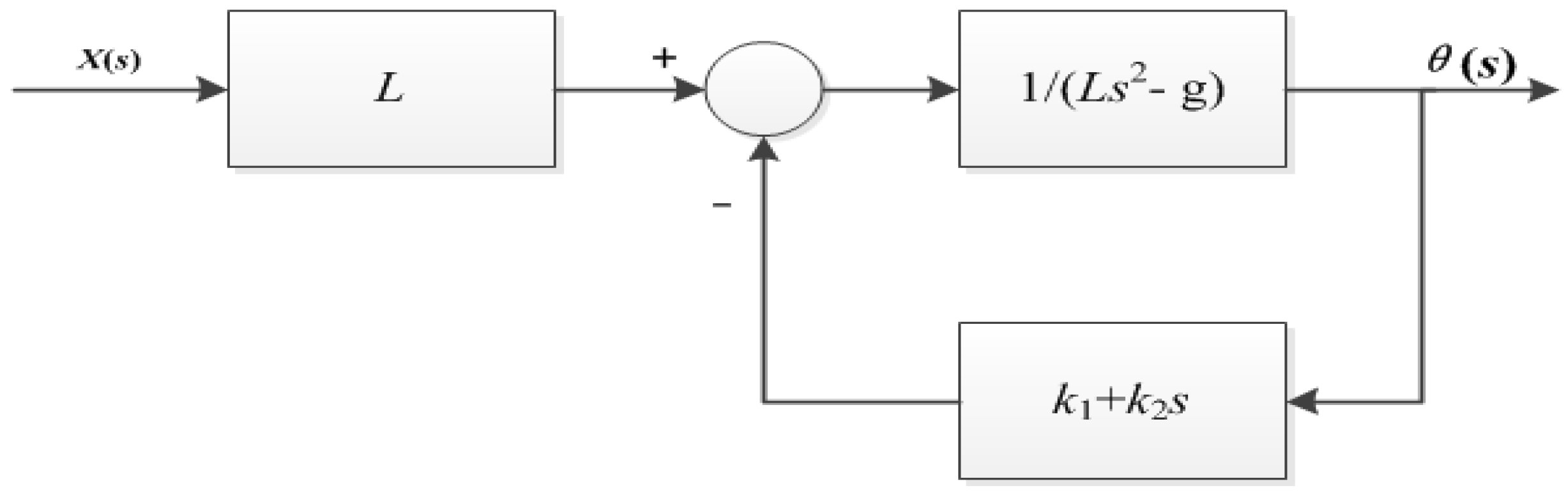
3.1. Force Analysis of the Two-Wheel Self-Balancing Model
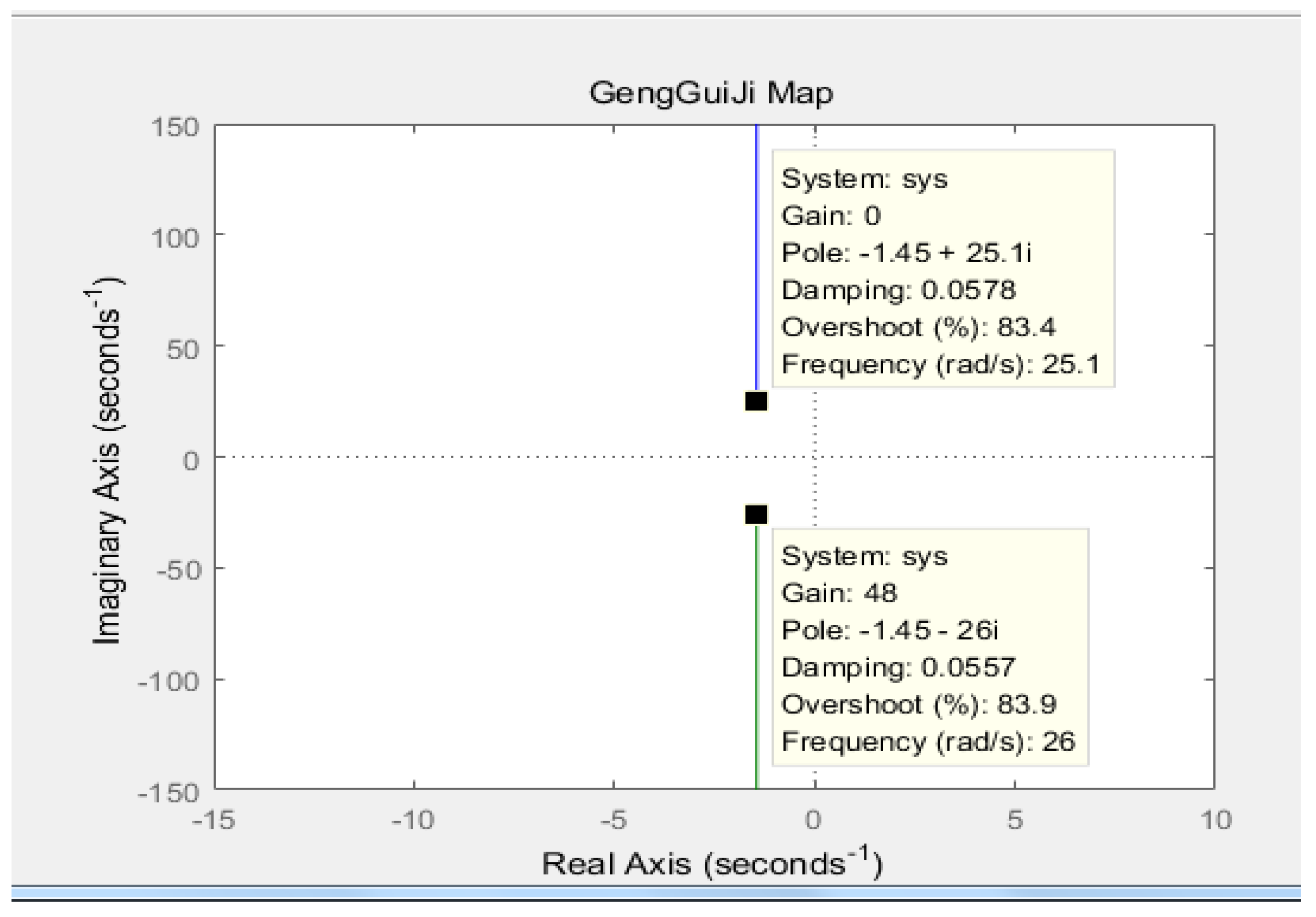
3.2. Modeling and Analysis of the Two-Wheel Self-Balancing Robot System
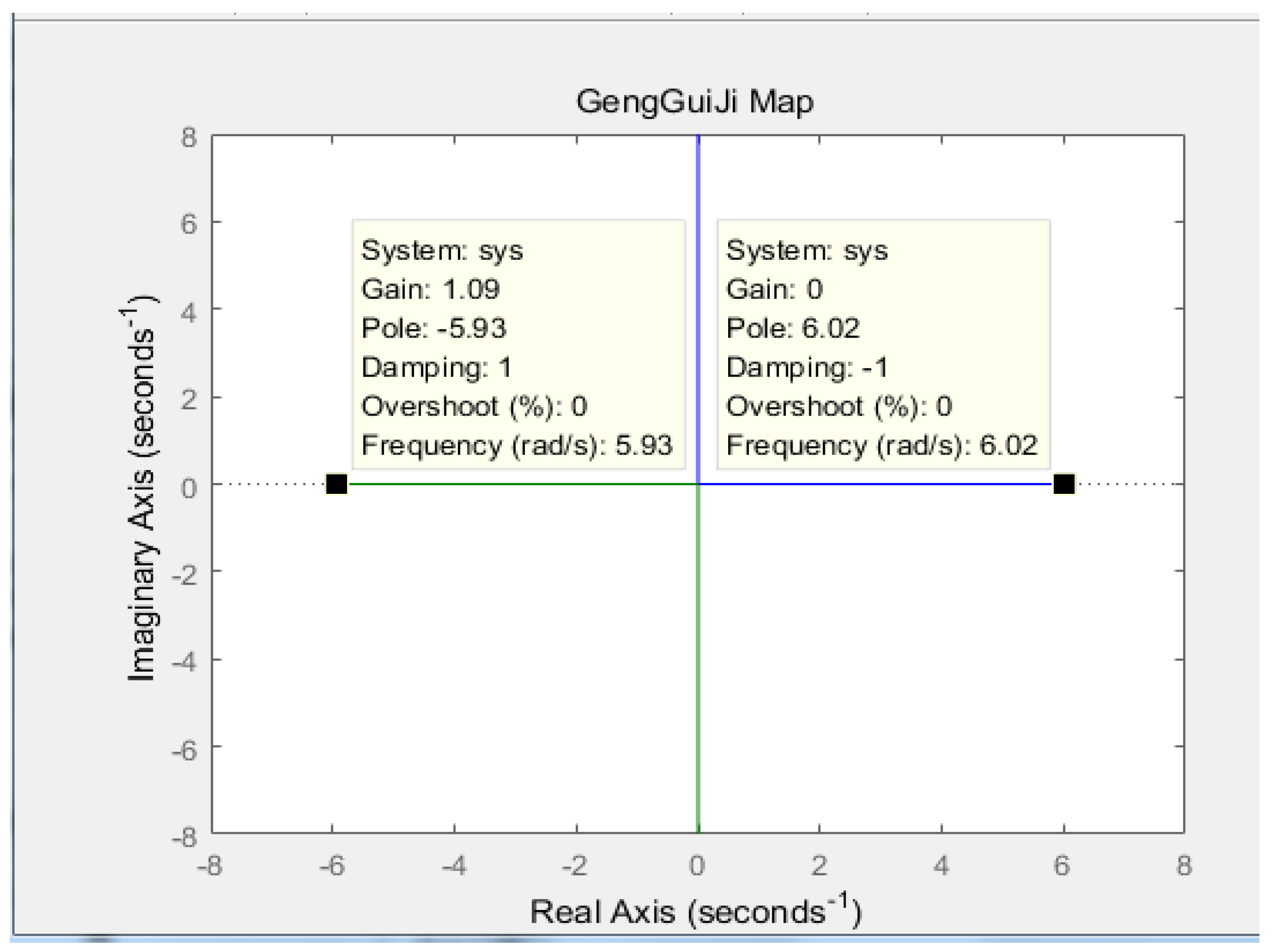
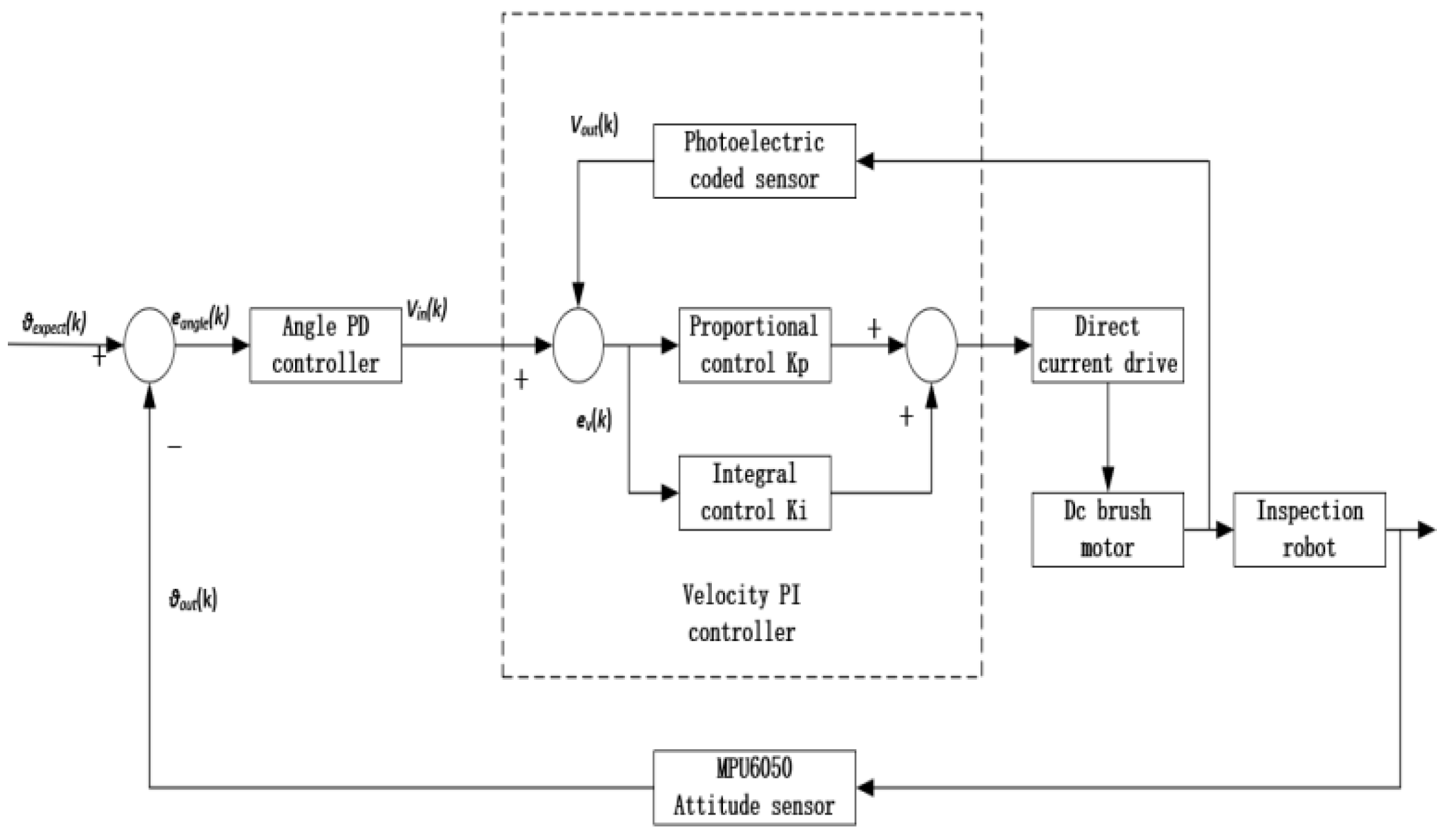
3.3. Design of the Self-Balancing Algorithm for the Two-Wheel Robot
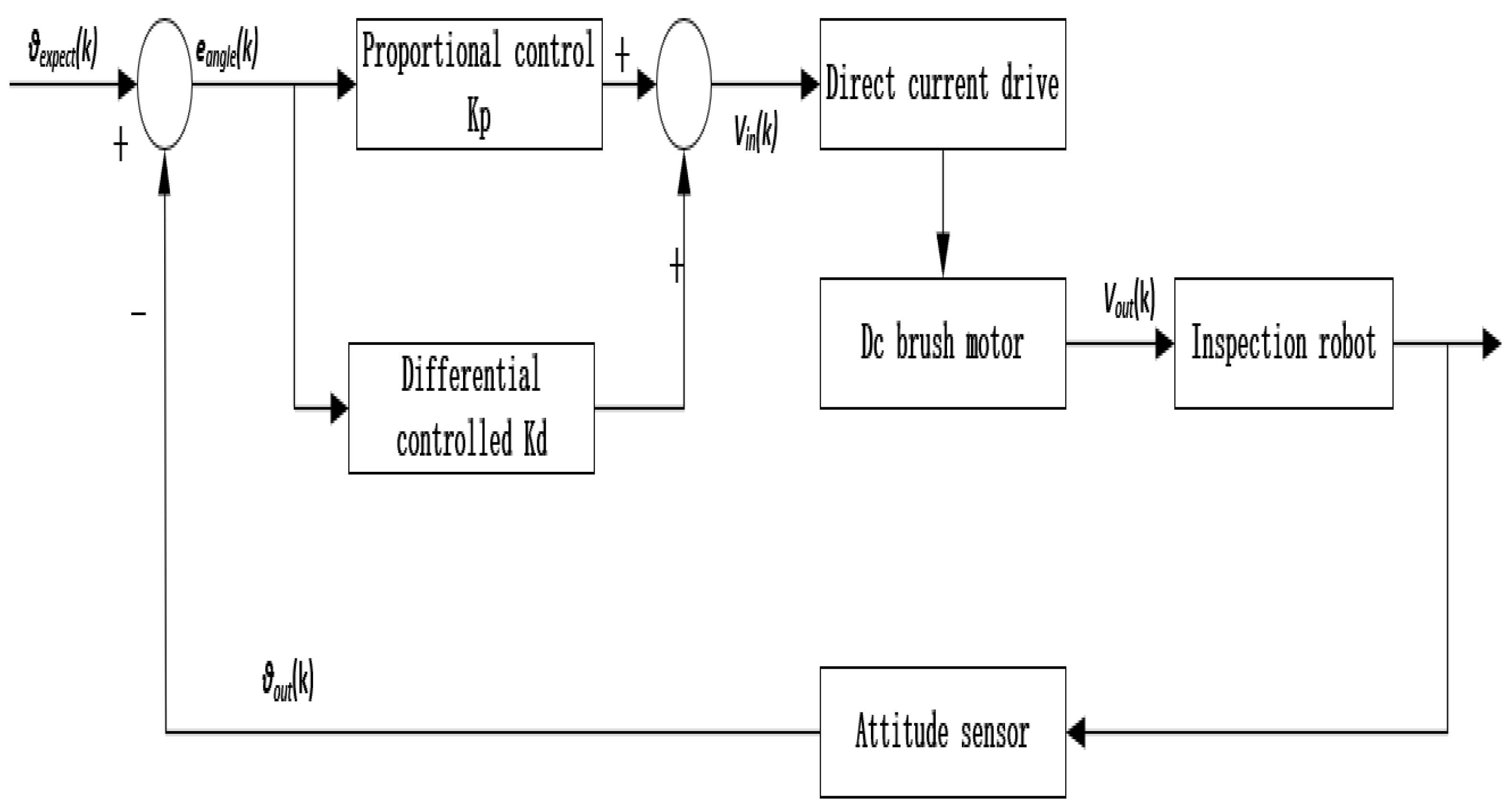
3.3.1. Two-Wheel Self-Balancing Robot Upright Ring Control
3.3.2. Two-Wheel Self-Balancing Robot Speed Loop Control
4. Research on Two Rounds of the Self-Balancing Robotic LiDAR SLAM
4.1. Two Rounds of the Self-Balancing Laser SLAM Research
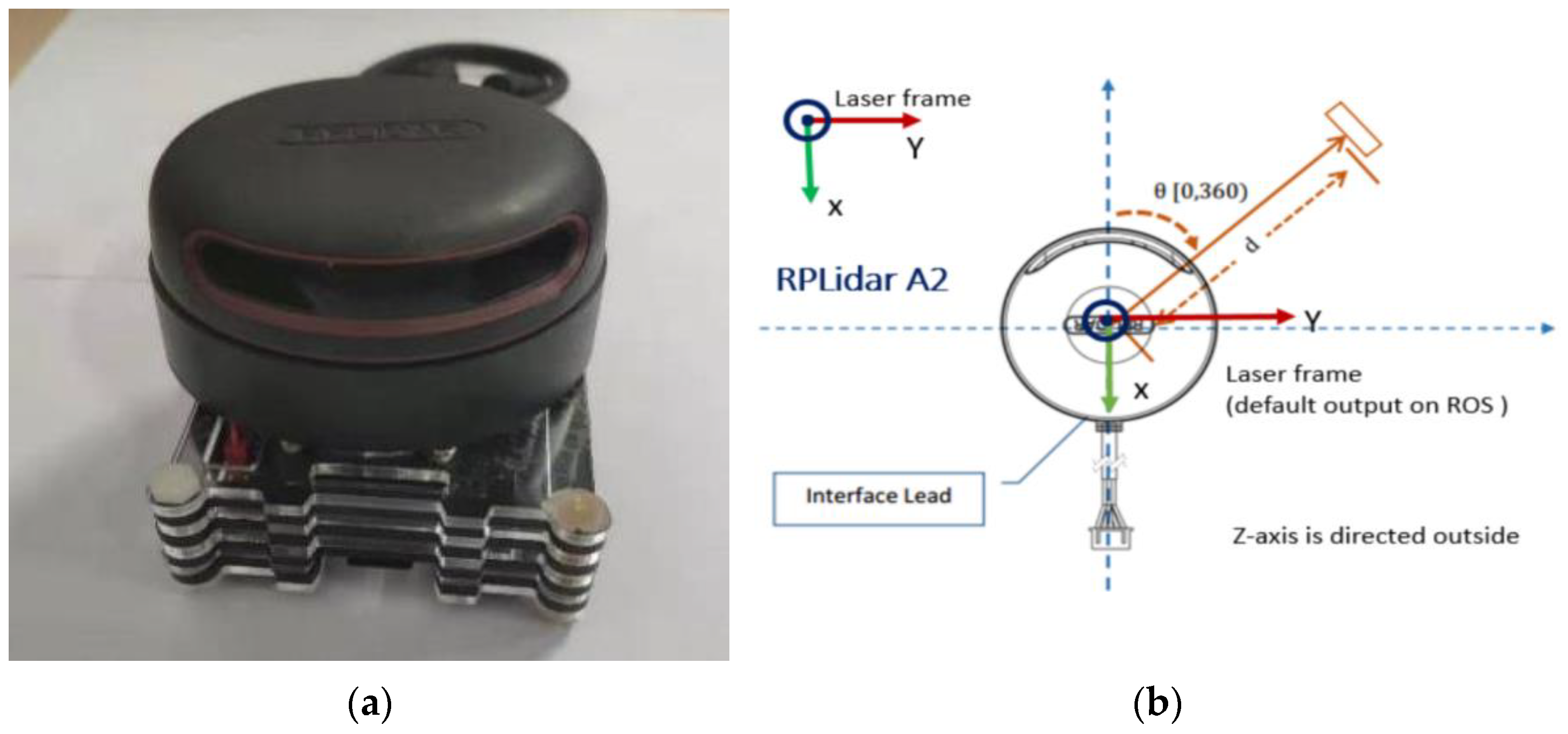
4.2. Two-Wheel Self-Balancing Robotic LiDAR Sensor
4.3. Research on the Gmapping Algorithm of the Two-Wheel Self-Balancing Robot Based on the 2D LiDAR
4.3.1. Particle Filter
4.3.2. The Gmapping Algorithm Based on RBPF
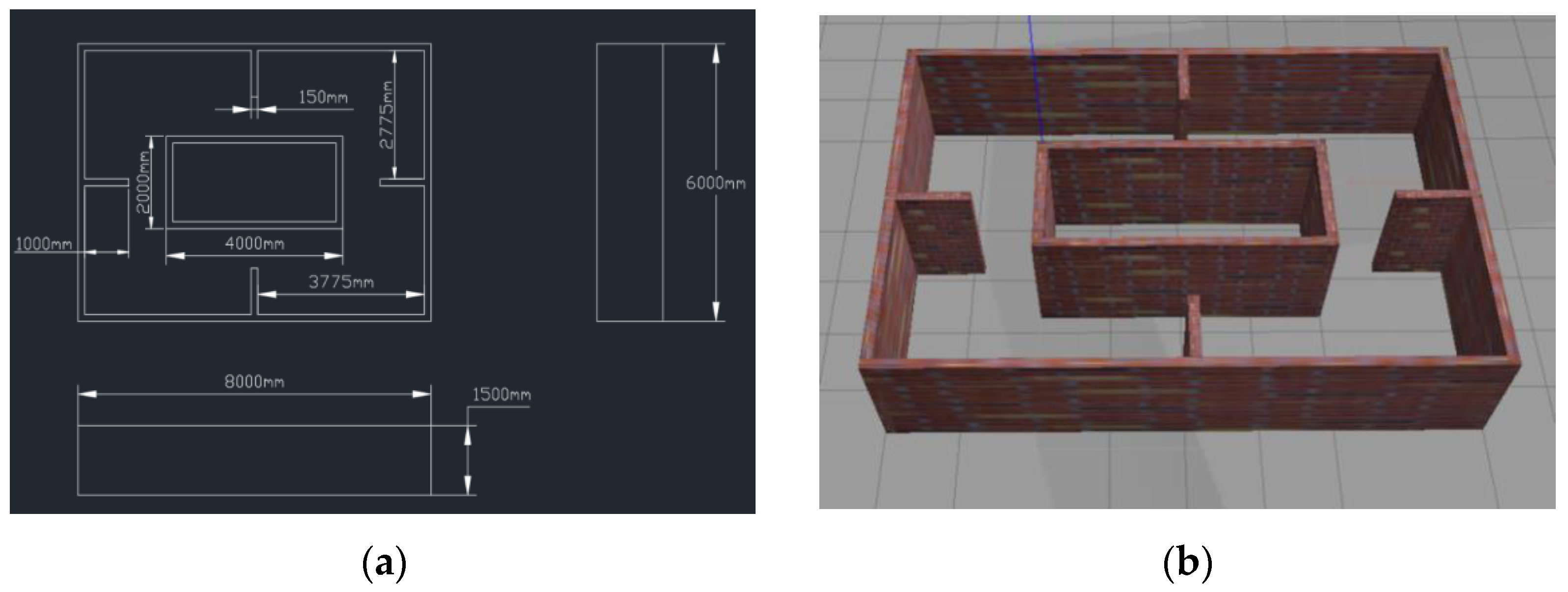
4.4. A Simulation Experiment of the Inspection Robot Based on the Gmapping Algorithm
5. The Experiment and Analysis of the Two-Wheel Self-Balancing Inspection Robot
5.1. Test and Analysis of the Robot Self-Balancing Algorithm
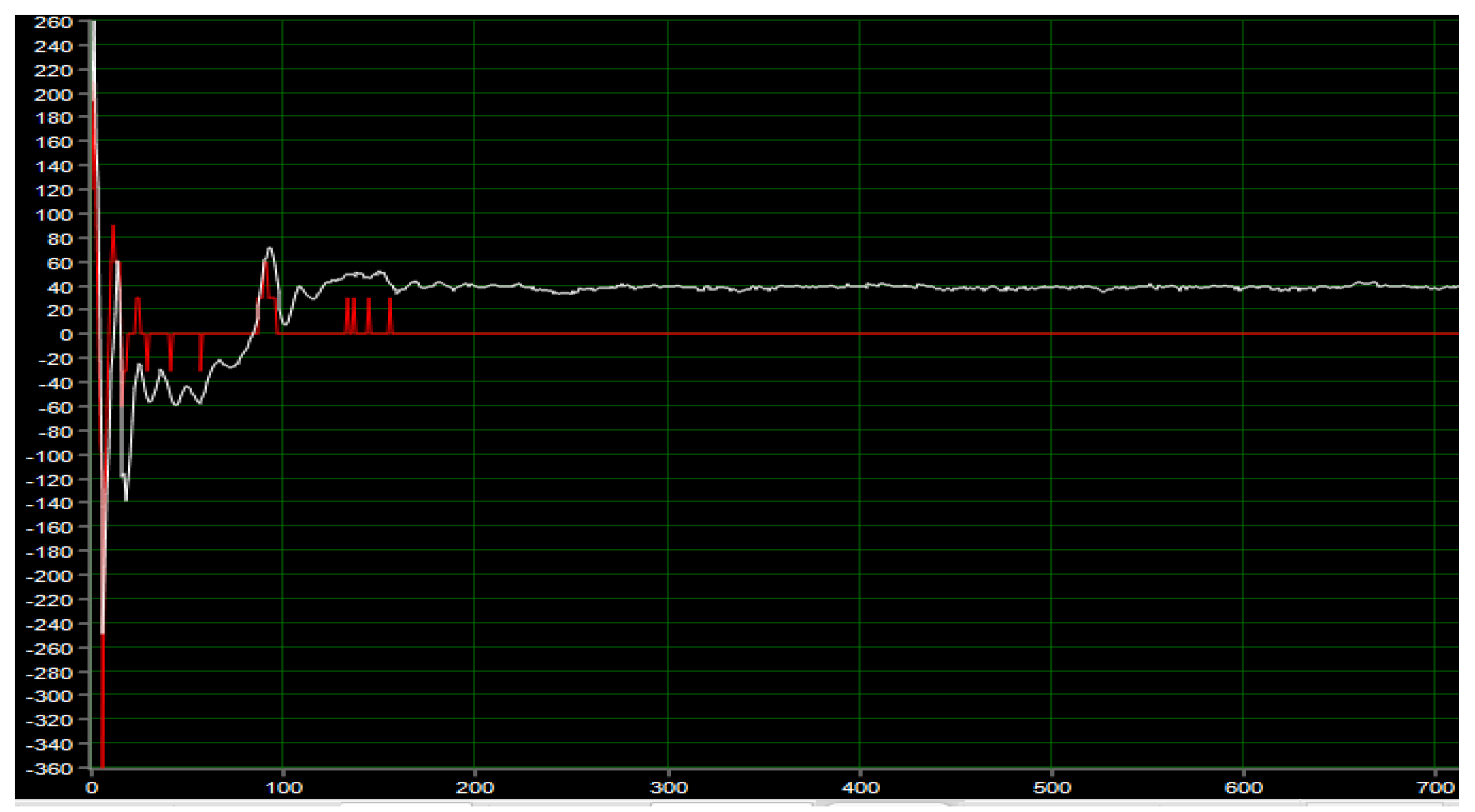
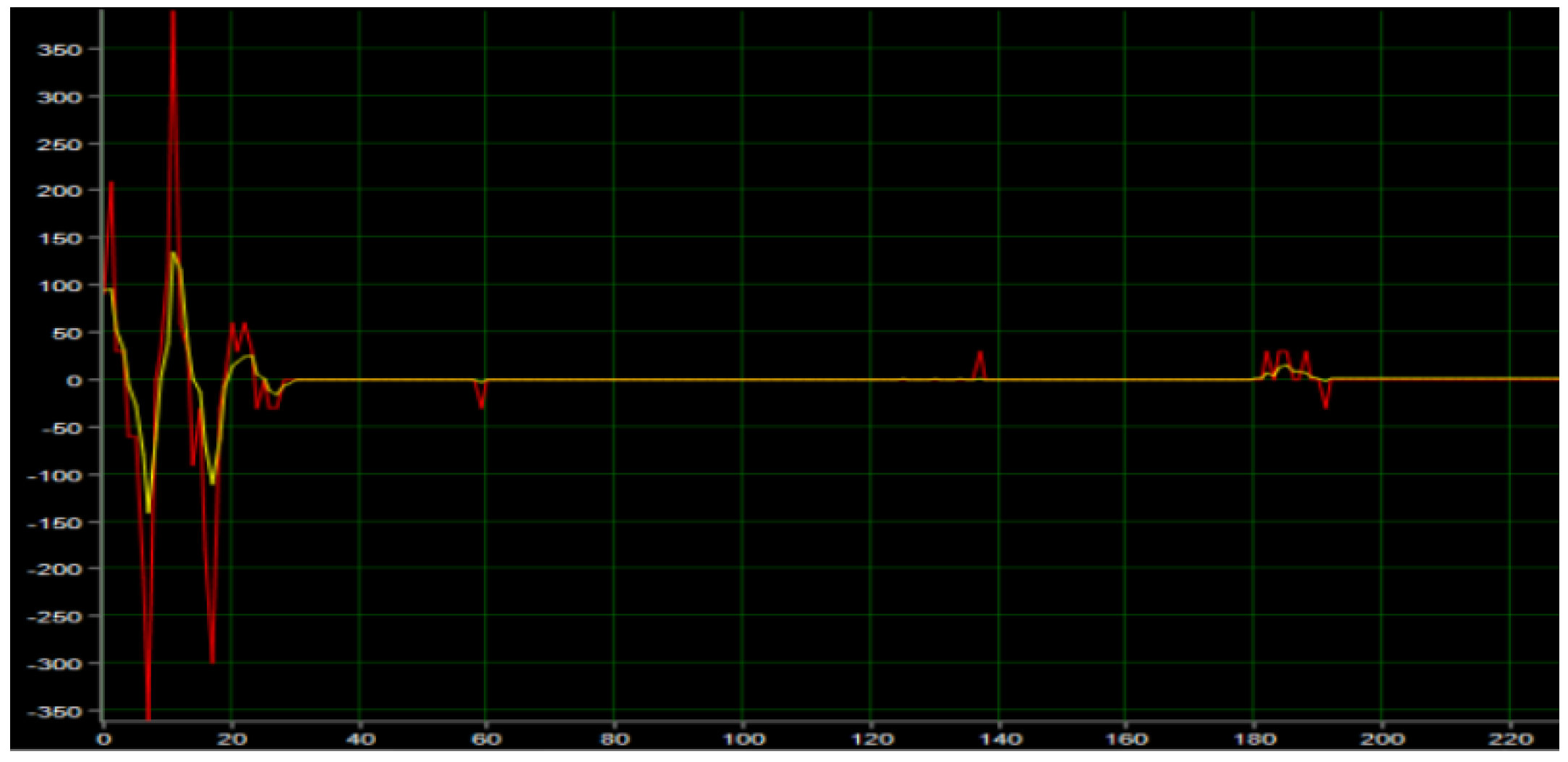
5.1.1. Pose Test of Robot at Rest
5.1.2. Posture Experiment in a Self-Balancing Stable State
5.1.3. Robot Attitude Experiment after Adding the Load
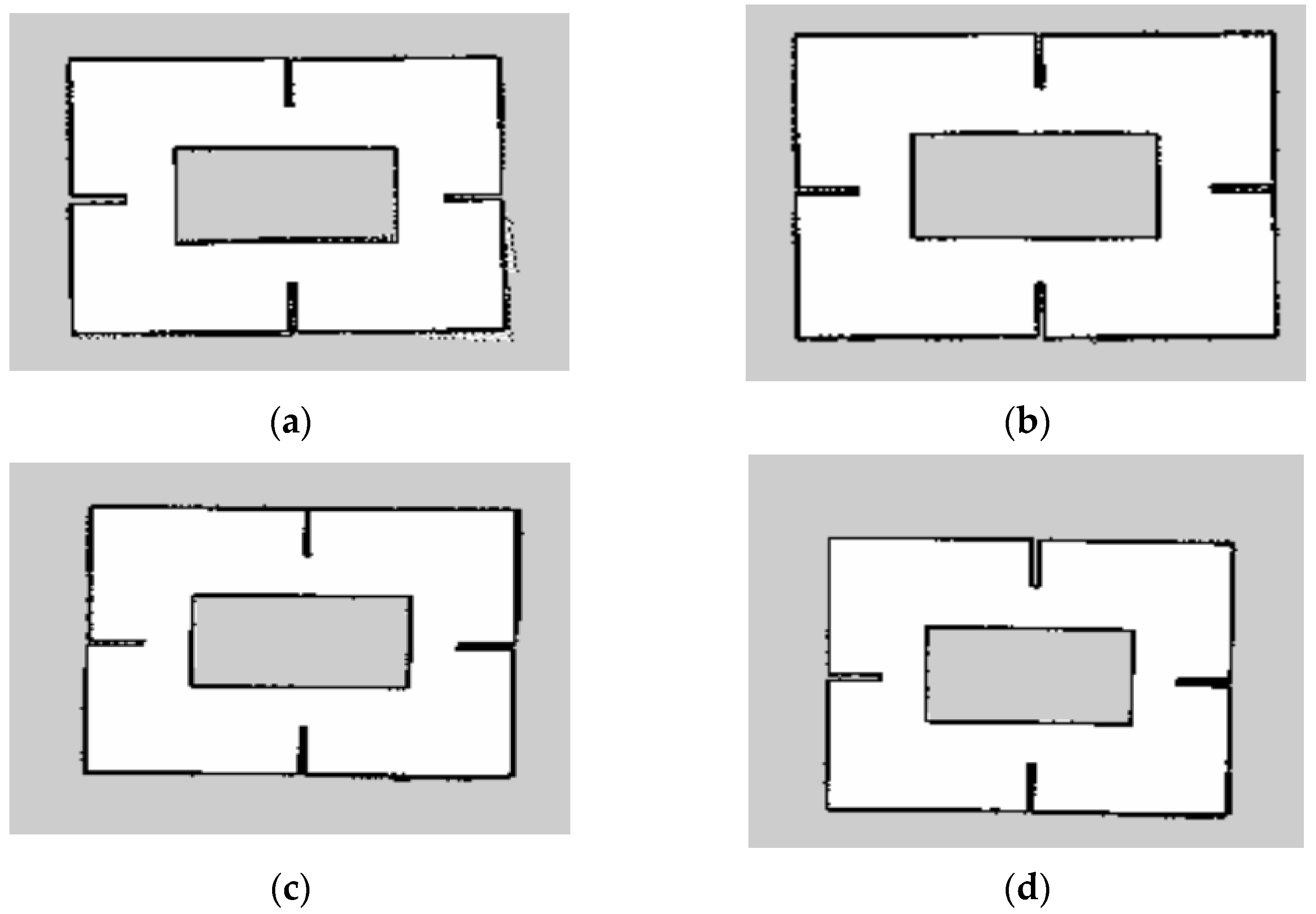
5.2. Map Construction Experiment of the Two-Wheel Self-Balancing Robot
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zu, L.; Zhang, Q.; Liang, J.; Wang, J. A Research of substation inspection robot navigation method. Sci. Technol. Eng. 2014, 14, 198–201. [Google Scholar]
- Daisuke, K.; Satoki, T.; Gustavo Alfonso Garcia, R.; Jun, T.; Tsukasa, O. Alignment of Occupancy Grid and Floor Maps Using Graph Matching. In Proceedings of the 2017 IEEE 11th International Conference on Semantic Computing (ICSC), San Diego, CA, USA, 30 Janaury–1 February 2017; pp. 57–60. [Google Scholar]
- Qiu, J.; Wu, J.; Jin, S.; Jin, Y.; Shi, J. Research on Inspection robot of Coal mine Water pump House based on Optimized Fast-SLAM. Coal Eng. 2021, 53, 139–145. [Google Scholar]
- Qiao, L. Research On Control Strategy of Two-Wheeled Self-Balancing Robot. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2019. [Google Scholar]
- Lin, X.; Zhang, S.; Chen, J.; Zhao, Z. Finite element simulation analysis integrated information model based on Design Reuse. Comput. Integr. Manuf. Syst. 2009, 15, 2296–2302. [Google Scholar]
- Wang, X. Design of Two-Wheel Balancing Vehicle System Based on Genetic PD Control. Ph.D. Thesis, Harbin University of Science and Technology, Harbin, China, 2018. [Google Scholar]
- Tang, L. Modeling and Control of Inverted Pendulum System. Ph.D. Thesis, Henan University, Kaifeng, China, 2013. [Google Scholar]
- Zhou, D. Structure and Control System Design of Weight Reduction Walking Aid Robot. Ph.D. Thesis, Anhui University of Science and Technology, Huainan, China, 2022. [Google Scholar]
- Chen, W.; Zhang, F. Research progress of synchronous self-localization and map creation for mobile robots. Control Theory Appl. 2005, 3, 455–460. [Google Scholar]
- Xu, B.; Xu, M.; Chen, L.; Tan, Y. A review of full coverage path planning algorithms for intelligent machinery. Comput. Meas. Control 2016, 24, 1−5+53. [Google Scholar]
- González, O.M.; Novel, C.; Said, A.; Ángel, T. Autonomous 2D SLAM and 3D Mapping of an Environment Using a Single 2D LIDAR and ROS. In Proceedings of the 2017 Latin American Robotics Symposium (LARS) and 2017 Brazilian Symposium on Robotics (SBR), Curitiba, Brazil, 8–10 November 2017. [Google Scholar]
- Li, W. Application of sensors in UAV flight control system. Professional 2019, 25, 122–123. [Google Scholar]
- Zhang, P. Research and Implementation of Indoor Path Planning Technology for Mobile Robots. Ph.D. Thesis, Xi’an University of Science and Technology, Xi’an, China, 2018. [Google Scholar]
- Yang, L.; Ma, H.; Wang, Y. SLAM Algorithm for underground Mobile Robot based on Laser Inertia Fusion. J. China Coal Soc. 2022, 47, 3523–3534. [Google Scholar]
- Du, Z. Research on SLAM and Navigation Technology of Indoor Mobile Robot Based on LiDAR. Ph.D. Thesis, Hubei University of Technology, Wuhan, China, 2019. [Google Scholar]
- Giorgio, G.; Cyrill, S.; Wolfram, B. Improved techniques for grid mapping with Rao-Blackwellized particle filters. IEEE Trans. Robot. 2007, 23, 34–46. [Google Scholar]
- Zhu, M. Research on Mobile Robot Closed-Loop Detection Algorithm Based on Vision SLAM. Ph.D. Thesis, Zhejiang Gongshang University, Hangzhou, China, 2022. [Google Scholar]
- Zhao, X. Robot Localization and Target Tracking Based on Particle Filter. Ph.D. Thesis, Ocean University of China, Qingdao, China, 2008. [Google Scholar]
- Qiu, H. Research on Semantic Map Construction Method of Cloud Mobile Robot. Ph.D. Thesis, Southeast University, Nanjing, China, 2021. [Google Scholar]
- Stephen, H.; Paul, D.; Kimberly, H. The Affordance Template ROS Package for Robot Task Programming. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; Volume 2015, pp. 6227–6234. [Google Scholar]
- Lopez, N.G.; Nuin YL, E.; Moral, E.B.; Juan LU, S.; Rueda, A.S.; Vilches, V.M.; Kojcev, R. Gym-gazebo2, a toolkit for reinforcement learning using ROS 2 and Gazebo. arXiv 2019, arXiv:1903.06278. [Google Scholar]
- Li, H.; Qiao, X.; Niu, K. Research on Building Mobile Robot Mapping Based on 2D Laser Radar. Available online: https://cpfd.cnki.com.cn/Article/CPFDTOTAL-SGJS202112001056.htm (accessed on 22 November 2022).










| The Material Properties | The Parameter Value | Unit |
|---|---|---|
| Modulus of Elasticity | 2.05 × 1011 | N/m2 |
| Poisson’s Ratio | 2.9 × 10−1 | None |
| The Shear Modulus | 8 × 1010 | N/m2 |
| Mass Density | 7.858 × 103 | kg/m3 |
| The Tension Strength | 4.25 × 108 | N/m2 |
| The Yield Strength | 2.82685 × 108 | N/m2 |
| The Material Properties | The Parameter Value | Unit |
|---|---|---|
| Modulus of Elasticity | 1.18 × 1011 | N/m2 |
| Poisson’s Ratio | 3.35 × 10−1 | None |
| The Shear Modulus | 3.32 × 109 | N/m2 |
| Mass Density | 2.0 × 103 | kg/m3 |
| The Tension Strength | 3.0 × 107 | N/m2 |
| The Yield Strength | 1.5 × 108 | N/m2 |
| Name | Type | The Minimum Value | The Maximum Value |
|---|---|---|---|
| Stress | VON: von Mises | 0 N/m2 | 1.29208 × 106 N/m2 |
| The Displacement | URES | 0 mm | 1.54699 ×10−2 mm |
| Strain | ESTRN | 0 | 7.60008 × 10−6 |
| Name | Type | The Minimum Value | The Maximum Value |
|---|---|---|---|
| Stress | VON: von Mises | 1.48067 × 103 N/m2 | 4.2585 × 106 |
| The Displacement | URES | 0 mm | 1.35066 × 10−2 mm |
| Strain | ESTRN | 1.27093 × 10−8 | 2.06188 × 10−5 |
| Measurement Reference Point | Label | The Actual Value/cm | Measured Value/cm | Absolute Error/cm | The Relative Error |
|---|---|---|---|---|---|
| A | 1 | 400 | 393.2 | 6.8 | 1.7% |
| B | 2 | 200 | 204.4 | 4.4 | 2.2% |
| C | 3 | 570 | 566.8 | 3.2 | 0.6% |
| D | 4 | 100 | 101.1 | 1.1 | 1.1% |
| E | 5 | 15 | 17.0 | 2 | 13.3% |
| F | 6 | 770 | 766.6 | 3.4 | 0.4% |
| G | 7 | 85 | 82.3 | 2.7 | 3.2% |
| H | 8 | 185 | 181.4 | 3.6 | 1.9% |
| I | 9 | 185 | 181.9 | 3.1 | 1.7% |
| Measurement Reference Point | Label | The Actual Value/cm | Measured Value/cm | Absolute Error/cm | The Relative Error |
|---|---|---|---|---|---|
| A | 1 | 400 | 404.5 | 4.5 | 1.1% |
| B | 2 | 200 | 198.8 | 1.2 | 2.2% |
| C | 3 | 570 | 565.5 | 3.5 | 0.6% |
| D | 4 | 100 | 96.5 | 3.5 | 1.1% |
| E | 5 | 15 | 17.3 | 2.3 | 15.3% |
| F | 6 | 770 | 766.1 | 3.9 | 0.5% |
| G | 7 | 85 | 82.1 | 2.9 | 3.4% |
| H | 8 | 185 | 182.9 | 2.1 | 1.1% |
| I | 9 | 185 | 182.8 | 2.2 | 1.2% |
| Measurement Reference Point | Label | The Actual Value/cm | Measured Value/cm | Absolute Error/cm | The Relative Error |
|---|---|---|---|---|---|
| A | 1 | 400 | 399.4 | 0.6 | 0.1% |
| B | 2 | 200 | 199.2 | 0.8 | 0.4% |
| C | 3 | 570 | 568.8 | 1.2 | 0.2% |
| D | 4 | 100 | 101.5 | 1.5 | 1.5% |
| E | 5 | 15 | 16.4 | 1.4 | 9.3% |
| F | 6 | 770 | 764.9 | 5.1 | 0.7% |
| G | 7 | 85 | 83.2 | 1.8 | 2.1% |
| H | 8 | 185 | 183.8 | 1.2 | 0.6% |
| I | 9 | 185 | 182.7 | 2.3 | 1.2% |
| Measurement Reference Point | Label | The Actual Value/cm | Measured Value/cm | Absolute Error/cm | The Relative Error |
|---|---|---|---|---|---|
| A | 1 | 400 | 402.7 | 2.7 | 0.7% |
| B | 2 | 200 | 204.3 | 4.3 | 2.2% |
| C | 3 | 570 | 567.5 | 2.5 | 0.4% |
| D | 4 | 100 | 103.1 | 3.1 | 3.1% |
| E | 5 | 15 | 17.2 | 2.2 | 14.7% |
| F | 6 | 770 | 767.1 | 2.9 | 0.4% |
| G | 7 | 85 | 84.0 | 1.0 | 1.2% |
| H | 8 | 185 | 183.3 | 1.7 | 0.9% |
| Measurement Reference Point | Label | The Actual Value/cm | Measured Value/cm | Absolute Error/cm | The Relative Error |
|---|---|---|---|---|---|
| I | 9 | 185 | 181.1 | 3.9 | 2.1% |
| Reference Point | Label | The Actual Value/cm | Measured Value/cm | Absolute Error/cm | The Relative Error |
|---|---|---|---|---|---|
| The length of the obstacle at point A | 1 | 84 | 85.2 | 1.2 | 1.43% |
| The width of the obstacle at point A | 2 | 48 | 48.9 | 0.9 | 1.88% |
| The length of the obstacle at point B | 3 | 44 | 45.4 | 1.4 | 3.18% |
| The width of the obstacle at point B | 4 | 35 | 36.5 | 1.5 | 4.28% |
| The length of the obstacle at point C | 5 | 92 | 90.3 | 1.7 | 1.85% |
| The width of the obstacle at point C | 6 | 15 | 14.6 | 0.4 | 2.67% |
| The length of the obstacle at point D | 7 | 32 | 33.7 | 1.7 | 5.31% |
| The width of the obstacle at point D | 8 | 32 | 33.8 | 1.8 | 5.63% |
| Width of passage | 9 | 204 | 204.5 | 0.5 | 0.25% |
| Reference Point | Label | The Actual Value/cm | Measured Value/cm | Absolute Error/cm | The Relative Error |
|---|---|---|---|---|---|
| The length of the obstacle at point A | 1 | 84 | 86.6 | 2.6 | 3.10% |
| The width of the obstacle at point A | 2 | 48 | 49.4 | 1.4 | 2.91% |
| The length of the obstacle at point B | 3 | 44 | 47.2 | 3.2 | 7.27% |
| The width of the obstacle at point B | 4 | 35 | 38.8 | 3.8 | 10.9% |
| The length of the obstacle at point C | 5 | 92 | 96.9 | 4.9 | 5.32% |
| The width of the obstacle at point C | 6 | 15 | 16.4 | 1.4 | 9.33% |
| The length of the obstacle at point D | 7 | 32 | 35.9 | 3.9 | 12.1% |
| The width of the obstacle at point D | 8 | 32 | 35.1 | 3.1 | 9.69% |
| Width of passage | 9 | 204 | 205.5 | 1.5 | 0.74% |
| Reference Point | Label | The Actual Value/cm | Measured Value/cm | Absolute Error/cm | The Relative Error |
|---|---|---|---|---|---|
| The length of the obstacle at point A | 1 | 84 | 84.3 | 0.3 | 0.36% |
| The width of the obstacle at point A | 2 | 48 | 48.4 | 0.4 | 0.83% |
| The length of the obstacle at point B | 3 | 44 | 44.6 | 0.6 | 1.36% |
| The width of the obstacle at point B | 4 | 35 | 34.5 | 0.5 | 1.43% |
| The length of the obstacle at point C | 5 | 92 | 91.3 | 0.7 | 0.76% |
| The width of the obstacle at point C | 6 | 15 | 14.7 | 0.3 | 2.00% |
| The length of the obstacle at point D | 7 | 32 | 32.9 | 0.9 | 2.81% |
| The width of the obstacle at point D | 8 | 32 | 33.8 | 1.8 | 5.62% |
| Width of passage | 9 | 204 | 204.5 | 0.5 | 0.25% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Li, J.; Zhou, J. Research on Two-Round Self-Balancing Robot SLAM Based on the Gmapping Algorithm. Sensors 2023, 23, 2489. https://doi.org/10.3390/s23052489
Zhao J, Li J, Zhou J. Research on Two-Round Self-Balancing Robot SLAM Based on the Gmapping Algorithm. Sensors. 2023; 23(5):2489. https://doi.org/10.3390/s23052489
Chicago/Turabian StyleZhao, Jianwei, Jinyu Li, and Jiaxin Zhou. 2023. "Research on Two-Round Self-Balancing Robot SLAM Based on the Gmapping Algorithm" Sensors 23, no. 5: 2489. https://doi.org/10.3390/s23052489
APA StyleZhao, J., Li, J., & Zhou, J. (2023). Research on Two-Round Self-Balancing Robot SLAM Based on the Gmapping Algorithm. Sensors, 23(5), 2489. https://doi.org/10.3390/s23052489







