Gaussian Process Regression for Single-Channel Sound Source Localization System Based on Homomorphic Deconvolution
Abstract
1. Introduction
2. Nonparametric and Parametric Homomorphic Deconvolution
3. Methodology
3.1. Feature Extraction
3.2. Gaussian Process Regression
4. Simulations
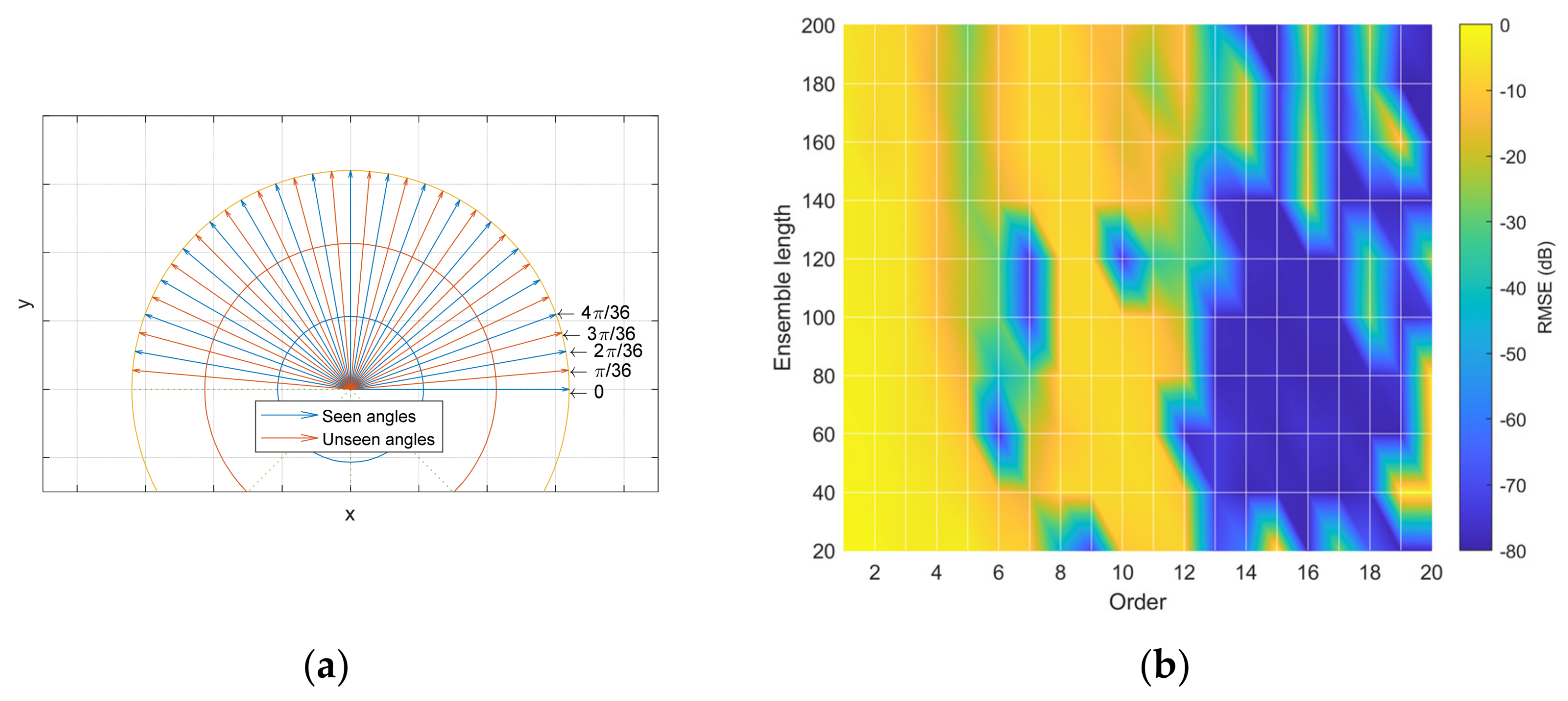
4.1. Receiver Locations
4.2. Localization Performance
5. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SSL | Sound source localization |
| AoA | Angle of arrival |
| 3D | Three-dimensional |
| ADC | Analog-to-digital converter |
| SCSSL | Single-channel sound source localization |
| HD | Homomorphic deconvolution |
| ToF | Time of flight |
| GPR | Gaussian process regression |
| DFT | Discrete Fourier transform |
| FFT | Fast Fourier transform |
| SNR | Signal-to-noise ratio |
| AR | Autoregressive |
| ARMA | Autoregressive moving average |
| RMSE | Root mean square error |
| CDF | Cumulative distribution function |
| PLA | Polylactic acid |
| ASIO | Audio stream input/output |
References
- Veen, B.D.V.; Buckley, K.M. Beamforming: A versatile approach to spatial filtering. IEEE ASSP Mag. 1988, 5, 4–24. [Google Scholar] [CrossRef]
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Blauert, J. Spatial Hearing: The Psychophysics of Human Sound Localization; Revised Edition; Massachusetts Institute of Technology: Cambridge, MA, USA, 1997. [Google Scholar]
- Wightman, F.L.; Kistler, D.J. Monaural sound localization revisited. J. Acoust. Soc. Am. 1997, 101, 1050–1063. [Google Scholar] [CrossRef] [PubMed]
- Stecker, G.; Gallun, F. Binaural hearing, sound localization, and spatial hearing. Transl. Perspect. Audit. Neurosci. Norm. Asp. Hear. 2012, 383, 433. [Google Scholar]
- Yang, B.; Liu, H.; Li, X. Learning Deep Direct-Path Relative Transfer Function for Binaural Sound Source Localization. IEEE/ACM Trans. Audio Speech Lang. Process. 2021, 29, 3491–3503. [Google Scholar] [CrossRef]
- Ding, J.; Li, J.; Zheng, C.; Li, X. Wideband sparse Bayesian learning for off-grid binaural sound source localization. Signal Process. 2020, 166, 107250. [Google Scholar] [CrossRef]
- Badawy, D.E.; Dokmanić, I. Direction of Arrival with One Microphone, a Few LEGOs, and Non-Negative Matrix Factorization. IEEE/ACM Trans. Audio Speech Lang. Process. 2018, 26, 2436–2446. [Google Scholar] [CrossRef]
- Pang, C.; Liu, H.; Zhang, J.; Li, X. Binaural sound localization based on reverberation weighting and generalized parametric mapping. IEEE/ACM Trans. Audio Speech Lang. Process. 2017, 25, 1618–1632. [Google Scholar] [CrossRef]
- Kim, U.-H.; Nakadai, K.; Okuno, H.G. Improved sound source localization in horizontal plane for binaural robot audition. Appl. Intell. 2015, 42, 63–74. [Google Scholar] [CrossRef]
- Baumann, C.; Rogers, C.; Massen, F. Dynamic binaural sound localization based on variations of interaural time delays and system rotations. J. Acoust. Soc. Am. 2015, 138, 635–650. [Google Scholar] [CrossRef]
- King, E.A.; Tatoglu, A.; Iglesias, D.; Matriss, A. Audio-visual based non-line-of-sight sound source localization: A feasibility study. Appl. Acoust. 2021, 171, 107674. [Google Scholar] [CrossRef]
- SongGong, K.; Wang, W.; Chen, H. Acoustic Source Localization in the Circular Harmonic Domain Using Deep Learning Architecture. IEEE/ACM Trans. Audio Speech Lang. Process. 2022, 30, 2475–2491. [Google Scholar] [CrossRef]
- Nguyen, T.N.T.; Watcharasupat, K.N.; Nguyen, N.K.; Jones, D.L.; Gan, W.S. SALSA: Spatial Cue-Augmented Log-Spectrogram Features for Polyphonic Sound Event Localization and Detection. IEEE/ACM Trans. Audio Speech Lang. Process. 2022, 30, 1749–1762. [Google Scholar] [CrossRef]
- Lee, S.Y.; Chang, J.; Lee, S. Deep Learning-Enabled High-Resolution and Fast Sound Source Localization in Spherical Microphone Array System. IEEE Trans. Instrum. Meas. 2022, 71, 2506112. [Google Scholar] [CrossRef]
- Tan, T.-H.; Lin, Y.-T.; Chang, Y.-L.; Alkhaleefah, M. Sound Source Localization Using a Convolutional Neural Network and Regression Model. Sensors 2021, 21, 8031. [Google Scholar] [CrossRef]
- Cheng, L.; Sun, X.; Yao, D.; Li, J.; Yan, Y. Estimation Reliability Function Assisted Sound Source Localization with Enhanced Steering Vector Phase Difference. IEEE/ACM Trans. Audio Speech Lang. Process. 2021, 29, 421–435. [Google Scholar] [CrossRef]
- Chun, C.; Jeon, K.M.; Choi, W. Configuration-Invariant Sound Localization Technique Using Azimuth-Frequency Representation and Convolutional Neural Networks. Sensors 2020, 20, 3768. [Google Scholar] [CrossRef]
- Wang, L.; Cavallaro, A. Deep-Learning-Assisted Sound Source Localization from a Flying Drone. IEEE Sens. J. 2022, 22, 20828–20838. [Google Scholar] [CrossRef]
- Ko, J.; Kim, H.; Kim, J. Real-Time Sound Source Localization for Low-Power IoT Devices Based on Multi-Stream CNN. Sensors 2022, 22, 4650. [Google Scholar] [CrossRef]
- Machhamer, R.; Dziubany, M.; Czenkusch, L.; Laux, H.; Schmeink, A.; Gollmer, K.U.; Naumann, S.; Dartmann, G. Online Offline Learning for Sound-Based Indoor Localization Using Low-Cost Hardware. IEEE Access 2019, 7, 155088–155106. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, H.; Wang, S.; Xu, J. A New Regional Localization Method for Indoor Sound Source Based on Convolutional Neural Networks. IEEE Access 2018, 6, 72073–72082. [Google Scholar] [CrossRef]
- Qureshi, S.A.; Hussain, L.; Alshahrani, H.M.; Abbas, S.R.; Nour, M.K.; Fatima, N.; Khalid, M.I.; Sohail, H.; Mohamed, A.; Hilal, A.M. Gunshots Localization and Classification Model Based on Wind Noise Sensitivity Analysis Using Extreme Learning Machine. IEEE Access 2022, 10, 87302–87321. [Google Scholar] [CrossRef]
- Marchegiani, L.; Newman, P. Listening for Sirens: Locating and Classifying Acoustic Alarms in City Scenes. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17087–17096. [Google Scholar] [CrossRef]
- He, W.; Motlicek, P.; Odobez, J.M. Neural Network Adaptation and Data Augmentation for Multi-Speaker Direction-of-Arrival Estimation. IEEE/ACM Trans. Audio Speech Lang. Process. 2021, 29, 1303–1317. [Google Scholar] [CrossRef]
- Komen, D.F.V.; Howarth, K.; Neilsen, T.B.; Knobles, D.P.; Dahl, P.H. A CNN for Range and Seabed Estimation on Normalized and Extracted Time-Series Impulses. IEEE J. Oceanic. Eng. 2022, 47, 833–846. [Google Scholar] [CrossRef]
- El-Banna, A.A.A.; Wu, K.; ElHalawany, B.M. Application of Neural Networks for Dynamic Modeling of an Environmental-Aware Underwater Acoustic Positioning System Using Seawater Physical Properties. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Huang, Z.; Xu, J.; Gong, Z.; Wang, H.; Yan, Y. Multiple Source Localization in a Shallow Water Waveguide Exploiting Subarray Beamforming and Deep Neural Networks. Sensors 2019, 19, 4768. [Google Scholar] [CrossRef]
- Grumiaux, P.-A.; Kitić, S.; Girin, L.; Guérin, A. A survey of sound source localization with deep learning methods. J. Acoust. Soc. Am. 2022, 152, 107–151. [Google Scholar] [CrossRef]
- Park, Y.; Choi, A.; Kim, K. Parametric Estimations Based on Homomorphic Deconvolution for Time of Flight in Sound Source Localization System. Sensors 2020, 20, 925. [Google Scholar] [CrossRef]
- George, A.D.; Kim, K. Parallel Algorithms for Split-Aperture Conventional Beamforming. J. Comput. Acoust. 1999, 7, 225–244. [Google Scholar] [CrossRef]
- George, A.D.; Garcia, J.; Kim, K.; Sinha, P. Distributed Parallel Processing Techniques for Adaptive Sonar Beamforming. J. Comput. Acoust. 2002, 10, 1–23. [Google Scholar] [CrossRef]
- Sinha, P.; George, A.D.; Kim, K. Parallel Algorithms for Robust Broadband MVDR Beamforming. J. Comput. Acoust. 2002, 10, 69–96. [Google Scholar] [CrossRef]
- Kim, K.; George, A.D. Parallel Subspace Projection Beamforming for Autonomous, Passive Sonar Signal Processing. J. Comput. Acoust. 2003, 11, 55–74. [Google Scholar] [CrossRef]
- Cho, K.; George, A.D.; Subramaniyan, R.; Kim, K. Parallel Algorithms for Adaptive Matched-Field Processing on Distributed Array Systems. J. Comput. Acoust. 2004, 12, 149–174. [Google Scholar] [CrossRef]
- Cho, K.; George, A.D.; Subramaniyan, R.; Kim, K. Fault-Tolerant Matched-Field Processing in the Presence of Element Failures. J. Comput. Acoust. 2006, 14, 299–319. [Google Scholar] [CrossRef]
- Kim, K. Lightweight Filter Architecture for Energy Efficient Mobile Vehicle Localization Based on a Distributed Acoustic Sensor Network. Sensors 2013, 13, 11314–11335. [Google Scholar] [CrossRef]
- Kim, K.; Choi, A. Binaural Sound Localizer for Azimuthal Movement Detection Based on Diffraction. Sensors 2012, 12, 10584–10603. [Google Scholar] [CrossRef]
- Kim, K.; Kim, Y. Monaural Sound Localization Based on Structure-Induced Acoustic Resonance. Sensors 2015, 15, 3872–3895. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, K. Near-Field Sound Localization Based on the Small Profile Monaural Structure. Sensors 2015, 15, 28742–28763. [Google Scholar] [CrossRef]
- Park, Y.; Choi, A.; Kim, K. Monaural Sound Localization Based on Reflective Structure and Homomorphic Deconvolution. Sensors 2017, 17, 2189. [Google Scholar] [CrossRef]
- Park, Y.; Choi, A.; Kim, K. Single-Channel Multiple-Receiver Sound Source Localization System with Homomorphic Deconvolution and Linear Regression. Sensors 2021, 21, 760. [Google Scholar] [CrossRef] [PubMed]
- Kim, K. Design and analysis of experimental anechoic chamber for localization. J. Acoust. Soc. Korea 2012, 31, 10. [Google Scholar] [CrossRef]
- Oppenheim, A.V.; Schafer, R.W.; Stockham, T.G. Nonlinear filtering of multiplied and convolved signals. Proc. IEEE 1968, 56, 1264–1291. [Google Scholar] [CrossRef]
- Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing; Prentice Hall: Upper Saddle River, NJ, USA, 1989. [Google Scholar]
- Rabiner, L.R.; Schafer, R.W. Theory and Applications of Digital Speech Processing; Pearson: San Antonio, TX, USA, 2011. [Google Scholar]
- Yule, G.U. VII. On a method of investigating periodicities disturbed series, with special reference to Wolfer’s sunspot numbers. Philos. Trans. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1927, 226, 267–298. [Google Scholar]
- Kim, K. Conceptual Digital Signal Processing with MATLAB, 1st ed.; Signals and Communication Technology; Springer Nature: Singapore, 2021; p. 690. [Google Scholar]
- Parks, T.W.; Burrus, C.S. Digital Filter Design; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Steiglitz, K.; McBride, L. A technique for the identification of linear systems. IEEE Trans. Autom. Control 1965, 10, 461–464. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Evaluation of Gaussian Processes and Other Methods for Non-Linear Regression; University of Toronto: Toronto, ON, Canada, 1997. [Google Scholar]
- Rasmussen, C.E. Gaussian Processes in Machine Learning. In Advanced Lectures on Machine Learning: ML Summer Schools 2003, Canberra, Australia, February 2–14, 2003, Tübingen, Germany, August 4–16, 2003; Revised Lectures; Bousquet, O., von Luxburg, U., Rätsch, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 63–71. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Williams, C.K.I. Prediction with Gaussian Processes: From Linear Regression to Linear Prediction and Beyond. In Learning in Graphical Models; Jordan, M.I., Ed.; Springer: Dordrecht, The Netherlands, 1998; pp. 599–621. [Google Scholar]
- Ebden, M. Gaussian processes: A quick introduction. arXiv 2015, arXiv:1505.02965. [Google Scholar]
- Fonnesbeck, C. Fitting Gaussian Process Models in Python. Available online: https://www.dominodatalab.com/blog/fitting-gaussian-process-models-python (accessed on 17 March 2022).
- Görtler, J.; Kehlbeck, R.; Deussen, O. A Visual Exploration of Gaussian Processes. Available online: https://distill.pub/2019/visual-exploration-gaussian-processes/ (accessed on 10 April 2022).
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Schölkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA; London, UK, 2002. [Google Scholar]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence properties of the Nelder—Mead simplex method in low dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Lawrence, N.; Seeger, M.; Herbrich, R. Fast sparse Gaussian process methods: The informative vector machine. Adv. Neural Inf. Process. Syst. 2002, 15. [Google Scholar]
- Smola, A.; Schölkopf, B. Sparse Greedy Matrix Approximation for Machine Learning. In Proceedings of the Seventeenth International Conference on Machine Learning, Stanford, CA, USA, 29 June–2 July 2000. [Google Scholar]
- Gilbert, J.R.; Peierls, T. Sparse Partial Pivoting in Time Proportional to Arithmetic Operations. SIAM J. Sci. Stat. Comput. 1988, 9, 862–874. [Google Scholar] [CrossRef]
- Vetterling, W.T.; Press, W.H.; Press, W.H.; Teukolsky, S.A.; Flannery, B.P. Numerical Recipes: Example Book C, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Steele, J.M. The Cauchy-Schwarz Master Class: An Introduction to the Art of Mathematical Inequalities; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- ISO 3745:2003; International Organization for Standardization. Acoustics—Determination of Sound Power Levels of Noise Sources Using Sound Pressure—Precision Methods for Anechoic and Hemi-Anechoic Rooms. ISO: Geneva, Switzerland, 2003.









| Kernel Name | with Parameter |
|---|---|
| Squared exponential | |
| Exponential | |
| Matern 3/2 | |
| Matern 5/2 | |
| Rational quadratic |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Sampling frequency | 48,000 Hz | Angle range | |
| Frame length | 1024 samples | Angle resolution | rad (10°) |
| Overlap length | 768 samples (210–28) | Seen angles | 0, |
| Sound speed | 34,613 cm/s | Unseen angles | Seen angles + |
| Number of receivers | 3 | # of seen angles | 18 (=1 angle set) |
| SNR | 20 dB | # of unseen angles | 18 (=1 angle set) |
| HD window length | 5 samples | Training iterations | 1998 iter. (111 angle sets) |
| Max time delay (nmax) | 90 samples | Validation iter. (Seen angles) | 3996 iter.(222 angle sets) |
| Audio source | Wideband signal ~12,000 Hz | Validation iter. (Unseen angles) | 3996 iter.(222 angle sets) |
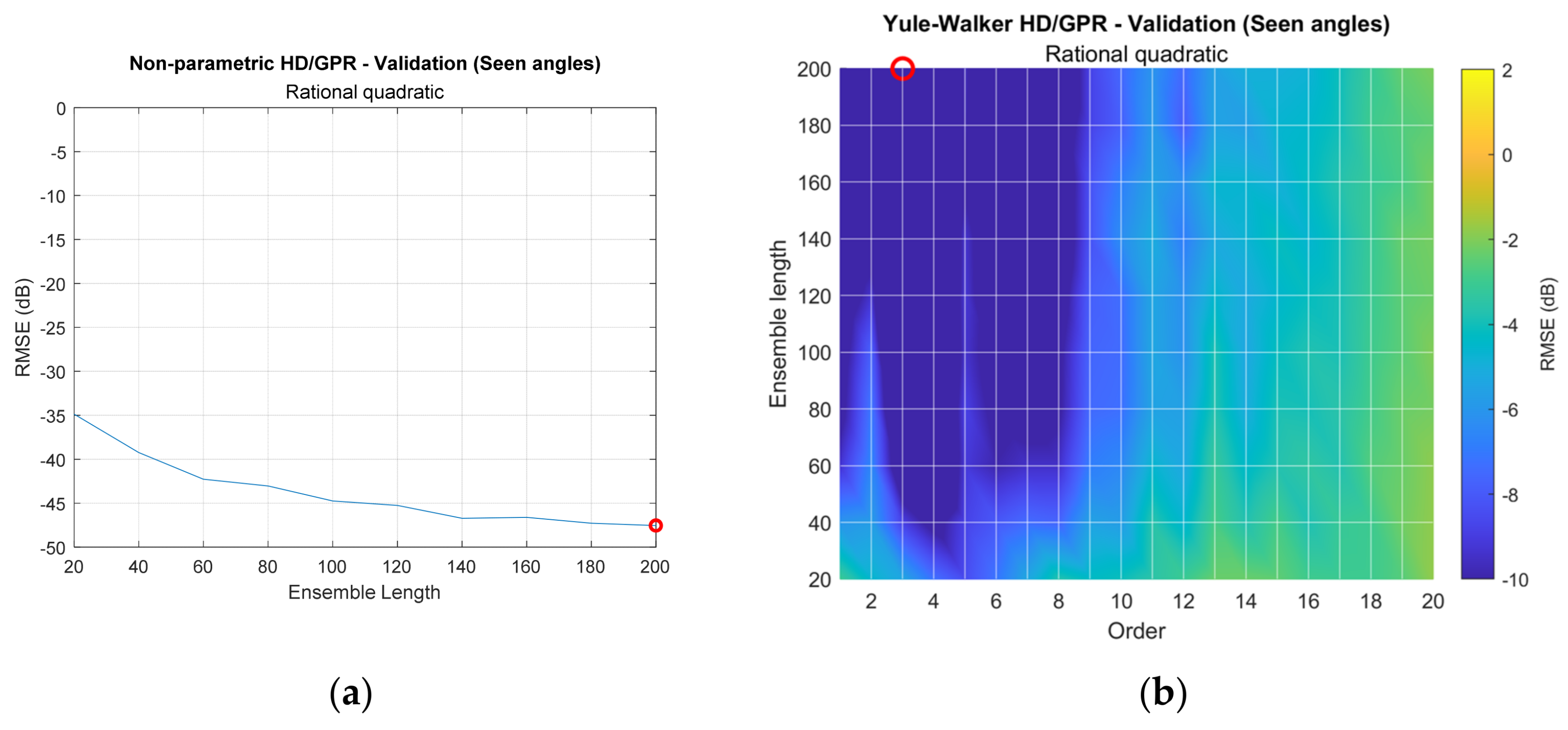
| SCSSL Method (Kernel Function) | Validation (Seen Angles) Best Parameter Corresponding RMSE | Training RMSE ← @ Parameter 1 [Best] | Validation (Unseen Angles) RMSE ← @ Parameter 1 [Best] |
|---|---|---|---|
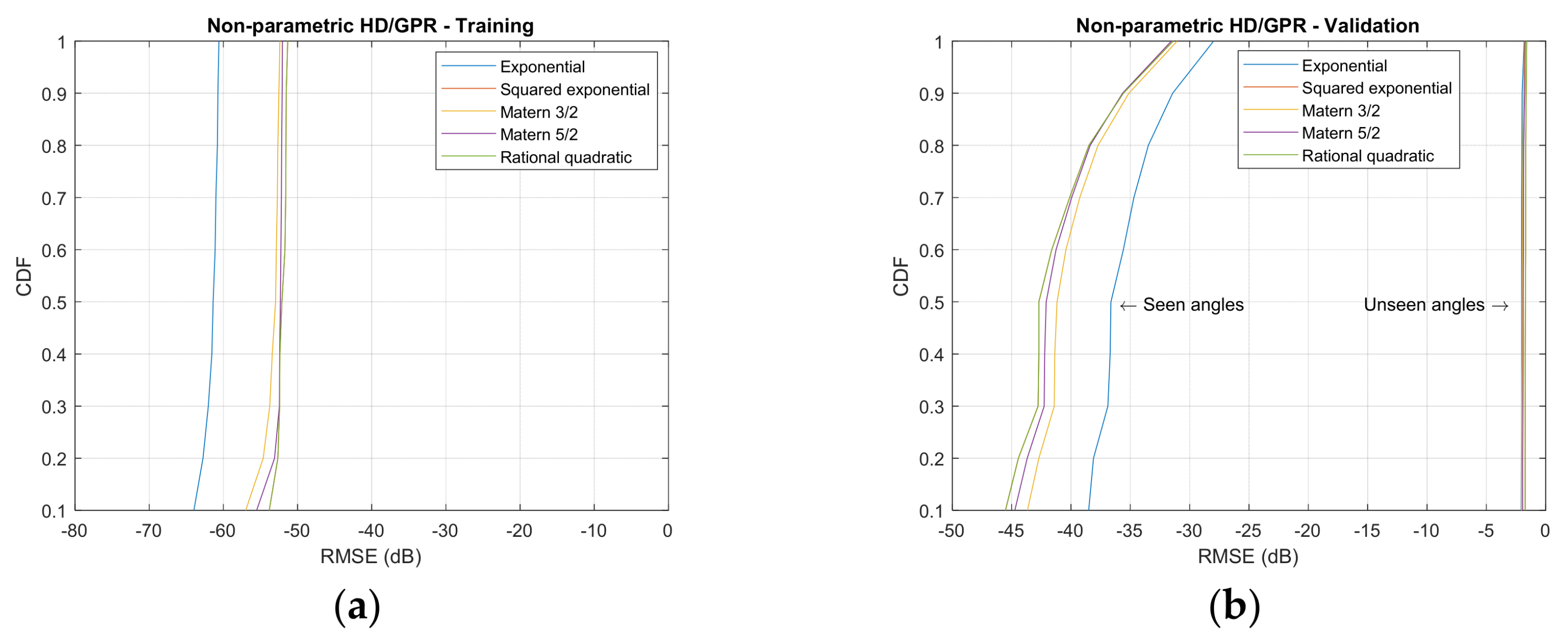
| Non-para. HD/GPR (Rat. quad.) | 200 Len. | −52.43 dB [−53.83 dB] | −1.74 dB [−1.74 dB] |
| −45.52 dB | |||
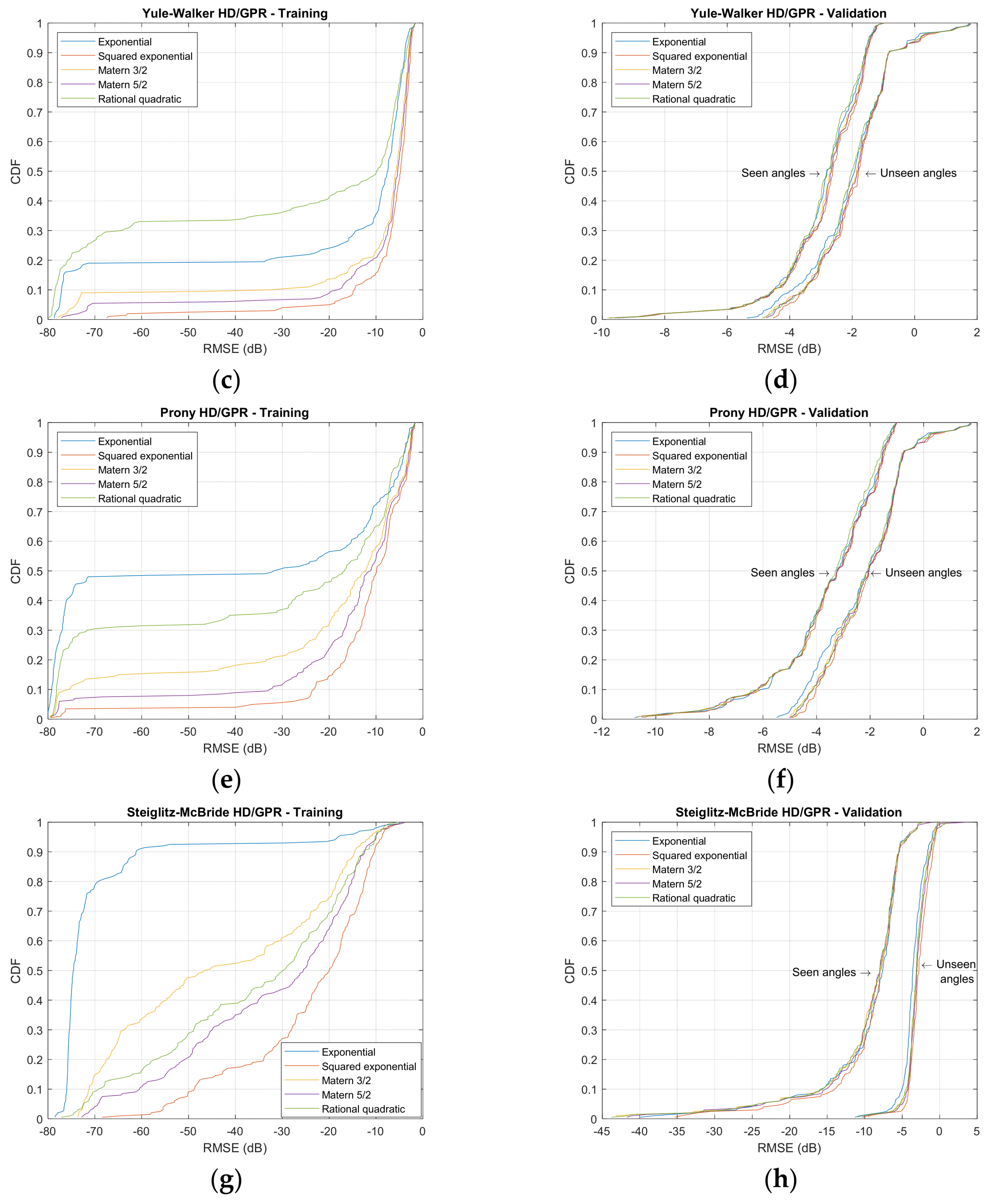
| YW HD/GPR (Rat. quad.) | 4 Ord. and 200 Len. | −15.90 dB [−79.78 dB] | −3.99 dB [−4.88 dB] |
| −9.77 dB | |||
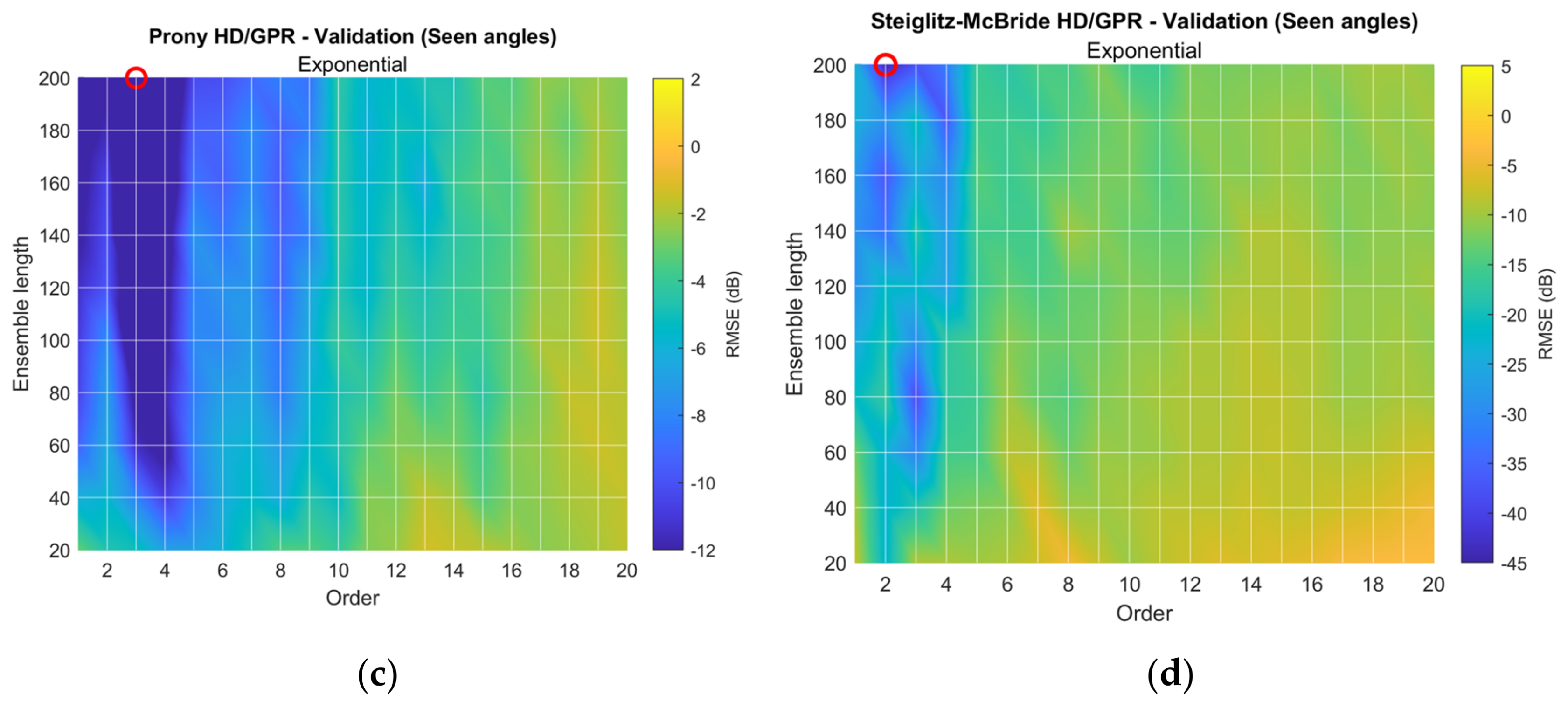
| Prony HD/GPR (Exponential) | 4 Ord. and 200 Len. | −71.69 dB [−80.06 dB] | −4.71 dB [−5.49 dB] |
| −10.79 dB | |||
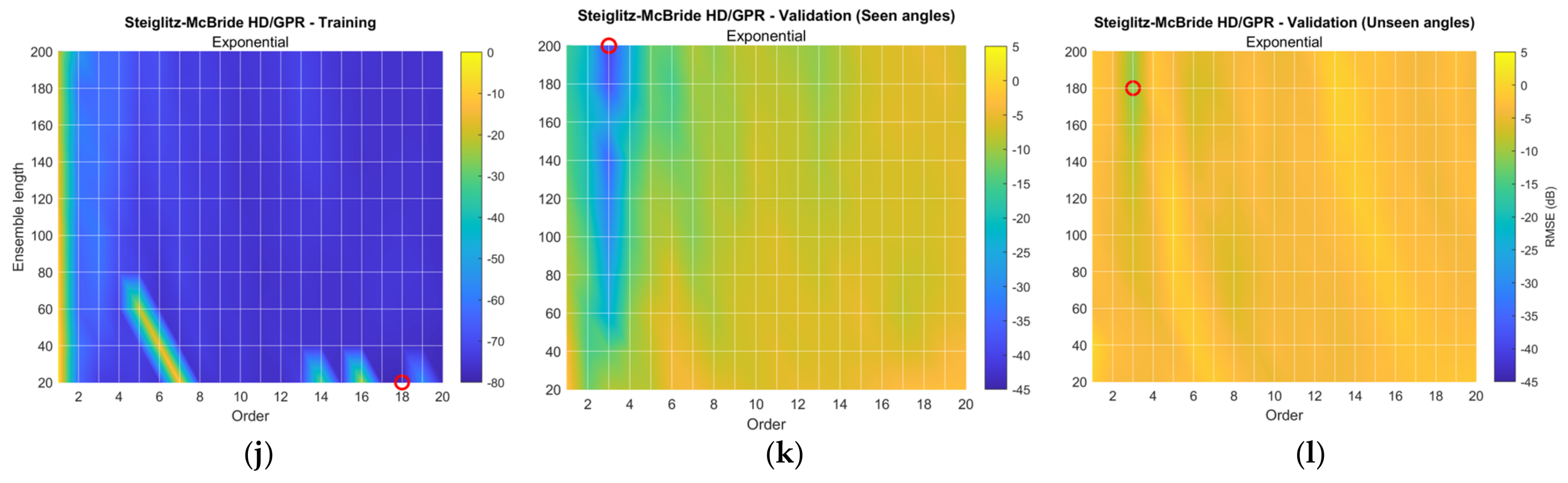
| SM HD/GPR (Exponential) | 3 Ord. and 200 Len. | −63.48 dB [−75.77 dB] | −10.73 dB [−11.32 dB] |
| −39.91 dB |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Sampling frequency | 48,000 Hz | Angle range | |
| Frame length | 1024 samples | Angle resolution | rad (20°) |
| Overlap length | 768 samples (210–28) | Seen angles | 0, |
| Sound speed | 34,613 cm/sec | Unseen angles | Seen angles + |
| Number of receivers | 3 | # of seen angles | 9 (=1 angle set) |
| SNR | Not applicable | # of unseen angles | 9 (=1 angle set) |
| HD window length | 5 samples | Training iterations | 999 iter. (111 angle sets) |
| Max time delay (nmax) | 90 samples | Validation iter. (Seen angles) | 999 iter. (111 angle sets) |
| Audio source | Wideband signal ~12,000 Hz | Validation iter. (Unseen angles) | 999 iter. (111 angle sets) |
| SSL Method (Kernel Function) | Parameter | Validation (Seen Angles) RMSE | Validation (Unseen Angles) RMSE |
|---|---|---|---|
| Non-para. HD/GPR (Rat. quad.) | 200 Len. | −47.54 dB | −1.95 dB |
| YW HD/GPR (Rat. quad.) | 4 Ord. and 200 Len. | −15.75 dB | −3.04 dB |
| Prony HD/GPR (Exponential) | 4 Ord. and 200 Len. | −15.50 dB | −0.24 dB |
| SM HD/GPR (Exponential) | 3 Ord. and 200 Len. | −37.56 dB | −9.11 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.; Hong, Y. Gaussian Process Regression for Single-Channel Sound Source Localization System Based on Homomorphic Deconvolution. Sensors 2023, 23, 769. https://doi.org/10.3390/s23020769
Kim K, Hong Y. Gaussian Process Regression for Single-Channel Sound Source Localization System Based on Homomorphic Deconvolution. Sensors. 2023; 23(2):769. https://doi.org/10.3390/s23020769
Chicago/Turabian StyleKim, Keonwook, and Yujin Hong. 2023. "Gaussian Process Regression for Single-Channel Sound Source Localization System Based on Homomorphic Deconvolution" Sensors 23, no. 2: 769. https://doi.org/10.3390/s23020769
APA StyleKim, K., & Hong, Y. (2023). Gaussian Process Regression for Single-Channel Sound Source Localization System Based on Homomorphic Deconvolution. Sensors, 23(2), 769. https://doi.org/10.3390/s23020769







