Robust Control Based on Adaptive Neural Network for the Process of Steady Formation of Continuous Contact Force in Unmanned Aerial Manipulator
Abstract
:1. Introduction
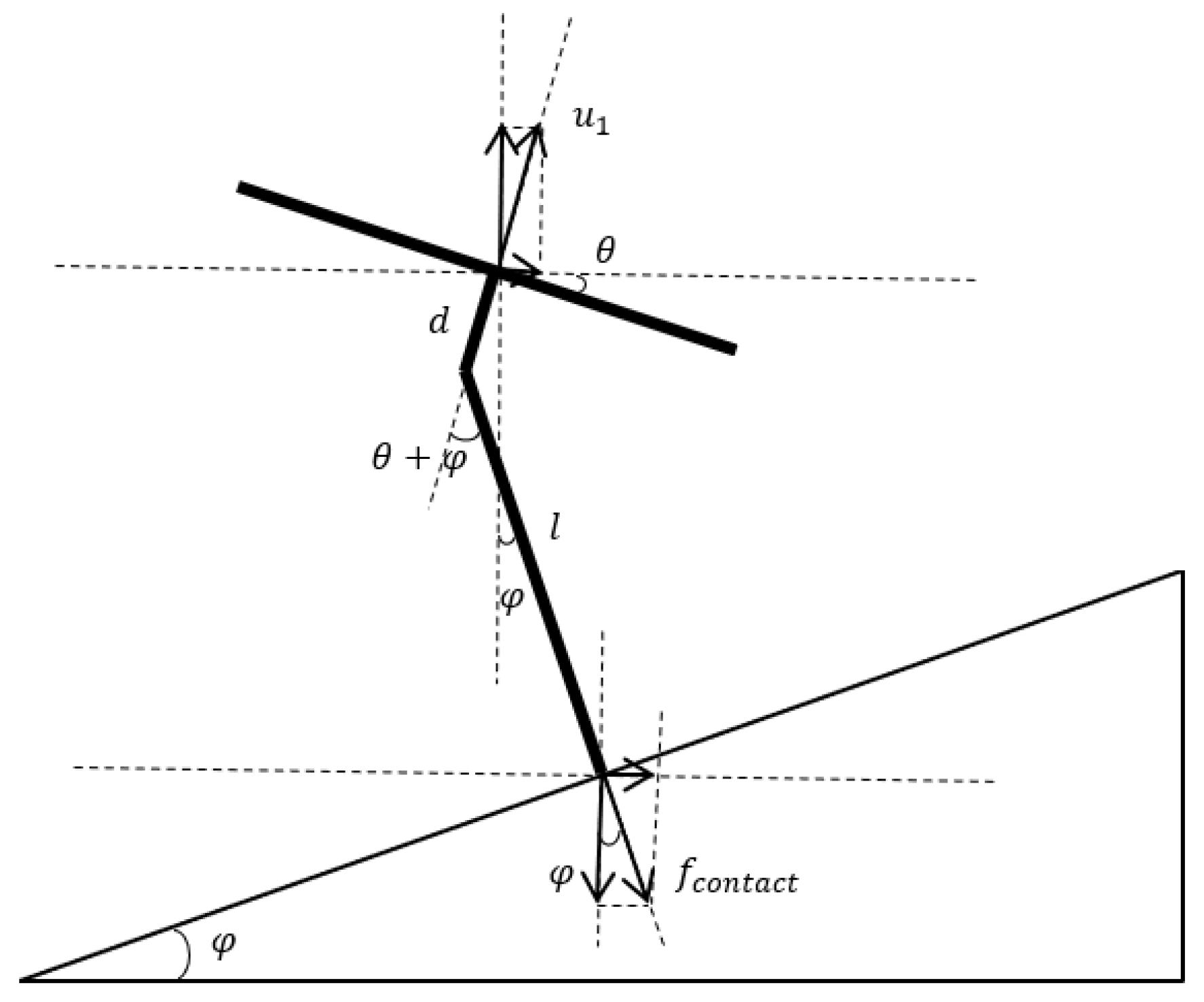
- A force/position hybrid control framework is designed for the contact process between the UAM and the inclined target. This method will generate the desired trajectory according to the formation process of the contact force.
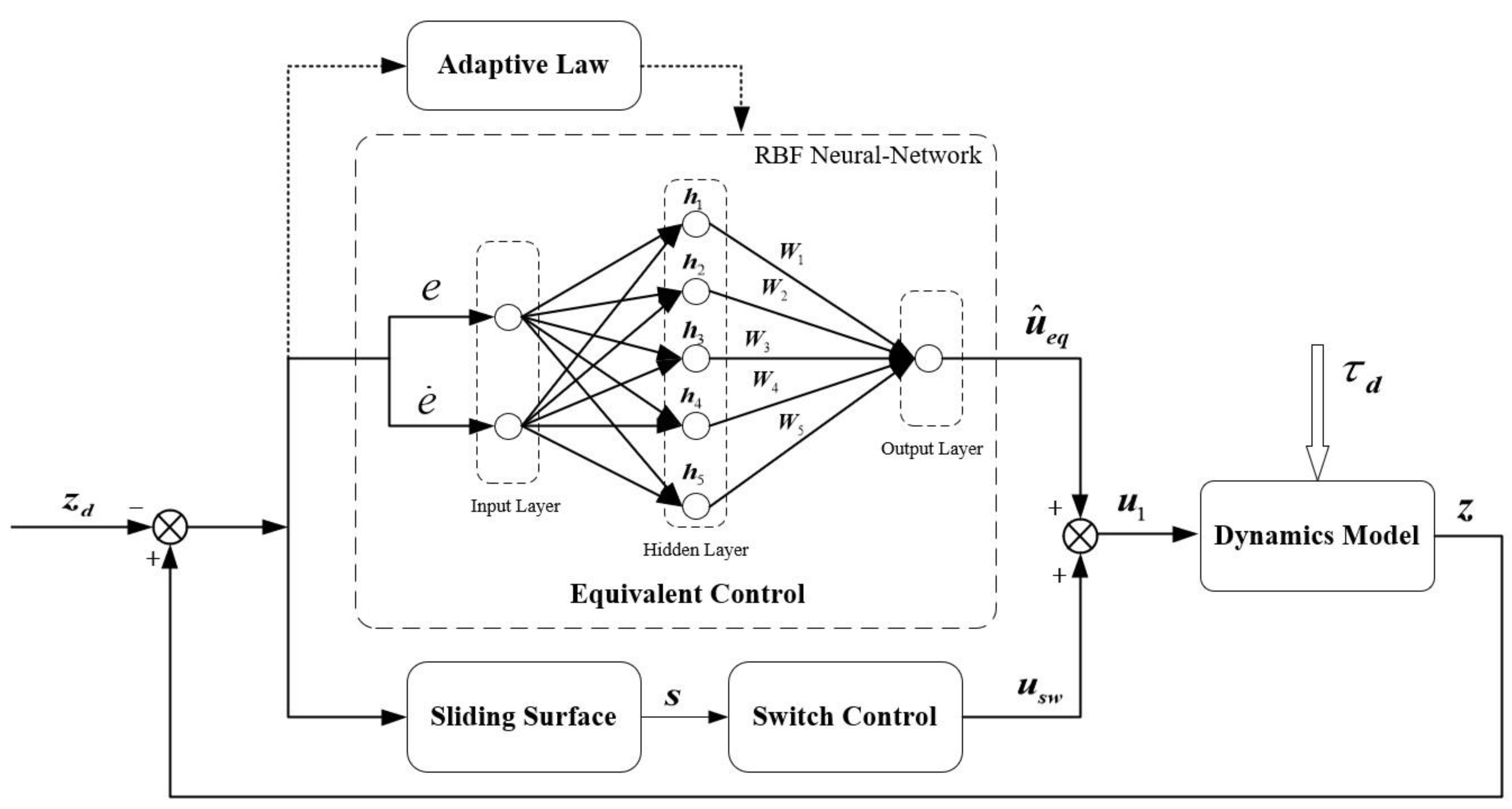
- A robust non-singular global fast terminal sliding mode controller (NGFTSMC) is proposed to make the system error converge rapidly during the whole process of trajectory tracking. Furthermore, since an adaptive RBFNN is used to estimate the equivalent part of the controller, the improved controller does not need any prior knowledge of the system dynamics and external disturbances, and can reduce the system chattering effectively.
2. Related Work
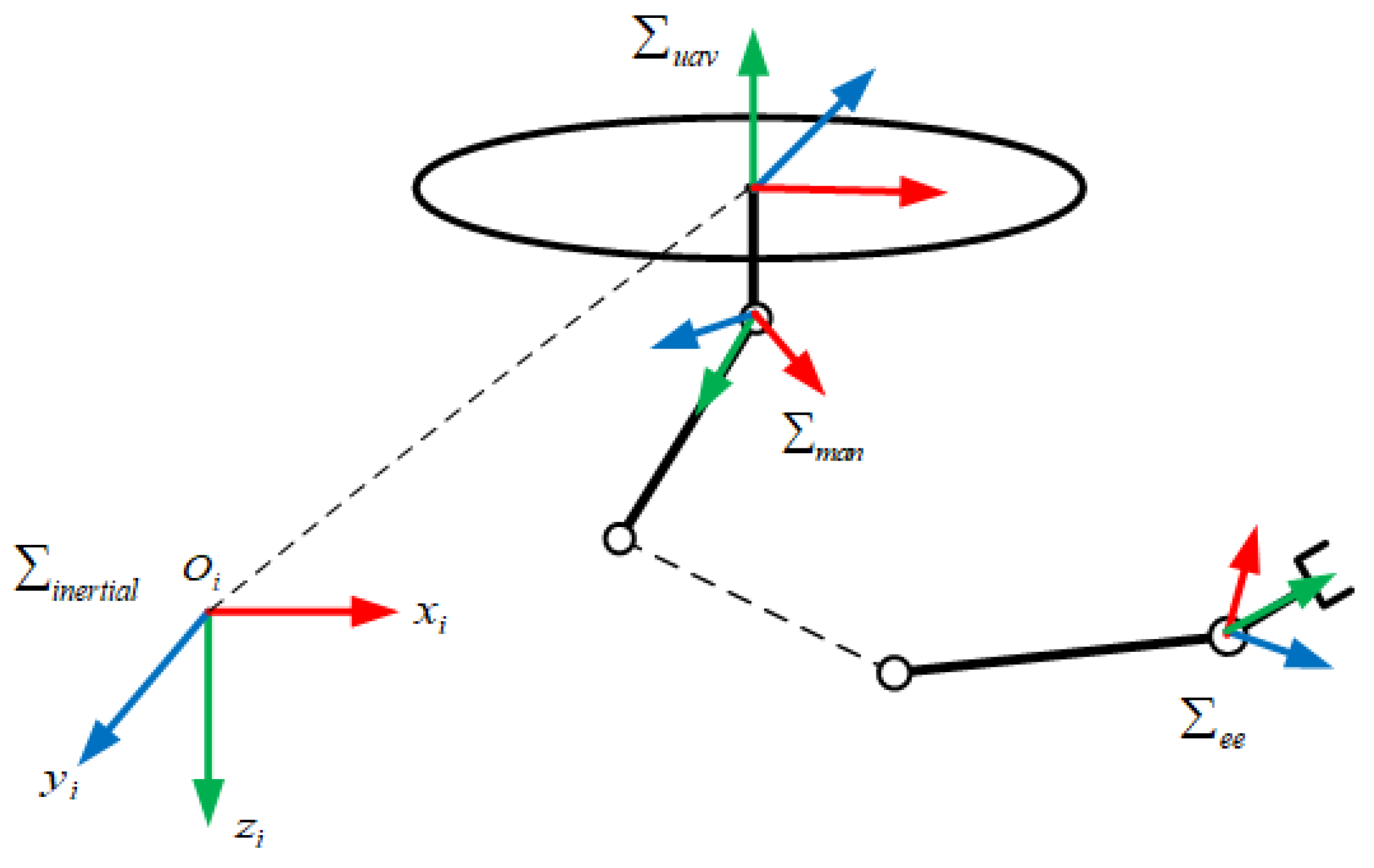
3. System Modeling
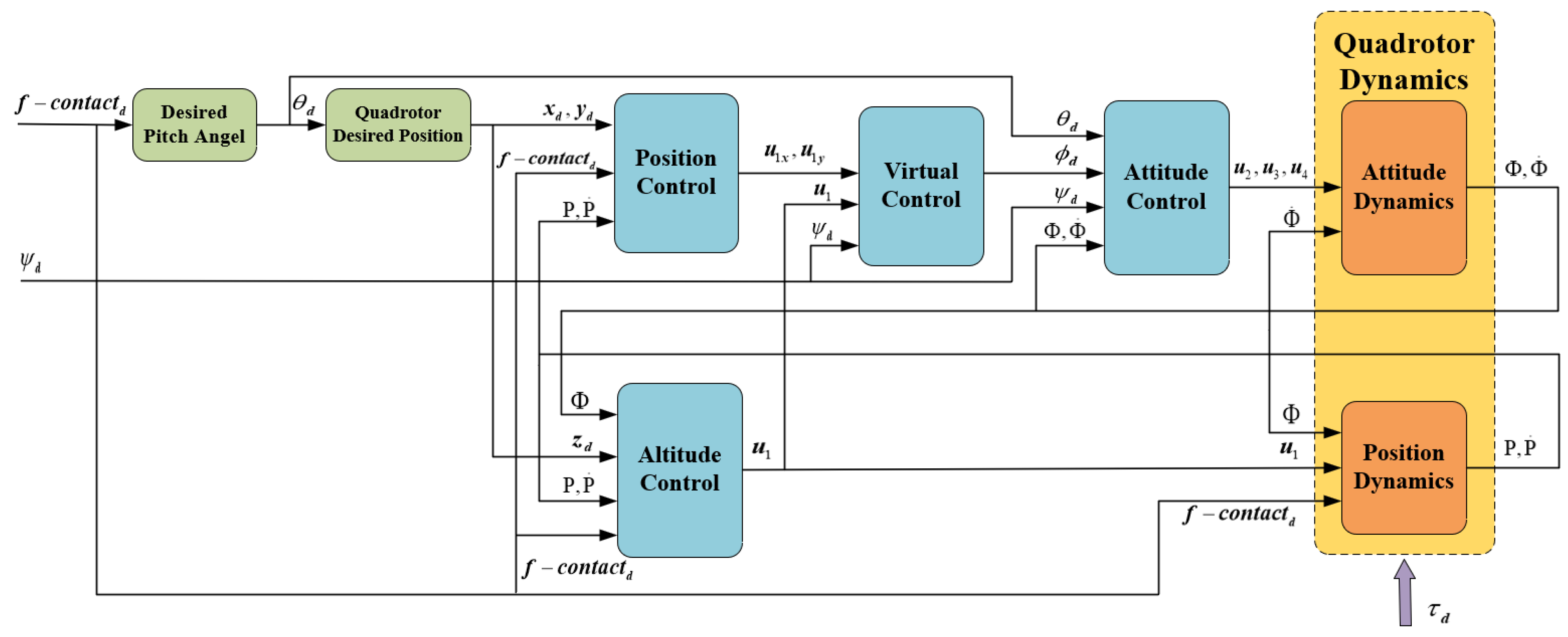
4. Controller Design
4.1. Altitude Control
4.2. Horizontal Position Control
4.3. Attitude Control
5. Simulation
5.1. Simulation Settings
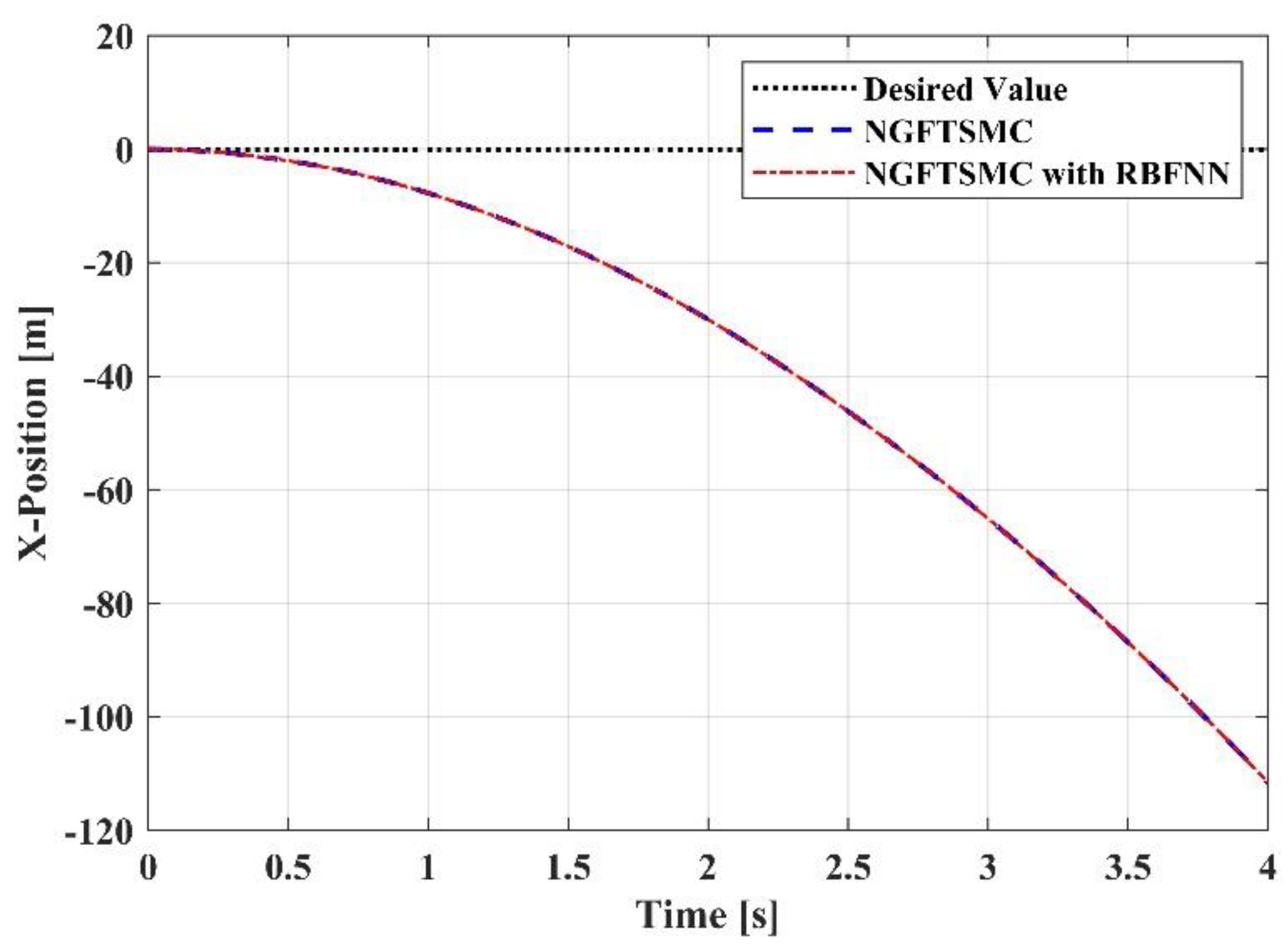
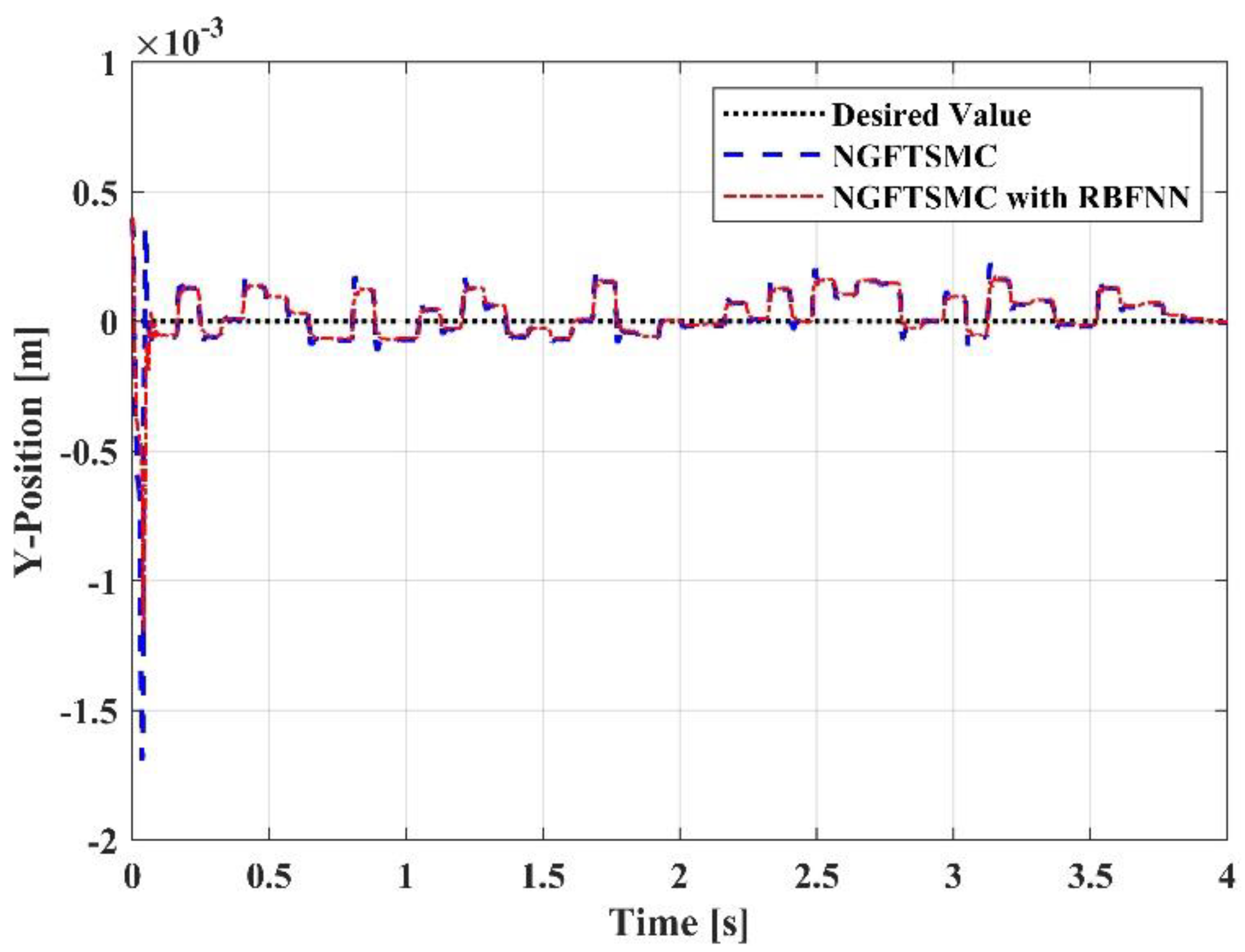
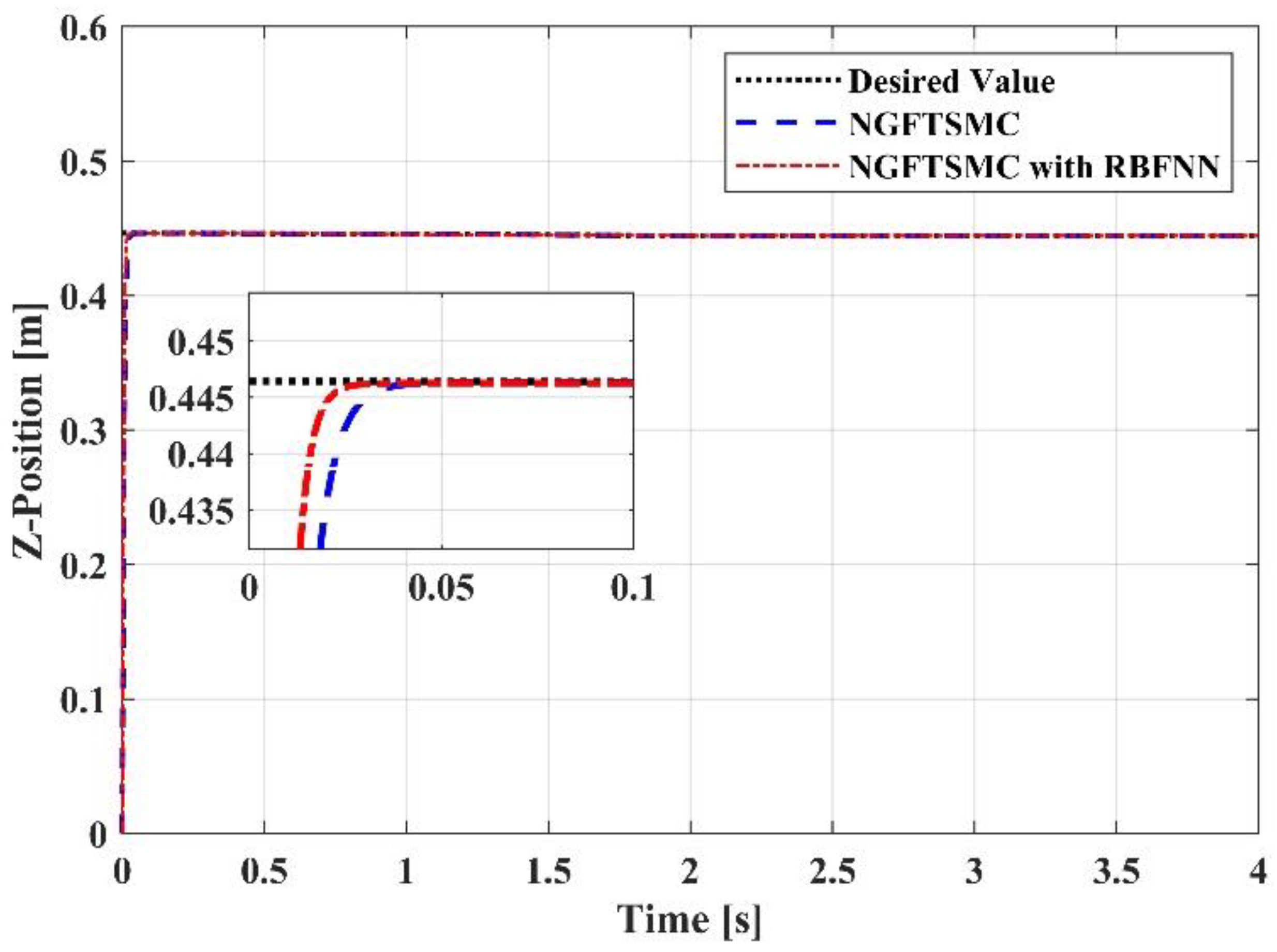
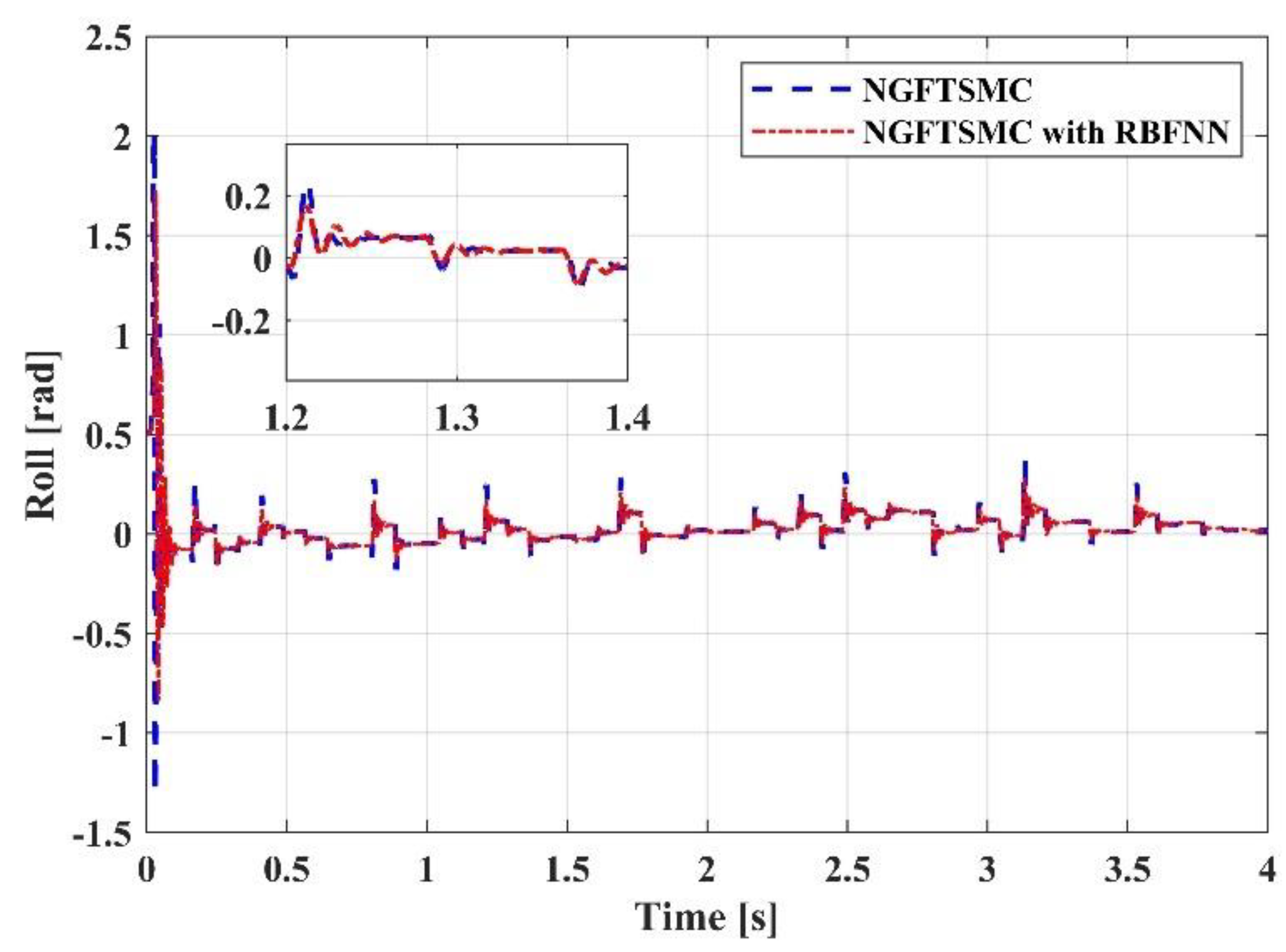
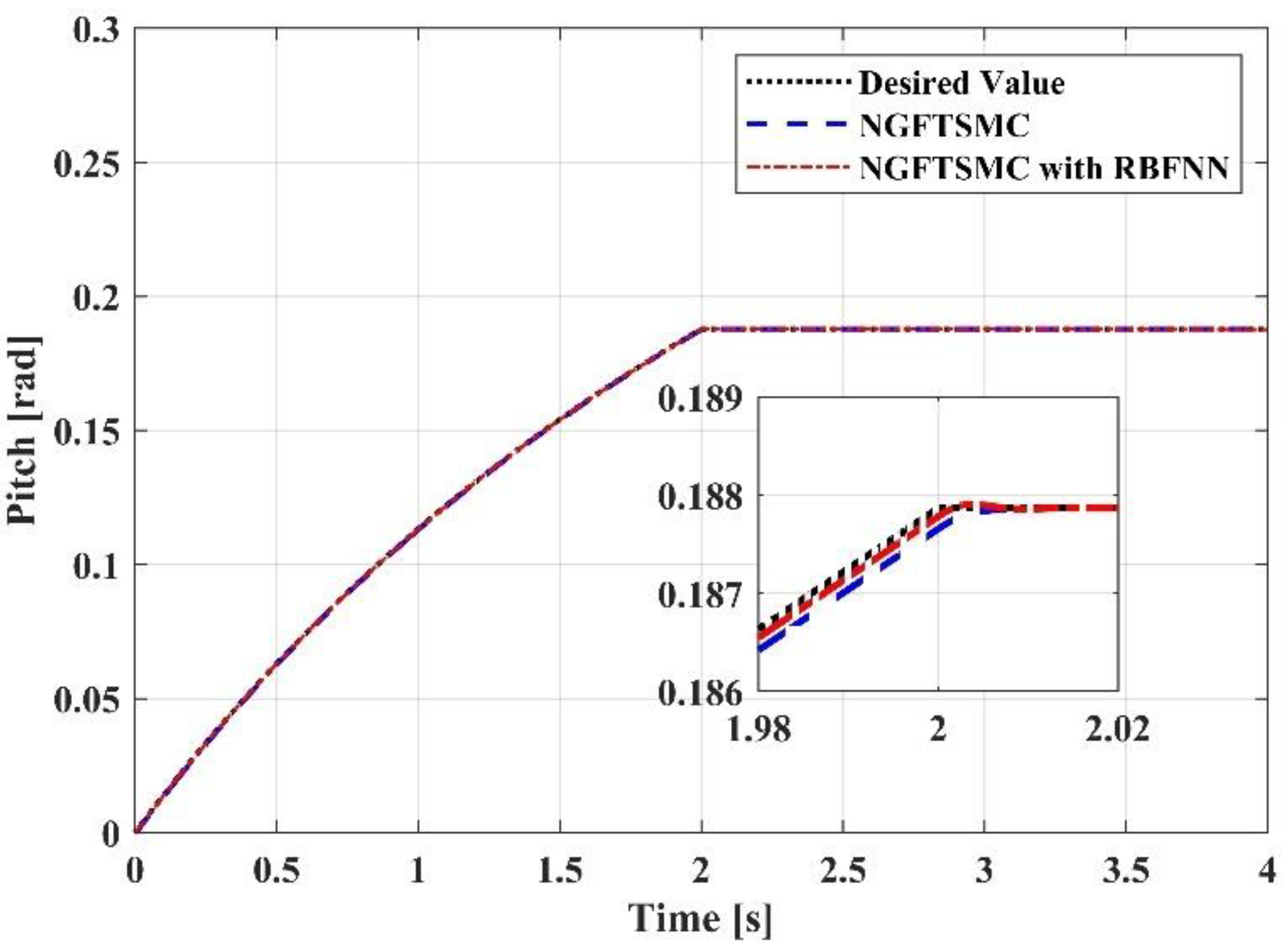
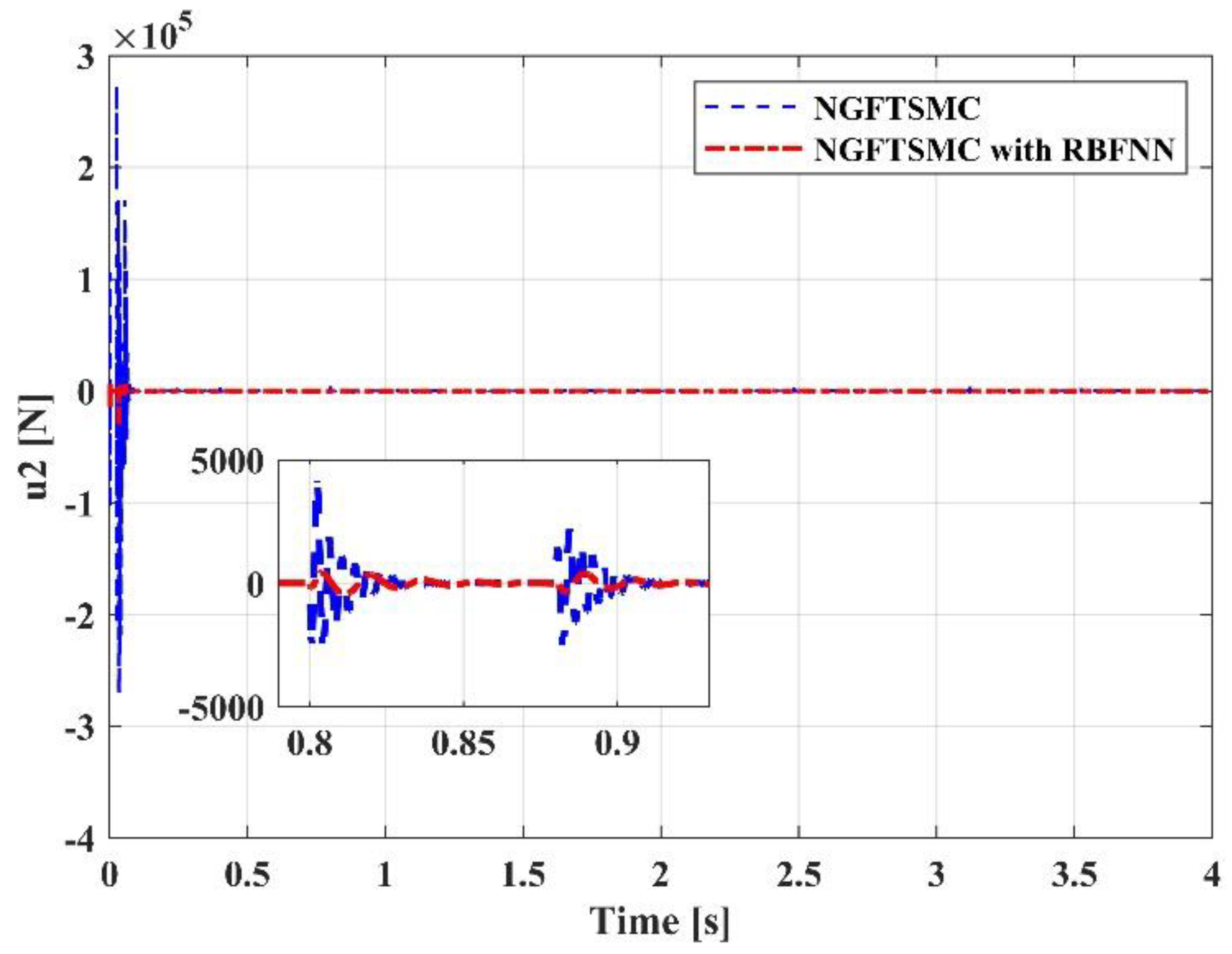
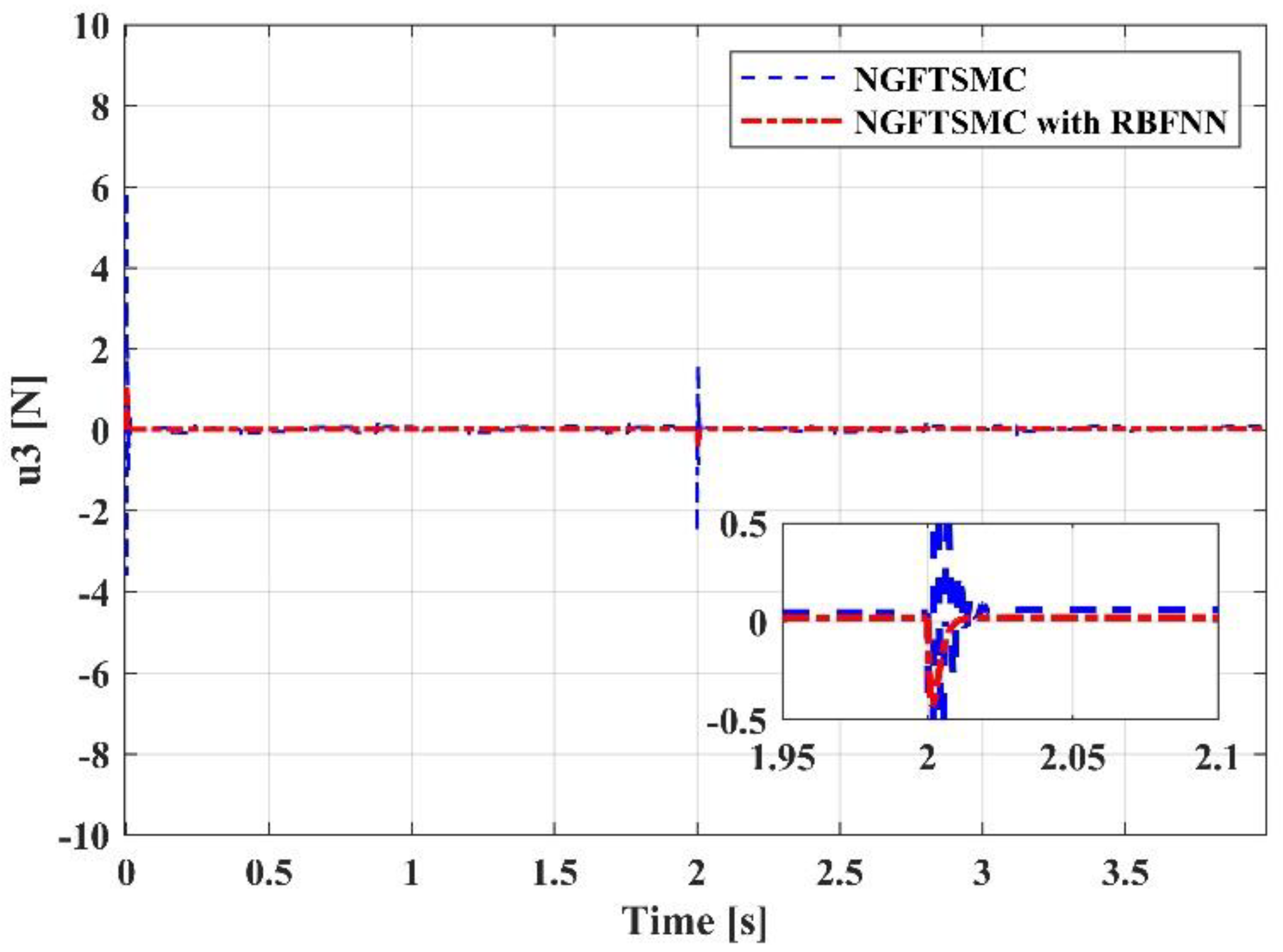
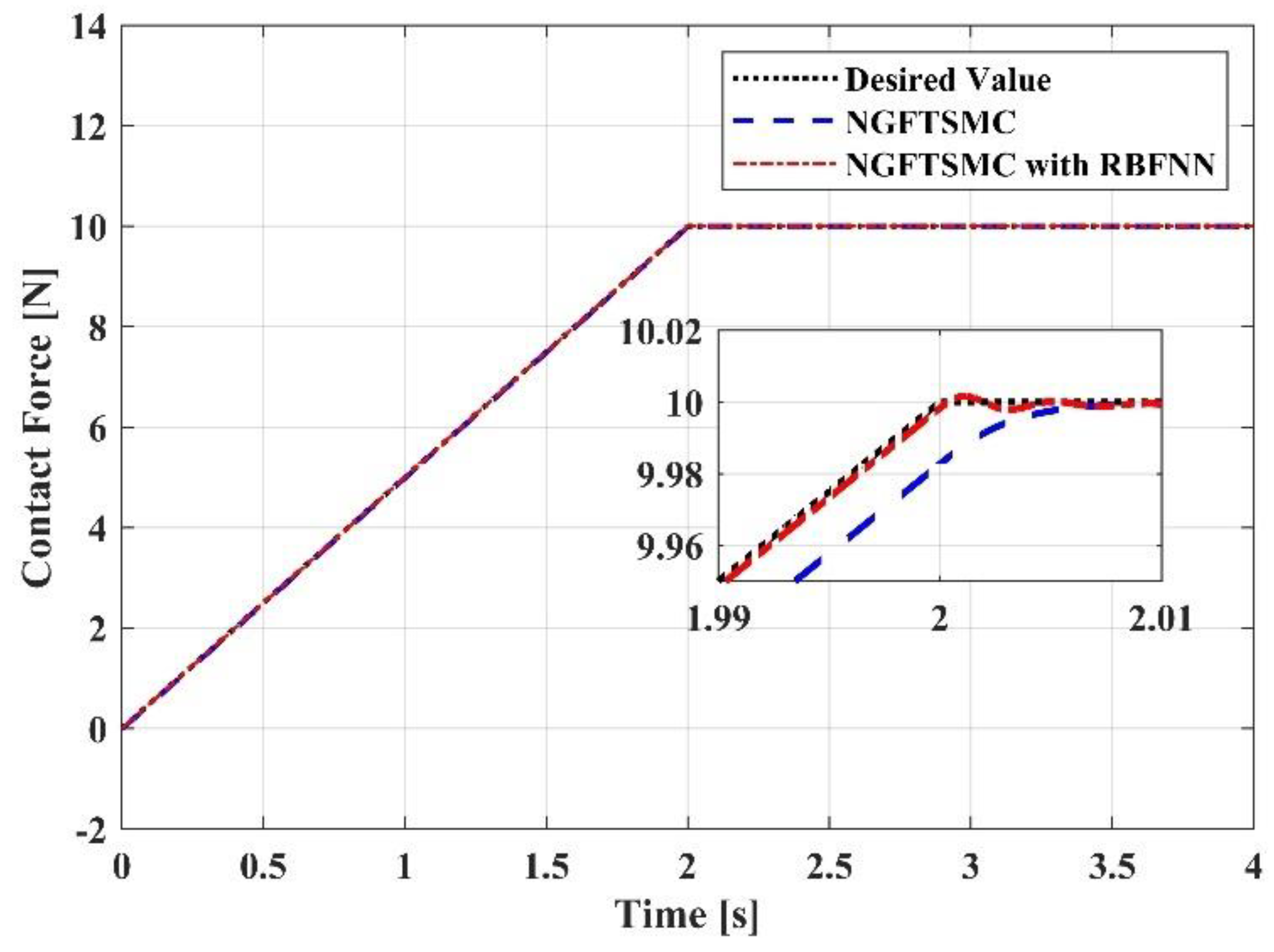
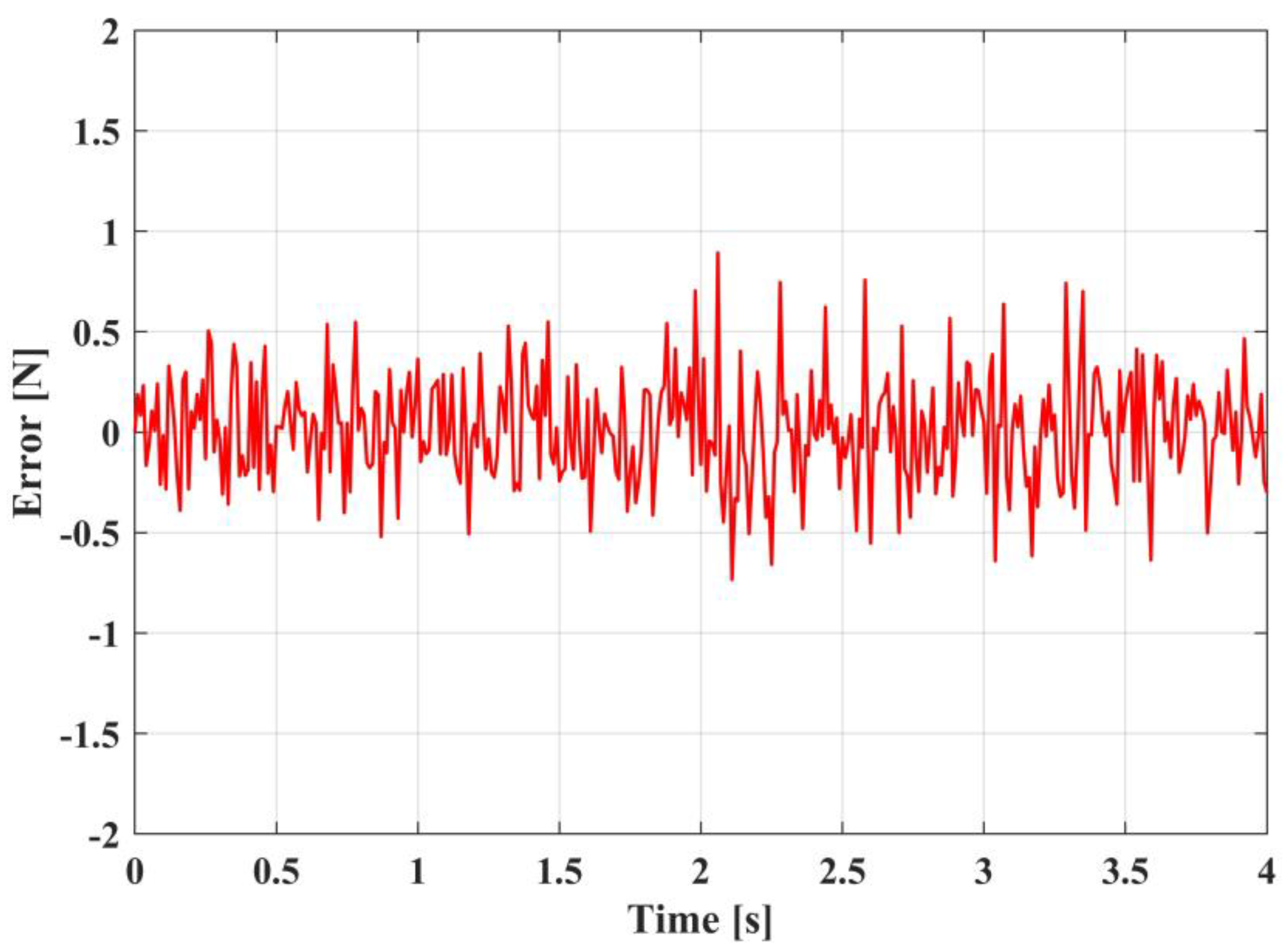
5.2. Simulation Results and Analysis
6. Experiment
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| UAV | Unmanned Aerial Vehicle |
| UAM | Unmanned Aerial Manipulator |
| TSMC | Terminal Sliding Mode Controller |
| RBFNN | Radial Basis Function Neural Network |
| NGFTSMC | Non-singular Global Fast Terminal Sliding Mode Controller |
| The inertial coordinate system | |
| The UAV body coordinate system | |
| The coordinate system of the manipulator | |
| The coordinate system of the end effector | |
| The rotation matrix from the UAV body coordinate system to the inertial coordinate system | |
| The Euler angle of the UAV in the inertial coordinate system | |
| The rotation matrix from the end effector of the manipulator to the UAV | |
| The rotation matrix from the base of the manipulator to the UAV body | |
| The rotation matrix from the end effector to the base of the manipulator | |
| The position of the quadrotor | |
| The mass of the aerial manipulator | |
| The acceleration of gravity | |
| The mass moments of inertia in the x, y, and z axes | |
| The rotor inertia | |
| The total residual speed of the motor | |
| The lumped disturbance including modeling errors, parameter uncertainties, and external disturbances | |
| The input forces of the quadrotor | |
| The contact forces applied by the aerial manipulator to the target in the x, y, and z axes | |
| The angle between the target and the horizontal | |
| The length of the manipulator | |
| The distance from the base of the manipulator to the center of the quadrotor | |
| The contact force | |
| The position of the target | |
| The desired position | |
| The desired attitude | |
| The tracking errors | |
| The sliding surface function | |
| The parameters of the controller | |
| The equivalent control input | |
| The switching control input | |
| The input of RBFNN | |
| The approximate equivalent control output | |
| The weight of the RBFNN | |
| The nonlinear mapping of the RBFNN | |
| The ideal equivalent control | |
| The ideal weight of the RBFNN | |
| The approximation error of the neural network | |
| The equivalent control output error generated by the neural network estimation | |
| The weight error of the neural network | |
| The Lyapunov function | |
| The parameter of the neural network adaptation law | |
| The virtual input force of the horizontal subsystem |
References
- Xiao, M.; Liang, J.; Ji, L.; Sun, Z.; Li, Z. Aerial photography trajectory-tracking controller design for quadrotor UAV. Meas. Control 2022, 55, 738–745. [Google Scholar] [CrossRef]
- Budiharto, W.; Irwansyah, E.; Suroso, J.S.; Chowanda, A.; Ngarianto, H.; Gunawan, A.A.S. Mapping and 3D modelling using quadrotor drone and GIS software. J. Big Data 2021, 8, 48. [Google Scholar] [CrossRef]
- Hegde, A.; Ghose, D. Multi-Quadrotor Distributed Load Transportation for Autonomous Agriculture Spraying Operations. J. Guid. Control Dyn. 2022, 45, 944–951. [Google Scholar] [CrossRef]
- Wang, S.; Chen, J.; He, X. An adaptive composite disturbance rejection for attitude control of the agricultural quadrotor UAV. ISA Trans. 2022, 129, 564–579. [Google Scholar] [CrossRef] [PubMed]
- Nekoo, S.R.; Acosta, J.Á.; Heredia, G.; Ollero, A. A benchmark mechatronics platform to assess the inspection around pipes with variable pitch quadrotor for industrial sites. Mechatronics 2021, 79, 102641. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, L.; Fan, S.; Zhang, Y. Design of Gas Monitoring Terminal Based on Quadrotor UAV. Sensors 2022, 22, 5350. [Google Scholar] [CrossRef]
- Feng, L.; Katupitiya, J. Vector Field based Control of Quadrotor UAVs for Wildfire Boundary Monitoring. J. Intell. Robot. Syst. 2022, 106, 27. [Google Scholar] [CrossRef]
- Gul, O.M.; Erkmen, A.M.; Kantarci, B. UAV-Driven sustainable and Quality-Aware data collection in robotic wireless sensor networks. IEEE Internet Things J. 2022, 9, 25150–25164. [Google Scholar] [CrossRef]
- Gul, O.M.; Erkmen, A.M. Energy-efficient cluster-based data collection by a UAV with a limited-capacity battery in robotic wireless sensor networks. Sensors 2020, 20, 5865. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Quan, F.; Fang, L.; Zhang, S. Aerial grasping with a lightweight manipulator based on multi-objective optimization and visual compensation. Sensors 2019, 19, 4253. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; He, Y.; Dai, B.; Gu, F.; Yang, L.; Han, J.; Liu, G.; Qi, J. Grasp a moving target from the air: System & control of an aerial manipulator. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 1681–1687. [Google Scholar] [CrossRef]
- Baraban, G.; Sheckells, M.; Kim, S.; Kobilarov, M. Adaptive parameter estimation for aerial manipulation. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 614–619. [Google Scholar] [CrossRef]
- Lee, H.; Kim, H.; Kim, W.; Kim, H.J. An integrated framework for cooperative aerial manipulators in unknown environments. IEEE Robot. Autom. Lett. 2018, 3, 2307–2314. [Google Scholar] [CrossRef]
- Thapa, S.; Bai, H.; Acosta, J.A. Cooperative aerial load transport with force control. IFAC-PapersOnLine 2018, 51, 38–43. [Google Scholar] [CrossRef]
- Sanchez-Cuevas, P.J.; Gonzalez-Morgado, A.; Cortes, N.; Gayango, D.B.; Jimenez-Cano, A.E.; Ollero, A.; Heredia, G. Fully-actuated aerial manipulator for infrastructure contact inspection: Design, modeling, localization, and control. Sensors 2020, 20, 4708. [Google Scholar] [CrossRef]
- Zeng, J.; Zhong, H.; Wang, Y.; Fan, S.; Zhang, H. Autonomous control design of an unmanned aerial manipulator for contact inspection. Robotica 2022, 1–14. [Google Scholar] [CrossRef]
- Hamaza, S.; Georgilas, I.; Fernandez, M.; Sanchez, P.; Richardson, T.; Heredia, G.; Ollero, A. Sensor installation and retrieval operations using an unmanned aerial manipulator. IEEE Robot. Autom. Lett. 2019, 4, 2793–2800. [Google Scholar] [CrossRef] [Green Version]
- Ivanovic, A.; Markovic, L.; Car, M.; Duvnjak, I.; Orsag, M. Towards Autonomous Bridge Inspection: Sensor Mounting Using Aerial Manipulators. Appl. Sci. 2021, 11, 8279. [Google Scholar] [CrossRef]
- Hamaza, S.; Georgilas, I.; Heredia, G.; Ollero, A.; Richardson, T. Design, modeling, and control of an aerial manipulator for placement and retrieval of sensors in the environment. J. Field Robot. 2020, 37, 1224–1245. [Google Scholar] [CrossRef]
- Ding, C.; Lu, L.; Wang, C.; Ding, C. Design, sensing, and control of a novel UAV platform for aerial drilling and screwing. IEEE Robot. Autom. Lett. 2021, 6, 3176–3183. [Google Scholar] [CrossRef]
- Fumagalli, M.; Naldi, R.; Macchelli, A.; Forte, F.; Keemink, A.Q.; Stramigioli, S.; Carloni, R.; Marconi, L. Developing an aerial manipulator prototype: Physical interaction with the environment. IEEE Robot. Autom. Mag. 2014, 21, 41–50. [Google Scholar] [CrossRef]
- Meng, X.; He, Y.; Li, Q.; Gu, F.; Yang, L.; Yan, T.; Han, J. Contact force control of an aerial manipulator in pressing an emergency switch process. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), USA, Madrid, Spain, 1–5 October 2018; IEEE: Piscataway, NJ, USA, 2019; pp. 2107–2113. [Google Scholar] [CrossRef]
- Yang, B.; He, Y.; Han, J.; Liu, G. Rotor-flying manipulator: Modeling, analysis, and control. Math. Probl. Eng. 2014, 2014, 492965. [Google Scholar] [CrossRef] [Green Version]
- Escareno, J.; Rakotondrabe, M.; Flores, G.; Lozano, R. Rotorcraft mav having an onboard manipulator: Longitudinal modeling and robust control. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 3258–3263. [Google Scholar] [CrossRef] [Green Version]
- Di Lucia, S.; Tipaldi, G.D.; Burgard, W. Attitude stabilization control of an aerial manipulator using a quaternion-based backstepping approach. In Proceedings of the 2015 European Conference on Mobile Robots (ECMR), Lincoln, UK, 2–4 September 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Lunni, D.; Santamaria-Navarro, A.; Rossi, R.; Rocco, P.; Bascetta, L.; Andrade-Cetto, J. Nonlinear model predictive control for aerial manipulation. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 87–93. [Google Scholar] [CrossRef] [Green Version]
- Feng, Y.; Yu, X.; Han, F. On nonsingular terminal sliding-mode control of nonlinear systems. Automatica 2013, 49, 1715–1722. [Google Scholar] [CrossRef]
- Riache, S.; Kidouche, M.; Rezoug, A. Adaptive robust nonsingular terminal sliding mode design controller for quadrotor aerial manipulator. TELKOMNIKA Telecommun. Comput. Electron. Control 2019, 17, 1501–1512. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, Y.; Wang, D.; Ju, F.; Chen, B.; Wu, H. Practical continuous nonsingular terminal sliding mode control of a cable-driven manipulator developed for aerial robots. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2020, 234, 1011–1023. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, Y.; Celler, B.G.; Su, S.W. Neural adaptive backstepping control of a robotic manipulator with prescribed performance constraint. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 3572–3583. [Google Scholar] [CrossRef]
- Ren, B.; Wang, Y.; Chen, J. Trajectory-tracking-based adaptive neural network sliding mode controller for robot manipulators. J. Comput. Inf. Sci. Eng. 2020, 20, 031009. [Google Scholar] [CrossRef]
- Nubert, J.; Köhler, J.; Berenz, V.; Allgöwer, F.; Trimpe, S. Safe and fast tracking on a robot manipulator: Robust mpc and neural network control. IEEE Robot. Autom. Lett. 2020, 5, 3050–3057. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Yang, J. Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems. Int. J. Robust Nonlinear Control 2011, 21, 1865–1879. [Google Scholar] [CrossRef]
- Boukattaya, M.; Mezghani, N.; Damak, T. Adaptive nonsingular fast terminal sliding-mode control for the tracking problem of uncertain dynamical systems. Isa Trans. 2018, 77, 1–19. [Google Scholar] [CrossRef]











| Parameter | Value | Units |
|---|---|---|
| 1.8 | ||
| 9.8 | ||
| 1.24 | ||
| 1.24 | ||
| 2.48 | ||
| 0.1 | ||
| 0.4 | ||
| (0, 0, 0) | ||
| 30 | ||
| 10 |
| Parameter in the Position Loop | Value | Parameter in the Attitude Loop | Value | Parameter of the RBFNN Observer | Value |
|---|---|---|---|---|---|
| 200 | 1000 | ||||
| 10 | 60 | ||||
| 3 | 3 | ||||
| 5 | 5 | ||||
| 800 | 400 | ||||
| 100 | 100 | ||||
| 3 | 3 | ||||
| 5 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Q.; Mao, P.; Shen, L.; Wang, J. Robust Control Based on Adaptive Neural Network for the Process of Steady Formation of Continuous Contact Force in Unmanned Aerial Manipulator. Sensors 2023, 23, 989. https://doi.org/10.3390/s23020989
Fang Q, Mao P, Shen L, Wang J. Robust Control Based on Adaptive Neural Network for the Process of Steady Formation of Continuous Contact Force in Unmanned Aerial Manipulator. Sensors. 2023; 23(2):989. https://doi.org/10.3390/s23020989
Chicago/Turabian StyleFang, Qian, Pengjun Mao, Lirui Shen, and Jun Wang. 2023. "Robust Control Based on Adaptive Neural Network for the Process of Steady Formation of Continuous Contact Force in Unmanned Aerial Manipulator" Sensors 23, no. 2: 989. https://doi.org/10.3390/s23020989
APA StyleFang, Q., Mao, P., Shen, L., & Wang, J. (2023). Robust Control Based on Adaptive Neural Network for the Process of Steady Formation of Continuous Contact Force in Unmanned Aerial Manipulator. Sensors, 23(2), 989. https://doi.org/10.3390/s23020989





