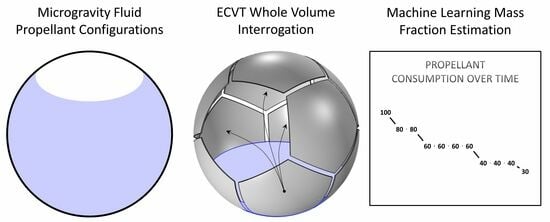
Propellant Mass Gauging in a Spherical Tank under Micro-Gravity Conditions Using Capacitance Plate Arrays and Machine Learning
Abstract
:1. Introduction
2. Sensor Description and Fill Types
3. Different Approaches for Mass Fraction Estimation
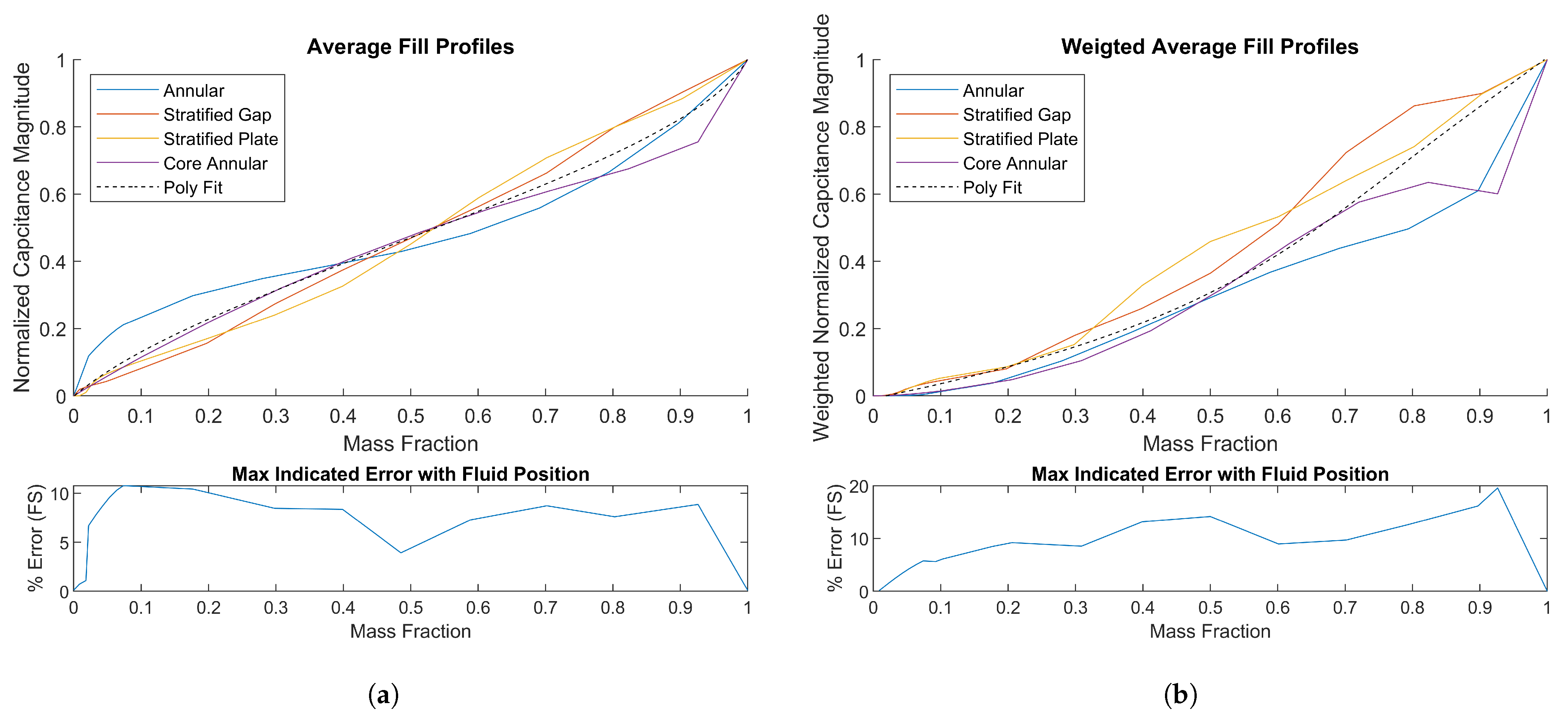
3.1. Average-Capacitance-Based Approach
| Algorithm 1 Steps for average-capacitance-based mass fraction estimation. |
|
3.2. Weighted Average Capacitance by Channel Type Approach
| Algorithm 2 Stepsfor weighted average-capacitance-based mass fraction estimation. |
|
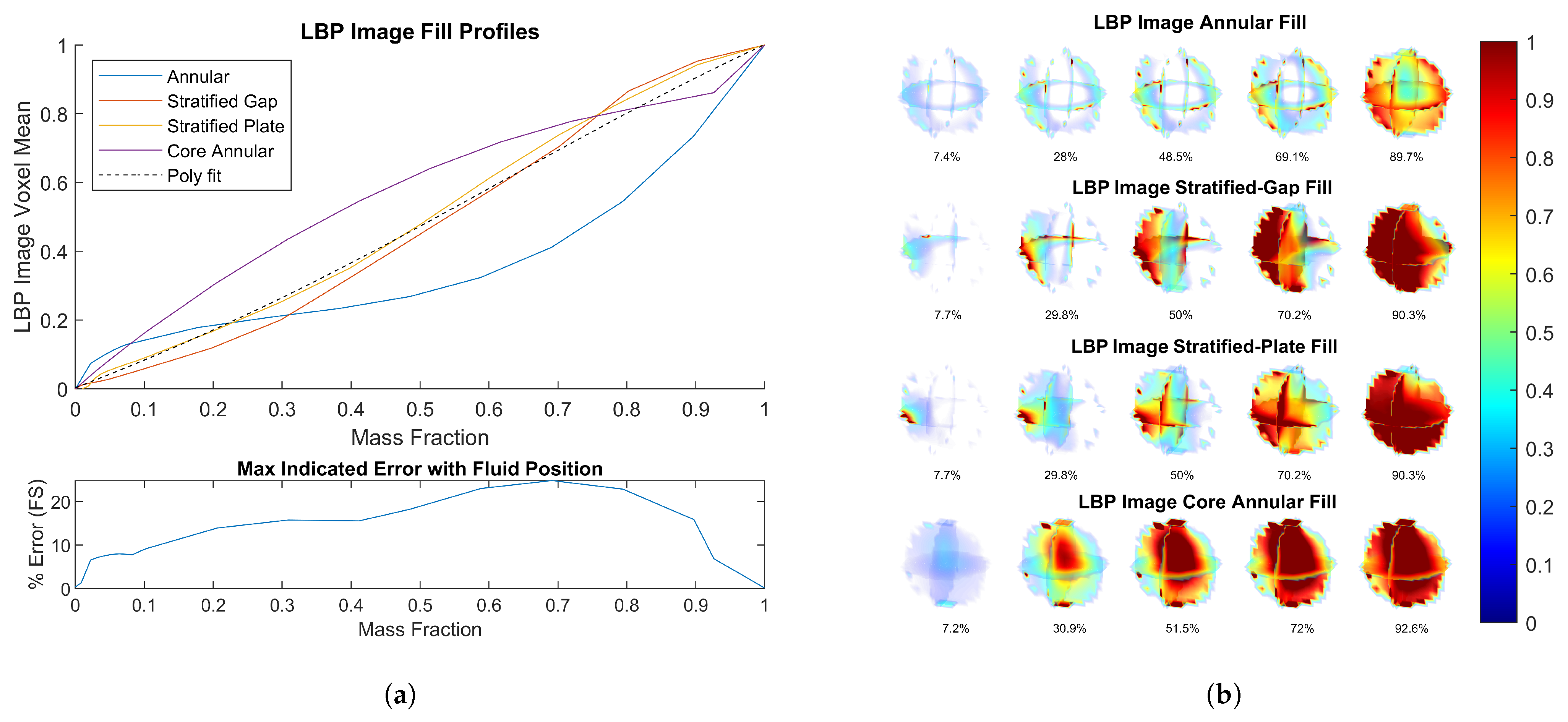
3.3. Linear Back Projection Image Voxel Mean Approach
| Algorithm 3 Stepsfor linear back projection voxel mean (LBP-VM)-based mass fraction estimation. |
|
3.4. Capacitance-Norm-Based Approach
| Algorithm 4 Steps for capacitance-norm-based mass fraction estimation. |
|
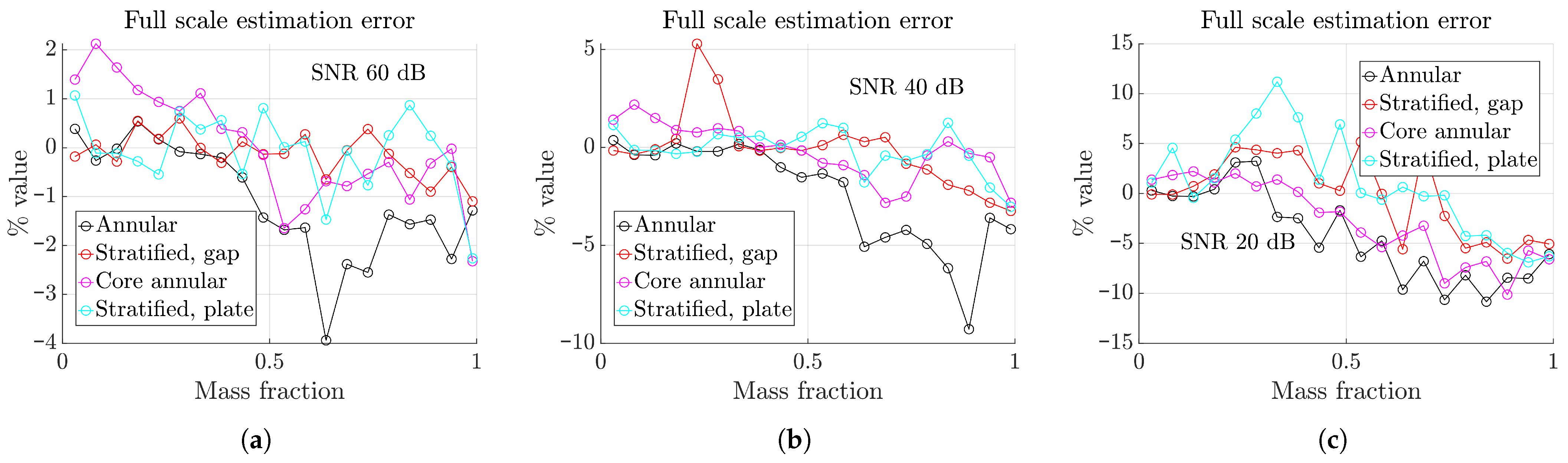
3.5. Machine-Learning-Based Approach
| Algorithm 5 Steps for machine-learning-based mass fraction estimation. |
|
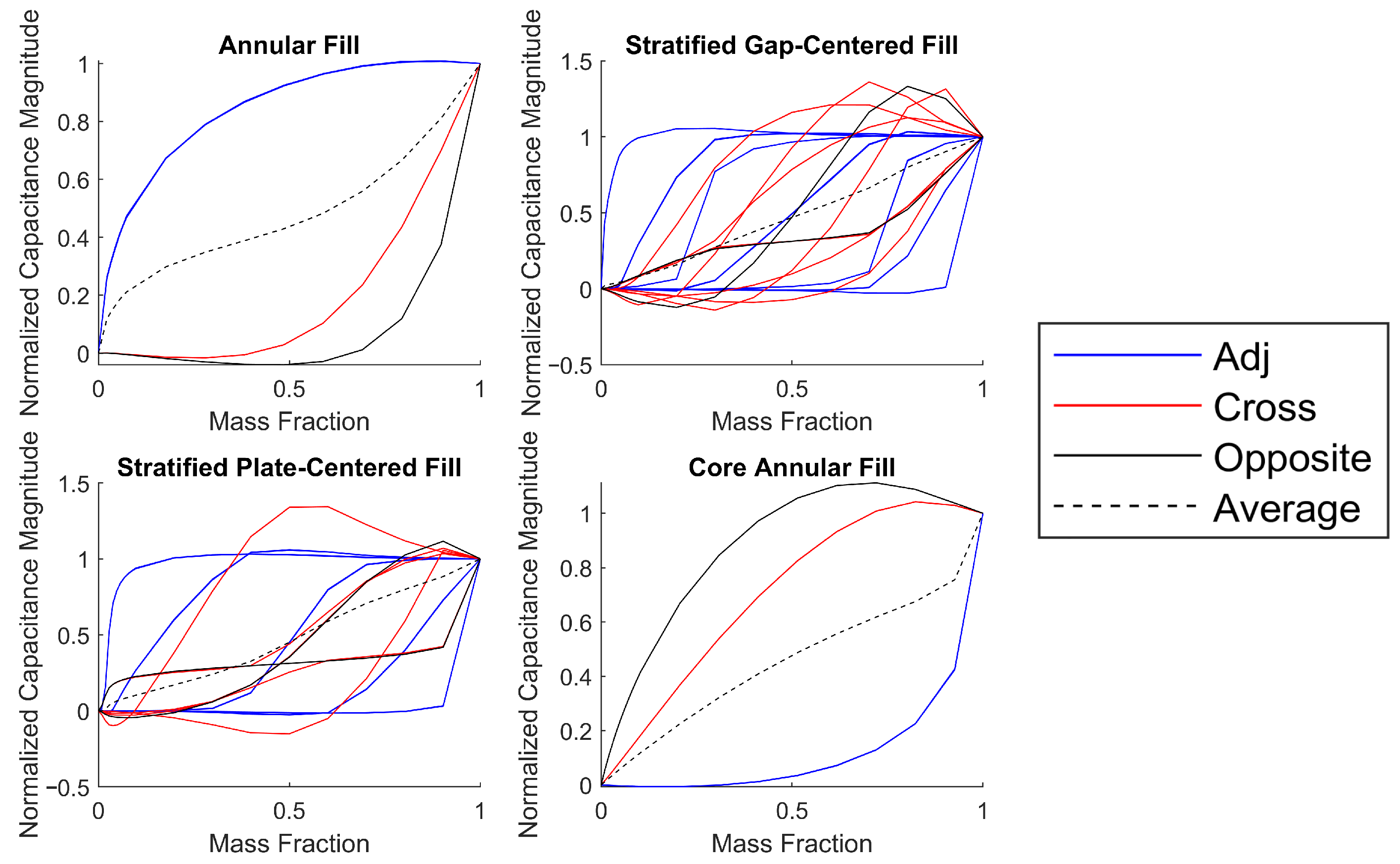
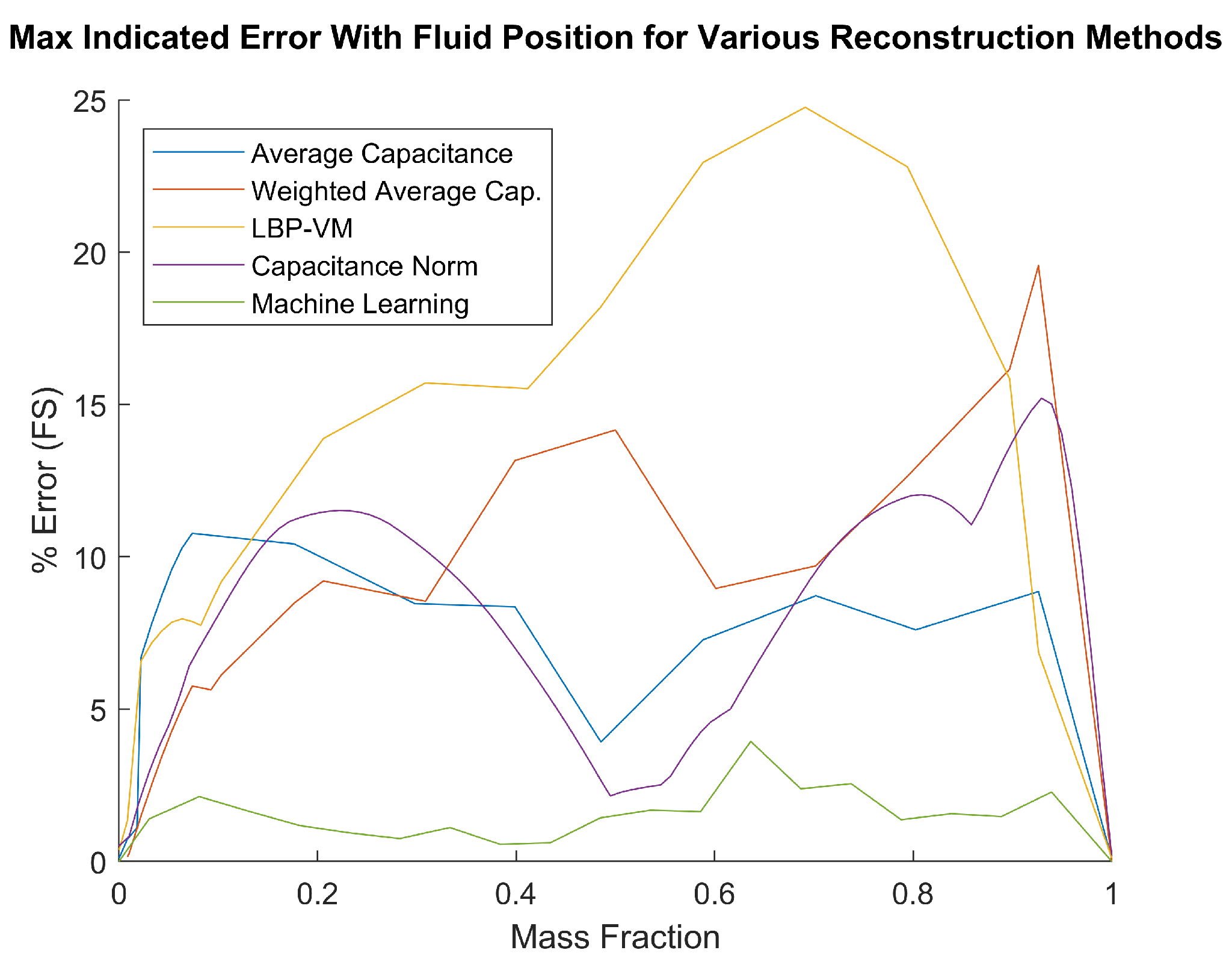
4. Experimental Results
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dodge, F. Propellant Mass Gauging: Database of vehicle Applications and Research and Development Studies; Technical Report; National Aeronautics and Space Administration: San Antonio, TX, USA, 2008.
- Aeronautics, N.; Administration, S. 2020 NASA Technology Taxonomy; Technical Report; National Aeronautics and Space Administration: Washington, DC, USA, 2020.
- Yendler, B. Review of Propellant Gauging Methods. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar]
- Zimmerli, G.A.; Vaden, K.R.; Herlacher, M.D.; Buchanan, D.A.; Van Dresar, N.T. Radio Frequency Mass Gauging of Propellants. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- Crosby, K.M.; Welink, R.J.; Hurlbert, E.A. Liquid Propellant Mass Measurement in Microgravity. Gravitational Space Res. 2021, 9, 50–61. [Google Scholar] [CrossRef]
- Zimmerli, G.A. Propellant Gauging for Exploration. In Proceedings of the 54th JANNAF Propulsion Meeting, Denver, CO, USA, 14–17 May2007. [Google Scholar]
- Storey, J.; Marsell, B.; Elmore, M.; Clark, S. Preliminary Results from Propellant Mass Gauging in Microgravity with Electrical Capacitance Tomography; Technical Report; National Aeronautics and Space Administration: Washington, DC, USA, 2022.
- Gut, Z. Using Electrical Capacitance Tomography System for Determination of Liquids in Rocket and Satellite Tanks. Trans. Aerosp. Res. 2020, 2020, 18–33. [Google Scholar] [CrossRef]
- Youngquist, R.; Storey, J.M.; Nurge, M.A.; Biagi, C.J. A Derivation of the Electrical Capacitance Tomography Sensitivity Matrix. Meas. Sci. Technol. 2022, 34, 025404. [Google Scholar] [CrossRef]
- Chowdhury, S.M.; Marashdeh, Q.M.; Teixeira, F.L.; Fan, L.S. Electrical capacitance tomography. In Industrial Tomography: Systems and Applications, 2nd ed.; Wang, M., Ed.; Woodhead/Elsevier: Cambridge, UK, 2022; Chapter 1; pp. 3–29. [Google Scholar]
- Warsito, W.; Marashdeh, Q.M.; Fan, L.S. Electrical capacitance volume tomography. IEEE Sens. J. 2007, 7, 525–535. [Google Scholar] [CrossRef]
- Park, C.; Chowdhury, S.M.; Pottimurthy, Y.; Marashdeh, Q.M.; Tong, A.; Teixeira, F.L.; Fan, L.S. Velocity Profiling of a Gas–Solid Fluidized Bed Using Electrical Capacitance Volume Tomography. IEEE Trans. Instrum. Meas. 2022, 71, 1–16. [Google Scholar] [CrossRef]
- Guo, Q.; Ye, M.; Yang, W.; Liu, Z. A machine learning approach for electrical capacitance tomography measurement of gas–solid fluidized beds. AIChE J. 2019, 65, e16583. [Google Scholar] [CrossRef]
- Li, W.; Song, W.; Yin, G.; Ong, M.C.; Han, F. Flow regime identification in the subsea jumper based on electrical capacitance tomography and convolution neural network. Ocean Eng. 2022, 266, 113152. [Google Scholar] [CrossRef]
- Zheng, J.; Peng, L. A Deep Learning Compensated Back Projection for Image Reconstruction of Electrical Capacitance Tomography. IEEE Sens. J. 2020, 20, 4879–4890. [Google Scholar] [CrossRef]
- Lei, J.; Liu, Q.B.; Wang, X.Y. Ensemble learning-based computational imaging method for electrical capacitance tomography. Appl. Math. Modell. 2020, 82, 521–545. [Google Scholar] [CrossRef]
- Tian, Z.N.; Gao, X.X.; Qiu, L.m.; Zhang, X.B. Experimental imaging and algorithm optimization based on deep neural network for electrical capacitance tomography for LN2-VN2 flow. Cryogenics 2022, 127, 103568. [Google Scholar] [CrossRef]
- Jaworek, A.; Krupa, A.; Trela, M. Capacitance sensor for void fraction measurement in water/steam flows. Flow Meas. Instrum. 2004, 15, 317–324. [Google Scholar] [CrossRef]
- Chowdhury, S.M.; Marashdeh, Q.M.; Teixeira, F.L. Electronic Scanning Strategies in Adaptive Electrical Capacitance Volume Tomography: Tradeoffs and Prospects. IEEE Sens. J. 2020, 20, 9253–9264. [Google Scholar] [CrossRef]
- Charleston, M.A.; Chowdhury, S.M.; Marashdeh, Q.M.; Straiton, B.J.; Teixeira, F.L. Towards Microgravity Mass Gauging in Spherical Tanks using ECVT. In Proceedings of the 30th Space Cryogenics Workshop in the Journal Cryogenics, Kailua-Kona, HI, USA, 16–18 July 2023. [Google Scholar]
- Behruzi, P.; Hunt, A.; Foster-Turner, R. Evaluation of Liquid Sloshing using Electrical Capacitance Tomography. In AIAA Propulsion and Energy 2020 Forum; AIAA Propulsion and Energy Forum, American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2020. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
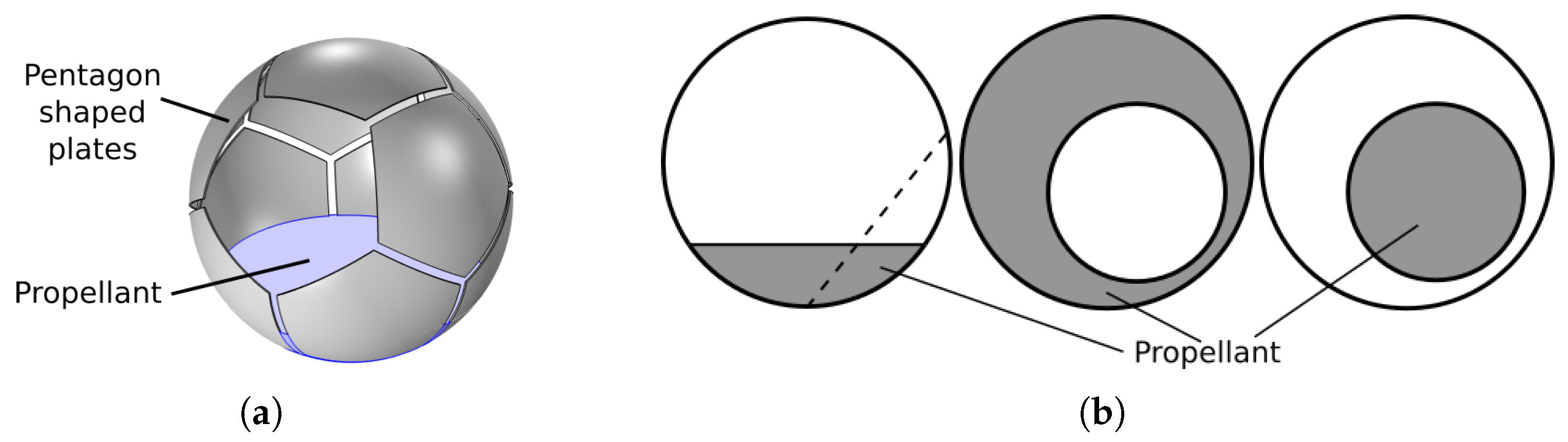
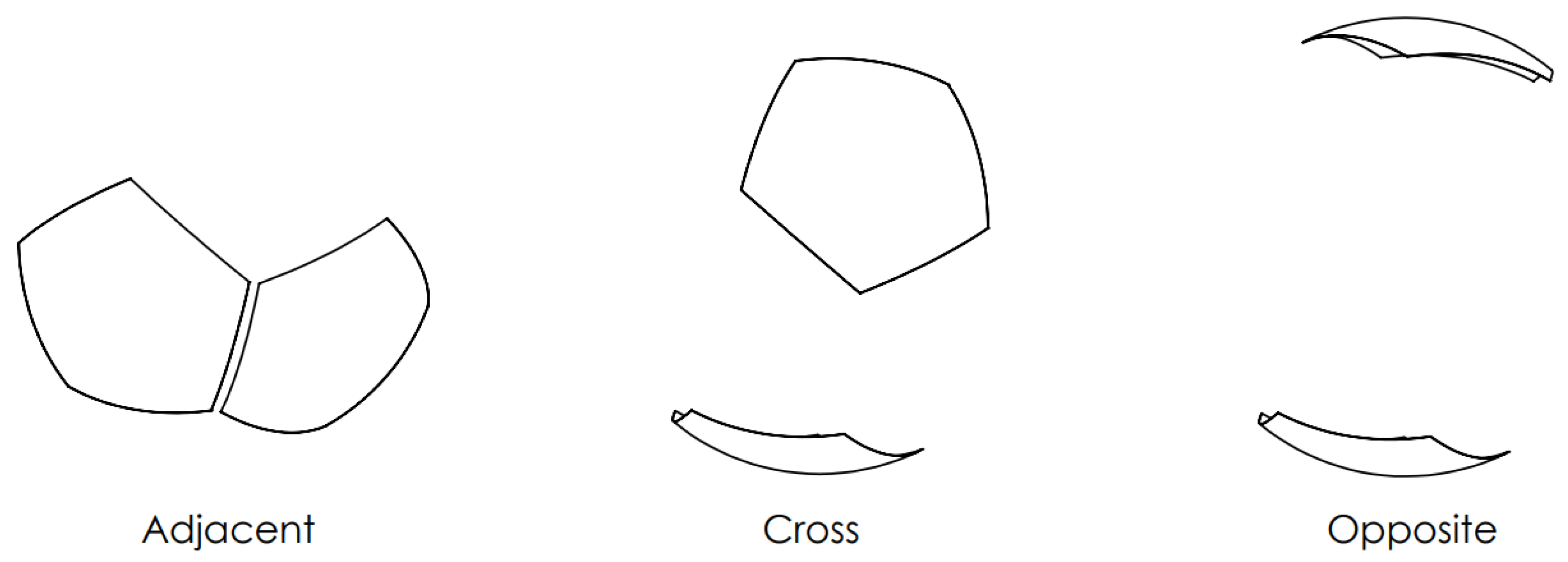


| Fill Type | Object Center Distance from Sensor Origin, r | Number of Directions/ Locations, (), L | Mass Fraction Range | Number of Data Points, N | Total Number of Data Points, |
|---|---|---|---|---|---|
| Stratified | N/A | 26 | 0.0–1.0 | 100 | 2600 |
| Core-annular | N/A | 1 | 0.0–1.0 | 100 | 100 |
| Core-annular, off-centered | 1/8 | 32 | 0.0–0.62 | 60 | 1920 |
| 1/4 | 32 | 0.0–0.36 | 40 | 1280 | |
| 3/8 | 32 | 0.0–0.21 | 20 | 640 | |
| 1/2 | 32 | 0.0–0.10 | 10 | 320 | |
| 5/8 | 32 | 0.0–0.04 | 5 | 160 | |
| Annular | N/A | 1 | 0.0–1.0 | 100 | 100 |
| Annular, off-centered | 1/8 | 32 | 0.38–1.0 | 60 | 1920 |
| 1/4 | 32 | 0.64–1.0 | 40 | 1280 | |
| 3/8 | 32 | 0.79–1.0 | 20 | 640 | |
| 1/2 | 32 | 0.90–1.0 | 10 | 320 | |
| Total | N/A | 316 | N/A | N/A | 11,280 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chowdhury, S.M.; Charleston, M.A.; Marashdeh, Q.M.; Teixeira, F.L. Propellant Mass Gauging in a Spherical Tank under Micro-Gravity Conditions Using Capacitance Plate Arrays and Machine Learning. Sensors 2023, 23, 8516. https://doi.org/10.3390/s23208516
Chowdhury SM, Charleston MA, Marashdeh QM, Teixeira FL. Propellant Mass Gauging in a Spherical Tank under Micro-Gravity Conditions Using Capacitance Plate Arrays and Machine Learning. Sensors. 2023; 23(20):8516. https://doi.org/10.3390/s23208516
Chicago/Turabian StyleChowdhury, Shah M., Matthew A. Charleston, Qussai M. Marashdeh, and Fernando L. Teixeira. 2023. "Propellant Mass Gauging in a Spherical Tank under Micro-Gravity Conditions Using Capacitance Plate Arrays and Machine Learning" Sensors 23, no. 20: 8516. https://doi.org/10.3390/s23208516
APA StyleChowdhury, S. M., Charleston, M. A., Marashdeh, Q. M., & Teixeira, F. L. (2023). Propellant Mass Gauging in a Spherical Tank under Micro-Gravity Conditions Using Capacitance Plate Arrays and Machine Learning. Sensors, 23(20), 8516. https://doi.org/10.3390/s23208516