Data Augmentation Techniques for Machine Learning Applied to Optical Spectroscopy Datasets in Agrifood Applications: A Comprehensive Review
Abstract
:1. Introduction
2. A Brief Introduction to AI: Training and Evaluation
2.1. Backpropagation in Training
- It takes a mini-batch from the training dataset.
- It sends the mini-batch though the network’s input layer, on to the first hidden layer, and computes the outputs of all neurons in this layer. This result is then passed to the next layer. This process continues until it reaches the output layer. This is the forward pass, similar to making predictions, but intermediate values are kept for calculations.
- A loss function, which compares the desired output with the actual output of the network, is used, and it returns an error metric.
- It calculates how much each output connection contributes to the error. It measures how many error contributions come from each connection of the previous layer. This process is performed all the way back to the input layer.
- The gradient descent process is applied to adjust the weights of the network using the error gradients that were just calculated.
2.2. Model Performance Evaluation
2.2.1. Metrics for Regression Models
2.2.2. Metrics for Classification Models
- True positives (TPs): Number of positive observations the model correctly predicted as positive.
- False positives (FPs): Number of negative observations the model incorrectly predicted as positive.
- True negatives (TNs): Number of negative observations the model correctly predicted as negative.
- False negatives (FNs): Number of positive observations the model incorrectly predicted as negative.
3. DA to Enhance the Dataset
3.1. DA Based on Non-DL Algorithms
- Blending spectra: combines samples with variations to create artificial admixtures.
- Spectral intensifier: modifies the intensity of a spectrum to control baseline variations.
- Shifting along the x-axis: applies random shifts to data points in spectra to mimic instrumental variations.
- Adding noise: increases the variability of a class by including slightly noisy spectra based on the original spectra.
3.2. Generative Adversarial Networks (GANs)
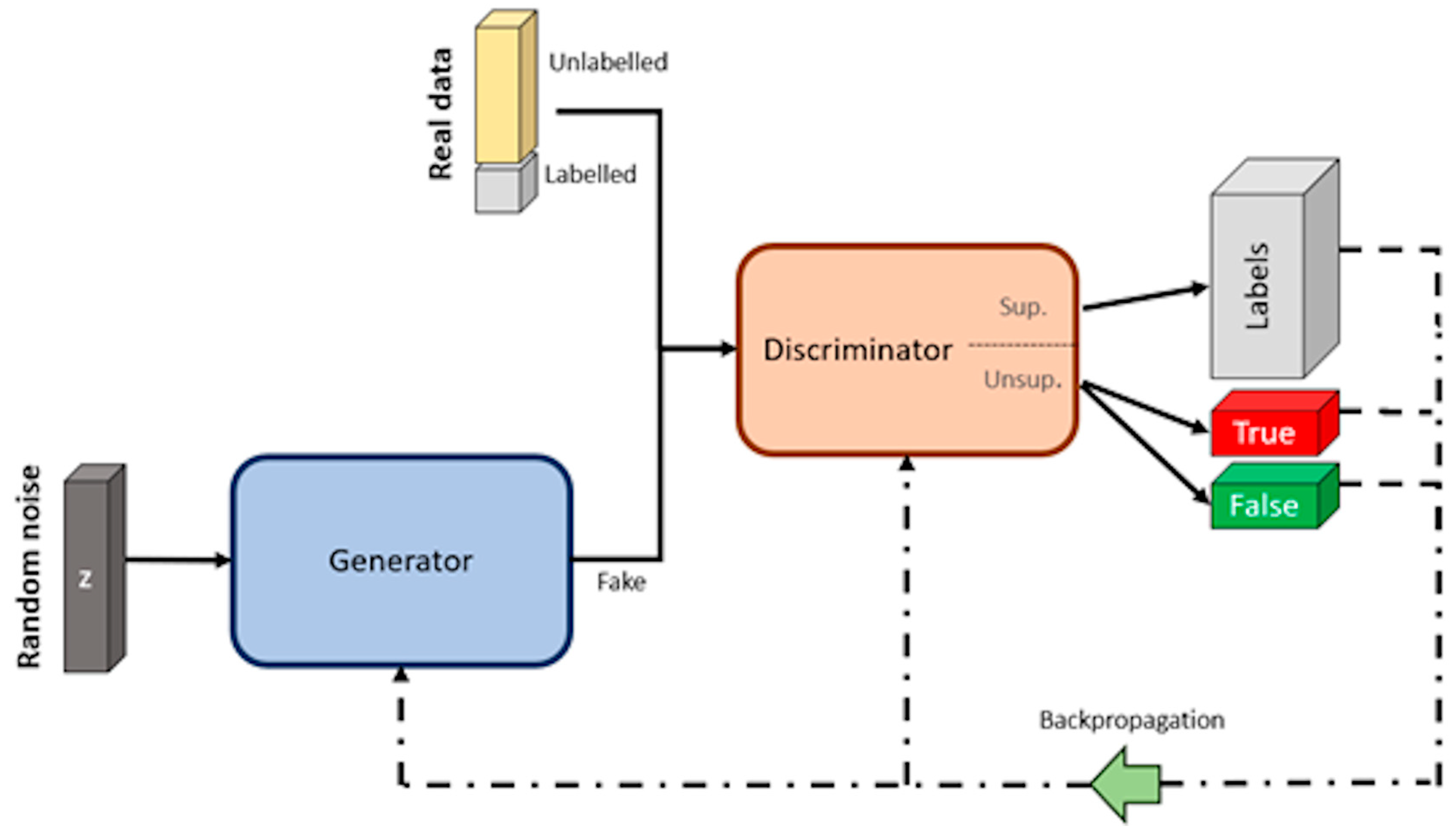
Semi-Supervised Learning—SGANs for DA and Classification
3.3. Comparative Analysis of DA Techniques: Merits and Disadvantages
- Non-DL-based methods: The explained methods encompass the addition of various types of noise to the existing data: shifting along the wavelength axis, modifying the spectral intensity of the samples, or applying SMOTE, among others. These methods are useful and simple to apply but may not achieve the precise discernment of spectral features if not applied correctly, resulting in a lack of real semantic variability. This means that the diversity in the generated data can be non-meaningful or irrelevant to the task.
- GAN and SGAN methods: Their main strength is their ability to learn complex data distributions to generate more realistic data with real semantic variability. In contrast, these methods require considerable expertise in tuning and training, as well as the availability of computational resources.
4. Conclusions
- Take a set of samples and perform the optical spectroscopy measurements in the range where the samples present the most relevant information for the target.
- Apply non-DL-based techniques to enhance the dataset, adding new synthetic data to the dataset. Develop a model and check the performance with these new synthetic data.
- Apply DL-based techniques (GANs or SGANs) to generate new fake data and evaluate the final model in order to check if there was an improvement in its performance.
- Release the model and apply it to the agrifood industry particular application case to evaluate the model in situ.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pavia, D.L.; Lampman, G.M.; Kriz, G.S.; Vyvyan, J.A. Introduction to Spectroscopy. Google Libros. Available online: https://books.google.es/books?hl=es&lr=&id=N-zKAgAAQBAJ&oi=fnd&pg=PP1&dq=spectroscopy+&ots=XfmebVhP2L&sig=ressCoxB7WEneEerzZzaUmQfThs#v=onepage&q=spectroscopy&f=false (accessed on 20 December 2022).
- Manley, M. Near-Infrared Spectroscopy and Hyperspectral Imaging: Non-Destructive Analysis of Biological Materials. Chem. Soc. Rev. 2014, 43, 8200–8214. [Google Scholar] [CrossRef]
- Herrero, A.M. Raman Spectroscopy a Promising Technique for Quality Assessment of Meat and Fish: A Review. Food Chem. 2008, 107, 1642–1651. [Google Scholar] [CrossRef]
- Gaudiuso, R.; Dell’Aglio, M.; de Pascale, O.; Senesi, G.S.; de Giacomo, A. Laser Induced Breakdown Spectroscopy for Elemental Analysis in Environmental, Cultural Heritage and Space Applications: A Review of Methods and Results. Sensors 2010, 10, 7434–7468. [Google Scholar] [CrossRef]
- Wang, H.; Peng, J.; Xie, C.; Bao, Y.; He, Y. Fruit Quality Evaluation Using Spectroscopy Technology: A Review. Sensors 2015, 15, 11889–11927. [Google Scholar] [CrossRef]
- Rossman, G.R. Optical Spectroscopy. Rev. Mineral. Geochem. 2014, 78, 371–398. [Google Scholar] [CrossRef]
- Rolinger, L.; Rüdt, M.; Hubbuch, J. A Critical Review of Recent Trends, and a Future Perspective of Optical Spectroscopy as PAT in Biopharmaceutical Downstream Processing. Anal. Bioanal. Chem. 2020, 412, 2047–2064. [Google Scholar] [CrossRef]
- Childs, P.R.N.; Greenwood, J.R.; Long, C.A. Review of Temperature Measurement. Rev. Sci. Instrum. 2000, 71, 2959–2978. [Google Scholar] [CrossRef]
- Moerner, W.E.; Basché, T. Optical Spectroscopy of Single Impurity Molecules in Solids. Angew. Chem. Int. Ed. Engl. 1993, 32, 457–476. [Google Scholar] [CrossRef]
- Osborne, B.G. Near-Infrared Spectroscopy in Food Analysis; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Lin, T.; Yu, H.Y.; Ying, Y.B. Review of Progress in Application Visible/near-Infrared Spectroscopy in Liquid Food Detection. Spectrosc. Spectr. Anal. 2008, 28, 285–290. [Google Scholar]
- Gong, Y.M.; Zhang, W. Recent Progress in NIR Spectroscopy Technology and Its Application to the Field of Forestry. Spectrosc. Spectr. Anal. 2008, 28, 1544–1548. [Google Scholar]
- Sun, T.; Xu, H.R.; Ying, Y.B. Progress in Application of near Infrared Spectroscopy to Nondestructive On-Line Detection of Products/Food Quality. Spectrosc. Spectr. Anal. 2009, 29, 122–126. [Google Scholar]
- Cozzolino, D.; Murray, I.; Paterson, R.; Scaife, J.R. Visible and near Infrared Reflectance Spectroscopy for the Determination of Moisture, Fat and Protein in Chicken Breast and Thigh Muscle. J. Near Infrared Spectrosc. 1996, 4, 213–223. [Google Scholar] [CrossRef]
- Zaroual, H.; Chénè, C.; El Hadrami, E.M.; Karoui, R. Application of New Emerging Techniques in Combination with Classical Methods for the Determination of the Quality and Authenticity of Olive Oil: A Review. Crit. Rev. Food Sci. Nutr. 2022, 62, 4526–4549. [Google Scholar] [CrossRef] [PubMed]
- Armenta, S.; Moros, J.; Garrigues, S.; de la Guardia, M. The Use of Near-Infrared Spectrometry in the Olive Oil Industry. Crit. Rev. Food Sci. Nutr. 2010, 50, 567–582. [Google Scholar] [CrossRef]
- Franz, A.W.; Kronemayer, H.; Pfeiffer, D.; Pilz, R.D.; Reuss, G.; Disteldorf, W.; Gamer, A.O.; Hilt, A. Formaldehyde. Ullmann’s Encycl. Ind. Chem. 2016, A11, 1–34. [Google Scholar] [CrossRef]
- Alishahi, A.; Farahmand, H.; Prieto, N.; Cozzolino, D. Identification of Transgenic Foods Using NIR Spectroscopy: A Review. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2010, 75, 1–7. [Google Scholar] [CrossRef]
- Chauhan, N.K.; Singh, K. A Review on Conventional Machine Learning vs Deep Learning. In Proceedings of the 2018 International Conference on Computing, Power and Communication Technologies, GUCON 2018, Greater Noida, India, 28–29 September 2018; pp. 347–352. [Google Scholar] [CrossRef]
- Shinde, P.P.; Shah, S. A Review of Machine Learning and Deep Learning Applications. In Proceedings of the 2018 4th International Conference on Computing, Communication Control and Automation, ICCUBEA 2018, Pune, India, 16–18 August 2018. [Google Scholar] [CrossRef]
- Meza Ramirez, C.A.; Greenop, M.; Ashton, L.; ur Rehman, I. Applications of Machine Learning in Spectroscopy. Appl. Spectrosc. Rev. 2020, 56, 733–763. [Google Scholar] [CrossRef]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine Learning in Agriculture: A Review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef]
- Su, W.H. Advanced Machine Learning in Point Spectroscopy, RGB- and Hyperspectral-Imaging for Automatic Discriminations of Crops and Weeds: A Review. Smart Cities 2020, 3, 767–792. [Google Scholar] [CrossRef]
- Prell, J.S.; O’Brien, J.T.; Williams, E.R. IRPD Spectroscopy and Ensemble Measurements: Effects of Different Data Acquisition and Analysis Methods. J. Am. Soc. Mass. Spectrom. 2010, 21, 800–809. [Google Scholar] [CrossRef]
- Gao, L.; Smith, R.T. Optical Hyperspectral Imaging in Microscopy and Spectroscopy—A Review of Data Acquisition. J. Biophotonics 2015, 8, 441–456. [Google Scholar] [CrossRef] [PubMed]
- Ur-Rahman, A.; Choudhary, M.I.; Wahab, A.-T. Solving Problems with NMR Spectroscopy. Google Libros. Available online: https://books.google.es/books?hl=es&lr=&id=2PujBwAAQBAJ&oi=fnd&pg=PP1&dq=problems+spectroscopy&ots=TETTQ5BDlo&sig=exLWLZSyJKQMl6bJcrmhoiP2M8M#v=onepage&q=problems%20spectroscopy&f=false (accessed on 20 December 2022).
- Aasen, H.; Honkavaara, E.; Lucieer, A.; Zarco-Tejada, P.J. Quantitative Remote Sensing at Ultra-High Resolution with UAV Spectroscopy: A Review of Sensor Technology, Measurement Procedures, and Data Correction Workflows. Remote Sens. 2018, 10, 1091. [Google Scholar] [CrossRef]
- Chawla, N.V. Data Mining for Imbalanced Datasets: An Overview. In Data Mining and Knowledge Discovery Handbook; Springer: Berlin/Heidelberg, Germany, 2009; pp. 875–886. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Heaton, J. Ian Goodfellow, Yoshua Bengio, and Aaron Courville: Deep Learning. Genet. Program. Evolvable Mach. 2017, 19, 305–307. [Google Scholar] [CrossRef]
- He, H.; Garcia, E.A. Learning from Imbalanced Data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar] [CrossRef]
- Shorten, C.; Khoshgoftaar, T.M. A Survey on Image Data Augmentation for Deep Learning. J. Big Data 2019, 6, 1–48. [Google Scholar] [CrossRef]
- Maharana, K.; Mondal, S.; Nemade, B. A Review: Data Pre-Processing and Data Augmentation Techniques. Glob. Transit. Proc. 2022, 3, 91–99. [Google Scholar] [CrossRef]
- Hernández-García, A.; König, P. Further Advantages of Data Augmentation on Convolutional Neural Networks. In Artificial Neural Networks and Machine Learning—ICANN 2018, Proceedings of the 27th International Conference on Artificial Neural Networks, Rhodes, Greece, 4–7 October 2018; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; Volume 11139, pp. 95–103. [Google Scholar] [CrossRef]
- Wong, S.C.; Gatt, A.; Stamatescu, V.; McDonnell, M.D. Understanding Data Augmentation for Classification: When to Warp? In Proceedings of the 2016 International Conference on Digital Image Computing: Techniques and Applications, DICTA 2016, Gold Coast, QLD, Australia, 30 November–2 December 2016. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q.; Sun, J.Q. Intelligent Rotating Machinery Fault Diagnosis Based on Deep Learning Using Data Augmentation. J. Intell. Manuf. 2020, 31, 433–452. [Google Scholar] [CrossRef]
- Learning Internal Representations by Error Propagation. Available online: https://apps.dtic.mil/sti/citations/ADA164453 (accessed on 28 July 2023).
- Kishore, R.; Kaur, T. Backpropagation Algorithm: An Artificial Neural Network Approach for Pattern Recognition. Int. J. Sci. Eng. Res. 2012, 3, 1–4. [Google Scholar]
- Ruder, S. An Overview of Gradient Descent Optimization Algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Haji, S.H.; Abdulazeez, A.M. Comparison of Optimization Techniques Based on Gradient Descent Algorithm: A Review. PalArch’s J. Archaeol. Egypt/Egyptol. 2021, 18, 2715–2743. [Google Scholar]
- Steurer, M.; Hill, R.J.; Pfeifer, N. Metrics for Evaluating the Performance of Machine Learning Based Automated Valuation Models. J. Prop. Res. 2021, 38, 99–129. [Google Scholar] [CrossRef]
- Vickery, R. 8 Metrics to Measure Classification Performance. Towards Data Science. Available online: https://towardsdatascience.com/8-metrics-to-measure-classification-performance-984d9d7fd7aa (accessed on 28 July 2023).
- Flach, P.A.; Kull, M. Precision-Recall-Gain Curves: PR Analysis Done Right. In Proceedings of the Advances in Neural Information Processing Systems 28 (NIPS 2015), Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Conlin, A.K.; Martin, E.B.; Morris, A.J. Data Augmentation: An Alternative Approach to the Analysis of Spectroscopic Data. Chemom. Intell. Lab. Syst. 1998, 44, 161–173. [Google Scholar] [CrossRef]
- Mehmood, T.; Liland, K.H.; Snipen, L.; Sæbø, S. A Review of Variable Selection Methods in Partial Least Squares Regression. Chemom. Intell. Lab. Syst. 2012, 118, 62–69. [Google Scholar] [CrossRef]
- Sáiz-Abajo, M.J.; Mevik, B.H.; Segtnan, V.H.; Næs, T. Ensemble Methods and Data Augmentation by Noise Addition Applied to the Analysis of Spectroscopic Data. Anal. Chim. Acta 2005, 533, 147–159. [Google Scholar] [CrossRef]
- Bjerrum, E.J.; Glahder, M.; Skov, T. Data Augmentation of Spectral Data for Convolutional Neural Network (CNN) Based Deep Chemometrics. arXiv 2017, arXiv:1710.01927. [Google Scholar]
- Nallan Chakravartula, S.S.; Moscetti, R.; Bedini, G.; Nardella, M.; Massantini, R. Use of Convolutional Neural Network (CNN) Combined with FT-NIR Spectroscopy to Predict Food Adulteration: A Case Study on Coffee. Food Control 2022, 135, 108816. [Google Scholar] [CrossRef]
- Denham, M.C. Prediction Intervals in Partial Least Squares. J. Chemom. 1997, 11, 39–52. Available online: https://analyticalsciencejournals.onlinelibrary.wiley.com/doi/abs/10.1002/(SICI)1099-128X(199701)11:1%3C39::AID-CEM433%3E3.0.CO;2-S?casa_token=HtDWzpx3_j4AAAAA:jk4BoYhY5QUSeUbcbBMAj9BPowvpa2V4HxzWT8yKpj00nuQ6fkApa9liJVLUafRRKyZ3WMyQmhokWi8 (accessed on 1 August 2023). [CrossRef]
- Workman, J. A Review of Process near Infrared Spectroscopy: 1980–1994. J. Near Infrared Spectrosc. 1993, 1, 221–245. [Google Scholar] [CrossRef]
- Momeny, M.; Jahanbakhshi, A.; Neshat, A.A.; Hadipour-Rokni, R.; Zhang, Y.D.; Ampatzidis, Y. Detection of Citrus Black Spot Disease and Ripeness Level in Orange Fruit Using Learning-to-Augment Incorporated Deep Networks. Ecol. Inform. 2022, 71, 101829. [Google Scholar] [CrossRef]
- Naranjo-Torres, J.; Mora, M.; Hernández-García, R.; Barrientos, R.J.; Fredes, C.; Valenzuela, A. A Review of Convolutional Neural Network Applied to Fruit Image Processing. Appl. Sci. 2020, 10, 3443. [Google Scholar] [CrossRef]
- Georgouli, K.; Osorio, M.T.; Martinez Del Rincon, J.; Koidis, A. Data Augmentation in Food Science: Synthesising Spectroscopic Data of Vegetable Oils for Performance Enhancement. J. Chemom. 2018, 32, e3004. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority over-Sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Wang, S.; Liu, S.; Zhang, J.; Che, X.; Yuan, Y.; Wang, Z.; Kong, D. A New Method of Diesel Fuel Brands Identification: SMOTE Oversampling Combined with XGBoost Ensemble Learning. Fuel 2020, 282, 118848. [Google Scholar] [CrossRef]
- Bogner, C.; Kühnel, A.; Huwe, B. Predicting with Limited Data—Increasing the Accuracy in Vis-Nir Diffuse Reflectance Spectroscopy by Smote. In Proceedings of the Workshop on Hyperspectral Image and Signal Processing, Evolution in Remote Sensing, Lausanne, Switzerland, 24–27 June 2014. [Google Scholar] [CrossRef]
- Kumar, A.; Goel, S.; Sinha, N.; Bhardwaj, A. A Review on Unbalanced Data Classification. In Proceedings of the International Joint Conference on Advances in Computational Intelligence: IJCACI 2021, Online Streaming, 23–24 October 2021; pp. 197–208. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative Adversarial Networks: An Overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing Systems 27 (NIPS 2014), Montreal, QC, Canada, 8–13 December 2015. [Google Scholar]
- Lu, Y.; Chen, D.; Olaniyi, E.; Huang, Y. Generative Adversarial Networks (GANs) for Image Augmentation in Agriculture: A Systematic Review. Comput. Electron. Agric. 2022, 200, 107208. [Google Scholar] [CrossRef]
- Aldausari, N.; Sowmya, A.; Marcus, N.; Mohammadi, G. Video Generative Adversarial Networks: A Review. ACM Comput. Surv. 2022, 55, 1–25. [Google Scholar] [CrossRef]
- Otter, D.W.; Medina, J.R.; Kalita, J.K. A Survey of the Usages of Deep Learning for Natural Language Processing. IEEE Trans. Neural. Netw. Learn. Syst. 2021, 32, 604–624. [Google Scholar] [CrossRef]
- Wali, A.; Alamgir, Z.; Karim, S.; Fawaz, A.; Ali, M.B.; Adan, M.; Mujtaba, M. Generative Adversarial Networks for Speech Processing: A Review. Comput. Speech Lang. 2022, 72, 101308. [Google Scholar] [CrossRef]
- Chadha, A.; Kumar, V.; Kashyap, S.; Gupta, M. Deepfake: An Overview. In Proceedings of the Second International Conference on Computing, Communications, and Cyber-Security, Ghaziabad, India, 3–4 October 2020; Lecture Notes in Networks and Systems. Springer: Singapore, 2021; Volume 203, pp. 557–566. [Google Scholar] [CrossRef]
- Mirza, M.; Osindero, S. Conditional Generative Adversarial Nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Zhao, W.; Chen, X.; Bo, Y.; Chen, J. Semisupervised Hyperspectral Image Classification with Cluster-Based Conditional Generative Adversarial Net. IEEE Geosci. Remote Sens. Lett. 2020, 17, 539–543. [Google Scholar] [CrossRef]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks. In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016—Conference Track Proceedings, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar] [CrossRef]
- Kingma, D.P.; Rezende, D.J.; Mohamed, S.; Welling, M. Semi-Supervised Learning with Deep Generative Models. Adv. Neural. Inf. Process. Syst. 2014, 4, 3581–3589. [Google Scholar]
- Odena, A. Semi-Supervised Learning with Generative Adversarial Networks. arXiv 2016, arXiv:1606.01583. [Google Scholar]
- Zhang, Z.; Liu, S.; Li, M.; Zhou, M.; Chen, E. Bidirectional Generative Adversarial Networks for Neural Machine Translation. In Proceedings of the CoNLL 2018—22nd Conference on Computational Natural Language Learning, Brussels, Belgium, 31 October–1 November 2018; pp. 190–199. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Wei, Y.; An, D. Near-Infrared Hyperspectral Imaging Technology Combined with Deep Convolutional Generative Adversarial Network to Predict Oil Content of Single Maize Kernel. Food Chem. 2022, 370, 131047. [Google Scholar] [CrossRef]
- Yang, B.; Chen, C.; Chen, F.; Chen, C.; Tang, J.; Gao, R.; Lv, X. Identification of Cumin and Fennel from Different Regions Based on Generative Adversarial Networks and near Infrared Spectroscopy. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2021, 260, 119956. [Google Scholar] [CrossRef] [PubMed]
- Roselló, S.; Díez, M.J.; Nuez, F. Viral Diseases Causing the Greatest Economic Losses to the Tomato Crop. I. The Tomato Spotted Wilt Virus—A Review. Sci. Hortic. 1996, 67, 117–150. [Google Scholar] [CrossRef]
- Wang, D.; Vinson, R.; Holmes, M.; Seibel, G.; Bechar, A.; Nof, S.; Luo, Y.; Tao, Y. Early Tomato Spotted Wilt Virus Detection Using Hyperspectral Imaging Technique and Outlier Removal Auxiliary Classifier Generative Adversarial Nets (OR-AC-GAN). In Proceedings of the ASABE 2018 Annual International Meeting, Detroit, MI, USA, 29 July–1 August 2018; pp. 1–14. [Google Scholar] [CrossRef]
- Yu, S.; Li, H.; Li, X.; Fu, Y.V.; Liu, F. Classification of Pathogens by Raman Spectroscopy Combined with Generative Adversarial Networks. Sci. Total Environ. 2020, 726, 138477. [Google Scholar] [CrossRef]
- Du, Y.; Han, D.; Liu, S.; Sun, X.; Ning, B.; Han, T.; Wang, J.; Gao, Z. Raman Spectroscopy-Based Adversarial Network Combined with SVM for Detection of Foodborne Pathogenic Bacteria. Talanta 2022, 237, 122901. [Google Scholar] [CrossRef]
- Ouali, Y.; Hudelot, C.; Tami, M. An Overview of Deep Semi-Supervised Learning. arXiv 2020, arXiv:2006.05278. [Google Scholar]
- He, R.; Tian, Z.; Zuo, M.J. A Semi-Supervised GAN Method for RUL Prediction Using Failure and Suspension Histories. Mech. Syst. Signal Process. 2022, 168, 108657. [Google Scholar] [CrossRef]
- Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X.; Chen, X. Improved Techniques for Training GANs. In Proceedings of the Advances in Neural Information Processing Systems 29 (NIPS 2016), Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Miyato, T.; Maeda, S.I.; Koyama, M.; Ishii, S. Virtual Adversarial Training: A Regularization Method for Supervised and Semi-Supervised Learning. IEEE Trans. Pattern. Anal. Mach. Intell. 2019, 41, 1979–1993. [Google Scholar] [CrossRef] [PubMed]
- Schlegl, T.; Seeböck, P.; Waldstein, S.M.; Schmidt-Erfurth, U.; Langs, G. Unsupervised Anomaly Detection with Generative Adversarial Networks to Guide Marker Discovery. In Information Processing in Medical Imaging, Proceedings of the 25th International Conference, IPMI 2017, Boone, NC, USA, 25–30 June 2017; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2017; Volume 10265, pp. 146–157. [Google Scholar] [CrossRef]
- Yang, X.; Lin, Y.; Wang, Z.; Li, X.; Cheng, K.T. Bi-Modality Medical Image Synthesis Using Semi-Supervised Sequential Generative Adversarial Networks. IEEE J. Biomed. Health Inform. 2020, 24, 855–865. [Google Scholar] [CrossRef]
- Madani, A.; Moradi, M.; Karargyris, A.; Syeda-Mahmood, T. Semi-Supervised Learning with Generative Adversarial Networks for Chest X-ray Classification with Ability of Data Domain Adaptation. In Proceedings of the International Symposium on Biomedical Imaging, Washington, DC, USA, 4–7 April 2018; pp. 1038–1042. [Google Scholar] [CrossRef]
- Xu, M.; Wang, Y. An Imbalanced Fault Diagnosis Method for Rolling Bearing Based on Semi-Supervised Conditional Generative Adversarial Network with Spectral Normalization. IEEE Access 2021, 9, 27736–27747. [Google Scholar] [CrossRef]
- Springenberg, J.T. Unsupervised and Semi-Supervised Learning with Categorical Generative Adversarial Networks. arXiv 2015, arXiv:1511.06390. [Google Scholar]
- Olmschenk, G.; Zhu, Z.; Tang, H. Generalizing Semi-Supervised Generative Adversarial Networks to Regression Using Feature Contrasting. Comput. Vis. Image Underst. 2019, 186, 1–12. [Google Scholar] [CrossRef]
- Kerdegari, H.; Razaak, M.; Argyriou, V.; Remagnino, P. Semi-Supervised GAN for Classification of Multispectral Imagery Acquired by UAVs. arXiv 2019, arXiv:1905.10920. [Google Scholar]
- Sa, I.; Chen, Z.; Popovic, M.; Khanna, R.; Liebisch, F.; Nieto, J.; Siegwart, R. WeedNet: Dense Semantic Weed Classification Using Multispectral Images and MAV for Smart Farming. IEEE Robot. Autom. Lett. 2017, 3, 588–595. [Google Scholar] [CrossRef]
- Khan, S.; Tufail, M.; Khan, M.T.; Khan, Z.A.; Iqbal, J.; Alam, M. A Novel Semi-Supervised Framework for UAV Based Crop/Weed Classification. PLoS ONE 2021, 16, e0251008. [Google Scholar] [CrossRef]
- Zhan, Y.; Hu, D.; Wang, Y.; Yu, X. Semisupervised Hyperspectral Image Classification Based on Generative Adversarial Networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 212–216. [Google Scholar] [CrossRef]
- He, Z.; Liu, H.; Wang, Y.; Hu, J. Generative Adversarial Networks-Based Semi-Supervised Learning for Hyperspectral Image Classification. Remote Sens. 2017, 9, 1042. [Google Scholar] [CrossRef]















| Noise Augmentation (%) | RMSE | |
|---|---|---|
| Calibration | Validation | |
| 0 | 10.96 | 15.04 |
| 5 | 6.52 | 17.45 |
| 10 | 5.92 | 16.95 |
| 15 | 10.10 | 14.61 |
| 20 | 7.60 | 14.40 |
| 25 | 13.81 | 6.52 |
| 30 | 15.76 | 5.68 |
| PLS | CNN | ||||
|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | ||
| Without DA | Train | 0.97 | 2.97 | 0.97 | 3.02 |
| Test | 0.94 | 4.43 | 0.97 | 4.01 | |
| With DA | Train | 0.97 | 3.20 | 0.98 | 1.10 |
| Test | 0.95 | 4.23 | 0.97 | 2.44 | |
| Sample Type | Preprocessing | Model | RMSEP (%) | F1 Score |
|---|---|---|---|---|
| Chicory (without DA) | AS + iPLS | - | 1.06 | 0.99 |
| Chicory (with DA) | DA + AS | CNN | 0.76 | 0.99 |
| Chicory (with DA) | DA | CNN | 1.06 | 0.98 |
| Barley (without DA) | iPLS + SNV + AS | - | 1.06 | 0.99 |
| Barley (with DA) | DA + AS | CNN | 0.80 | 0.99 |
| Barley (with DA) | DA + SNV + AS | PLS | 0.75 | 0.99 |
| Barley (with DA) | DA + SNV + AS | iPLS | 0.60 | 1.00 |
| Barley (with DA) | DA + SNV + AS | CNN | 0.76 | 1.00 |
| Maize (without DA) | SNV + AS | iPLS | 0.73 | 0.99 |
| Maize (with DA) | DA + AS | CNN | 0.82 | 0.99 |
| Maize (with DA) | DA + SNV + AS | iPLS | 0.71 | 0.99 |
| Maize (with DA) | DA + SNV + AS | PLS | 0.83 | 0.99 |
| Maize (with DA) | DA + SNV + AS | CNN | 0.98 | 0.99 |
| Class | Methodology | Sensitivity (%) | Precision (%) | Recall (%) | F1 Score |
|---|---|---|---|---|---|
| Orange Infected with Black Spot Disease | ResNet50 with DA | 100 | 100 | 100 | 100 |
| Orange (Unripe) | ResNet50 with DA | 100 | 98 | 100 | 99 |
| Orange (Half-Ripe) | ResNet50 with DA | 98.5 | 100 | 98.5 | 99.3 |
| Orange (Ripe) | ResNet50 with DA | 100 | 100 | 100 | 100 |
| Model | Without DA | With DA |
|---|---|---|
| PLS | 63% | 88% |
| Model Calibration | RMSEP | R2 |
|---|---|---|
| Air-dried spectra only | 6.18 | −0.53 |
| Air-dried spectra with synthetic field spectra | 2.12 | 0.82 |
| Model | Accuracy (%) | AUC/ROC |
|---|---|---|
| Tree-XGBoost | 80.67 | 0.78 |
| Tree-SMOTE-XGBoost | 94.96 | 0.97 |
| Application Domain | Dataset | DA Technique | Ref. |
|---|---|---|---|
| F: Adulteration of commercial ‘espresso’ coffee with chicory, barley, and maize. | NIR (1000–2500 nm) | Adding random offset, multiplication, and slope effects. | [47] |
| F: Identification of vegetable oil species in oil admixtures. | Far IR (2500–18,000 nm) | Noise adding, weighted sum of samples, modify the intensity of the spectra and shift along wavelength axis. | [52] |
| A: Citrus black spot disease and ripeness level detection in orange fruit. | VIS (440–650 nm) | Noise adding (Gaussian, salt-and-pepper, speckle, and Poisson). | [50] |
| A: Predicting soil properties in situ with diffuse reflectance spectroscopy | VIS–NIR (350–2500 nm) | Use of SMOTE with different hyperparameters. | [55] |
| A: Identification of diesel oil brands to ensure the normal operation of diesel engines. | NIR (750–1550 nm) | Use of SMOTE to balance the dataset. | [54] |
| C: Analysis of drug content in tablets from pharmaceutical industries. | NIR (600–1800 nm) | Adding random variations in offset, multiplication, and slope. | [46] |
| I: Analysis of an industrial batch polymerization process to monitor end group properties. | NIR (1000–2100 nm) | Noise adding, weighted sum of samples, linear drift adding, smoothing techniques and baseline shifts. | [43] |
| Zhengdan958 | Nongda616 | |||
|---|---|---|---|---|
| PLSR | SVR | PLSR | SVR | |
| R2 Increase (%) | 3.47 | 1.69 | 3.50 | 5.34 |
| RMSE Decrease (%) | 12.78 | 6.77 | 12.03 | 15.29 |
| PCA-QDA | PCA-MLP | CNN | GAN | |
|---|---|---|---|---|
| Cumin Accuracy (%) | 100.0 | 97.8 | 96.7 | 100.0 |
| Fennel Accuracy (%) | 97.8 | 96.7 | 92.2 | 100.0 |
| OR-AC-GAN | |
|---|---|
| Plant-Level Classification Sensitivity (%) | 92.59 |
| Plant-Level Classification Specificity (%) | 100.00 |
| Average Classification Accuracy (%) | 96.25 |
| Bacteria | Accuracy (%) |
|---|---|
| Salmonella typhimurium | 85.0 |
| Vibrio parahaemolyticus | 91.2 |
| E. coli | 94.0 |
| Overall Accuracy | 90.0 |
| Labeled Data (%) | 50 | 40 | 30 | |||
|---|---|---|---|---|---|---|
| Crop | Weed | Crop | Weed | Crop | Weed | |
| F1 scores | 0.857 | 0.865 | 0.837 | 0.834 | 0.823 | 0.815 |
| Labeled Data (%) | Model | 20% | 40% | 60% | 80% |
|---|---|---|---|---|---|
| Cropland Pea (%) | ResNet50 | 87.67 | 89.69 | 92.83 | 95.98 |
| Cropland Strawberry (%) | 88.03 | 89.91 | 93.89 | 96.82 | |
| Cropland Pea (%) | ResNet18 | 87.11 | 89.42 | 92.47 | 95.63 |
| Cropland Strawberry (%) | 87.51 | 89.77 | 93.47 | 96.53 | |
| Cropland Pea (%) | VGG-16 | 86.24 | 89.13 | 92.23 | 95.01 |
| Cropland Strawberry (%) | 87.13 | 89.37 | 93.08 | 96.21 |
| PCA-KNN | CNN | HSGAN | ||
|---|---|---|---|---|
| 5% Supervised Samples | Overall Accuracy (%) | 71.50 | 72.00 | 74.92 |
| Average Accuracy (%) | 64.91 | 66.93 | 70.97 | |
| 10% Supervised Samples | Overall Accuracy (%) | 75.93 | 78.44 | 83.53 |
| Average Accuracy (%) | 70.76 | 75.60 | 79.27 |
| Indian Pines | University of Pavia | Salinas | ||||
|---|---|---|---|---|---|---|
| Spec-GAN | 3DBF-GAN | Spec-GAN | 3DBF-GAN | Spec-GAN | 3DBF-GAN | |
| Overall Accuracy (%) | 56.51 | 75.62 | 63.66 | 77.94 | 77.17 | 87.63 |
| Average Accuracy (%) | 70.04 | 81.05 | 72.85 | 81.36 | 73.18 | 92.30 |
| F1 Score | 60.60 | 79.10 | 66.97 | 77.30 | 81.09 | 91.09 |
| Application Domain | Dataset | DA Method | Ref. |
|---|---|---|---|
| F: Generate realistic synthetic samples with GAN to predict oil content of single maize kernel. | NIR (866–1701 nm) | DCGAN to generate samples and balance the dataset | [71] |
| F: Use GANs to improve the model performance to accurately distinguish cumin and fennel from three different regions. | MIR (1000–2500 nm) | DCGAN to generate samples and balance the dataset | [72] |
| F: Use a GAN to enhance the dataset to achieve early detection of tomato spotted wilt virus. | VIS-NIR (395–1005 nm) | DCGAN to generate samples and balance the dataset | [73] |
| F: Enhance a Raman spectra dataset for detection of foodborne pathogenic bacteria. | MIR (2857–25,000 nm) | GAN for Raman spectroscopy | [76] |
| A: Enhance HSIs dataset to identify and help to preserve fields from weed infestations. | NIR (660 and 790 nm) | SGAN based on DCGAN as generator of HSIs | [87] |
| A: Enhance a multispectral images dataset to differentiate between fields with crops and weeds. | VIS–NIR (350–1050 nm) | SGAN based on DCGAN as generator of HSIs | [89] |
| A: Enhance a multispectral images dataset with a bilateral filter. | VIS–NIR (430–860 nm) | DCGAN for hyperspectral images | [91] |
| B: Development of a rapid identification method for pathogens in water. | MIR (5556–16,667 nm) | DCGAN to enhance the dataset | [75] |
| MC: Improving the accuracy and efficiency of hyperspectral image classification in the field of remote sensing. | VIS–NIR (400–2200 nm) | DCGAN for hyperspectral images | [90] |
| Method | Advantages | Disadvantages |
|---|---|---|
| Non-DL-Based Methods | Easy to implement. Quick to apply. Creates semantic variability. Useful for class imbalance, can enhance the minority class representation. | May degrade data quality. May generate unrealistic data. Does not add real semantic variability. Sensitive to noise and outliers. |
| GAN-Based Methods | Generates realistic data. Adds real semantic variability. Ability to learn complex data distributions. | Time and computational resource consuming. Can be challenging to train. Difficult to evaluate the model’s generator. |
| SGANs Methods | Utilizes both labeled und unlabeled data. May enhance generation quality. Could improve model generalization. Ability to learn complex data distributions. | More complex to implement and train. Requires time and computational resources. Difficult to evaluate the generator performance. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gracia Moisés, A.; Vitoria Pascual, I.; Imas González, J.J.; Ruiz Zamarreño, C. Data Augmentation Techniques for Machine Learning Applied to Optical Spectroscopy Datasets in Agrifood Applications: A Comprehensive Review. Sensors 2023, 23, 8562. https://doi.org/10.3390/s23208562
Gracia Moisés A, Vitoria Pascual I, Imas González JJ, Ruiz Zamarreño C. Data Augmentation Techniques for Machine Learning Applied to Optical Spectroscopy Datasets in Agrifood Applications: A Comprehensive Review. Sensors. 2023; 23(20):8562. https://doi.org/10.3390/s23208562
Chicago/Turabian StyleGracia Moisés, Ander, Ignacio Vitoria Pascual, José Javier Imas González, and Carlos Ruiz Zamarreño. 2023. "Data Augmentation Techniques for Machine Learning Applied to Optical Spectroscopy Datasets in Agrifood Applications: A Comprehensive Review" Sensors 23, no. 20: 8562. https://doi.org/10.3390/s23208562
APA StyleGracia Moisés, A., Vitoria Pascual, I., Imas González, J. J., & Ruiz Zamarreño, C. (2023). Data Augmentation Techniques for Machine Learning Applied to Optical Spectroscopy Datasets in Agrifood Applications: A Comprehensive Review. Sensors, 23(20), 8562. https://doi.org/10.3390/s23208562







