Assessing Vehicle Wandering Effects on the Accuracy of Weigh-in-Motion Measurement Based on In-Pavement Fiber Bragg Sensors through a Hybrid Sensor-Camera System
Abstract
:1. Introduction
2. Methodology
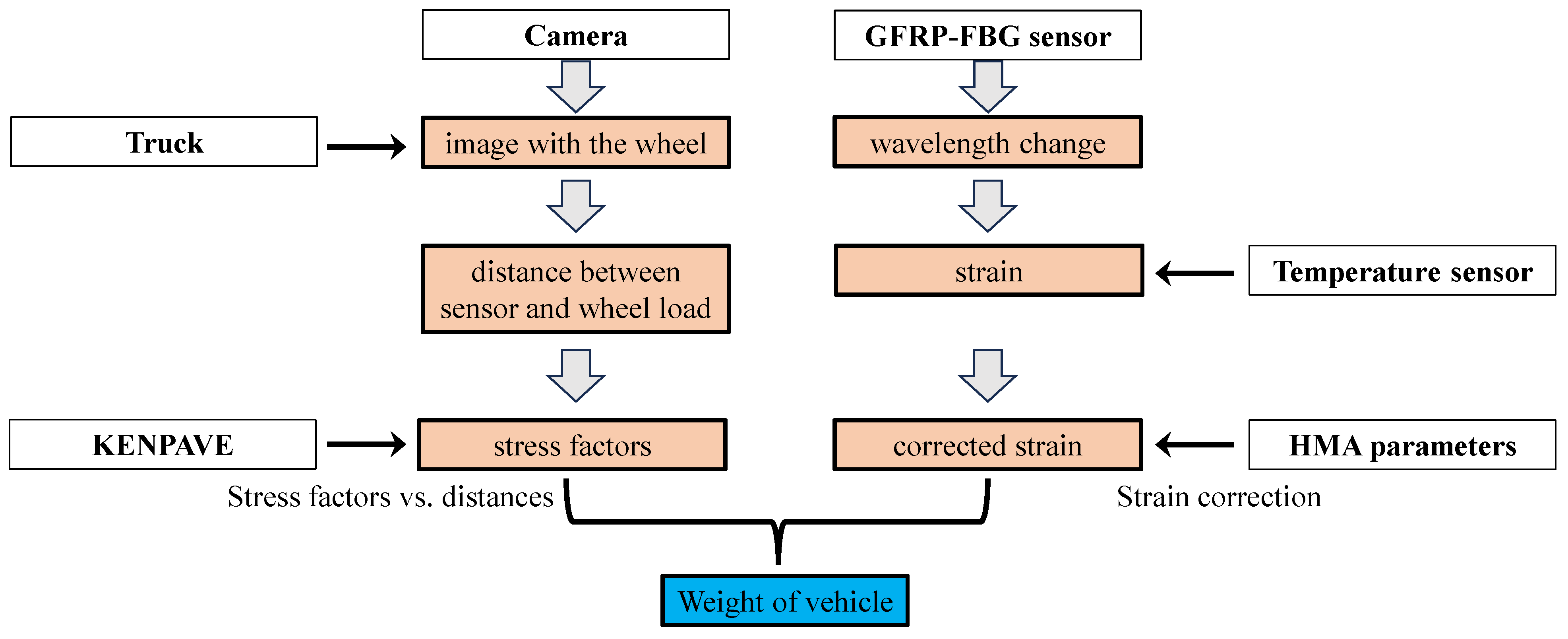
2.1. Framework for Weigh-in-Motion Using Camera Data and GFRP-FBG Sensors Fusion
2.2. Wheel Load Measurement by GFRP-FBG Sensor
2.2.1. Strain Collection by GFRP-FBG Sensor
2.2.2. Strain Correction Based on the Host Material
2.3. Integration of Image-Based Distance Determination and KENPAVE Analysis to Determine the Stress Factor
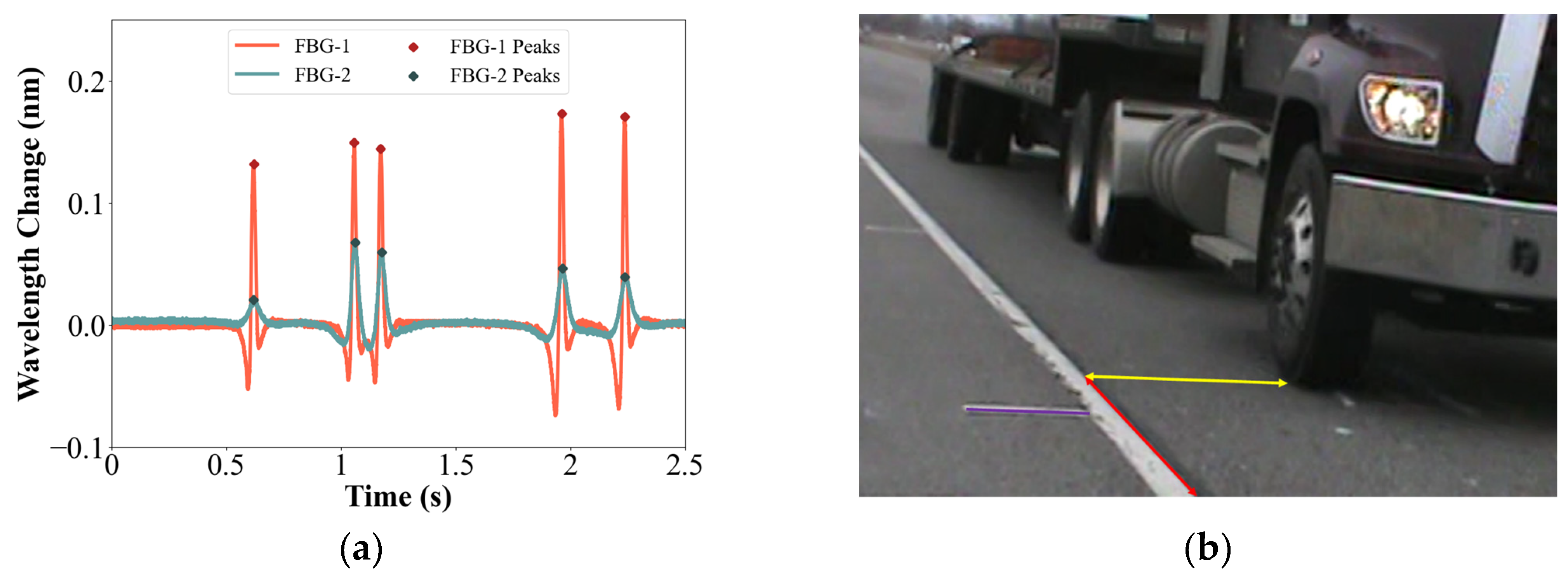
2.3.1. Determining Wheel Load Position Using Camera-Captured Figures
- Purple calibration line: White lines usually exist on the side of the highway edge line, which is used as the purple calibration line, deliberately positioned consistently above the same spot and meant to align with the white line. If the purple calibration line fails to align with the white line, it signifies the potential for camera position shifts caused by windy conditions, leading to the possibility of inaccurate determinations of locations;
- Red calibration line: The highway edge lines (red line) can be used as another reference as they determine the wheel loading position of trucks in the direction parallel to the edge line;
- Yellow calibration line: The lines perpendicular to the highway edge lines (yellow line) can be used to determine the wheel loading position of trucks in the direction vertical to the edge line.
2.3.2. Stress Factor Determination Using KENPAVE Software
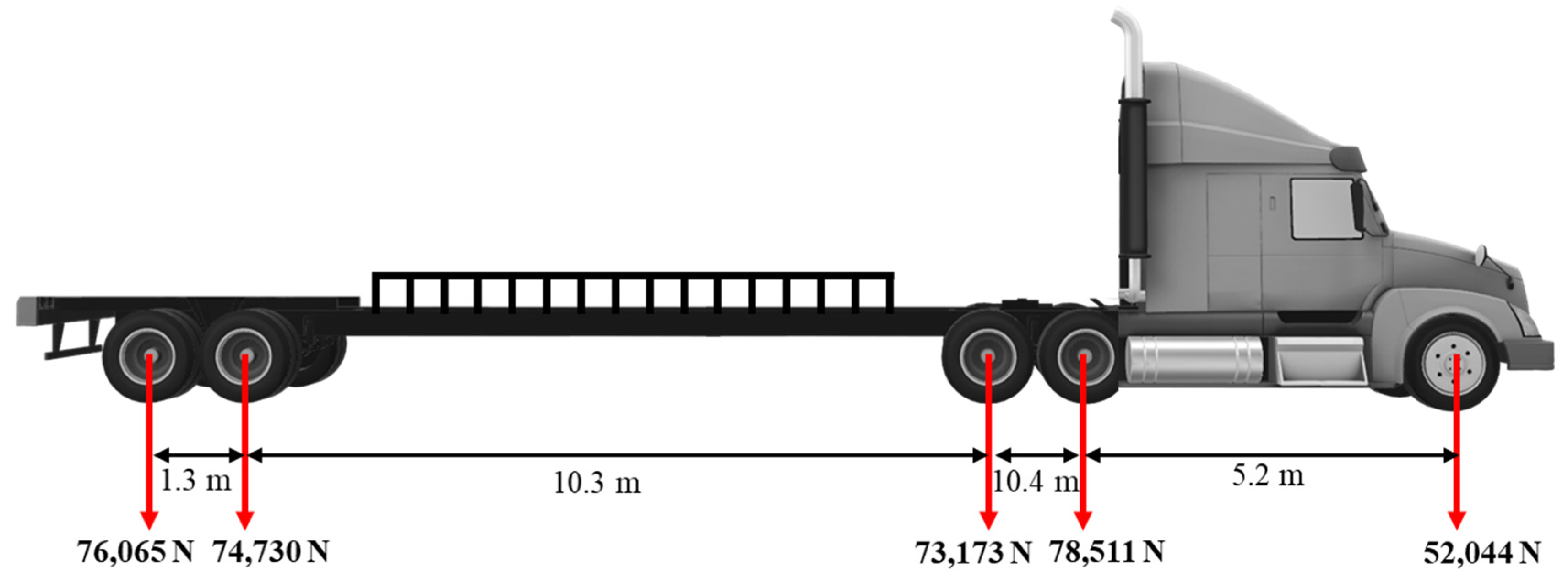
3. Materials and Field Validation Testing
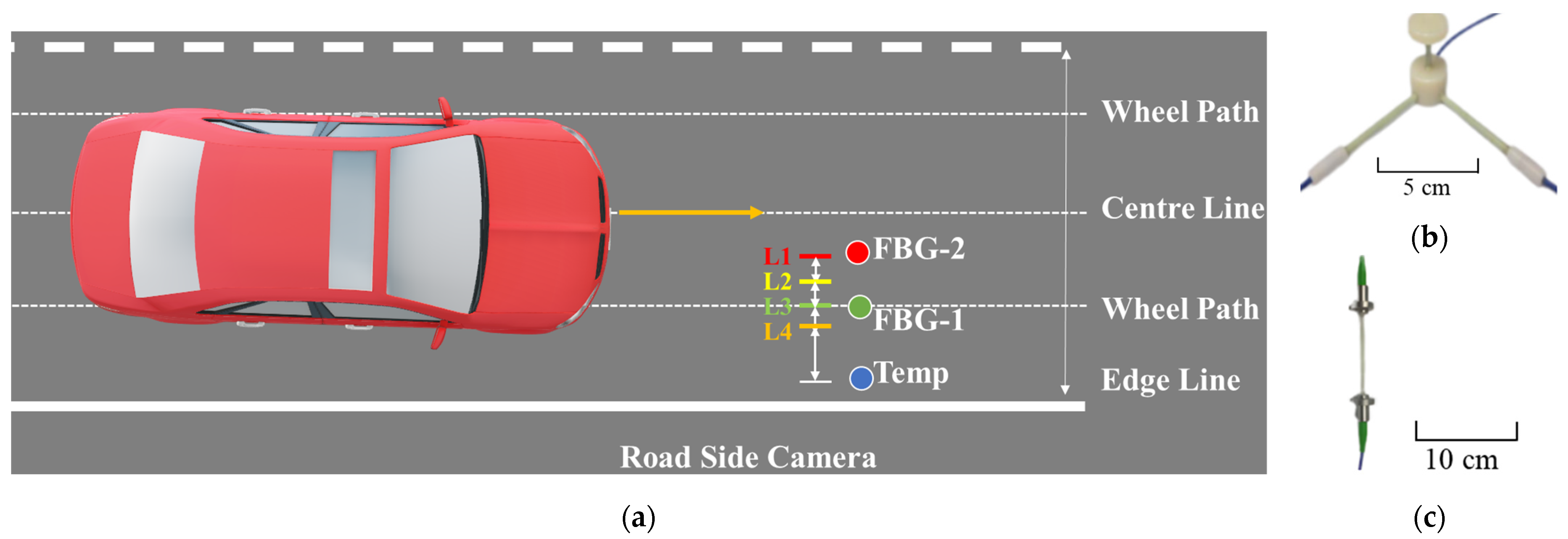
3.1. Field Experiment Setup
3.2. Field Installed GFRP-FBG Sensors
3.3. Experimental Setup
4. Experimental Results and Discussion
4.1. Utilizing GFRP-FBG Sensors for Wavelength-Based Strain Calculation
4.2. Calibration Line Utilization and Modeling for Distance Calculation
4.3. Stress Analysis with KENPAVE Software in Pavement Structures
4.4. Accuracy Assessment of Vehicle Load Monitoring
5. Conclusions and Future Work
- Applying a calibration line to generate a model for distance prediction: This study employed distinct marked lines (L1, L2, L3, and L4) to develop a linear regression model accurately estimating the distance from the edge line to the wheel loading position. This model’s reliability is supported by a strong R-squared value of 0.9989 when the confidence interval is set at 95%, providing a solid basis for precise distance calculations;
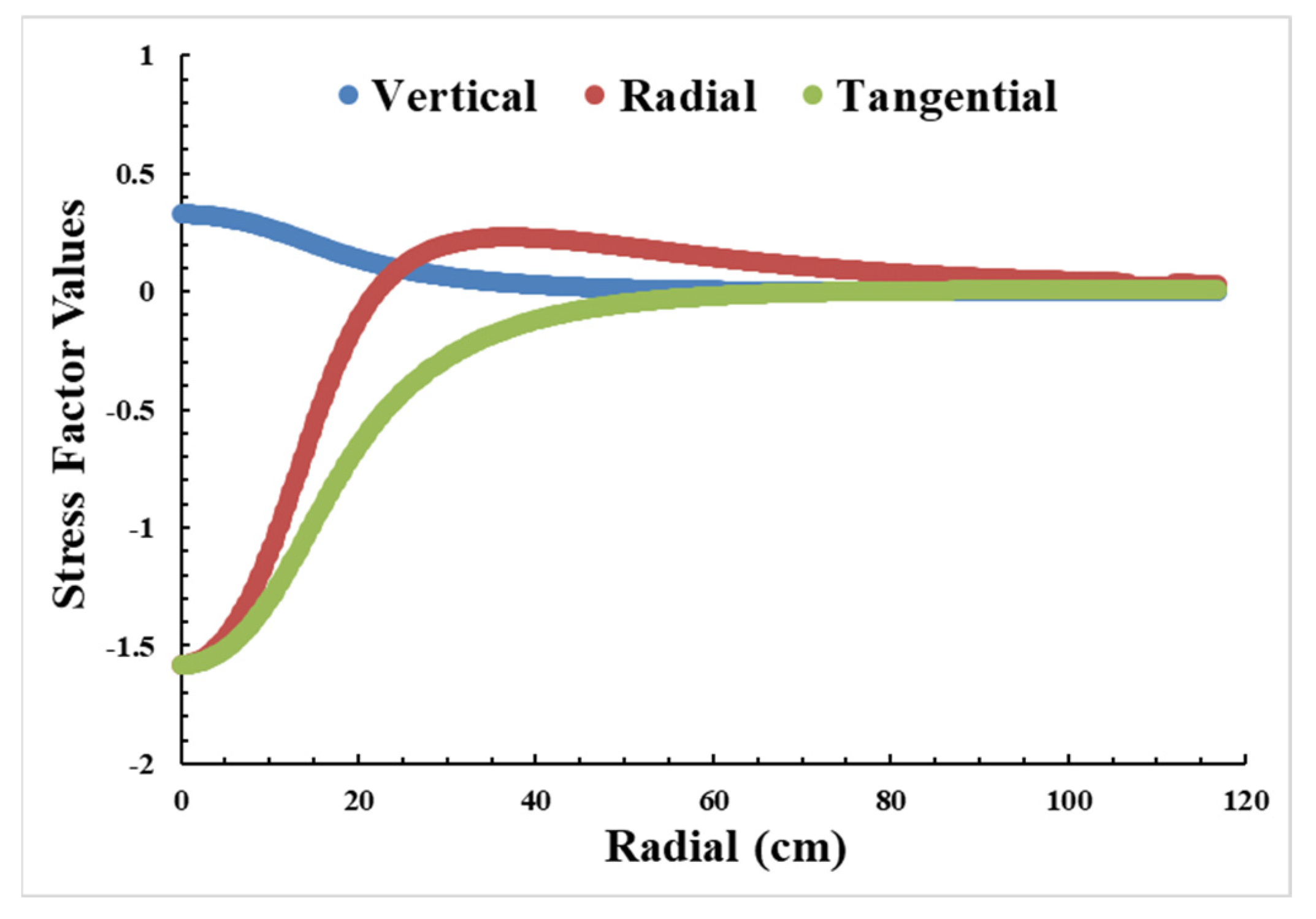
- Investigation of the wander effect: Given the fixed position of the sensor and the significant impact of varying wheel loading positions on the collected signals, this study accounted for the wandering effect using KENPAVE software. The outputs encompassed vertical, radial, and tangential stress, covering a sensor-wheel loading distance range of 0 to 116.8 m. Vertical, radial, and tangential factors were derived relative to weight, contributing to the determination of vehicle weight;
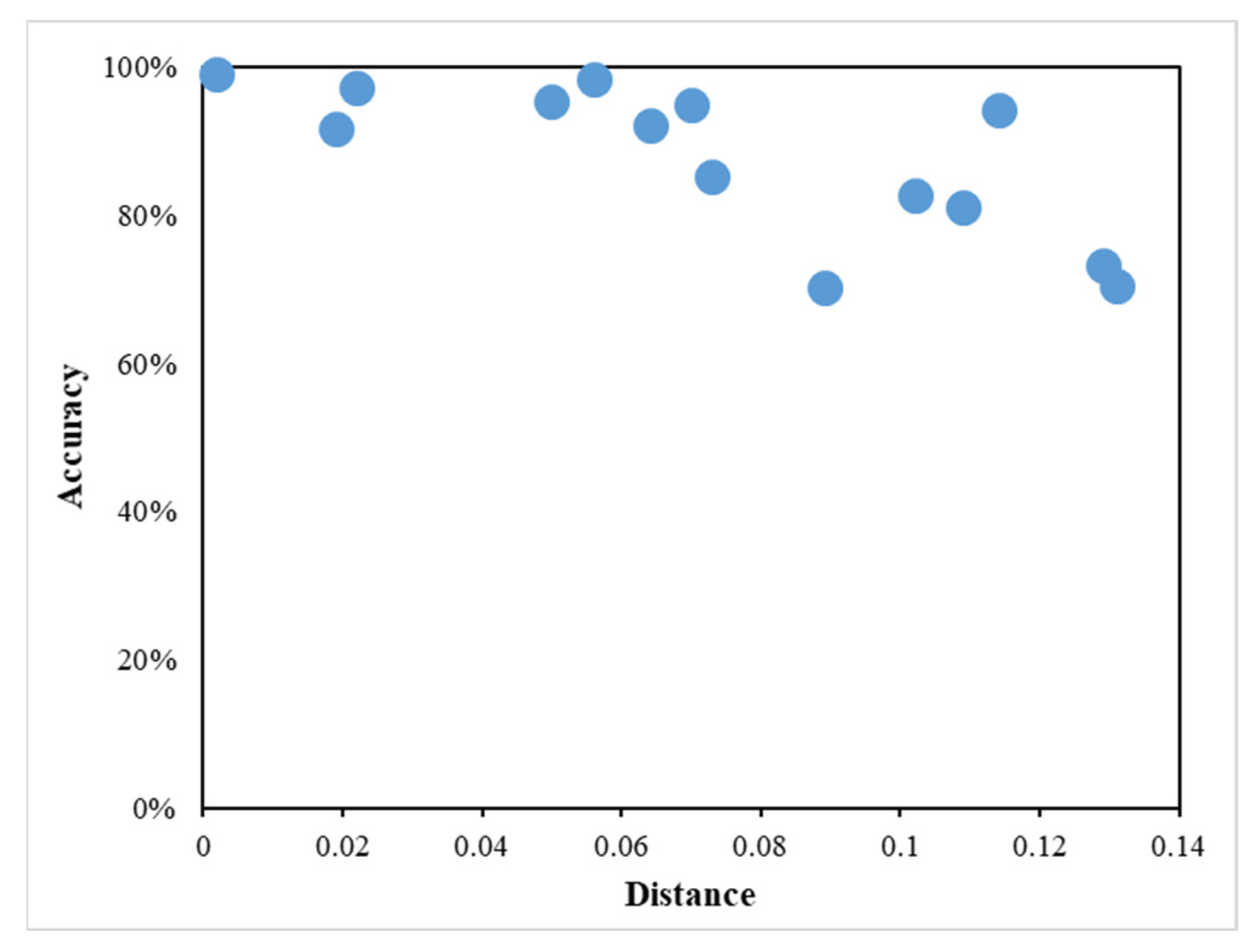
- High-accuracy WIM measurement: Highly accurate measurement was achieved by taking into account factors such as the GFRP-FBG sensor-assessed strain, distance between the sensor and wheel loading position, and KENPAVE software-derived stress factors. Accuracy is closely tied to the proximity of the wheel loading point to sensors. FBG-1 achieves an average accuracy of 87.831% for distances under 0.089 m, decreasing to 84.206% when the distance is less than 0.131 m. In contrast, FBG-2 achieves 94.645% accuracy for distances less than 0.070 m and maintains 91.027% accuracy for distances under 0.109 m.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Statista Research Department Number of Motor Vehicles in U.S. Available online: https://www.statista.com/statistics/183505/number-of-vehicles-in-the-united-states-since-1990/ (accessed on 24 May 2023).
- Duan, G.; Ma, X.; Wang, J.; Wang, Z.; Wang, Y. Optimization of Urban Bus Stops Setting Based on Data Mining. Int. J. Pattern Recognit. Artif. Intell. 2021, 35, 2159028. [Google Scholar] [CrossRef]
- Xiong, Z.; Li, J.; Wu, H. Understanding Operation Patterns of Urban Online Ride-Hailing Services: A Case Study of Xiamen. Transp. Policy 2021, 101, 100–118. [Google Scholar] [CrossRef]
- Guangnian, X.; Qiongwen, L.; Anning, N.; Zhang, C. Research on Carbon Emissions of Public Bikes Based on the Life Cycle Theory. Transp. Lett. 2023, 15, 278–295. [Google Scholar] [CrossRef]
- Wang, J.; Wu, M. An Overview of Research on Weigh-in-Motion System. In Proceedings of the Fifth World Congress on Intelligent Control and Automation (IEEE cat. no. 04EX788), Hangzhou, China, 15–19 June 2004; Volume 6, pp. 5241–5244. [Google Scholar]
- Lansdell, A.; Song, W.; Dixon, B. Development and Testing of a Bridge Weigh-in-Motion Method Considering Nonconstant Vehicle Speed. Eng. Struct. 2017, 152, 709–726. [Google Scholar] [CrossRef]
- Bajwa, R.; Rajagopal, R.; Coleri, E.; Varaiya, P.; Flores, C. In-Pavement Wireless Weigh-in-Motion. In Proceedings of the 12th International Conference on Information Processing in Sensor Networks, Philadelphia, PA, USA, 8–11 April 2013; pp. 103–114. [Google Scholar]
- Liu, X.; Al-Qadi, I.L. Development of a Simulated Three-Dimensional Truck Model to Predict Excess Fuel Consumption Resulting from Pavement Roughness. Transp. Res. Rec. 2021, 2675, 1444–1456. [Google Scholar] [CrossRef]
- US Department of Transportation. Weigh-In-Motion Pocket Guide: Part 1; US Department of Transportation: Washington, DC, USA, 2018. Available online: https://www.fhwa.dot.gov/policyinformation/knowledgecenter/wim_guide/wim_guidebook_part1_070918_(508_compliant).pdf (accessed on 2 October 2023).
- Al-Tarawneh, M.; Huang, Y.; Lu, P.; Bridgelall, R. Weigh-In-Motion System in Flexible Pavements Using Fiber Bragg Grating Sensors Part A: Concept. IEEE Trans. Intell. Transp. Syst. 2019, 21, 5136–5147. [Google Scholar] [CrossRef]
- Kuang, K.S.C.; Quek, S.T.; Koh, C.G.; Cantwell, W.J.; Scully, P.J. Plastic Optical Fibre Sensors for Structural Health Monitoring: A Review of Recent Progress. J. Sens. 2009, 2009, 312053. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, D.; Huang, Y.; Shi, S.; Pan, H.; Bao, Y. Monitoring Epoxy Coated Steel under Combined Mechanical Loads and Corrosion Using Fiber Bragg Grating Sensors. Sensors 2022, 22, 8034. [Google Scholar] [CrossRef]
- Xu, L.; Shi, S.; Yan, F.; Huang, Y.; Bao, Y. Experimental Study on Combined Effect of Mechanical Loads and Corrosion Using Tube-Packaged Long-Gauge Fiber Bragg Grating Sensors. Struct. Health Monit. 2023, 22, 14759217231164960. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, T.; Lu, J.; Lin, R.; Chen, C.; He, Z.; Cui, S.; Liu, Z.; Wang, X.; Liu, B. Static and Ultrasonic Structural Health Monitoring of Full-Size Aerospace Multi-Function Capsule Using FBG Strain Arrays and PSFBG Acoustic Emission Sensors. Opt. Fiber Technol. 2023, 78, 103316. [Google Scholar] [CrossRef]
- Hong, C.-Y.; Zhang, Y.-F.; Zhang, M.-X.; Leung, L.M.G.; Liu, L.-Q. Application of FBG Sensors for Geotechnical Health Monitoring, a Review of Sensor Design, Implementation Methods and Packaging Techniques. Sens. Actuators A Phys. 2016, 244, 184–197. [Google Scholar] [CrossRef]
- Jiao, T.; Pu, C.; Xing, W.; Lv, T.; Li, Y.; Wang, H.; He, J. Characterization of Engineering-Suitable Optical Fiber Sensors Packaged with Glass Fiber-Reinforced Polymers. Symmetry 2022, 14, 973. [Google Scholar] [CrossRef]
- Available online: https://www.dot.state.mn.us/traffic/data/reports/wim/WIM_for_Screening.pdf (accessed on 2 October 2023).
- Feng, M.Q.; Leung, R.Y.; Eckersley, C.M. Non-Contact Vehicle Weigh-in-Motion Using Computer Vision. Measurement 2020, 153, 107415. [Google Scholar] [CrossRef]
- Kong, X.; Zhang, J.; Wang, T.; Deng, L.; Cai, C.S. Non-Contact Vehicle Weighing Method Based on Tire-Road Contact Model and Computer Vision Techniques. Mech. Syst. Signal Process. 2022, 174, 109093. [Google Scholar] [CrossRef]
- Lawton, W.L. Static Load Contact Pressure Patterns under Airplane Tires. Highw. Res. Board Proc. 1957, 36, 233–239. [Google Scholar]
- Lister, N.W.; Nunn, D.E. Contact Areas of Commercial Vehicle Tyres; Road Research Laboratory: London, UK, 1968. [Google Scholar]
- Van Vuuren, J.D. Relationship between Tire Inflation Pressure and Mean Tire Contact Pressure. Transp. Res. Rec. 1974, 523, 76–87. [Google Scholar]
- Yoder, E.J.; Witczak, M.W. Principles of Pavement Design; John Wiley & Sons: Hoboken, NJ, USA, 1991; ISBN 0-471-97780-2. [Google Scholar]
- Ejsmont, J.; Taryma, S.; Ronowski, G.; Swieczko-Zurek, B. Influence of Temperature on the Tyre Rolling Resistance. Int. J. Automot. Technol. 2018, 19, 45–54. [Google Scholar] [CrossRef]
- ASTM E1318-09; Standard Specification for Highway Weigh-in-Motion (WIM) Systems with User Requirements and Test Methods; 2007 Annual Book of ASTM Standards. Edited by ASTM Committee E17-52 on Traffic Monitoring; ASTM International: West Conshohocken, PA, USA, 2009.
- Zhang, Z. An Integrated System for Road Condition and Weigh-in-Motion Measurements Using in-Pavement Strain Sensors. Ph.D. Thesis, North Dakota State University, Fargo, ND, USA, 2016. [Google Scholar]
- Zhou, Z.; Liu, W.; Huang, Y.; Wang, H.; Jianping, H.; Huang, M.; Jinping, O. Optical Fiber Bragg Grating Sensor Assembly for 3D Strain Monitoring and Its Case Study in Highway Pavement. Mech. Syst. Signal Process. 2012, 28, 36–49. [Google Scholar] [CrossRef]
- Yuan, H.; Yuan, J.; Du, J. The Sensing Principle of FBG and Its Experimental Application in Structure Strengthening Detection. J. Wuhan Univ. Technol. Mater. Sci. Ed. 2003, 18, 94–96. [Google Scholar]
- Fan, L.; Le, K.; Guo, C.; Sun, C.; Chen, G. Magnet-Assisted Hybrid EFPI/FBG Sensor for Internal Corrosion Monitoring of Steel Pipelines. Opt. Fiber Technol. 2022, 73, 103064. [Google Scholar] [CrossRef]
- Liao, M.; Liang, S.; Luo, R.; Xiao, Y. The Cooperative Deformation Test of an Embedded FBG Sensor and Strain Correction Curve Verification. Constr. Build. Mater. 2022, 342, 128029. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, J.; Ou, J. Interface Transferring Mechanism and Error Modification of Embedded FBG Strain Sensors. Front. Electr. Electron. Eng. China 2007, 2, 92–98. [Google Scholar] [CrossRef]
- Michalczyk, R. Implementation of Generalized Viscoelastic Material Model in Abaqus Code. Logistyka 2011, 6, 2883–2890. [Google Scholar]
- Huang, Y.H. Pavement Analysis and Design; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2004; Volume 2. [Google Scholar]
- Alkasawneh, W.; Pan, E.; Green, R. The Effect of Loading Configuration and Footprint Geometry on Flexible Pavement Response Based on Linear Elastic Theory. Road Mater. Pavement Des. 2008, 9, 159–179. [Google Scholar] [CrossRef]
- Kou, H.-L.; Li, W.; Zhang, W.-C.; Zhou, Y.; Zhou, X.-L. Stress Monitoring on GFRP Anchors Based on Fiber Bragg Grating Sensors. Sensors 2019, 19, 1507. [Google Scholar] [CrossRef] [PubMed]
- Bonaquist, R.; Christensen, D.W. Practical Procedure for Developing Dynamic Modulus Master Curves for Pavement Structural Design. Transp. Res. Rec. 2005, 1929, 208–217. [Google Scholar] [CrossRef]
- Olidis, C.; Hein, D. Guide for the Mechanistic-Empirical Design of New and Rehabilitated Pavement Structures Materials Characterization: Is Your Agency Ready. In Proceedings of the 2004 Annual Conference of the Transportation Association of Canada, Quebec City, QC, Canada, 19–22 September 2004. [Google Scholar]
- Islam, M.R.; Kalevela, S.A.; Mendel, G. How the Mix Factors Affect the Dynamic Modulus of Hot-Mix Asphalt. J. Compos. Sci. 2019, 3, 72. [Google Scholar] [CrossRef]
- Bennert, T. Dynamic Modulus of Hot Mix Asphalt: Final Report, June 2009; Department of Transportation: Washington, DC, USA, 2009.
- Thornton, T.; Calvert, J.; Vrtis, M. Forensic Investigation of HMA Test Sections for Laboratory and Field Comparisons; National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 2021. [Google Scholar]
- Marasteanu, M.; Turos, M.; Ghosh, D.; Matias de Oliveira, J.L.; Yan, T. Investigation of Cracking Resistance of Asphalt Mixtures and Binders; Department of Transportation: Washington, DC, USA, 2019.
- Kong, X.; Wang, T.; Zhang, J.; Deng, L.; Zhong, J.; Cui, Y.; Xia, S. Tire Contact Force Equations for Vision-Based Vehicle Weight Identification. Appl. Sci. 2022, 12, 4487. [Google Scholar] [CrossRef]
- Schaertl, G.J.; Edil, T.B.; Benson, C.H. Falling Weight Deflectometer Data Analysis—Recycled Asphalt Pavement and Recycled Concrete Aggregate; University of Wisconsin–Madison: Madison, WI, USA, 2010; Available online: https://www.dot.state.mn.us/mnroad/projects/recycled-unbound-pavement-materials/files/tpf-5-129-task-2b-fwd-report.pdf (accessed on 2 October 2023).




| Temp (°C) | 25 Hz | 10 Hz | 5 Hz | 1 Hz | 0.5 Hz | 0.1 Hz | 0.05 Hz | 0.01 Hz |
|---|---|---|---|---|---|---|---|---|
| −12 | 15.520 | 11.830 | 10.410 | 9.490 | 9.000 | 8.190 | 7.900 | 6.990 |
| 12 | 7.580 | 7.830 | 7.340 | 4.550 | 3.990 | 2.120 | 1.570 | 0.570 |
| 36 | 1.660 | 1.350 | 1.070 | 0.420 | 0.300 | 0.160 | 0.130 | 0.040 |
| (GPa) | (mm) | (GPa) | (mm) | (mm) | (mm) | |
|---|---|---|---|---|---|---|
| Longitudinal | 70 | 0.0625 | 5.0 | 2.5 | 25 | 70 |
| Vehicle Number | Wavelength Change (FBG-1) | Wavelength Change (T) | Strain (×10−4) | Vehicle Number | Wavelength Change (FBG-2) | Wavelength Change (T) | Strain (×10−4) |
|---|---|---|---|---|---|---|---|
| 1 | 0.143 | −0.002 | 1.194 | 8 | 0.143 | 0.001 | 1.186 |
| 2 | 0.132 | −0.003 | 1.111 | 9 | 0.153 | 0.002 | 1.260 |
| 3 | 0.142 | −0.002 | 1.183 | 10 | 0.127 | 0.000 | 1.057 |
| 4 | 0.151 | −0.001 | 1.252 | 11 | 0.136 | −0.002 | 1.153 |
| 5 | 0.105 | −0.001 | 0.875 | 12 | 0.121 | 0.001 | 0.988 |
| 6 | 0.113 | −0.002 | 0.951 | 13 | 0.126 | −0.001 | 1.055 |
| 7 | 0.112 | −0.001 | 0.931 | 14 | 0.082 | −0.002 | 0.696 |
| Number | Red Calibration Line | Yellow Calibration Line (L1) | Yellow Calibration Line (L2) | Yellow Calibration Line (L3) | Yellow Calibration Line (L4) |
|---|---|---|---|---|---|
| 1 | 0.030 | 0.114 | 0.102 | 0.089 | 0.073 |
| 2 | 0.032 | 0.113 | 0.100 | 0.087 | 0.072 |
| 3 | 0.033 | 0.112 | 0.099 | 0.086 | 0.071 |
| 4 | 0.035 | 0.111 | 0.098 | 0.085 | 0.069 |
| 5 | 0.037 | 0.110 | 0.097 | 0.084 | 0.068 |
| 6 | 0.038 | 0.109 | 0.096 | 0.083 | 0.067 |
| 7 | 0.040 | 0.108 | 0.095 | 0.082 | 0.066 |
| 8 | 0.041 | 0.106 | 0.093 | 0.080 | 0.065 |
| 9 | 0.043 | 0.105 | 0.092 | 0.079 | 0.064 |
| 10 | 0.045 | 0.104 | 0.091 | 0.078 | 0.063 |
| 11 | 0.046 | 0.103 | 0.090 | 0.077 | 0.062 |
| 12 | 0.048 | 0.102 | 0.089 | 0.076 | 0.061 |
| 13 | 0.049 | 0.101 | 0.087 | 0.074 | 0.060 |
| 14 | 0.051 | 0.100 | 0.086 | 0.073 | 0.059 |
| 15 | 0.052 | 0.099 | 0.085 | 0.072 | 0.058 |
| Vehicle Number | Distance (FBG-1) | Revised Distance (FBG-1) | Vehicle Number | Distance (FBG-2) | Revised Distance (FBG-2) |
|---|---|---|---|---|---|
| 1 | −0.125 | −0.022 | 8 | −0.101 | 0.002 |
| 2 | −0.159 | −0.056 | 9 | −0.084 | 0.019 |
| 3 | −0.176 | −0.073 | 10 | −0.053 | 0.050 |
| 4 | −0.192 | −0.089 | 11 | −0.040 | 0.064 |
| 5 | 0.011 | 0.114 | 12 | −0.033 | 0.070 |
| 6 | −0.232 | −0.129 | 13 | −0.205 | −0.102 |
| 7 | 0.027 | 0.131 | 14 | −0.212 | −0.109 |
| Layer | Thickness (m) | Poisson’s Ratio | Dynamic Modulus (GPa) |
|---|---|---|---|
| HMA | 0.127 | 0.35 | 4.826 |
| granular base | 0.305 | 0.35 | 0.414 |
| sub-base clay loam | 0.305 | 0.35 | 0.276 |
| granular | 0.178 | 0.4 | 0.083 |
| clay loam | 0.089 | 0.4 | 0.083 |
| Vehicle Number | Revised Distance (FBG-1) | Weight (FBG-1) | Accuracy (%) | Vehicle Number | Revised Distance (FBG-2) | Weight (FBG-2) | Accuracy (%) |
|---|---|---|---|---|---|---|---|
| 1 | −0.022 | 26,750.916 | 97.199 | 8 | 0.002 | 26,275.504 | 99.026 |
| 2 | −0.056 | 26,429.119 | 98.435 | 9 | 0.019 | 28,168.385 | 91.752 |
| 3 | −0.073 | 29,826.825 | 85.378 | 10 | 0.050 | 24,817.696 | 95.372 |
| 4 | −0.089 | 33,747.883 | 70.310 | 11 | 0.064 | 28,061.367 | 92.163 |
| 5 | 0.114 | 27,505.864 | 94.298 | 12 | 0.070 | 24,698.723 | 94.915 |
| 6 | −0.129 | 32,990.593 | 73.220 | 13 | −0.102 | 30,495.575 | 82.808 |
| 7 | 0.131 | 33,672.318 | 70.601 | 14 | −0.109 | 21,117.985 | 81.154 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Wang, X.; Podolsky, J.; Huang, Y.; Lu, P. Assessing Vehicle Wandering Effects on the Accuracy of Weigh-in-Motion Measurement Based on In-Pavement Fiber Bragg Sensors through a Hybrid Sensor-Camera System. Sensors 2023, 23, 8707. https://doi.org/10.3390/s23218707
Yang X, Wang X, Podolsky J, Huang Y, Lu P. Assessing Vehicle Wandering Effects on the Accuracy of Weigh-in-Motion Measurement Based on In-Pavement Fiber Bragg Sensors through a Hybrid Sensor-Camera System. Sensors. 2023; 23(21):8707. https://doi.org/10.3390/s23218707
Chicago/Turabian StyleYang, Xinyi, Xingyu Wang, Joseph Podolsky, Ying Huang, and Pan Lu. 2023. "Assessing Vehicle Wandering Effects on the Accuracy of Weigh-in-Motion Measurement Based on In-Pavement Fiber Bragg Sensors through a Hybrid Sensor-Camera System" Sensors 23, no. 21: 8707. https://doi.org/10.3390/s23218707
APA StyleYang, X., Wang, X., Podolsky, J., Huang, Y., & Lu, P. (2023). Assessing Vehicle Wandering Effects on the Accuracy of Weigh-in-Motion Measurement Based on In-Pavement Fiber Bragg Sensors through a Hybrid Sensor-Camera System. Sensors, 23(21), 8707. https://doi.org/10.3390/s23218707








