Recurrent Neural Network Methods for Extracting Dynamic Balance Variables during Gait from a Single Inertial Measurement Unit
Abstract
:1. Introduction
2. Data Collection and Pre-Processing
2.1. Subjects
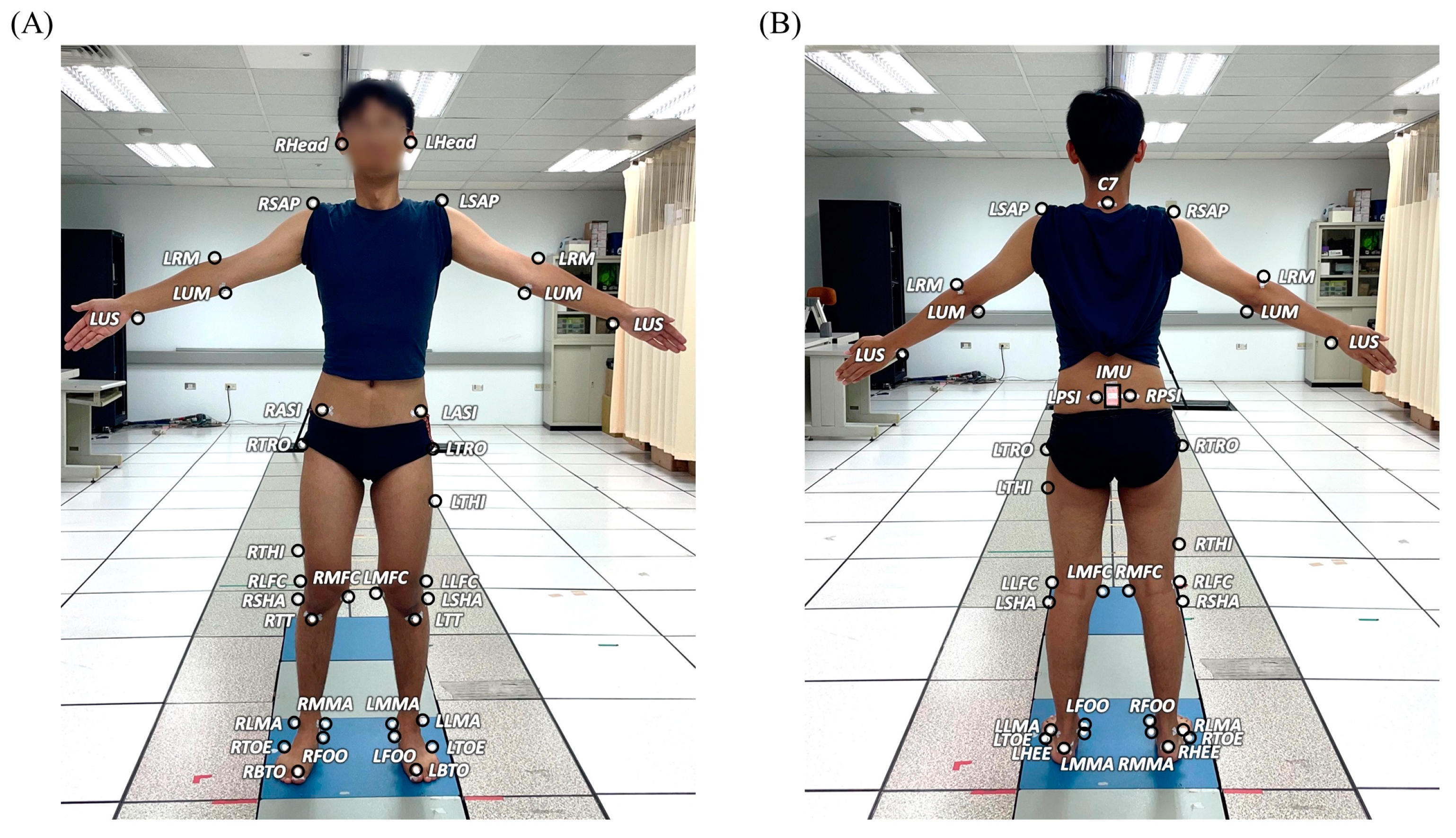
2.2. Gait Experiments
2.3. Calculation of COM–COP IA and RCIA
2.4. IMU Data Processing
3. Recurrent Neural Network (RNN) Modelling
3.1. Training Data Preparation
3.2. Machine Learning Models
3.2.1. RNN Cell Types: LSTM vs. GRU
3.2.2. The Architecture of RNN Models
3.2.3. Flow of Information: Uni-Directional vs. Bi-Directional
3.3. Loss Functions and Model Training
3.4. Validation Metrics
3.5. Statistical Analysis
4. Results
4.1. Prediction Accuracy
4.2. Performance in Between-Group Comparison
4.3. Number of Parameters and Computational Efficiency
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Santiago, J.; Cotto, E.; Jaimes, L.G.; Vergara-Laurens, I. Fall detection system for the elderly. In Proceedings of the 2017 IEEE 7th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 9–11 January 2017; pp. 1–4. [Google Scholar]
- World Health Organization; Ageing, and Life Course Unit. WHO Global Report on Falls Prevention in Older Age; World Health Organization: Geneva, Switzerland, 2008. [Google Scholar]
- Gryfe, C.; Amies, A.; Ashley, M. A longitudinal study of falls in an elderly population: I. Incidence and morbidity. Age Ageing 1977, 6, 201–210. [Google Scholar] [CrossRef]
- Sattin, R.W.; Huber, D.A.L.; Devito, C.A.; Rodriguez, J.G.; Ros, A.; Bacchelli, S.; Stevens, J.A.; Waxweiler, R.J. The incidence of fall injury events among the elderly in a defined population. Am. J. Epidemiol. 1990, 131, 1028–1037. [Google Scholar] [CrossRef] [PubMed]
- Sander, R. Risk factors for falls. Nurs. Older People 2009, 21, 15. [Google Scholar] [CrossRef] [PubMed]
- Tinetti, M.E.; Speechley, M. Prevention of falls among the elderly. N. Engl. J. Med. 1989, 320, 1055–1059. [Google Scholar] [PubMed]
- Rubenstein, L.Z. Falls in older people: Epidemiology, risk factors and strategies for prevention. Age Ageing 2006, 35 (Suppl. 2), ii37–ii41. [Google Scholar] [CrossRef]
- Luukinen, H.; Koski, K.; Laippala, P.; Kivelä, S.L.K. Factors predicting fractures during falling impacts among home-dwelling older adults. J. Am. Geriatr. Soc. 1997, 45, 1302–1309. [Google Scholar] [CrossRef]
- Caplan, B.; Bogner, J.; Brenner, L.; Yang, Y.; Mackey, D.C.; Liu-Ambrose, T.; Leung, P.-M.; Feldman, F.; Robinovitch, S.N. Clinical risk factors for head impact during falls in older adults: A prospective cohort study in long-term care. J. Head Trauma Rehabil. 2017, 32, 168–177. [Google Scholar]
- Siracuse, J.J.; Odell, D.D.; Gondek, S.P.; Odom, S.R.; Kasper, E.M.; Hauser, C.J.; Moorman, D.W. Health care and socioeconomic impact of falls in the elderly. Am. J. Surg. 2012, 203, 335–338. [Google Scholar] [CrossRef]
- Carey, D.; Laffoy, M. Hospitalisations due to falls in older persons. Ir. Med. J. 2005, 98, 179–181. [Google Scholar]
- Hindmarsh, J.J.; Estes, E.H. Falls in older persons: Causes and interventions. Arch. Intern. Med. 1989, 149, 2217–2222. [Google Scholar] [CrossRef]
- King, M.B.; Tinetti, M.E. Falls in community-dwelling older persons. J. Am. Geriatr. Soc. 1995, 43, 1146–1154. [Google Scholar] [CrossRef] [PubMed]
- Deshpande, N.; Metter, E.J.; Lauretani, F.; Bandinelli, S.; Guralnik, J.; Ferrucci, L. Activity restriction induced by fear of falling and objective and subjective measures of physical function: A prospective cohort study. J. Am. Geriatr. Soc. 2008, 56, 615–620. [Google Scholar] [CrossRef] [PubMed]
- Kempen, G.I.; van Haastregt, J.C.; McKee, K.J.; Delbaere, K.; Zijlstra, G.R. Socio-demographic, health-related and psychosocial correlates of fear of falling and avoidance of activity in community-living older persons who avoid activity due to fear of falling. BMC Public Health 2009, 9, 170. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, P.C.; Guthrie, D.M.; Berg, K.; Hirdes, J.P. Risk factors for restriction in activity associated with fear of falling among seniors within the community. J. Patient Saf. 2010, 6, 187–191. [Google Scholar] [CrossRef]
- Shafizadeh, M.; Manson, J.; Fowler-Davis, S.; Ali, K.; Lowe, A.C.; Stevenson, J.; Parvinpour, S.; Davids, K. Effects of enriched physical activity environments on balance and fall prevention in older adults: A scoping review. J. Aging Phys. Act. 2020, 29, 178–191. [Google Scholar] [CrossRef]
- Hamm, J.; Money, A.G.; Atwal, A.; Paraskevopoulos, I. Fall prevention intervention technologies: A conceptual framework and survey of the state of the art. J. Biomed. Inform. 2016, 59, 319–345. [Google Scholar] [CrossRef]
- Lee, H.-J.; Chou, L.-S. Detection of gait instability using the center of mass and center of pressure inclination angles. Arch. Phys. Med. Rehabil. 2006, 87, 569–575. [Google Scholar] [CrossRef]
- Chien, H.-L.; Lu, T.-W.; Liu, M.-W. Control of the motion of the body’s center of mass in relation to the center of pressure during high-heeled gait. Gait Posture 2013, 38, 391–396. [Google Scholar] [CrossRef]
- Paul, J.C.; Patel, A.; Bianco, K.; Godwin, E.; Naziri, Q.; Maier, S.; Lafage, V.; Paulino, C.; Errico, T.J. Gait stability improvement after fusion surgery for adolescent idiopathic scoliosis is influenced by corrective measures in coronal and sagittal planes. Gait Posture 2014, 40, 510–515. [Google Scholar] [CrossRef]
- Huang, S.-C.; Lu, T.-W.; Chen, H.-L.; Wang, T.-M.; Chou, L.-S. Age and height effects on the center of mass and center of pressure inclination angles during obstacle-crossing. Med. Eng. Phys. 2008, 30, 968–975. [Google Scholar] [CrossRef]
- Lee, P.-A.; Wu, K.-H.; Lu, H.-Y.; Su, K.-W.; Wang, T.-M.; Liu, H.-C.; Lu, T.-W. Compromised balance control in older people with bilateral medial knee osteoarthritis during level walking. Sci. Rep. 2021, 11, 3742. [Google Scholar] [CrossRef] [PubMed]
- Hong, S.-W.; Leu, T.-H.; Wang, T.-M.; Li, J.-D.; Ho, W.-P.; Lu, T.-W. Control of body’s center of mass motion relative to center of pressure during uphill walking in the elderly. Gait Posture 2015, 42, 523–528. [Google Scholar] [CrossRef] [PubMed]
- Chou, L.-S.; Kaufman, K.R.; Hahn, M.E.; Brey, R.H. Medio-lateral motion of the center of mass during obstacle crossing distinguishes elderly individuals with imbalance. Gait Posture 2003, 18, 125–133. [Google Scholar] [CrossRef] [PubMed]
- De Jong, L.; van Dijsseldonk, R.; Keijsers, N.; Groen, B. Test-retest reliability of stability outcome measures during treadmill walking in patients with balance problems and healthy controls. Gait Posture 2020, 76, 92–97. [Google Scholar] [CrossRef]
- Toebes, M.J.; Hoozemans, M.J.; Furrer, R.; Dekker, J.; van Dieën, J.H. Local dynamic stability and variability of gait are associated with fall history in elderly subjects. Gait Posture 2012, 36, 527–531. [Google Scholar] [CrossRef] [PubMed]
- Bizovska, L.; Svoboda, Z.; Janura, M.; Bisi, M.C.; Vuillerme, N. Local dynamic stability during gait for predicting falls in elderly people: A one-year prospective study. PLoS ONE 2018, 13, e0197091. [Google Scholar] [CrossRef]
- Pierleoni, P.; Belli, A.; Palma, L.; Pellegrini, M.; Pernini, L.; Valenti, S. A high reliability wearable device for elderly fall detection. IEEE Sens. J. 2015, 15, 4544–4553. [Google Scholar] [CrossRef]
- Khojasteh, S.B.; Villar, J.R.; Chira, C.; González, V.M.; De la Cal, E. Improving fall detection using an on-wrist wearable accelerometer. Sensors 2018, 18, 1350. [Google Scholar] [CrossRef]
- Cheng, J.; Chen, X.; Shen, M. A framework for daily activity monitoring and fall detection based on surface electromyography and accelerometer signals. IEEE J. Biomed. Health Inform. 2012, 17, 38–45. [Google Scholar] [CrossRef]
- Zongxing, L.; Baizheng, H.; Yingjie, C.; Bingxing, C.; Ligang, Y.; Haibin, H.; Zhoujie, L. Human-machine interaction technology for simultaneous gesture recognition and force assessment: A Review. IEEE Sens. J. 2023. [Google Scholar] [CrossRef]
- Guo, L.; Lu, Z.; Yao, L. Human-machine interaction sensing technology based on hand gesture recognition: A review. IEEE Trans. Hum. Mach. Syst. 2021, 51, 300–309. [Google Scholar] [CrossRef]
- Wang, X.; Ellul, J.; Azzopardi, G. Elderly fall detection systems: A literature survey. Front. Robot. AI 2020, 7, 71. [Google Scholar] [CrossRef] [PubMed]
- Yan, X.; Li, H.; Li, A.R.; Zhang, H. Wearable IMU-based real-time motion warning system for construction workers’ musculoskeletal disorders prevention. Autom. Constr. 2017, 74, 2–11. [Google Scholar] [CrossRef]
- Yang, B.; Lee, Y.; Lin, C. On developing a real-time fall detecting and protecting system using mobile device. In Proceedings of the International Conference on Fall Prevention and Protection, Tokyo, Japan, 23–25 October 2013; pp. 151–156. [Google Scholar]
- Lin, H.-C.; Chen, M.-J.; Lee, C.-H.; Kung, L.-C.; Huang, J.-T. Fall Recognition Based on an IMU Wearable Device and Fall Verification through a Smart Speaker and the IoT. Sensors 2023, 23, 5472. [Google Scholar] [CrossRef] [PubMed]
- Mioskowska, M.; Stevenson, D.; Onu, M.; Trkov, M. Compressed gas actuated knee assistive exoskeleton for slip-induced fall prevention during human walking. In Proceedings of the 2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 6–9 July 2020; pp. 735–740. [Google Scholar]
- Kapsalyamov, A.; Jamwal, P.K.; Hussain, S.; Ghayesh, M.H. State of the art lower limb robotic exoskeletons for elderly assistance. IEEE Access 2019, 7, 95075–95086. [Google Scholar] [CrossRef]
- Aminian, K.; Najafi, B.; Büla, C.; Leyvraz, P.-F.; Robert, P. Spatio-temporal parameters of gait measured by an ambulatory system using miniature gyroscopes. J. Biomech. 2002, 35, 689–699. [Google Scholar] [CrossRef]
- Mariani, B.; Hoskovec, C.; Rochat, S.; Büla, C.; Penders, J.; Aminian, K. 3D gait assessment in young and elderly subjects using foot-worn inertial sensors. J. Biomech. 2010, 43, 2999–3006. [Google Scholar] [CrossRef]
- Schlachetzki, J.C.; Barth, J.; Marxreiter, F.; Gossler, J.; Kohl, Z.; Reinfelder, S.; Gassner, H.; Aminian, K.; Eskofier, B.M.; Winkler, J. Wearable sensors objectively measure gait parameters in Parkinson’s disease. PLoS ONE 2017, 12, e0183989. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, Z.; Qiu, S.; Shen, Y.; Wang, J. IMU-based gait analysis for rehabilitation assessment of patients with gait disorders. In Proceedings of the 2017 4th International Conference on Systems and Informatics (ICSAI), Hangzhou, China, 11–13 November 2017; pp. 622–626. [Google Scholar]
- Zhou, L.; Tunca, C.; Fischer, E.; Brahms, C.M.; Ersoy, C.; Granacher, U.; Arnrich, B. Validation of an IMU gait analysis algorithm for gait monitoring in daily life situations. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 4229–4232. [Google Scholar]
- O’Brien, M.K.; Hidalgo-Araya, M.D.; Mummidisetty, C.K.; Vallery, H.; Ghaffari, R.; Rogers, J.A.; Lieber, R.; Jayaraman, A. Augmenting clinical outcome measures of gait and balance with a single inertial sensor in age-ranged healthy adults. Sensors 2019, 19, 4537. [Google Scholar] [CrossRef]
- Najafi, B.; Aminian, K.; Paraschiv-Ionescu, A.; Loew, F.; Bula, C.J.; Robert, P. Ambulatory system for human motion analysis using a kinematic sensor: Monitoring of daily physical activity in the elderly. IEEE Trans. Biomed. Eng. 2003, 50, 711–723. [Google Scholar] [CrossRef]
- Chebel, E.; Tunc, B. Deep neural network approach for estimating the three-dimensional human center of mass using joint angles. J. Biomech. 2021, 126, 110648. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.-C.; Chen, Y.-J.; Hsu, C.-S.; Wen, Y.-T.; Lee, Y.-J. Multiple inertial measurement unit combination and location for center of pressure prediction in gait. Front. Bioeng. Biotechnol. 2020, 8, 566474. [Google Scholar] [CrossRef] [PubMed]
- Berwald, J.; Gedeon, T.; Sheppard, J. Using machine learning to predict catastrophes in dynamical systems. J. Comput. Appl. Math. 2012, 236, 2235–2245. [Google Scholar] [CrossRef]
- de Arquer Rilo, J.; Hussain, A.; Al-Taei, M.; Baker, T.; Al-Jumeily, D. Dynamic neural network for business and market analysis. In Proceedings of the Intelligent Computing Theories and Application: 15th International Conference, ICIC 2019, Nanchang, China, 3–6 August 2019; pp. 77–87. [Google Scholar]
- Andersson, Å.E. Economic structure of the 21st century. In The Cosmo-Creative Society: Logistical Networks in a Dynamic Economy; Springer: Berlin/Heidelberg, Germany, 1993; pp. 17–29. [Google Scholar]
- Mao, W.; Liu, M.; Salzmann, M.; Li, H. Learning trajectory dependencies for human motion prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9489–9497. [Google Scholar]
- Martinez, J.; Black, M.J.; Romero, J. On human motion prediction using recurrent neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2891–2900. [Google Scholar]
- Sung, J.; Han, S.; Park, H.; Cho, H.-M.; Hwang, S.; Park, J.W.; Youn, I. Prediction of lower extremity multi-joint angles during overground walking by using a single IMU with a low frequency based on an LSTM recurrent neural network. Sensors 2021, 22, 53. [Google Scholar] [CrossRef] [PubMed]
- Alemayoh, T.T.; Lee, J.H.; Okamoto, S. LocoESIS: Deep-Learning-Based Leg-Joint Angle Estimation from a Single Pelvis Inertial Sensor. In Proceedings of the 2022 9th IEEE RAS/EMBS International Conference for Biomedical Robotics and Biomechatronics (BioRob), Seoul, Republic of Korea, 21–24 August 2022; pp. 1–7. [Google Scholar]
- Hossain, M.S.B.; Dranetz, J.; Choi, H.; Guo, Z. Deepbbwae-net: A cnn-rnn based deep superlearner for estimating lower extremity sagittal plane joint kinematics using shoe-mounted imu sensors in daily living. IEEE J. Biomed. Health Inform. 2022, 26, 3906–3917. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Yang, S.; Yu, X.; Zhou, Y. Lstm and gru neural network performance comparison study: Taking yelp review dataset as an example. In Proceedings of the 2020 International Workshop on Electronic Communication and Artificial Intelligence (IWECAI), Shanghai, China, 12–14 June 2020; pp. 98–101. [Google Scholar]
- World Medical Association. World Medical Association Declaration of Helsinki: Ethical principles for medical research involving human subjects. JAMA 2013, 310, 2191–2194. [Google Scholar] [CrossRef]
- Erdfelder, E.; Faul, F.; Buchner, A. GPOWER: A general power analysis program. Behav. Res. Methods Instrum. Comput. 1996, 28, 1–11. [Google Scholar] [CrossRef]
- Lu, S.-H.; Kuan, Y.-C.; Wu, K.-W.; Lu, H.-Y.; Tsai, Y.-L.; Chen, H.-H.; Lu, T.-W. Kinematic strategies for obstacle-crossing in older adults with mild cognitive impairment. Front. Aging Neurosci. 2022, 14, 950411. [Google Scholar] [CrossRef]
- Wu, K.-W.; Yu, C.-H.; Huang, T.-H.; Lu, S.-H.; Tsai, Y.-L.; Wang, T.-M.; Lu, T.-W. Children with Duchenne muscular dystrophy display specific kinematic strategies during obstacle-crossing. Sci. Rep. 2023, 13, 17094. [Google Scholar] [CrossRef] [PubMed]
- Ghoussayni, S.; Stevens, C.; Durham, S.; Ewins, D. Assessment and validation of a simple automated method for the detection of gait events and intervals. Gait Posture 2004, 20, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Cavanagh, P.R. ISB recommendations for standardization in the reporting of kinematic data. J. Biomech. 1995, 28, 1257–1262. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.-C.; Hsieh, H.-J.; Lu, T.-W.; Tseng, C.-H. A method for estimating subject-specific body segment inertial parameters in human movement analysis. Gait Posture 2011, 33, 695–700. [Google Scholar] [CrossRef]
- Lu, T.-W.; O’connor, J. Bone position estimation from skin marker co-ordinates using global optimisation with joint constraints. J. Biomech. 1999, 32, 129–134. [Google Scholar] [CrossRef]
- Besser, M.; Kowalk, D.; Vaughan, C. Mounting and calibration of stairs on piezoelectric force platforms. Gait Posture 1993, 1, 231–235. [Google Scholar] [CrossRef]
- Woltring, H.J. A Fortran package for generalized, cross-validatory spline smoothing and differentiation. Adv. Eng. Softw. 1986, 8, 104–113. [Google Scholar] [CrossRef]
- Kristianslund, E.; Krosshaug, T.; Van den Bogert, A.J. Effect of low pass filtering on joint moments from inverse dynamics: Implications for injury prevention. J. Biomech. 2012, 45, 666–671. [Google Scholar] [CrossRef]
- Yu, B.; Gabriel, D.; Noble, L.; An, K.-N. Estimate of the optimum cutoff frequency for the Butterworth low-pass digital filter. J. Appl. Biomech. 1999, 15, 318–329. [Google Scholar] [CrossRef]
- Kaur, M.; Mohta, A. A review of deep learning with recurrent neural network. In Proceedings of the 2019 International Conference on Smart Systems and Inventive Technology (ICSSIT), Tirunelveli, India, 27–29 November 2019; pp. 460–465. [Google Scholar]
- Graves, A. Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–45. [Google Scholar]
- Olah, C. Understanding lstm networks. Colah’s Blog, 27 August 2015. [Google Scholar]
- Horn, R.A. The hadamard product. Proc. Symp. Appl. Math. 1990, 40, 87–169. [Google Scholar]
- Gruber, N.; Jockisch, A. Are GRU cells more specific and LSTM cells more sensitive in motive classification of text? Front. Artif. Intell. 2020, 3, 40. [Google Scholar] [CrossRef] [PubMed]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Jordán, K. Calculus of Finite Differences; Chelsea Publishing Company: New York, NY, USA, 1965; Volume 33. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L. Pytorch: An imperative style, high-performance deep learning library. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Sawilowsky, S.S. New effect size rules of thumb. J. Mod. Appl. Stat. Methods 2009, 8, 26. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Parikh, R.; Mathai, A.; Parikh, S.; Sekhar, G.C.; Thomas, R. Understanding and using sensitivity, specificity and predictive values. Indian J. Ophthalmol. 2008, 56, 45. [Google Scholar] [CrossRef] [PubMed]
- Alcaraz, J.C.; Moghaddamnia, S.; Peissig, J. Efficiency of deep neural networks for joint angle modeling in digital gait assessment. EURASIP J. Adv. Signal Process. 2021, 2021, 10. [Google Scholar] [CrossRef]
- Choi, A.; Jung, H.; Mun, J.H. Single inertial sensor-based neural networks to estimate COM-COP inclination angle during walking. Sensors 2019, 19, 2974. [Google Scholar] [CrossRef]
- Renani, M.S.; Eustace, A.M.; Myers, C.A.; Clary, C.W. The use of synthetic imu signals in the training of deep learning models significantly improves the accuracy of joint kinematic predictions. Sensors 2021, 21, 5876. [Google Scholar] [CrossRef]
- Yu, Y.; Tian, N.; Hao, X.; Ma, T.; Yang, C. Human motion prediction with gated recurrent unit model of multi-dimensional input. Appl. Intell. 2022, 52, 6769–6781. [Google Scholar] [CrossRef]
- Ying, X. An overview of overfitting and its solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Myung, I.J. The importance of complexity in model selection. J. Math. Psychol. 2000, 44, 190–204. [Google Scholar] [CrossRef] [PubMed]
- Al Borno, M.; O’Day, J.; Ibarra, V.; Dunne, J.; Seth, A.; Habib, A.; Ong, C.; Hicks, J.; Uhlrich, S.; Delp, S. OpenSense: An open-source toolbox for inertial-measurement-unit-based measurement of lower extremity kinematics over long durations. J. Neuroeng. Rehabil. 2022, 19, 22. [Google Scholar] [CrossRef] [PubMed]
- Mundt, M.; Koeppe, A.; David, S.; Witter, T.; Bamer, F.; Potthast, W.; Markert, B. Estimation of gait mechanics based on simulated and measured IMU data using an artificial neural network. Front. Bioeng. Biotechnol. 2020, 8, 41. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.L.; Odom, C.; Ben-Asher, M. Knee angle estimation based on imu data and artificial neural networks. In Proceedings of the 2013 29th Southern Biomedical Engineering Conference, Miami, FL, USA, 3–5 May 2013; pp. 111–112. [Google Scholar]
- Karatsidis, A.; Bellusci, G.; Schepers, H.M.; De Zee, M.; Andersen, M.S.; Veltink, P.H. Estimation of ground reaction forces and moments during gait using only inertial motion capture. Sensors 2016, 17, 75. [Google Scholar] [CrossRef]
- Fleron, M.K.; Ubbesen, N.C.H.; Battistella, F.; Dejtiar, D.L.; Oliveira, A.S. Accuracy between optical and inertial motion capture systems for assessing trunk speed during preferred gait and transition periods. Sports Biomech. 2018, 18, 366–377. [Google Scholar] [CrossRef]
- Lin, C.-S.; Hsu, H.C.; Lay, Y.-L.; Chiu, C.-C.; Chao, C.-S. Wearable device for real-time monitoring of human falls. Measurement 2007, 40, 831–840. [Google Scholar] [CrossRef]
- Pham, C.; Diep, N.N.; Phuong, T.M. A wearable sensor based approach to real-time fall detection and fine-grained activity recognition. J. Mob. Multimed. 2013, 9, 15–26. [Google Scholar]
- Sharifi-Renani, M.; Mahoor, M.H.; Clary, C.W. BioMAT: An Open-Source Biomechanics Multi-Activity Transformer for Joint Kinematic Predictions Using Wearable Sensors. Sensors 2023, 23, 5778. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Flagg, C.; Frieder, O.; MacAvaney, S.; Motamedi, G. Real-time streaming of gait assessment for Parkinson’s disease. In Proceedings of the 14th ACM International Conference on Web Search and Data Mining, Virtual, 8–12 March 2021; pp. 1081–1084. [Google Scholar]






| Variable Number | Gait Event | Groups | Effect Size | p-Value | |
|---|---|---|---|---|---|
| Old | Young | ||||
| Sagittal IA (°) | |||||
| 1 | HS | 7.61 (2.06) | 7.96 (1.57) | 0.19 | 0.64 |
| 2 | CTO | −6.92 (1.39) | −7.24 (1.02) | 0.26 | 0.53 |
| 3 | CHS | 6.49 (1.31) | 6.10 (1.29) | 0.30 | 0.47 |
| 4 | TO | −7.69 (1.04) | −7.16 (0.62) | 0.61 | 0.15 |
| Frontal IA (°) | |||||
| 5 | HS | 4.89 (1.36) | 4.37 (1.04) | 0.43 | 0.31 |
| 6 | CTO | −3.43 (1.13) | −3.48 (0.80) | 0.05 | 0.91 |
| 7 | CHS | −4.18 (1.37) | −3.96 (1.09) | 0.18 | 0.67 |
| 8 | TO | 3.62 (1.17) | 3.43 (0.82) | 0.19 | 0.65 |
| Sagittal RCIA (°/s) | |||||
| 9 | HS | 39.45 (16.34) | 45.29 (9.34) | 0.44 | 0.29 |
| 10 | CTO | −37.93 (26.53) | 0.24 (21.58) | 1.58 | <0.01 * |
| 11 | CHS | −149.58 (48.03) | −131.63 (28.05) | 0.46 | 0.28 |
| 12 | TO | −34.63 (25.08) | −7.38 (53.08) | 0.66 | 0.12 |
| Frontal RCIA (°/s) | |||||
| 13 | HS | 7.80 (5.64) | 5.28 (2.82) | 0.56 | 0.18 |
| 14 | CTO | −31.78 (15.38) | −14.42 (8.68) | 1.39 | <0.01 * |
| 15 | CHS | 74.18 (25.33) | 69.94 (19.68) | 0.19 | 0.65 |
| 16 | TO | 28.35 (15.04) | 18.47 (20.31) | 0.55 | 0.19 |
| Variable Number | Sub- Phase | Groups | Effect Size | p-Value | |
|---|---|---|---|---|---|
| Old | Young | ||||
| Sagittal IA (°) | |||||
| 17 | iDLS | −0.34 (0.79) | −0.79 (0.81) | 0.55 | 0.19 |
| 18 | SLS | 0.22 (0.77) | 0.00 (0.42) | 0.37 | 0.37 |
| 19 | tDLS | −0.25 (1.02) | −0.41 (1.15) | 0.14 | 0.73 |
| 20 | SW | −0.29 (0.68) | 0.26 (0.49) | 0.93 | 0.03 * |
| Frontal IA (°) | |||||
| 21 | iDLS | 0.57 (0.55) | 0.40 (0.54) | 0.31 | 0.46 |
| 22 | SLS | −3.86 (0.98) | −3.69 (0.91) | 0.18 | 0.66 |
| 23 | tDLS | −0.53 (0.64) | −0.38 (0.75) | 0.21 | 0.61 |
| 24 | SW | 3.88 (1.08) | 3.58 (0.91) | 0.30 | 0.47 |
| Sagittal RCIA (°/s) | |||||
| 25 | iDLS | −93.95 (25.76) | −89.52 (19.07) | 0.20 | 0.64 |
| 26 | SLS | 29.46 (6.26) | 32.48 (3.59) | 0.59 | 0.16 |
| 27 | tDLS | −102.65 (33.67) | −96.08 (19.46) | 0.24 | 0.56 |
| 28 | SW | 32.37 (6.18) | 34.67 (4.41) | 0.43 | 0.31 |
| Frontal RCIA (°/s) | |||||
| 29 | iDLS | −53.78 (13.87) | −51.54 (10.62) | 0.18 | 0.66 |
| 30 | SLS | −2.84 (1.94) | −2.07 (1.52) | 0.44 | 0.29 |
| 31 | tDLS | 54.36 (20.17) | 52.60 (12.68) | 0.10 | 0.80 |
| 32 | SW | 3.21 (1.48) | 2.46 (1.15) | 0.56 | 0.18 |
| Variable Number | Sub-Phase | Groups | Effect Size | p-Value | |
|---|---|---|---|---|---|
| Old | Young | ||||
| Sagittal IA (°) | |||||
| 33 | iDLS | 11.85 (2.15) | 12.38 (1.50) | 0.28 | 0.49 |
| 34 | SLS | 15.09 (1.74) | 14.35 (1.14) | 0.50 | 0.23 |
| 35 | tDLS | 13.55 (1.40) | 13.01 (1.53) | 0.37 | 0.38 |
| 36 | SW | 15.05 (2.00) | 14.73 (1.64) | 0.17 | 0.68 |
| Frontal IA (°) | |||||
| 37 | iDLS | 7.00 (1.85) | 7.18 (1.41) | 0.11 | 0.79 |
| 38 | SLS | 1.74 (0.78) | 1.44 (0.57) | 0.44 | 0.30 |
| 39 | tDLS | 7.36 (2.17) | 7.10 (1.46) | 0.14 | 0.74 |
| 40 | SW | 1.55 (0.62) | 1.17 (0.38) | 0.75 | 0.08 |
| Sagittal RCIA (°/s) | |||||
| 41 | iDLS | 138.09 (56.37) | 168.94 (53.67) | 0.56 | 0.18 |
| 42 | SLS | 111.38 (38.46) | 89.13 (24.63) | 0.69 | 0.11 |
| 43 | tDLS | 149.33 (47.45) | 170.72 (53.22) | 0.42 | 0.31 |
| 44 | SW | 84.74 (28.59) | 66.06 (52.59) | 0.44 | 0.29 |
| Frontal RCIA (°/s) | |||||
| 45 | iDLS | 64.58 (32.42) | 68.85 (22.43) | 0.15 | 0.71 |
| 46 | SLS | 57.39 (22.94) | 41.13 (15.14) | 0.84 | 0.06 |
| 47 | tDLS | 62.86 (27.57) | 68.35 (20.98) | 0.22 | 0.59 |
| 48 | SW | 35.36 (15.61) | 25.72 (19.75) | 0.54 | 0.20 |
| Model | False Negative | False Positive | Sensitivity (%) | Specificity (%) | Accuracy (%) | Pearson’s r for Effect Sizes |
|---|---|---|---|---|---|---|
| Bi-GRU | 3/3 (10, 14, 20) | 4/45 (4, 35, 43, 47) | 0.00 | 91.11 | 85.42 | 0.28 |
| Uni-GRU | 0/3 (−) | 8/45 (2, 3, 4, 30, 35, 38, 40, 41) | 100.00 | 82.22 | 83.33 | 0.47 |
| Bi-LSTM | 2/3 (14, 20) | 0/45 (−) | 33.33 | 100.00 | 95.83 | 0.48 |
| Uni-LSTM | 0/3 (−) | 0/45 (−) | 100.00 | 100.00 | 100.00 | 0.65 |
| Cell Type | Flow of Information | |
|---|---|---|
| Uni-Direction | Bi-Direction | |
| LSTM | 3.17 × 106 | 8.43 × 106 |
| GRU | 2.38 × 106 | 6.32 × 106 |
| Loss Function | Machine Learning Model | p-Value | ||||
|---|---|---|---|---|---|---|
| Uni-LSTM | Uni-GRU | Bi-LSTM | Bi-GRU | PL | PC, PD | |
| Running Time (sec) | ||||||
| Standard MSE | 0.10 (0.01) | 0.07 (0.01) | 0.20 (0.01) | 0.16 (0.02) | 0.72, 0.09, | <0.01 *, |
| Weighted MSE | 0.10 (0.01) | 0.08 (0.01) | 0.21 (0.02) | 0.16 (0.01) | 0.09, 0.55 | <0.01 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, C.-H.; Yeh, C.-C.; Lu, Y.-F.; Lu, Y.-L.; Wang, T.-M.; Lin, F.Y.-S.; Lu, T.-W. Recurrent Neural Network Methods for Extracting Dynamic Balance Variables during Gait from a Single Inertial Measurement Unit. Sensors 2023, 23, 9040. https://doi.org/10.3390/s23229040
Yu C-H, Yeh C-C, Lu Y-F, Lu Y-L, Wang T-M, Lin FY-S, Lu T-W. Recurrent Neural Network Methods for Extracting Dynamic Balance Variables during Gait from a Single Inertial Measurement Unit. Sensors. 2023; 23(22):9040. https://doi.org/10.3390/s23229040
Chicago/Turabian StyleYu, Cheng-Hao, Chih-Ching Yeh, Yi-Fu Lu, Yi-Ling Lu, Ting-Ming Wang, Frank Yeong-Sung Lin, and Tung-Wu Lu. 2023. "Recurrent Neural Network Methods for Extracting Dynamic Balance Variables during Gait from a Single Inertial Measurement Unit" Sensors 23, no. 22: 9040. https://doi.org/10.3390/s23229040
APA StyleYu, C.-H., Yeh, C.-C., Lu, Y.-F., Lu, Y.-L., Wang, T.-M., Lin, F. Y.-S., & Lu, T.-W. (2023). Recurrent Neural Network Methods for Extracting Dynamic Balance Variables during Gait from a Single Inertial Measurement Unit. Sensors, 23(22), 9040. https://doi.org/10.3390/s23229040







