Practical Considerations for Laser-Induced Graphene Pressure Sensors Used in Marine Applications
Abstract
:1. Introduction
2. Materials and Methods
2.1. LIG Sensor Fabrication
2.2. SEM Imaging
2.3. Compression Testing
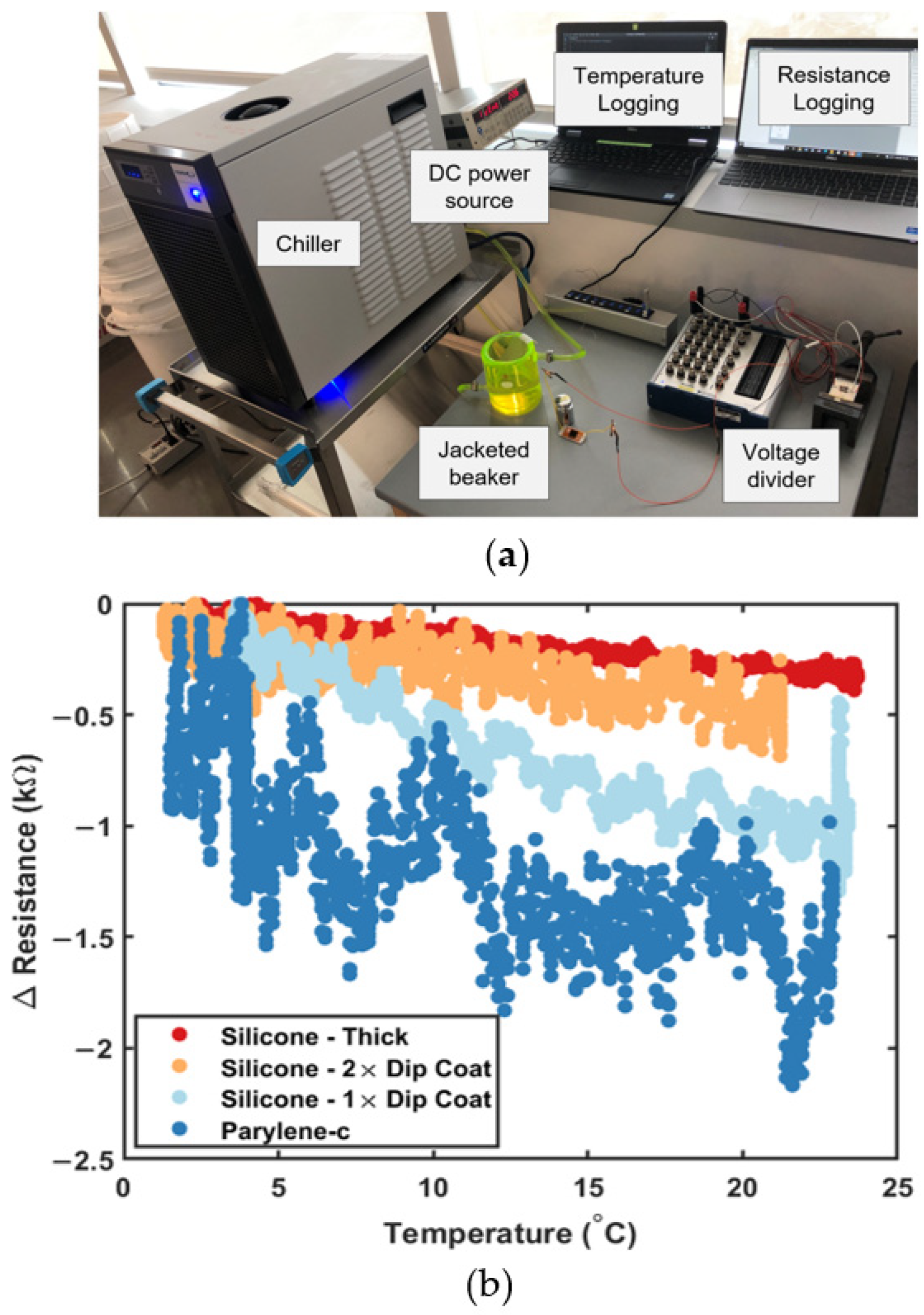
2.4. Thermal Testing
3. Results
3.1. LIG Characterization
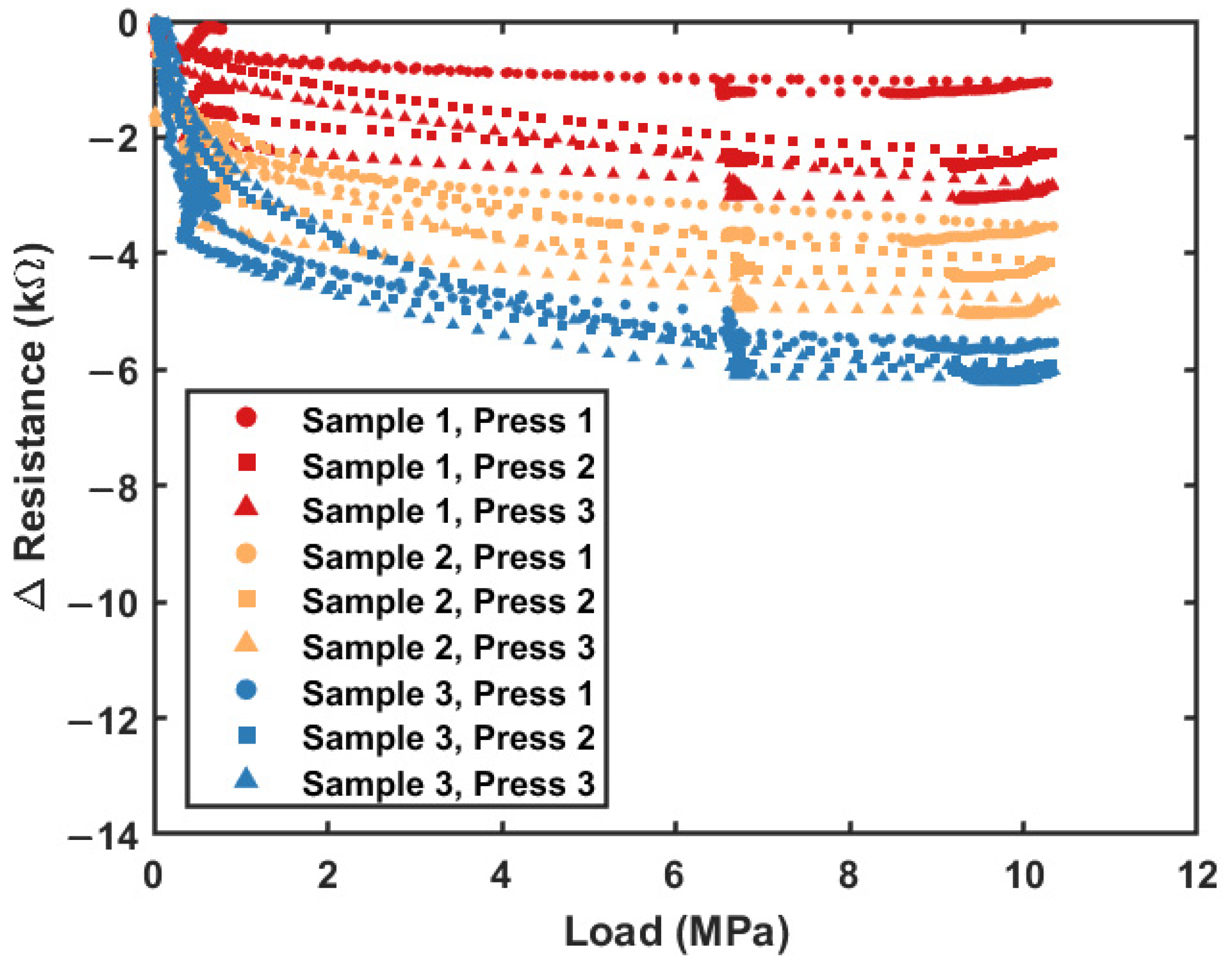
3.2. Uniaxial Compression Testing
3.3. Thermal Testing
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aravamudhan, S.; Bhansali, S. Reinforced Piezoresistive Pressure Sensor for Ocean Depth Measurements. Sens. Actuators A Phys. 2008, 142, 111–117. [Google Scholar] [CrossRef]
- Li, T.; Shang, H.; Wang, B.; Mao, C.; Wang, W. High-Pressure Sensor with High Sensitivity and High Accuracy for Full Ocean Depth Measurements. IEEE Sens. J. 2022, 22, 3994–4003. [Google Scholar] [CrossRef]
- Lin, M.; Yang, C. Ocean Observation Technologies: A Review. Chin. J. Mech. Eng. 2020, 33, 32. [Google Scholar] [CrossRef]
- Treasure, A.M.; Roquet, F.; Ansorge, I.J.; Bester, M.N.; Boehme, L.; Bornemann, H.; Charrassin, J.-B.; Chevallier, D.; Costa, D.P.; Fedak, M.A.; et al. Marine Mammals Exploring the Oceans Pole to Pole: A Review of the MEOP Consortium. Oceanography 2017, 30, 132–138. [Google Scholar] [CrossRef]
- Yoon, S.-T.; Lee, W.Y. Quality Control Methods for CTD Data Collected by Using Instrumented Marine Mammals: A Review and Case Study. Ocean Polar Res. 2021, 43, 321–334. [Google Scholar] [CrossRef]
- Paradis, R.; Wood, S.L. Inexpensive Expendable Conductivity Temperature and Depth (CTD) Sensor. In Proceedings of the 2013 OCEANS, San Diego, CA, USA, 23–27 September 2013; pp. 1–12. [Google Scholar]
- Conductivity, Temperature, Depth (CTD) Sensors-Woods Hole Oceanographic Institution. Available online: https://www.whoi.edu/ (accessed on 15 July 2023).
- Wang, Y.; Liu, Y.; Guo, Z. Three-Dimensional Ocean Sensor Networks: A Survey. J. Ocean Univ. China 2012, 11, 436–450. [Google Scholar] [CrossRef]
- Tyler, R.H.; Boyer, T.P.; Minami, T.; Zweng, M.M.; Reagan, J.R. Electrical Conductivity of the Global Ocean. Earth Planets Space 2017, 69, 156. [Google Scholar] [CrossRef]
- Key Physical Variables in the Ocean: Temperature, Salinity, and Density|Learn Science at Scitable. Available online: https://www.nature.com/scitable/knowledge/library/key-physical-variables-in-the-ocean-temperature-102805293/ (accessed on 22 March 2023).
- Xiao, S.; Zhang, M.; Liu, C.; Jiang, C.; Wang, X.; Yang, F. CTD Sensors for Ocean Investigation Including State of Art and Commercially Available. Sensors 2023, 23, 586. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, X.; Miao, Y.; Jiang, G.; Tong, L.; Tao, P.; Yu, Q.; Peng, W. Integrated and Compact Fiber-Optic Conductivity-Temperature-Depth (CTD) Sensor for Marine Detection. Opt. Laser Technol. 2023, 164, 109523. [Google Scholar] [CrossRef]
- Lin, J.; Peng, Z.; Liu, Y.; Ruiz-Zepeda, F.; Ye, R.; Samuel, E.L.G.; Yacaman, M.J.; Yakobson, B.I.; Tour, J.M. Laser-Induced Porous Graphene Films from Commercial Polymers. Nat. Commun. 2014, 5, 5714. [Google Scholar] [CrossRef]
- Kaidarova, A.; Kosel, J. Physical Sensors Based on Laser-Induced Graphene: A Review. IEEE Sens. J. 2021, 21, 12426–12443. [Google Scholar] [CrossRef]
- Ben-Shimon, Y.; Sharma, C.P.; Arnusch, C.J.; Ya’akobovitz, A. Freestanding Laser-Induced Graphene Ultrasensitive Resonative Viral Sensors. ACS Appl. Mater. Interfaces 2022, 14, 44713–44723. [Google Scholar] [CrossRef] [PubMed]
- Erçarıkcı, E.; Dağcı Kıranşan, K.; Topçu, E. A Flexible Graphene Paper Electrochemical Sensor with Electrodeposited Ag and Ni Nanoparticles for H2O2 Detection. IEEE Sens. J. 2023, 23, 7087–7094. [Google Scholar] [CrossRef]
- Ye, R.; James, D.K.; Tour, J.M. Laser-Induced Graphene. Acc. Chem. Res. 2018, 51, 1609–1620. [Google Scholar] [CrossRef] [PubMed]
- Tavakkoli Gilavan, M.; Rahman, M.S.; Minhas-Khan, A.; Nambi, S.; Grau, G. One-Step Fabrication of Low-Resistance Conductors on 3D-Printed Structures by Laser-Induced Graphene. ACS Appl. Electron. Mater. 2021, 3, 3867–3875. [Google Scholar] [CrossRef]
- Kaidarova, A.; Marengo, M.; Geraldi, N.R.; Duarte, C.M.; Kosel, J. Flexible Conductivity, Temperature, and Depth Sensor for Marine Environment Monitoring. In Proceedings of the 2019 IEEE SENSORS, Montreal, QC, Canada, 27–30 October 2019; pp. 1–4. [Google Scholar]
- Duy, L.X.; Peng, Z.; Li, Y.; Zhang, J.; Ji, Y.; Tour, J.M. Laser-Induced Graphene Fibers. Carbon 2018, 126, 472–479. [Google Scholar] [CrossRef]
- Fu, H.; Xiao, Y.; Song, R.; Wang, Z.; Ji, H.; He, D. Rapid Soldering of Flexible Graphene Assembled Films at Low Temperature in Air with Ultrasonic Assistance. Carbon 2020, 158, 55–62. [Google Scholar] [CrossRef]
- Chen, B.; Johnson, Z.T.; Sanborn, D.; Hjort, R.G.; Garland, N.T.; Soares, R.R.A.; Van Belle, B.; Jared, N.; Li, J.; Jing, D.; et al. Tuning the Structure, Conductivity, and Wettability of Laser-Induced Graphene for Multiplexed Open Microfluidic Environmental Biosensing and Energy Storage Devices. ACS Nano 2022, 16, 15–28. [Google Scholar] [CrossRef]
- Vivaldi, F.M.; Dallinger, A.; Bonini, A.; Poma, N.; Sembranti, L.; Biagini, D.; Salvo, P.; Greco, F.; Di Francesco, F. Three-Dimensional (3D) Laser-Induced Graphene: Structure, Properties, and Application to Chemical Sensing. ACS Appl. Mater. Interfaces 2021, 13, 30245–30260. [Google Scholar] [CrossRef]
- Tiliakos, A.; Ceaus, C.; Iordache, S.M.; Vasile, E.; Stamatin, I. Morphic Transitions of Nanocarbons via Laser Pyrolysis of Polyimide Films. J. Anal. Appl. Pyrolysis 2016, 121, 275–286. [Google Scholar] [CrossRef]
- Fusion Pro Laser Machines. Available online: https://www.epiloglaser.com/assets/downloads/manuals/fusion-manual-web.pdf (accessed on 21 March 2023).
- Laser, E. Fusion Pro Laser Series. Available online: https://www.epiloglaser.com/laser-machines/fusion-pro-laser-series/ (accessed on 7 September 2023).
- Sales, F.C.P.; Ariati, R.M.; Noronha, V.T.; Ribeiro, J.E. Mechanical Characterization of PDMS with Different Mixing Ratios. Procedia Struct. Integr. 2022, 37, 383–388. [Google Scholar] [CrossRef]
- Hosseini, E.S.; Chakraborty, M.; Roe, J.; Petillot, Y.; Dahiya, R.S. Porous Elastomer Based Wide Range Flexible Pressure Sensor for Autonomous Underwater Vehicles. IEEE Sens. J. 2022, 22, 9914–9921. [Google Scholar] [CrossRef]
- Resistivity and Conductivity-Temperature Coefficients Common Materials. Available online: https://www.engineeringtoolbox.com/resistivity-conductivity-d_418.html (accessed on 21 March 2023).
- Dallinger, A.; Steinwender, F.; Gritzner, M.; Greco, F. Different Roles of Surface Chemistry and Roughness of Laser-Induced Graphene: Implications for Tunable Wettability. ACS Appl. Nano Mater. 2023, 6, 16201–16211. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Zhang, T.; Li, Z.H.; Jia, J.W.; Deng, Y.; Xu, P.L.; Shao, Y.; Deng, D.Y.; Hu, B.W. Temperature Characteristic and Compensation Algorithm for a Marine High Accuracy Piezoresistive Pressure Sensor. J. Mar. Eng. Technol. 2020, 19, 207–214. [Google Scholar] [CrossRef]
- Li, Y.; Villada, A.; Lu, S.-H.; Sun, H.; Xiao, J.; Wang, X. Soft, Flexible Pressure Sensors for Pressure Monitoring under Large Hydrostatic Pressure and Harsh Ocean Environments. Soft Matter 2023, 19, 5772–5780. [Google Scholar] [CrossRef]
- Eisape, A.; Rennoll, V.; Van Volkenburg, T.; Xia, Z.; West, J.E.; Kang, S.H. Soft CNT-Polymer Composites for High Pressure Sensors. Sensors 2022, 22, 5268. [Google Scholar] [CrossRef] [PubMed]
- Kaidarova, A.; Alsharif, N.; Oliveira, B.N.M.; Marengo, M.; Geraldi, N.R.; Duarte, C.M.; Kosel, J. Laser-Printed, Flexible Graphene Pressure Sensors. Glob. Chall. 2020, 4, 2000001. [Google Scholar] [CrossRef]
- Kaidarova, A.; Khan, M.A.; Marengo, M.; Swanepoel, L.; Przybysz, A.; Muller, C.; Fahlman, A.; Buttner, U.; Geraldi, N.R.; Wilson, R.P.; et al. Wearable Multifunctional Printed Graphene Sensors. NPJ Flex. Electron. 2019, 3, 15. [Google Scholar] [CrossRef]
- Tetik, H.; Markgraf, E.; Kato, K.; Chan, V.N.; Malakooti, M.H. Highly Conductive Laser-Induced Graphene through the Deposition of Liquid Metal Particles for Flexible Electronics. Flex. Print. Electron. 2023, 8, 035001. [Google Scholar] [CrossRef]
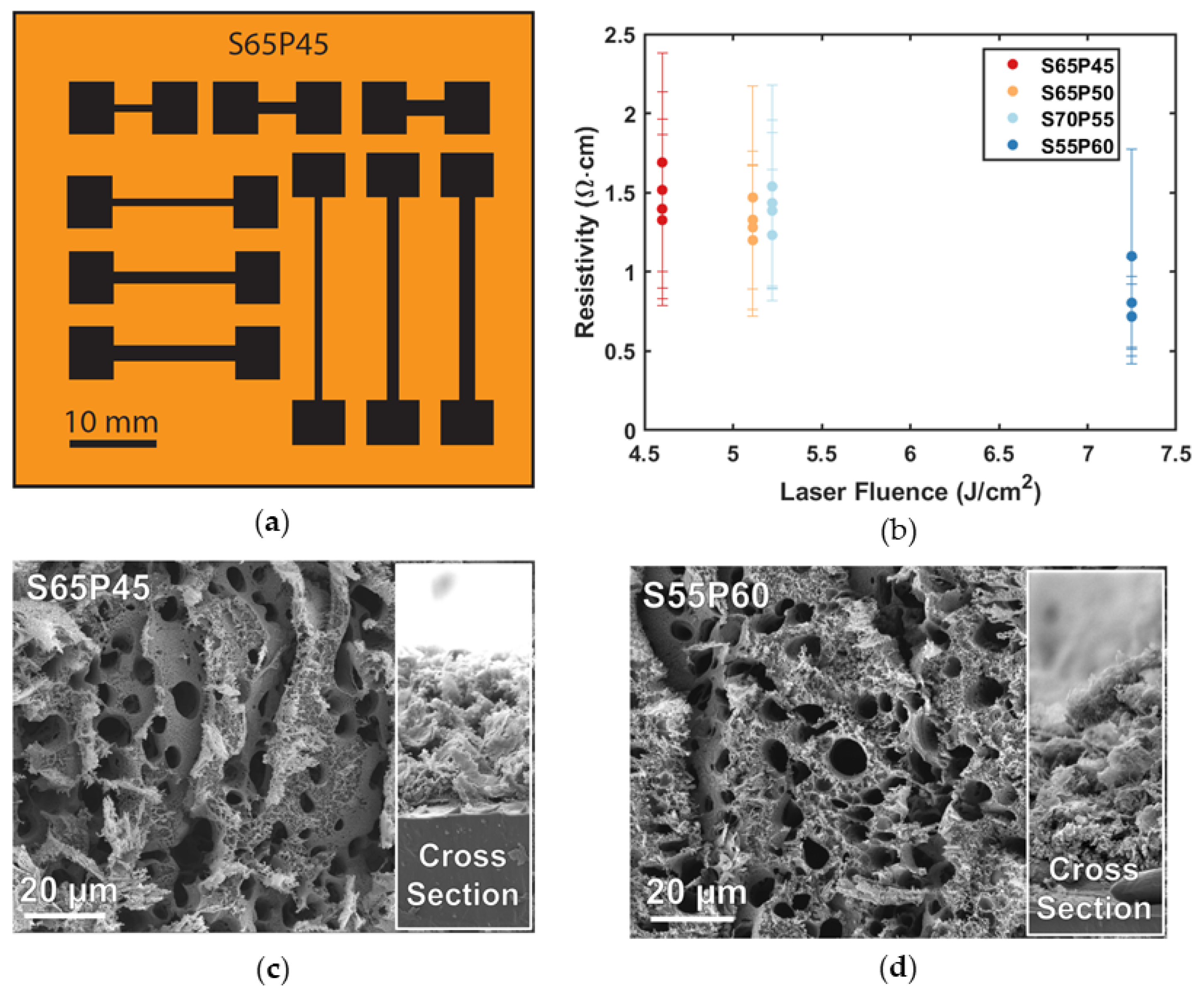


| Name | Power (%) 1 | Speed (%) 2 | Approximate Laser Fluence (J/cm2) |
|---|---|---|---|
| S65P45 | 45 | 65 | 4.6 |
| S65P50 | 50 | 65 | 5.1 |
| S70P55 | 55 | 70 | 5.2 |
| S55P60 | 60 | 55 | 7.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Volkenburg, T.; Ayoub, D.; Alemán Reyes, A.; Xia, Z.; Hamilton, L. Practical Considerations for Laser-Induced Graphene Pressure Sensors Used in Marine Applications. Sensors 2023, 23, 9044. https://doi.org/10.3390/s23229044
Van Volkenburg T, Ayoub D, Alemán Reyes A, Xia Z, Hamilton L. Practical Considerations for Laser-Induced Graphene Pressure Sensors Used in Marine Applications. Sensors. 2023; 23(22):9044. https://doi.org/10.3390/s23229044
Chicago/Turabian StyleVan Volkenburg, Tessa, Daniel Ayoub, Andrea Alemán Reyes, Zhiyong Xia, and Leslie Hamilton. 2023. "Practical Considerations for Laser-Induced Graphene Pressure Sensors Used in Marine Applications" Sensors 23, no. 22: 9044. https://doi.org/10.3390/s23229044
APA StyleVan Volkenburg, T., Ayoub, D., Alemán Reyes, A., Xia, Z., & Hamilton, L. (2023). Practical Considerations for Laser-Induced Graphene Pressure Sensors Used in Marine Applications. Sensors, 23(22), 9044. https://doi.org/10.3390/s23229044





