A Smart System for an Assessment of the Remaining Useful Life of Ball Bearings by Applying Chaos-Based Health Indicators and a Self-Selective Regression Model
Abstract
1. Introduction
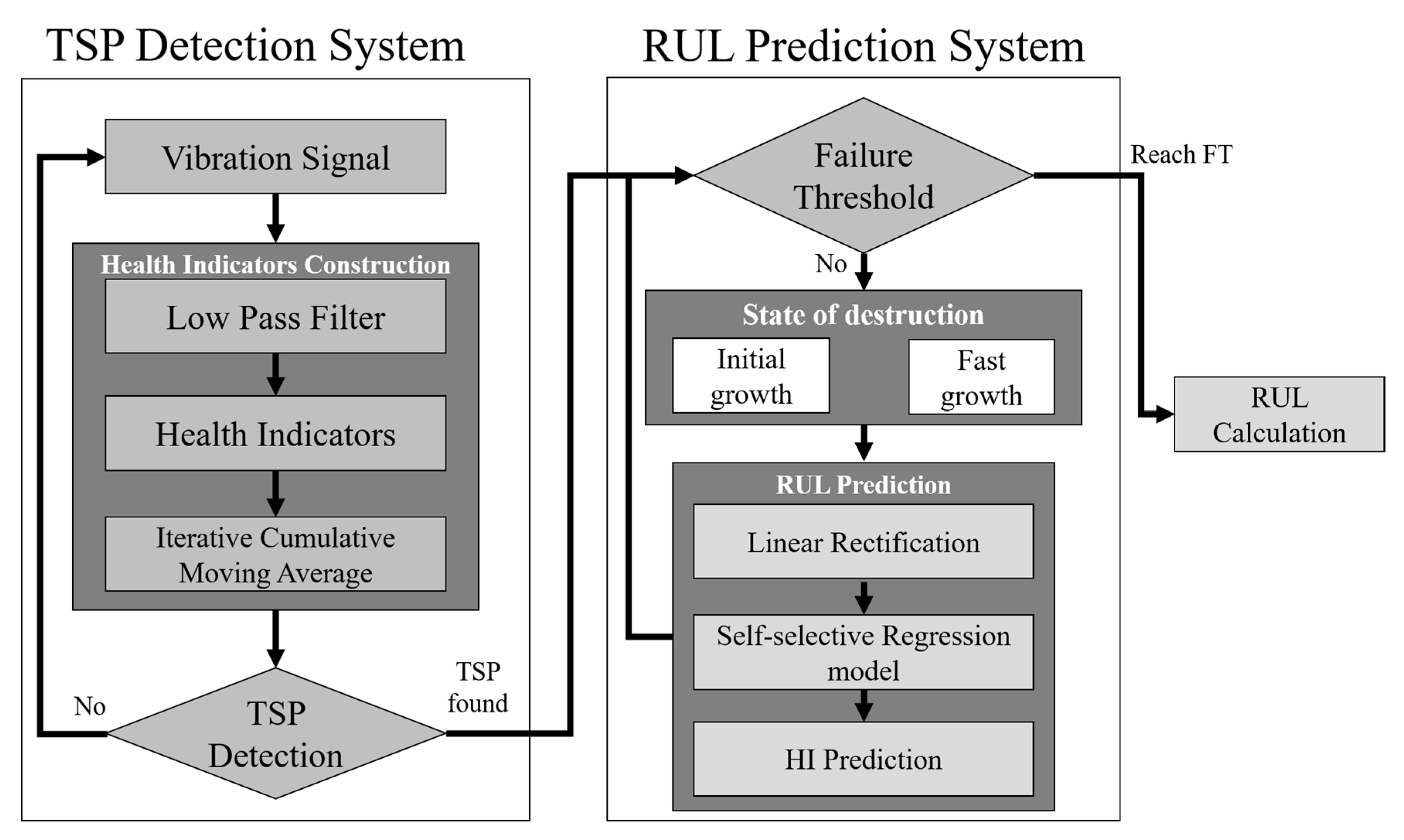
2. Materials and Methods
2.1. Data Experiment Platform
2.1.1. IMS Database
2.1.2. The PRONOSTIA (Also Called FEMTO-ST) Bearing Dataset
2.2. Construction of Health Indicators
2.2.1. Low-Pass Filter
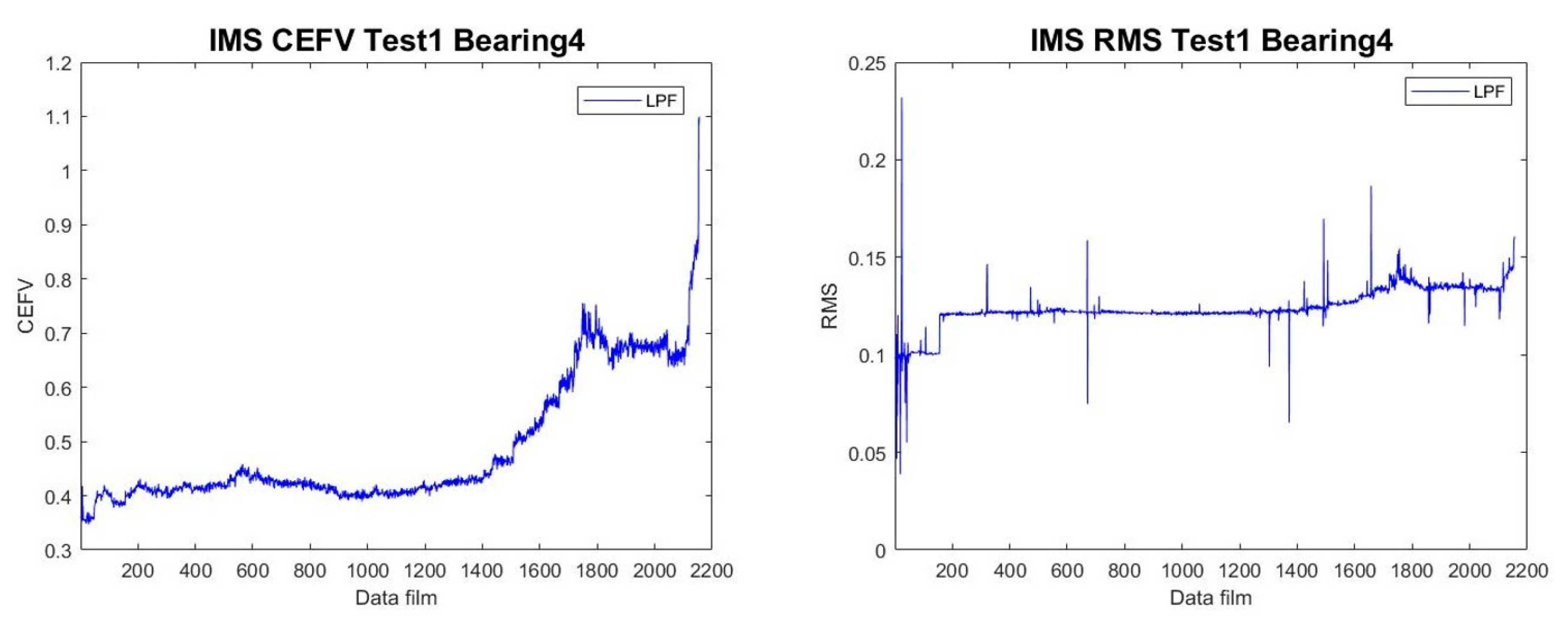
2.2.2. Chaotic Euclidean Feature Values
2.2.3. Iterative Cumulative Moving Average
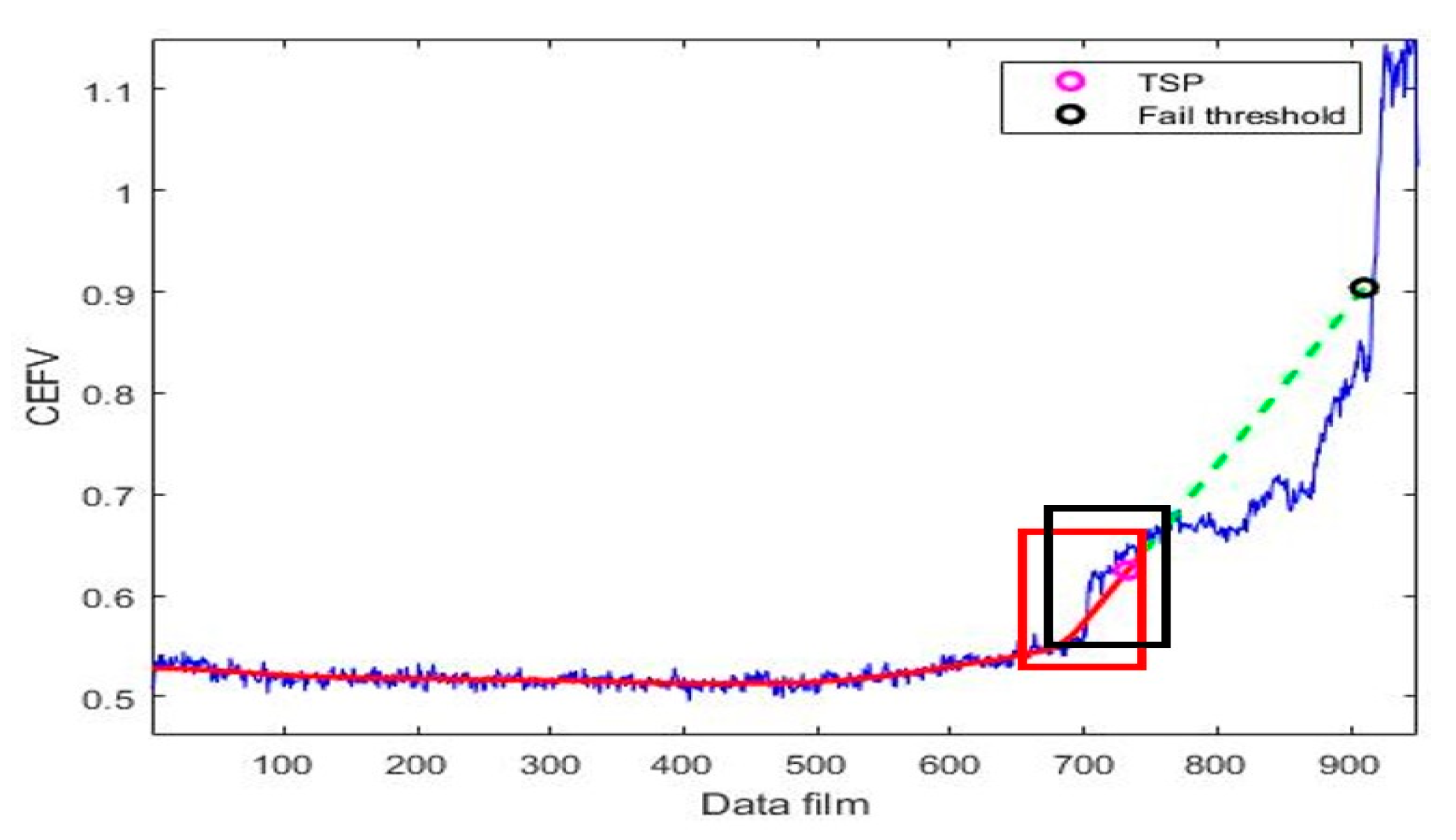
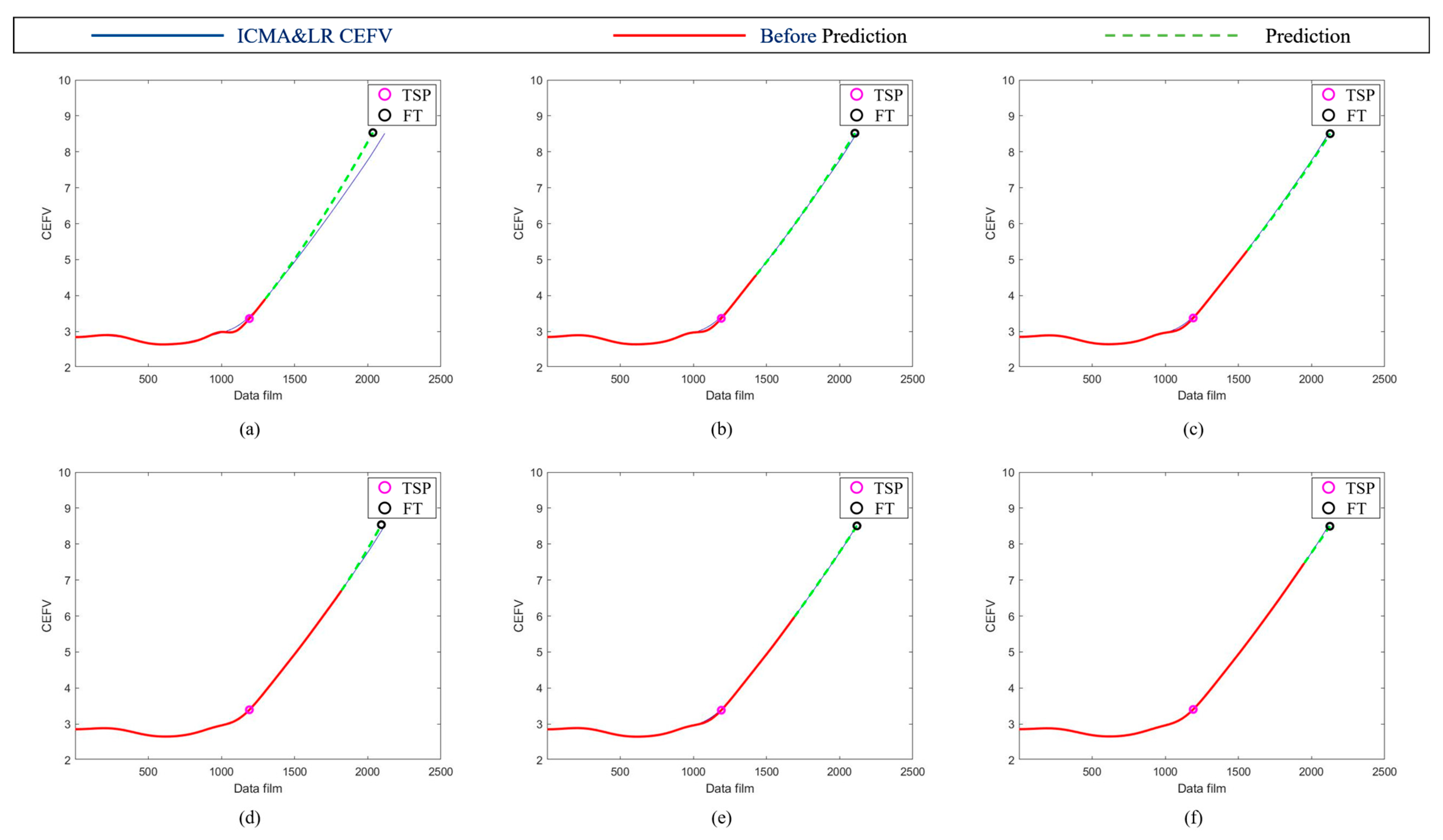
2.3. Time-to-Start Prediction
2.3.1. Euclidean Norm
2.3.2. Gradient
2.4. Failure Threshold
2.5. RUL Prediction
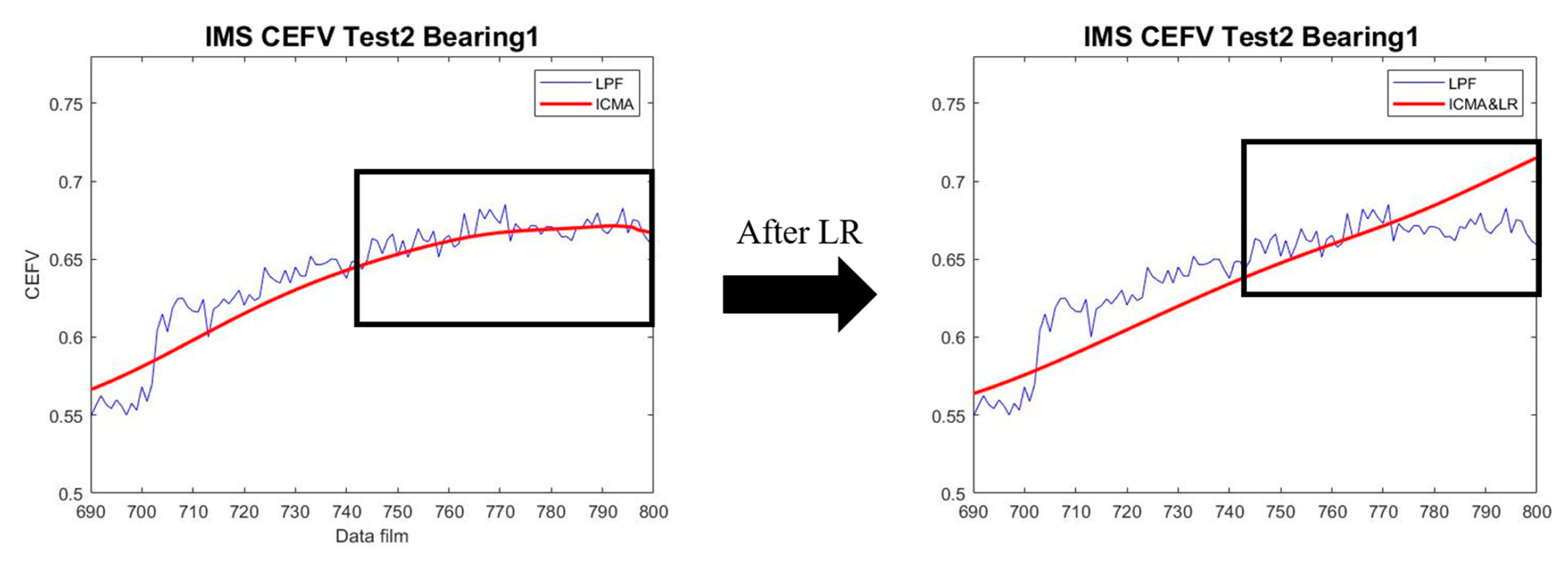
2.5.1. Linear Rectification
2.5.2. Self-Selective Regression Model
3. Results and Discussion
3.1. Performance Evolution
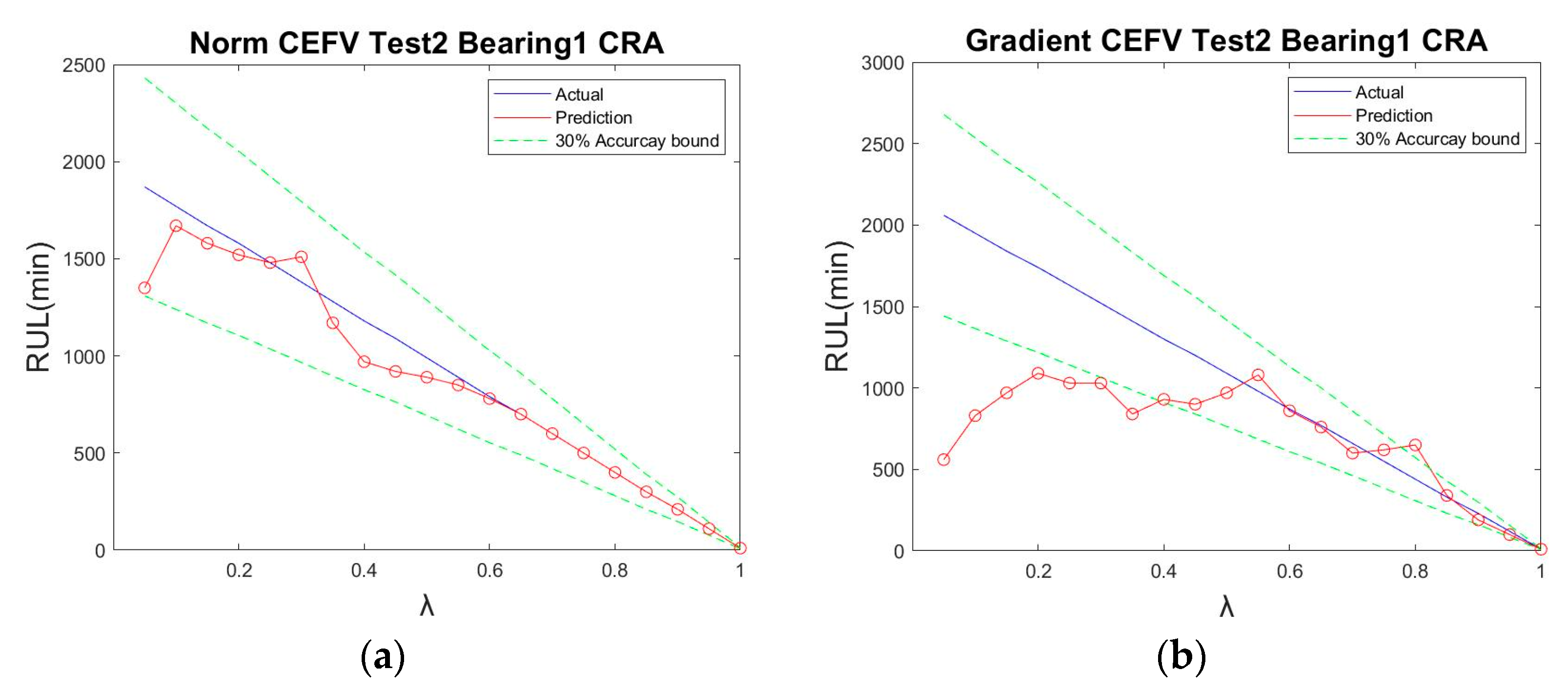
3.2. IMS Prediction Results
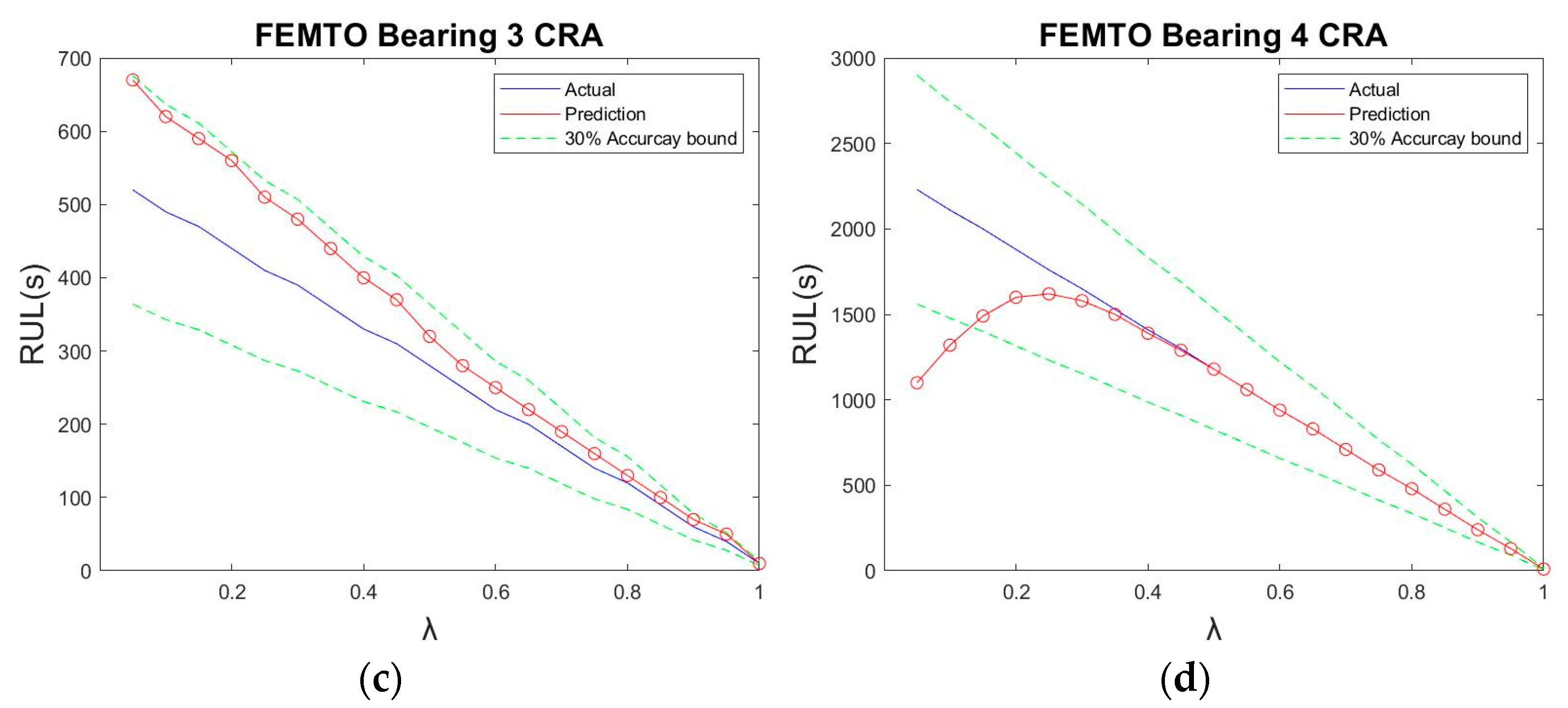
3.3. FEMTO-ST Prediction Result
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, N.H.; An, D.; Choi, J.H. Prognostics and Health Management of Engineering Systems; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Zhang, J.L. A review on prognostics and health monitoring of Li-ion battery. J. Power Sources 2011, 196, 6007–6014. [Google Scholar] [CrossRef]
- Dong, W.; Tsui, K.; Miao, Q. Prognostics and health management: A review of vibration based bearing and gear health indicators. IEEE Access 2017, 6, 665–676. [Google Scholar]
- Williams, T.; Ribadeneira, X.; Billington, S.; Kurfess, T. Rolling element bearing diagnostics in run-to-failure lifetime testing. Mech. Syst. Signal Process. 2001, 15, 979–993. [Google Scholar] [CrossRef]
- Antoni, J. The spectral kurtosis: A useful tool for characterising non-stationary signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X. Approximate entropy as a diagnostic tool for machine health monitoring. Mech. Syst. Signal Process. 2007, 21, 824–839. [Google Scholar] [CrossRef]
- Jin, X.; Wang, Y.; Chow, T.W.; Sun, Y. MD-based approaches for system health monitoring: A review. IET Sci. Meas. Technol. 2017, 11, 371–379. [Google Scholar] [CrossRef]
- Gebraeel, N.Z.; Lawley, M.A.; Li, R.; Ryan, J.K. Residual-life distributions from component degradation signals: A Bayesian approach. IiE Trans. 2005, 37, 543–557. [Google Scholar] [CrossRef]
- Li, N.; Lei, Y.; Lin, J.; Ding, S.X. An improved exponential model for predicting remaining useful life of rolling element bearings. IEEE Trans. Ind. Electron. 2015, 62, 7762–7773. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Gontarz, S.; Lin, J.; Radkowski, S.; Dybala, J. A model-based method for remaining useful life prediction of machinery. IEEE Trans. Reliab. 2016, 65, 1314–1326. [Google Scholar] [CrossRef]
- Loutas, T.H.; Roulias, D.; Georgoulas, G. Remaining Useful Life Estimation in Rolling Bearings Utilizing Data-Driven Probabilistic E-Support Vectors Regression. IEEE Trans. Reliab. 2013, 62, 821–832. [Google Scholar] [CrossRef]
- Tran, V.T.; Pham, H.T.; Yang, B.S.; Nguyen, T.T. Machine performance degradation assessment and remaining useful life prediction using proportional hazard model and support vector machine. Mech. Syst. Signal Process. 2012, 32, 320–330. [Google Scholar] [CrossRef]
- Ren, L.; Cui, J.; Sun, Y.; Cheng, X. Multi-bearing remaining useful life collaborative prediction: A deep learning approach. J. Manuf. Syst. 2017, 43, 248–256. [Google Scholar] [CrossRef]
- Jiang, J.R.; Lee, J.E.; Zeng, Y.M. Time series multiple channel convolutional neural network with attention-based long short-term memory for predicting bearing remaining useful life. Sensors 2020, 20, 166. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; Li, N.; Jia, F.; Lei, Y.; Lin, J. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- Caesarendra, W.; Widodo, A.; Thom, P.H.; Yang, B.S.; Setiawan, J.D. Combined probability approach and indirect data-driven method for bearing degradation prognostics. IEEE Trans. Reliab. 2011, 60, 14–20. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, Y.; Zi, Y.; Jin, X.; Tsui, K.L. A two-stage data-driven-based prognostic approach for bearing degradation problem. IEEE Trans. Ind. Inform. 2016, 12, 924–932. [Google Scholar] [CrossRef]
- Ahmad, W.; Khan, S.A.; Kim, J.M. A hybrid prognostics technique for rolling element bearings using adaptive predictive models. IEEE Trans. Ind. Electron. 2017, 65, 1577–1584. [Google Scholar] [CrossRef]
- Wang, F.K.; Mamo, T. Hybrid approach for remaining useful life prediction of ball bearings. Qual. Reliab. Eng. Int. 2019, 35, 2494–2505. [Google Scholar] [CrossRef]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. Comput. Lang. 2014, arXiv:1406.1078. Available online: https://arxiv.org/abs/1406.1078 (accessed on 3 September 2014).
- Zhao, R.; Wang, D.; Yan, R.; Mao, K.; Shen, F.; Wang, J. Machine health monitoring using local feature-based gated recurrent unit networks. IEEE Trans. Ind. Electron. 2018, 65, 1539–1548. [Google Scholar] [CrossRef]
- Caesarendra, W.; Widodo, A.; Yang, B. Application of relevance vector machine and logistic regression for machine degradation assessment. Mech. Syst. Signal Process. 2010, 24, 1161–1171. [Google Scholar] [CrossRef]
- Feng, K.; Ji, J.; Ni, Q. A novel gear fatigue monitoring indicator and its application to remaining useful life prediction for spur gear in intelligent manufacturing systems. Int. J. Fatigue 2023, 168, 107459. [Google Scholar] [CrossRef]
- Li, S.Y.; Gu, K.R. Smart fault-detection machine for ball-bearing system with chaotic mapping strategy. Sensors 2019, 19, 2178. [Google Scholar] [CrossRef] [PubMed]
- Li, S.Y.; Gu, K.R.; Chen, C.S. A novel smart fault-diagnosis method with procedures of feature productions and extractions. In Proceedings of the 2019 IEEE 4th International Conference on Advanced Robotics and Mechatronics (ICARM), Toyonaka, Japan, 3–5 July 2019; pp. 268–273. [Google Scholar]
- Chen, C.S.; Ke, Y.C.; Tam, L.M.; Li, S.Y. A Smart Real-Time Monitoring System for Fault-Diagnosis of Ball-Bearing. In Proceedings of the 2019 IEEE International Conference on Consumer Electronics-Taiwan (ICCE-TW), Yilan, Taiwan, 20–22 May 2019; pp. 1–2. [Google Scholar]
- Saxena, A.; Celaya, J.; Balaban, E.; Goebel, K.; Saha, B.; Saha, S.; Schwabacher, M. Metrics for evaluating performance of prognostic techniques. In Proceedings of the 2008 International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008; pp. 1–17. [Google Scholar]
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Chebel-Morello, B.; Zerhouni, N.; Varnier, C. PRONOSTIA: An experimental platform for bearings accelerated degradation tests. In Proceedings of theIEEE International Conference on Prognostics and Health Management, PHM’12, Denver, CO, USA, 18–21 June 2012; pp. 1–8. [Google Scholar]
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics. J. Sound Vib. 2006, 289, 1066–1090. [Google Scholar] [CrossRef]
- Qiu, H.; Lee, J.; Yu, G.; Lin, J. Rexnord Technical Services, “Bearing Data Set”, IMS, University of Cincinnati, NASA Ames Prognostics Data Repository; NASA Ames: Moffett Field, CA, USA, 2007. Available online: http://ti.arc.nasa.gov/project/prognosticdata-repository (accessed on 4 January 2023).
- IEEE PHM 2012 Prognostic Challenge. Outline, Experiments, Scoring of Results, Winners. Available online: http://www.femto-st.fr/f/d/IEEEPHM2012-Challenge-Details.pdf (accessed on 4 January 2023).
- Li, S.Y.; Gu, K.R. A smart fault-detection approach with feature production and extraction processes. Inf. Sci. 2020, 513, 553–564. [Google Scholar] [CrossRef]
- Chen, H.K.; Lee, C.I. Anti-control of chaos in rigid body motion. Chaos Solitons Fractals 2004, 21, 957–965. [Google Scholar] [CrossRef]
- Qian, Y.; Yan, R.; Gao, R.X. A multi-time scale approach to remaining useful life prediction in rolling bearing. Mech. Syst. Signal Process. 2017, 83, 549–567. [Google Scholar] [CrossRef]
- Wen, J.; Gao, H.; Zhang, J. Bearing remaining useful life prediction based on a nonlinear wiener process model. Shock. Vib. 2018, 2018, 4068431. [Google Scholar] [CrossRef]









| System Information | Conditions | ||
|---|---|---|---|
| Test | 1 | 2 | 3 |
| Speed | 2000 rpm | ||
| Load | 6000 lb | ||
| Sampling rate | 20 kHz | ||
| Recording interval | 1 s/every 10 min | ||
| Channels | 8 | 4 | 4 |
| File | 2156 | 984 | 6324 |
| System Information | Conditions | ||
|---|---|---|---|
| Test | 1 | 2 | 3 |
| Speed | 1800 rpm | 1650 rpm | 1500 rpm |
| Load | 4000 N | 4200 N | 5000 N |
| Sampling rate | 25.6 kHz | ||
| Recording interval | 0.1 s/every 10 s | ||
| Training data | Bearing 1_1 Bearing 1_2 | Bearing 2_1 Bearing 2_2 | Bearing 3_1 Bearing 3_2 |
| Test data | Bearing 1_3 Bearing 1_4 Bearing 1_5 Bearing 1_6 Bearing 1_7 | Bearing 2_3 Bearing 2_4 Bearing 2_5 Bearing 2_6 Bearing 2_7 | Bearing 3_3 |
| Parameter | Conditions | |
|---|---|---|
| HI | CEFV | |
| Tracking values | Norm | Gradient |
| Window box | 60 | 60 |
| ICMA | 7 | 20 |
| TSP | 0.00055 | |
| Fast growth | 0.00077 | |
| Failure threshold | 0.00095 | |
| Parameter | Condition | |
|---|---|---|
| HI | CEFV | |
| Track value | Norm | Gradient |
| Test 2 Bearing 1 CRA | 0.9450 | 0.7459 |
| Test 1 Bearing 4 CRA | 0.8355 | 0.8206 |
| Test 3 Bearing 3 CRA | 0.9230 | 0.5507 |
| CRA AVG | 0.9012 | 0.7057 |
| Parameter | Conditions |
|---|---|
| HI | CEFV |
| Tracking values | Norm |
| Window box | 60 |
| ICMA | 11 |
| TSP | |
| Fast growth | |
| Failure threshold |
| Gebraeel Method | Linear Method | NWP Method | Our Method | |
|---|---|---|---|---|
| Bearing 1 | 0.6230 | 0.5890 | 0.6960 | 0.9259 |
| Bearing 2 | 0.5411 | 0.7771 | 0.8429 | 0.8361 |
| Bearing 3 | 0.6961 | 0.6402 | 0.7808 | 0.8222 |
| Bearing 4 | 0.6876 | 0.7573 | 0.7647 | 0.9276 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.-Y.; Li, H.-A.; Tam, L.-M.; Chen, C.-S. A Smart System for an Assessment of the Remaining Useful Life of Ball Bearings by Applying Chaos-Based Health Indicators and a Self-Selective Regression Model. Sensors 2023, 23, 1267. https://doi.org/10.3390/s23031267
Li S-Y, Li H-A, Tam L-M, Chen C-S. A Smart System for an Assessment of the Remaining Useful Life of Ball Bearings by Applying Chaos-Based Health Indicators and a Self-Selective Regression Model. Sensors. 2023; 23(3):1267. https://doi.org/10.3390/s23031267
Chicago/Turabian StyleLi, Shih-Yu, Hao-An Li, Lap-Mou Tam, and Chin-Sheng Chen. 2023. "A Smart System for an Assessment of the Remaining Useful Life of Ball Bearings by Applying Chaos-Based Health Indicators and a Self-Selective Regression Model" Sensors 23, no. 3: 1267. https://doi.org/10.3390/s23031267
APA StyleLi, S.-Y., Li, H.-A., Tam, L.-M., & Chen, C.-S. (2023). A Smart System for an Assessment of the Remaining Useful Life of Ball Bearings by Applying Chaos-Based Health Indicators and a Self-Selective Regression Model. Sensors, 23(3), 1267. https://doi.org/10.3390/s23031267









