Temperature and Humidity Stability of Fibre Optic Sensor Cables for High Resolution Measurements
Abstract
1. Introduction
2. Experimental Programme and Measurement
2.1. FOS Cables
2.2. Calibration Test Specification
2.3. FOS Data Capture and Analysis
3. Evaluation of the Cable Calibration Factors
3.1. Calibration Factor for Strain Exposure
3.2. Calibration Factor for Temperature Exposure
3.3. Calibration Factor for Humidity Exposure
4. Frequency Drifts and Fluctuations under Sustained Conditions
4.1. Frequency Drifts and Fluctuations
4.2. Frequency Drift with Time and Temperature
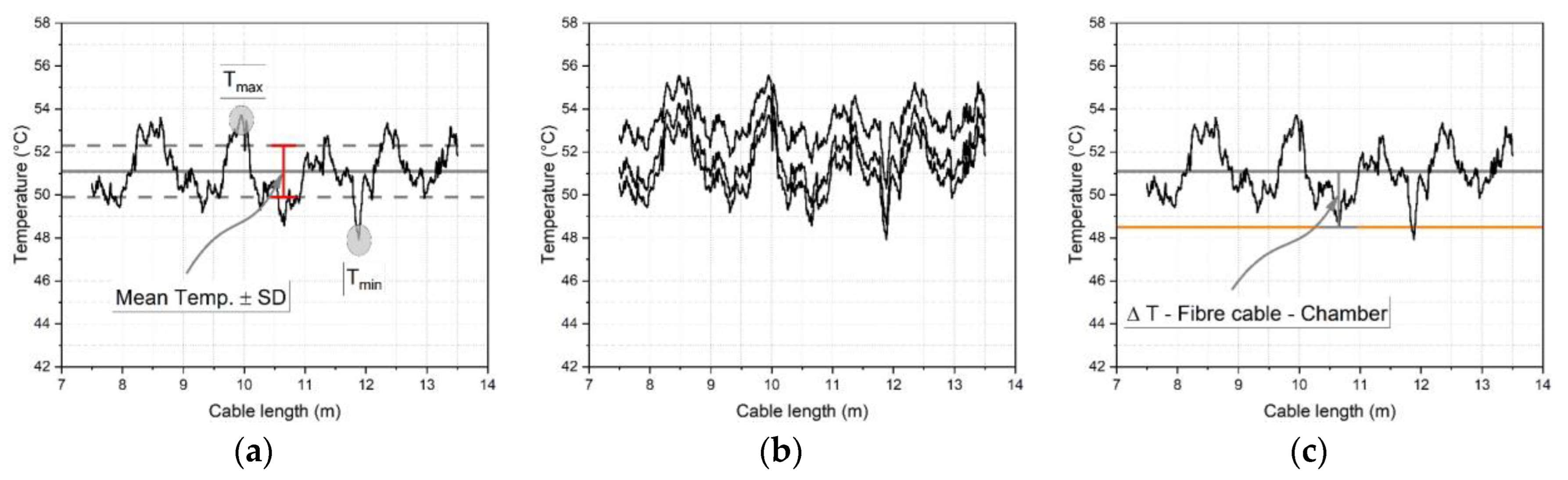
4.3. Frequency Fluctuations along the Cable Length
4.4. Chamber Humidity and Temperature Measurement
5. Time- and Length Dependent Temperature and Humidity Stability
5.1. Time Dependent Temperature and Humidity Drift
5.2. Length Dependent Temperature and Humidity Fluctuations
5.3. Accuracy of FOS Measurements
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. DFOS Temperature or Humidity Exposure Frequency Versus Time Plots
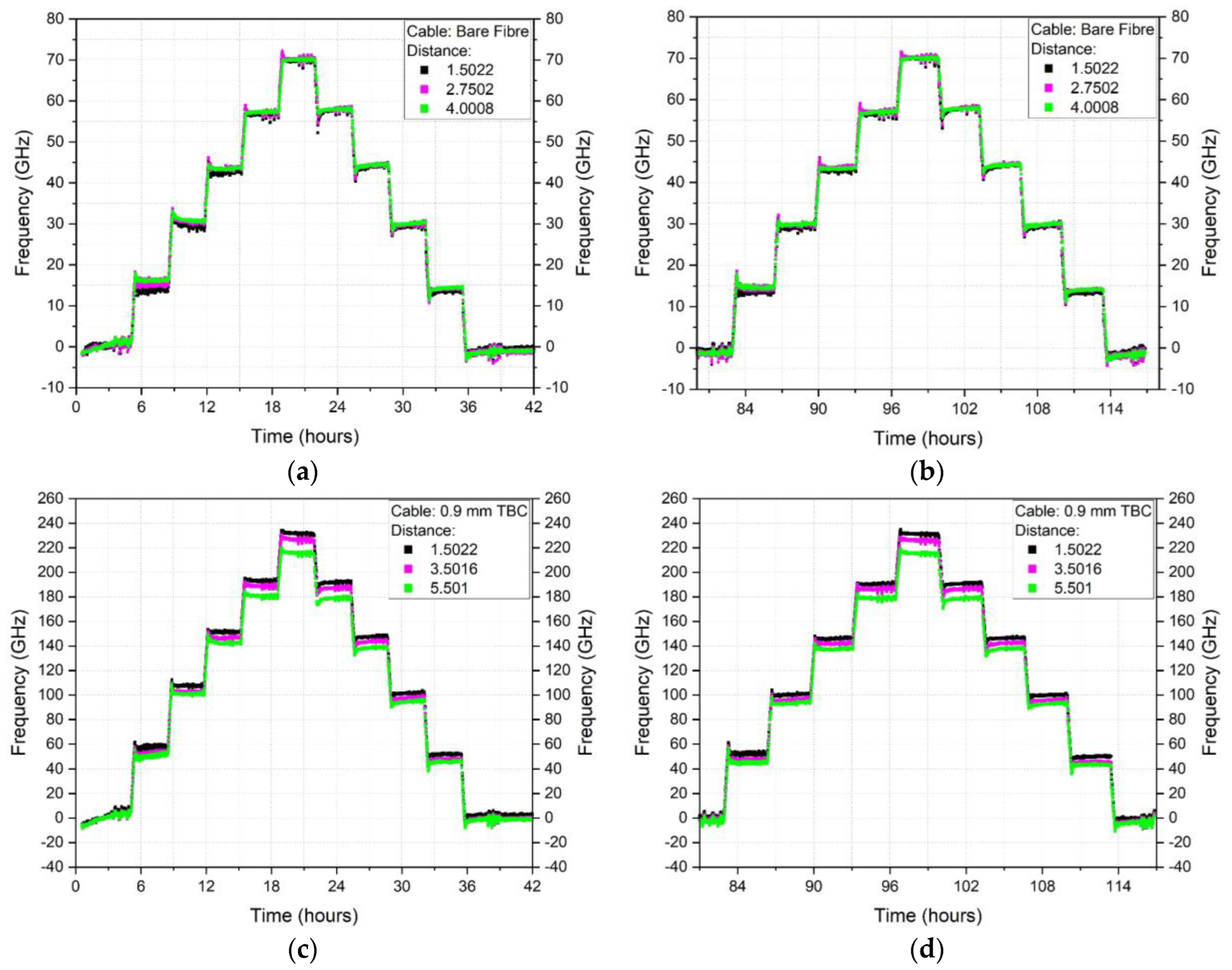

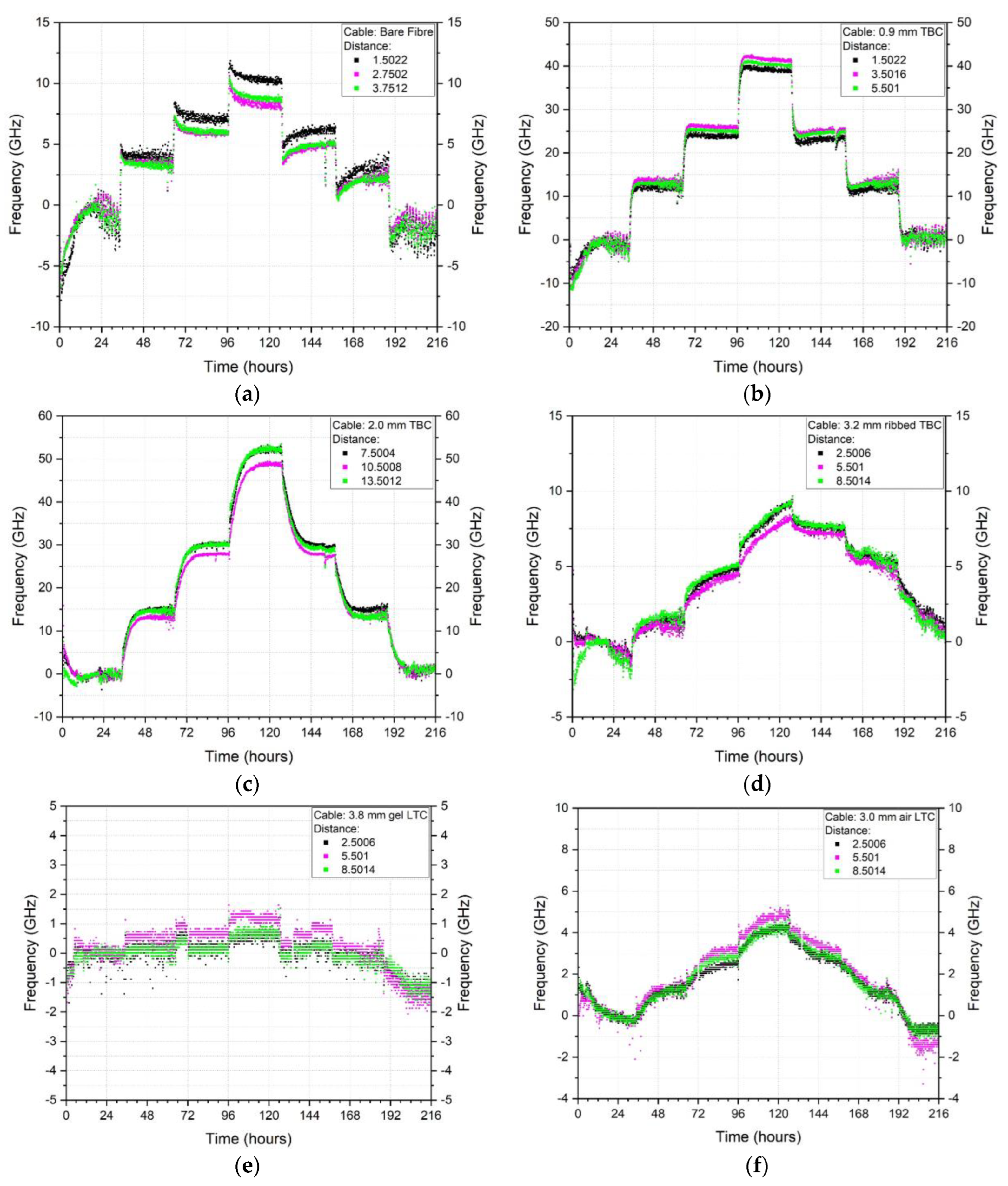
Appendix B. Longitudinal DFOS Temperature and Humidity Frequency Variations



References
- Monsberger, C.M.; Lienhart, W. Distributed fiber optic shape sensing along shotcrete tunnel linings: Methodology, field applications, and monitoring results. J. Civ. Struct. Health Monit. 2021, 11, 337–350. [Google Scholar] [CrossRef]
- Woschitz, H.; Klug, F.; Lienhart, W. Design and Calibration of a Fiber-Optic Monitoring System for the Determination of Segment Joint Movements Inside a Hydro Power Dam. J. Light. Technol. 2015, 33, 2652–2657. [Google Scholar] [CrossRef]
- Mohamad, H.; Soga, K.; Amatya, B. Thermal strain sensing of concrete piles using brillouin optical time domain reflectometry. Geotech. Test. J. 2014, 37, 333–346. [Google Scholar] [CrossRef]
- Pelecanos, L.; Soga, K.; Chunge, M.P.M.; Ouyang, Y.; Kwan, V.; Kechavarzi, C.; Nicholson, D. Distributed fibre-optic monitoring of an Osterberg-cell pile test in London. Géotechnique Lett. 2017, 7, 152–160. [Google Scholar] [CrossRef]
- Leung, C.K.Y.; Wan, K.T.; Inaudi, D.; Bao, X.; Habel, W.; Zhou, Z.; Ou, J.; Ghandehari, M.; Wu, H.C. Review: Optical fiber sensors for civil engineering applications. Mater. Struct./Mater. Constr. 2015, 48, 871–906. [Google Scholar] [CrossRef]
- Min, R.; Liu, Z.; Pereira, L.; Yang, C.; Sui, Q.; Marques, C. Optical fiber sensing for marine environment and marine structural health monitoring: A review. Opt. Laser Technol. 2021, 140, 107082. [Google Scholar] [CrossRef]
- Bado, M.F.; Casas, J.R. A Review of Recent Distributed Optical Fiber Sensors Applications for Civil Engineering Structural Health Monitoring. Sensors 2021, 21, 1818. [Google Scholar] [CrossRef]
- Barrias, A.; Casas, J.R.; Villalba, S. A review of distributed optical fiber sensors for civil engineering applications. Sensors 2016, 16, 748. [Google Scholar] [CrossRef]
- Kechavarzi, C.; Soga, K.; de Battista, N.; Pelecanos, L.; Elshafie, M.Z.E.B.; Mair, R.J. Distributed Fibre Optic Strain Sensing for Monitoring Civil Infrastructure; ICE Publishing: Johor, Malaysia, 2016. [Google Scholar] [CrossRef]
- Fenta, M.C.; Potter, D.K.; Szanyi, J. Fibre Optic Methods of Prospecting: A Comprehensive and Modern Branch of Geophysics; Springer: The Netherlands, 2021. [Google Scholar] [CrossRef]
- Kuznetsov, A.G.; Babin, S.A.; Shelemba, I.S. Fibreoptic distributed temperature sensor with spectral filtration by directional fibre couplers. Quantum Electron. 2009, 39, 1078–1081. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, H.; Coulibaly, A.A.S.; DeJong, M. Fiber optic sensing of concrete cracking and rebar deformation using several types of cable. Struct. Control Health Monit. 2021, 28, e2664. [Google Scholar] [CrossRef]
- Her, S.C.; Huang, C.Y. Effect of coating on the strain transfer of optical fiber sensors. Sensors 2011, 11, 6926–6941. [Google Scholar] [CrossRef] [PubMed]
- Sien, R.; Sien, S.; Zych, M.; Bednarski, Ł.; Howiacki, T. Strain and crack analysis within concrete members using distributed fibre optic sensors. Struct. Health Monit. 2019, 18, 1510–1526. [Google Scholar] [CrossRef]
- Ge, Y.; Elshafie, M.Z.E.B.; Dirar, S.; Middleton, C.R. The response of embedded strain sensors in concrete beams subjected to thermal loading. Constr. Build. Mater. 2014, 70, 279–290. [Google Scholar] [CrossRef]
- Roman, M.; Balogun, D.; Zhuang, Y.; Gerald, R.E.; Bartlett, L.; O’Malley, R.J.; Huang, J. A spatially distributed fiber-optic temperature sensor for applications in the steel industry. Sensors 2020, 20, 3900. [Google Scholar] [CrossRef]
- Alj, I.; Quiertant, M.; Khadour, A.; Grando, Q.; Terrade, B.; Renaud, J.C.; Benzarti, K. Experimental and numerical investigation on the strain response of distributed optical fiber sensors bonded to concrete: Influence of the adhesive stiffness on crack monitoring performance. Sensors 2020, 20, 5144. [Google Scholar] [CrossRef]
- Barrias, A.; Casas, J.R.; Villalba, S. Fatigue performance of distributed optical fiber sensors in reinforced concrete elements. Constr. Build. Mater. 2019, 218, 214–223. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, H.; Cheng, J.; DeJong, M.J. A mechanical model to interpret distributed fiber optic strain measurement at displacement discontinuities. Struct. Health Monit. 2020, 20, 2584–2603. [Google Scholar] [CrossRef]
- Bassil, A.; Chapeleau, X.; Leduc, D.; Abraham, O. Concrete crack monitoring using a novel strain transfer model for distributed fiber optics sensors. Sensors 2020, 20, 2220. [Google Scholar] [CrossRef]
- Monsberger, C.M. Distributed Fiber Optic Shape Sensing of Concrete Structures. Sensors 2021, 21, 6098. [Google Scholar] [CrossRef]
- Bielak, J. Application of fiber optic measurement in textile-reinforced concrete testing. Struct. Concr. 2022, 23, 2600–2614. [Google Scholar] [CrossRef]
- Davis, M.; Hoult, N.A.; Scott, A. Distributed strain sensing to determine the impact of corrosion on bond performance in reinforced concrete. Constr. Build. Mater. 2016, 114, 481–491. [Google Scholar] [CrossRef]
- Bado, M.F.; Casas, J.R.; Dey, A.; Berrocal, C.G. Distributed optical fiber sensing bonding techniques performance for embedment inside reinforced concrete structures. Sensors 2020, 20, 5788. [Google Scholar] [CrossRef]
- Wood, T.W.; Blake, B.; Blue, T.E.; Petrie, C.M.; Hawn, D. Evaluation of the performance of distributed temperature measurements with single-mode fiber using rayleigh backscatter up to 1000 °C. IEEE Sens. J. 2014, 14, 124–128. [Google Scholar] [CrossRef]
- Bado, M.F.; Casas, J.R.; Barrias, A. Performance of rayleigh-based distributed optical fiber sensors bonded to reinforcing bars in bending. Sensors 2018, 18, 3125. [Google Scholar] [CrossRef]


















| Cable Type | Outer Dia-Meter (mm) | Coating or Sheath Material | Weight (kg/km) | Min Bend Radius (mm) | Total Cable Length (m) | Cable Length in Chamber (m) |
|---|---|---|---|---|---|---|
| Bare fibre | 0.25 | 250 μm acrylate | n.a | n.a | 4.50 | 1.1–4.5 |
| 0.9 mm TBC 1 | 0.9 | Hytrel (TPC-ET thermoplastic elastomer) | 0.9 | 20 | 5.25 | 1.0–5.25 |
| 2.0 mm TBC 1 | 2.0 | Hytrel polyurethane | 4.1 | 30 | 18.50 | 2.1–18.5 |
| 3.2 mm ribbed TBC 1 | 3.2 | stainless steel tube/ structured polyamide | 10.5 | 48 | 9.70 | 1.3–9.7 |
| 3.0 mm air filled LTC 2 | 3.0 | air filled steel conduit LSZH 3 thermoplastic | 30 | 30 | 9.70 | 1.1–9.7 |
| 3.8 mm gel filled LTC 2 | 3.8 | gel filled stainless steel tube/polyamide | 26 | 57 | 9.70 | 1.7–9.7 |
| Datapoints Used for Each Sustained Step | Analysis Cable Length (mm) | Spacing between Sampled Data Points for Analysis (mm) | # of Length Data Points | Duration, ttotal, of Each Step (min) | Increment, Δt, within Each Time Step (min) | Analysed Time from-to (min) | # of Time Data Points |
|---|---|---|---|---|---|---|---|
| Strain | 900 * 1500 | 150 * 250 | 6 * 6 | 2 * 2 | 1/60 * 1/60 | 0–2 * 0–2 | 12 * 12 |
| Temperature | 3000 | 250 | 13 | 180 | 10 | 15–165 | 16 |
| Humidity | 3000 | 250 | 13 | 1800 | 10 | 50–1750 | 171 |
| Strain Calibration Factor | Difference [%] | Average Strain Calibration Factor | ||
|---|---|---|---|---|
| Fibre Type | Increasing | Decreasing | Increasing-Decreasing Cycle | Increasing-Decreasing Cycle |
| Bare fibre | 0.150 ± 9.04 × 10−5 | 0.149 ± 6.48 × 10−5 | 0.7 | 0.150 |
| 0.9 mm TBC | 0.148 ± 5.04 × 10−5 | 0.152 ± 7.03 × 10−5 | 2.7 | 0.150 |
| 2.0 mm TBC | 0.153 ± 5.27 × 10−5 | 0.154 ± 2.78 × 10−5 | 0.7 | 0.154 |
| 3.2 ribbed TBC | 0.148 ± 1.10 × 10−4 | 0.146 ± 2.21 × 10−4 | 1.4 | 0.147 |
| 3.8 gel LTC | 0.022 ± 1.22 × 10−4 | 0.016 ± 2.86 × 10−4 | 27.3 | 0.019 |
| 3.0 air LTC | 0.079 ± 1.36 × 10−4 | 0.085 ± 6.05 × 10−4 | 7.6 | 0.082 |
| Fibre Type | Cycle | Temperature Calibration Factor (GHz/°C) | Difference Heating-Cooling Coefficient | Average Temperature Calibration Factor Increasing- Decreasing Cycle (GHz/°C) | |
|---|---|---|---|---|---|
| Heating Coefficient | Cooling Coefficient | ||||
| Bare Fibre | 1 | 1.382 ± 0.002 | 1.441 ± 0.002 | 4.27% | |
| 2 | 1.426 ± 0.002 | 1.434 ± 0.002 | 0.56% | ||
| 3 | 1.442 ± 0.002 | 1.444 ± 0.002 | 0.14% | 1.443 | |
| 0.9 mm TBC | 1 | 4.509 ± 0.011 | 4.605 ± 0.007 | 2.13% | |
| 2 | 4.608 ± 0.009 | 4.633 ± 0.007 | 0.54% | ||
| 3 | 4.645 ± 0.008 | 4.641 ± 0.007 | 0.09% | 4.643 | |
| 2.0 mm TBC | 1 | 5.697 ±0.021 | 5.836 ± 0.011 | 2.44% | |
| 2 | 5.764 ±0.011 | 5.828 ± 0.011 | 1.11% | ||
| 3 | 5.795 ±0.011 | 5.972 ± 0.014 | 3.05% | 5.884 | |
| 3.2 mm ribbed TBC | 1 | 4.580 ± 0.009 | 4.792 ± 0.007 | 4.63% | |
| 2 | 4.773 ± 0.007 | 4.776 ± 0.007 | 0.06% | ||
| 3 | 4.793 ± 0.007 | 4.802 ± 0.007 | 0.19% | 4.798 | |
| 3.8 mm gel LTC | 1 | 1.596 ± 0.005 | 1.679 ± 0.005 | 5.20% | |
| 2 | 1.676 ± 0.003 | 1.674 ± 0.004 | 0.12% | ||
| 3 | 1.674 ± 0.004 | 1.662 ± 0.004 | 0.72% | 1.668 | |
| 3.0 mm air LTC | 1 | 2.520 ± 0.016 | 2.600 ± 0.012 | 3.17% | |
| 2 | 2.560 ± 0.011 | 2.608 ± 0.012 | 1.88% | ||
| 3 | 2.592 ± 0.012 | 2.585 ± 0.012 | 0.27% | 2.589 | |
| Moisture Calibration Factor (GHz/% rel. H) | Difference [%] | Average Moisture Calibration Factor (GHz/% rel. H) | ||
|---|---|---|---|---|
| Fibre type | Increasing | Decreasing | Increasing-Decreasing Cycle | Increasing-Decreasing Cycle |
| Bare fibre | 0.163 ± 5.02 × 10−4 | 0.172 ± 3.88 × 10−4 | 5.5 | 0.168 |
| 0.9 mm TBC | 0.687 ± 8.92 × 10−4 | 0.643 ± 9.22 × 10−4 | 6.4 | 0.665 |
| 2.0 mm TBC | 0.792 ± 0.10 × 10−4 | 0.770 ± 0.10 × 10−4 | 2.8 | 0.781 |
| 3.2 ribbed TBC | 0.133 ± 4.49 × 10−4 | 0.104 ± 5.53 × 10−4 | 21.8 | 0.119 |
| 3.8 gel LTC | 0.012 ± 1.18 × 10−4 | 0.025 ± 2.01 × 10−4 | 108.3 | 0.019 |
| 3.0 air LTC | 0.070 ± 3.91 × 10−4 | 0.083 ± 4.25 × 10−4 | 18.6 | 0.077 |
| Datapoints Used for Each Sustained Step | Analysis Length (mm) | Increment, ΔL, along Cable Length (mm) | # of Length Data Points | Duration, ttotal, of Each Step (min) | Increment, Δt, within Each Time Step (min) | Analysis Times from-to (min) | # of Time Data Points |
|---|---|---|---|---|---|---|---|
| Frequency drift with time | |||||||
| Temperature | 2500 * 4000+ 6000 | 1250 2000 3000 | 3 | 180 | 1 | 15–165 | 150 |
| Humidity | 2500 * 4000+ 6000 | 1250 2000 3000 | 3 | 1800 | 1 | 15–1785 | 1770 |
| Frequency fluctuation along length | |||||||
| Temperature | 2500 * 4000+ 6000 | 2.6 2.6 2.6 | 2308 2308 2308 | 180 | 75 | 15–165 | 3 |
| Humidity | 2500 * 4000+ 6000 | 2.6 2.6 2.6 | 2308 2308 2308 | 1800 | 875 | 15–1785 | 3 |
| Cable | Max/Min Humidity Drift over 30 h | Max/Min Peak Humidity along Cable | Max. SD Humidity Fluctuation along Cable | Cycle | Max/Min. Temp Drift over 2.5 h | Max/Min Peak Temperature Along Cable | Max. SD Temp Fluctuation Along Cable |
|---|---|---|---|---|---|---|---|
| [% rel. H] | [% rel. H] | [% rel. H] | [°C] | [°C] | [°C] | ||
| Bare fibre | 12.31 ± 2.94 −10.78 ± 0.79 | 17.47 ± 4.27 −12.41 ± 13.05 | ±8.45 | 1 | 0.60 ± 0.16 −0.73 ± 0.23 | 1.18 ± 0.55 −1.06 ± 0.38 | ±0.78 |
| 2 | 0.45 ± 0.09 −0.31 ± 0.13 | 1.01 ± 0.18 −0.98 ± 0.19 | ±0.66 | ||||
| 3 | 0.67 ± 0.14 −0.39 ± 0.10 | 1.16 ± 0.18 −1.06 ± 0.27 | ±0.64 | ||||
| 0.9 mm TBC | 6.80 ± 0.89 −5.08 ± 0.84 | 5.58 ± 2.13 −7.12 ± 2.77 | ±4.57 | 1 | 0.43 ± 0.04 −0.57 ± 0.23 | 2.34 ± 0.46 −2.43 ± 0.42 | ±0.80 |
| 2 | 0.36 ± 0.20 −0.37 ± 0.04 | 2.37 ± 0.29 −2.37 ± 0.28 | ±0.57 | ||||
| 3 | 0.42 ± 0.06 −0.44 ± 0.07 | 2.45 ± 0.13 −2.37 ± 0.12 | ±0.49 | ||||
| 2.0 mm TBC | 18.48 ± 1.82 −18.79 ± 0.45 | 8.94 ± 10.19 −6.11 ± 11.09 | ±11.41 | 1 | 1.52 ± 1.02 −2.83 ± 0.12 | 3.51 ± 0.24 −3.28 ± 1.22 | ±1.42 |
| 2 | 0.25 ± 0.20 −0.57 ± 0.05 | 4.07 ± 0.52 −3.32 ± 0.17 | ±0.34 | ||||
| 3 | 0.46 ± 0.07 −0.22 ± 0.08 | 4.01 ± 0.63 −3.38 ± 0.08 | ±0.40 | ||||
| 3.2 mm ribbed TBC | 24.03 ± 0.73 −26.53 ± 0.71 | 22.43 ± 13.21 −40.97 ± 16.52 | ±13.71 | 1 | 0.36 ± 0.09 −0.90 ± 0.13 | 2.02 ± 0.04 −1.80 ± 0.10 | ±0.32 |
| 2 | 0.25 ± 0.14 −0.23 ± 0.11 | 2.11 ± 0.02 −1.78 ± 0.12 | ±0.27 | ||||
| 3 | 0.26 ± 0.13 −0.19 ± 0.01 | 2.10 ± 0.02 −1.83 ± 0.14 | ±0.28 | ||||
| 3.8 mm gel LTC | 19.69 ± 5.38 −23.00 ± 15.87 | 62.96 ± 4.88 −72.45 ± 9.56 | ±18.58 | 1 | 0.55 ± 0.15 −1.11 ± 0.10 | 7.23 ± 0.79 −1.74 ± 0.64 | ±0.49 |
| 2 | 0.25 ± 0.09 −0.22 ± 0.37 | 5.39 ± 1.00 −1.44 ± 0.36 | ±0.51 | ||||
| 3 | 1.52 ± 0.10 −0.26 ± 0.11 | 4.97 ± 0.78 −1.54 ± 0.38 | ±0.29 | ||||
| 3.0 mm air LTC | 16.15 ± 3.58 −20.58 ± 3.40 | 27.16 ± 4.76 −24.58 ± 15.78 | ±9.62 | 1 | 0.39 ± 0.40 −0.82 ± 0.07 | 5.91 ± 0.22 −5.33 ± 0.14 | ±0.46 |
| 2 | 1.16 ± 1.41 −0.19 ± 0.16 | 5.58 ± 0.42 −5.33 ± 0.14 | ±0.67 | ||||
| 3 | 0.39 ± 0.07 −0.29 ± 0.12 | 5.41 ± 0.17 −5.31 ± 0.16 | ±0.44 |
| Cable | Cycle Path | Max/Min. Deviation from Chamber Humidity | Humidity Level for Min/Max Deviation | Deviation from Chamber in% | Cycle | Cycle Stage | Max/Min. Deviation from Chamber Temp | Temperature Level for Min/Max Deviation | Deviation from Chamber in% |
|---|---|---|---|---|---|---|---|---|---|
| [% rel. H] | [% rel. H] | [%] | [°C] | [°C] | [%] | ||||
| Bare fibre | Increasing decreasing | −6.05 −11.0 | 30 30 | 20.1 36.7 | 1 | Increasing decreasing | −1.88 −1.96 | 60 10 | 3.1 19.6 |
| 2 | Increasing decreasing | −2.11 −2.06 | 60 10 | 3.5 20.6 | |||||
| 3 | Increasing decreasing | −2.07 −1.65 | 60 10 | 3.5 16.5 | |||||
| 0.9 mm tight buffered | Increasing decreasing | −3.70 −2.49 | 30 70 | 12.3 3.6 | 1 | Increasing decreasing | 2.20 −1.00 | 40 10 | 5.5 1.0 |
| 2 | Increasing decreasing | −1.49 −1.11 | 60 10 | 2.5 11.1 | |||||
| 3 | Increasing decreasing | −1.50 −1.13 | 60 10 | 2.5 11.3 | |||||
| 2.0 mm tight buffered | Increasing decreasing | −7.24 4.93 | 70 30 | −10.3 16.4 | 1 | Increasing decreasing | 6.02 −2.32 | 40 10 | 15.1 23.2 |
| 2 | Increasing decreasing | 3.28 2.81 | 60 10 | 5.5 28.1 | |||||
| 3 | Increasing decreasing | 3.81 −3.24 | 60 10 | 6.4 −32.4 | |||||
| 3.2 mm ribbed tight buffered | Increasing decreasing | −10.86 24.2 | 50 70 | −21.7 34.6 | 1 | Increasing decreasing | 1.76 −1.60 | 30 10 | 5.9 16.0 |
| 2 | Increasing decreasing | −1.69 −1.53 | 60 10 | 2.8 15.3 | |||||
| 3 | Increasing decreasing | −1.78 −1.72 | 60 10 | 3.0 17.2 | |||||
| 3.8 mm gel filled loose tube | Increasing decreasing | −31.81 −47.35 | 90 30 | −35.3 −157.8 | 1 | Increasing decreasing | 3.4 −4.0 | 60 50 | 5.7 8.0 |
| 2 | Increasing decreasing | 1.51 −2.22 | 30 50 | 5.0 4.4 | |||||
| 3 | Increasing decreasing | 2.05 −2.32 | 60 50 | 3.4 4.6 | |||||
| 3.0 mm air filled loose tube | Increasing decreasing | −10.47 −11.97 | 50 30 | −20.9 −39.9 | 1 | Increasing decreasing | 8.68 3.48 | 30 30 | 28.9 11.6 |
| 2 | Increasing decreasing | 5.26 4.53 | 30 30 | 17.5 15.1 | |||||
| 3 | Increasing decreasing | 5.32 4.33 | 30 30 | 17.7 14.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maier, M.; Kechavarzi, C.; Xu, X.; Lees, J.M. Temperature and Humidity Stability of Fibre Optic Sensor Cables for High Resolution Measurements. Sensors 2023, 23, 1296. https://doi.org/10.3390/s23031296
Maier M, Kechavarzi C, Xu X, Lees JM. Temperature and Humidity Stability of Fibre Optic Sensor Cables for High Resolution Measurements. Sensors. 2023; 23(3):1296. https://doi.org/10.3390/s23031296
Chicago/Turabian StyleMaier, Marcus, Cedric Kechavarzi, Xiaomin Xu, and Janet M. Lees. 2023. "Temperature and Humidity Stability of Fibre Optic Sensor Cables for High Resolution Measurements" Sensors 23, no. 3: 1296. https://doi.org/10.3390/s23031296
APA StyleMaier, M., Kechavarzi, C., Xu, X., & Lees, J. M. (2023). Temperature and Humidity Stability of Fibre Optic Sensor Cables for High Resolution Measurements. Sensors, 23(3), 1296. https://doi.org/10.3390/s23031296








