Revisiting Link Quality Metrics and Models for Multichannel Low-Power Lossy Networks
Abstract
:1. Introduction
2. Related Works
2.1. Link Quality Estimation for Single Channel
2.2. Multichannel Communication
2.3. Link Quality Estimation for Multichannel
3. Popular Link Quality Metrics and Models
4. Experimental Setup
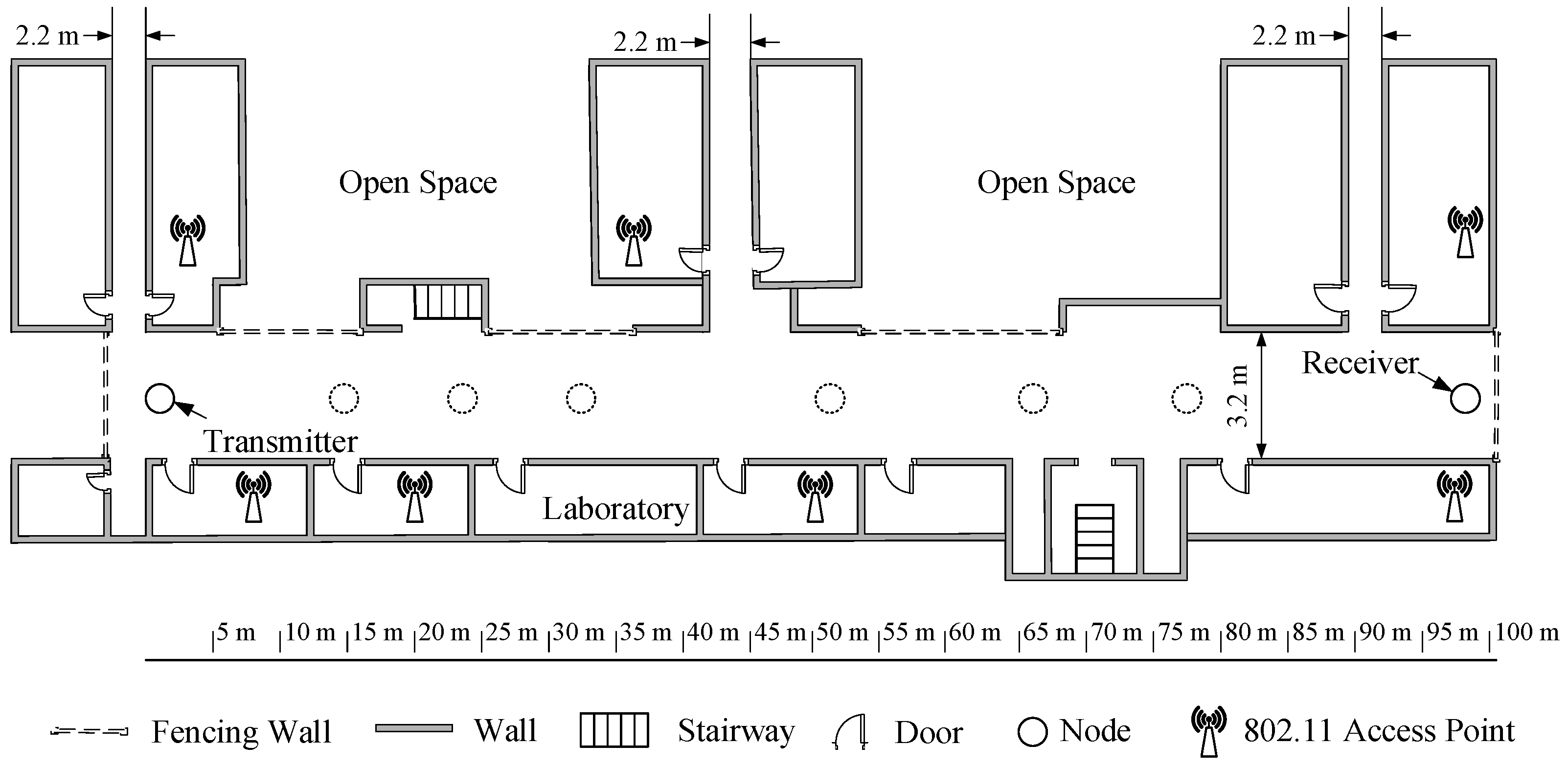
4.1. Experimental Field
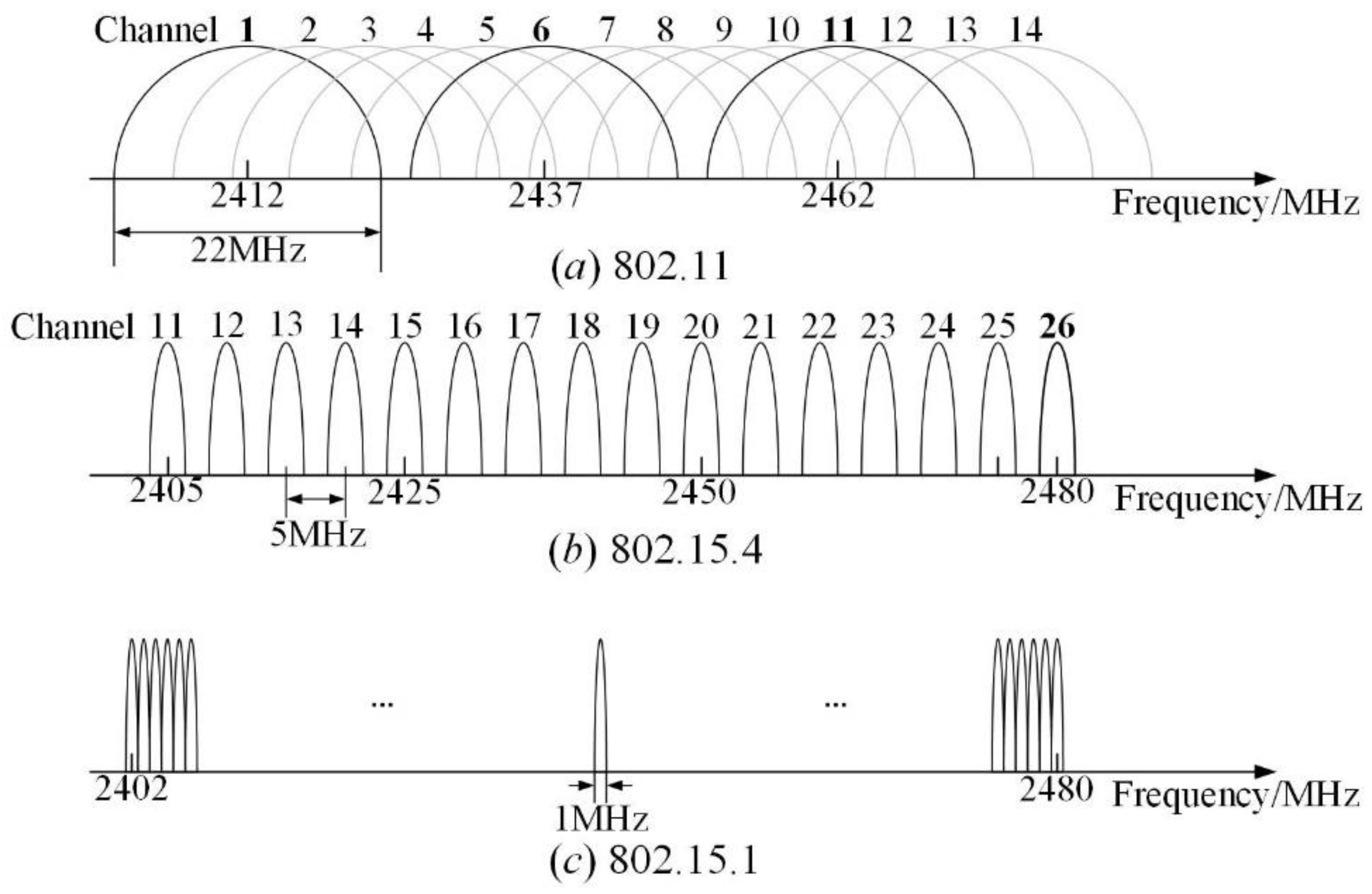
4.2. Channel Selection
4.3. Methodology
5. Spatial Characteristics and Models under Multichannel Scenario
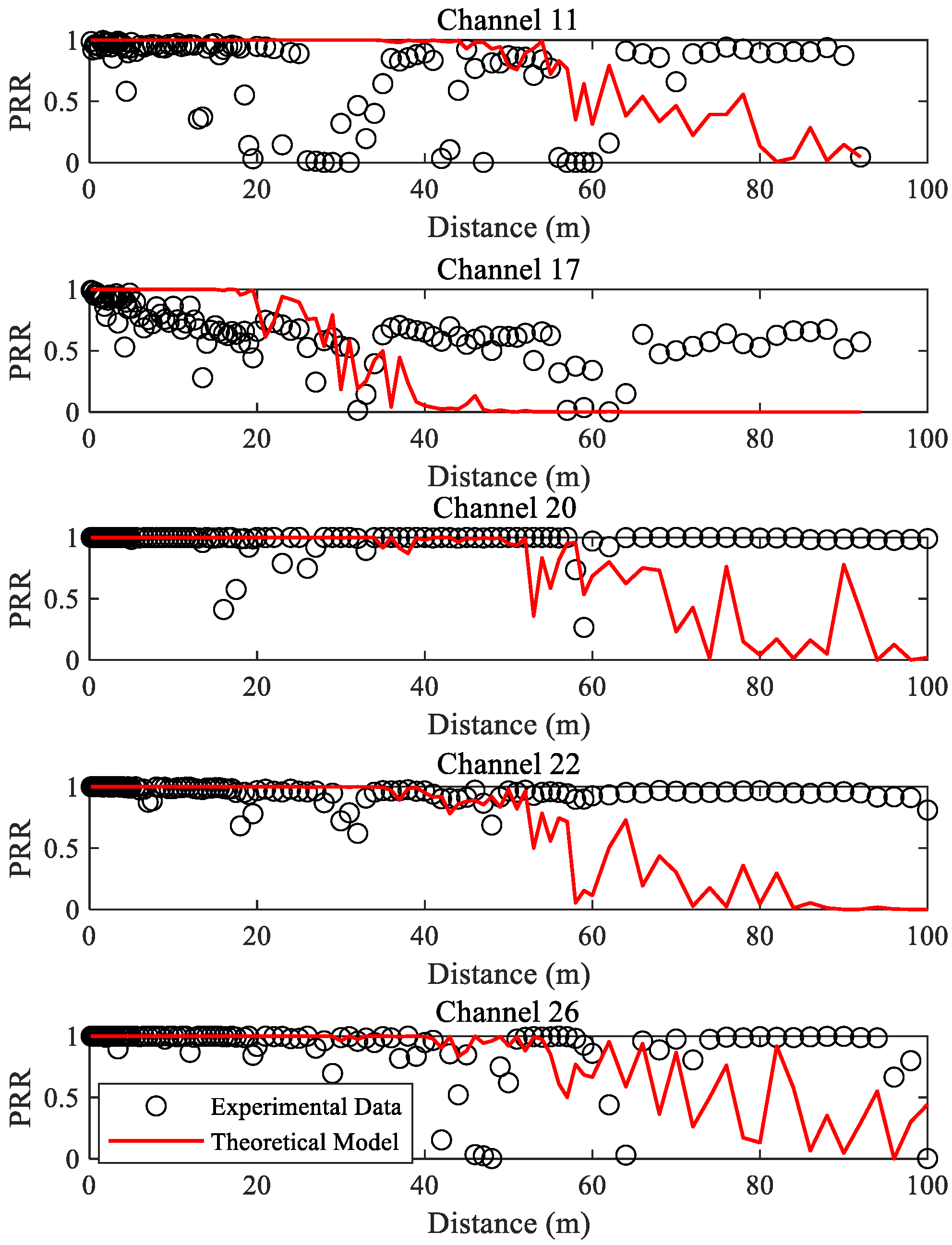
5.1. Spatial Characteristics of Low-Power Links
5.2. Spatial Distribution Model of PRR
6. Physical Layer Metrics and Models under Multichannel Scenario
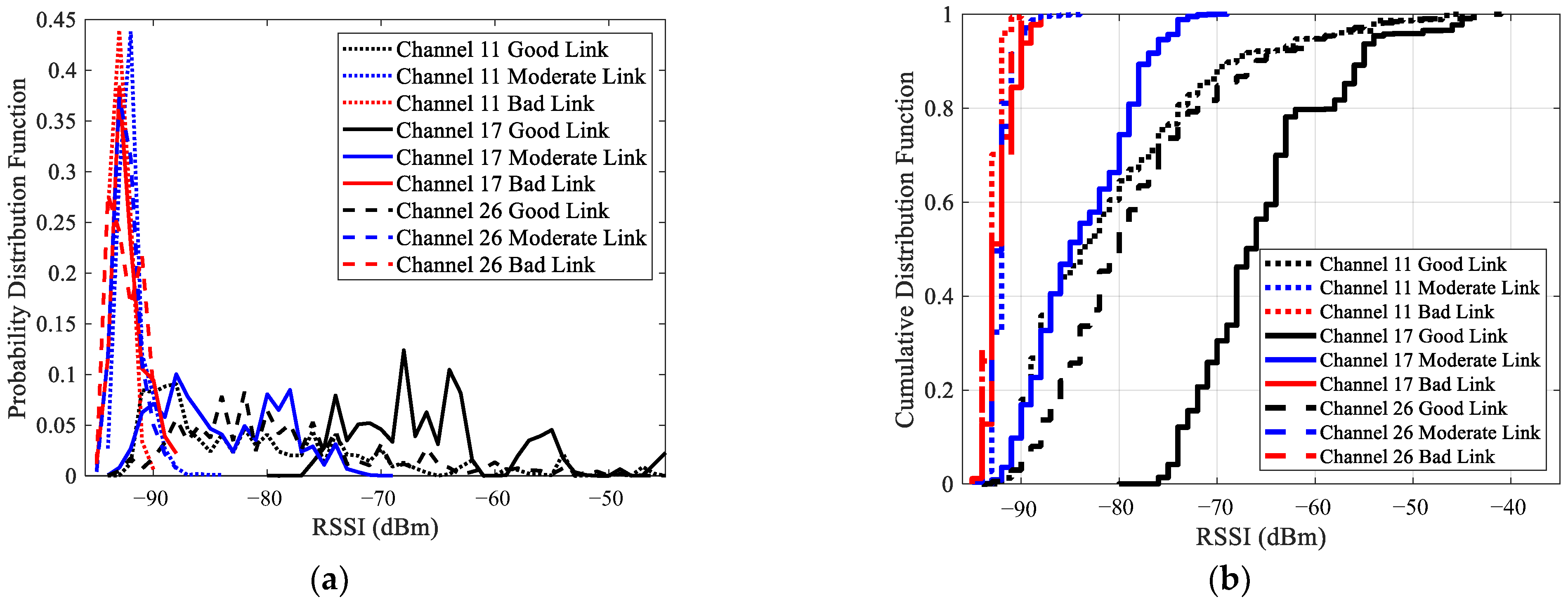
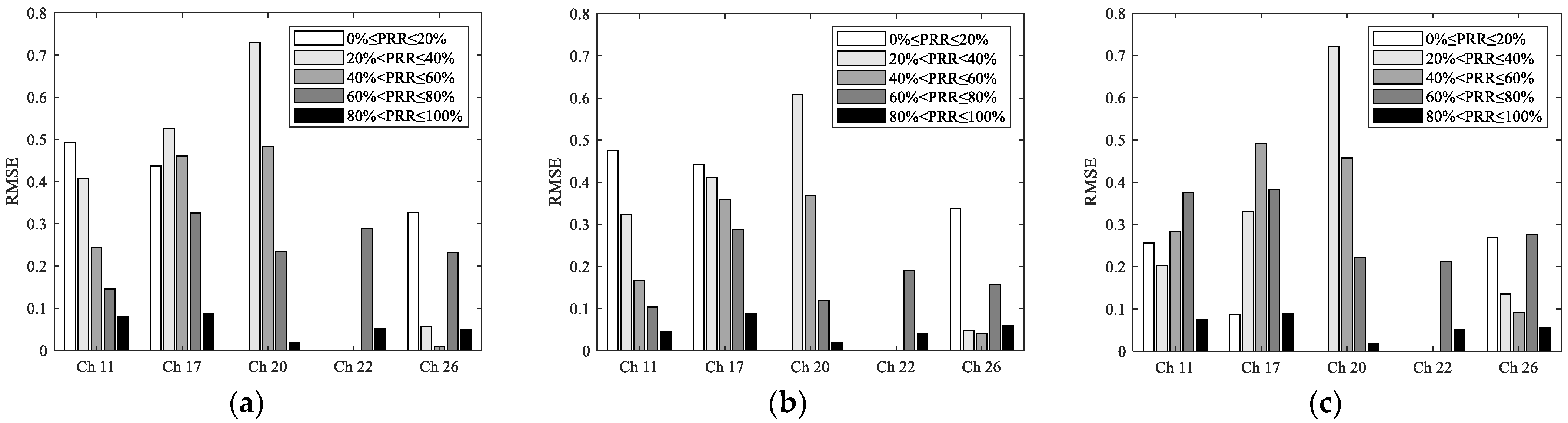
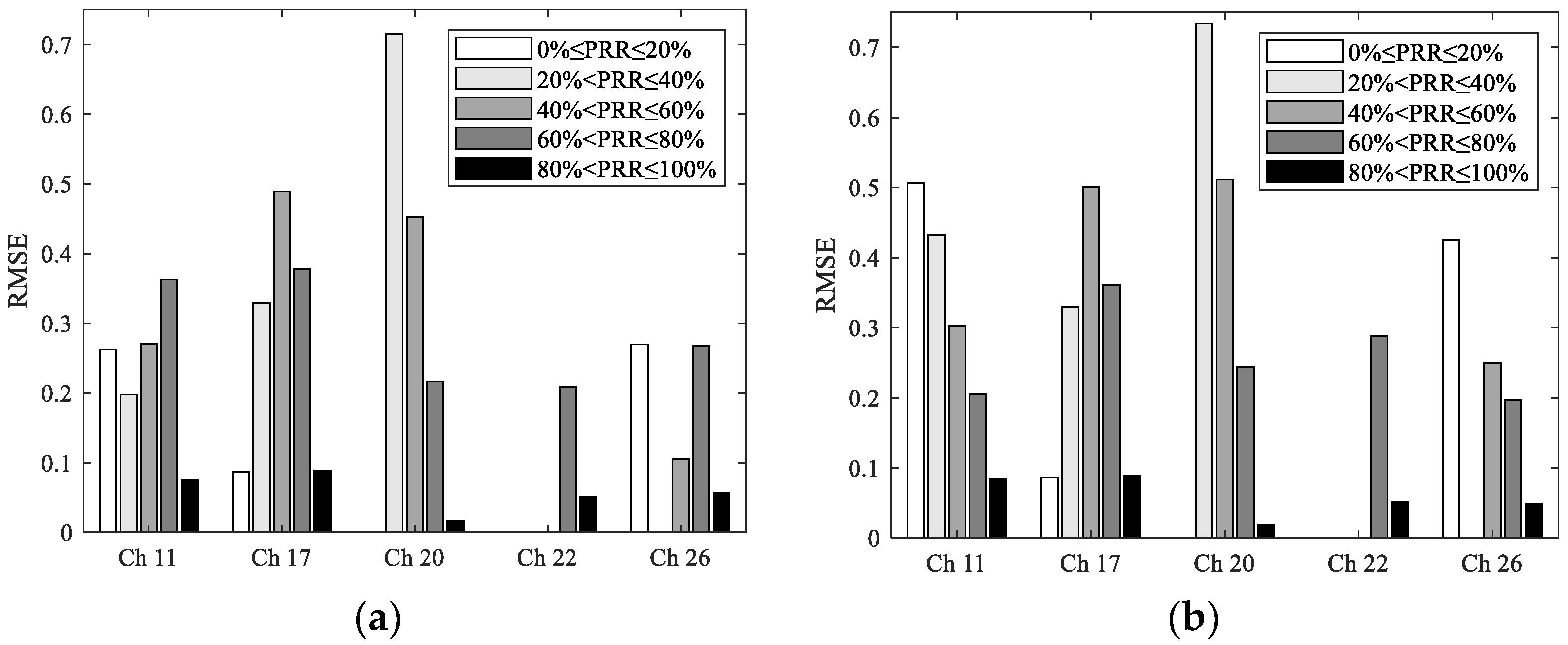
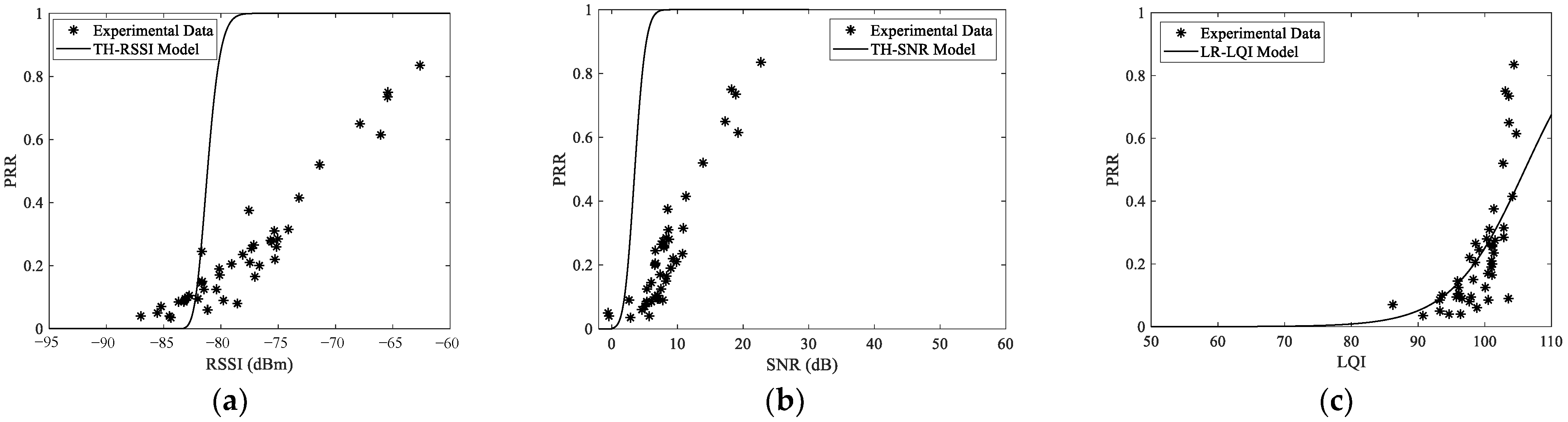
6.1. RSSI and RSSI-Based Models
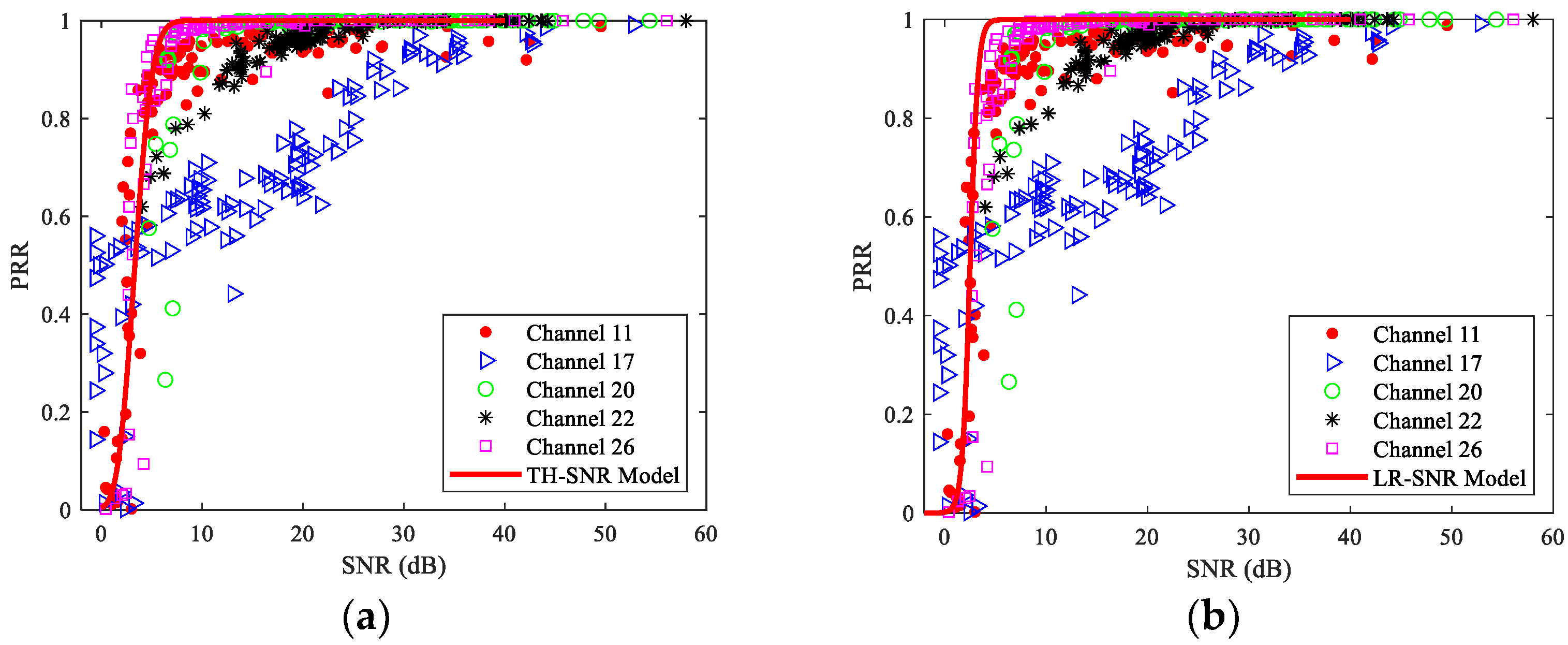
6.2. SNR and SNR-Based Models
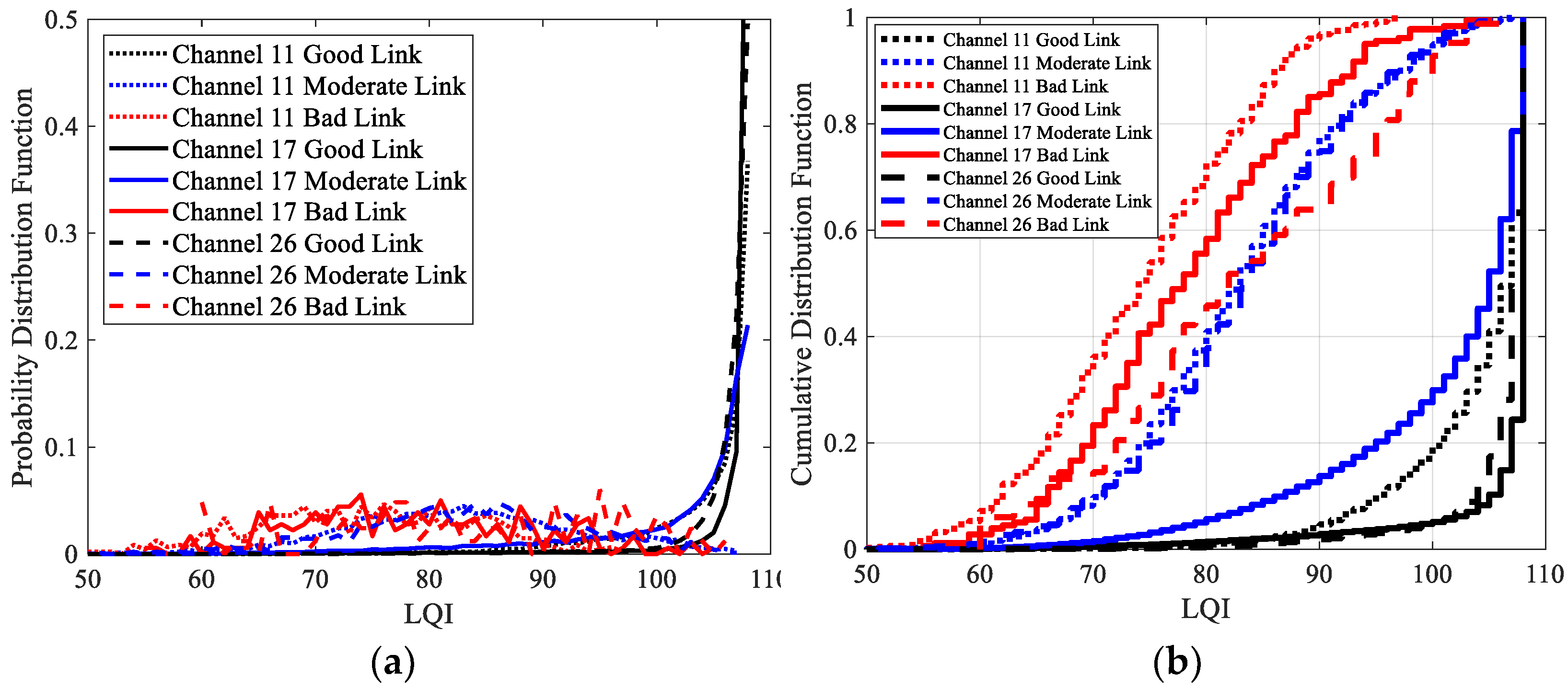
6.3. LQI and LQI-Based Models
7. Generality of The Conclusions
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, H.S.; Ko, J.; Culler, D.E.; Paek, J. Challenging the IPv6 routing protocol for low-power and lossy networks (RPL): A survey. IEEE Commun. Surv. Tutor. 2017, 19, 2502–2525. [Google Scholar] [CrossRef]
- Kim, S.; Kim, H.S.; Kim, C. ALICE: Autonomous link-based cell scheduling for TSCH. In Proceedings of the ACM/IEEE IPSN 2019, Montreal, QC, Canada, 16 April 2019; pp. 121–132. [Google Scholar]
- Wu, Y.; Liu, K.S.; Stankovic, J.A.; He, T.; Lin, S. Efficient multichannel communications in wireless sensor networks. ACM Trans. Sen. Netw. 2016, 12, 12–23. [Google Scholar] [CrossRef]
- Tang, L.; Sun, Y.; Gurewitz, O.; Johnson, D.B. EM-MAC: A dynamic multichannel energy-efficient MAC protocol for wireless sensor networks. In Proceedings of the ACM MobiHoc 2011, New York, NY, USA, 17 May 2011; pp. 1–11. [Google Scholar]
- Zanella, A.; Bardella, A. RSS-based ranging by multichannel RSS averaging. IEEE Wirel. Commun. Lett. 2014, 3, 10–13. [Google Scholar] [CrossRef]
- Kim, S.; Kim, H.S.; Kim, C. A3: Adaptive autonomous allocation of TSCH slots. In Proceedings of the ACM IPSN 2021, New York, NY, USA, 18 May 2021; pp. 299–314. [Google Scholar]
- Duquennoy, S.; Nahas, B.A.; Landsiedel, O.; Watteyne, T. Orchestra: Robust mesh networks through autonomously scheduled TSCH. In Proceedings of the ACM SenSys 2015, New York, NY, USA, 1 November 2015; pp. 337–350. [Google Scholar]
- Vallati, C.; Brienza, S.; Anastasi, G.; Das, S.K. Improving network formation in 6TiSCH networks. IEEE Trans. on Mobile Comput. 2019, 18, 98–110. [Google Scholar] [CrossRef]
- Baccour, N.; Koubaa, A.; Mottola, L.; Youssef, H.; Boano, C.A.; Alves, M. Radio link quality estimation in wireless sensor networks: A survey. ACM Trans. Sens. Netw. 2012, 8, 1–33. [Google Scholar] [CrossRef]
- Sun, W.; Yuan, X.; Wang, J.; Li, Q.; Chen, L.; Mu, D. End-to-end data delivery reliability model for estimating and optimizing the link quality of industrial WSNs. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1127–1137. [Google Scholar] [CrossRef]
- Sun, W.; Lu, W.; Li, Q.; Chen, L.; Mu, D.; Yuan, X. WNN-LQE: Wavelet-neural-network-based link quality estimation for smart grid WSNs. IEEE Access 2017, 5, 12788–12797. [Google Scholar] [CrossRef]
- Liu, T.; Cerpa, A.E. Data-driven link quality prediction using link features. ACM Trans. Sens. Netw. 2014, 10, 1–35. [Google Scholar] [CrossRef]
- Ye, R.; Boukerche, A.; Wang, H.; Zhou, X.; Yan, B. RECODAN: An efficient redundancy coding-based data transmission scheme for wireless sensor networks. Comput. Netw. 2016, 110, 351–363. [Google Scholar] [CrossRef]
- Liu, W.; Xia, Y.; Xie, J.; Xu, M.; Luo, R.; Hu, S.; Dang, X.; Huang, D. Simplified theoretical model based self-adaptive packet reception rate estimation in sensor networks. In Proceedings of the WCNC 2020, Seoul, Republic of Korea, 25 April 2020; pp. 1–6. [Google Scholar]
- Gomez, C.; Boix, A.; Paradells, J. Impact of LQI-Based routing metrics on the performance of a one-to-one routing protocol for IEEE 802.15.4 multihop networks. Eurasip J. Wirel. Commun. Netw. 2010, 6, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Luo, J.; Yu, L.; Zhang, D.; Xia, Z.; Chen, W. A new link quality estimation mechanism based on LQI in WSN. Inf. Technol. J. 2013, 12, 1626–1631. [Google Scholar] [CrossRef] [Green Version]
- Gomes, R.D.; Queiroz, D.V.; Filho, A.C.L.; Fonseca, I.E. Real-time link quality estimation for industrial wireless sensor networks using dedicated nodes. Ad. Hoc. Netw. 2017, 59, 116–133. [Google Scholar] [CrossRef]
- Srinivasan, K.; Dutta, P.; Tavakoli, A.; Levis, P. An empirical study of low-power wireless. ACM Trans. Sens. Netw. 2010, 6, 1–49. [Google Scholar] [CrossRef] [Green Version]
- Wen, J.; Dargie, W. Characterization of link quality fluctuation in mobile wireless sensor networks. ACM Trans. on Cyber-Phys. Syst. 2021, 5, 1–24. [Google Scholar] [CrossRef]
- Barać, F.; Gidlund, M.; Zhang, T. Ubiquitous, yet deceptive hardware-based channel metrics on interfered WSN links. IEEE Trans. on Veh. Technol. 2015, 64, 1766–1778. [Google Scholar] [CrossRef]
- Liu, W.; Xia, Y.; Zheng, D.; Xie, J.; Luo, R.; Hu, S. Environmental impacts on hardware-based link quality estimators in wireless sensor networks. Sensors 2020, 20, 5327. [Google Scholar] [CrossRef]
- Zamalloa, M.Z.; Krishnamachari, B. An analysis of unreliability and asymmetry in low-power wireless links. ACM Trans. Sens. Netw. 2007, 3, 7-es. [Google Scholar] [CrossRef] [Green Version]
- Gonga, A.; Landsiedel, O.; Soldati, P.; Johansson, M. Revisiting multi-channel communication to mitigate interference and link dynamics in wireless sensor networks. In Proceedings of the IEEE DCOSS 2012, Hangzhou, China, 16 May 2012; pp. 186–193. [Google Scholar]
- Gunatilaka, D.; Sha, M.; Lu, C. Impacts of channel selection on industrial wireless sensor-actuator networks. In Proceedings of the IEEE INFOCOM 2017, Atlanta, GA, USA, 1 May 2017; pp. 1–9. [Google Scholar]
- Hermeto, R.T.; Gallais, A.; Laerhoven, K.V.; Tholeyre, F. Passive link quality estimation for accurate and stable parent selection in dense 6TiSCH networks. In Proceedings of the EWSN 2018, Madrid, Spain, 14 February 2018; pp. 114–125. [Google Scholar]
- Kotsiou, V.; Papadopoulos, G.Z.; Chatzimisios, P.; Theoleyre, F. LABeL: Link-based adaptive blacklisting technique for 6TiSCH wireless industrial networks. In Proceedings of the ACM MSWiM 2017, New York, NY, USA, 21 November 2017; pp. 25–33. [Google Scholar]
- Gall, G.L.; Montavont, N.; Papadopoulos, G.Z. Enabling IEEE 802.15.4-2015 TSCH based wireless network for electric vehicle battery management. In Proceedings of the IEEE ISCC 2020, Rennes, France, 7 July 2020; pp. 1–6. [Google Scholar]
- Tavakoli, R.; Nabi, M.; Basten, T.; Goossen, K. Dependable interference-aware time-slotted channel hopping for wireless sensor networks. ACM Trans. Sen. Netw. 2018, 14, 1–35. [Google Scholar] [CrossRef] [Green Version]
- Mavromatis, A.; Papadopoulos, G.Z.; Fafoutis, X.; Goulianos, A.; Oikonomou, G.; Chatzimisios, P.; Tryfonas, T. Link quality and path based clustering in IEEE 802.15.4-2015 TSCH networks. In Proceedings of the IEEE ISCC 2017, Heraklion, Greece, 3 July 2017; pp. 798–803. [Google Scholar]
- Farahmand, M.; Nabi, M. Channel quality prediction for TSCH blacklisting in highly dynamic networks: A self-supervised deep learning approach. IEEE Sens. J. 2021, 21, 21059–21068. [Google Scholar] [CrossRef]
- Boucetta, C.; Nour, B.; Cusin, A.; Moungla, H. QoS in IoT networks based on link quality prediction. In Proceedings of the IEEE ICC 2021, Montreal, QC, Canada, 14 June 2021; pp. 1–6. [Google Scholar]
- Kotsiou, V.; Papadopoulos, G.Z.; Zorbas, D.; Chatzimisios, P.; Theoleyre, F. Blacklisting-based channel hopping approaches in low-power and lossy networks. IEEE Commun. Mag. 2019, 57, 48–53. [Google Scholar] [CrossRef] [Green Version]
- Tavakoli, R.; Nabi, M.; Basten, T.; Goossens, K. Topology management and TSCH scheduling for low-latency convergecast in in-vehicle WSNs. IEEE Trans. on Industrial Informatics 2019, 15, 1082–1093. [Google Scholar] [CrossRef] [Green Version]
- Jin, M.; He, Y.; Zheng, X.; Fang, D.; Xu, D.; Xing, T.; Chen, X. Exploiting interference fingerprints for predictable wireless concurrency. IEEE Trans. on Mobile Comput. 2021, 20, 2354–2366. [Google Scholar] [CrossRef]
- Gomes, P.H.; Chen, Y.; Watteyne, T.; Krishnamachari, B. Insights into frequency diversity from measurements on an indoor low power wireless network testbed. In Proceedings of the IEEE GLOBECOM Workshops 2016, Washington, DC, USA, 4 December 2016; pp. 1–6. [Google Scholar]
- Orfanidis, C.; Pop, P.; Fafoutis, X. Active connectivity fundamentals for TSCH networks of mobile robots. In Proceedings of the DCOSS 2022, Los Angeles, CA, USA, 1 June 2022; pp. 191–198. [Google Scholar]
- Tavakoli, R.; Nabi, M.; Basten, T.; Goossens, K. Enhanced time-slotted channel hopping in WSNs using non-intrusive channel-quality estimation. In Proceedings of the IEEE MASS 2015, Dallas, TX, USA, 19 October 2015; pp. 217–225. [Google Scholar]
- Tavakoli, R.; Nabi, M.; Basten, T.; Goossens, K. An experimental study of cross-technology interference in in-vehicle wireless sensor networks. In Proceedings of the ACM MSWiM 2016, New York, NY, USA, 13 November 2016; pp. 195–204. [Google Scholar]
- Kotsiou, V.; Papadopoulos, G.Z.; Chatzimisios, P.; Tholeyre, F. Is local blacklisting relevant in slow channel hopping low-power wireless networks? In Proceedings of the IEEE ICC 2017, Paris, France, 21 May 2017; pp. 1–6. [Google Scholar]
- Chen, G.; Dong, W.; Zhao, Z.; Gu, T. Accurate corruption estimation in ZigBee under cross-technology interference. IEEE Trans. on Mobile Comput. 2019, 18, 2243–2256. [Google Scholar] [CrossRef]
- Hithnawi, A.; Shafagh, H.; Duquennoy, S. Understanding the impact of cross technology interference on IEEE 802.15.4. In Proceedings of the ACM WiNTECH 2014, New York, NY, USA, 7 September 2014; pp. 49–56. [Google Scholar]
- Texas Instruments, Inc. CC2420. Available online: http://www.ti.com/lit/ds/symlink/cc2420.pdf (accessed on 1 October 2022).
- Bildea, A.; Alphand, O.; Rousseau, F.; Duda, A. Link quality metrics in large scale indoor wireless sensor networks. In Proceedings of the IEEE PIMRC 2013, London, UK, 8 September 2013; pp. 1888–1892. [Google Scholar]
- Wen, J.; Dargie, W. Evaluation of the quality of aerial links in low-power wireless sensor networks. IEEE Sens. J. 2021, 21, 13924–13934. [Google Scholar] [CrossRef]





| Parameter | Lc | n | σ | Pn (Ch 11) |
| Value | 36.6957 | 1.5896 | 1.4725 | −95.76 dBm |
| Parameter | Pn (Ch 17) | Pn (Ch 20) | Pn (Ch 22) | Pn (Ch 26) |
| Value | −90.35 dBm | −96.27 dBm | −94.89 dBm | −96.23 dBm |
| Channel | 11 | 17 | 20 | 22 | 26 |
| RMSE | 0.4558 | 0.3819 | 0.3263 | 0.3677 | 0.3130 |
| Channel | 11 | 17 | 20 | 22 | 26 | Multichannel |
|---|---|---|---|---|---|---|
| LR-RSSI | 0.2324 | 0.3435 | 0.1020 | 0.0800 | 0.1049 | 0.1985 |
| PN-RSSI | 0.2117 | 0.2920 | 0.0793 | 0.0581 | 0.1057 | 0.1723 |
| TH-RSSI | 0.1622 | 0.3512 | 0.0984 | 0.0697 | 0.1038 | 0.1856 |
| Channel | 11 | 17 | 20 | 22 | 26 | Multichannel |
|---|---|---|---|---|---|---|
| TH-SNR | 0.1615 | 0.3482 | 0.0975 | 0.0689 | 0.1026 | 0.1840 |
| LR-SNR | 0.1662 | 0.3636 | 0.0969 | 0.0687 | 0.1324 | 0.2042 |
| Parameter | e1 | e2 | e3 | e4 | e5 | e6 |
| Value | −0.000013918 | 0.002948 | −0.1626 | 1.6928 | 70.4 | 100.5 |
| Parameter | f1 | f2 | f3 | f4 | f5 | f6 |
| Value | 0.01875 | −0.875 | 0.04913 | −3.4269 | 0.00061 | −0.0305 |
| Parameter | f7 | f8 | f9 | g1 | g2 | |
| Value | 100 | 84 | 70 | −0.2331 | 19.3453 |
| Channel | 11 | 17 | 20 | 22 | 26 | Multichannel |
|---|---|---|---|---|---|---|
| CU-LQI | 0.1200 | 0.2859 | 0.0601 | 0.0671 | 0.0889 | 0.1486 |
| LR-LQI | 0.1131 | 0.2834 | 0.0658 | 0.0673 | 0.0865 | 0.1468 |
| ML-LQI | 0.1319 | 0.2951 | 0.0650 | 0.0666 | 0.0932 | 0.1548 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, J.; Zhao, Y.; Xia, Y.; Yang, Z.; Xu, C.; Liu, W.; Huang, D. Revisiting Link Quality Metrics and Models for Multichannel Low-Power Lossy Networks. Sensors 2023, 23, 1303. https://doi.org/10.3390/s23031303
Mao J, Zhao Y, Xia Y, Yang Z, Xu C, Liu W, Huang D. Revisiting Link Quality Metrics and Models for Multichannel Low-Power Lossy Networks. Sensors. 2023; 23(3):1303. https://doi.org/10.3390/s23031303
Chicago/Turabian StyleMao, Jing, Yan Zhao, Yu Xia, Zhuopeng Yang, Cheng Xu, Wei Liu, and Daqing Huang. 2023. "Revisiting Link Quality Metrics and Models for Multichannel Low-Power Lossy Networks" Sensors 23, no. 3: 1303. https://doi.org/10.3390/s23031303
APA StyleMao, J., Zhao, Y., Xia, Y., Yang, Z., Xu, C., Liu, W., & Huang, D. (2023). Revisiting Link Quality Metrics and Models for Multichannel Low-Power Lossy Networks. Sensors, 23(3), 1303. https://doi.org/10.3390/s23031303







