Region Anomaly Detection via Spatial and Semantic Attributed Graph in Human Monitoring †
Abstract
:1. Introduction
- (1)
- We propose a spatial and semantic attributed graph to characterize the regions with their contexts by exploring their spatial and semantic relationships among regions co-occurring in an image.
- (2)
- We devise a novel graph auto-encoder-based framework, SSGAE, which adopts the sum aggregation strategy to discriminate the node neighbors containing similar node attributes, to tackle the region anomaly detection task by jointly reconstructing the node features and structures in the graph.
- (3)
- We construct three real-world datasets, including two human monitoring datasets collected by an autonomous mobile robot and one region anomaly dataset AnoVisualGenome from a large-scale visual dataset VisualGenome [21] to evaluate the performance of SSGAE. Extensive experimental results demonstrate that SSGAE outperforms other advanced anomaly detection methods on the region anomaly detection task.
2. Related Work
2.1. Image and Region Anomaly Detection
2.2. Graph Anomaly Detection
3. Problem Formulation
4. Methodology
4.1. Spatial and Semantic Attributed Graph
4.1.1. Localizing and Describing Regions in an Image
4.1.2. Construction of Spatial and Semantic Attributed Graph
4.2. Spatial and Semantic Graph Auto-Encoder
| Algorithm 1 Overall procedure of SSGAE. |
| Input: Graph , ; Learnable parameter ; Hyper-parameter ; Number L of the hidden layers in SSGAE; Number T of the training epochs. Output: Anomaly score for each node via function .
|
4.2.1. Sum Neighborhood Aggregation Strategy
4.2.2. Attributed Graph Encoder
4.2.3. Graph Structure Decoder
4.2.4. Graph Attribute Decoder
4.2.5. Optimization and Anomaly Score
5. Experiments
5.1. Datasets
- LabPatrolling [14] is constructed from the video clips when the mobile robot patrols around the laboratory. It includes various single anomalies, such as a man holding a baseball bat and a man holding an umbrella in the room, as well as a small number of contextual anomalies, such as a man making a phone call in the working area. It contains 5146 normal images for training, as well as 373 normal images and 21 abnormal images for testing.
- BehaviorMonitoring [14] is constructed from another large-scale human monitoring dataset of video clips (almost 100 h) when the mobile robot is navigated to designated locations by a program to monitor diverse human behaviors in the laboratory. It includes a wide range of contextual anomalies of many human behaviors, such as eating and sleeping in the working and resting areas, which are defined as normal and abnormal activities. It contains 5548 normal images for training, as well as 585 normal images and 106 abnormal images for testing.
- AnoVisualGenome is constructed from Visual Genome [21], which provides dense annotations for regions on over 108K images. It includes several kinds of human activities in inappropriate environments as contextual anomalies, such as watching TV on the street and sitting on a couch on the beach. It contains 1427 normal images for training, as well as 218 normal images and 31 abnormal images for testing.
5.2. Experimental Setup
5.2.1. Preprocessing
5.2.2. Baseline Algorithms
- AE [42] is a classical reconstruction-based method for anomaly detection. Both the encoder and the decoder are designed with fully-connected layers.
- GANomaly [36] is a popular generative anomaly detection method. It adopts an encoder-decoder-encoder module as a generator and three loss functions to jointly reconstruct images and features in a latent space.
- AIRD [7] is a one-class region anomaly detection method. It combines the visual, caption, and coordinate features of each region as its representation and employs an incremental clustering method to model normal regions.
- FSTAD [8] employs AIRD as its fast module for detecting single anomalies and devises a slow module recording neighboring regions with their visual features for detecting anomalous region pairs.
- VGAE [18] is the first model to extend the auto-encoder framework on graph data. It encodes node representations by GCN layers and utilizes an inner product decoder for reconstructing the adjacency matrix of graph data.
- DOMINANT [19] is the state-of-the-art graph auto-encoder for detecting anomalous nodes in attributed graphs by devising GCN-based components and adopting reconstruction errors as the anomaly scores.
- GATE [35] is a graph auto-encoder variant that stacks graph attention layers in its encoder and decoder for graph classification tasks.
5.2.3. Implementation Details
5.3. Experimental Results and Analysis
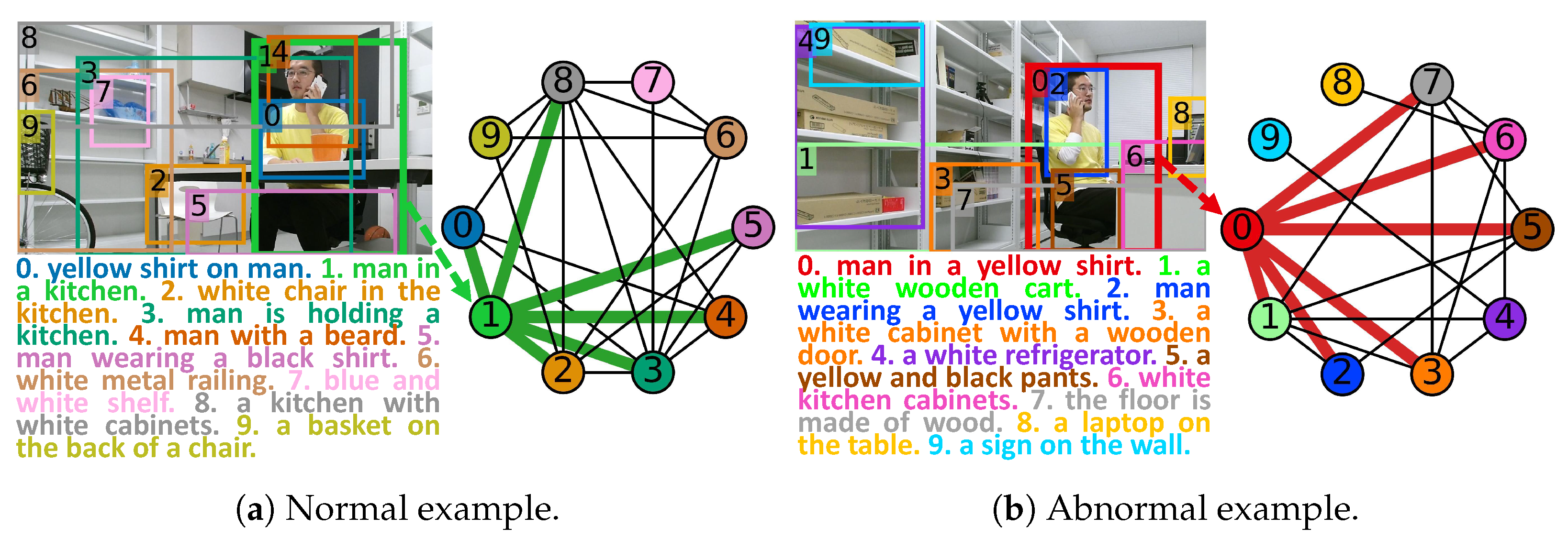
- SSGAE outperforms all the baseline methods on the three datasets, which achieves , , and improvements in terms of their AUC scores on LabPatrolling, BehaviorMonitoring, and AnoVisualGenome, respectively. This validates the superiority of our method for the region anomaly detection task. The main reason is that SSGAE is capable of discriminating node representations from the spatial and semantic graphs and thus generates separated reconstruction errors to measure the abnormalities of regions, as shown in the example in Figure 8.
- The previous methods, which do not consider region contexts, i.e., AE, GANomaly, and AIRD, achieve competitive performance on LabPatrolling, where most of the anomalies are single anomalies. This fact proves their effectiveness in detecting single anomalies that are dissimilar to normal regions, e.g., normal and abnormal regions in the upper row in Figure 8. However, these methods do not perform well on BehaviorMonitoring and AnoVisual Genome, where there exist a large number of contextual anomalies. For instance, GANomaly achieves an AUC score of on LabParolling, while it only achieves and on the other two datasets. The distributions of the anomaly scores on the two datasets shown in (b) and (c) in Figure 7 demonstrate that AE, GANomaly, and AIRD are unable to separate the normal and abnormal regions very well. We think the reason would be that without considering the region contexts, the contextual anomalies include similar human behaviors as normal regions, which are difficult to detecte with these methods. To confirm the reason, we investigate the anomaly scores of the examples, including a normal region and a contextual anomaly, i.e., the no. 0 regions in the upper and bottom images in the left part of Figure 8. Compared with SSGAE, which outputs the anomaly score of on the normal/abnormal regions in Figure 8, AE, GANomaly, and AIRD output , , and , respectively. These findings indicate that the methods that do not consider region contexts have deficiencies in detecting contextual anomalies compared with SSGAE.
- Compared with other graph auto-encoder variants, SSGAE achieves significant performance gains with the improvements of , , and on the three datasets in terms of AUC scores. Accordingly, the anomaly scores of normal and abnormal regions generated by SSGAE are better separated compared with these baseline methods, as shown in Figure 7. The main difference between SSGAE and other graph auto-encoders is the sum aggregation strategy, which plays a critical role in discriminating the representations of node neighbors. We verify the effectiveness of the sum aggregation strategy in SSGAE by substituting it with the aggregation strategies in other graph auto-encoders, as illustrated in Section 5.5.
- We observe that VGAE performs worst on the target task, although its encoder is similar to the encoders in other graph auto-encoders. We notice that compared with DOMINANT, GATE, and SSGAE, the decoder in VGAE only aims at reconstructing the graph structure without considering the reconstruction of node attributes in the graph. This fact implies that both the structure and the attribute reconstructions are necessary for our method of the task.
5.4. Parameter Sensitivity Study
5.5. Effectiveness of Components
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sultani, W.; Chen, C.; Shah, M. Real-World Anomaly Detection in Surveillance Videos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6479–6488. [Google Scholar] [CrossRef] [Green Version]
- Luo, W.; Liu, W.; Lian, D.; Gao, S. Future Frame Prediction Network for Video Anomaly Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 7505–7520. [Google Scholar] [CrossRef] [PubMed]
- Yu, M.; Li, G.; Jiang, D.; Jiang, G.; Tao, B.; Chen, D. Hand Medical Monitoring System Based on Machine Learning and Optimal EMG Feature Set. Pers. Ubiquitous Comput. 2019, 1–17. [Google Scholar] [CrossRef]
- Wu, P.; Liu, J.; Shi, Y.; Sun, Y.; Shao, F.; Wu, Z.; Yang, Z. Not Only Look, but Also Listen: Learning Multimodal Violence Detection under Weak Supervision. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 322–339. [Google Scholar] [CrossRef]
- Deguchi, Y.; Takayama, D.; Takano, S.; Scuturici, V.M.; Petit, J.M.; Suzuki, E. Skeleton Clustering by Multi-Robot Monitoring for Fall Risk Discovery. J. Intell. Inf. Syst. 2017, 48, 75–115. [Google Scholar] [CrossRef]
- Meng, F.; Yuan, G.; Lv, S.; Wang, Z.; Xia, S. An Overview on Trajectory Outlier Detection. Artif. Intell. Rev. 2019, 52, 2437–2456. [Google Scholar] [CrossRef]
- Hatae, Y.; Yang, Q.; Fadjrimiratno, M.F.; Li, Y.; Matsukawa, T.; Suzuki, E. Detecting Anomalous Regions from an Image based on Deep Captioning. In Proceedings of the International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications, Valletta, Malta, 27–29 February 2020; Volume 5, pp. 326–335. [Google Scholar] [CrossRef]
- Fadjrimiratno, M.F.; Hatae, Y.; Matsukawa, T.; Suzuki, E. Detecting Anomalies from Human Activities by an Autonomous Mobile Robot based on “Fast and Slow” Thinking. In Proceedings of the International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications, Online Streaming, 8–10 February 2021; Volume 5, pp. 943–953. [Google Scholar] [CrossRef]
- Dong, N.; Suzuki, E. GIAD-ST: Detecting Anomalies in Human Monitoring Based on Generative Inpainting via Self-Supervised Multi-Task Learning. J. Intell. Inf. Syst. 2022, 59, 733–754. [Google Scholar] [CrossRef]
- Yi, J.; Yoon, S. Patch SVDD: Patch-level SVDD for Anomaly Detection and Segmentation. In Proceedings of the Asian Conference on Computer Vision, Kyoto, Japan, 30 November–4 December 2020. [Google Scholar] [CrossRef]
- Li, C.L.; Sohn, K.; Yoon, J.; Pfister, T. CutPaste: Self-Supervised Learning for Anomaly Detection and Localization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Kyoto, Japan, 30 November 2020; pp. 9664–9674. [Google Scholar] [CrossRef]
- Wu, K.; Zhu, L.; Shi, W.; Wang, W.; Wu, J. Self-Attention Memory-Augmented Wavelet-CNN for Anomaly Detection. IEEE Trans. Circuits Syst. Video Technol. 2022. early access. [Google Scholar] [CrossRef]
- Mu, H.; Sun, R.; Wang, M.; Chen, Z. Spatio-Temporal Graph-Based CNNs for Anomaly Detection in Weakly-Labeled Videos. Inf. Process. Manag. 2022, 59, 102983. [Google Scholar] [CrossRef]
- Zhang, K.; Fadjrimiratno, M.F.; Suzuki, E. Context-Based Anomaly Detection via Spatial Attributed Graphs in Human Monitoring. In Proceedings of the International Conference on Neural Information Processing, Sanur, Bali, Indonesia, 8 December 2021; pp. 450–463. [Google Scholar] [CrossRef]
- Choi, M.J.; Torralba, A.; Willsky, A.S. Context Models and Out-of-Context Objects. Pattern Recognit. Lett. 2012, 33, 853–862. [Google Scholar] [CrossRef] [Green Version]
- Pasini, A.; Baralis, E. Detecting Anomalies in Image Classification by means of Semantic Relationships. In Proceedings of the 2019 IEEE Second International Conference on Artificial Intelligence and Knowledge Engineering (AIKE), Sardinia, Italy, 3–5 June 2019; pp. 231–238. [Google Scholar] [CrossRef]
- Johnson, J.; Karpathy, A.; Fei-Fei, L. DenseCap: Fully Convolutional Localization Networks for Dense Captioning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4565–4574. [Google Scholar] [CrossRef] [Green Version]
- Kipf, T.N.; Welling, M. Variational Graph Auto-Encoders. arXiv 2016, arXiv:1611.07308. [Google Scholar]
- Ding, K.; Li, J.; Bhanushali, R.; Liu, H. Deep Anomaly Detection on Attributed Networks. In Proceedings of the 2019 SIAM International Conference on Data Mining, Calgary, AB, Canada, 2–4 May 2019; pp. 594–602. [Google Scholar] [CrossRef] [Green Version]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How Powerful are Graph Neural Networks? In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Krishna, R.; Zhu, Y.; Groth, O.; Johnson, J.; Hata, K.; Kravitz, J.; Chen, S.; Kalantidis, Y.; Li, L.J.; Shamma, D.A.; et al. Visual Genome: Connecting Language and Vision Using Crowdsourced Dense Image Annotations. Int. J. Comput. Vis. 2017, 123, 32–73. [Google Scholar] [CrossRef] [Green Version]
- Bergmann, P.; Fauser, M.; Sattlegger, D.; Steger, C. MVTec AD—A Comprehensive Real-World Dataset for Unsupervised Anomaly Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9592–9600. [Google Scholar] [CrossRef]
- Seeböck, P.; Waldstein, S.; Klimscha, S.; Gerendas, B.S.; Donner, R.; Schlegl, T.; Schmidt-Erfurth, U.; Langs, G. Identifying and Categorizing Anomalies in Retinal Imaging Data. arXiv 2016, arXiv:1612.00686. [Google Scholar]
- Schlegl, T.; Seeböck, P.; Waldstein, S.M.; Schmidt-Erfurth, U.; Langs, G. Unsupervised Anomaly Detection with Generative Adversarial Networks to Guide Marker Discovery. In Proceedings of the International Conference on Information Processing in Medical Imaging, Boone, NC, USA, 25–30 June 2017; pp. 146–157. [Google Scholar] [CrossRef] [Green Version]
- Venkataramanan, S.; Peng, K.C.; Singh, R.V.; Mahalanobis, A. Attention Guided Anomaly Localization in Images. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 485–503. [Google Scholar] [CrossRef]
- Gong, D.; Liu, L.; Le, V.; Saha, B.; Mansour, M.R.; Venkatesh, S.; Hengel, A.v.d. Memorizing Normality to Detect Anomaly: Memory-augmented Deep Autoencoder for Unsupervised Anomaly Detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1705–1714. [Google Scholar] [CrossRef] [Green Version]
- Sun, C.; Jia, Y.; Hu, Y.; Wu, Y. Scene-Aware Context Reasoning for Unsupervised Abnormal Event Detection in Videos. In Proceedings of the 28th ACM International Conference on Multimedia, Seattle, WA, USA, 12–16 October 2020; pp. 184–192. [Google Scholar] [CrossRef]
- Pourreza, M.; Salehi, M.; Sabokrou, M. Ano-Graph: Learning Normal Scene Contextual Graphs to Detect Video Anomalies. arXiv 2021, arXiv:2103.10502. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Li, Z.; Pan, S.; Gong, C.; Zhou, C.; Karypis, G. Anomaly Detection on Attributed Networks via Contrastive Self-Supervised Learning. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 2378–2392. [Google Scholar] [CrossRef]
- Zheng, Y.; Jin, M.; Liu, Y.; Chi, L.; Phan, K.T.; Chen, Y.P.P. Generative and Contrastive Self-Supervised Learning for Graph Anomaly Detection. IEEE Trans. Knowl. Data Eng. 2021. early access. [Google Scholar] [CrossRef]
- Jin, M.; Liu, Y.; Zheng, Y.; Chi, L.; Li, Y.F.; Pan, S. ANEMONE: Graph Anomaly Detection with Multi-Scale Contrastive Learning. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Queensland, Australia, 1–5 November 2021; pp. 3122–3126. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Fan, H.; Zhang, F.; Li, Z. AnomalyDAE: Dual Autoencoder for Anomaly Detection on Attributed Networks. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 5685–5689. [Google Scholar] [CrossRef] [Green Version]
- Salehi, A.; Davulcu, H. Graph Attention Auto-Encoders. In Proceedings of the IEEE 32nd International Conference on Tools with Artificial Intelligence (ICTAI), Baltimore, MD, USA, 9–11 November 2020; pp. 989–996. [Google Scholar] [CrossRef]
- Akcay, S.; Atapour-Abarghouei, A.; Breckon, T.P. GANomaly: Semi-Supervised Anomaly Detection via Adversarial Training. In Proceedings of the Asian Conference on Computer Vision, Perth, Australia, 2–6 December 2018; pp. 622–637. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]
- Reimers, N.; Gurevych, I. Sentence-Bert: Sentence Embeddings Using Siamese Bert-Networks. arXiv 2019, arXiv:1908.10084. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Liu, Y.; Ott, M.; Goyal, N.; Du, J.; Joshi, M.; Chen, D.; Levy, O.; Lewis, M.; Zettlemoyer, L.; Stoyanov, V. Roberta: A robustly optimized bert pretraining approach. arXiv 2019, arXiv:1907.11692. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. ImageNet: A Large-Scale Hierarchical Image Database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar] [CrossRef] [Green Version]
- Bengio, Y.; Lamblin, P.; Popovici, D.; Larochelle, H. Greedy Layer-Wise Training of Deep Networks. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 4–7 December 2006; pp. 153–160. [Google Scholar]
- Shlens, J. A Tutorial on Principal Component Analysis. arXiv 2014, arXiv:1404.1100. [Google Scholar]
- Li, G.; Jung, J.J. Entropy-based dynamic graph embedding for anomaly detection on multiple climate time series. Sci. Rep. 2021, 11, 13819. [Google Scholar] [CrossRef] [PubMed]









| Notation | Description |
|---|---|
| The image | |
| The region in the image | |
| The caption of the region | |
| The visual feature vector of the region | |
| The semantic feature vector of caption of the region | |
| The attributed graph for image | |
| The node in the graph | |
| The set of the neighbors adjacent to node | |
| The adjacency matrix of graph | |
| The edge, i.e., structure, information of node in | |
| The node attribute matrix of graph | |
| The node feature vector of node | |
| n | The number of regions in image and nodes in graph |
| d | The dimension of node feature |
| The dimensions of the visual feature and the semantic feature | |
| The hidden representation matrix of graph in the layer of the attributed graph encoder in SSGAE | |
| The hidden representation vector of node in | |
| The final hidden embedding matrix of nodes in graph | |
| The final hidden embedding vector of node | |
| The hidden representation matrix of graph in the layer of the graph attribute decoder in SSGAE | |
| The hidden representation vector of node in | |
| The learnable parameter vector in the layer | |
| The learnable parameter in | |
| The multi-layer perception modules in the layer of the attributed graph encoder and the graph attribute decoder | |
| The multi-layer perception module in the graph structure decoder | |
| L | The number of the hidden layers |
| The hyper-parameter to balance the attribute and the structure reconstruction errors in the objective function | |
| The dimensions of hidden representation and final hidden embedding | |
| The reconstructions of and | |
| The reconstructions of and for node | |
| The anomaly score of node in the test phase |
| Dataset | |||
|---|---|---|---|
| Method | LabPatrolling | BehaviorMonitoring | AnoVisualGenome |
| AE | 0.813 | 0.631 | 0.709 |
| GANomaly | 0.911 | 0.794 | 0.687 |
| AIRD | 0.881 | 0.745 | 0.794 |
| FSTAD | 0.868 | 0.772 | 0.701 |
| VGAE | 0.540 | 0.517 | 0.524 |
| DOMINANT | 0.767 | 0.695 | 0.709 |
| GATE | 0.884 | 0.777 | 0.826 |
| SSGAE1 | 0.927 | 0.832 | 0.869 |
| Dataset | |||
|---|---|---|---|
| LabPatrolling | BehaviorMonitoring | AnoVisualGenome | |
| Spatial Attributed Graph | 0.915 | 0.807 | 0.833 |
| Semantic Attributed Graph | 0.924 | 0.778 | 0.791 |
| Mean-pooling Aggregation | 0.922 | 0.798 | 0.821 |
| Max-pooling Aggregation | 0.923 | 0.805 | 0.836 |
| SSGAE1 | 0.927 | 0.832 | 0.869 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Fadjrimiratno, M.F.; Suzuki, E. Region Anomaly Detection via Spatial and Semantic Attributed Graph in Human Monitoring. Sensors 2023, 23, 1307. https://doi.org/10.3390/s23031307
Zhang K, Fadjrimiratno MF, Suzuki E. Region Anomaly Detection via Spatial and Semantic Attributed Graph in Human Monitoring. Sensors. 2023; 23(3):1307. https://doi.org/10.3390/s23031307
Chicago/Turabian StyleZhang, Kang, Muhammad Fikko Fadjrimiratno, and Einoshin Suzuki. 2023. "Region Anomaly Detection via Spatial and Semantic Attributed Graph in Human Monitoring" Sensors 23, no. 3: 1307. https://doi.org/10.3390/s23031307
APA StyleZhang, K., Fadjrimiratno, M. F., & Suzuki, E. (2023). Region Anomaly Detection via Spatial and Semantic Attributed Graph in Human Monitoring. Sensors, 23(3), 1307. https://doi.org/10.3390/s23031307







