A Joint-Parameter Estimation and Bayesian Reconstruction Approach to Low-Dose CT †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Bayesian Image Reconstruction for CT
2.1.1. Multivariate Gaussian Distribution Data Model
2.1.2. Multivariate Gaussian MRF Prior Model
2.2. Unobservable Parameter Estimation by Joint-Parameter-Bayes
| Algorithm 1. Joint-MAP-Bayes | |
| Initialization: | |
| Initialize and by Equations (14) and (15) with | |
| For each iteration: | |
| While (Stopping criterion is not met) | |
| For each voxel j: | |
| end | |
| Update and by Equations (14) and (15) | |
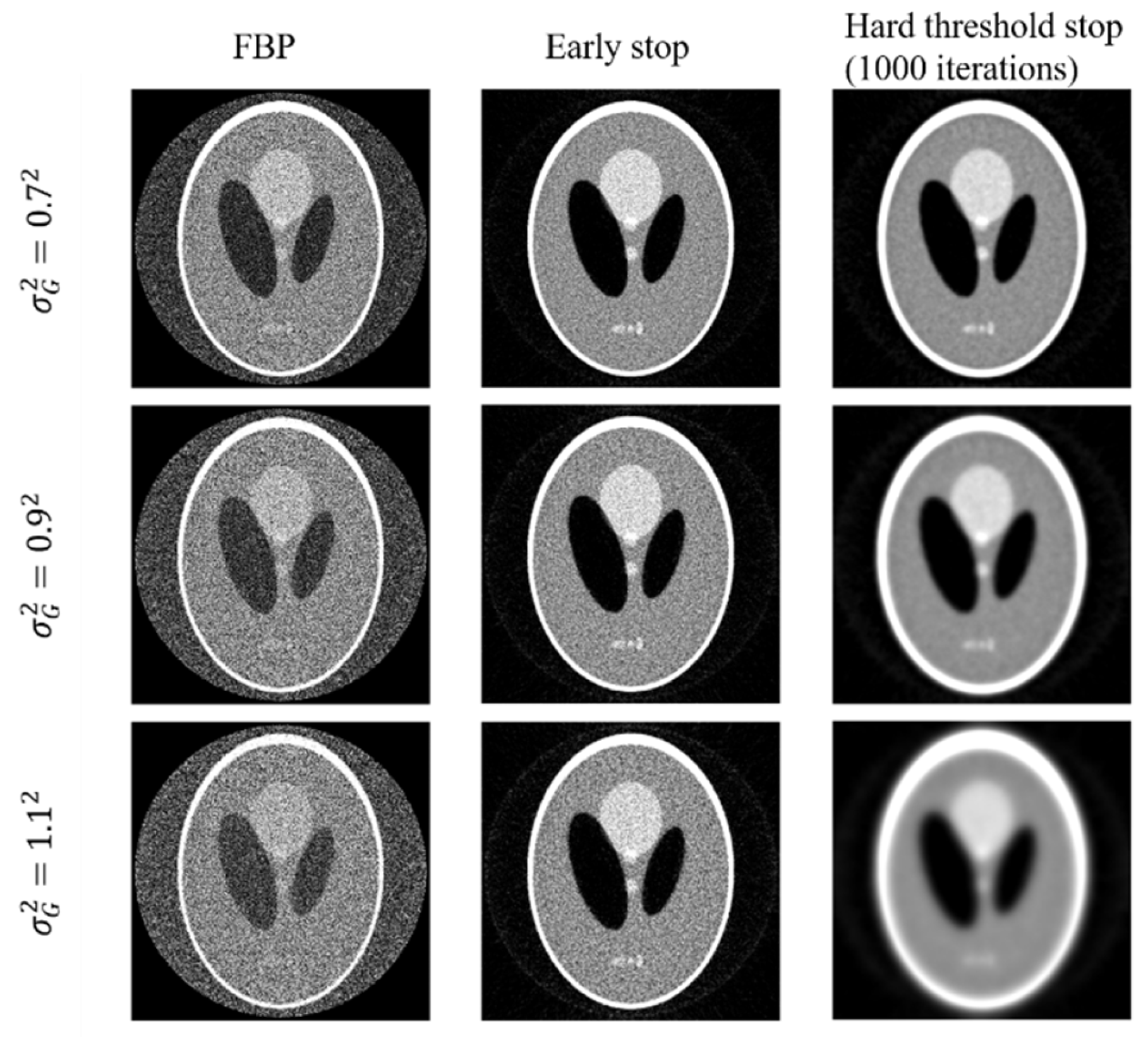
2.3. Stopping Criterion Investigation
2.4. Stability Investigation
2.5. Phantom Simulation and Patient Data Acquisition
3. Results
3.1. Results of Numerical Simulation Data
3.1.1. Reconstruction Comparison
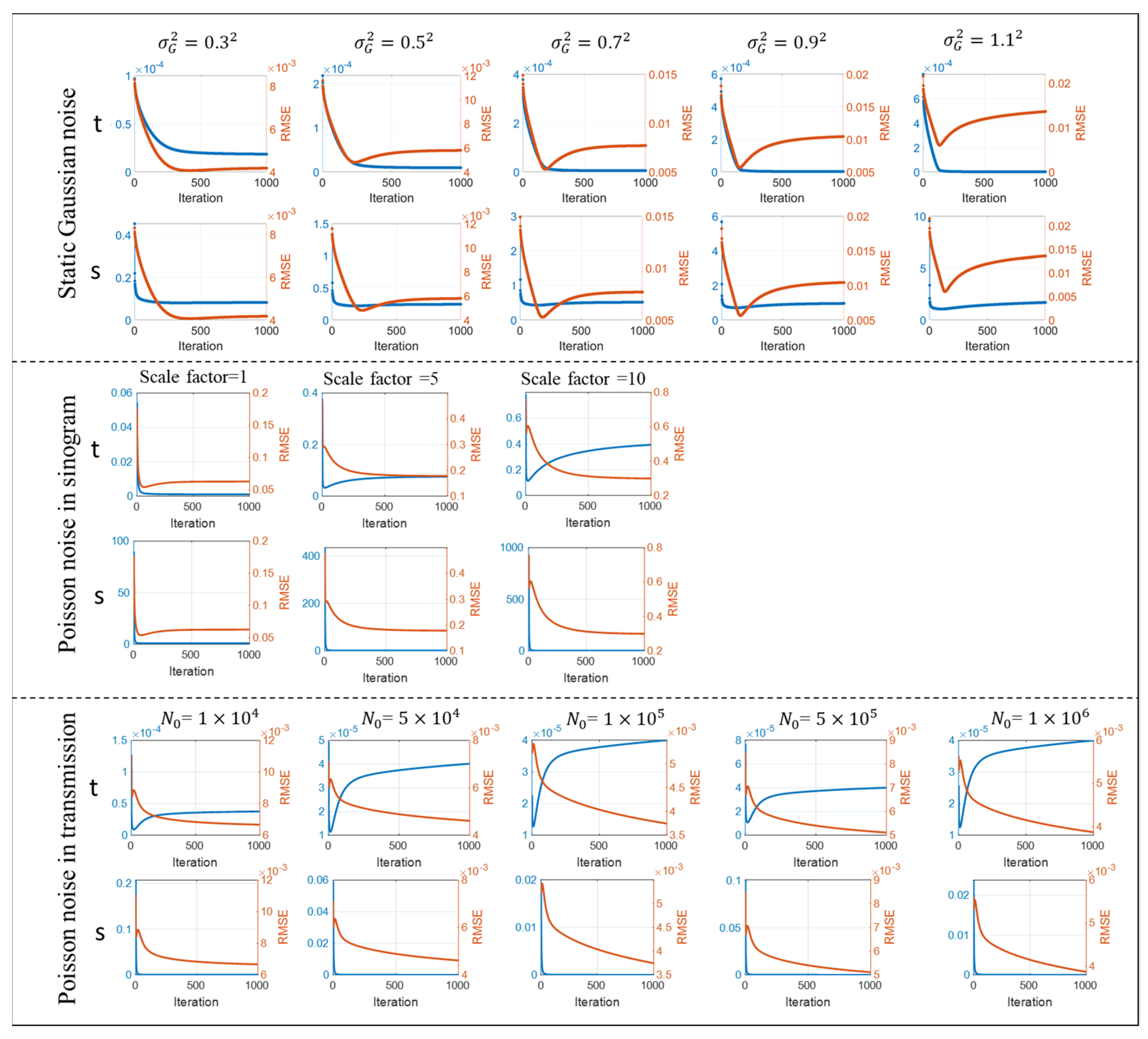
3.1.2. Stopping Criterion Investigation
3.1.3. Stability Investigation
- (a)
- Effect of Initialization
- (b)
- Effects of Variance Normalization
3.2. Results of Clinical Patient Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
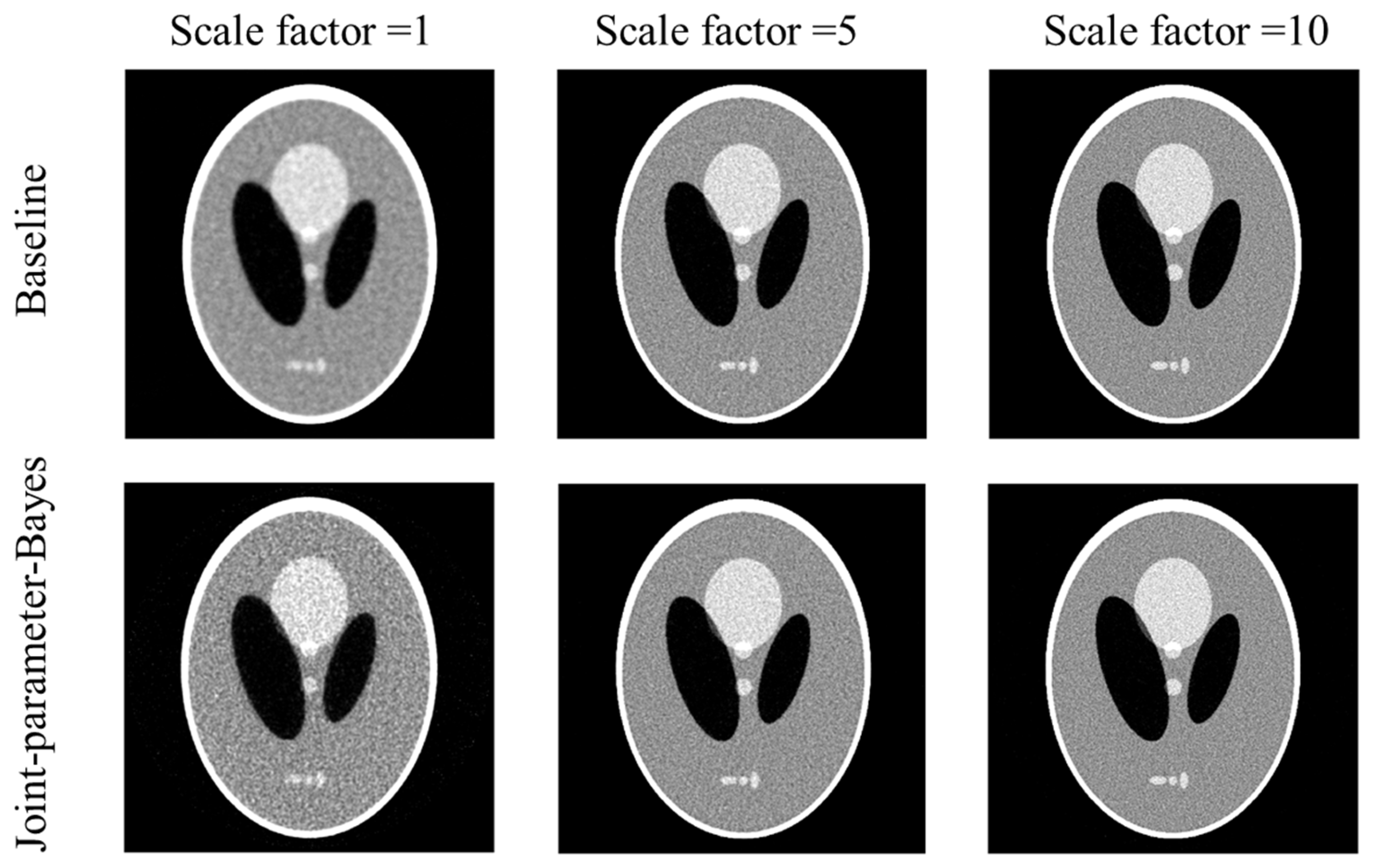
| Conventional MAP (Baseline) | Joint-Parameter-Bayes | |||||||
|---|---|---|---|---|---|---|---|---|
| Scale Factor | RMSE | SSIM | PSNR | Iterations | RMSE | SSIM | PSNR | Iterations |
| 0.0643 | 0.9109 | 23.84 | 1000 * trial number | 0.0547 | 0.8249 | 25.24 | 81 | |
| 0.1844 | 0.6445 | 14.68 | 1000 * trial number | 0.1848 | 0.6358 | 14.67 | 1000 | |
| 0.2994 | 0.6091 | 10.48 | 1000 * trial number | 0.3073 | 0.5904 | 10.25 | 1000 | |

| Conventional MAP (Baseline) | Joint-Parameter-Bayes | |||||||
|---|---|---|---|---|---|---|---|---|
| Incident Flux | RMSE | SSIM | PSNR | Iterations | RMSE | SSIM | PSNR | Iterations |
| 0.0065 | 0.9744 | 43.69 | 1000 * trial number | 0.0067 | 0.9731 | 43.53 | 1000 | |
| 0.0048 | 0.9864 | 46.36 | 1000 * trial number | 0.0051 | 0.9853 | 45.83 | 1000 | |
| 0.0042 | 0.9898 | 47.46 | 1000 * trial number | 0.0046 | 0.9885 | 46.73 | 1000 | |
| 0.0033 | 0.9941 | 49.68 | 1000 * trial number | 0.0038 | 0.9931 | 48.25 | 1000 | |
| 0.0031 | 0.9946 | 50.04 | 1000 * trial number | 0.0037 | 0.9937 | 48.53 | 1000 | |
References
- Schwenzer, N.F.; Springer, F.; Schraml, C.; Stefan, N.; Machann, J.; Schick, F. Non-invasive assessment and quantification of liver steatosis by ultrasound, computed tomography and magnetic resonance. J. Hepatol. 2009, 51, 433–445. [Google Scholar] [CrossRef] [PubMed]
- Deans, S.R. The Radon Transform and Some of Its Applications; Courier Corporation: Chelmsford, MA, USA, 2007. [Google Scholar]
- Shepp, L.A.; Logan, B.F. The Fourier reconstruction of a head section. IEEE Trans. Nucl. Sci. 1974, 21, 21–43. [Google Scholar] [CrossRef]
- Liang, Z.; La Riviere, P.; El Fakhri, G.; Glick, S.; Siewerdsen, J. Low-Dose CT: What Has Been Done, and What Challenges Remain. IEEE Trans. Med. Imaging 2017, 36, 2409–2416. [Google Scholar] [CrossRef]
- Jin, B.; Zhao, Y.; Zou, J. Iterative parameter choice by discrepancy principle. IMA J. Numer. Anal. 2012, 32, 1714–1732. [Google Scholar] [CrossRef]
- Golub, G.H.; Wahba, G. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics 1979, 21, 215–223. [Google Scholar] [CrossRef]
- Hansen, P.C. Analysis of discrete ill-posed problems by means of the L-curve. SIAM Rev. 1992, 34, 561–580. [Google Scholar] [CrossRef]
- Kazufumi, I.; Jin, B.; Takeuchi, T. A regularization parameter for nonsmooth Tikhonov regularization. SIAM J. Sci. Comput. 2011, 33, 1415–1438. [Google Scholar]
- Bai, T.; Yan, H.; Jia, X.; Jiang, S.; Wang, G.; Mou, X. Z-index parameterization for volumetric CT image reconstruction via 3-D dictionary learning. IEEE Trans. Med. Imaging 2017, 36, 2466–2478. [Google Scholar] [CrossRef]
- Mou, X.; Bai, T.; Chen, X.; Yu, H.; Yang, Q.; Wang, G. Optimal Selection for Regularization Parameter in Iterative CT Reconstruction Based on the Property of Natural Image Statistics. Fully 3D 2015, 13, 383–386. [Google Scholar]
- Johnson, V.E.; Wong, W.H.; Hu, X.; Chen, C.T. Image restoration using Gibbs priors: Boundary modeling, treatment of blurring, and selection of hyperparameter. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 5, 413–425. [Google Scholar] [CrossRef]
- Hsiao, T.; Rangarajan, A.; Gindi, G.R. Bayesian image reconstruction for transmission tomography using deterministic annealing. J. Electron. Imaging 2003, 12, 7–17. [Google Scholar]
- Cai, C.; Rodet, T.; Legoupil, S.; Mohammad-Djafari, A. A full-spectral Bayesian reconstruction approach based on the material decomposition model applied in dual-energy computed tomography. Med. Phys. 2013, 40, 111916. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, F.; Liu, J.; Luo, J.; Xie, Y.; Bai, J.; Xing, L. Cone beam X-ray luminescence computed tomography based on Bayesian method. IEEE Trans. Med. Imaging 2016, 36, 225–235. [Google Scholar] [CrossRef]
- Veklerov, E.; Llacer, J. Stopping rule for the MLE algorithm based on statistical hypothesis testing. IEEE Trans. Med. Imaging 1987, 6, 313–319. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Herbert, T.J. Statistical stopping criteria for iterative maximum likelihood reconstruction of emission images. Phys. Med. Biol. 1990, 35, 1221. [Google Scholar] [CrossRef]
- Gaitanis, A.; Kontaxakis, G.; Spyrou, G.; Panayiotakis, G.; Tzanakos, G. PET image reconstruction: A stopping rule for the MLEM algorithm based on properties of the updating coefficients. Comput. Med. Imaging Graph. 2010, 34, 131–141. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Liang, Z.; Lu, S.; Shi, Y.; Chang, S.; Hou, W. Hyperparameter Selection for Bayesian Image Reconstruction by Mimicking Physical Crystallization. In Proceedings of the 2020 IEEE Symposium on Nuclear Science (NSS/MIC), Boston, MA, USA, 31 October–7 November 2020. [Google Scholar]
- Gao, Y.; Liang, Z.; Xing, Y.; Zhang, H.; Pomeroy, M.; Lu, S.; Ma, J.; Lu, H.; Moore, W. Characterization of tissue-specific pre-log Bayesian CT reconstruction by texture–dose relationship. Med. Phys. 2020, 47, 5032–5047. [Google Scholar] [CrossRef]
- Ma, J.; Liang, Z.; Fan, Y.; Liu, Y.; Huang, J.; Chen, W.; Lu, H. Variance Analysis of X-ray CT Sinograms in the Presence of Electronic Noise Background. Med. Phys. 2012, 39, 4051–4065. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Li, T.; Lu, H.; Liang, Z. Penalized Weighted Least-squares Approach to Sinogram Noise Reduction and Image Reconstruction for Low-dose X-ray CT. IEEE Trans. Med. Imaging 2006, 25, 1272–1283. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Han, H.; Wang, J.; Ma, J.; Liu, Y.; Moore, W.; Liang, Z. Deriving Adaptive MRF Coefficients from Previous Normal-dose CT Scan for Low-dose Image Reconstruction via Penalized Weighted Least-squares Minimization. Med. Phys. 2014, 41, 041916. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Han, H.; Liang, Z.; Hu, Y.; Moore, W.; Ma, J.; Lu, H. Extracting Information from Previous Full-dose CT Scan for Knowledge-based Bayesian Reconstruction of Current Low-dose CT Images. IEEE Trans. Med. Imaging 2016, 35, 860–870. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, Y.; Liang, Z.; Moore, W.; Zhang, H.; Pomeroy, M.J.; Ferretti, J.A.; Bilfinger, T.V.; Ma, J.; Lu, H. A Feasibility Study of Extracting Tissue Textures from a Previous Full-Dose CT Database as Prior Knowledge for Bayesian Reconstruction of Current Low-dose CT Images. IEEE Trans. Med. Imaging 2019, 38, 1981–1992. [Google Scholar] [CrossRef] [PubMed]
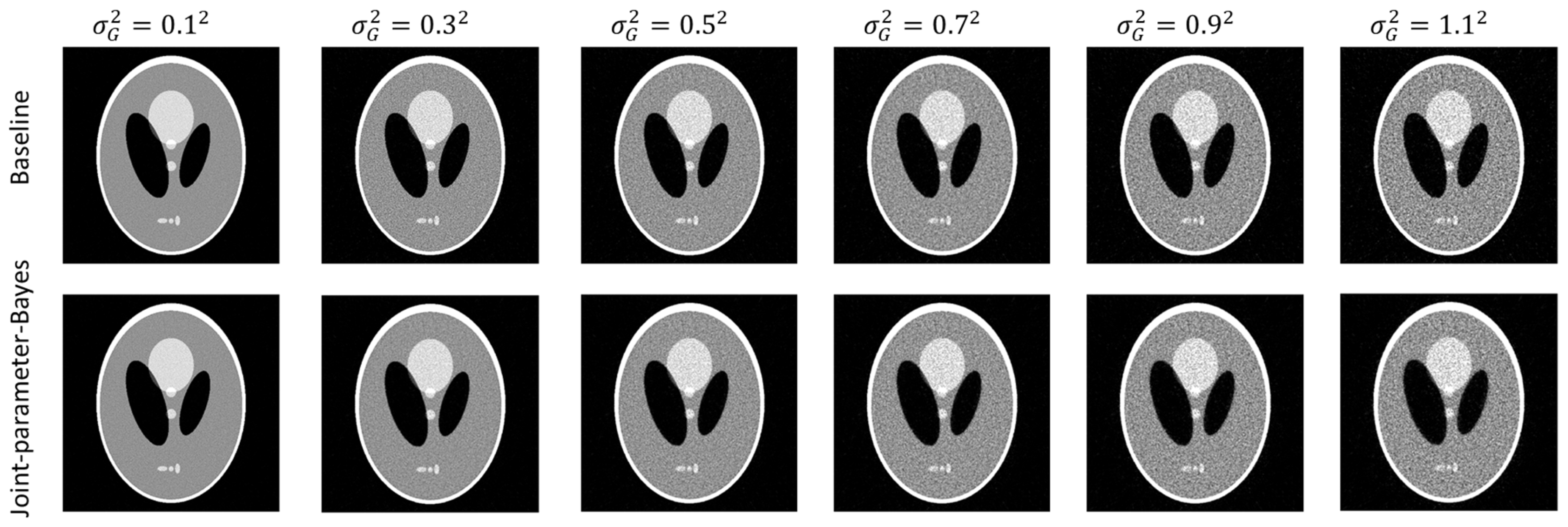






| Conventional MAP (Baseline) | Joint-Parameter-Bayes | |||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | SSIM | PSNR | Iterations | RMSE | SSIM | PSNR | Iterations | |
| 0.002397 | 0.9970 | 52.41 | 1000 * trial number | 0.002264 | 0.9972 | 52.90 | 1000 | |
| 0.003581 | 0.9911 | 48.92 | 1000 * trial number | 0.004125 | 0.9918 | 47.69 | 339 | |
| 0.004440 | 0.9894 | 47.05 | 1000 * trial number | 0.004778 | 0.9881 | 46.42 | 200 | |
| 0.004995 | 0.9867 | 46.03 | 1000 * trial number | 0.00518 | 0.9853 | 45.71 | 157 | |
| 0.005190 | 0.9844 | 45.67 | 1000 * trial number | 0.005501 | 0.9829 | 45.19 | 132 | |
| 0.005426 | 0.9815 | 45.31 | 1000 * trial number | 0.005786 | 0.9805 | 44.75 | 115 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Lu, S.; Shi, Y.; Chang, S.; Zhang, H.; Hou, W.; Li, L.; Liang, Z. A Joint-Parameter Estimation and Bayesian Reconstruction Approach to Low-Dose CT. Sensors 2023, 23, 1374. https://doi.org/10.3390/s23031374
Gao Y, Lu S, Shi Y, Chang S, Zhang H, Hou W, Li L, Liang Z. A Joint-Parameter Estimation and Bayesian Reconstruction Approach to Low-Dose CT. Sensors. 2023; 23(3):1374. https://doi.org/10.3390/s23031374
Chicago/Turabian StyleGao, Yongfeng, Siming Lu, Yongyi Shi, Shaojie Chang, Hao Zhang, Wei Hou, Lihong Li, and Zhengrong Liang. 2023. "A Joint-Parameter Estimation and Bayesian Reconstruction Approach to Low-Dose CT" Sensors 23, no. 3: 1374. https://doi.org/10.3390/s23031374





