Resonant-Based Wireless Power Transfer System Using Electric Coupling for Transparent Wearable Devices and Null Power Points
Abstract
:Simple Summary
Abstract
1. Introduction
- Metal mesh (flexible and transparent material) is used as an ER-WPT coupler and its performance is compared with conventional copper plate material.
- A null power point analysis is conducted and clarifies the reason why the null power point occurs in ER-WPT.
2. WPT System Model
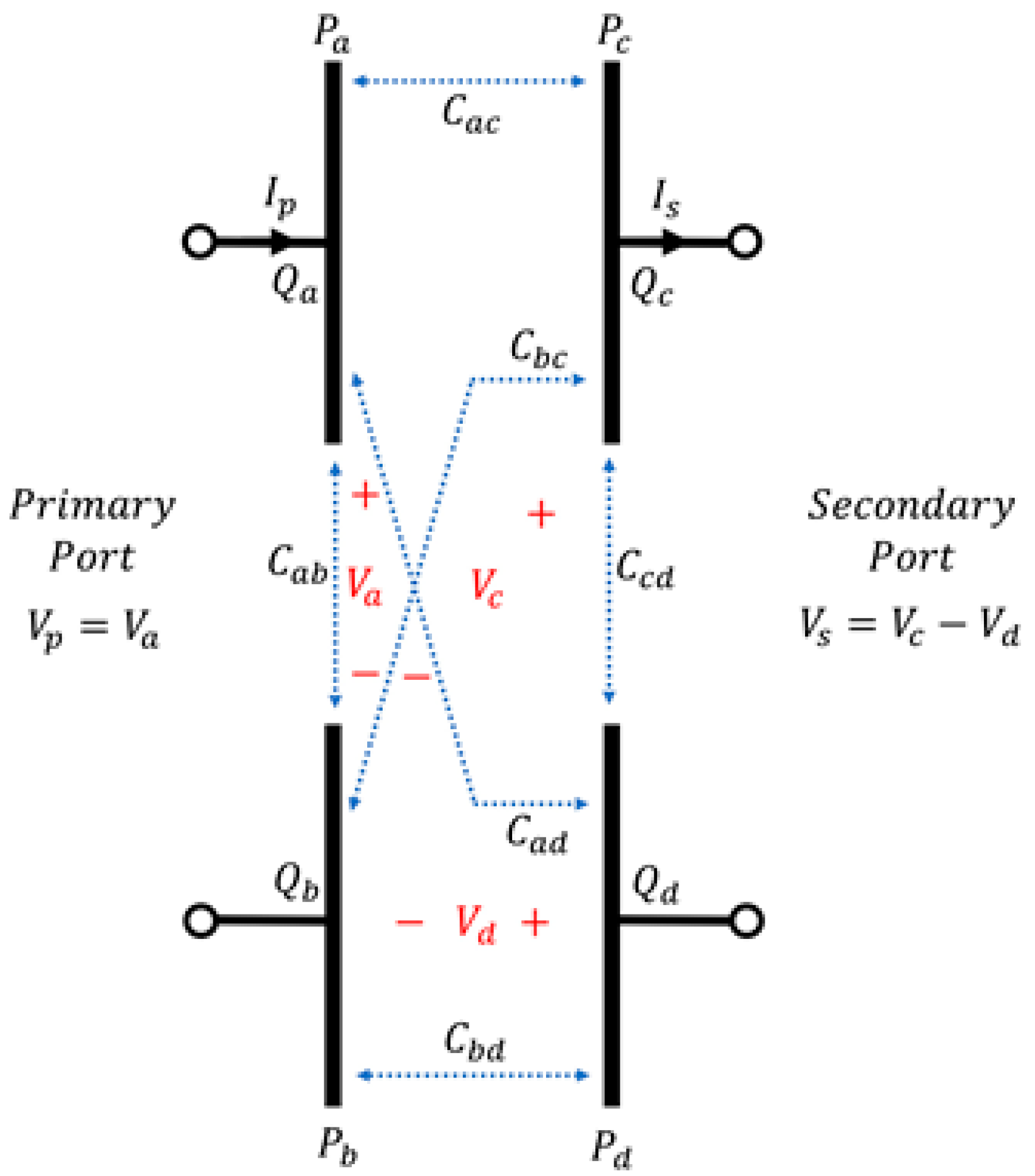
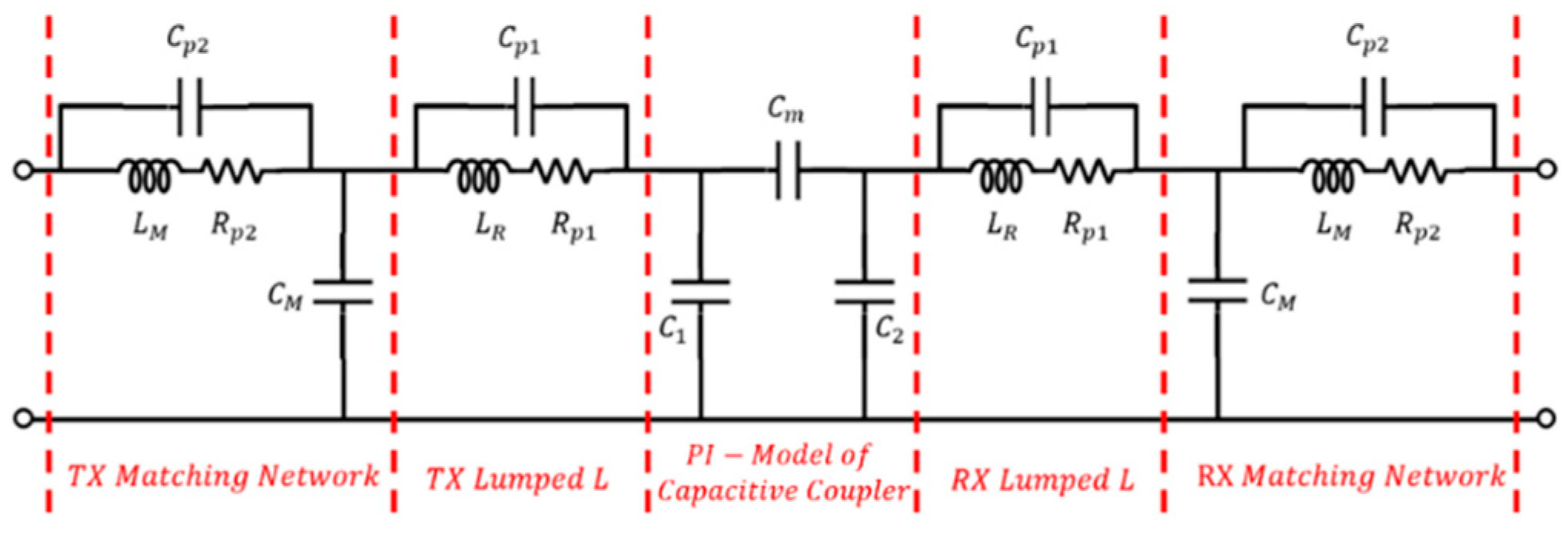
2.1. Configuration of ER-WPT System
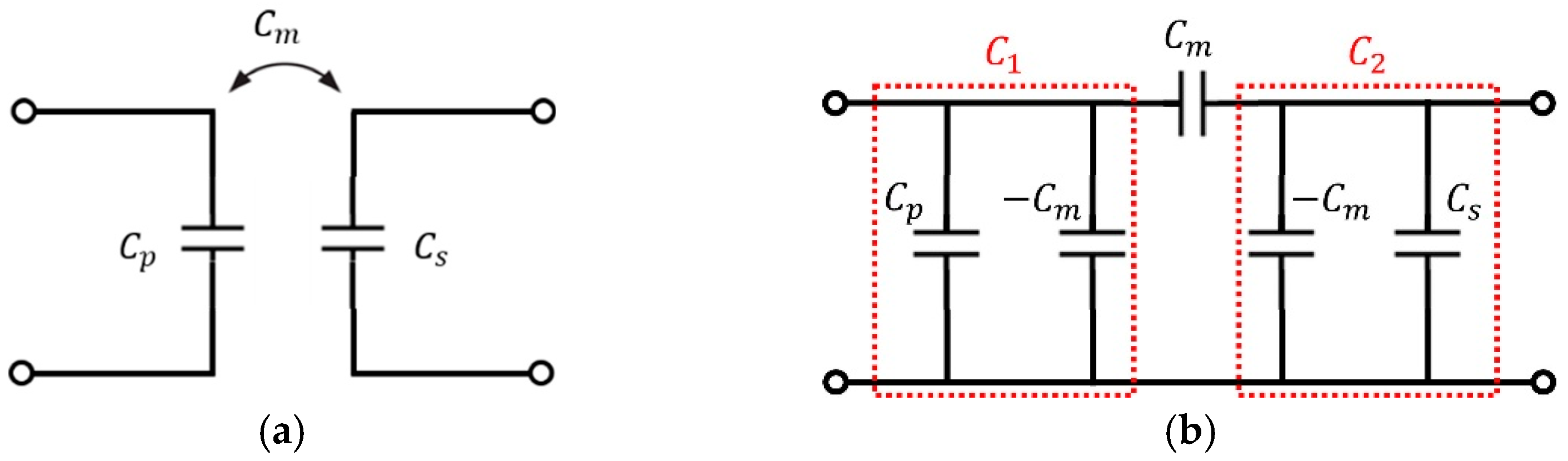
2.2. Structure of Capacitive Coupler
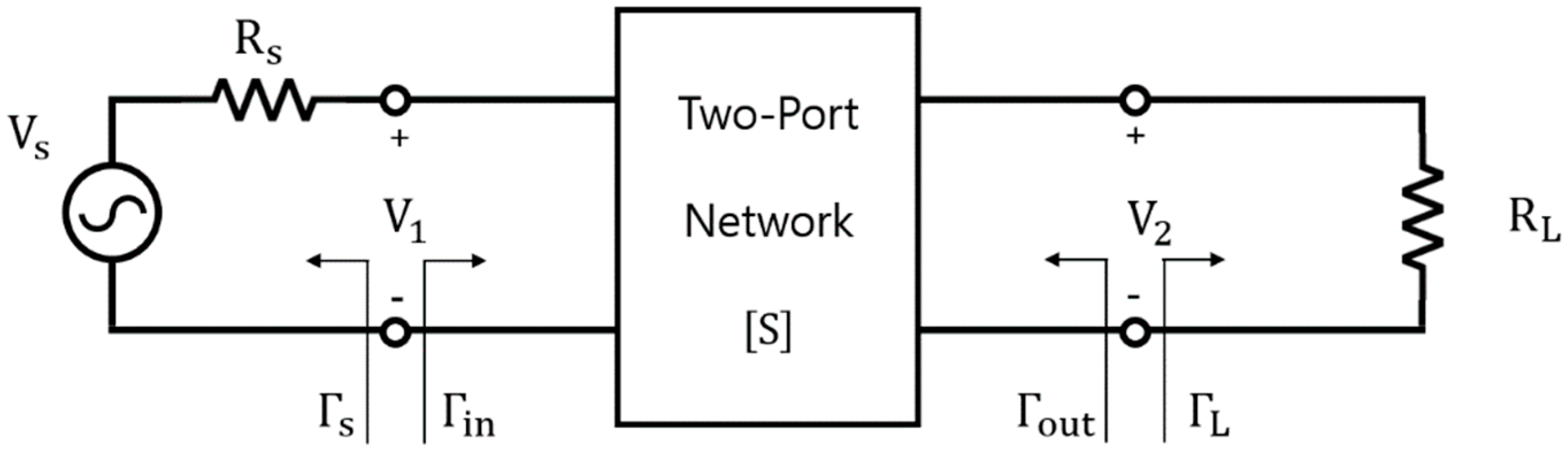
2.3. Measured Equivalent Circuit Model and Power Efficiency
2.4. Null-Power Point and Mutual Capacitance
3. Results and Discussion
3.1. Verification of the Proposed Approach
3.1.1. Fabricated Model
3.1.2. Experimental and Simulation Results
3.2. Power Efficiency Calculated Based on the Proposed Approach
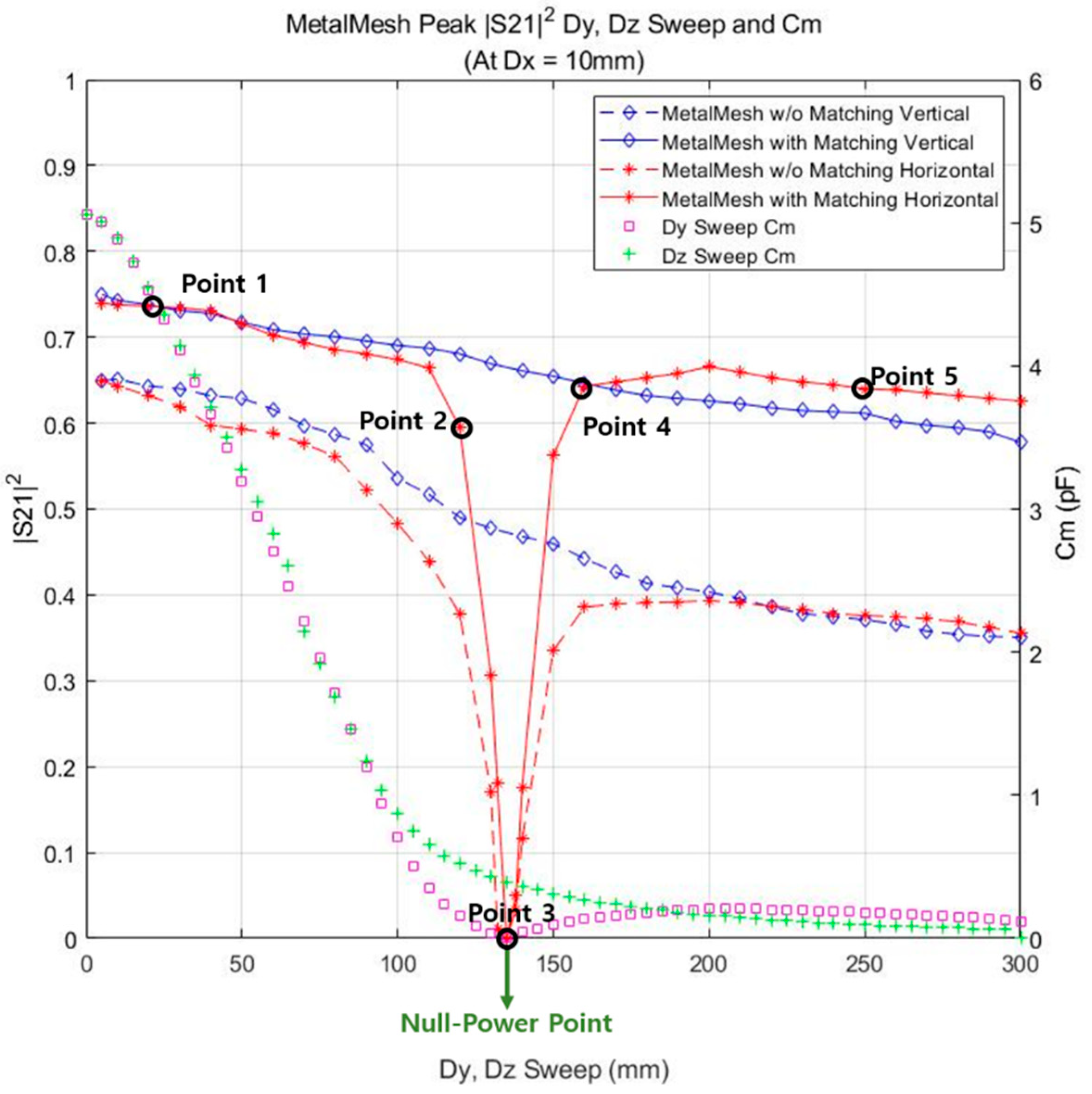
3.3. Null Power Point
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Covic, G.A.; Boys, J.T. Modern Trends in Inductive Power Transfer for Transportation Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 28–41. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, Y.; Kan, T.; Lu, F.; Zhang, K.; Song, B.; Mi, C.C. Frequency Optimization of a Loosely Coupled Underwater Wireless Power Transfer System Considering Eddy Current Loss. IEEE Trans. Ind. Electron. 2018, 66, 3468–3476. [Google Scholar] [CrossRef]
- Chen-Yang, X.; Chao-Wei, L.; Juan, Z. Analysis of power transfer characteristic of capacitive power transfer system and inductively coupled power transfer system. In Proceedings of the 2011 International Conference on Mechatronic Science, Electric Engineering and Computer (MEC), Jilin, China, 19–21 August 2011; pp. 1281–1285. [Google Scholar]
- Maji, S.; Sinha, S.; Regensburger, B.; Monticone, F.; Afridi, K.K. Reduced-Fringing-Field Multi-MHz Capacitive Wireless Power Transfer System Utilizing a Metasurface-based Coupler. In Proceedings of the 2020 IEEE 21st Workshop on Control and Modeling for Power Electronics (COMPEL), Aalborg, Denmark, 9–12 November 2020; pp. 1–6. [Google Scholar]
- Tarek, M.T.; Muharam, A.; Hattori, R. Wireless battery charging system for drones via capacitive power transfer. In Proceedings of the 2017 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW). IEEE, Chongqing, China, 20–22 May 2017; pp. 1–6. [Google Scholar]
- Koruprolu, A.; Nag, S.; Erfani, R.; Mohseni, P. Capacitive Wireless Power and Data Transfer for Implantable Medical Devices. In Proceedings of the 2018 IEEE Biomedical Circuits and Systems Conference (BioCAS), Cleveland, OH, USA, 17–19 October 2018; pp. 1–4. [Google Scholar]
- Zhang, H.; Lu, F.; Hofmann, H.; Liu, W.; Mi, C.C. A four-plate compact capacitive coupler design and LCL-compensated topology for capacitive power transfer in electric vehicle charging application. IEEE Trans. Power Electron. 2016, 31, 8541–8551. [Google Scholar] [CrossRef]
- Kang, S.H.; Park, S.; Jung, C.W. Textile resonators using a sintered metal conductor for wearable MR-WPT with high efficiency and wearability. Microw. Opt. Technol. Lett. 2017, 59, 668–672. [Google Scholar] [CrossRef]
- Lee, H.H.; Jung, C.W. Magnetic resonant-wireless power transfer for transparent laptop applications using μ-metal mesh film. Microw. Opt. Technol. Lett. 2017, 59, 2781–2785. [Google Scholar] [CrossRef]
- Yang, L.; Feng, B.; Zhang, Y.; Li, X.; Zhang, L.; Chen, X.; Nie, J.; Wen, H.; Tian, J.; Jian, J.; et al. Single Wire Capacitive Wireless Power Transfer System for Wearable Biomedical Sensors based on Flexible Graphene Film Material. IEEE Trans. Biomed. Circuits Syst. 2022, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Reatti, A.; Pugi, L.; Corti, F.; Grasso, F. Effect of misalignment in a four plates capacitive wireless power transfer system. In proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC / I&CPS Europe), Madrid, Spain, 9–12 June 2020.
- Lu, F.; Zhang, H.; Hofmann, H.; Mi, C.C. A Double-Sided LC-Compensation Circuit for Loosely Coupled Capacitive Power Transfer. IEEE Trans. Power Electron. 2017, 33, 1633–1643. [Google Scholar] [CrossRef]
- Lu, F.; Zhang, H.; Hofmann, H.; Mi, C. A Double-Sided LCLC-Compensated Capacitive Power Transfer System for Electric Vehicle Charging. IEEE Trans. Power Electron. 2015, 30, 6011–6014. [Google Scholar] [CrossRef]
- Masuda, M.; Kusunoki, M.; Umegami, H.; Hattori, F.; Yamamoto, M. Wireless Power Transfer via Electric Field Resonance Coupling. J. Jpn. Inst. Electron. Packag. 2015, 18, 327–330. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; Hu, A. Defining the mutual coupling of capacitive power transfer for wireless power transfer. Electron. Lett. 2015, 51, 1806–1807. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 558–563. [Google Scholar]
- Park, C.; Park, J.; Shin, Y.; Kim, J.; Huh, S.; Kim, D.; Park, S.; Ahn, S. Separated Circular Capacitive Coupler for Reducing Cross-Coupling Capacitance in Drone Wireless Power Transfer System. IEEE Trans. Microw. Theory Tech. 2020, 68, 3978–3985. [Google Scholar] [CrossRef]
- Bertoluzzo, M.; Buja, G.; Dashora, H. Avoiding null power point in DD coils. In Proceedings of the IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), London, UK, 18–21 June 2019. [Google Scholar]




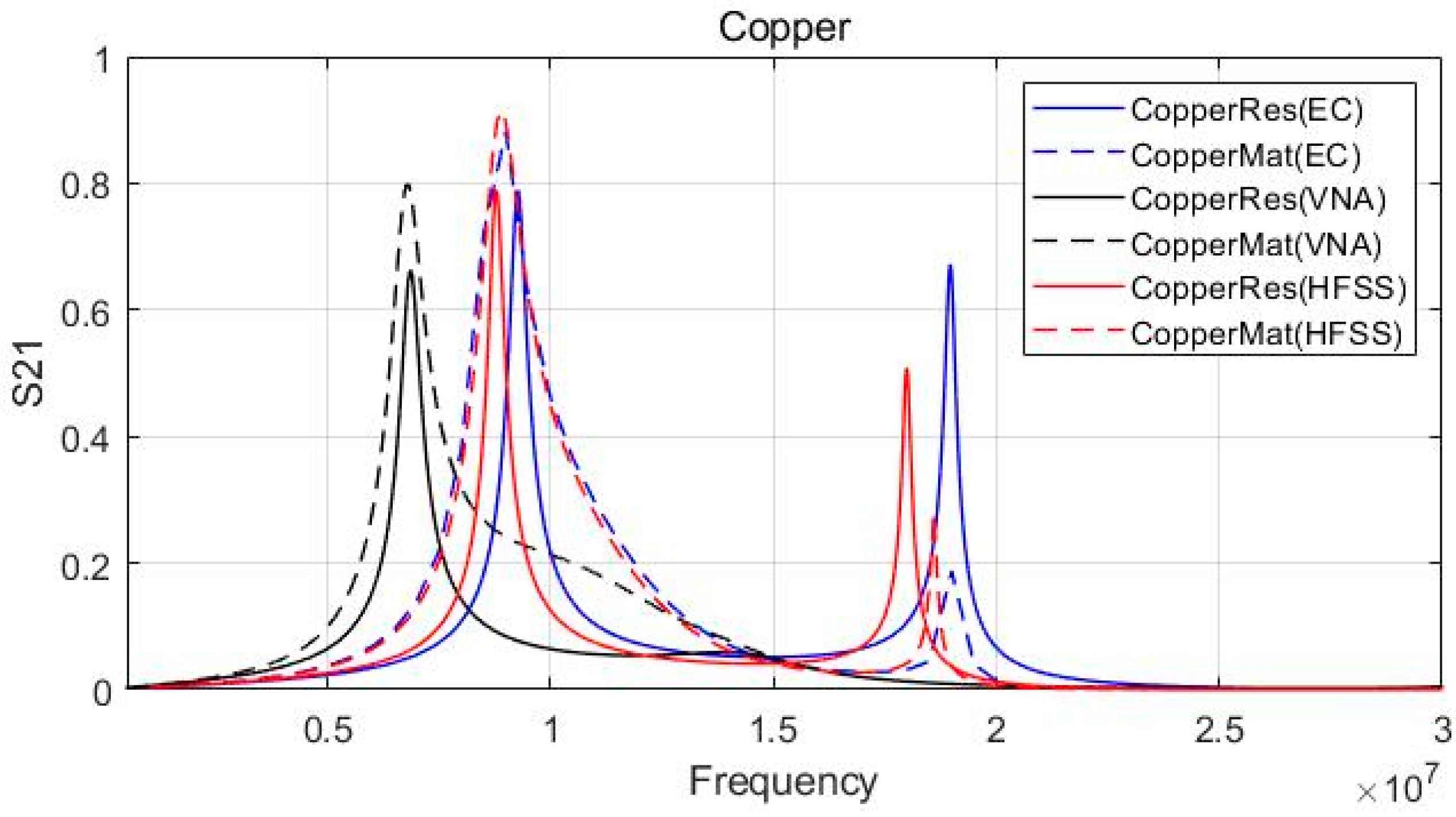


| Parameter | ||
|---|---|---|
| , | 12.552 pF, 12.472 pF | 12.275 pF, 12.213 pF |
| , | 1.401 pF, 1.418 pF | 1.282 pF, 1.316 pF |
| , | 1.325 pF, 1.408 pF | 1.237 pF, 1.221 pF |
| 5.57 pF | 5.5 pF | |
| , | 2.8 pF | 2.5 pF |
| Parameter | Copper Plate | Metal Mesh |
|---|---|---|
| 20 μH | 20 μH | |
| 180 pF | 180 pF | |
| 1.2 μH | 1 μH | |
| 10 , 1.5 | 10, 1.2 | |
| 2 pF, 1 pF | 2 pF, 0.8 pF |
| Point 1 20 mm | Point 2 120 mm | Point 3 135 mm | Point 4 160 mm | Point 5 250 mm | |
|---|---|---|---|---|---|
| 9.33 pF | 1.41 pF | 1.09 pF | 0.766 pF | 0.286 pF | |
| 0.39 pF | 4.02 pF | 5.40 pF | 7.65 pF | 6.82 pF | |
| 0.18 pF | 0.22 pF | 0.23 pF | 0.24 pF | 0.21 pF | |
| 87.05 pF | 1.988pF | 1.21 pF | 0.587 pF | 0.082 pF | |
| 0.070 pF | 0.884 pF | 1.242 pF | 1.836 pF | 1.432 pF | |
| 86.98 pF | 1.104 pF | 0.032 pF | 1.249 pF | 1.35 pF | |
| 4.528 pF | 0.156 pF | 0.006 pF | 0.134 pF | 0.180 pF |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bang, K.; Bae, H.; Park, S. Resonant-Based Wireless Power Transfer System Using Electric Coupling for Transparent Wearable Devices and Null Power Points. Sensors 2023, 23, 1535. https://doi.org/10.3390/s23031535
Bang K, Bae H, Park S. Resonant-Based Wireless Power Transfer System Using Electric Coupling for Transparent Wearable Devices and Null Power Points. Sensors. 2023; 23(3):1535. https://doi.org/10.3390/s23031535
Chicago/Turabian StyleBang, Kyeungwon, Hongguk Bae, and Sangwook Park. 2023. "Resonant-Based Wireless Power Transfer System Using Electric Coupling for Transparent Wearable Devices and Null Power Points" Sensors 23, no. 3: 1535. https://doi.org/10.3390/s23031535





