Comparison of Heuristic Algorithms in Identification of Parameters of Anomalous Diffusion Model Based on Measurements from Sensors
Abstract
:1. Introduction
2. Anomalous Diffusion Model
3. Numerical Solution of Direct Problem
4. Inverse Problem and the Procedure for Its Solution
5. Meta-Heuristic Algorithms
5.1. ACO for Continuous Function Optimization
- Solution (pheromone) representation. Points from the search area are identified as pheromone patches. In other words, the pheromone spot plays the role of a solution. Thus, k-th pheromone spot (or approximate solution) can be represented as . Each solution (pheromone spot) has its quality calculated on the basis of fitness function . In each iteration of the algorithm, we store a fixed number of pheromone spots in the set of solutions (establish at the start of the algorithm).
- Transformation of the solution by the ant. The procedure of constructing a new solution, in the first place, consists in choosing one of the current solutions (pheromone spots) with a certain probability. The quality of the solution is a factor that determines the probability. The relationship here is as follows: with the increase in the quality of the solution, the probability of selection increases. In this paper, the following formula is adopted to calculate the probability (based on the rank) of the k-th solution:where L denotes number of all pheromone spots, and is expressed by the formula:The symbol in the Equation (11) denotes the rank of the k-th solution in the set of solutions. The parameter q is a parameter that narrows the search area. In case of small value of q, the choice of the best solution is preferred. The greater q, the closer the probabilities of choosing each of the solutions. After choosing k-th solution, it is required to perform Gaussian sampling using the formula:where is i-th coordinate of k-th solution and is the calculated average distance between the chosen k-th solution and all the other solutions.
- Pheromone spots update. In each iteration of the ACO algorithm, M of new solutions is created (M denotes the number of ants). These solutions should be included in the solution set. In total, there are of pheromone spots in the set. Then the spots (solutions) are sorted by quality. The worst solutions in the M set are removed. Thus, the solution set always has a fixed number of elements equal to L.
| Algorithm 1 Pseudocode of ACO algorithm. |
| 1: Initialization part. |
| 2: Configuration of ACO algorithm parameters. |
| 3: Initialization of starting population in a random way. |
| 4: Calculation value of the fitness function F for all pheromone spots and sorting them according to their rank (quality). |
| 5: Iterative part. |
| 6: for do |
| 7: Assignment of probability to pheromone spots according to the Equation (10). |
| 8: for do |
| 9: The ant chooses the k-th () solution with probability . |
| 10: for do |
| 11: Using the probability density function (12) in the sampling process, the ant changes the j-th coordinate of the k-th solution. |
| 12: end for |
| 13: end for |
| 14: Calculation the value of the fitness function F for M new solutions. |
| 15: Adding M new solutions to the set of archive of old, sorting the archive by quality and then rejection of the M worst solutions. |
| 16: end for |
| 17: return best solution . |
5.2. Dynamic Butterfly Optimization Algorithm
- Butterflies in the considered environment emit fragrances that differ in intensity, which results from the quality of the solution. Communication between these animals takes place through sensing the emitted fragrances.
- There are two ways of movement of a butterfly, namely: towards a more intense fragrance emitted by another butterfly and in a random direction.
- Global search is represented by:where is the position of the butterfly (agent) before the move, and is the transformation position of the butterfly, is the position of the best butterfly in the current population, and f is the fragrance of a butterfly and r denotes a number from the range selected in a random way.
- Local search move is formulated by:where , are randomly selected butterflies from the population.
| Algorithm 2 Pseudocode of LSAM operator. |
| 1: —random solution among the top half best agents in population (obtained from BOA). |
| 2: —value of the fitness function for . |
| 3: I—number of iterations, —mutation rate. |
| 4: Iterative part. |
| 5: for do |
| 6: Calculate: Mutate(), . |
| 7: if then |
| 8: , . |
| 9: else |
| 10: Set a random solution from the population, but not . |
| 11: Compute the fitness function . |
| 12: if then |
| 13: |
| 14: end if |
| 15: end if |
| 16: end for |
| Algorithm 3 Pseudocode of DBOA. |
| 1: Initialization part. |
| 2: Determine parameters of BOA algorithm. N—number of butterfly in population, n—dimension, c—sensor modality and a, , p parameters. |
| 3: Random generate starting population . |
| 4: Calculate the value of the fitness function F (hence intensity of the stimulus ) for each butterfly in population. |
Iterative part. |
| for do |
| for do |
| Calculate value of fragnance for with the use of Equation (13). |
| 5: end for |
| Set the best agent among the butterflies. |
| for do |
| Set a random number r from range . |
| if then |
| 10: Convert solution in accordance with the Equation (14). |
| else |
| Convert solution in accordance with the Equation (15). |
| end if |
| end for |
| 15: Change value of the parameter a. |
| Adopt the LSAM algorithm to convert the agents population with mutation rate . |
| end for |
| return . |
5.3. Aquila Optimizer
- Expanded exploration. In the case that a predator is high in the air and wants to hunt other birds, it tilts vertically. After locating the victim from a height, Aquila begins nosediving with increasing speed. We can express this phenomenon with the use of the following equation:where is solution after transformation, is the best solution so far and symbolizes position of the prey, i is current iteration, I is number of maximum iteration and is random number from . In this case can also be defined as the optimization goal or approximate solution. Vector is mean solution from all population:
- Narrowed exploration. This technique involves circling the prey in flight and preparing to drop the earth and attack the prey. It is also known as short stroke contour flight. This is described in the algorithm by the equation:where and denotes the same as in expanded exploration point, is a random solution from population and is a random number from interval . Term simulates spiral flight of Aquila. Expression is random value of the Levy flight distribution:where are constants denote random numbers from range , and is formulated as follows [34]:In above equation denotes gamma function. In order to determine the values of the parameters r and the following formula is used:where is a fixed integer from , are small constants, is an integer from .
- Expanded exploitation. This hunting technique begins with a vertical attack on a prey, which location is known within some approximation defining the search area. Thanks to this information, Aquila gets as close to its prey as possible. It can be described as follows:where is the solution after transformation, is the best solution at the moment and is the mean solution in all population determined with the use of the formula (18). As before, denotes a random number from range , while , are lower and upper bound, and are constants parameters of exploitation regulation.
- Narrowed exploitation. The characteristic feature of this technique are the stochastic movements of the bird, which attacks the prey in close proximity. It can be described by the formula:where denotes solution before transformation, is quality function:and are described by:We can adjust the algorithm with the above parameters.
| Algorithm 4 Pseudocode of AO. |
| 1: Initialization part. |
| 2: Set up parameters of AO algorithm. |
| 3: Initialize population in a random way . |
| 4: Iterative part. |
| 5: for do |
| 6: Determine values of the fitness function F for each agent in the population. |
| 7: Establish the best solution in the population. |
| 8: for do |
| 9: Calculate mean solution in the population. |
| 10: Improve parameters of the algorithm. |
| 11: if then |
| 12: if then |
| 13: Perform step expanded exploration (17) by updating solution . |
| 14: In the result solution is obtained. |
| 15: if then make substitution |
| 16: end if |
| 17: if then make substitution |
| 18: end if |
| 19: else |
| 20: Perform step narrowed exploration (19) by updating solution . |
| 21: In the result solution is obtained. |
| 22: if then make substitution . |
| 23: end if |
| 24: if then make substitution . |
| 25: end if |
| 26: end if |
| 27: else |
| 28: if then |
| 29: Perform step Expanded exploitation (23) by updating solution . |
| 30: In the result solution is obtained. |
| 31: if then make substitution . |
| 32: end if |
| 33: if then make substitution . |
| 34: end if |
| 35: else |
| 36: Perform step narrowed exploitation (24) by updating solution . |
| 37: In the result solution is obtained. |
| 38: if then make substitution . |
| 39: end if |
| 40: if then make substitution . |
| 41: end if |
| 42: end if |
| 43: end if |
| 44: end for |
| 45: end for |
| 46: return . |
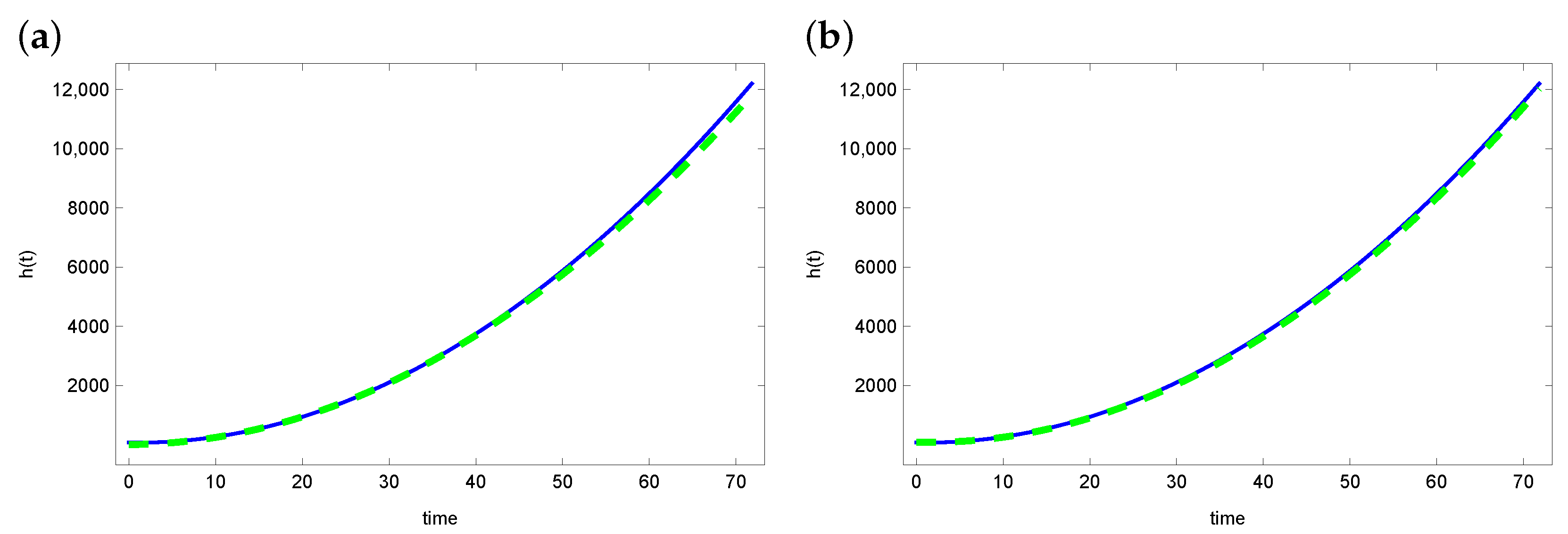
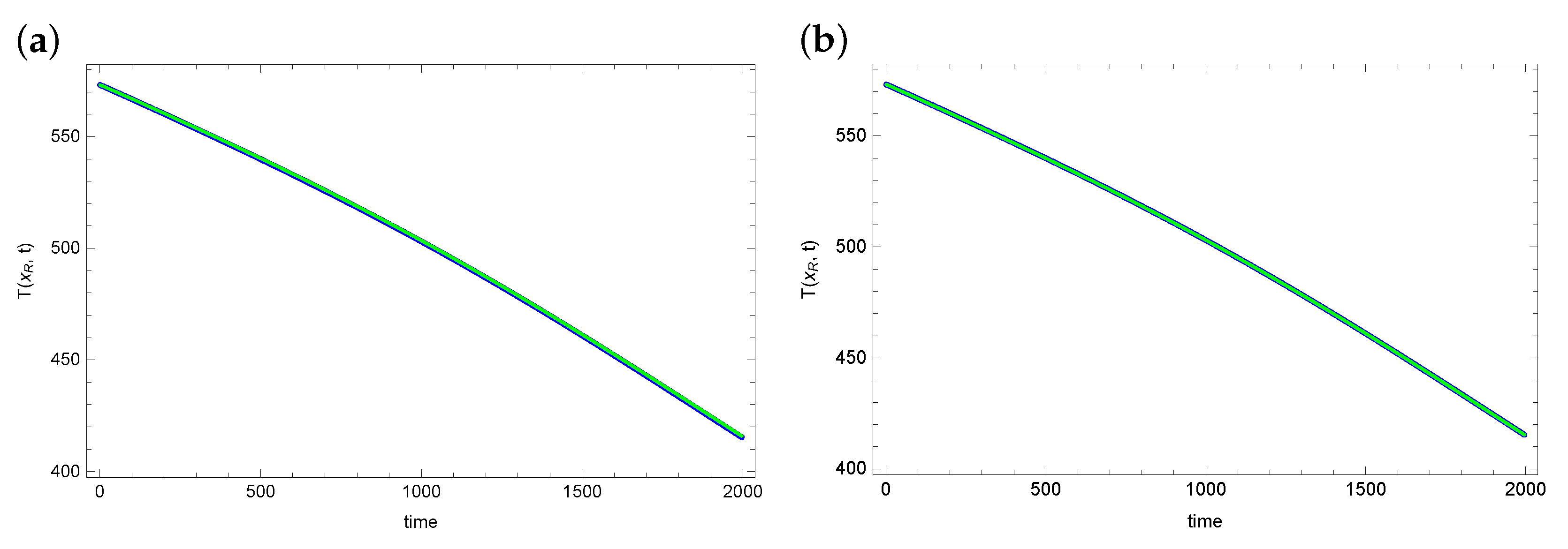
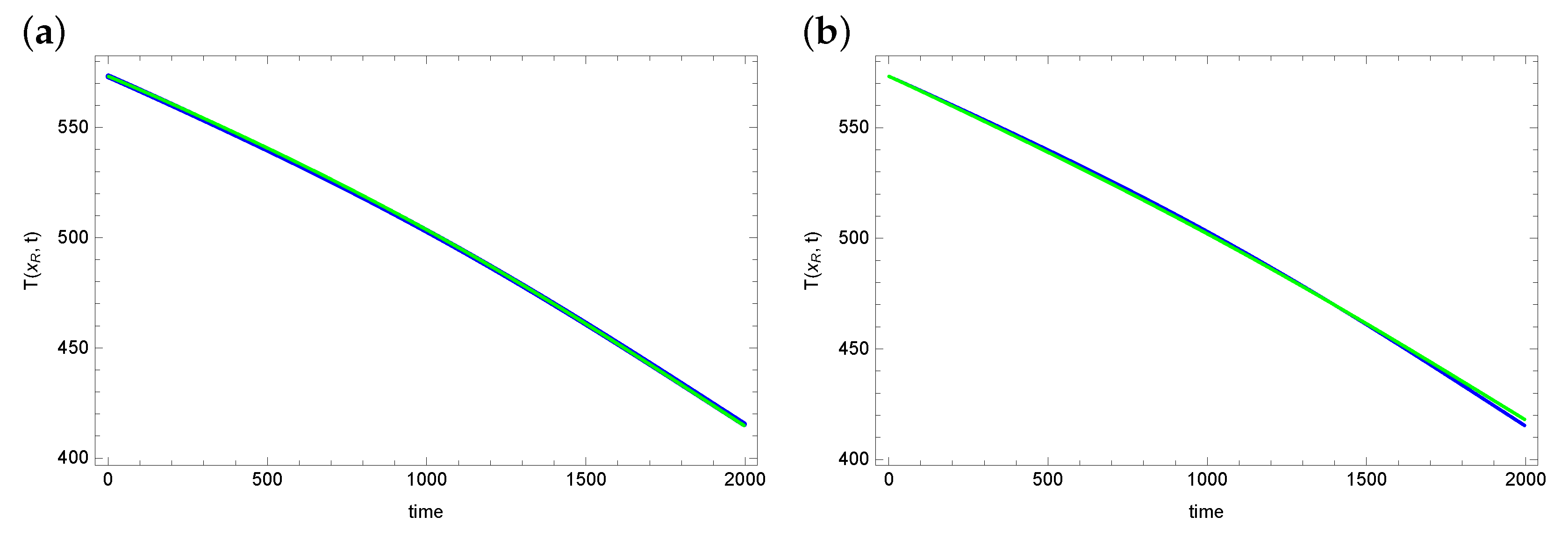
6. Numerical Example and Test of Algorithms
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ketelbuters, J.J.; Hainaut, D. CDS pricing with fractional Hawkes processes. Eur. J. Oper. Res. 2022, 297, 1139–1150. [Google Scholar] [CrossRef]
- Ming, H.; Wang, J.; Fečkan, M. The Application of Fractional Calculus in Chinese Economic Growth Models. Appl. Math. Comput. 2019, 7, 665. [Google Scholar] [CrossRef]
- Bas, E.; Ozarslan, R. Real world applications of fractional models by Atangana–Baleanu fractional derivative. Chaos Solitons Fractals 2018, 116, 121–125. [Google Scholar] [CrossRef]
- Ozkose, F.; Yılmaz, S.; Yavuz, M.; Ozturk, I.; Şenel, M.T.; Bağcı, B.S.; Dogan, M.; Onal, O. A Fractional Modeling of Tumor–Immune System Interaction Related to Lung Cancer with Real Data. Eur. Phys. J. Plus 2022, 137, 1–28. [Google Scholar] [CrossRef]
- De Gaetano, A.; Sakulrang, S.; Borri, A.; Pitocco, D.; Sungnul, S.; Moore, E.J. Modeling continuous glucose monitoring with fractional differential equations subject to shocks. J. Theor. Biol. 2021, 526, 110776. [Google Scholar] [CrossRef] [PubMed]
- Singh, H.; Kumar, D.; Baleanu, D. Methods of Mathematical Modelling. Fractional Differential Equations; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Meng, R. Application of Fractional Calculus to Modeling the Non-Linear Behaviors of Ferroelectric Polymer Composites: Viscoelasticity and Dielectricity. Membranes 2021, 11, 409. [Google Scholar] [CrossRef] [PubMed]
- Maslovskaya, A.; Moroz, L. Time-fractional Landau–Khalatnikov model applied to numerical simulation of polarization switching in ferroelectrics. Nonlinear Dyn. 2023, 111, 4543–4557. [Google Scholar] [CrossRef]
- Kaipio, J.; Somersalo, E. Statistical and Computational Inverse Problems; Springer: New York, NY, USA, 2005. [Google Scholar]
- Marinov, T.; Marinova, R. An inverse problem solution for thermal conductivity reconstruction. Wseas Trans. Syst. 2021, 20, 187–195. [Google Scholar] [CrossRef]
- Brociek, R.; Słota, D.; Król, M.; Matula, G.; Kwaśny, W. Comparison of mathematical models with fractional derivative for the heat conduction inverse problem based on the measurements of temperature in porous aluminum. Int. J. Heat Mass Transf. 2019, 143, 118440. [Google Scholar] [CrossRef]
- Liang, D.; Cheng, J.; Ke, Z.; Ying, L. Deep Magnetic Resonance Image Reconstruction: Inverse Problems Meet Neural Networks. IEEE Signal Process. Mag. 2020, 37, 141–151. [Google Scholar] [CrossRef] [PubMed]
- Drezet, J.M.; Rappaz, M.; Grün, G.U.; Gremaud, M. Determination of thermophysical properties and boundary conditions of direct chill-cast aluminum alloys using inverse methods. Metall. Mater. Trans. A 2000, 31, 1627–1634. [Google Scholar] [CrossRef]
- Zielonka, A.; Słota, D.; Hetmaniok, E. Application of the Swarm Intelligence Algorithm for Reconstructing the Cooling Conditions of Steel Ingot Continuous Casting. Energies 2020, 13, 2429. [Google Scholar] [CrossRef]
- Okamoto, K.; Li, B. A regularization method for the inverse design of solidification processes with natural convection. Int. J. Heat Mass Transf. 2007, 50, 4409–4423. [Google Scholar] [CrossRef]
- Özişik, M.; Orlande, H. Inverse Heat Transfer: Fundamentals and Applications; Taylor & Francis: New York, NY, USA, 2000. [Google Scholar]
- Neto, F.M.; Neto, A.S. An Introduction to Inverse Problems with Applications; Springer: Berlin, Germany, 2013. [Google Scholar]
- Brociek, R.; Pleszczyński, M.; Zielonka, A.; Wajda, A.; Coco, S.; Sciuto, G.L.; Napoli, C. Application of Heuristic Algorithms in the Tomography Problem for Pre-Mining Anomaly Detection in Coal Seams. Sensors 2022, 22, 7297. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Yang, D. Modeling and Inversion of Airborne and Semi-Airborne Transient Electromagnetic Data with Inexact Transmitter and Receiver Geometries. Remote Sens. 2022, 14, 915. [Google Scholar] [CrossRef]
- Gao, H.; Zahr, M.J.; Wang, J.X. Physics-informed graph neural Galerkin networks: A unified framework for solving PDE-governed forward and inverse problems. Comput. Methods Appl. Mech. Eng. 2022, 390, 114502. [Google Scholar] [CrossRef]
- Kukla, S.; Siedlecka, U.; Ciesielski, M. Fractional Order Dual-Phase-Lag Model of Heat Conduction in a Composite Spherical Medium. Materials 2022, 15, 7251. [Google Scholar] [CrossRef]
- Žecová, M.; Terpák, J. Heat conduction modeling by using fractional-order derivatives. Appl. Math. Comput. 2015, 257, 365–373. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Socha, K.; Dorigo, M. Ant colony optimization for continuous domains. Eur. J. Oper. Res. 2008, 185, 1155–1173. [Google Scholar] [CrossRef]
- Ojha, V.K.; Abraham, A.; Snášel, V. ACO for continuous function optimization: A performance analysis. In Proceedings of the 14th International Conference on Intelligent Systems Design and Applications, Okinawa, Japan, 28–30 November 2014; pp. 145–150. [Google Scholar] [CrossRef] [Green Version]
- Moradi, B.; Kargar, A.; Abazari, S. Transient stability constrained optimal power flow solution using ant colony optimization for continuous domains (ACOR). IET Gener. Transm. Distrib. 2022, 16, 3734–3747. [Google Scholar] [CrossRef]
- Omran, M.G.; Al-Sharhan, S. Improved continuous Ant Colony Optimization algorithms for real-world engineering optimization problems. Eng. Appl. Artif. Intell. 2019, 85, 818–829. [Google Scholar] [CrossRef]
- Brociek, R.; Chmielowska, A.; Słota, D. Comparison of the Probabilistic Ant Colony Optimization Algorithm and Some Iteration Method in Application for Solving the Inverse Problem on Model With the Caputo Type Fractional Derivative. Entropy 2020, 22, 555. [Google Scholar] [CrossRef]
- Tubishat, M.; Alswaitti, M.; Mirjalili, S.; Al-Garadi, M.A.; Alrashdan, M.T.; Rana, T.A. Dynamic Butterfly Optimization Algorithm for Feature Selection. IEEE Access 2020, 8, 194303–194314. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Chen, S.; Chen, R.; Gao, J. A Monarch Butterfly Optimization for the Dynamic Vehicle Routing Problem. Algorithms 2017, 10, 107. [Google Scholar] [CrossRef]
- Xia, Q.; Ding, Y.; Zhang, R.; Liu, M.; Zhang, H.; Dong, X. Blind Source Separation Based on Double-Mutant Butterfly Optimization Algorithm. Sensors 2022, 22, 3979. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Wang, D.; Yang, J. Hybrid-Flash Butterfly Optimization Algorithm with Logistic Mapping for Solving the Engineering Constrained Optimization Problems. Entropy 2022, 24, 525. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-qaness, M.A.; Gandomi, A.H. Aquila Optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Wang, Y.; Xiao, Y.; Guo, Y.; Li, J. Dynamic Chaotic Opposition-Based Learning-Driven Hybrid Aquila Optimizer and Artificial Rabbits Optimization Algorithm: Framework and Applications. Processes 2022, 10, 2703. [Google Scholar] [CrossRef]


| Algorithm | F | ||||||
|---|---|---|---|---|---|---|---|
| ACO | |||||||
| DBOA | |||||||
| AO | |||||||
| BOA |
| Algorithm | ||
|---|---|---|
| ACO | ||
| DBOA | ||
| AO | ||
| BOA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brociek , R.; Wajda, A.; Słota, D. Comparison of Heuristic Algorithms in Identification of Parameters of Anomalous Diffusion Model Based on Measurements from Sensors. Sensors 2023, 23, 1722. https://doi.org/10.3390/s23031722
Brociek R, Wajda A, Słota D. Comparison of Heuristic Algorithms in Identification of Parameters of Anomalous Diffusion Model Based on Measurements from Sensors. Sensors. 2023; 23(3):1722. https://doi.org/10.3390/s23031722
Chicago/Turabian StyleBrociek , Rafał, Agata Wajda, and Damian Słota. 2023. "Comparison of Heuristic Algorithms in Identification of Parameters of Anomalous Diffusion Model Based on Measurements from Sensors" Sensors 23, no. 3: 1722. https://doi.org/10.3390/s23031722
APA StyleBrociek , R., Wajda, A., & Słota, D. (2023). Comparison of Heuristic Algorithms in Identification of Parameters of Anomalous Diffusion Model Based on Measurements from Sensors. Sensors, 23(3), 1722. https://doi.org/10.3390/s23031722









