Figure 1.
Unmanned delivery robots enable fast, efficient, and contactless delivery services. (a) Meituan delivery robots deliver living supplies to epidemic-stricken areas; (b) JD delivery robot cargo transportation test; (c) UISEE delivery robot enables unmanned delivery service at KAUST.
Figure 1.
Unmanned delivery robots enable fast, efficient, and contactless delivery services. (a) Meituan delivery robots deliver living supplies to epidemic-stricken areas; (b) JD delivery robot cargo transportation test; (c) UISEE delivery robot enables unmanned delivery service at KAUST.
Figure 2.
Hierarchy of the Gray Wolf Pack (dominance decreases from top down).
Figure 2.
Hierarchy of the Gray Wolf Pack (dominance decreases from top down).
Figure 3.
Position update of wolf groups in GWO algorithm.
Figure 3.
Position update of wolf groups in GWO algorithm.
Figure 4.
The small period nature of Tent chaotic mapping. (a) At a = 0.5 and initial values of 0.2, 0.4, and 0.8, the Tent chaotic mapping falls into a small loop, resulting in a sequence that is not chaotic in nature. (b) The random sequence generated by the Tent chaos mapping with a = 0.45 and initial values of 0.2, 0.3, and 0.15.
Figure 4.
The small period nature of Tent chaotic mapping. (a) At a = 0.5 and initial values of 0.2, 0.4, and 0.8, the Tent chaotic mapping falls into a small loop, resulting in a sequence that is not chaotic in nature. (b) The random sequence generated by the Tent chaos mapping with a = 0.45 and initial values of 0.2, 0.3, and 0.15.
Figure 5.
Distribution of generated sequences for Tent–Sine chaotic mapping with different parameters. (a) Tent–Sine chaotic mapping at a = 0.5, = 0.7, and initial value of 0.2. (b) Tent–Sine chaotic mapping at a = 0.5, = 0.8, and initial value of 0.2. (c) Tent–Sine chaotic mapping at a = 0.5, = 0.95, and initial value of 0.2.
Figure 5.
Distribution of generated sequences for Tent–Sine chaotic mapping with different parameters. (a) Tent–Sine chaotic mapping at a = 0.5, = 0.7, and initial value of 0.2. (b) Tent–Sine chaotic mapping at a = 0.5, = 0.8, and initial value of 0.2. (c) Tent–Sine chaotic mapping at a = 0.5, = 0.95, and initial value of 0.2.
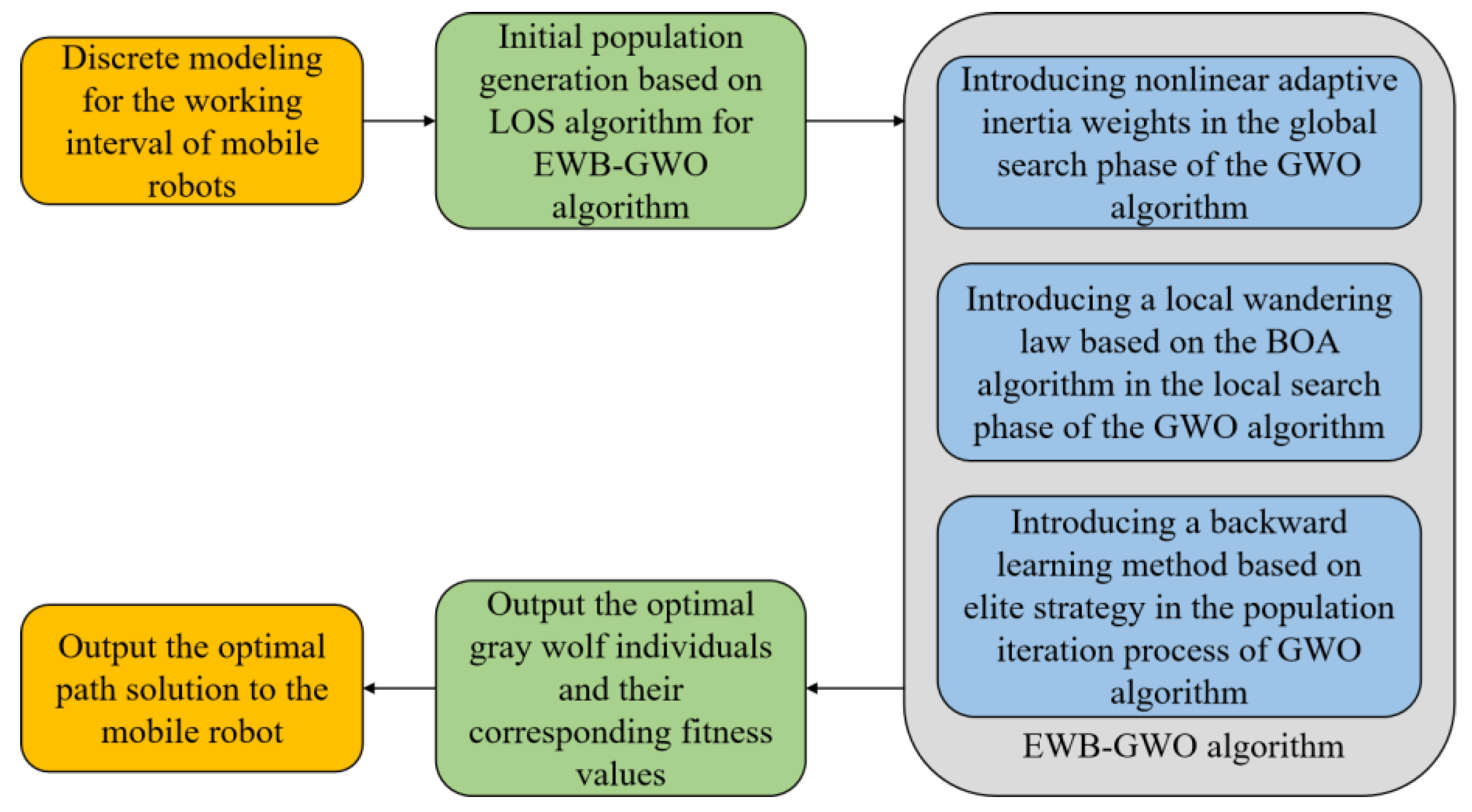
Figure 6.
Workflow for mobile robot path planning based on EWB-GWO algorithm.
Figure 6.
Workflow for mobile robot path planning based on EWB-GWO algorithm.
Figure 7.
Mobile robot workspace based on grid slice.
Figure 7.
Mobile robot workspace based on grid slice.
Figure 8.
Determine if the current node needs to be retained by LOS detection.
Figure 8.
Determine if the current node needs to be retained by LOS detection.
Figure 9.
Complete path example for unmanned delivery robot path planning.
Figure 9.
Complete path example for unmanned delivery robot path planning.
Figure 10.
Comparison of convergence curves of GWO, E−GWO, W−GWO, B−GWO, and EWB−GWO with Dim = 50.
Figure 10.
Comparison of convergence curves of GWO, E−GWO, W−GWO, B−GWO, and EWB−GWO with Dim = 50.
Figure 11.
Comparison of convergence curves of GWO, E−GWO, W−GWO, B−GWO, and EWB−GWO with Dim = 100.
Figure 11.
Comparison of convergence curves of GWO, E−GWO, W−GWO, B−GWO, and EWB−GWO with Dim = 100.
Figure 12.
Comparison of convergence curves of GWO, E−GWO, W−GWO, B−GWO, and EWB−GWO in fixed-dimensional multimodal function tests.
Figure 12.
Comparison of convergence curves of GWO, E−GWO, W−GWO, B−GWO, and EWB−GWO in fixed-dimensional multimodal function tests.
Figure 13.
Comparison of convergence curves of GWO, I−GWO, GWO−CS, PSO−GWO, and EWB−GWO.
Figure 13.
Comparison of convergence curves of GWO, I−GWO, GWO−CS, PSO−GWO, and EWB−GWO.
Figure 14.
Comparison of convergence curves of GWO, B−GWO, W−GWO, E−GWO, EWB−GWO, GA, PSO, BOA, and ABC.
Figure 14.
Comparison of convergence curves of GWO, B−GWO, W−GWO, E−GWO, EWB−GWO, GA, PSO, BOA, and ABC.
Figure 15.
Simulation diagram of drone path planning experiment.
Figure 15.
Simulation diagram of drone path planning experiment.
Table 1.
The benchmark functions used in this article.
Table 1.
The benchmark functions used in this article.
| No. | Name | Formula | Dim | Range | |
|---|
| Unimodal benchmark functions. |
| Exponential | | 50 | [−10, 10] | 0 |
| Quartic | | 50 | [−1.28, 1.28] | 0 |
| Step | | 50 | [−10, 10] | 0 |
| Sum square | | 50 | [−10, 10] | 0 |
| Zakharov | | 50 | [−1, 1] | 0 |
| Rosenbrock | | 50 | [−10, 10] | 0 |
| Schwefel 1.2 | | 50 | [−100, 100] | 0 |
| Cigar | | 50 | [−1, 1] | 0 |
| Multimodal benchmark functions |
| Schwefel 2.26 | | 50 | [−500, 500] | −12,569.5 |
| Rastrigin | | 50 | [−5.12, 5.12] | 0 |
| Ackley | | 50 | [−32, 32] | 0 |
| Bohachevsky | | 50 | [−10, 10] | 0 |
| Solomon | | 50 | [−100, 100] | 0 |
| Griewank | | 50 | [−500, 500] | 0 |
| NCRastrigin | | 50 | [−5.12, 5.12] | 0 |
|
| Alpine | | 50 | [−10, 10] | 0 |
| Fixed-dimension multimodal benchmark functions |
| Cross-in-Tray | | 2 | [−10, 10] | −2.06261 |
| Drop-Wave | | 2 | [−5.12, 5.12] | −1 |
| Eggholder | | 2 | [−512, 512] | −959.641 |
| Holder Table | | 2 | [−10, 10] | −19.2085 |
| Schaffer N.4 | | 2 | [−100, 100] | 0 |
| Levy N.13 | | 2 | [−10, 10] | 0 |
| Schaffer N.2 | | 2 | [−100, 100] | 0 |
| Shubert | | 2 | [−10, 10] | −186.731 |
Table 2.
Test results of the algorithm at Dim = 50.
Table 2.
Test results of the algorithm at Dim = 50.
| Functions | GWO | B-GWO | W-GWO | E-GWO | EWB-GWO |
|---|
| Avg | 6.955 × 10−100 | 1.934 × 10−102 | 1.733 × 10−77 | 1.491 × 10−105 | 3.087 × 10−102 |
| Std | 1.237 × 10−99 | 2.802 × 10−102 | 3.466 × 10−77 | 2.955 × 10−105 | 6.157 × 10−102 |
| Best | 3.302 × 10−109 | 1.766 × 10−105 | 1.732 × 10−94 | 3.153 × 10−109 | 5.015 × 10−107 |
| Avg | 6.102 × 10−01 | 8.754 × 10−01 | 3.101 × 1000 | 9.996 × 10−02 | 9.806 × 10−02 |
| Std | 3.719 × 10−01 | 3.710 × 10−01 | 5.146 × 10−01 | 1.999 × 10−01 | 1.959 × 10−01 |
| Best | 2.499 × 10−01 | 4.970 × 10−01 | 2.250 × 1000 | 6.503 × 10−06 | 4.672 × 10−06 |
| Avg | 2.079 × 10−76 | 2.287 × 10−79 | 8.434 × 10−76 | 1.325 × 10−118 | 2.514 × 10−139 |
| Std | 1.302 × 10−76 | 4.574 × 10−79 | 1.246 × 10−75 | 2.650 × 10−118 | 3.219 × 10−139 |
| Best | 4.806 × 10−77 | 6.646 × 10−88 | 3.605 × 10−77 | 6.180 × 10−140 | 1.241 × 10−148 |
| Avg | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 |
| Std | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 |
| Best | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 |
| Avg | 9.611 × 10−18 | 6.771 × 10−76 | 1.325 × 10−128 | 2.521 × 10−139 | 9.621 × 10−140 |
| Std | 1.922 × 10−17 | 9.590 × 10−76 | 2.650 × 10−128 | 3.224 × 10−139 | 1.920 × 10−139 |
| Best | 2.007 × 10−77 | 3.605 × 10−77 | 6.180 × 10−140 | 1.415 × 10−147 | 1.325 × 10−147 |
| Avg | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 |
| Std | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 |
| Best | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 |
Table 3.
Test results of the algorithm at Dim = 100.
Table 3.
Test results of the algorithm at Dim = 100.
| Functions | GWO | B-GWO | W-GWO | E-GWO | EWB-GWO |
|---|
| Avg | 1.587 × 10−188 | 1.052 × 10−185 | 1.077 × 10−119 | 9.641 × 10−191 | 4.069 × 10−181 |
| Std | 0.000 × 1000 | 0.000 × 1000 | 2.153 × 10−119 | 0.000 × 1000 | 0.000 × 1000 |
| Best | 3.559 × 10−196 | 1.925 × 10−203 | 1.550 × 10−143 | 4.826 × 10−199 | 2.116 × 10−194 |
| Avg | 4.473 × 1000 | 5.816 × 1000 | 1.167 × 1001 | 4.388 × 1000 | 1.564 × 1000 |
| Std | 2.294 × 10−01 | 9.534 × 10−01 | 7.229 × 10−01 | 6.501 × 10−01 | 2.234 × 10−01 |
| Best | 4.204 × 1000 | 4.735 × 1000 | 1.075 × 1001 | 3.720 × 1000 | 1.231 × 1000 |
| Avg | 1.514 × 10−48 | 7.696 × 10−37 | 3.172 × 10−38 | 2.528 × 10−48 | 7.847 × 10−86 |
| Std | 1.454 × 10−48 | 1.366 × 10−37 | 6.343 × 10−38 | 3.170 × 10−48 | 1.569 × 10−85 |
| Best | 3.418 × 10−49 | 5.485 × 10−37 | 3.470 × 10−98 | 2.607 × 10−49 | 5.068 × 10−99 |
| Avg | 6.422 × 10−13 | 0.000 × 1000 | 0.000 × 1000 | 7.276 × 10−14 | 0.000 × 1000 |
| Std | 9.060 × 10−13 | 0.000 × 1000 | 0.000 × 1000 | 8.794 × 10−14 | 0.000 × 1000 |
| Best | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 |
| Avg | 9.051 × 10−40 | 5.933 × 10−27 | 3.172 × 10−38 | 2.931 × 10−47 | 7.891 × 10−86 |
| Std | 1.810 × 10−39 | 3.291 × 10−27 | 6.343 × 10−38 | 5.340 × 10−47 | 1.578 × 10−85 |
| Best | 3.418 × 10−49 | 8.430 × 10−37 | 3.470 × 10−38 | 2.607 × 10−49 | 5.068 × 10−99 |
| Avg | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 |
| Std | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 |
| Best | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 |
Table 4.
Test results of the algorithm in fixed-dimensional multimodal function tests.
Table 4.
Test results of the algorithm in fixed-dimensional multimodal function tests.
| Functions | GWO | B-GWO | W-GWO | E-GWO | EWB-GWO |
|---|
| Avg | −1.000 × 1000 | −1.000 × 1000 | −1.000 × 1000 | −1.000 × 1000 | −1.000 × 1000 |
| Std | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 |
| Best | −1.000 × 1000 | −1.000 × 1000 | −1.000 × 1000 | −1.000 × 1000 | −1.000 × 1000 |
| Avg | −9.596 × 1002 | −9.596 × 1002 | −9.596 × 1002 | −9.596 × 1002 | −9.596 × 1002 |
| Std | 0.000 × 10+00 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 |
| Best | −9.596 × 1002 | −9.596 × 1002 | −9.596 × 1002 | −9.596 × 1002 | −9.596 × 1002 |
| Avg | −1.921 × 1001 | −1.921 × 1001 | −1.921 × 1001 | −1.921 × 1001 | −1.921 × 1001 |
| Std | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 |
| Best | −1.921 × 1001 | −1.921 × 1001 | −1.921 × 1001 | −1.921 × 1001 | −1.921 × 1001 |
| Avg | 2.926 × 10−01 | 2.926 × 10−01 | 2.926 × 10−01 | 2.926 × 10−01 | 2.926 × 10−01 |
| Std | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 |
| Best | 2.926 × 10−01 | 2.926 × 10−01 | 2.926 × 10−01 | 2.926 × 10−01 | 2.926 × 10−01 |
| Avg | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 |
| Std | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 |
| Best | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 |
| Avg | −1.867 × 1002 | −1.867 × 1002 | −1.867 × 1002 | −1.867 × 1002 | −1.867 × 1002 |
| Std | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 | 0.000 × 1000 |
| Best | −1.867 × 1002 | −1.867 × 1002 | −1.867 × 1002 | −1.867 × 1002 | −1.867 × 1002 |
Table 5.
Test results of the GWO-improved algorithms.
Table 5.
Test results of the GWO-improved algorithms.
| Functions | GWO | I-GWO | GWO-CS | PSO-GWO | EWB-GWO |
|---|
| Avg | 1.057 × 10−05 | 2.447 × 10−06 | 7.562 × 10−06 | 2.088 × 10−05 | 2.981 × 10−06 |
| Std | 3.851 × 10−06 | 9.850 × 10−07 | 1.935 × 10−06 | 2.072 × 10−05 | 5.594 × 10−07 |
| Best | 7.139 × 10−06 | 1.225 × 10−06 | 4.964 × 10−06 | 3.222 × 10−06 | 2.306 × 10−06 |
| Time | 3.352 × 10−01 | 7.030 × 10+00 | 6.236 × 10+00 | 6.470 × 10+00 | 1.973 × 10+00 |
| Avg | 2.073 × 10−78 | 8.802 × 10−79 | 1.070 × 10−80 | 2.408 × 10−01 | 8.261 × 10−121 |
| Std | 2.436 × 10−78 | 9.312 × 10−79 | 5.351 × 10−81 | 3.405 × 10−01 | 5.791 × 10−121 |
| Best | 2.048 × 10−79 | 2.478 × 10−80 | 5.074 × 10−81 | 2.124 × 10−44 | 2.106 × 10−122 |
| Time | 2.110 × 10+00 | 1.097 × 10+01 | 1.192 × 10+01 | 1.068 × 10+01 | 3.616 × 10+00 |
| Avg | 4.329 × 10−39 | 2.338 × 10−32 | 5.938 × 10−41 | 2.284 × 10+00 | 1.754 × 10−50 |
| Std | 4.904 × 10−39 | 1.216 × 10−32 | 5.987 × 10−41 | 3.211 × 10+00 | 8.684 × 10−51 |
| Best | 2.380 × 10−40 | 1.098 × 10−32 | 6.222 × 10−42 | 4.707 × 10−26 | 7.574 × 10−51 |
| Time | 2.305 × 10+00 | 1.178 × 10+01 | 1.186 × 10+01 | 1.284 × 10+01 | 3.809 × 10+00 |
| Avg | 4.546 × 10−01 | 4.024 × 10−01 | 3.164 × 10−01 | 4.819 × 10−01 | 1.648 × 10+00 |
| Std | 1.113 × 10−02 | 2.577 × 10−03 | 2.705 × 10−01 | 3.388 × 10−02 | 1.720 × 10+00 |
| Best | 4.426 × 10−01 | 3.991 × 10−01 | 1.223 × 10−01 | 4.473 × 10−01 | 4.023 × 10−01 |
| Time | 2.179 × 10+00 | 1.126 × 10+01 | 1.216 × 10+01 | 1.173 × 10+01 | 3.746 × 10+00 |
| Avg | 1.257 × 10−22 | 5.937 × 10−13 | 9.554 × 10−24 | 5.874 × 10−03 | 7.805 × 10−42 |
| Std | 1.581 × 10−22 | 6.696 × 10−13 | 7.650 × 10−24 | 6.662 × 10−03 | 5.491 × 10−42 |
| Best | 8.025 × 10−24 | 5.653 × 10−15 | 1.167 × 10−24 | 1.080 × 10−15 | 8.996 × 10−43 |
| Time | 5.552 × 10+00 | 1.846 × 10+01 | 1.524 × 10+01 | 1.595 × 10+01 | 1.348 × 10+01 |
| Avg | −1.016 × 10+04 | −1.244 × 10+04 | −2.095 × 10+04 | −1.267 × 10+04 | −1.129 × 10+04 |
| Std | 1.178 × 10+03 | 3.257 × 10+03 | 1.843 × 10−01 | 1.295 × 10+03 | 1.849 × 10+03 |
| Best | −1.167 × 10+04 | −1.534 × 10+04 | −2.095 × 10+04 | −1.385 × 10+04 | −1.267 × 10+04 |
| Time | 2.585 × 10+00 | 1.352 × 10+01 | 1.347 × 10+01 | 1.345 × 10+01 | 5.322 × 10+00 |
| Avg | 1.510 × 10−14 | 1.391 × 10−14 | 1.510 × 10−14 | 6.163 × 10+00 | 5.994 × 10−15 |
| Std | 0.000 × 10+00 | 1.675 × 10−15 | 0.000 × 10+00 | 8.705 × 10+00 | 2.828 × 10−15 |
| Best | 1.510 × 10−14 | 1.155 × 10−14 | 1.510 × 10−14 | 5.773 × 10−14 | 1.994 × 10−15 |
| Time | 2.293 × 10+00 | 1.170 × 10+01 | 1.243 × 10+01 | 1.317 × 10+01 | 3.908 × 10+00 |
| Avg | 1.999 × 10−01 | 1.999 × 10−01 | 1.999 × 10−01 | 3.952 × 10−01 | 2.000 × 10−07 |
| Std | 0.000 × 10+00 | 0.000 × 10+00 | 0.000 × 10+00 | 8.146 × 10−02 | 2.087 × 10−07 |
| Best | 1.999 × 10−01 | 1.999 × 10−01 | 1.999 × 10−01 | 2.938 × 10−01 | 1.348 × 10−08 |
| Time | 2.216 × 10+00 | 1.163 × 10+01 | 1.216 × 10+01 | 1.278 × 10+01 | 3.822 × 10+00 |
| Avg | 0.000 × 10+00 | 0.000 × 10+00 | 0.000 × 10+00 | 2.185 × 10+01 | 0.000 × 10+00 |
| Std | 0.000 × 10+00 | 0.000 × 10+00 | 0.000 × 10+00 | 3.090 × 10+01 | 0.000 × 10+00 |
| Best | 0.000 × 10+00 | 0.000 × 10+00 | 0.000 × 10+00 | 2.220 × 10−16 | 0.000 × 10+00 |
| Time | 2.603 × 10+00 | 1.212 × 10+01 | 1.247 × 10+01 | 1.328 × 10+01 | 5.649 × 10+00 |
| Avg | 2.156 × 10−24 | 4.105 × 10−05 | 1.631 × 10−45 | 3.616 × 10+00 | 1.902 × 10−69 |
| Std | 3.050 × 10−24 | 3.767 × 10−05 | 1.690 × 10−45 | 1.380 × 10+00 | 1.318 × 10−69 |
| Best | 4.470 × 10−40 | 2.328 × 10−06 | 1.169 × 10−46 | 1.856 × 10+00 | 4.990 × 10−70 |
| Time | 2.384 × 10+00 | 1.129 × 10+01 | 1.216 × 10+01 | 1.299 × 10+01 | 3.915 × 10+00 |
| Avg | −2.063 × 10+00 | −2.063 × 10+00 | −2.063 × 10+00 | −2.063 × 10+00 | −2.063 × 10+00 |
| Std | 0.000 × 10+00 | 0.000 × 10+00 | 0.000 × 10+00 | 0.000 × 10+00 | 0.000 × 10+00 |
| Best | −2.063 × 10+00 | −2.063 × 10+00 | −2.063 × 10+00 | −2.063 × 10+00 | −2.063 × 10+00 |
| Time | 2.001 × 10−01 | 6.308 × 10+00 | 2.925 × 10+00 | 5.237 × 10+00 | 2.597 × 10+00 |
| Avg | 9.201 × 10−10 | 1.350 × 10−31 | 9.208 × 10−09 | 4.439 × 10−09 | 3.475 × 10−08 |
| Std | 4.977 × 10−10 | 0.000 × 10+00 | 7.000 × 10−09 | 5.726 × 10−09 | 4.496 × 10−08 |
| Best | 2.166 × 10−10 | 1.350 × 10−31 | 1.092 × 10−09 | 1.873 × 10−11 | 1.091 × 10−12 |
| Time | 1.786 × 10−01 | 6.120 × 10+00 | 2.819 × 10+00 | 3.247 × 10−01 | 2.434 × 10+00 |
Table 6.
The parameter setting of each algorithm.
Table 6.
The parameter setting of each algorithm.
| Name | Source | Parameter |
|---|
| EWB-GWO | [23] | ; ; ; . Elite individuals select 10 percent of the total population. |
| PSO | [39] | Learning factor of PSO algorithm , ; the maximum value of inertia weight ; the minimum value of inertia weight . |
| BOA | [31] | Perceptual modality ; power index ; conversion probability . |
| ABC | [40] | , where denotes the maximum number of update-free iterations of the ABC algorithm for detecting bee solutions, denotes the number of food sources, and denotes the problem dimension. |
| GA | [41] | Crossover probability ; variance probability . |
Table 7.
BOA-SA, BOA-AIW, BOA-RV, BOA-TSAR, GA, PSO, GWO, and ABC test results on the 50 dimensional functions in Experiment 2.
Table 7.
BOA-SA, BOA-AIW, BOA-RV, BOA-TSAR, GA, PSO, GWO, and ABC test results on the 50 dimensional functions in Experiment 2.
| Functions | GWO | B-GWO | W-GWO | E-GWO | EWB-GWO | BOA | PSO | ABC | GA |
|---|
| Avg | 1.35 × 10−104 | 6.46 × 10−103 | 8.26 × 10−84 | 3.40 × 10−107 | 5.66 × 10−107 | 1.33 × 10−28 | 5.61 × 10−73 | 1.79 × 10−101 | 5.61 × 10−73 |
| Std | 1.33 × 10−104 | 5.12 × 10−103 | 1.17 × 10−83 | 2.39 × 10−107 | 7.06 × 10−107 | 1.88 × 10−28 | 7.94 × 10−73 | 1.25 × 10−101 | 7.93 × 10−73 |
| Avg | 2.14 × 10−04 | 1.60 × 10−05 | 2.02 × 10−05 | 1.73 × 10−05 | 2.90 × 10−06 | 3.07 × 10−04 | 3.64 × 10−01 | 2.01 × 1000 | 1.38 × 1000 |
| Std | 9.98 × 10−05 | 1.26 × 10−05 | 2.99 × 10−06 | 1.44 × 10−05 | 1.73 × 10−06 | 8.00 × 10−05 | 6.58 × 10−02 | 4.48 × 10−01 | 2.47 × 10−01 |
| Avg | 6.38 × 10−01 | 1.00 × 1000 | 3.81 × 1000 | 7.03 × 10−01 | 3.98 × 10−01 | 9.18 × 1000 | 1.22 × 1000 | 3.43 × 1000 | 1.51 × 1001 |
| Std | 1.61 × 10−01 | 4.11 × 10−01 | 4.97 × 10−01 | 7.06 × 10−02 | 7.55 × 10−02 | 1.93 × 10−01 | 2.99 × 10−02 | 4.31 × 10−01 | 1.13 × 1001 |
| Avg | 1.39 × 10−78 | 4.02 × 10−59 | 1.11 × 10−120 | 7.05 × 10−132 | 2.15 × 10−142 | 1.35 × 10−14 | 6.28 × 1000 | 4.35 × 1001 | 2.45 × 1002 |
| Std | 7.00 × 10−79 | 2.62 × 10−59 | 1.07 × 10−120 | 9.97 × 10−132 | 3.04 × 10−142 | 3.69 × 10−16 | 3.79 × 1000 | 4.73 × 1000 | 1.21 × 1002 |
| Avg | 2.10 × 10−39 | 8.31 × 10−26 | 9.67 × 10−34 | 1.06 × 10−38 | 2.20 × 10−51 | 1.13 × 10−14 | 1.98 × 10−01 | 6.46 × 1000 | 9.92 × 1000 |
| Std | 1.18 × 10−39 | 6.06 × 10−26 | 1.36 × 10−33 | 1.41 × 10−38 | 3.11 × 10−51 | 5.10 × 10−16 | 3.79 × 10−02 | 6.16 × 10−01 | 1.68 × 1000 |
| Avg | 4.51 × 1001 | 4.62 × 1001 | 4.71 × 1001 | 4.44 × 1001 | 4.17 × 1001 | 4.89 × 1001 | 2.81 × 1002 | 5.23 × 1004 | 7.38 × 1003 |
| Std | 8.40 × 10−01 | 1.77 × 10−02 | 6.93 × 10−01 | 5.34 × 10−01 | 1.19 × 1000 | 4.18 × 10−02 | 6.17 × 1001 | 1.85 × 1003 | 7.35 × 1003 |
| Avg | 5.46 × 10−23 | 9.34 × 10−18 | 2.51 × 10−44 | 7.58 × 10−53 | 3.99 × 10−50 | 1.44 × 10−14 | 3.42 × 1001 | 8.20 × 1004 | 3.97 × 1004 |
| Std | 5.32 × 10−23 | 1.21 × 10−17 | 3.29 × 10−53 | 1.01 × 10−52 | 5.64 × 10−50 | 1.62 × 10−16 | 4.71 × 1000 | 7.45 × 1003 | 6.11 × 1003 |
| Avg | 1.78 × 10−76 | 2.70 × 10−56 | 5.70 × 10−77 | 1.38 × 10−137 | 6.39 × 10−138 | 1.18 × 10−14 | 3.90 × 10−01 | 8.48 × 1000 | 4.91 × 1000 |
| Std | 2.08 × 10−76 | 3.11 × 10−56 | 4.41 × 10−77 | 9.54 × 10−138 | 8.80 × 10−138 | 6.86 × 10−16 | 1.10 × 10−01 | 2.19 × 10−01 | 1.69 × 1000 |
| Avg | −1.07 × 1004 | −1.20 × 1004 | −8.98 × 1003 | −1.02 × 1004 | −1.33 × 1004 | −6.68 × 1003 | −4.30 × 1003 | 2.19 × 1003 | 5.02 × 1003 |
| Std | 1.45 × 1003 | 7.64 × 1002 | 6.41 × 1002 | 5.08 × 1002 | 1.29 × 1003 | 3.47 × 1002 | 1.19 × 1004 | 6.73 × 1003 | 1.32 × 1004 |
| Avg | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 8.08 × 1001 | 4.55 × 1002 | 8.16 × 1001 |
| Std | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 9.20 × 1000 | 1.02 × 1001 | 4.82 × 1000 |
| Avg | 1.48 × 10−14 | 2.27 × 10−14 | 7.66 × 10−15 | 1.76 × 10−16 | 8.06 × 10−15 | 6.55 × 10−12 | 2.79 × 1000 | 5.89 × 1000 | 5.14 × 1000 |
| Std | 3.96 × 10−16 | 6.60 × 10−16 | 4.71 × 10−16 | 3.51 × 10−15 | 7.12 × 10−16 | 4.63 × 10−12 | 7.86 × 10−01 | 2.81 × 10−01 | 8.84 × 10−01 |
| Avg | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 7.75 × 10−01 | 6.86 × 10−01 | 9.24 × 1000 | 3.13 × 1001 |
| Std | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 3.14 × 10−02 | 3.50 × 10−02 | 6.48 × 10−01 | 1.90 × 1001 |
| Avg | 1.92 × 10−01 | 8.52 × 10−08 | 9.99 × 10−02 | 1.13 × 10−02 | 3.90 × 10−08 | 3.00 × 10−01 | 9.56 × 10−01 | 5.24 × 1000 | 1.42 × 1001 |
| Std | 1.08 × 10−02 | 3.68 × 10−08 | 0.00 × 1000 | 7.36 × 10−03 | 4.98 × 10−08 | 3.78 × 10−04 | 4.17 × 10−02 | 2.32 × 10−01 | 3.56 × 1000 |
| Avg | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 1.37 × 1000 | 5.47 × 10−02 | 3.05 × 1000 | 3.72 × 1000 |
| Std | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 1.94 × 1000 | 6.06 × 10−03 | 1.56 × 10−01 | 1.14 × 1000 |
| Avg | 1.92 × 10−01 | 8.52 × 10−08 | 9.99 × 10−02 | 1.13 × 10−02 | 3.90 × 10−08 | 3.00 × 10−01 | 9.56 × 10−01 | 5.24 × 1000 | 1.42 × 1001 |
| Std | 1.08 × 10−02 | 3.68 × 10−08 | 0.00 × 1000 | 7.36 × 10−03 | 4.98 × 10−08 | 3.78 × 10−04 | 4.17 × 10−02 | 2.32 × 10−01 | 3.56 × 1000 |
| Avg | 6.16 × 10−38 | 2.98 × 10−07 | 5.17 × 10−40 | 4.76 × 10−80 | 8.64 × 10−66 | 1.72 × 10−15 | 3.89 × 1000 | 3.91 × 1001 | 1.20 × 1000 |
| Std | 8.63 × 10−38 | 4.21 × 10−07 | 4.38 × 10−80 | 6.73 × 10−40 | 1.22 × 10−65 | 1.31 × 10−16 | 2.43 × 10−01 | 2.02 × 10−01 | 5.86 × 10−01 |
| Avg | −2.06 × 1000 | −2.06 × 1000 | −2.06 × 1000 | −2.06 × 1000 | −2.06 × 1000 | −2.06 × 1000 | −2.06 × 1000 | −2.06 × 1000 | −2.06 × 1000 |
| Std | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 |
| Avg | −1.00 × 1000 | −1.00 × 1000 | −1.00 × 1000 | −1.00 × 1000 | −1.00 × 1000 | −9.96 × 10−01 | −1.00 × 1000 | −1.00 × 1000 | 2.91 × 10−01 |
| Std | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 1.24 × 10−03 | 0.00 × 1000 | 0.00 × 1000 | 9.13 × 10−01 |
| Avg | −9.60 × 1002 | −9.60 × 1002 | −9.60 × 1002 | −9.60 × 1002 | −9.60 × 1002 | −9.60 × 1002 | −9.38 × 1002 | −9.60 × 1002 | −9.28 × 1002 |
| Std | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 2.74 × 10−02 | 3.07 × 1001 | 0.00 × 1000 | 2.93 × 1001 |
| Avg | −1.92 × 1001 | −1.92 × 1001 | −1.92 × 1001 | −1.92 × 1001 | −1.92 × 1001 | −1.92 × 1001 | −1.92 × 1001 | −1.92 × 1001 | −1.92 × 1001 |
| Std | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 3.65 × 10−03 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 |
| Avg | 2.93 × 10−01 | 2.93 × 10−01 | 2.93 × 10−01 | 2.93 × 10−01 | 2.93 × 10−01 | 2.93 × 10−01 | 2.93 × 10−01 | 2.93 × 10−01 | 2.93 × 10−01 |
| Std | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 8.16 × 10−06 | 0.00 × 1000 | 0.00 × 1000 | 2.12 × 10−04 |
| Avg | 1.59 × 10−09 | 6.26 × 10−09 | 2.06 × 10−09 | 1.45 × 10−09 | 3.58 × 10−08 | 1.22 × 10−05 | 1.35 × 10−31 | 1.35 × 10−31 | 7.62 × 10−16 |
| Std | 2.89 × 10−10 | 3.99 × 10−09 | 7.96 × 10−10 | 1.10 × 10−09 | 4.62 × 10−08 | 6.84 × 10−06 | 0.00 × 1000 | 0.00 × 1000 | 5.11 × 10−16 |
| Avg | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 5.92 × 10−16 | 0.00 × 1000 | 0.00 × 1000 | 2.10 × 10−03 |
| Std | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 | 3.77 × 10−16 | 0.00 × 1000 | 0.00 × 1000 | 2.39 × 10−03 |
| Avg | −1.87 × 1002 | −1.87 × 1002 | −1.87 × 1002 | −1.87 × 1002 | −1.87 × 1002 | −1.87 × 1002 | −1.87 × 1002 | −1.87 × 1002 | −1.87 × 1002 |
| Std | 0.00 × 1000 | 2.22 × 10−03 | 8.82 × 10−03 | 0.00 × 1000 | 1.76 × 1003 | 1.30 × 10−02 | 0.00 × 1000 | 0.00 × 1000 | 0.00 × 1000 |
Table 8.
Wilcoxon rank test order.
Table 8.
Wilcoxon rank test order.
| Functions | Rank |
|---|
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
Table 9.
Friedman test statistical results of nine algorithms.
Table 9.
Friedman test statistical results of nine algorithms.
| Functions | Sum of Squares | Degree of Freedom | Mean Squares | p-Value |
|---|
| 119.25 | 8 | 14.9063 | 0.0429 |
| 116 | 8 | 15.47 | 0.0407 |
| 100 | 8 | 13.33 | 0.1009 |
| 120 | 8 | 15 | 0.0424 |
| 120 | 8 | 15 | 0.0424 |
| 121 | 8 | 16.375 | 0.0404 |
| 117 | 8 | 14.625 | 0.0485 |
| 119 | 8 | 14.875 | 0.0443 |
| 88 | 8 | 11 | 0.1635 |
| 84 | 8 | 15.81 | 0.0452 |
| 102 | 8 | 13.6 | 0.0928 |
| 99 | 8 | 12.375 | 0.0447 |
| 109 | 8 | 13.625 | 0.0489 |
| 97 | 8 | 15.52 | 0.0498 |
| 109 | 8 | 14.53 | 0.0489 |
| 112 | 8 | 14 | 0.0405 |
| 0 | 8 | 0 | 1 |
| 64 | 8 | 8 | 0.0424 |
| 68.25 | 8 | 8.53125 | 0.0662 |
| 9 | 8 | 1.125 | 0.4335 |
| 16 | 8 | 2 | 0.4335 |
| 116 | 8 | 14.5 | 0.0485 |
| 64 | 8 | 8 | 0.0424 |
| 25 | 8 | 3.125 | 0.4335 |
Table 10.
Map information selected for the dataset.
Table 10.
Map information selected for the dataset.
| Map Name | Map Size (m) | Number of Obstacles | Max Length (m) |
|---|
| City Map | Boston | 256 × 256 | 48,286 | 363.4579 |
| Denver | 256 × 256 | 48,202 | 375.5584 |
| Milan | 256 × 256 | 47,331 | 362.6001 |
| Moscow | 256 × 256 | 48,101 | 362.9137 |
| New York | 256 × 256 | 48,299 | 362.9015 |
| Shanghai | 256 × 256 | 48,708 | 347.7005 |
| Warcraft III | battleground | 256 × 256 | 23,067 | 231.8498 |
| harvestmoon | 256 × 256 | 28,648 | 283.9665 |
| duskwood | 256 × 256 | 31,807 | 215.9625 |
| frostsabre | 256 × 256 | 22,845 | 223.2813 |
| golemsinthemist | 256 × 256 | 27,707 | 259.4772 |
| plainsofsnow | 256 × 256 | 26,458 | 211.6589 |
Table 11.
Experimental results of path planning under city maps.
Table 11.
Experimental results of path planning under city maps.
| Map | Algorithm Type | Path Length (m) | Total Turning Angle of the Path (°) | Calculation Time (s) | Memory Usage (kb) | Number of Nodes |
|---|
| Boston | A* | 267.8772 | 990.0000 | 7.138933 | 1852.9219 | 19 |
| JPS | 267.8772 | 135.0000 | 0.3088 | 1059.2578 | 19 |
| RRT | 408.5665 | 3338.5940 | 186.8712 | 572.4229 | 94 |
| Theta* | 256.6033 | 49.9276 | 7.3710 | 1899.1718 | 4 |
| BOA | 297.7898 | 120.9959 | 1.1564 | 1564.0421 | 4 |
| EWB-GWO | 250.5955 | 48.1721 | 1.8218 | 1561.8130 | 4 |
| Denver | A* | 276.1615 | 1170.0000 | 11.2521 | 1951.9844 | 219 |
| JPS | 276.1615 | 315.0000 | 0.4641 | 1077.7109 | 33 |
| RRT | 436.7546 | 3034.6210 | 61.4231 | 533.5322 | 100 |
| Theta* | 258.3104 | 52.7972 | 11.5335 | 1102.2732 | 6 |
| BOA | 270.1912 | 270.1927 | 2.5235 | 1585.8192 | 4 |
| EWB-GWO | 258.8289 | 62.9828 | 2.7950 | 1582.1092 | 4 |
| Milan | A* | 270.8356 | 1620.0000 | 13.6309 | 2035.2344 | 229 |
| JPS | 270.8356 | 495.0000 | 0.7813 | 1132.5547 | 29 |
| RRT | 407.7956 | 3108.8480 | 142.7865 | 558.5557 | 93 |
| Theta* | 258.1860 | 38.9810 | 13.9132 | 1190.1270 | 6 |
| BOA | 262.6911 | 44.6869 | 2.1344 | 1578.7026 | 4 |
| EWB-GWO | 255.9445 | 35.6227 | 1.9219 | 1574.6176 | 3 |
| Moscow | A* | 300.2447 | 1530.0000 | 13.0021 | 1710.5781 | 229 |
| JPS | 298.2447 | 405.0000 | 0.6125 | 1089.5781 | 39 |
| RRT | 405.3163 | 3039.8970 | 132.5529 | 555.3838 | 95 |
| Theta* | 289.0161 | 83.1341 | 13.2845 | 1785.5801 | 6 |
| BOA | 290.7984 | 46.5618 | 5.8887 | 1537.7820 | 3 |
| EWB-GWO | 289.8957 | 46.3224 | 5.0168 | 1568.8093 | 3 |
| New York | A* | 310.4335 | 3960.0000 | 18.6781 | 2478.4688 | 257 |
| JPS | 310.4335 | 675.0000 | 0.5872 | 1103.343 | 30 |
| RRT | 368.6966 | 3173.0940 | 110.6314 | 548.5400 | 87 |
| Theta* | 285.4566 | 44.7358 | 19.8253 | 2501.4208 | 10 |
| BOA | 283.3957 | 39.4442 | 1.4239 | 1540.5 | 4 |
| EWB-GWO | 283.0304 | 34.7131 | 1.5010 | 1502.2 | 3 |
| Shanghai | A* | 300.6173 | 2160.0000 | 19.6747 | 2105.7344 | 236 |
| JPS | 300.6173 | 495.0000 | 0.5586 | 1061.5781 | 26 |
| RRT | 366.1955 | 2851.8291 | 48.8274 | 529.2666 | 86 |
| Theta* | 282.7505 | 54.8031 | 19.9811 | 2180.3429 | 5 |
| BOA | 302.7648 | 102.0262 | 3.1015 | 1554.8193 | 4 |
| EWB-GWO | 282.6029 | 24.0939 | 2.8359 | 1555.7849 | 3 |
Table 12.
Experimental results of path planning under game maps.
Table 12.
Experimental results of path planning under game maps.
| Map | Algorithm Type | Path Length (m) | Total Turning Angle of the Path (°) | Calculation Time (s) | Memory Usage (kb) | Number of Nodes |
|---|
| battleground | A* | 176.7817 | 630.0000 | 5.2977 | 2221.2031 | 154 |
| JPS | 176.7817 | 171.6604 | 1.0484 | 1870.9609 | 27 |
| RRT | 222.3185 | 1683.270 | 80.1531 | 522.3135 | 52 |
| Theta* | 171.6604 | 89.7732 | 5.6248 | 2301.4532 | 6 |
| BOA | 174.2078 | 93.3885 | 2.6984 | 1579.2133 | 4 |
| EWB-GWO | 170.6907 | 90.1226 | 2.6910 | 15,787.7810 | 4 |
| harvestmoon | A* | 191.0955 | 1080.0000 | 4.6075 | 2089.2813 | 165 |
| JPS | 191.0955 | 1035.0000 | 0.7749 | 1705.7109 | 43 |
| RRT | 263.8107 | 2049.297 | 98.1736 | 521.9932 | 61 |
| Theta* | 186.7259 | 656.6668 | 4.8306 | 2020.3452 | 114 |
| BOA | 182.8787 | 66.8938 | 2.9988 | 1556.7690 | 4 |
| EWB-GWO | 183.7229 | 63.8977 | 3.0292 | 1554.1269 | 5 |
| duskwood | A* | 216.7766 | 1170.0000 | 0.5311 | 1812.1250 | 165 |
| JPS | 216.7766 | 585.0000 | 8.3422 | 1579.6875 | 39 |
| RRT | 338.8771 | 2269.2270 | 45.0792 | 673.2666 | 78 |
| Theta* | 216.7398 | 102.0471 | 8.5788 | 1880.4324 | 11 |
| BOA | 217.2969 | 104.7780 | 5.4616 | 1557.4368 | 4 |
| EWB-GWO | 215.2443 | 95.2199 | 4.9328 | 1555.6790 | 4 |
| frostsabre | A* | 234.5046 | 2160.0000 | 7.1108 | 2303.5469 | 179 |
| JPS | 232.5046 | 1125.0000 | 1.1715 | 1891.9922 | 63 |
| RRT | 285.8457 | 2162.9054 | 76.6554 | 522.1338 | 67 |
| Theta* | 211.1609 | 74.6927 | 7.3739 | 1384.3443 | 12 |
| BOA | 230.4921 | 46.5942 | 5.0096 | 1576.9384 | 4 |
| EWB-GWO | 228.7364 | 46.4878 | 4.0595 | 1574.6754 | 4 |
| golemsinthemist | A* | 199.4508 | 1170.0000 | 11.2086 | 2184.5938 | 163 |
| JPS | 199.4508 | 225.0000 | 1.1425 | 1718.7734 | 27 |
| RRT | 251.4762 | 2157.0730 | 95.4560 | 545.0088 | 59 |
| Theta* | 186.2028 | 110.7750 | 11.7007 | 2231.4853 | 10 |
| BOA | 196.0223 | 89.0916 | 5.6584 | 1558.1250 | 4 |
| EWB-GWO | 196.7637 | 81.6472 | 3.7590 | 1556.6089 | 5 |
| plainsofsnow | A* | 209.5391 | 3330.0000 | 10.7168 | 2483.0938 | 188 |
| JPS | 209.5391 | 585.0000 | 0.8499 | 1822.6953 | 24 |
| RRT | 314.9667 | 2852.405 | 99.2433 | 587.4385 | 72 |
| Theta* | 192.8992 | 82.9728 | 11.0657 | 2520.2432 | 7 |
| BOA | 194.1490 | 60.2447 | 5.7059 | 1561.8362 | 3 |
| EWB-GWO | 192.8901 | 60.1029 | 5.2394 | 1560.0021 | 3 |