Multi-Core Time-Triggered OCBP-Based Scheduling for Mixed Criticality Periodic Task Systems
Abstract
:1. Introduction
- The extension of a mixed criticality uniprocessor table-driven scheduling algorithm to a mixed criticality algorithm for periodic tasks on a multiprocessor platform (Section 4.1, Section 4.2 and Section 4.6). The original method has been modified to employ a periodic mixed criticality job model (Section 4.4 and Section 4.5).
- The proposal of a task partitioning heuristic for the multiprocessor mixed criticality system (Section 4.3).
- The comparison of the newly developed algorithm in terms of success ratio with two state-of-the-art methods (Section 5).
- This current paper aims to demonstrate the efficiency of algorithm [6] through:
- More experiments and comparisons.
- Additional details about the algorithm implementation.
2. Related Work
2.1. Event-Driven Scheduling Algorithms
2.2. Time-Triggered Scheduling Algorithms
3. Model and Problem Statement
- An MCS executes in either of two modes: Hi-criticality mode or Lo-criticality mode.
- Each mixed-criticality task τi is characterized by a set of parameters [7,14]:where Ti, Di and Li denote, respectively, the period, the deadline and the criticality level (i.e., Lo or Hi) of the task i; Ci,Lj is a vector containing the worst-case execution times (WCETs) for each criticality level; and Si,Lj is a vector where each element represents the execution start time, relative to its release time, for each criticality level that is lower than or equal to the task criticality level Li, with Si,Lj < Di.
- A task consists of a series of jobs that inherit some of the parameters of the task (Ti,Di,Li). Furthermore, each job adds its own parameters, which means that the k-th job of task i is characterized by the following:where:
- ○
- ai,k represents the arrival time of job k, with ai,k+1 − ai,k ≥ Ti.
- ○
- di,k is the absolute deadline of job k and can be obtained using di,k = ai,k + Di.
- ○
- ci,k expresses the execution time and depends on the criticality mode of the system (e.g., for L = Lo, ci,k = Ci,Lo).
- ○
- si,k offers the absolute execution start time corresponding to job k and, similar to ci,k, also depends on the criticality mode of the system.
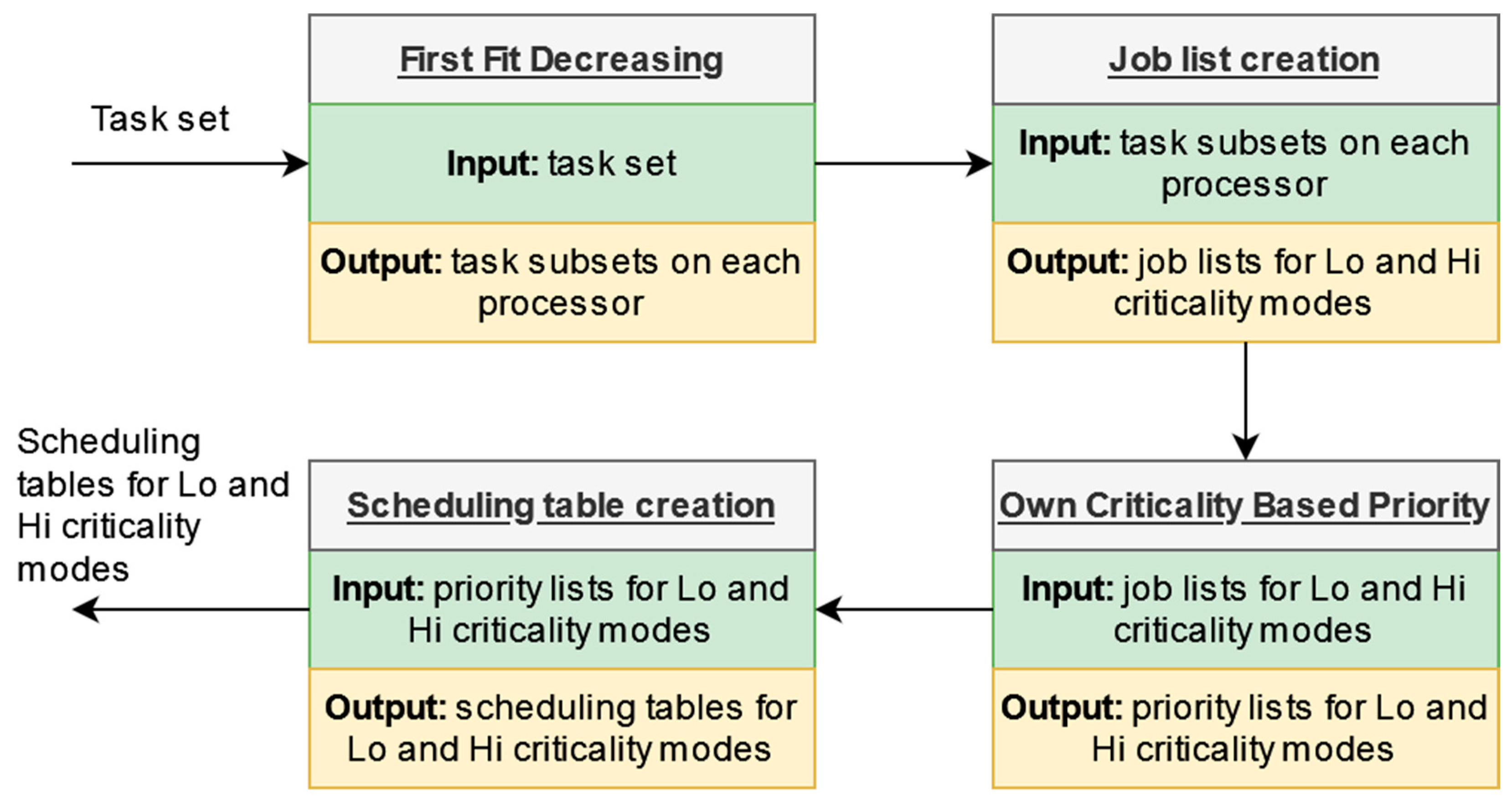
4. Algorithm P-TT-OCBP
4.1. Original Algorithm
| Algorithm 1: Own Criticality Based Priority. |
| Input: (the job list for processor ) |
| Output: (the priority list for processor ) |
| sort in non-decreasing order by for do |
| for do if then if then end if end if end for if and then add to end if if and and then add to end if end for |
4.2. Working Hypothesis
- A dual criticality system is defined to execute in one of two modes: Lo-criticality mode and Hi-criticality mode.
- Each job is characterized by the set of parameters described in (2), with C(Lo) ≤ C(Hi).
- The system starts in Lo-criticality mode and does not change as long as jobs execute within their Lo-criticality WCETs.
- If any job overruns its Lo-criticality WCET, then a criticality mode change occurs.
- As the system instantly moves to Hi-criticality mode, all Lo-criticality jobs are dropped (they are no longer executed). Hi-criticality jobs are allowed to run according to their Hi-criticality WCETs.
- The system remains in Hi-criticality mode.
- In this paper, we only consider the mode change from Lo-criticality to Hi-criticality.
4.3. Partitioning Tasks to Processors
- The utilization of each task is computed based on the criticality level (3): for Hi-criticality tasks there will be two utilizations (one for each criticality level).
- Tasks are selected one by one from the task set and added into each processor where a test is performed.
- Two conditions must be verified (4):
- (1)
- The current total processor utilization in Lo-criticality mode must not exceed 1.
- (2)
- The current total processor utilization in Hi-criticality mode must not exceed 1.
- If the above two conditions are met, the task will be assigned to Pq and the total processor utilizations are updated.
- If one of the two conditions returns failure, the task is removed from Pq and added into the next processor, where the same test is performed
4.4. Constructing the List of Jobs at the Processor Level
4.5. Scheduling at the Processor Level
- The job list to be prioritized must be parsed in non-decreasing order of deadlines di,k.
- The criticality level of the first job k from the list is verified:
- ○
- If the criticality level is Lo we compute the sum of the Lo-criticality WCETs (sum(Lo)) for the rest of the jobs.
- ○
- If the criticality level is Hi we compute two sums, one for Lo-criticality WCETs (sum(Lo)) and one for Hi-criticality WCETs (sum(Hi)) for the rest of the jobs.
- Next, the algorithm checks if job k can be added in the priority list, depending on its criticality level:
- ○
- For a Lo-criticality level:
- ○
- For a Hi-criticality level, two conditions must be met:
- If these conditions are met, job k is moved from the list of jobs to the priority list. Otherwise, the next job k + 1 in the list is taken, until the entire list of jobs is verified.
- If jobs are still in the list after the list of jobs is parsed at least once, the same algorithm is computed again, until no more jobs are left.
- If at least two jobs remain in the list of jobs which cannot be prioritized, the set of tasks is deemed not schedulable.
- The resulting priority list is sorted in non-decreasing order of deadlines. The schedule is constructed based on the priority list as follows:
- The first job is extracted from the priority list, with si,k = 0.
- We then compute the completion time (cti,k) of the job:
- For the next k − 1 jobs, we compare the arrival time with the previous job completion time: if the completion time is greater than the arrival time, then the start time will take on the value of the previous job completion time; otherwise, the start time will be equal to the current job arrival time. The completion time is computed using Equation (9).
4.6. System Execution
5. Evaluation
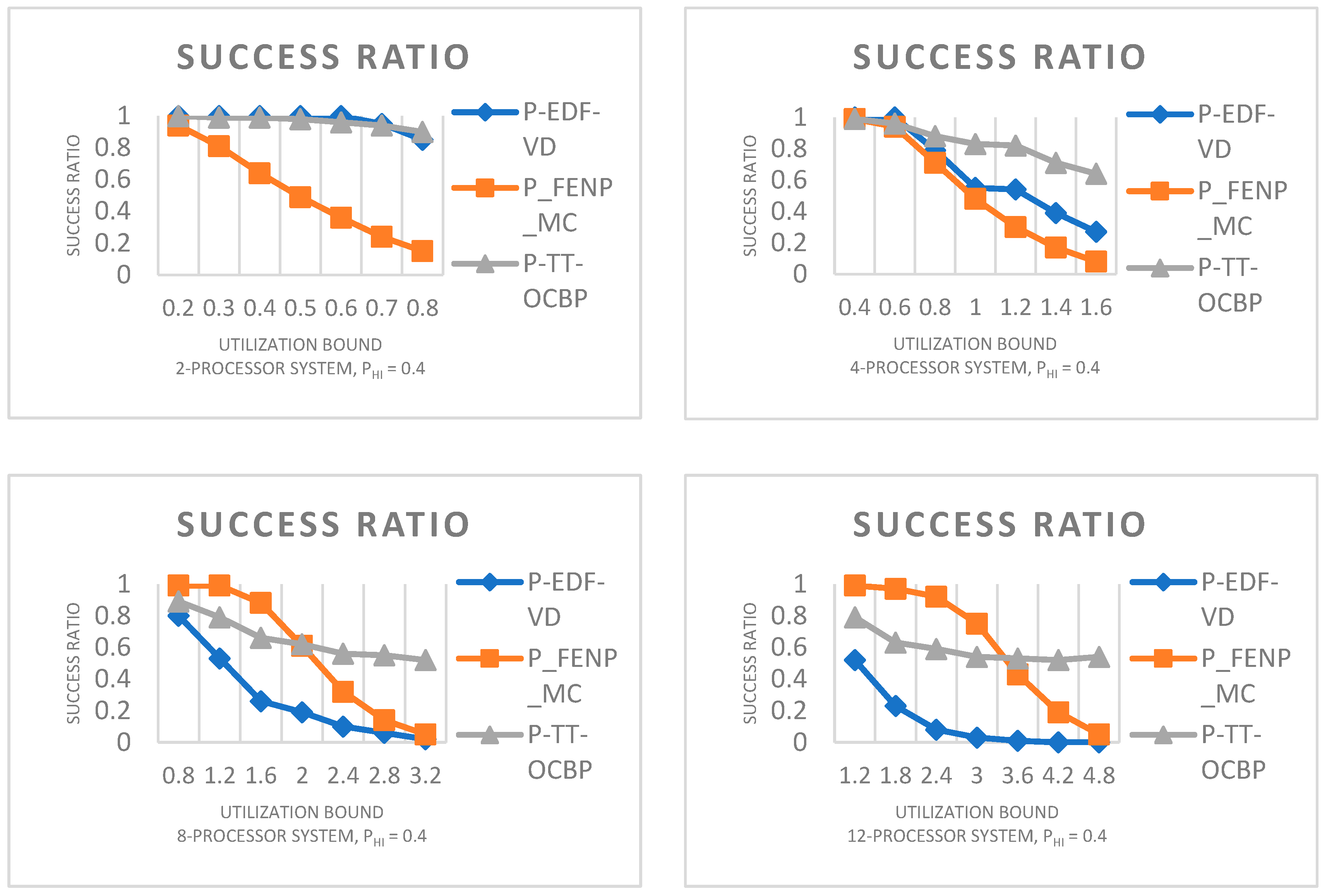
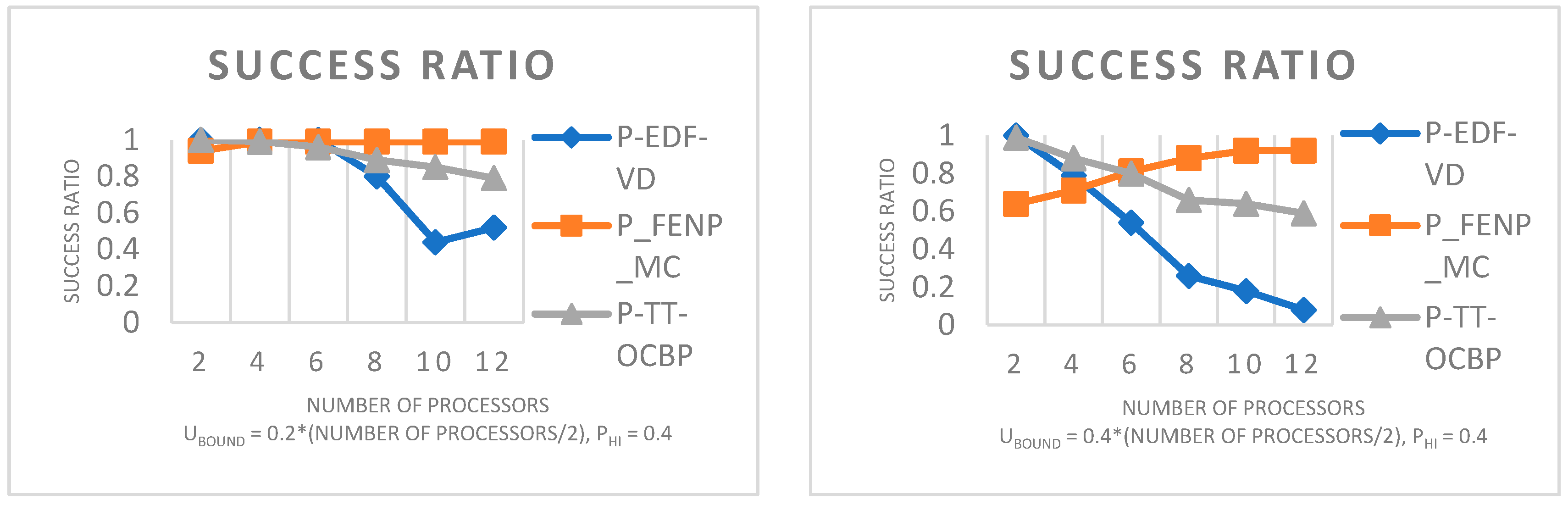
5.1. Task Set Generation
- Period: Ti is drawn using a uniform distribution on [10, 50].
- Deadline: Di = Ti.
- Criticality level: Li = Hi with a given probability PHi; otherwise, Li = Lo.
- Utilization: Ui,Lj (see Equation (3)), is a vector of size l, where l is the number of criticality levels. The utilizations are generated using five input parameters [28]:
- ○
- Ubound:where Hi(τ) is the subset of the entire task set τ which contains only the Hi-criticality tasks.
- ○
- [UL,UU]: The range of the task utilization, with 0 ≤ UL ≤ UU ≤ 1.
- ○
- [ZL,ZU]: The range of the ratio between Hi-criticality utilization of a task and Lo-criticality utilization, where 0 ≤ ZL ≤ ZU.
- WCET: (a) for Lo-criticality level: and (b) for Hi-criticality level: if Li = Hi, otherwise .
- Start time:
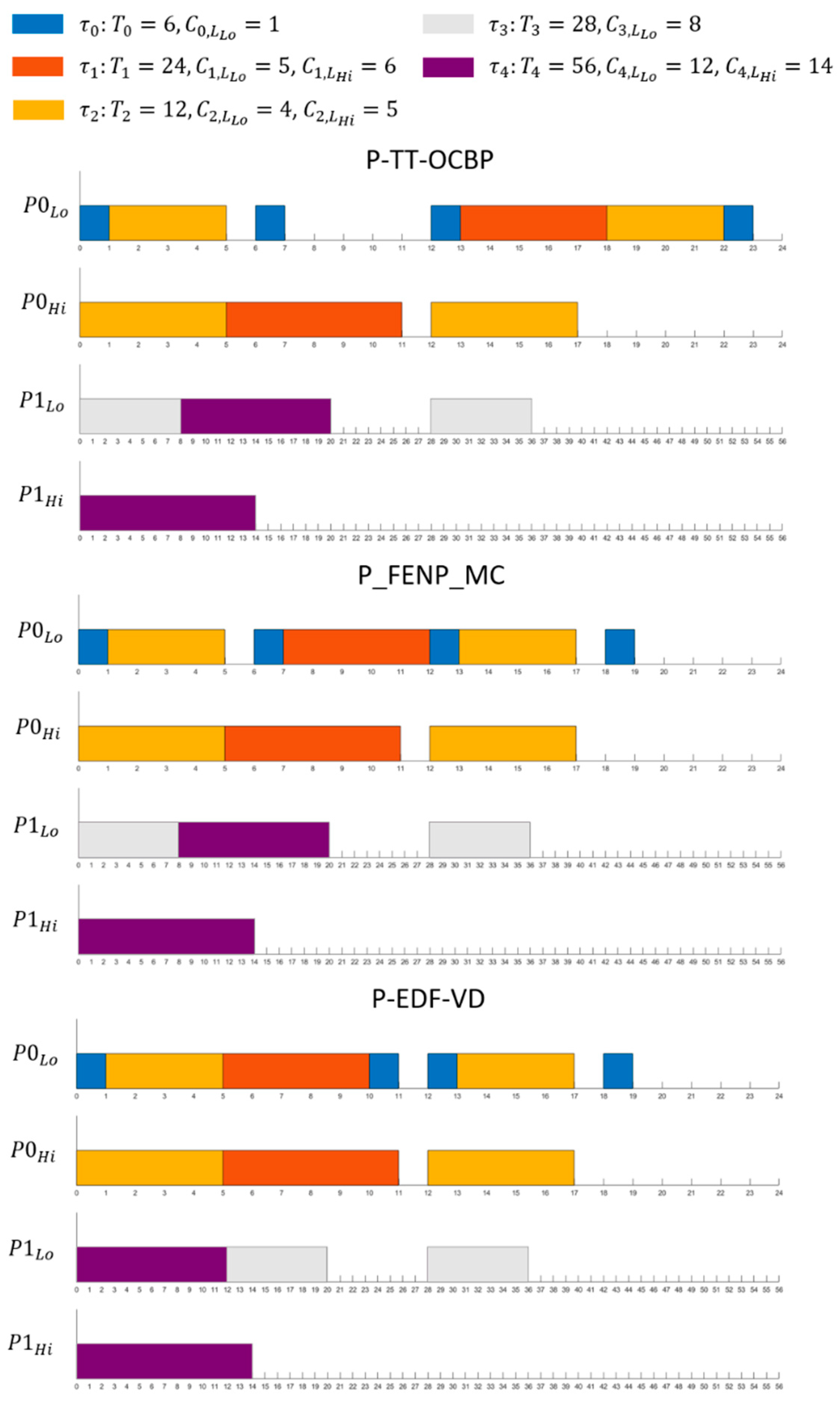
5.2. Execution Example and Comparison
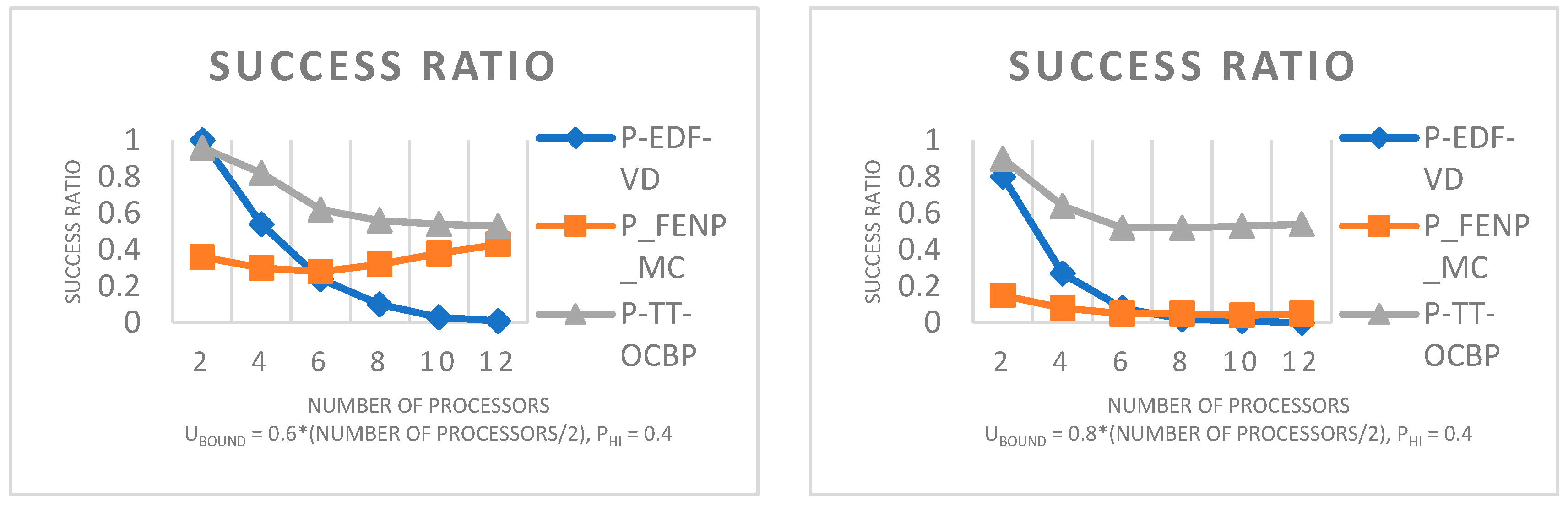
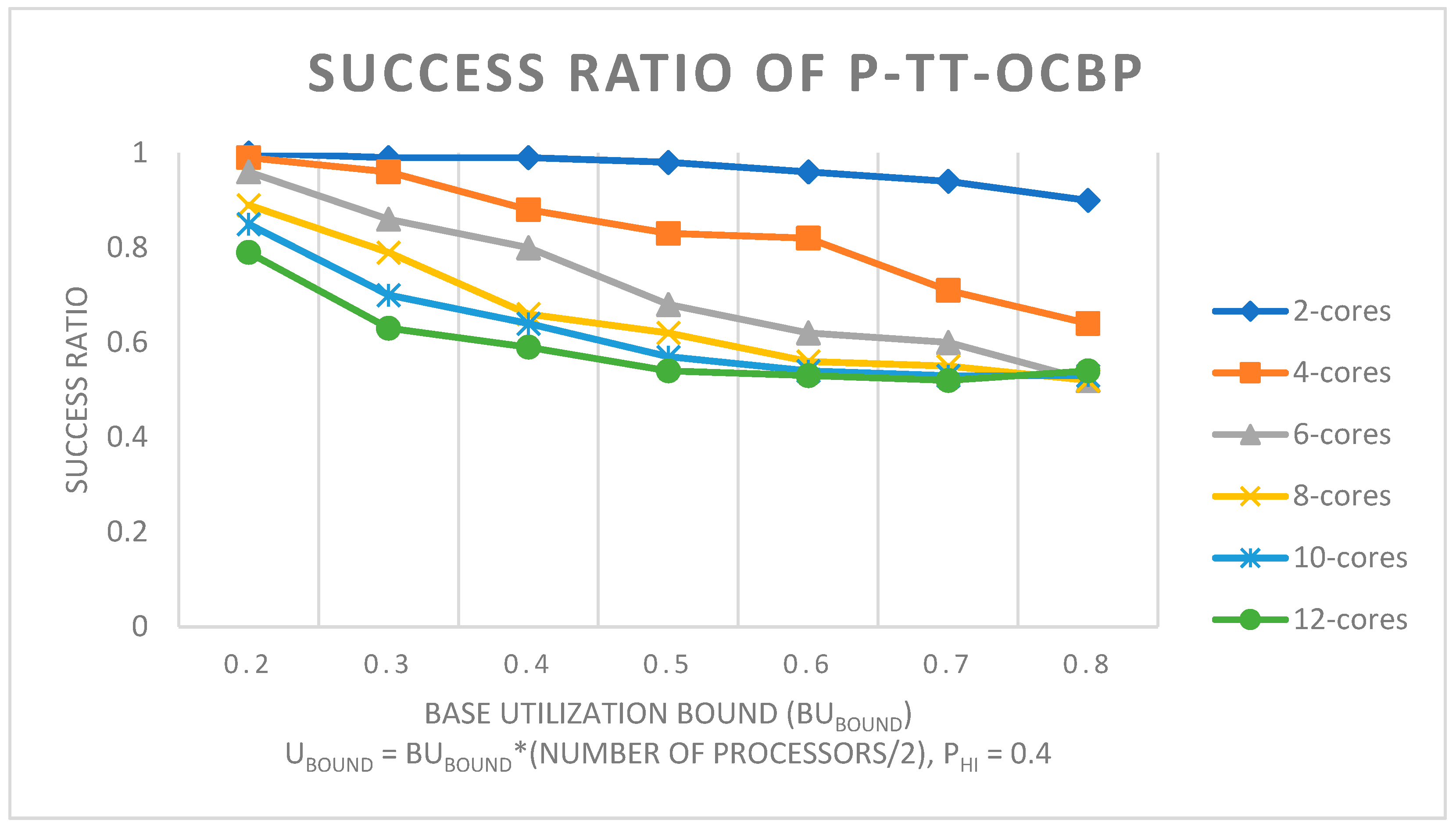
5.3. Success Ratio
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ernst, R.; Di Natale, M. Mixed Criticality Systems—A History of Misconceptions? IEEE Des. Test 2016, 33, 65–74. [Google Scholar] [CrossRef]
- Burns, A.; Davis, R.I. A Survey of Research into Mixed Criticality Systems. ACM Comput. Surv. 2017, 50, 1–37. [Google Scholar] [CrossRef]
- Capota, E.A.; Stangaciu, C.S.; Micea, M.V.; Curiac, D.-I. Towards mixed criticality task scheduling in cyber physical systems: Challenges and perspectives. J. Syst. Softw. 2019, 156, 204–216. [Google Scholar]
- Goswami, D.; Lukasiewycz, M.; Schneider, R.; Chakraborty, S. Time-triggered implementations of mixed-criticality automotive software. In Proceedings of the 2012 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 12–16 March 2012; pp. 1227–1232. [Google Scholar]
- Baruah, S.; Fohler, G. Certification-cognizant time-triggered scheduling of mixed-criticality systems. In Proceedings of the 2011 IEEE 32nd Real-Time Systems Symposium, Vienna, Austria, 29 November–2 December 2011; pp. 3–12. [Google Scholar]
- Baciu, M.D.; Capota, E.A.; Stangaciu, C.S.; Curiac, C.-D.; Micea, M.V. Multi-Core Time-Triggered OCBP-Based Scheduling for Mixed Criticality Periodic Task Systems. In Proceedings of the 2022 IEEE International Symposium on Electronics and Telecommunications (ISETC2022), Timisoara, Romania, 10–11 November 2022. [Google Scholar]
- Vestal, S. Preemptive scheduling of multi-criticality systems with varying degrees of execution time assurance. In Proceedings of the 28th IEEE International Real-Time Systems Symposium (RTSS 2007), Tucson, AZ, USA, 3–6 December 2007; pp. 239–243. [Google Scholar]
- Giannopoulou, G.; Stoimenov, N.; Huang, P.; Thiele, L. Scheduling of mixed-criticality applications on resource-sharing multicore systems. In Proceedings of the 2013 International Conference on Embedded Software (EMSOFT), Montreal, QC, Canada, 29 September–4 October 2013; pp. 1–15. [Google Scholar]
- Baruah, S.; Bonifaci, V.; d’Angelo, G.; Marchetti-Spaccamela, A.; Van Der Ster, S.; Stougie, L. Mixed-criticality scheduling of sporadic task systems. In European Symposium on Algorithms; Springer: Berlin/Heidelberg, Germany, 2011; pp. 555–566. [Google Scholar]
- Lee, J.; Chwa, H.S.; Phan, L.T.; Shin, I.; Lee, I. MC-ADAPT: Adaptive task dropping in mixed-criticality scheduling. ACM Trans. Embed. Comput. Syst. 2017, 16, 1–21. [Google Scholar]
- Yang, K.; Bhuiyan, A.; Guo, Z. F2VD: Fluid rates to virtual deadlines for precise mixed-criticality scheduling on a varying-speed processor. In Proceedings of the 2020 IEEE/ACM International Conference on Computer Aided Design (ICCAD), San Diego, CA, USA, 2–5 November 2020; pp. 1–9. [Google Scholar]
- Lee, J.; Ramanathan, S.; Phan, K.-M.; Easwaran, A.; Shin, I.; Lee, I. MC-Fluid: Multi-Core Fluid-Based Mixed-Criticality Scheduling. IEEE Trans. Comput. 2017, 67, 469–483. [Google Scholar] [CrossRef]
- Capota, E.A.; Stangaciu, C.S.; Micea, M.V.; Curiac, D.-I. Towards Fully Jitterless Applications: Periodic Scheduling in Multiprocessor MCSs Using a Table-Driven Approach. Appl. Sci. 2020, 10, 6702. [Google Scholar] [CrossRef]
- Ramanathan, S.; Easwaran, A. Mixed-criticality scheduling on multiprocessors with service guarantees. In Proceedings of the 2018 IEEE 21st International Symposium on Real-Time Distributed Computing (ISORC), Singapore, 29–31 May 2018; pp. 17–24. [Google Scholar]
- Behera, L.; Bhaduri, P. An energy-efficient time-triggered scheduling algorithm for mixed-criticality systems. Des. Autom. Embed. Syst. 2019, 24, 79–109. [Google Scholar] [CrossRef]
- Behera, L.; Bhaduri, P. Time-triggered scheduling for multiprocessor mixed-criticality systems. In Proceedings of the International Conference on Distributed Computing and Internet Technology, Bhubaneswar, India, 11–13 January 2018; Springer: Cham, Switzerland; pp. 135–151. [Google Scholar]
- Socci, D.; Poplavko, P.; Bensalem, S.; Bozga, M. Time-triggered mixed-critical scheduler on single and multi-processor platforms. In Proceedings of the 2015 IEEE 17th International Conference on High Performance Computing and Communications, 2015 IEEE 7th International Symposium on Cyberspace Safety and Security, and 2015 IEEE 12th International Conference on Embedded Software and Systems, New York, NY, USA, 24–26 August 2015; pp. 684–687. [Google Scholar]
- Zhang, Y.-W.; Cai, N. Energy efficient EDF-VD-based mixed-criticality scheduling with shared resources. J. Syst. Arch. 2021, 119, 102246. [Google Scholar]
- Baruah, S.; Li, H.; Stougie, L. Towards the design of certifiable mixed-criticality systems. In Proceedings of the 2010 16th IEEE Real-Time and Embedded Technology and Applications Symposium, Stockholm, Sweden, 12–15 April 2010; pp. 13–22. [Google Scholar]
- Stângaciu, C.S.; Capota, E.A.; Stângaciu, V.; Micea, M.V.; Curiac, D.I. A Hardware-Aware Application Execution Model in Mixed-Criticality Internet of Things. Mathematics 2022, 10, 1537. [Google Scholar]
- Baruah, S.; Burns, A.; Davis, R.I. Response-time analysis for mixed criticality systems. In Proceedings of the 2011 IEEE 32nd Real-Time Systems Symposium, Vienna, Austria, 29 November–2 December 2011; pp. 34–43. [Google Scholar]
- Baruah, S.; Bonifaci, V.; D’Angelo, G.; Li, H.; Marchetti-Spaccamela, A.; Megow, N.; Stougie, L. Scheduling real-time mixed-criticality jobs. In Proceedings of the International Symposium on Mathematical Foundations of Computer Science, Brno, Czech Republic, 23–27 August 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 90–101. [Google Scholar]
- Baruah, S.; Li, H.; Stougie, L. Mixed-criticality scheduling: Improved resource-augmentation results. In Proceedings of the CATA, Honolulu, HI, USA, 24–26 March 2010; pp. 217–223. [Google Scholar]
- Blake, G.; Dreslinski, R.G.; Mudge, T. A survey of multicore processors. IEEE Signal Process. Mag. 2009, 26, 26–37. [Google Scholar]
- Alahmadi, A.; Alnowiser, A.; Zhu, M.M.; Che, D.; Ghodous, P. Enhanced first-fit decreasing algorithm for energy-aware job scheduling in cloud. In Proceedings of the 2014 International Conference on Computational Science and Computational Intelligence, Las Vegas, NV, USA, 10–13 March 2014; Volume 2, pp. 69–74. [Google Scholar]
- Pathan, R.M. Improving the quality-of-service for scheduling mixed-criticality systems on multiprocessors. In Proceedings of the 29th Euromicro Conference on Real-Time Systems (ECRTS 2017), Dubrovnik, Croatia, 27–30 June 2017. [Google Scholar]
- Su, H.; Zhu, D.; Mossé, D. Scheduling algorithms for elastic mixed-criticality tasks in multicore systems. In Proceedings of the 2013 IEEE 19th International Conference on Embedded and Real-Time Computing Systems and Applications, Taipei, Taiwan, 19–21 August 2013; pp. 352–357. [Google Scholar]
- Li, H.; Baruah, S. Outstanding paper award: Global mixed-criticality scheduling on multiprocessors. In Proceedings of the 2012 24th Euromicro Conference on Real-Time Systems, Pisa, Italy, 11–13 July 2012; pp. 166–175. [Google Scholar]
- Guan, N.; Ekberg, P.; Stigge, M.; Yi, W. Improving the scheduling of certifiable mixed-criticality sporadic task systems. In Technical Report 2013–008; Department of Information Technology, Uppsala University: Uppsala, Sweden, 2013. [Google Scholar]
| Task | |||||
|---|---|---|---|---|---|
| 8 | 8 | 1 | 4 | - | |
| 12 | 12 | 2 | 5 | 7 | |
| 16 | 16 | 1 | 5 | - | |
| 24 | 24 | 2 | 1 | 4 |
| TaskID | JobID | StartTime |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 4 |
| 2 | 0 | 5 |
| 0 | 1 | 10 |
| 3 | 0 | 14 |
| 1 | 1 | 15 |
| 0 | 2 | 16 |
| 2 | 1 | 20 |
| 0 | 3 | 25 |
| 1 | 2 | 29 |
| 0 | 4 | 32 |
| 3 | 1 | 36 |
| 2 | 2 | 37 |
| 1 | 3 | 42 |
| 0 | 5 | 43 |
| TaskID | JobID | StartTime |
|---|---|---|
| 1 | 0 | 0 |
| 3 | 0 | 3 |
| 1 | 1 | 12 |
| 1 | 2 | 24 |
| 3 | 1 | 27 |
| 1 | 3 | 36 |
| Task | |||||
|---|---|---|---|---|---|
| 6 | 6 | 1 | 1 | - | |
| 24 | 24 | 2 | 5 | 6 | |
| 12 | 12 | 2 | 4 | 5 | |
| 28 | 28 | 1 | 8 | - | |
| 56 | 56 | 2 | 12 | 14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baciu, M.D.; Capota, E.A.; Stângaciu, C.S.; Curiac, D.-I.; Micea, M.V. Multi-Core Time-Triggered OCBP-Based Scheduling for Mixed Criticality Periodic Task Systems. Sensors 2023, 23, 1960. https://doi.org/10.3390/s23041960
Baciu MD, Capota EA, Stângaciu CS, Curiac D-I, Micea MV. Multi-Core Time-Triggered OCBP-Based Scheduling for Mixed Criticality Periodic Task Systems. Sensors. 2023; 23(4):1960. https://doi.org/10.3390/s23041960
Chicago/Turabian StyleBaciu, Marian D., Eugenia A. Capota, Cristina S. Stângaciu, Daniel-Ioan Curiac, and Mihai V. Micea. 2023. "Multi-Core Time-Triggered OCBP-Based Scheduling for Mixed Criticality Periodic Task Systems" Sensors 23, no. 4: 1960. https://doi.org/10.3390/s23041960
APA StyleBaciu, M. D., Capota, E. A., Stângaciu, C. S., Curiac, D. -I., & Micea, M. V. (2023). Multi-Core Time-Triggered OCBP-Based Scheduling for Mixed Criticality Periodic Task Systems. Sensors, 23(4), 1960. https://doi.org/10.3390/s23041960







