Weighted Sparseness-Based Anomaly Detection for Hyperspectral Imagery
Abstract
:1. Introduction
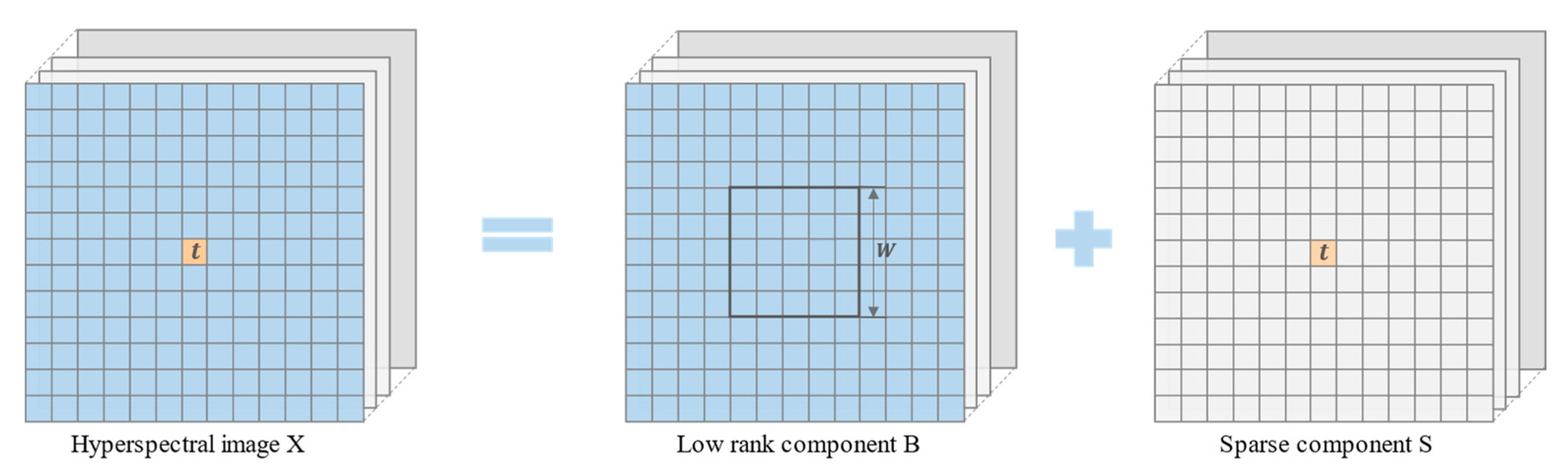
2. Low-Rank and Sparse Decomposition
3. Proposed Method
3.1. Spectral Sparsity Coefficient Divergence Index Weighting Factor
3.2. Spatial Sparsity Coefficient Divergence Index Weighting Factor
3.3. Anomalies Detection Based on Weighted Sparse Matrix
| Algorithm 1 WSA |
| Input: (1) The original HSI data ; (2) The restriction value of the rank ; (3) The restriction value of the sparseness ; Step 1. Solve the Equation (2) with Godec. Step 2. Construct the dictionary with matrix , reconstruct initial HSI , extract sparse coefficient, and calculate with Equations (6) and (8)–(10). Step 3. Calculate for each pixel with matrix according to Equation (11). Step 4. Calculate the final anomaly detection operator with Equation (12). Step 5. Calculate the threshold value with Equation (13) and traverse the image. Output: Abnormal detection results. |
4. Experimental Results
4.1. Hyperspectral Data
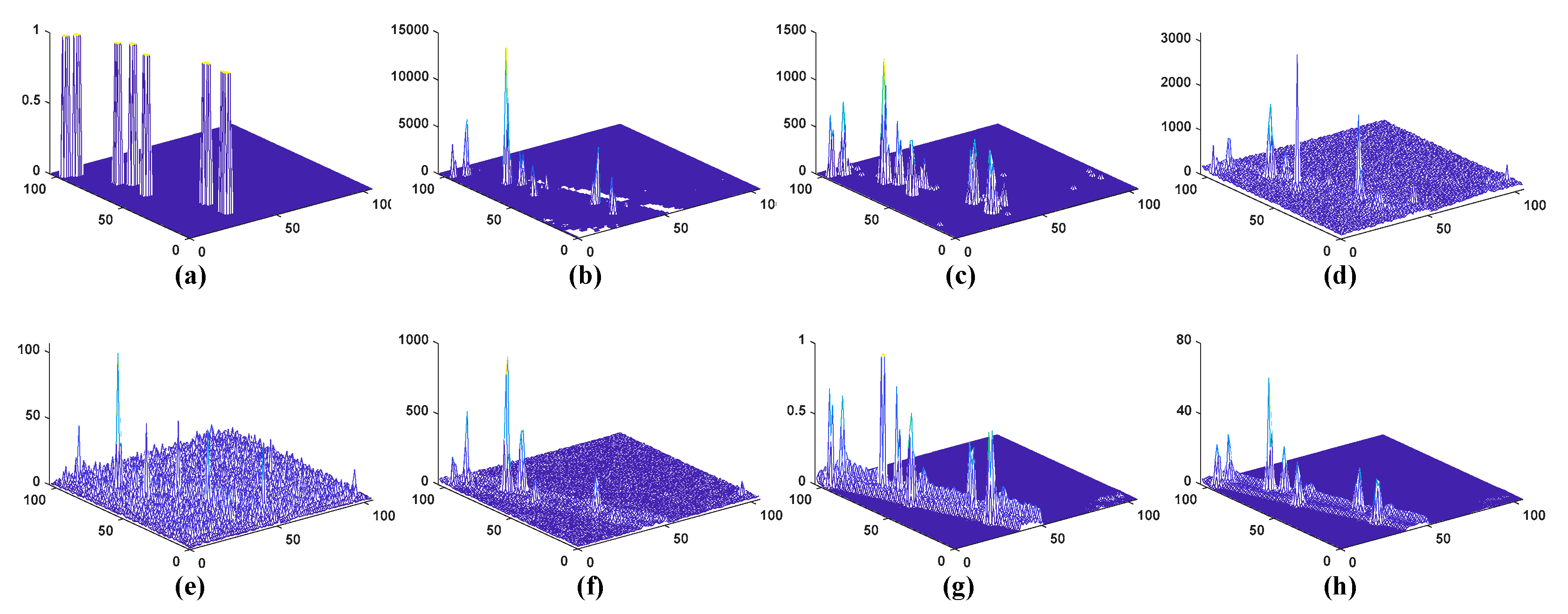
4.2. Experimental Results and Discussion
4.2.1. Effects from the Rank and Sparsity Level on Detection Performance
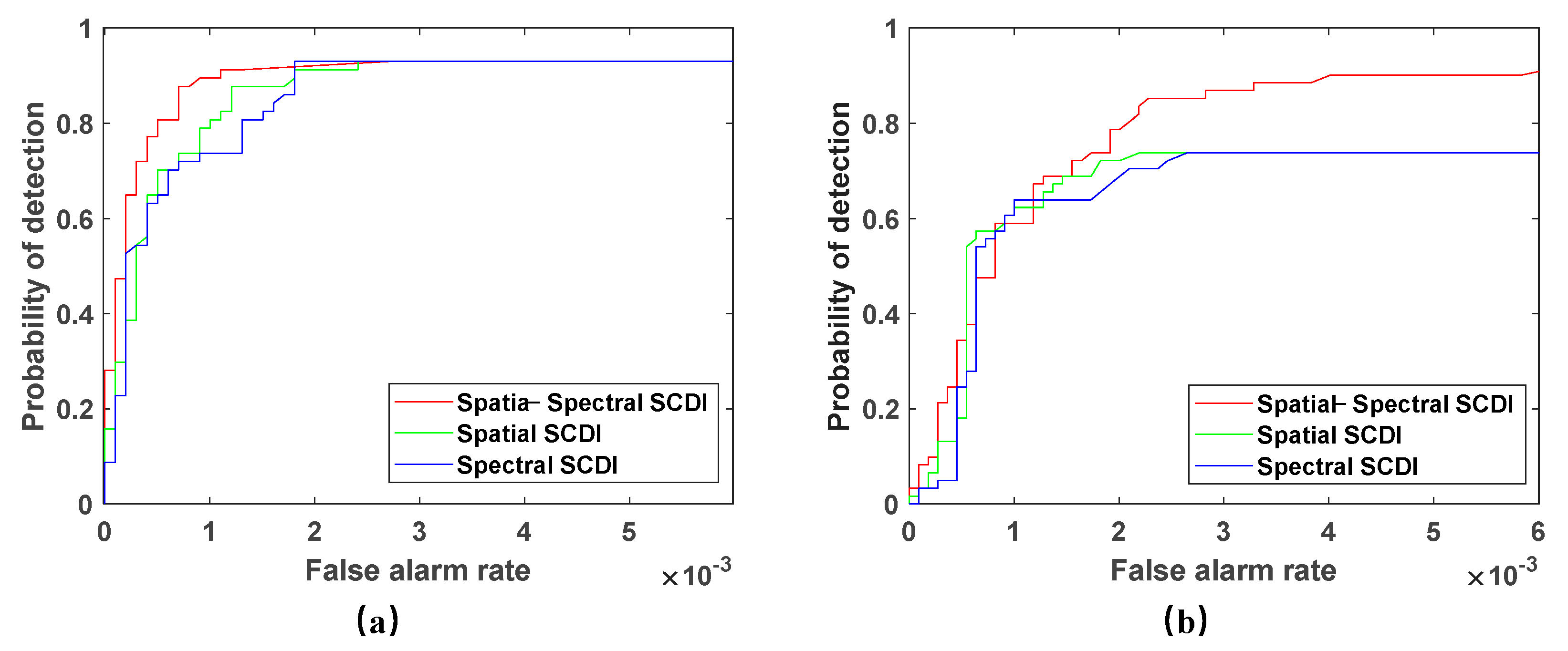
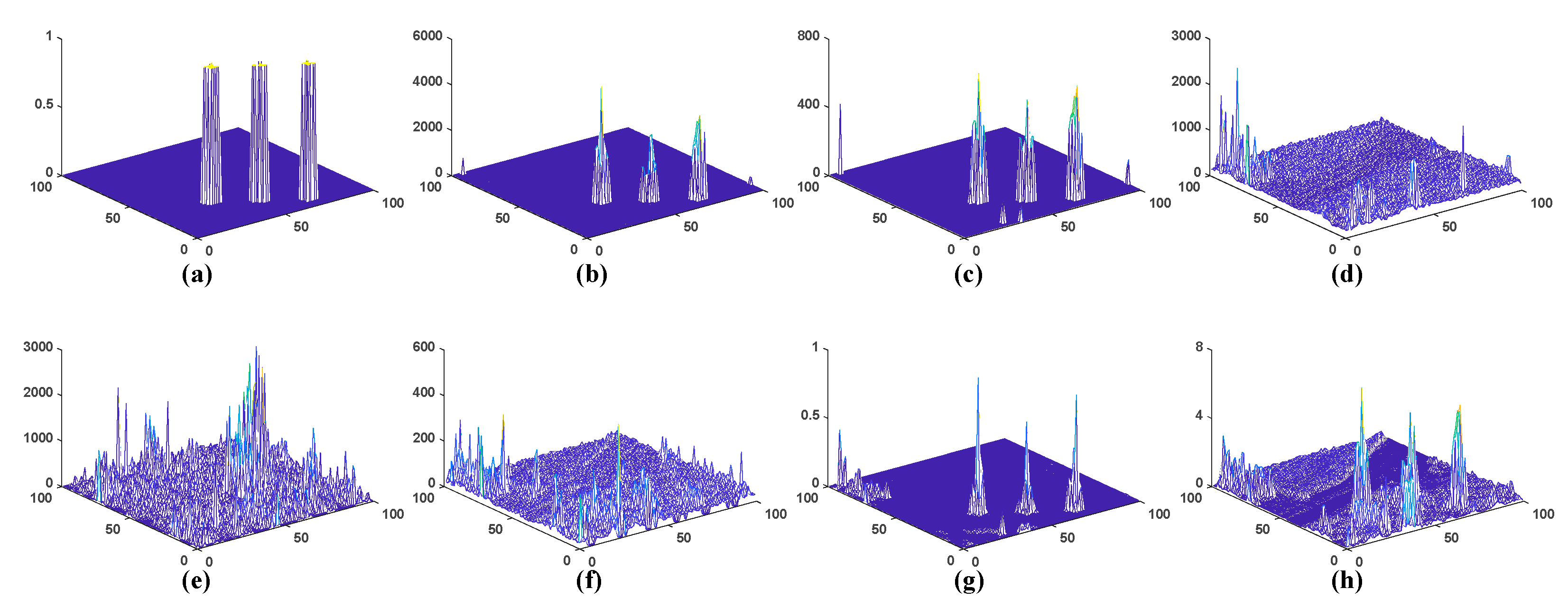
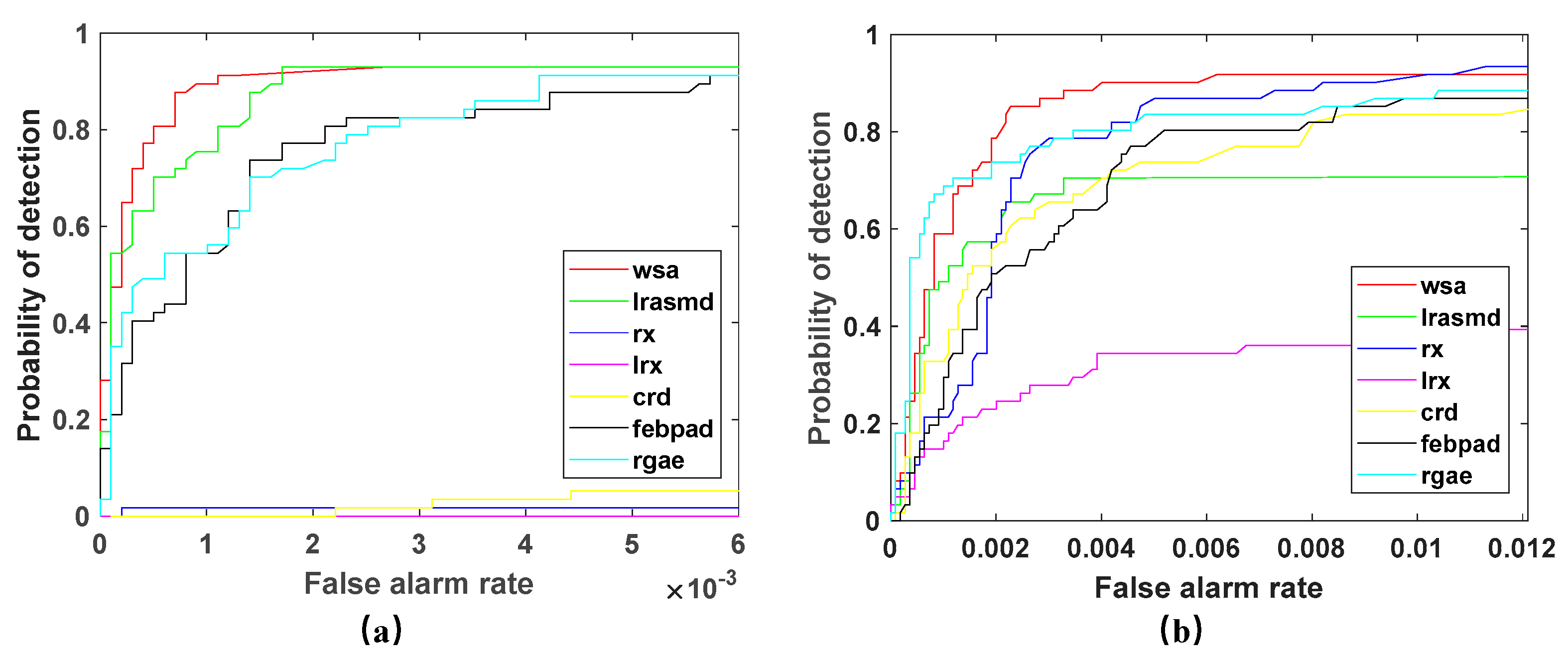
4.2.2. Detection Performance of WSA
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tong, Q.X.; Zhang, B.; Zhang, L.F. Current progress of hyperspectral remote sensing in China. J. Remote Sens. 2016, 20, 689–707. [Google Scholar]
- Zhang, L.; Zhang, L.; Du, B.; You, J.; Tao, D. Hyperspectral image unsupervised classification by robust manifold matrix factorization. Inf. Sci. 2019, 485, 154–169. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral remote sensing data analysis and future challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Shaw, G.; Manolakis, D. Signal processing for hyperspectral image exploitation. IEEE Trans. Signal Process. 2002, 19, 12–16. [Google Scholar] [CrossRef]
- Du, B.; Zhang, L. Random-selection-based anomaly detector for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1578–1589. [Google Scholar] [CrossRef]
- Liu, C.; Li, J.; He, L. Superpixel-based semisupervised active learning for hyperspectral image classification. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2019, 12, 357–370. [Google Scholar] [CrossRef]
- Huang, X.; Dong, M.; Li, J.; Guo, X. A 3-d-swin transformer-based hierarchical contrastive learning method for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification using dictionary-based sparse representation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3973–3985. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, B.; Zhang, L.; Wang, S. A low-rank and sparse matrix decomposition-based Mahalanobis distance method for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1376–1389. [Google Scholar] [CrossRef]
- Lee, L.C.; Paylor, D.; Chang, C.I. Anomaly discrimination and classification for hyperspectral imagery. In Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing; IEEE: Tokyo, Japan, 2015; pp. 2158–6276. [Google Scholar] [CrossRef]
- Zhao, R.; Du, B.; Zhang, L. A robust nonlinear hyperspectral anomaly detection approach. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2014, 7, 1227–1234. [Google Scholar] [CrossRef]
- Sudharsan, S.; Hemalatha, R.; Radha, S. A survey on hyperspectral imaging for mineral exploration using machine learning algorithms. In International Conference on Wireless Communications Signal Processing and Networking; IEEE: Chennai, India, 2019; pp. 206–212. [Google Scholar] [CrossRef]
- Booysen, R.; Gloaguen, R.; Lorenz, S.; Zimmermann, R.; Andreani, L.; Nex, P.A. The Potential of Multi-Sensor Remote Sensing Mineral Exploration: Examples from Southern Africa. In International Geoscience and Remote Sensing Symposium; IEEE: Yokohama, Japan, 2019; pp. 6027–6030. [Google Scholar] [CrossRef]
- Wang, Q.; Lin, J.; Yuan, Y. Salient band selection for hyperspectral image classification via manifold ranking. IEEE Trans. Neural Networks Learn. Syst. 2017, 27, 1279–1289. [Google Scholar] [CrossRef]
- de Almeida, D.R.A.; Broadbent, E.; Zambrano, A.M.A.; Ferreira, M.P.; Brancalion, P.H.S. Fusion of Lidar and Hyperspectral Data from Drones for Ecological Questions: The Gatoreye Atlantic Forest Restoration Case Study. In International Geoscience and Remote Sensing Symposium; IEEE: Brussels, Belgium, 2021; pp. 714–715. [Google Scholar] [CrossRef]
- Yu, R.; Lyu, M.; Lu, J.; Yang, Y.; Shen, G.; Li, F. Spatial Coordinates Correction Based on Multi-Sensor Low-Altitude Remote Sensing Image Registration for Monitoring Forest Dynamics. IEEE Access 2020, 8, 18483–18496. [Google Scholar] [CrossRef]
- Liu, Y.; Lin, C.H.; Kuo, Y.C. Low-Rank Representation With Morphological-Attribute-Filter Based Regularization For Hyperspectral Anomaly Detection. In Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing; IEEE: Rome, Italy, 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Ke, C. Military object detection using multiple information extracted from hyperspectral imagery. In International Conference on Progress in Informatics and Computing; IEEE: Nanjing, China, 2017; pp. 124–128. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y. Hyperspectral Anomaly Detection Based on Improved RX with CNN Framework. In International Geoscience and Remote Sensing Symposium; IEEE: Yokohama, Japan, 2019; pp. 2244–2247. [Google Scholar] [CrossRef]
- Yang, X.; Huang, X.; Zhu, M.; Xu, S.; Liu, Y. Ensemble and Random RX With Multiple Features Anomaly Detector for Hyperspectral Image. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Hidalgo, J.A.P.; Pérez-Suay, A.; Nar, F.; Camps-Valls, G. Efficient Nonlinear RX Anomaly Detectors. IEEE Geosci. Remote Sens. Lett. 2021, 18, 231–235. [Google Scholar] [CrossRef]
- Ren, L.; Zhao, L.; Wang, Y. A Superpixel-Based Dual Window RX for Hyperspectral Anomaly Detection. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1233–1237. [Google Scholar] [CrossRef]
- Li, L.; Li, W.; Du, Q.; Tao, R. Low-Rank and Sparse Decomposition with Mixture of Gaussian for Hyperspectral Anomaly Detection. IEEE Trans Cybern. 2021, 51, 4363–4372. [Google Scholar] [CrossRef]
- Wang, X.; Wang, L.; Wang, Q. Local Spatial–Spectral Information-Integrated Semisupervised Two-Stream Network for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Theiler, J.; Grosklos, G. Cracks in KRX: When more distant points are less anomalous. In Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing; IEEE: Los Angeles, CA, USA, 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Theiler, J.; Grosklos, G. Problematic Projection to the In-Sample Subspace for a Kernelized Anomaly Detector. IEEE Geosci. Remote Sens. Lett. 2016, 13, 485–489. [Google Scholar] [CrossRef]
- Zhou, J.; Kwan, C.; Ayhan, B.; Eismann, M.T. A novel cluster kernel RX algorithm for anomaly and change detection using hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6497–6504. [Google Scholar] [CrossRef]
- Hatipoğlu, P.U.; Özparlak, L. Elimination of unwanted anomalies in a hyperspectral image using modified subspace RX algorithm. In International Geoscience and Remote Sensing Symposium; IEEE: Milan, Italy, 2015; pp. 3505–3508. [Google Scholar] [CrossRef]
- Khaoula, R.; Mohamed, M. Improving Intrusion Detection Using PCA And K-Means Clustering Algorithm. In International Conference on Wireless Networks and Mobile Communication; IEEE: Morocco, Rabat, 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.; Zhang, J. Hyperspectral Anomaly Detection for Spectral Anomaly Targets via Spatial and Spectral Constraints. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, J.; Song, S.; Liu, D. Hyperspectral Anomaly Detection via Dictionary Construction-Based Low-Rank Representation and Adaptive Weighting. Remote Sens. 2019, 11, 192. [Google Scholar] [CrossRef] [Green Version]
- Tu, B.; Yang, X.; Li, N.; Zhou, C.; He, D. Hyperspectral anomaly detection via density peak clustering. Pattern Recognit. Lett. 2020, 129, 144–149. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. Collaborative representation for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1463–1474. [Google Scholar] [CrossRef]
- Tu, B.; Yang, X.; Zhou, C.; He, D.; Plaza, A. Hyperspectral Anomaly Detection Using Dual Window Density. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8503–8517. [Google Scholar] [CrossRef]
- Chen, S.; Chang, C.I.; Li, X. Component Decomposition Analysis for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–22. [Google Scholar] [CrossRef]
- Wu, W.; Wu, Z.; Xu, Y.; Yang, J.; Liu, H.; Wei, Z. Multi-Scale Anomaly Detection in Hyperspectral Images Based on Sparse and Low Rank Representations. In Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing; IEEE: Amsterdam, The Netherlands, 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Zhang, Y.; He, K.; Dong, Y.; Wu, K.; Chen, T. Joint Sparse Representation and Multitask Learning for Hyperspectral Anomaly Detection. In International Geoscience and Remote Sensing Symposium; IEEE: Waikoloa, Hawaii, 2020; pp. 2424–2427. [Google Scholar] [CrossRef]
- Cheng, T.; Wang, B. Manifold Regularized Low-Rank Representation for Hyperspectral Anomaly Detection. In International Geoscience and Remote Sensing Symposium; IEEE: Valencia, Spain, 2018; pp. 2853–2856. [Google Scholar] [CrossRef]
- Ruhan, A.; Mu, X.; He, J. Enhance Tensor RPCA-Based Mahalanobis Distance Method for Hyperspectral Anomaly Detection. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Sun, W.; Liu, C.; Li, J.; Lai, Y.M.; Li, W. Low-rank and sparse matrix decomposition-based anomaly detection for hyperspectral imagery. J. Appl. Remote Sens. 2014, 8, 083641. [Google Scholar] [CrossRef]
- Zhu, L.; Wen, G.; Qiu, S. Low-Rank and sparse matrix decomposition with cluster weighting for hyperspectral anomaly detection. Remote Sens. 2018, 10, 707. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Fan, Y.; Xu, M.; Li, W.; Zhang, G.; Liu, L.; Yu, D. An Improved Low Rank and Sparse Matrix Decomposition-Based Anomaly Target Detection Algorithm for Hyperspectral Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2663–2672. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, J.; Song, S.; Zhang, C.; Liu, D. Low-Rank and Sparse Matrix Decomposition with Orthogonal Subspace Projection-Based Background Suppression for Hyperspectral Anomaly Detection. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1378–1382. [Google Scholar] [CrossRef]
- Ahmad, M.; Shabbir, S.; Roy, S.K.; Hong, D.; Wu, X.; Yao, J.; Khan, A.M.; Mazzara, M.; Distefano, S.; Chanussot, J. Hyperspectral image classification—Traditional to deep models: A survey for future prospects. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2022, 15, 968–999. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A.; Chanussot, J. SpectralFormer: Rethinking hyperspectral image classification with transformers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Qian, X.; Lin, S.; Cheng, G.; Yao, X.; Ren, H.; Wang, W. Object Detection in Remote Sensing Images Based on Improved Bounding Box Regression and Multi-Level Features Fusion. Remote Sens. 2020, 12, 143. [Google Scholar] [CrossRef]
- Xie, W.; Li, Y.; Lei, J.; Yang, J.; Chang, C.I.; Li, Z. Hyperspectral band selection for spectral–spatial anomaly detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3426–3436. [Google Scholar] [CrossRef]
- Coca, M.; Neagoe, I.C.; Datcu, M. Hybrid DNN-Dirichlet Anomaly Detection and Ranking: Case of Burned Areas Discovery. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, W.; Huang, J. Exploiting embedding manifold of autoencoders for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1527–1537. [Google Scholar] [CrossRef]
- Dong, Y.; Du, B.; Zhang, L. Target detection based on random forest metric learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1830–1838. [Google Scholar] [CrossRef]
- Zhou, T.; Tao, D. GoDec: Randomized Lowrank & sparse matrix decomposition in noisy case. In International Conference on Machine Learning; DBLP: Washington, DC, USA, 2011. [Google Scholar]
- Ma, Y.; Fan, G.; Jin, Q.; Huang, J.; Mei, X.; Ma, J. Hyperspectral anomaly detection via integration of feature extraction and background purification. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1436–1440. [Google Scholar] [CrossRef]
- Fan, G.; Ma, Y.; Mei, X.; Fan, F.; Huang, J.; Ma, J. Hyperspectral anomaly detection with robust graph autoencoders. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]


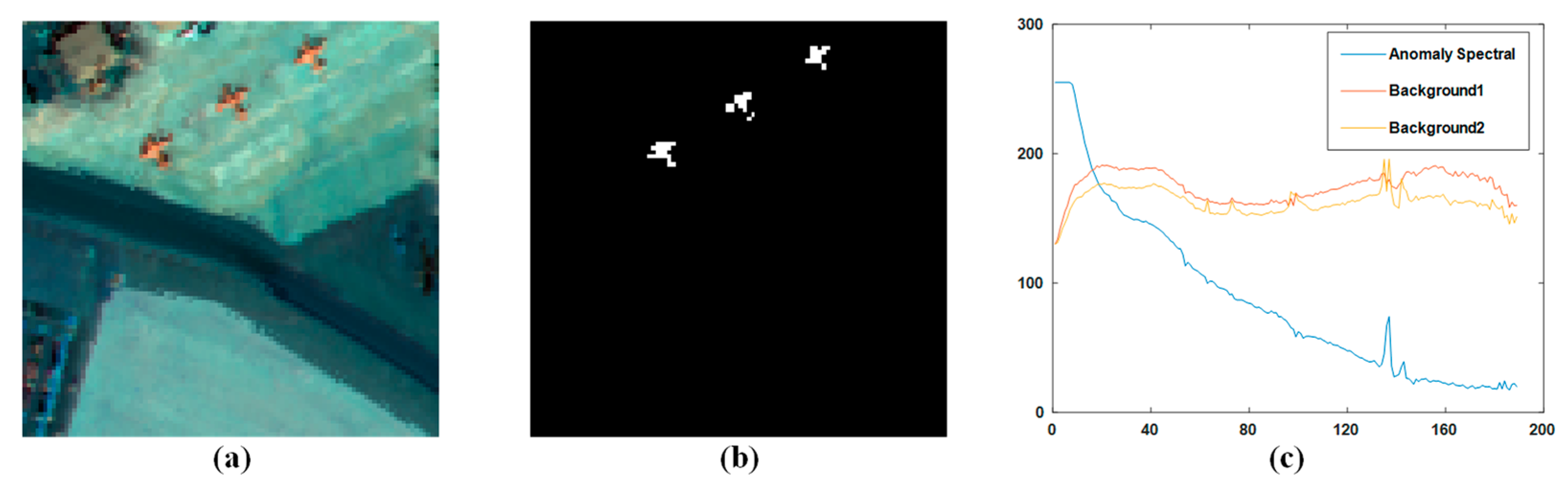





| Scene | San Diego Scene | PaviaC Scene |
|---|---|---|
| Size | ||
| Number of spectral bands | 189 | 102 |
| Target Description | Three stationary parked aircraft. | The landscape of San Diego airport, with buildings and roads in the background, and there is no drastic change in spectra |
| Background Description | Exposed mounds of soil with no vegetation growth and the cars on the bridge | The background mainly contains rivers, bridges and shadows, and there is no drastic change in spectra |
| Running Time of Detectors (s) | |||||||
|---|---|---|---|---|---|---|---|
| Datasets | WSA | LRaSMD | RX | LRX | CRD | FEBPAD | RGAE |
| San Diego | 45.3 | 15.5 | 1.2 | 30.2 | 3.7 | 3.5 | 87.3 |
| PaviaC | 40.1 | 11.2 | 1.1 | 15.3 | 3.5 | 3.2 | 65.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lian, X.; Zhao, E.; Zheng, W.; Peng, X.; Li, A.; Zhen, Z.; Wen, Y. Weighted Sparseness-Based Anomaly Detection for Hyperspectral Imagery. Sensors 2023, 23, 2055. https://doi.org/10.3390/s23042055
Lian X, Zhao E, Zheng W, Peng X, Li A, Zhen Z, Wen Y. Weighted Sparseness-Based Anomaly Detection for Hyperspectral Imagery. Sensors. 2023; 23(4):2055. https://doi.org/10.3390/s23042055
Chicago/Turabian StyleLian, Xing, Erwei Zhao, Wei Zheng, Xiaodong Peng, Ang Li, Zheng Zhen, and Yan Wen. 2023. "Weighted Sparseness-Based Anomaly Detection for Hyperspectral Imagery" Sensors 23, no. 4: 2055. https://doi.org/10.3390/s23042055
APA StyleLian, X., Zhao, E., Zheng, W., Peng, X., Li, A., Zhen, Z., & Wen, Y. (2023). Weighted Sparseness-Based Anomaly Detection for Hyperspectral Imagery. Sensors, 23(4), 2055. https://doi.org/10.3390/s23042055






