Design of MIR Dispersive Spectrograph System with Uncooled Microbolometer
Abstract
:1. Introduction
2. Configuration of the System
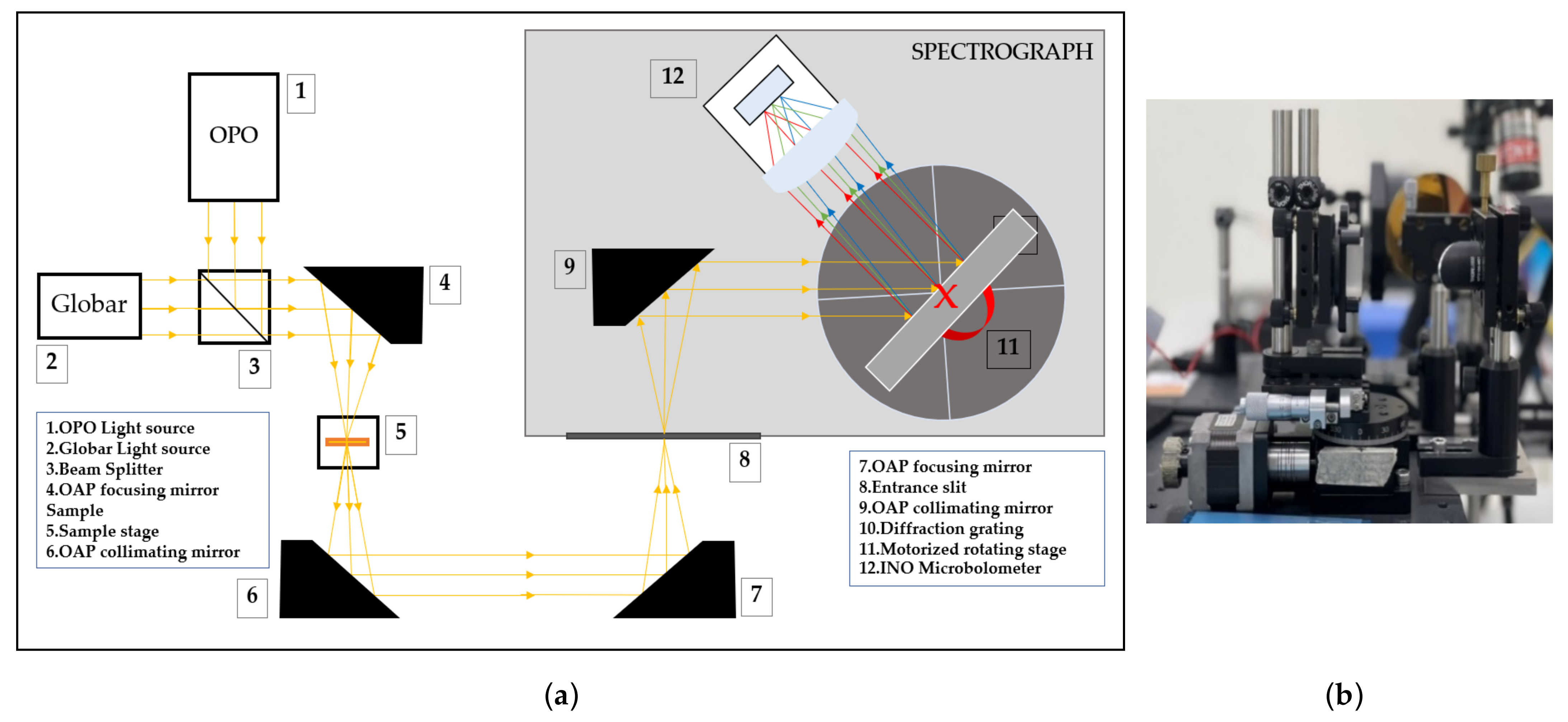
2.1. Optical Design
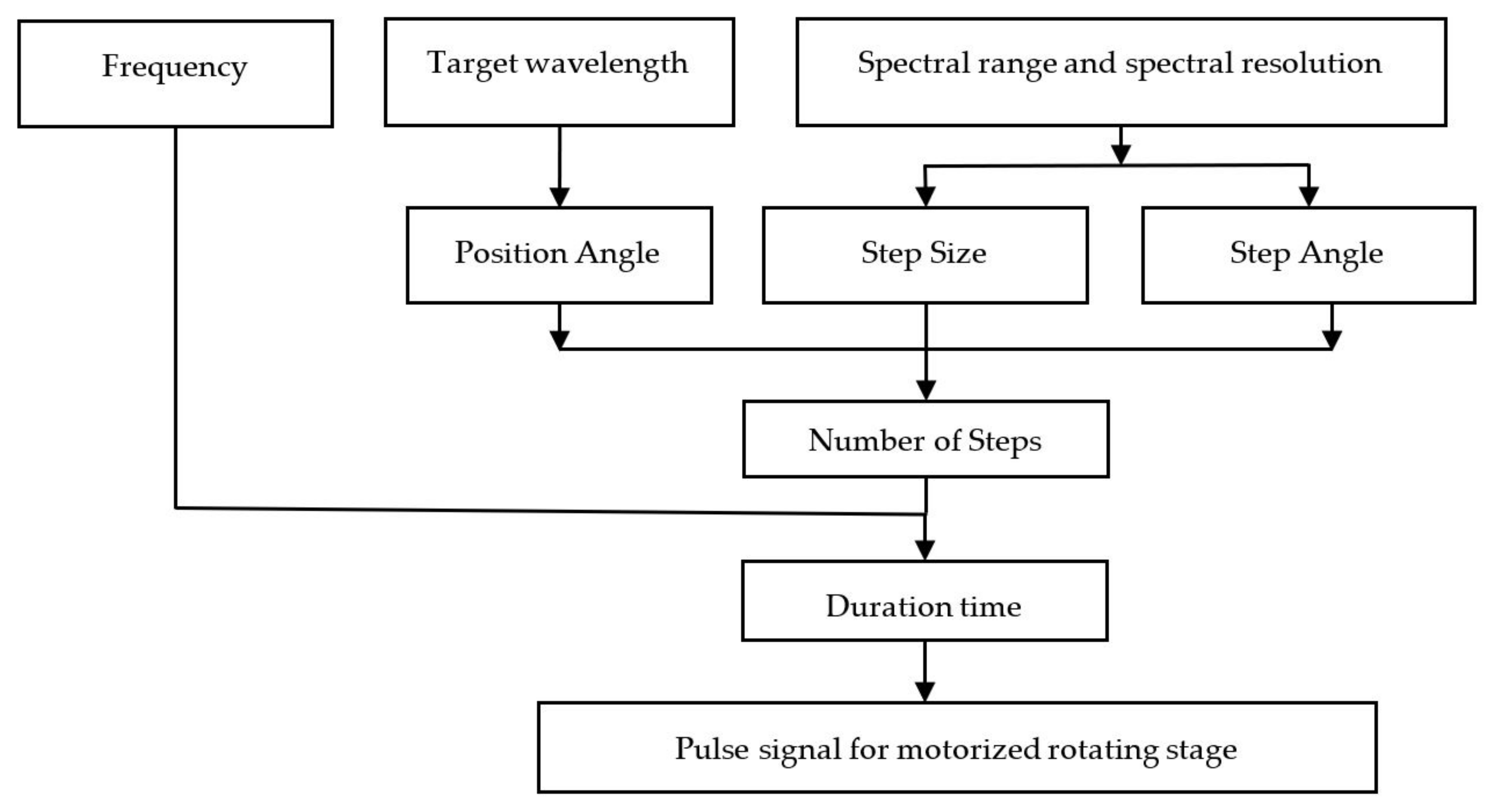
2.2. Programming Method
2.3. Program for Rotating Motorized Stage
2.4. Data Acquisition and Processing
3. Results and Discussion
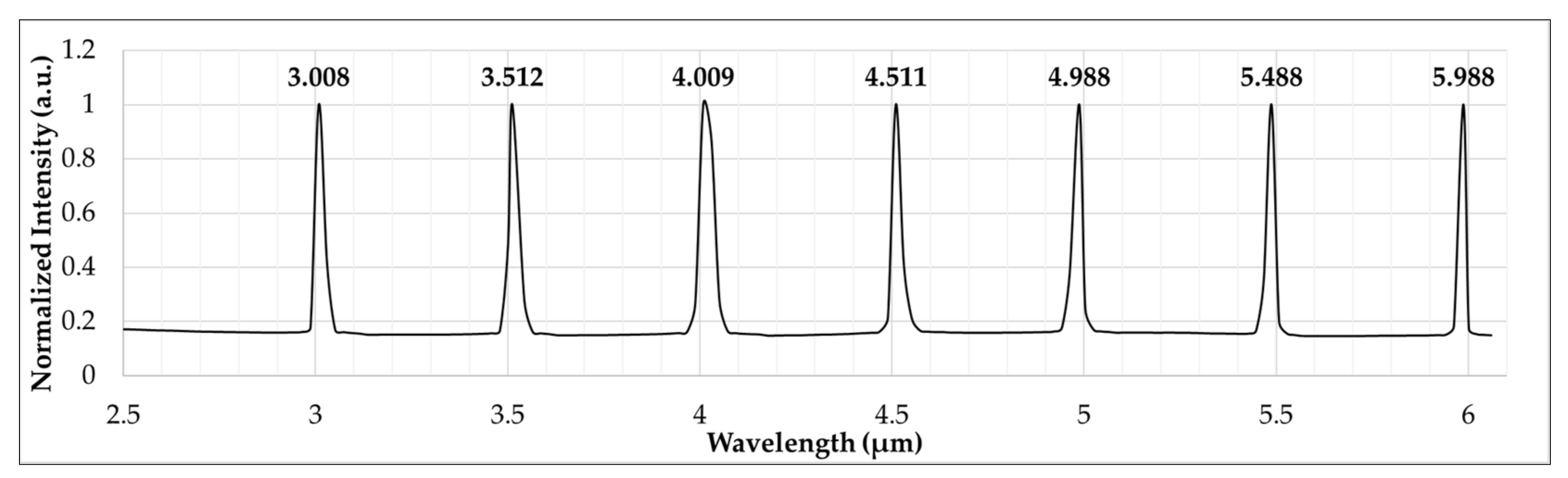
3.1. Spectral Characteristics
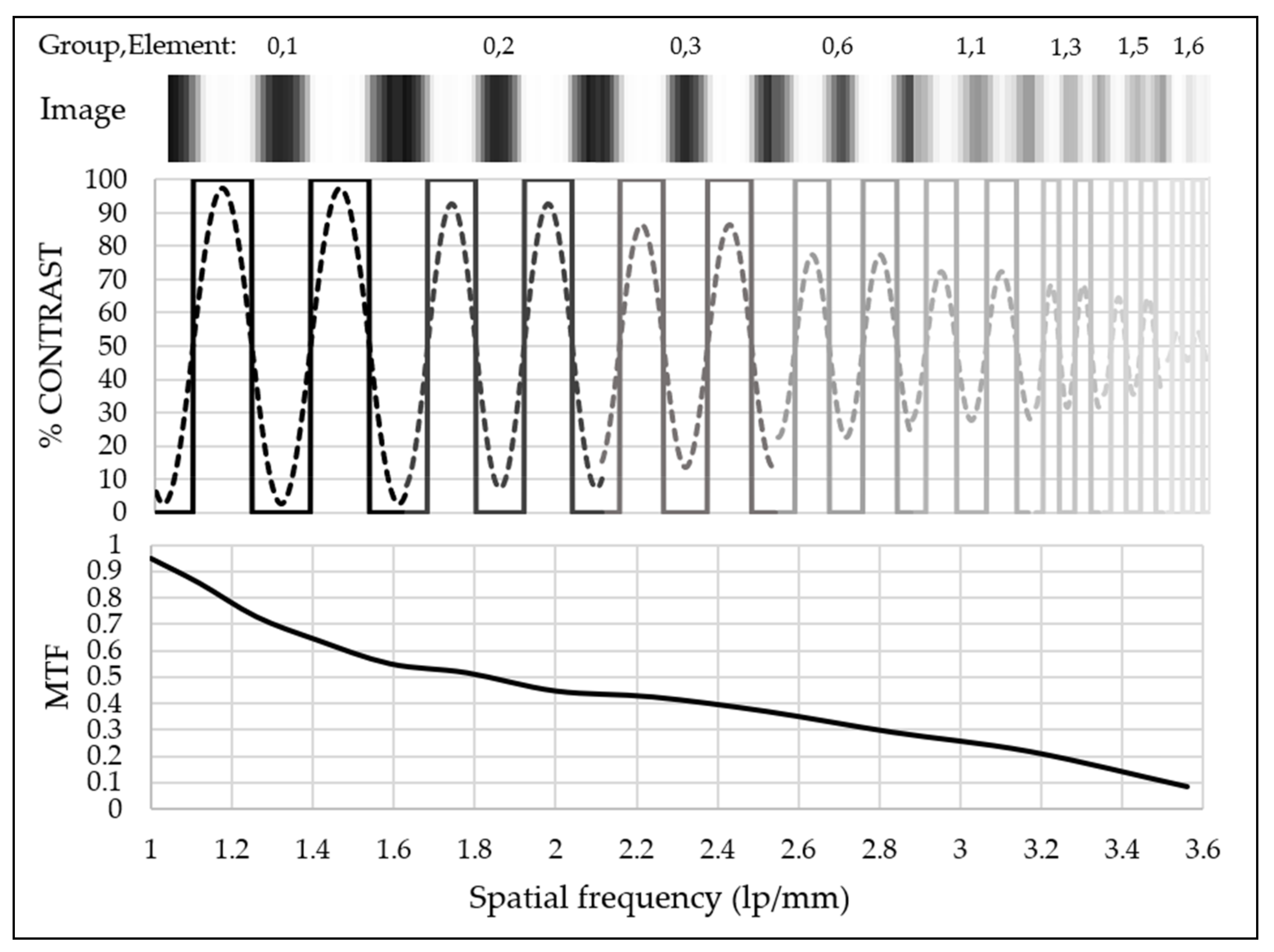
3.2. Spatial Resolution
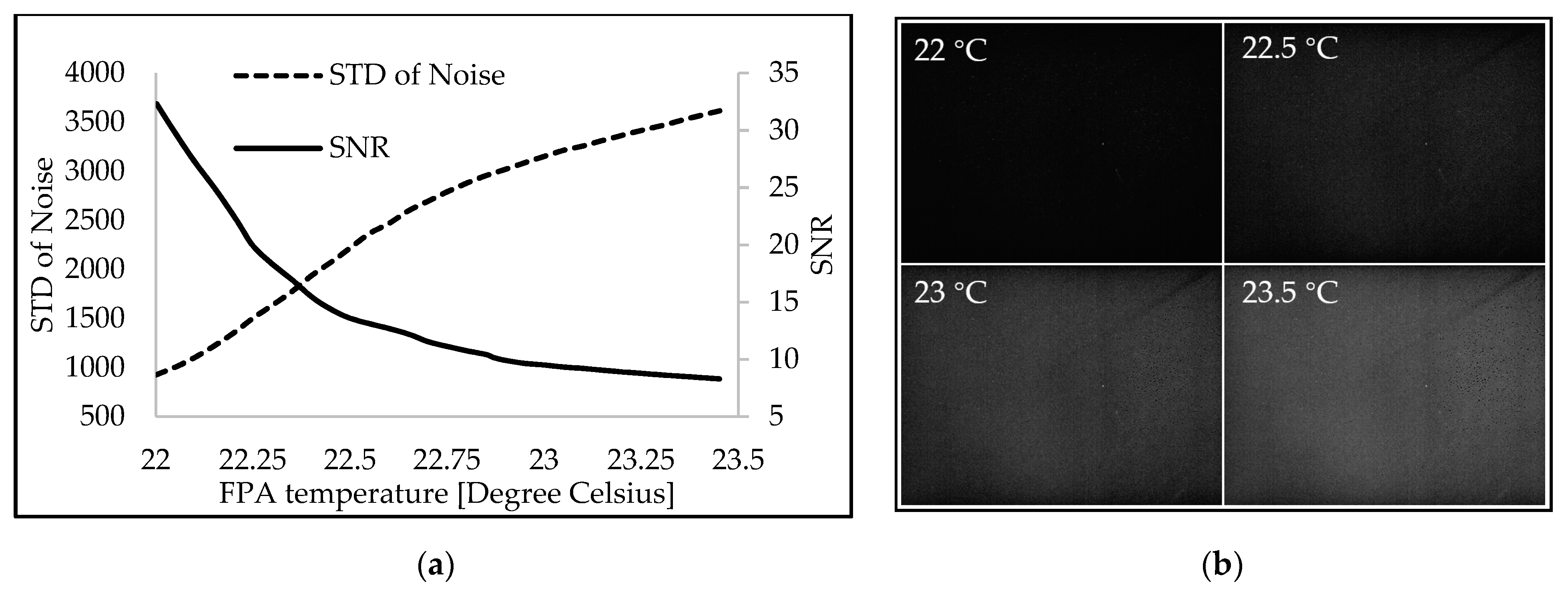
3.3. Signal-To-Noise Ratio
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hong, T.; Yin, J.; Nie, S.P.; Xie, M.Y. Applications of infrared spectroscopy in polysaccharide structural analysis: Progress, challenge and perspective. Food Chem. X 2021, 12, 100168. [Google Scholar] [CrossRef] [PubMed]
- Su, W.H.; Sun, D.W. MIR Spectroscopy for Quality Analysis of Liquid Foods. Food Eng. Rev. 2019, 11, 142–158. [Google Scholar] [CrossRef]
- Mendes, E.; Duarte, N. MIR Spectroscopy as a Valuable Tool to Tackle Food Analysis: A Literature Review on Coffee, Dairies, Honey, Olive Oil and Wine. Foods 2021, 10, 477. [Google Scholar] [CrossRef] [PubMed]
- Dumancas, G.; Ellis, H.; Neumann, J.; Smith, K. Comparison of Various Signal Processing Techniques and Spectral Regions for the Direct Determination of Syrup Adulterants in Honey Using Fourier Transform Infrared Spectroscopy and Chemometrics. Chemosensors 2022, 10, 51. [Google Scholar] [CrossRef]
- Hashimoto, A.; Kameoka, T. Applications of Infrared Spectros-copy to Biochemical, Food, and Agricultural Processes. Appl. Spectrosc. Rev. 2008, 43, 416–451. [Google Scholar] [CrossRef]
- Qin, J.; Kim, M.S.; Chao, K.; Chan, D.E.; Delwiche, S.R.; Cho, B.-K. Line-Scan Hyperspectral Imaging Techniques for Food Safety and Quality Applications. Appl. Sci. 2017, 7, 125. [Google Scholar] [CrossRef] [Green Version]
- Mohazzabi, P.; Mattson, D.J.; Ponce, J.A., Jr. Diffraction Pattern of a Rotated Grating. J. Appl. Math. Phys. 2019, 07, 1870–1876. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Wen, Q.; Nie, Q.; Chang, F.; Zhou, Y.; Wen, Z. Miniaturized NIR spectrometer based on novel MOEMS scanning tilted grating. Micromachines 2018, 9, 478. [Google Scholar] [CrossRef] [Green Version]
- Lanzarotta, A.; Marcott, C.; Story, G.; Dowrey, A.; Sommer, A. Infrared Microspectroscopy Using Prism-Based Spectrographs and Focal Plane Array Detection. Appl. Spectrosc. 2012, 66, 304–311. [Google Scholar] [CrossRef]
- Pellerin, C.; Snively, C.M.; Chase, D.B.; Rabolt, J.F. Performance and application of a new planar array infrared spectrograph operating in the MIR (2000–975 cm(-1)) fingerprint region. Appl. Spectrosc. 2004, 58, 639–646. [Google Scholar] [CrossRef]
- Elmore, D.; Tsao, M.W.; Frisk, S.; Chase, D.; Rabolt, J. Design and Performance of a Planar Array Infrared Spectrograph That Operates in the 3400 to 2000 cm−1 Region. Appl. Spectrosc. 2002, 56, 145–149. [Google Scholar] [CrossRef]
- William, R.J.; Simon, J.H.; Steven, M. Microbolometer imaging spectrometer. Opt. Lett. 2012, 37, 803–805. [Google Scholar] [CrossRef]
- Leijtens, J.; Helden, W.; Breussin, F.; Smorenburg, C.; Escudero, I.; Boslooper, E.; Visser, H. Microbolometer spectrometer opens hoist of new applications. In Proceedings of the International Conference on Space Optics, Toulouse, France, 21 November 2017. [Google Scholar] [CrossRef] [Green Version]
- Fisette, B.; Tremblay, M.; Oulachgar, H.; Généreux, F.; Béland, D.; Beaupre, P.; Julien, C.; Gay, D.; Deshaies, S.; Terroux, M.; et al. Novel vacuum packaged 384 × 288 broadband bolometer FPA with enhanced absorption in 3–14 μm wavelength. Proc. SPIE 2017, 101771, 407–421. [Google Scholar] [CrossRef]
- Fisette, B.; Généreux, F.; Béland, D.; Topart, P.; Tremblay, M.; Desroches, Y.; Terroux, M.; Marchese, L.; Proulx, C.; Picard, F.; et al. Customized packaged bolometers in niche applications at INO. Proc. SPIE 2018, 10656, 79–97. [Google Scholar] [CrossRef]
- Sánchez-Alvarez, A.; Luna-Moreno, D.; Hernández-Morales, J.A.; Zaragoza-Zambrano, J.O.; Castillo-Guerrero, D.H. Control of Stepper Motor Rotary Stages applied to optical sensing technique using LabView. Optik 2018, 164, 65–71. [Google Scholar] [CrossRef]
- Wang, S.; Han, H.; Gao, K.; Wang, Z.; Zhang, C.; Yang, M.; Wu, Z.; Wu, Z. A user-friendly LabVIEW software platform for grating based X-ray phase-contrast imaging. J. X-ray Sci. Technol. 2015, 23, 189–199. [Google Scholar] [CrossRef] [Green Version]
- Wu, Q.; Wang, L.; Zu, L. A LabVIEW-Based Virtual Instrument System for Laser-Induced Fluorescence Spectroscopy. J. Autom. Methods Manag. Chem. 2011, 2011, 457156. [Google Scholar] [CrossRef] [Green Version]
- Beussman, D.; Walters, J. Complete LabVIEW-Controlled HPLC Lab: An advanced undergraduate experience. J. Chem. Educ. 2017, 94, 1527–1532. [Google Scholar] [CrossRef]
- Robert, D.G.; Duncan, G.S. Encyclopedia of Modern Optics, 2nd ed.; Elsevier Academic Press: Cambridge, MA, USA; University of California: Los Angeles, CA, USA, 2005; pp. 845–857. [Google Scholar]
- Palmer, C.; Loewen, E. Diffraction Grating Handbook, 8th ed.; Newport Corporation: Irvine, CA, USA, 2020; pp. 76–236. [Google Scholar]
- Wang, Q.; Shen, H.; Liu, W.; Dai, P. A High-Resolution MIR Echelle Grating Spectrometer with a Three-Mirror Anastigmatic System. Appl. Sci. 2022, 12, 8013. [Google Scholar] [CrossRef]
- Floria, O.B.; Carlos, E.H.; Henrik, R.; Hans, M.; Hans, S.; Kristinn, B.G. Carbon dioxide absorption spectroscopy with a MIR silicon photonic waveguide. Opt. Lett. 2020, 45, 109–112. [Google Scholar] [CrossRef] [Green Version]
- Peter, L.; Dieter, N. Spatial resolution in infrared microspectroscopic imaging of tissues. Biochim. Biophys. Acta (BBA)-Biomembr. 2006, 1758, 814–829. [Google Scholar] [CrossRef] [Green Version]
- Deane, S.; Avdelidis, N.P.; Ibarra-Castanedo, C.; Zhang, H.; Nezhad, H.Y.; Williamson, A.A.; Mackley, T.; Maldague, X.; Tsourdos, A.; Nooralishahi, P. Comparison of Cooled and Uncooled IR Sensors by Means of Signal-to-Noise Ratio for NDT Diagnostics of Aerospace Grade Composites. Sensors 2020, 20, 3381. [Google Scholar] [CrossRef]
- Usamentiaga, R.; Ibarra-Castanedo, C.; Maldague, X.P. More than Fifty Shades of Grey: Quantitative Characterization of Defects and Interpretation Using SNR and CNR. J. Nondestruct. Eval. 2018, 37, 25. [Google Scholar] [CrossRef]





| Parameters | Values |
|---|---|
| Spectral range | 2–6 μm |
| Disperser | 300 grooves/mm grating |
| Detector type | Uncooled microbolometer VOx |
| Detector size | 35 μm pixel pitch |
| Spectral resolution | 12 nm/pixel at 3700 nm |
| Scan time | 4.5 s/μm for 10 mm spatial length |
| Spatial resolution | 3.5 lp/mm or 140 μm |
| Signal-to-noise ratio | 32 (SNR, operated at 20 °C) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sunongbua, P.; Aekram, S.; Lertsiriyothin, W. Design of MIR Dispersive Spectrograph System with Uncooled Microbolometer. Sensors 2023, 23, 2205. https://doi.org/10.3390/s23042205
Sunongbua P, Aekram S, Lertsiriyothin W. Design of MIR Dispersive Spectrograph System with Uncooled Microbolometer. Sensors. 2023; 23(4):2205. https://doi.org/10.3390/s23042205
Chicago/Turabian StyleSunongbua, Pattarapong, Suwan Aekram, and Weerasak Lertsiriyothin. 2023. "Design of MIR Dispersive Spectrograph System with Uncooled Microbolometer" Sensors 23, no. 4: 2205. https://doi.org/10.3390/s23042205
APA StyleSunongbua, P., Aekram, S., & Lertsiriyothin, W. (2023). Design of MIR Dispersive Spectrograph System with Uncooled Microbolometer. Sensors, 23(4), 2205. https://doi.org/10.3390/s23042205






