1. Introduction
Multi-messenger astrophysics is a novel scientific field that uses information carried by various and diverse cosmic messengers, electromagnetic waves, neutrinos, and gravitational waves, to observe and understand astrophysical phenomena. In order to effectively collect the multiple sources, distributed space systems are becoming extremely popular and useful, either as primary detectors or as localization sentinels to subsequently alert other instruments and observatories. In all these cases, the benefits guaranteed by miniaturized spacecraft are evident. In fact, these small platforms allow an easier and cost-effective access to space, with a reduced time scale from design to operations and with a pragmatic possibility to implement distributed space missions. Nano-satellites have lowered by several orders of magnitude the difficulties and the costs to realize orbital constellations or multi-element space observatories. In this way, they have facilitated and have made more accessible astrophysical studies from space that require an observation baseline, such as interferometry or localization by triangulation.
The positive influence of miniaturized space platforms on the multi-messenger astrophysics field has been deeply exploited by the High Energy Rapid Modular Ensemble of Satellites (HERMES) mission [
1]. HERMES is based on a constellation of nano-satellites in low-Earth orbit (LEO). The constellation is composed of 3U CubeSats, and it is built upon a twin project: the HERMES Technological Pathfinder (HERMES-TP), funded by the Italian Ministry for University and Research (MUR) and the Italian Space Agency (ASI); and the HERMES Scientific Pathfinder (HERMES-SP), funded by the European Union’s Horizon 2020 Research and Innovation Programme. Both the HERMES-TP and HERMES-SP projects provide three complete satellites to the constellation, for a total of six 3U CubeSats composing the space segment. The mission aims at the fast detection and localization of energetic astrophysical transients, such as gamma-ray bursts (GRBs), which are the electromagnetic counterparts of gravitational wave events, thanks to novel miniaturized detectors sensitive to X-rays and gamma-rays [
2].
The astrophysical events’ localization has to be accomplished with an accuracy level ranging from a few degrees to arcminutes, as a function of the number of spacecraft composing the full HERMES constellation. This is achieved in a field of view of several steradians exploiting the triangulation technique [
3]. In doing so, at least three spacecraft, separated by a minimum baseline of 1000 km, shall observe the same region of the sky by co-aligning the detectors’ lines of sight [
4]. This is achieved by maneuvering the individual elements of the constellation to orient their fields of view in the desired directions with an autonomous attitude determination and control subsystem (ADCS) [
5,
6]. Then, any HERMES spacecraft shall estimate its full orbital and attitude states on-board. The first is needed to understand if the minimum baseline requirement is respected and to feed the environment models used in the attitude determination functions [
7]. The latter is globally needed to have the ADCS properly working, achieving the expected mission goals. Specifically, the scientific requirements impose:
Therefore, despite the specific mission scenario analyzed, this research work can be applied and generalized to any spacecraft mission with similar attitude determination requirements, which are becoming common in complex and advanced nano-satellites.
However, this class of required performances is quite demanding for a nano-satellite because of its stringent mass, volume, power, and computation constraints. Moreover, the cost budget imposes a further difficulty to achieve the desired mission objectives. It is evident that the usage of extremely accurate sensors is typically not possible, and thus, an effective sensor architecture for full-attitude determination is needed. This paper discusses the one that was developed and verified for the HERMES satellites, but it is possible to state that the presented results are valid for CubeSat applications with the system constraints listed in
Table 1.
Existing literature studies have addressed the problem of sensor architectures for spacecraft attitude determination in real missions for many years [
8,
9,
10]. However, only in recent studies have the results been available for nano-satellites’ and CubeSats’ attitude determination subsystems. The work of Schmidt presented an attitude determination system based on Sun sensors, magnetometers, and gyroscopes to be processed by an extended Kalman filter (EKF) [
11]. The simulations results proved errors in the order of 10 deg to 20 deg, which are acceptable for an experimental pico-satellite in-orbit testing mission, but they are not for missions with imposed scientific requirements. Similarly, Scholz presented real flight data from a pico-satellite mission that is capable of estimating the orbital position with an ∼1 × 10
2 km accuracy [
12]. A few years later, Springmann discussed an attitude determination system that utilizes rate gyros, magnetometers, coarse Sun sensors, and an EKF [
13]. In this case, the attitude determination accuracy was about 2 deg to 3 deg in sunlight and decreased to about 7 deg to 8 deg when the states were estimated in eclipse. In the very last years, literature works about the ADCS in nano-satellites became more frequent, and they were often focused on improving the performance and the reliability of the developed system and sensor architectures. Byeon proposed a two-stage approach method for attitude determination that was robust to sensor faults [
14]. In nominal conditions, this method is accurate in the order of 10
1 arcsec, but it requires a star sensor, which may not respect the system constraints listed in
Table 1. With a different approach, the work of Zhang exploited independent vector and gyroscope measurements to efficiently determine the spacecraft attitude [
15]. This allowed reaching a high estimation accuracy, but it required a computational load and minimum sensor performances that are not suitable for nano-satellites. In these regards, the problem of attitude determination in nano-satellite was recently investigated by Fei [
16], Li [
17], and Ivanov [
18]. These research works exploited miniaturized sensors; however, the obtained accuracy was in the range of 1 deg to 10
1 deg, and they did not provide MIL or HIL test results. Experimental data were exploited in the work of Porras-Hermoso [
19], who proposed a simple, yet reliable method to estimate the Sun-pointing direction in a micro-satellite mission. Exploiting solar panels and photodiodes, this work achieved an estimation accuracy in the order of 10 deg. Similar conclusions are also possible analyzing the mission results of the NetSat satellites, whose overview is summarized in the work of Scharnagl [
20].
The effective sensor architecture proposed in this paper allows achieving a 1 deg attitude determination accuracy at
in any section of the orbit, together with a 10 m orbital position estimation at
. To achieve these results, the sensor architecture is composed of tactical-grade micro-electro-mechanical system (MEMS) gyroscopes, quadrant diode fine Sun sensors, photodiodes for coarse Sun estimations, and magnetometers. The system is also equipped with a GNSS receiver for precise on-board orbit estimation. The attitude determination is based on the classical Quaternion ESTimation (QUEST) algorithm [
21,
22,
23], which uses on-board calibrated sensor data. The orbit determination exploits GNSS measurements and an orbital propagator fused together in an EKF, which can be easily integrated with accelerometer measurements in the case of orbital control maneuvers.
List of Contributions
The paper describes the sensor architecture to guarantee the attitude determination performance. It illustrates the sensor selection process, focusing on the hardware typologies and specifications. The available data were obtained from hardware-in-the-loop (HIL) functional testing, and the sensor performance is representative of real commercial off-the-shelf (COTS) components.
First, the discussion presents the sensor architecture, with a schematic description of the whole attitude and orbit determination block. This part also covers the sensor configuration on the spacecraft, highlighting the hot redundancies in the architecture, while the effectiveness and the efficiency of the proposed subsystem are defined and discussed. Furthermore, the methods and the software elements to fully determine the attitude and orbital states are illustrated and critically discussed with respect to the available sensor measurements.
Then, the sensor selection process is extensively described, and for each sensor in the proposed architecture, the main component’s specifications are reported and analyzed together with the primary test results. This part is structured according to the different sensor typologies, examining the performance of the gyroscopes, Sun sensors, magnetometers, GNSS receivers, and accelerometers.
Finally, an example attitude determination performance is reported and discussed with respect to the sensor performance and specifications. In particular, the direct influence of the sensor architecture on the final output of the determination functions is highlighted. In this part, the presented results were derived from model-in-the-loop (MIL) with hardware calibrated simulations.
The aim of this study was to fully characterize the proposed sensor architecture, with respect to the available attitude and orbit determination performance. This was achieved thanks to an extensive analysis of the sensor test results, with particular attention on the critic performance for each sensor family and thanks to an end-to-end verification of the final attitude and orbit estimation accuracy. All the presented results were derived from HIL and MIL verification and testing activities, and they can serve as useful resources and a benchmark for future nano-satellite missions.
2. Effective Sensor Architecture
The effective sensor architecture for full-attitude determination in the HERMES nano-satellites was developed starting from the imposed mission requirements and system constraints. In addition to those described in the previous section, the system is required to determine its full orbital and attitude states in any point of the orbit, and it shall be capable of withstanding failures in the hardware components. For these reasons, the sensor architecture was selected to be operative both in sunlight and in eclipse and with a few degrees of hot redundancy.
First, the mass, power, and cost limitations indicated discarding the star sensors as the primary attitude determination sensors. The possibility to host this sensor typology in a redundant configuration is extremely remote for a nano-satellite. Moreover, the attitude determination accuracy requirement is not extremely strict to force the design to use star sensors. Then, since the attitude state estimation shall not be dependent on the relative attitude with respect to the Earth, the primary attitude sensors were selected to be Sun sensors and magnetometers.
The latter are also needed to actuate magnetic torquers, which are very common in nano-satellites. The maximum attitude estimation error drove the selection of fine Sun sensors with maximum measurement errors in the order of ∼1 deg. However, to avoid the presence of too many fine sensors for redundancy purposes, the sensor architecture was based on a combination of fine Sun sensors in the Sun’s primary axes and of distributed photodiodes to retrieve a coarse Sun direction. Note that the photodiodes shall also guarantee the detection of the Sun with a full-sphere field of view, with no blind spots.
The requirement to determine the full-attitude state in any section of the orbit imposed the inclusion of gyroscopes for dead-reckoning state propagation while in eclipse. The gyroscope measurements shall be continuously calibrated on-board in order to minimize attitude drifts due to the gyroscope’s bias. Analogously, to keep the desired performance, the magnetometers and the Sun sensors are also calibrated with on-board techniques. Specifically, the magnetic sensor’s measurements shall be corrected for bias and scale factor errors, while the fine Sun sensors’ measurements are adjusted for the presence of Earth’s albedo.
This sensor architecture requires also the estimation of the orbital position state. This is needed to feed the reference environment models for full-attitude determination and for sensors’ calibration. Moreover, this is needed in guidance functions, which need to compute reference attitude states relative to the Earth. Finally, it is fundamental to achieve the mission objectives with the imposed accuracy requirement also on the orbit determination. In the presented architecture, the primary sensor is a GNSS receiver. For redundancy purposes, the GNSS measurements are combined in an EKF with an on-board SGP4 orbital propagator [
24] and with the accelerometers’ measurements. The former can be updated with a two line element (TLE) set received from the ground. The latter were included because the accelerometers are typically embedded in MEMS inertial measurement units (IMUs) hosting gyroscopes and magnetometers, and they also enable the possibility to deal with orbital control maneuvers. In any case, the measured non-gravitational perturbation accelerations, despite being very disturbed due to the noise level of typical tactical-grade MEMS accelerometers, allow slightly improving the GNSS-based orbit determination accuracy, and they allow increasing the reliability of the on-board orbital propagation [
7].
The overall sensor architecture is reported in
Figure 1 together with the attitude determination blocks. In the scheme, the interfaces between the different elements and the hot redundancies are graphically reported. In particular, the gyroscopes, the magnetometers, and the Sun sensors have one degree of redundancy, each having on-board 2 three-axis gyroscopes, 4 fine Sun sensors, 12 photodiodes, and 2 magnetometers. The GNSS receiver has no redundant components, its failure being counteracted with the support of the three-axis accelerometer together with the SGP4 orbital propagation.
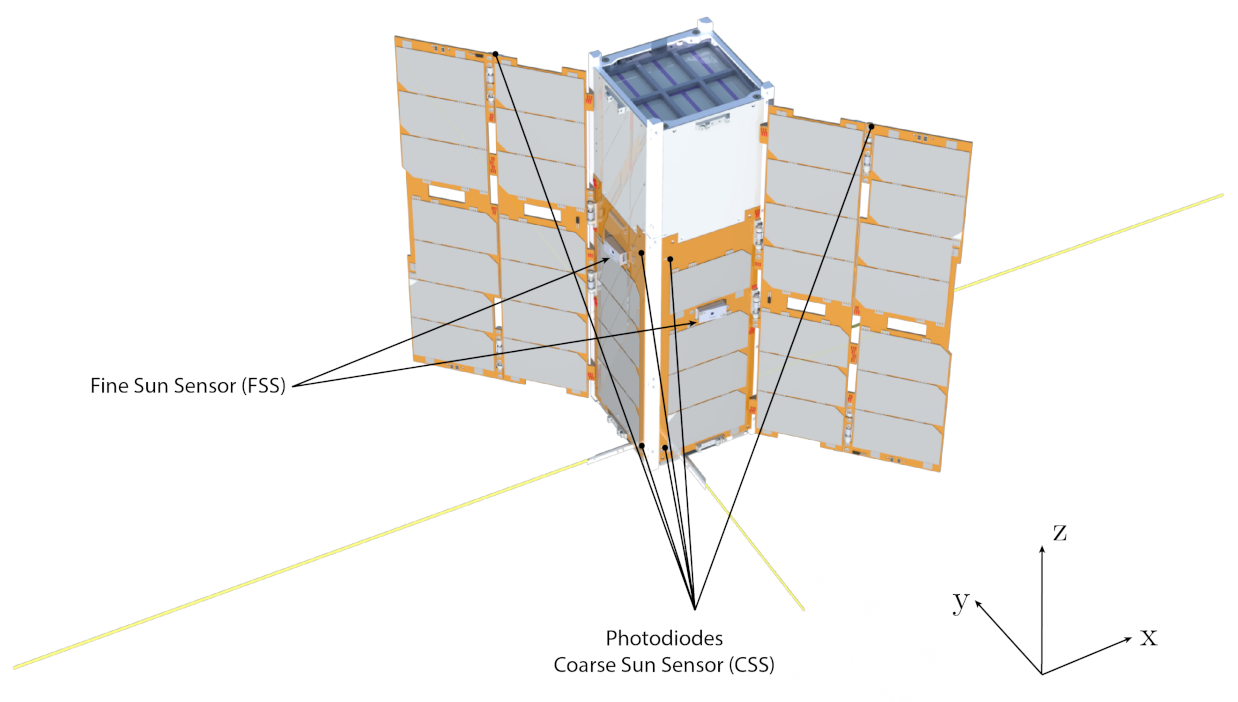
The sensor configuration further maximizes the efficiency of the sensor architecture, which is defined as the number of sensors per given attitude determination functionality. The fine Sun sensors are aligned with the four body axes contained in the plane orthogonal to the solar panel’s wings, in a way that, during the nominal attitude modes, at least one fine sensor is used. These are not installed on the surfaces not containing solar cells, where the Sun direction is detected with the coarse photodiode sensors. In this way, each of the four primary Sun directions has one main fine sensor and two redundant coarse photodiodes, while the remaining two directions have only the two redundant coarse photodiodes. Globally, the twelve photodiodes cover the full-sphere field of view around the spacecraft and act as redundant coarse Sun sensors (CSSs) in case one of the primary fine sensors fails.
Figure 2 shows the spacecraft configuration and highlights the position of the Sun sensors for the three illustrated surfaces. The photodiodes placed on the solar wings’ edges are those aligned with the
z axis, while those on the side panels are aligned with the
and
axes. The configuration is specular for the remaining six photodiodes on the other three faces. The fine Sun sensors (FSSs) are mounted on the side panels to be aligned with the four primary Sun directions. In reality, as shown in
Figure 3, they are inclined 6 deg with respect to these axes in order to have the entire field of view clear from interferences with the solar wings.
The other sensors are configured in a way to minimize disturbances and external interferences. Namely, the magnetometers are mounted as far as possible from the magnetic torquers and from the electronic boards, while the gyroscopes and the accelerometers are placed far from the sources of vibrations (e.g., rotating devices).
Full-Attitude Determination with Sensor Measurements
The proposed sensor architecture guarantees a continuous availability of measurements to estimate the attitude states. In fact, also in case of the failure of some sensors, the available redundant components can be exploited to continue with the nominal operations. The attitude determination section’s algorithms use the calibrated Sun and magnetic sensor measurements:
to statistically solve Wahba’s problem with the QUEST implementation for quaternions [
23]. The calibrated data were obtained from the raw measured ones as
where
and
are, respectively, the measured geomagnetic field and Sun direction,
is the estimated bias of the magnetometer,
is the fully populated matrix of scale factors and non-orthogonality magnetometer errors, and
is the estimated error in the Sun direction due to the influence of the Earth’s albedo. The magnetic calibration parameters are continuously estimated on-board with a sequential centered iterative algorithm [
25]. The Sun sensors’ correction for the albedo are computed knowing the position of the Earth and its irradiance and reflection models [
26], the spectral response of the photodiodes, and the measurement functions of the Sun sensors. These algorithms are valid in sunlight, where it is assumed to exploit the Sun and magnetic field measurements, with the addition of the position vector estimate by the orbit determination algorithms,
, and the current time,
t. These last two quantities are used in the environment models in order to compute the geomagnetic field and the Sun direction in the inertial reference frame:
and
. The environment models are based on the Chebyshev ephemerides of the Sun and on the IGRF model of the Earth’s magnetic field [
27]. Moreover, the spacecraft position vector is also used to compute the Earth parameters used in the albedo correction functions.
Whenever two independent vector measurements from the sensors are not available (e.g., during eclipses), a dead-reckoning attitude propagation is initialized from the last valid attitude state. The attitude kinematics is then propagated with the unbiased output of the gyroscopes. The gyroscope calibration function estimates the angular velocity biases,
, with a sequential complementary filter [
28], whose bias dynamics is expressed as follows:
where
is the estimated attitude quaternion with its vector and scalar parts. The angular velocity is then corrected with the current best estimate of the biases:
where
is the spacecraft’s measured angular rate vector. Note that the sensor calibration is not updated during the dead-reckoning propagation periods.
The static attitude determination logic uses the calibrated sensor measurements to implement the QUEST algorithm. The magnetometer and Sun sensors are weighted in this statistical implementation according to their quality, defined as the mean of the measurement’s variance computed in the sensor postprocessing functions:
where
and
are non-negative weights respecting
. The outcome of the statistical attitude determination is the best estimation of the spacecraft’s orientation, in terms of the quaternion,
, and angular velocity,
. The dynamic attitude determination complementary filter uses the output of this static attitude determination section, combined with the angular rates’ measurements, to obtain the updated bias values, as described before. At any time of the mission, the output of the full-attitude determination functions is the best estimate of the attitude state vector.
The orbit determination algorithm is based on a loosely coupled GNSS and inertial navigation system (INS) integration. Namely, the accelerometers and the SGP4 orbital propagator are exploited to update the orbital state vector generating the INS preliminary estimate, which is then compared with the GNSS measurements to calculate the measurement error. This measurement error signal is fed to an extended Kalman filter (EKF) [
29], which outputs an updated estimate of the position and velocity errors, as well as the accelerometer bias term estimate. Eventually, the output of the EKF is used to correct the INS preliminary estimate, whereas the bias term is fed back to the integration block of the accelerometer measurements. The orbit determination section’s algorithms provide a full orbital state estimate in terms of inertial position,
, and velocity,
, using positioning and acceleration measurements:
Note that the accelerometer bias term estimate is continuously updated to calibrate the accelerometer measurements:
Whenever the GNSS is experiencing an outage period or a fault, the on-board SGP4 orbit propagator is used as the synthetic measurement element for the INS input. In this case, the EKF exploits a different measurement model and covariance matrix with respect to the nominal mode with GNSS and accelerometer coupling. Obviously, the approximate orbital model introduces propagation errors, and an inherent position drift cannot be avoided. However, the coupling with the EKF helps in accounting for the orbital error dynamics, and it determines a slower divergence rate with respect to a pure on-board orbital propagation including the same perturbation terms.
4. Full-Attitude Determination Performance
The full-attitude determination accuracy is strongly dependent on the sensor performance. In fact, the quality of the available measurements sets a physical limit to the lowest determination error that can be achieved. For these reasons, a credible attitude determination design has to be founded on HIL testing results with the available sensors. Then, even if the attitude determination functions are going to be verified with MIL tests, or software-/processor-in-the-loop (SIL/PIL) analyses, the supporting system and dynamical simulators shall be calibrated with respect to real hardware performance.
The attitude determination performance was verified by means of numerical simulations composing a model-in-the-loop testing campaign, exploiting a functional engineering simulator (FES) developed for small satellite applications in Earth orbits. The HERMES nano-satellite dynamics accounts for realistic system characteristics, such as the measured inertia properties and dimensions. The nominal orbital environment is described according to international standards [
30] accounting for the nominal orbit of the spacecraft: an equatorial LEO with an altitude of 550 km. The simulation was run for four orbital periods, starting from a random attitude state. The nominal attitude mode was a nadir pointing mode, which is ideally tracked by an ideal controller (i.e., the pointing error was 0 deg). The FES contains detailed functional models of all the sensors composing the discussed architecture, whose parameters and performance were those discussed in the previous sections, retrieved from HIL testing activities. The full-attitude determination functions were executed at 10 Hz, and the sensor models were sampled at the same frequencies as the real hardware components. The output results were analyzed in terms of three-axis attitude determination error angle and three-axis orbit determination error position. The FES runs of MATLAB/Simulink with a fixed step numerical integrator with a sample time of 0.01 s. The numerical calculations of the attitude and orbit determination functions were executed with 32 bit floating numbers, to be representative of the numerical computations to be executed by the on-board processor.
Table 9 summarizes the main simulation parameters used in the presented analyses.
The attitude determination performance was assessed in several pointing modes, with random initial states and with realistic control performance. Moreover, the closed-loop determination and control functions were also verified together. However, to show and present the available attitude determination accuracy, an ideal attitude pointing control was exploited. In this condition, the attitude states, initialized with a random condition, were quickly aligned with the nominal operative nadir pointing. Then, along the orbit, the ideal controller made two yaw rotations in order to maintain the solar arrays’ fronts face the Sun. In this way, it was possible to study the attitude determination functions independently of the controller, and the resulting performance was only representative of the determination block. The proposed results were anyway significant and in line with the realistic results available for the entire HERMES mission.
The three-axis attitude determination error,
, satisfied the imposed requirements, as shown in
Figure 14. This performance evaluation parameter is defined as the angle between the desired pointing direction,
, and the actual one,
, as
This figure of merit is used in HERMES since the scientific requirement is formulated on the three-axis overall error angle in estimating the attitude state. Thus, it is not relevant to understand how this error is split into the classical roll, pith, and yaw components. As soon as the system was initialized, the estimated attitude states converged to the real ones with a determination error that was below 1 deg at
whenever the on-board determination functions were fully calibrated. Indeed, the attitude determination error stayed below 3 deg for the entire time, as visible in
Figure 14b, except for an instantaneous peak at
t ∼ 1.7 × 10
4 s and for the increasing error between 2000 s and 4000 s. The former was only a slightly larger jump in the determination functions, similar to the others that are commonly present during the attitude estimation process. These small peaks in the attitude determination error are typically due to a switch in the fine Sun sensor with the Sun currently in view. This sensor change happens during the yaw rotations and for attitude conditions in which the Sun is at the border of the field of view of one sensor. For instance, the same peaks would not be present in the case in which the attitude determination is executed in inertial attitude mode, whereas the initial attitude determination error rise was associated with the first dead-reckoning period during the first eclipse, when the gyroscope’s biases were still not completely estimated. Thus, along the first orbit, the attitude determination system was not fully calibrated yet. This small issue can be partially solved by initializing the calibration functions with ground-estimated biases, even if the launch event will for sure wreck the calibration values. In this regard and to minimize the risk of possible counter calibrations, the HERMES calibration functions were initialized with zero biases. However, whenever the biases were correctly estimated on-board, the dead-reckoning attitude propagation did not go over the
error threshold. This is visible in
Figure 14b for the following three eclipse periods at times
t ∼ 0.9 × 10
4 s,
t ∼ 1.4 × 10
4 s, and
t ∼ 2.0 × 10
4 s.
The sensor calibration was beneficial for the full-attitude determination functions, improving the estimation accuracy both in sunlight and in eclipse. The on-board autonomous calibration is continuously running, being able to calibrate the drifts in the sensor errors and to recalibrate the whole system, if the primary sensor fails and a redundant one is set in use. This is possible thanks to the relatively fast dynamics of the calibration algorithms.
Figure 15 and
Figure 16, respectively, report the residual error in the calibrated angular velocities and in the calibrated magnetic field. In both cases, the calibration functions, initialized from null initial conditions, were capable of canceling the measurement errors in less than 30 min, allowing a complete system calibration in less than one orbital period, which is a time scale relevant for the spacecraft operations and for the error drifts. Moreover, it is noted that the initial cold start trend, leading to the slower convergence of the calibration filters, was not present when the attitude determination functions were already up and running.
The orbit determination functions are fundamental in satisfying the imposed mission requirements, but they also guarantee the correct on-board environmental modeling to carry out the attitude determination calculations. In fact, the wrong position estimation may impact the computation of the Sun direction and of the geomagnetic field vector in the inertial reference frame, with a direct negative consequence on the attitude determination accuracy.
Figure 17 shows the absolute position error of the on-board determination functions, with performance fully in line with the imposed requirements. In fact, the three-axis orbit determination error was smaller than 10 m at all times the GNSS receiver was operational. The presence of the accelerometers and of the on-board orbit propagation functions did not significantly improve the GNSS measurements, but it made the overall orbit determination block robust with respect to GNSS failures and more reliable in the case of orbital control maneuvers. In fact, in this last case, the accelerometers provided a faster and more reliable convergence to the correct new orbital states.