Effect of Fractal Topology on the Resistivity Response of Thin Film Sensors
Abstract
1. Introduction
2. The Model
3. The Experiment
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Singh, A.K.; Chowdhury, N.K.; Roy, S.C.; Bhowmik, B. Review of Thin Film Transistor Gas Sensors: Comparison with Resistive and Capacitive Sensors. J. Electron. Mater. 2022, 51, 1974. [Google Scholar] [CrossRef]
- Dong, C.; Liang, X.; Gao, J.; Chen, H.; He, Y.; Wei, Y.; Zaeimbashi, M.; Matyushov, A.; Sun, C.; Sun, N.X. Thin Film Magnetoelectric Sensors Toward Biomagnetism: Materials, Devices, and Applications. Adv. Electron. Mater. 2022, 8, 2200013. [Google Scholar] [CrossRef]
- Liang, S.; Schwartzkopf, M.; Roth, S.V.; Müller-Buschbaum, P. State of the art of ultra-thin gold layers: Formation, fundamentals and applications. Nanoscale Adv. 2022, 4, 2533. [Google Scholar] [CrossRef] [PubMed]
- Lei, G.; Lou, C.; Liu, X.; Xie, J.; Li, Z.; Zheng, W.; Zhang, J. Thin films of tungsten oxide materials for advanced gas sensors. Sens. Actuators B Chem. 2021, 341, 129996. [Google Scholar] [CrossRef]
- Tian, F.; Jiang, A.; Yang, T.; Qian, J.; Liu, R.; Jiang, M. Application of Fractal Geometry in Gas Sensor: A Review. IEEE Sens. J. 2021, 21, 14587. [Google Scholar] [CrossRef]
- Liang, X.; Dong, C.; Chen, H.; Wang, J.; Wei, Y.; Zaeimbashi, M.; He, Y.; Matyushov, A.; Sun, C.; Sun, N. A Review of Thin-Film Magnetoelastic Materials for Magnetoelectric Applications. Sensors 2020, 20, 1532. [Google Scholar] [CrossRef]
- Mackin, C.; Fasoli, A.; Xue, M.; Lin, Y.; Adebiyi, A.; Bozano, L.; Palacios, T. Chemical sensor systems based on 2D and thin film materials. 2D Mater. 2020, 7, 022002. [Google Scholar] [CrossRef]
- Ohring, M. The Materials Science of Thin Films; Academic Press Inc.: Cambridge, MA, USA, 1992. [Google Scholar]
- Walton, D. Nucleation of Vapor Deposits. J. Chem. Phys. 1962, 37, 2182. [Google Scholar] [CrossRef]
- Aziz, M.J. Film growth mechanisms in pulsed laser deposition. Appl. Phys. A 2008, 93, 579. [Google Scholar] [CrossRef]
- Kapitulnik, A.; Deutscher, G. Percolation Characteristics in Discontinuous Thin Films of Pb. Phys. Rev. Lett. 1982, 49, 1444. [Google Scholar] [CrossRef]
- Voss, R.F.; Laibowitz, R.B.; Allessandrini, E.I. Fractal (Scaling) Clusters in Thin Gold Films near the Percolation Threshold. Phys. Rev. Lett. 1982, 49, 1441. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals: Form, Chance and Dimension; W.H. Freeman: San Francisco, CA, USA, 1977. [Google Scholar]
- Yehoda, J.E.; Messier, R. Are thin-film physical structures fractals. Appl. Surf. Sci. 1985, 590, 22–23. [Google Scholar]
- Zhou, W.; Cao, Y.; Zhao, H.; Li, Z.; Feng, P.; Feng, F. Fractal Analysis on Surface Topography of Thin Films: A Review. Fractal Fract. 2022, 6, 135. [Google Scholar] [CrossRef]
- Mwema, F.M.; Jen, T.-C.; Kaspar, P. Fractal Theory in Thin Films: Literature Review and Bibliometric Evidence on Applications and Trends. Fractal Fract. 2022, 6, 489. [Google Scholar] [CrossRef]
- Zhang, Z.; Lagally, M.G. Atomistic Processes in the Early Stages of Thin-Film Growth. Science 1997, 276, 377. [Google Scholar] [CrossRef]
- Deutscher, G. Percolation and superconductivity. In Percolation, Localization, and Superconductivity; Goldman, A.M., Wolf, S.A., Eds.; Plenum Press: New York, NY, USA, 1984; p. 95. [Google Scholar]
- Burger, J.; Senoussi, S.; Soufaché, B. Electrical and magnetic properties of palladium hydrides compared with those of pure palladium. J. Less Common Met. 1976, 49, 213. [Google Scholar] [CrossRef]
- Adams, B.D.; Chen, A. The role of palladium in a hydrogen economy. Mater. Today 2011, 14, 282. [Google Scholar] [CrossRef]
- Peisl, H. Lattice strains due to hydrogen in metals. In Hydrogen in Metals I; Topics in Applied Physics; Alefeld, G., Völkl, J., Eds.; Springer: Heidelberg, Germany, 1978; Volume 28, p. 53. [Google Scholar]
- Feenstra, R.; Griessen, R.; de Groot, D.G. Hydrogen induced lattice expansion and effective H-H interaction in single phase PdHc. J. Phys. F Met. Phys. 1986, 16, 1933. [Google Scholar] [CrossRef]
- Eastman, D.E.; Cashion, J.K.; Switendick, A.C. Photoemission Studies of Energy Levels in the Palladium-Hydrogen System. Phys. Rev. Lett. 1971, 27, 35. [Google Scholar] [CrossRef]
- Switendick, A.C. The change in electronic properties on hydrogen alloying and hydride formation. In Hydrogen in Metals I; Topics in Applied Physics; Alefeld, G., Völkl, J., Eds.; Springer: Heidelberg, Germany, 1978; Volume 28, p. 101. [Google Scholar]
- Geerken, B.M.; Griessen, R. Concentration and temperature dependence of the electrical resistivity of quenched PdHx. J. Phys. F Met. Phys. 1983, 13, 963. [Google Scholar] [CrossRef]
- Kirkpatrick, S. Percolation and conduction. Rev. Mod. Phys. 1973, 45, 574. [Google Scholar] [CrossRef]
- Bergman, D.J.; Stroud, D. Solid State Physics; Ehrenreich, H., Turnbull, D., Eds.; Academic Press Inc.: Cambridge, MA, USA, 1992; Volume 46. [Google Scholar]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; Taylor and Francis Group: London, UK, 2018. [Google Scholar]
- Fuchs, K. The conductivity of thin metallic films according to the electron theory of metals. Math. Proc. Camb. Philos. Soc. 1938, 34, 100. [Google Scholar] [CrossRef]
- Sondheimer, E.H. The mean free path of electrons in metals. Adv. Phys. 1952, 1, 1–42. [Google Scholar] [CrossRef]
- Das, S.S.; Kopnov, G.; Gerber, A. Detection of hydrogen by the extraordinary Hall effect in CoPd alloys. J. Appl. Phys. 2018, 124, 104502. [Google Scholar] [CrossRef]
- Lee, E.; Lee, J.M.; Koo, J.H.; Lee, W.; Lee, T. Hysteresis behavior of electrical resistance in Pd thin films during the process of absorption and desorption of hydrogen gas. Int. J. Hydrogen Energy 2010, 35, 6984. [Google Scholar] [CrossRef]
- Ramanathan, M.; Skudlarek, G.; Wang, H.H.; Darling, S.B. Crossover behavior in the hydrogen sensing mechanism for palladium ultrathin films. Nanotechnology 2010, 21, 125501. [Google Scholar] [CrossRef]
- Kiefer, T.; Villanueva, L.G.; Fargier, F.; Brugger, J. The transition in hydrogen sensing behavior in noncontinuous palladium films. Appl. Phys. Lett. 2010, 97, 121911. [Google Scholar] [CrossRef]
- Youngquist, R.C.; Nurge, M.A.; Fisher, B.H.; Malocha, D.C. A Resistivity Model for Ultrathin Films and Sensors. IEEE Sens. J. 2014, 15, 2412. [Google Scholar] [CrossRef]
- Das, S.S.; Kopnov, G.; Gerber, A. Positive vs negative resistance response to hydrogenation in palladium and its alloys. AIP Adv. 2020, 10, 065129. [Google Scholar] [CrossRef]
- Das, S.S.; Kopnov, G.; Gerber, A. Kinetics of the Lattice Response to Hydrogen Absorption in Thin Pd and CoPd Films. Molecules 2020, 25, 3597. [Google Scholar] [CrossRef] [PubMed]
- Gerber, A.; Kopnov, G.; Karpovski, M. Hall effect spintronics for gas detection. Appl. Phys. Lett. 2017, 111, 143505. [Google Scholar] [CrossRef]

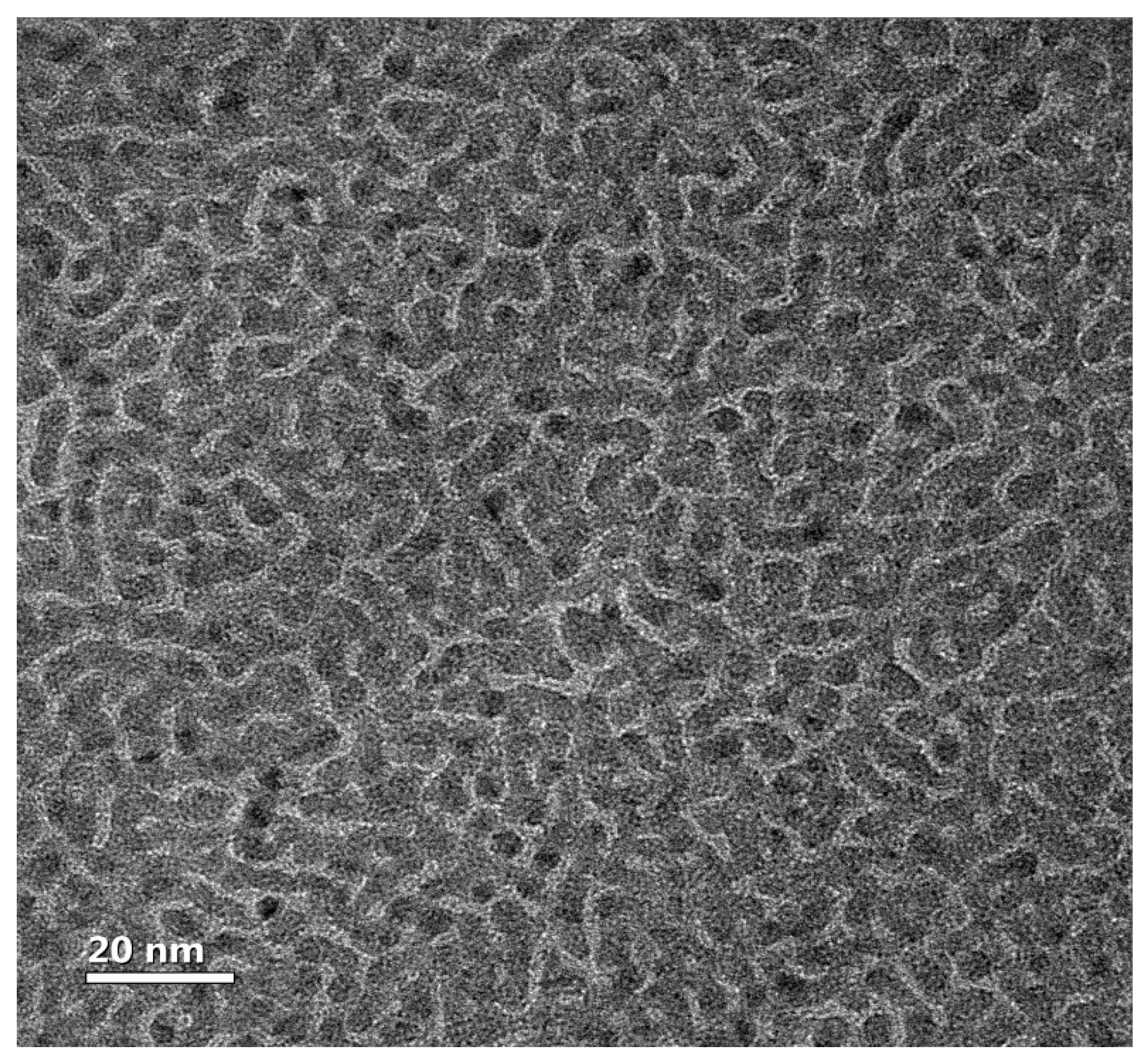

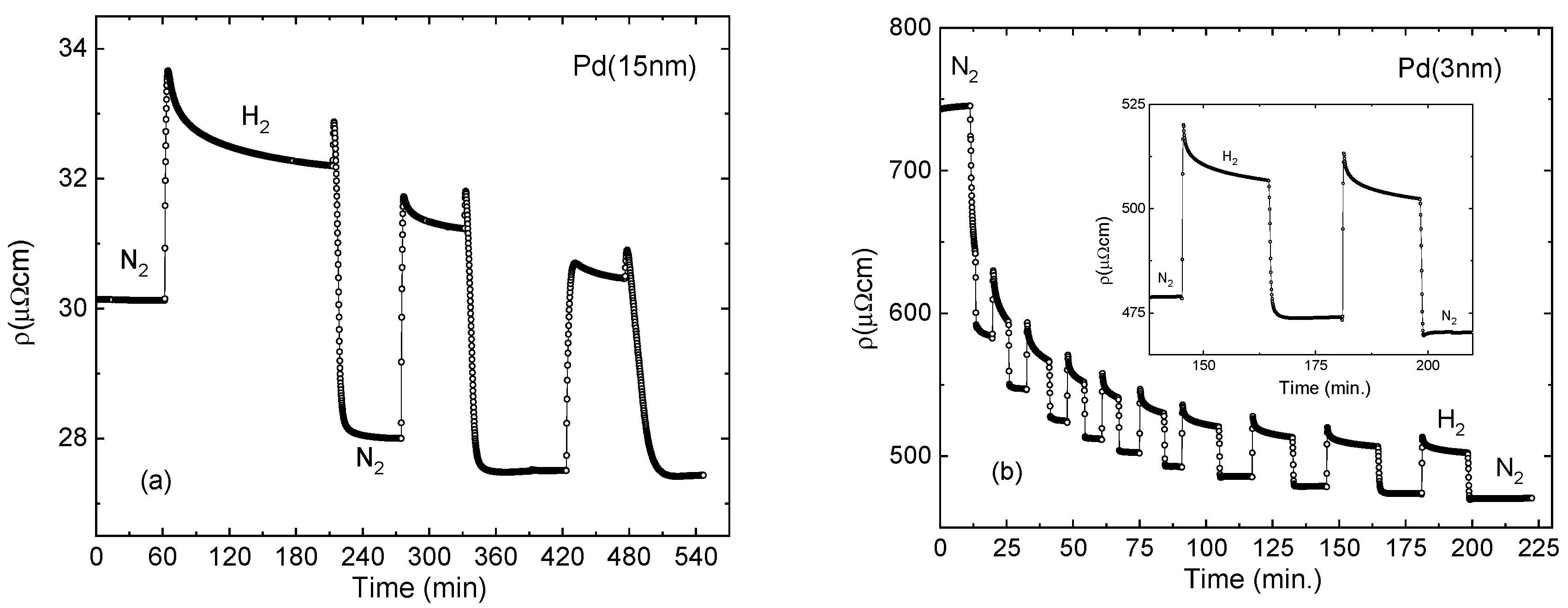


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kopnov, G.; Das, S.S.; Gerber, A. Effect of Fractal Topology on the Resistivity Response of Thin Film Sensors. Sensors 2023, 23, 2409. https://doi.org/10.3390/s23052409
Kopnov G, Das SS, Gerber A. Effect of Fractal Topology on the Resistivity Response of Thin Film Sensors. Sensors. 2023; 23(5):2409. https://doi.org/10.3390/s23052409
Chicago/Turabian StyleKopnov, Gregory, Sudhansu Sekhar Das, and Alexander Gerber. 2023. "Effect of Fractal Topology on the Resistivity Response of Thin Film Sensors" Sensors 23, no. 5: 2409. https://doi.org/10.3390/s23052409
APA StyleKopnov, G., Das, S. S., & Gerber, A. (2023). Effect of Fractal Topology on the Resistivity Response of Thin Film Sensors. Sensors, 23(5), 2409. https://doi.org/10.3390/s23052409






