An Interface ASIC Design of MEMS Gyroscope with Analog Closed Loop Driving
Abstract
:1. Introduction
2. Working Principle of the MEMS Gyroscope and Electrical Model Establishment
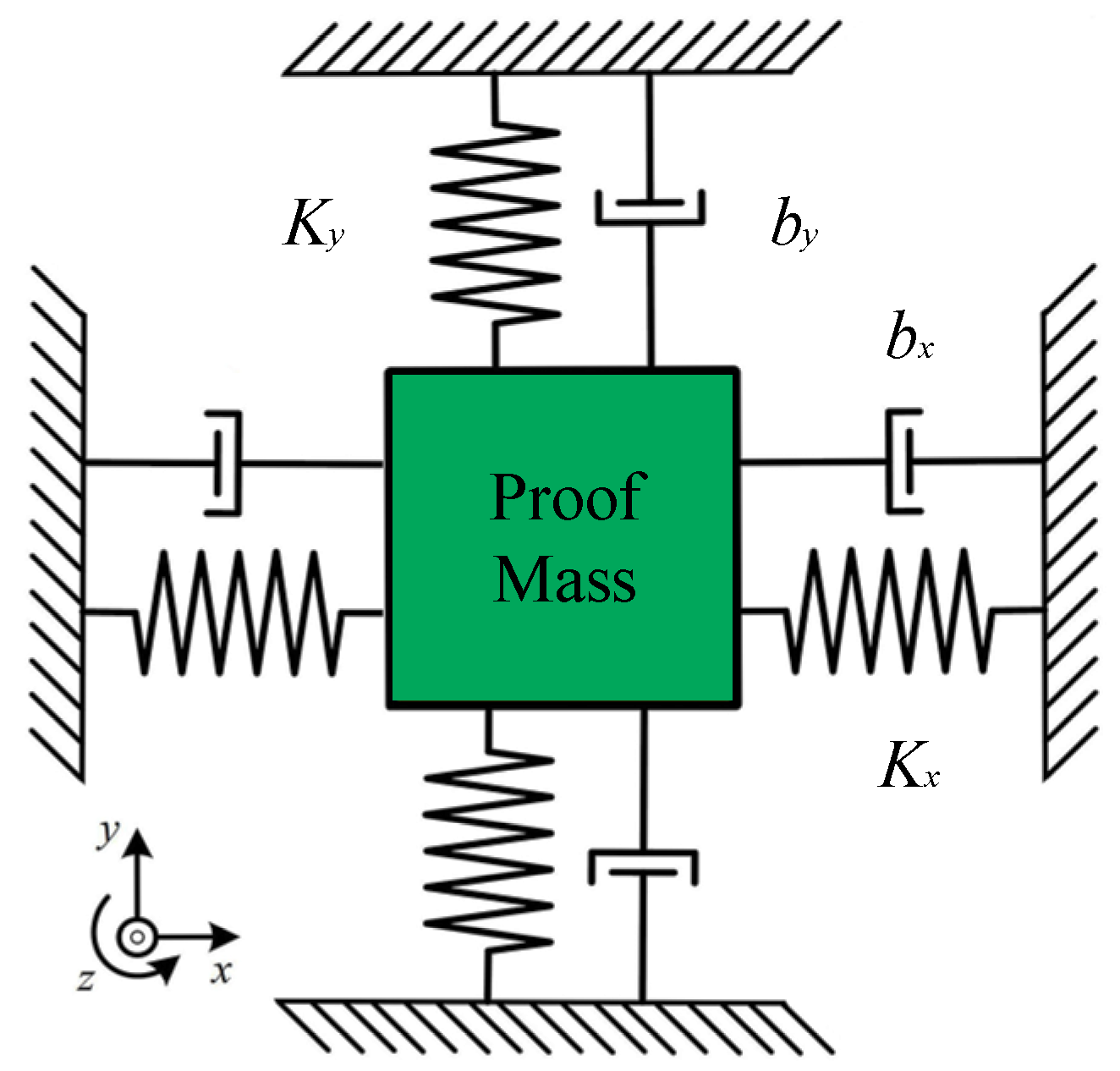
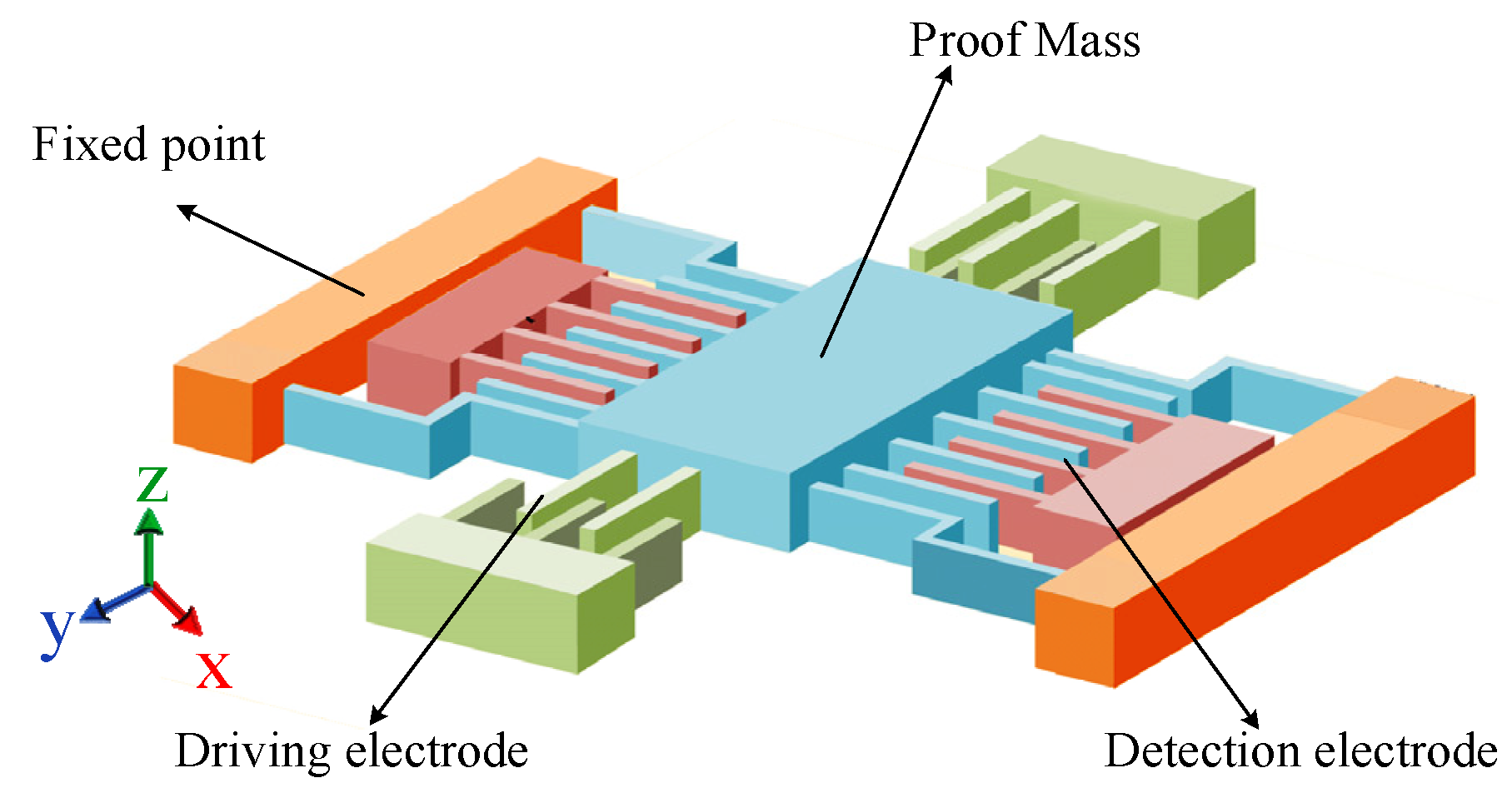
2.1. Dynamics Principle of the MEMS Gyroscope
2.2. Operating Principle of the MEMS Gyroscope Driving Mode
2.3. Working Principle of the MEMS Gyroscope Sense Mode
2.4. Equivalent Electrical Model of the MEMS Gyroscope
3. System-Level Modeling Design and Simulation
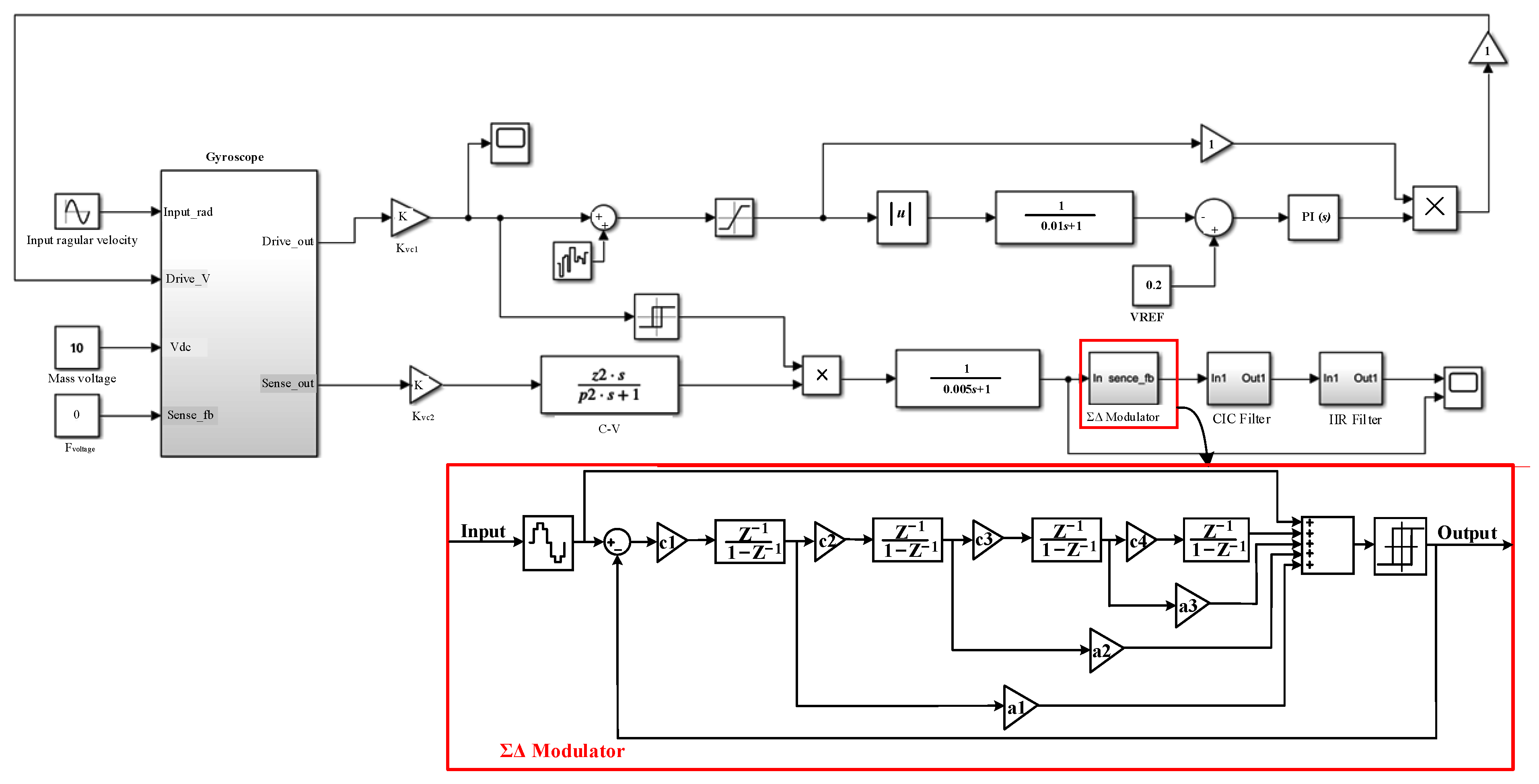
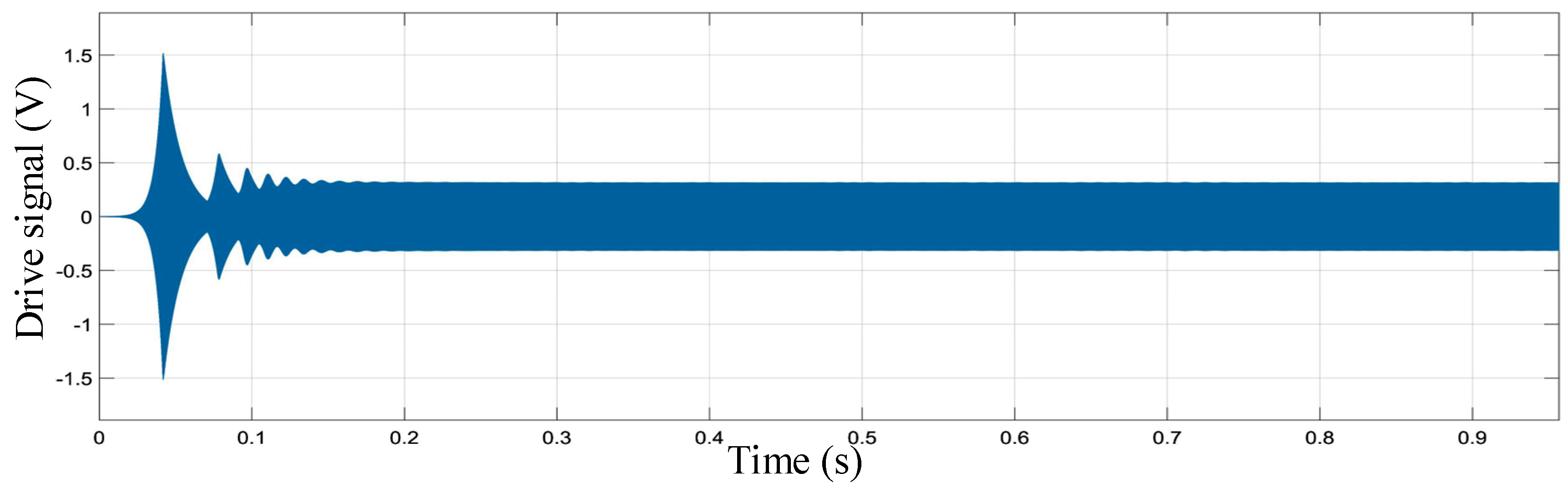
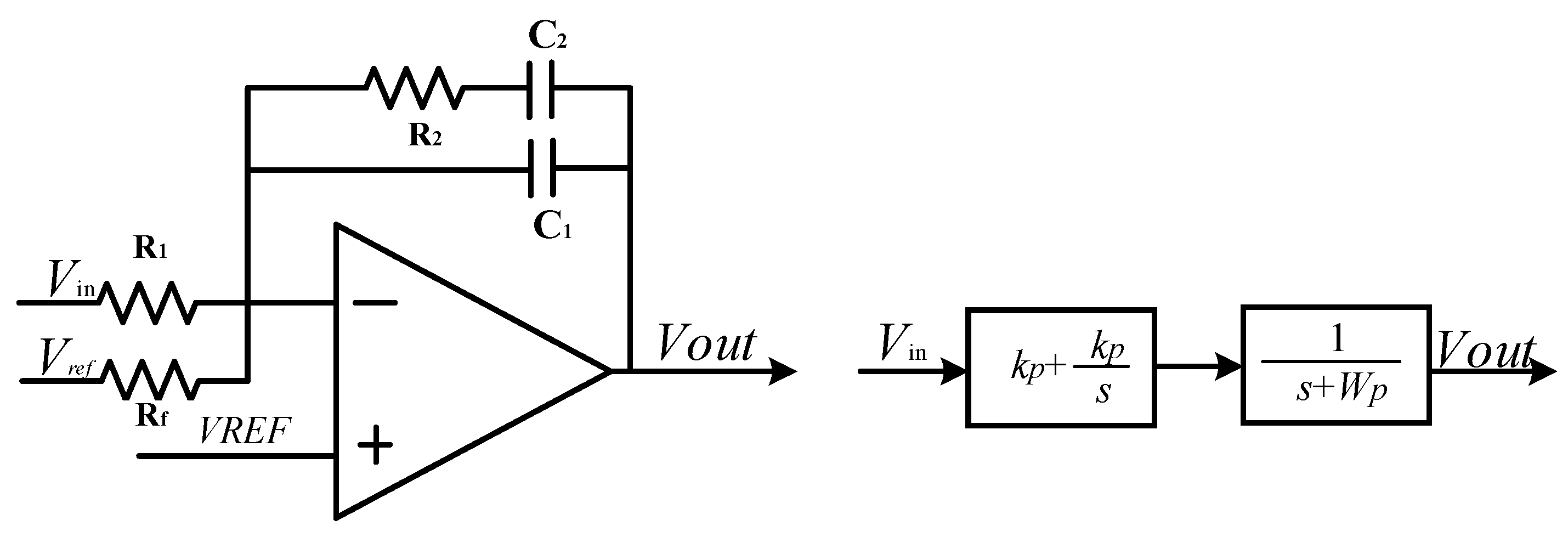
3.1. Modeling and Simulation of Driving Circuit
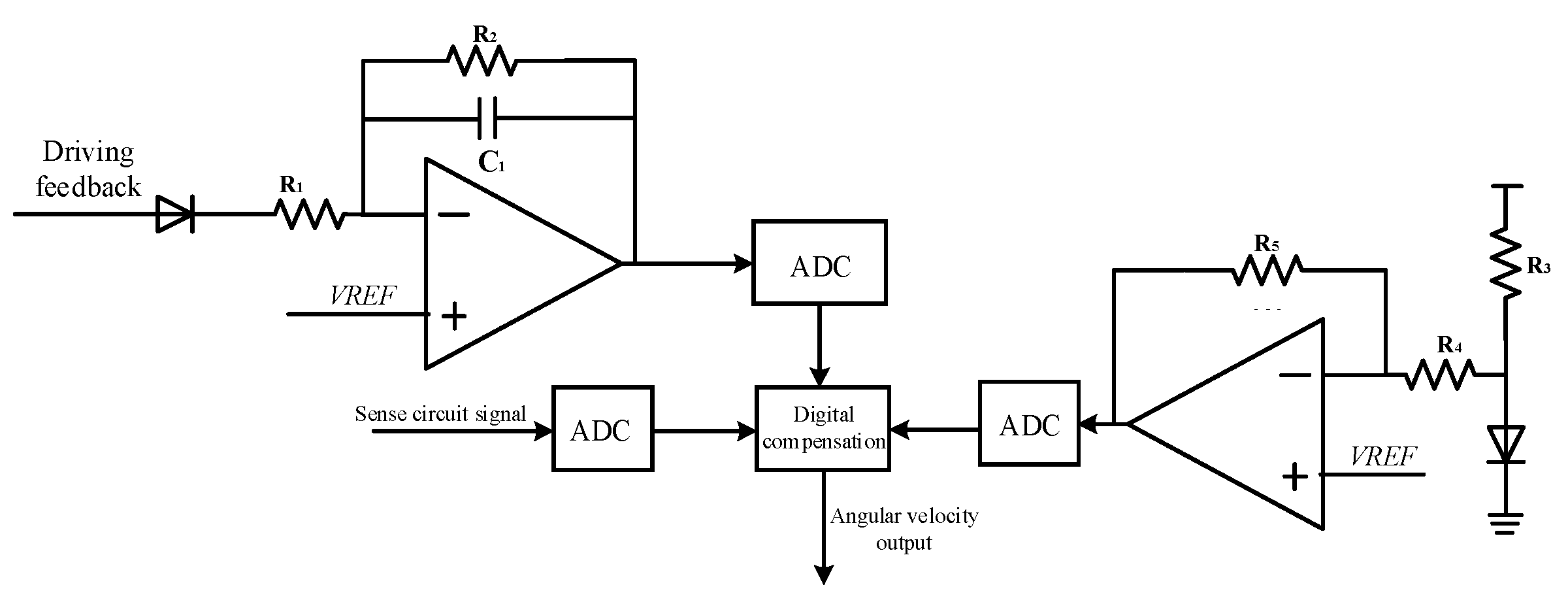
3.2. Modeling and Simulation of Sense Circuit
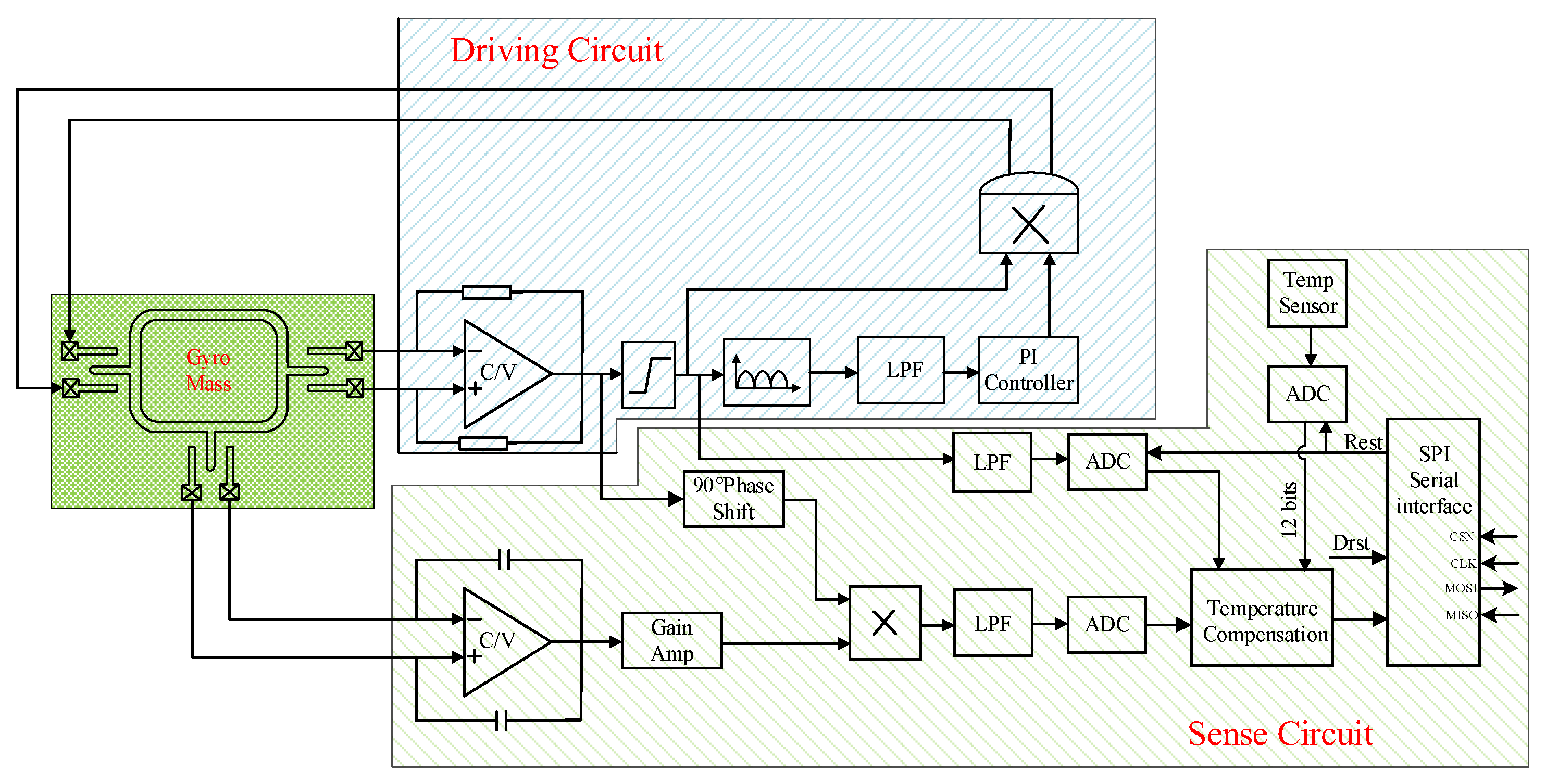
4. Design of the MEMS Gyroscope Interface Circuit
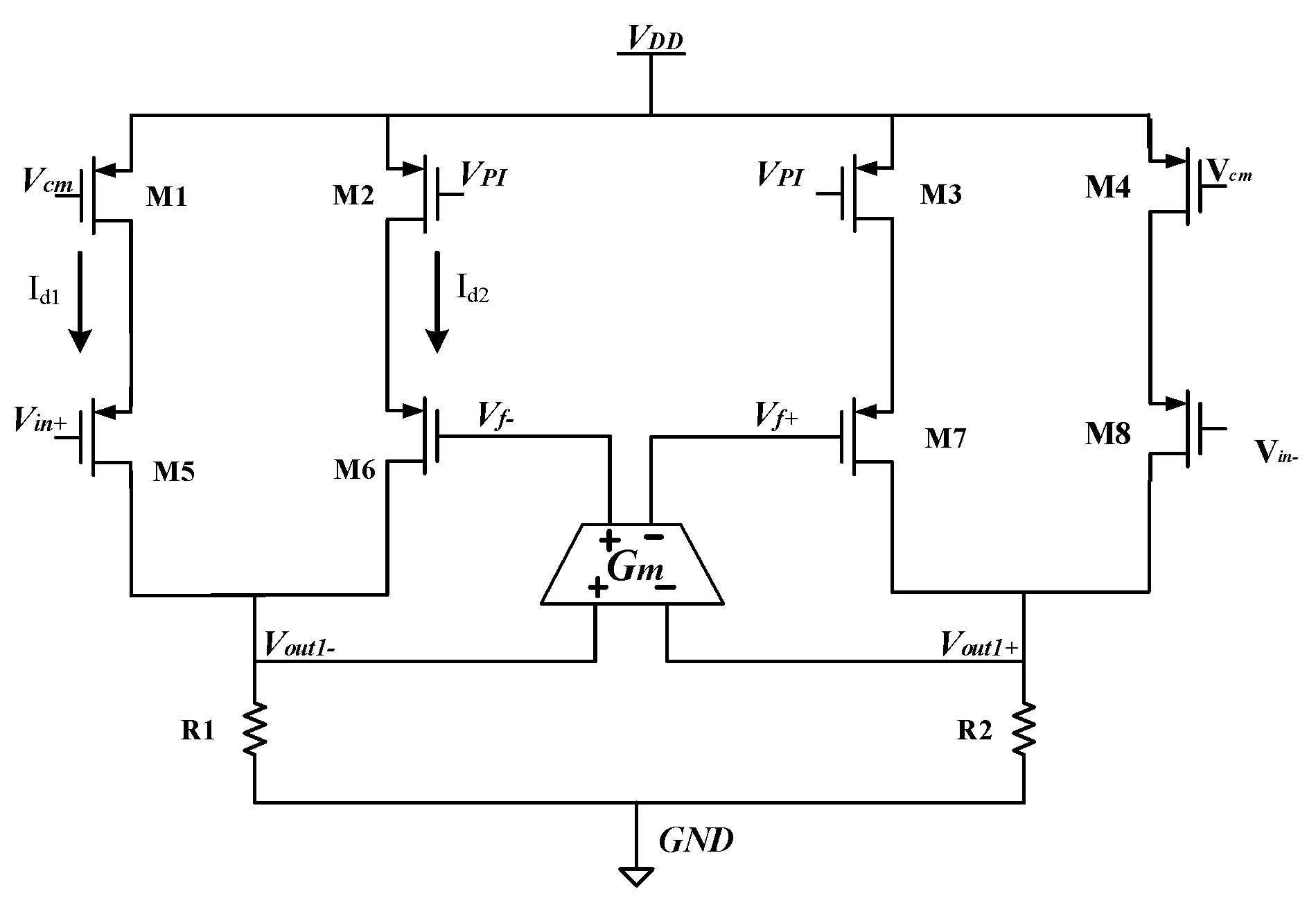
4.1. Design of AGC Circuit Module
4.2. Design and Analysis of Nonlinear Multiplier
4.3. Design of On-Chip Integrated Temperature Sensor
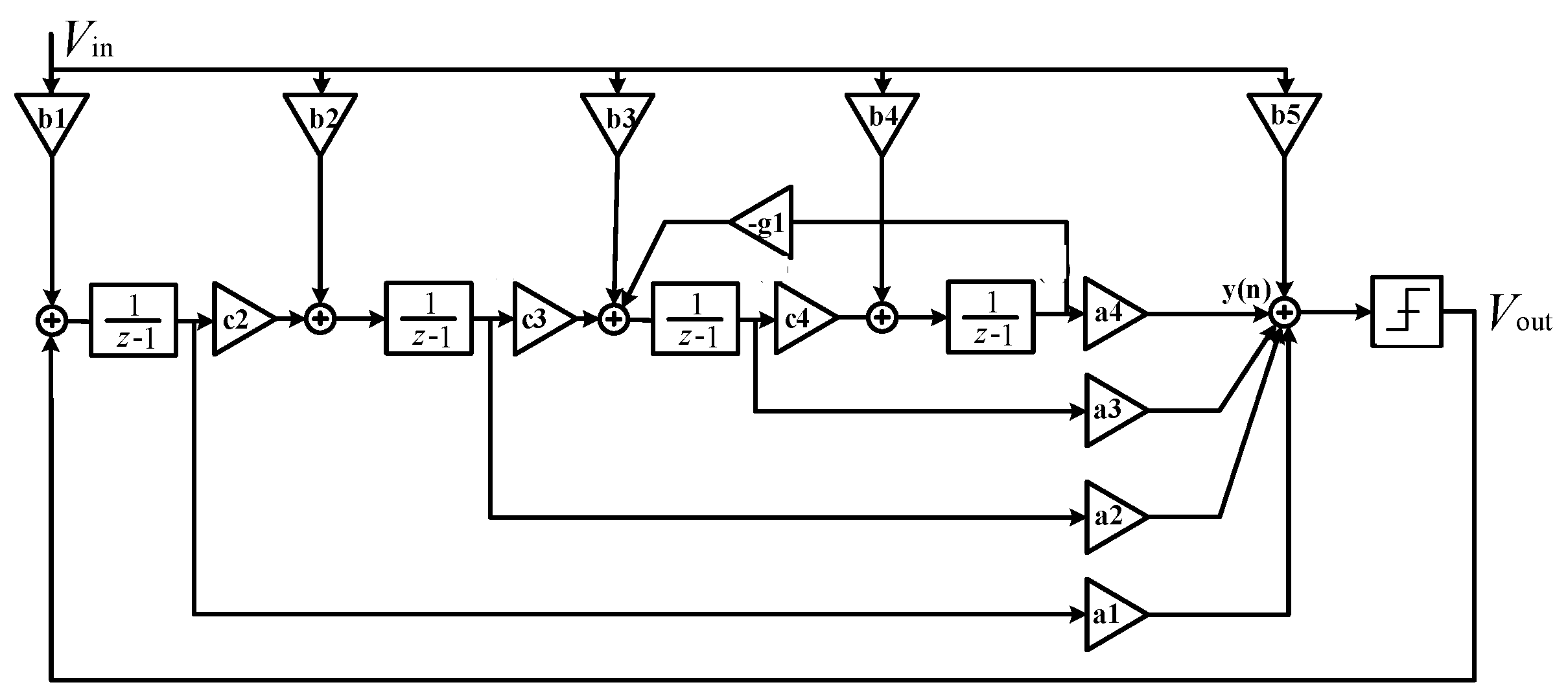
4.4. Circuit Design of ΣΔ Modulator
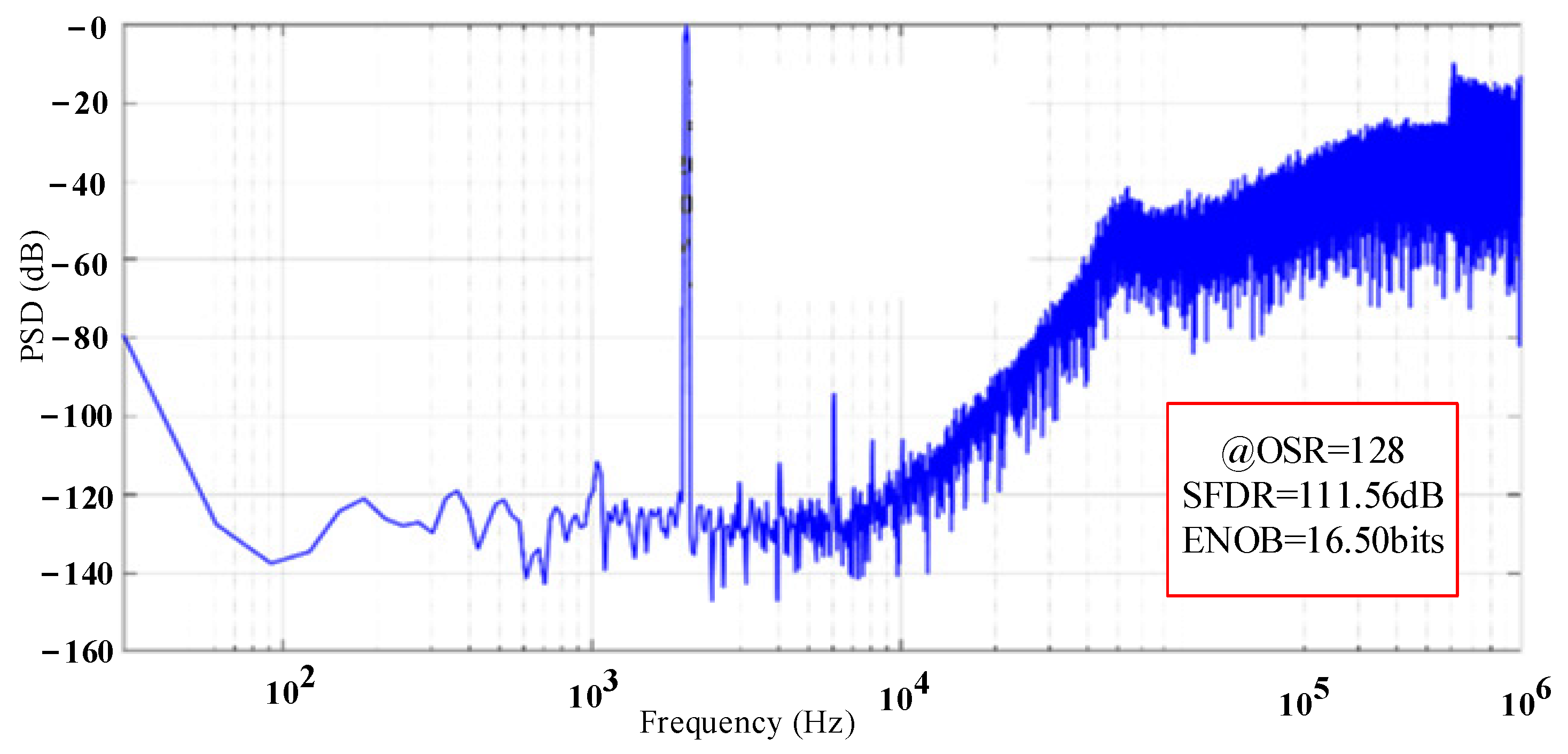
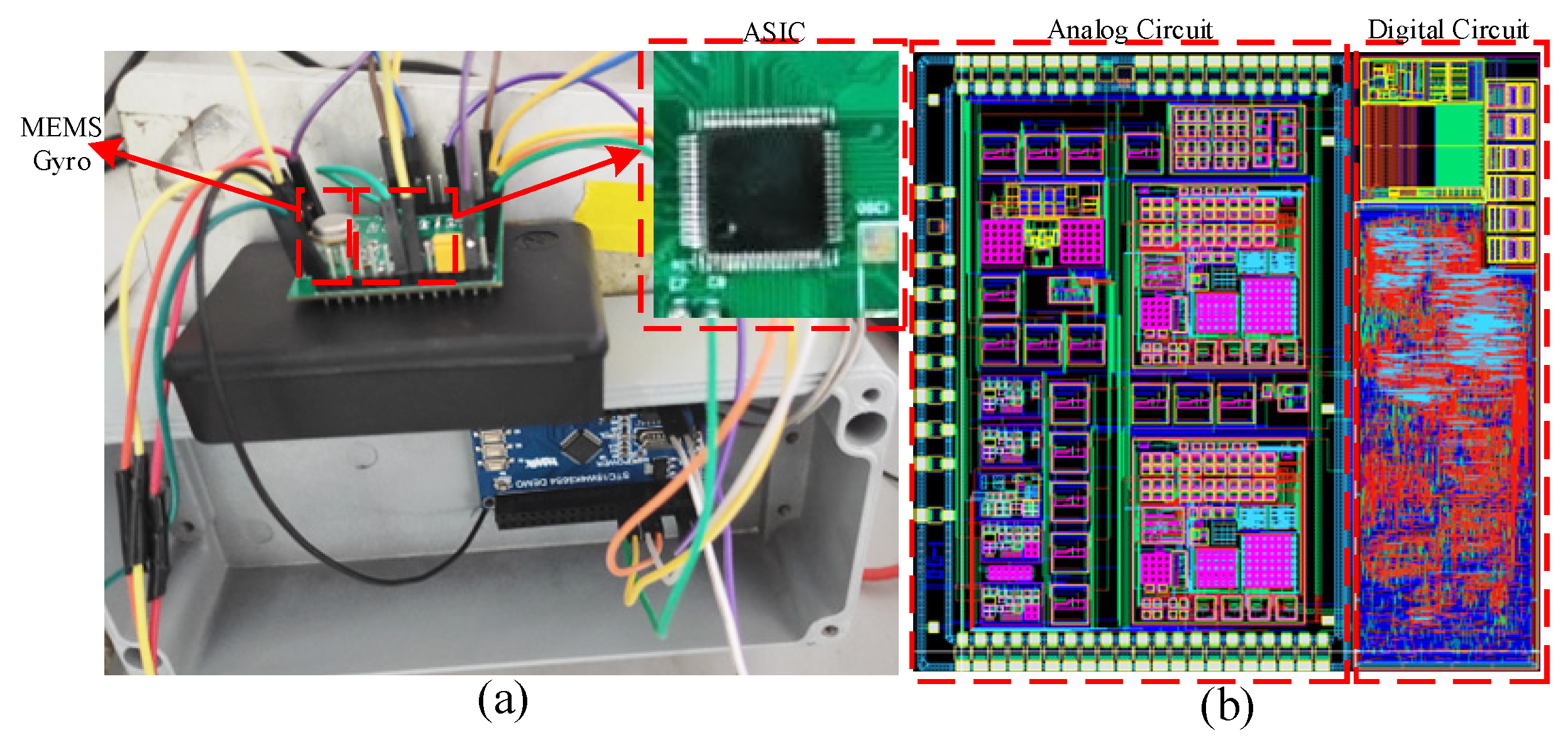
5. Experimental Results and Discussion of Gyroscope
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Prikhodko, I.P.; Nadig, S.; Gregory, J.; Clark, W.A.; Judy, M.W. Half-a-month stable 0.2 degree-per-hour mode-matched mems gyroscope. In Proceedings of the 2017 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Kauai, HI, USA, 28–30 March 2017; pp. 1–4. [Google Scholar]
- Zhu, J.X.; Liu, X.M.; Shi, Q.F.; He, T.Y.; Sun, Z.D.; Guo, X.E.; Liu, W.X.; Sulaiman, O.B.; Dong, B.W.; Lee, C.K. Development Trends and Perspectives of Future Sensors and MEMS/NEMS. Micromachines 2020, 11, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ren, X.J.; Zhou, X.; Yu, S.; Wu, X.Z.; Xiao, D.B. Frequency-Modulated MEMS Gyroscopes: A Review. IEEE Sens. J. 2021, 21, 26426–26446. [Google Scholar] [CrossRef]
- Singh, V.; Kumar, V.; Saini, A.; Khosla, P.; Mishra, S. Design and Development of the MEMS-Based High-g Acceleration Threshold Switch. J. Microelectromech. Syst. 2021, 30, 24–31. [Google Scholar] [CrossRef]
- Sheng, B.; Chen, F.; Qian, C.; Xu, D.; Guo, S.; Li, X. Design of a Dual Quantization Electromechanical Sigma–Delta Modulator MEMS Vibratory Wheel Gyroscope. IEEE/ASME J. Microelectromech. Syst. 2018, 27, 218–230. [Google Scholar] [CrossRef]
- Cao, H.; Xue, R.; Cai, Q.; Gao, J.; Zhao, R.; Shi, Y.; Shen, C. Design and Experiment for Dual-Mass MEMS Gyroscope Sensing Closed-Loop System. IEEE Access 2020, 8, 48074–48087. [Google Scholar] [CrossRef]
- Xi, Z.; Kong, N.; Nie, W.; Cao, Y.; Zheng, C. High g MEMS inertial switch capable of direction detection. Sens. Actuators A Phys. 2019, 296, 7–16. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, L.; Younis, M.I. Multi-Threshold Inertial Switch with Acceleration Direction Detection Capability. IEEE Trans. Ind. Electron. 2023, 70, 4226–4335. [Google Scholar] [CrossRef]
- Liu, M.; Wu, X.; Niu, Y.; Yang, H.; Zhu, Y.; Wang, W. Research Progress of MEMS Inertial Switches. Micromachines 2022, 13, 359. [Google Scholar] [CrossRef]
- Maeda, D.; Ono, K.; Giner, J.; Matsumoto, M.; Kanamaru, M.; Sekiguchi, T.; Hayashi, M. MEMS Gyroscope with Less Than 1-deg/h Bias Instability Variation in Temperature Range From −40 °C to 125 °C. IEEE Sens. J. 2018, 18, 1006–1015. [Google Scholar] [CrossRef]
- Li, Q.; Xiao, D.; Zhou, X.; Xu, Y.; Zhuo, M.; Hou, Z.; Wu, X. 0.04 degree-per-hour MEMS disk resonator gyroscope with high-quality factor (510 k) and long decaying time constant (74.9 s). Microsyst. Nanoeng. 2018, 4, 32. [Google Scholar] [CrossRef]
- Wang, Y.; Fu, Q.; Zhang, Y.; Zhang, W.; Chen, D.; Yin, L.; Liu, X. A Digital Closed-Loop Sense MEMS Disk Resonator Gyroscope Circuit Design Based on Integrated Analog Front-end. Sensors 2020, 20, 687. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, Y.; Li, Q.; Zhang, Y.; Zhou, X.; Wu, X.; Xiao, D. Honeycomb-Like Disk Resonator Gyroscope. IEEE Sens. J. 2020, 20, 85–94. [Google Scholar] [CrossRef]
- Khan, N.; Ahamed, M.J. Design and development of a MEMS butterfly resonator using synchronizing beam and out of plane actuation. Microsyst. Technol. 2019, 26, 1643–1652. [Google Scholar] [CrossRef]
- Lapadatu, D.; Blixhavn, B.; Holm, R.; Kvisteroy, T. SAR500-A high-precision high-stability butterfly gyroscope with north seeking capability. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Indian Wells, CA, USA, 4–6 May 2010; pp. 6–13. [Google Scholar]
- Su, J.; Xiao, D.; Wang, X.; Chen, Z.; Wu, X. Vibration sensitivity analysis of the ‘Butterfly-gyro’ structure. Microsyst. Technol. 2013, 20, 1281–1290. [Google Scholar] [CrossRef]
- Zhang, Y.S.; Yang, T. Modeling and compensation of MEMS gyroscope output data based on support vector machine. Measurement 2012, 45, 922–926. [Google Scholar]
- Tan, Z.; Nguyen, K.; Yan, J.; Samuels, H.; Keating, S.; Crocker, P.; Clark, B. A dual-axis MEMS vibratory gyroscope ASIC with 0.0061°/s/VHz noise floor over 480 Hz bandwidth. In Proceedings of the 2017 IEEE Asian Solid-State Circuits Conference (A-SSCC), Seoul, Republic of Korea, 6–8 November 2017; pp. 21–24. [Google Scholar]
- Chen, H.; Zhong, Y. Design of Readout Circuit with Quadrature Error and Auxiliary PLL for MEMS Vibratory Gyroscope. Sensors 2020, 20, 4564. [Google Scholar] [CrossRef]
- Xu, X.; Liu, X.; Zhang, Y. A Quick Start Method for MEMS Disk Resonant Gyroscope. Sensors 2021, 21, 7986. [Google Scholar] [CrossRef] [PubMed]
- Xiao, D.; Yu, D.; Xin, Z.; Hou, Z.; He, H.; Wu, X. Frequency Tuning of a Disk Resonator Gyroscope via Stiffness Perturbation. IEEE Sens. J. 2017, 17, 4725–4734. [Google Scholar] [CrossRef]
- Passaro, V.M.N.; Antonello, C.; Lorenzo, V.; Martino, D.C.; Edoardo, C.C. Gyroscope Technology and Applications: A Review in the Industrial Perspective. Sensors 2017, 17, 2284. [Google Scholar] [CrossRef] [Green Version]
- Zotov, S.A.; Simon, B.R.; Sharma, G.; Prikhodko, I.P.; Trusov, A.A.; Shkel, A.M. Utilization of mechanical quadrature in silicon MEMS vibratory gyroscope to increase and expand the long term in-run bias stability. In Proceedings of the 1st IEEE International Symposium on Inertial Sensors and Systems, ISISS, Laguna Beach, CA, USA, 25–26 February 2014; IEEE Sensors Council: Piscataway, NJ, USA, 2014. [Google Scholar]
- Rombach, S.; Marx, M.; Nessler, S.; De Dorigo, D.; Maurer, M.; Manoli, Y. An Interface ASIC for MEMS Vibratory Gyroscopes with a Power of 1.6 mW, 92 dB DR and 0.007°/s/Hz1/2 Noise Floor over a 40 Hz Band. IEEE J. Solid State Circuits 2016, 51, 1915–1927. [Google Scholar] [CrossRef]
- Marx, M.; De Dorigo, D.; Nessler, S.; Rombach, S.; Manoli, Y. A 0.06 mm2 Background Resonance Frequency Tuning Circuit Based on Noise Observation for a 1.71 mW CT-Delta Sigma MEMS Gyroscope Readout System with 0.9°/h Bias Instability. IEEE J. Solid-State Circuits 2018, 53, 174–186. [Google Scholar] [CrossRef]
- Taheri-Tehrani, P.; Challoner, A.D.; Horsley, D.A. Micromechanical Rate Integrating Gyroscope with Angle-Dependent Bias Compensation Using a Self-Precession Method. IEEE Sens. J. 2018, 18, 3533–3543. [Google Scholar] [CrossRef]
- Chen, C.; Wu, K.; Lu, K.; Li, Q.; Wang, C.; Wu, X. A Novel Mechanical Frequency Tuning Method Based on Mass-Stiffness Decoupling for MEMS Gyroscopes. Micromachines 2022, 13, 1052. [Google Scholar] [CrossRef]
- Huang, F.X.; Fu, Q.; Liu, X.L.; Zhang, Y.F.; Mao, Z.G. Research on digital silicon gyroscope interface circuit based on bandpass sigma-delta modulator. Int. J. Mod. Phys. B 2019, 33, 1950286. [Google Scholar] [CrossRef]
- Zhang, W.B.; Chen, W.P.; Yin, L.; Di, X.P.; Chen, D.L.; Fu, Q.; Zhang, Y.F.; Liu, X.W. Study of the Influence of Phase Noise on the MEMS Disk Resonator Gyroscope Interface Circuit. Sensors 2020, 20, 5470. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Li, H.; Yang, C.; Huang, L. Comparison of Three Automatic Mode-Matching Methods for Silicon Micro-Gyroscopes Based on Phase Characteristic. IEEE Sens. J. 2016, 16, 610–619. [Google Scholar] [CrossRef]
- Liu, Y.X.; Feng, W.L.; He, C.H.; Wang, L.; Dong, L.G.; Zhao, Q.C.; Yang, Z.C.; Yan, G.Z. Design of a digital closed control loop for the sense mode of a mode-matching MEMS vibratory gyroscope. In Proceedings of the 9th IEEE International Conference on Nano/Micro Engineered and Molecular Systems, IEEE-NEMS 2014, Waikiki Beach, HI, USA, 13–16 April 2014; pp. 199–203. [Google Scholar]
- Nitzan, S.; Su, T.H.; Ahn, C.; Ng, E.; Hong, V.; Yang, Y.; Kenny, T.; Horsley, D.A. Impact of gyroscope operation above the critical bifurcation threshold on scale factor and bias instability. In Proceedings of the IEEE International Conference on Micro Electro Mechanical Systems, San Francisco, CA, USA, 26–30 January 2014; pp. 749–752. [Google Scholar]
- Li, Q.; Xiao, D.; Xu, Y.; Zhuo, M.; Zhou, X.; Zhang, Y.; Yu, L.; Wu, X. Nonlinearity Reduction in Disk Resonator Gyroscopes Based on the Vibration Amplification Effect. IEEE Trans. Ind. Electron. 2020, 67, 6946–6954. [Google Scholar] [CrossRef]
- Balachandran, G.K.; Petkov, V.P.; Mayer, T.; Balslink, T. A 3-Axial Gyroscope for Electronic Stability Control for Continuous Self-Test. IEEE J. Solid State Circuits 2016, 51, 177–186. [Google Scholar]
- Tseng, K.; Li, M.; Li, S. A monolithic triaxial MEMS gyroscope working in air. In Proceedings of the IEEE International Symposium on Inertial Sensors and Systems 2020, Hiroshima, Japan, 23–26 March 2020. [Google Scholar]












| Sensitive to Structural Physical Parameters | Equivalent Electrical Parameters |
|---|---|
| Velocity v | Current i |
| Displacement x in the driving direction | The quantity of charge Qd on capacitor C |
| Effective mass m | Inductance L |
| Damping coefficient b | Resistance R |
| Elastic coefficient k | Capacitance C |
| Feedback driving force Fd /Coriolis force Fc | Constant pressure source U |
| Resultant force | Voltage droop on the inductor UL |
| Damping force Fb | Voltage droop on the resistor UR |
| Elastic force Fk | Voltage droop on the capacitor UC |
| Properties | [32] | [33] | [34] | [35] | This Work |
|---|---|---|---|---|---|
| Year | 2014 | 2016 | 2017 | 2020 | 2022 |
| Circuit type | PCB + FPGA | Analog + FPGA | ASIC | PCB | ASIC |
| Power (mW) | - | 27.3 | 21 | - | 25 |
| Chip area (mm2) | - | 2.3 | 7.3 | - | 5.7 |
| Input range (°/s) | - | ±100 | 500 | ±200 | ±200 |
| Bandwidth (Hz) | - | 80 | 480 | - | 100 |
| Bias instability (°/h) | 1.5 | 0.5 V | 5.5 | 11.3 | 5.1 |
| Nonlinearity (%) | 0.15 | 0.1 | - | - | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Chen, W.; Yin, L.; Fu, Q. An Interface ASIC Design of MEMS Gyroscope with Analog Closed Loop Driving. Sensors 2023, 23, 2615. https://doi.org/10.3390/s23052615
Zhang H, Chen W, Yin L, Fu Q. An Interface ASIC Design of MEMS Gyroscope with Analog Closed Loop Driving. Sensors. 2023; 23(5):2615. https://doi.org/10.3390/s23052615
Chicago/Turabian StyleZhang, Huan, Weiping Chen, Liang Yin, and Qiang Fu. 2023. "An Interface ASIC Design of MEMS Gyroscope with Analog Closed Loop Driving" Sensors 23, no. 5: 2615. https://doi.org/10.3390/s23052615
APA StyleZhang, H., Chen, W., Yin, L., & Fu, Q. (2023). An Interface ASIC Design of MEMS Gyroscope with Analog Closed Loop Driving. Sensors, 23(5), 2615. https://doi.org/10.3390/s23052615







