Fusing Expert Knowledge with Monitoring Data for Condition Assessment of Railway Welds
Abstract
:1. Introduction
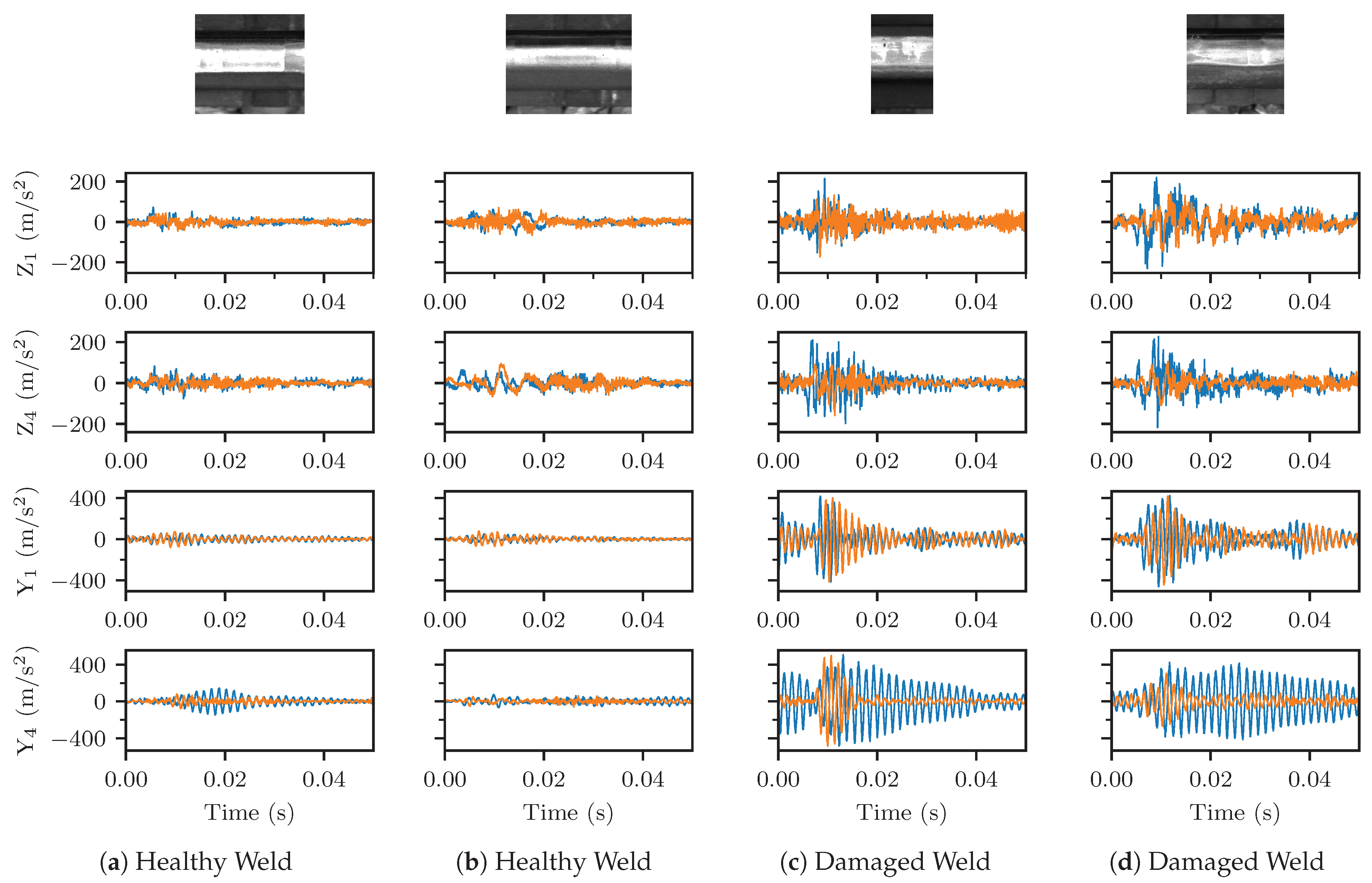
2. Description of the Measurement Data
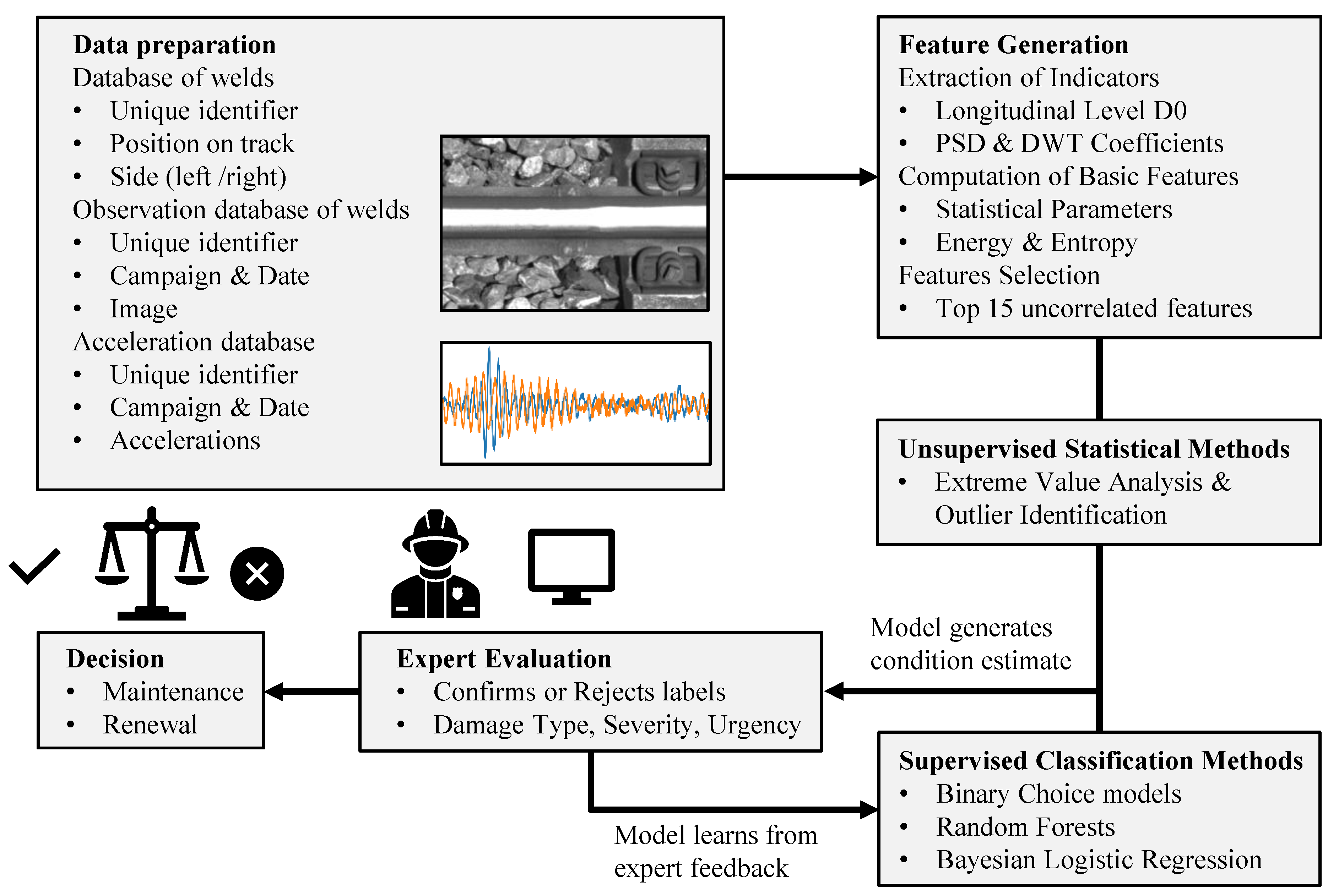
3. Methodological Approach
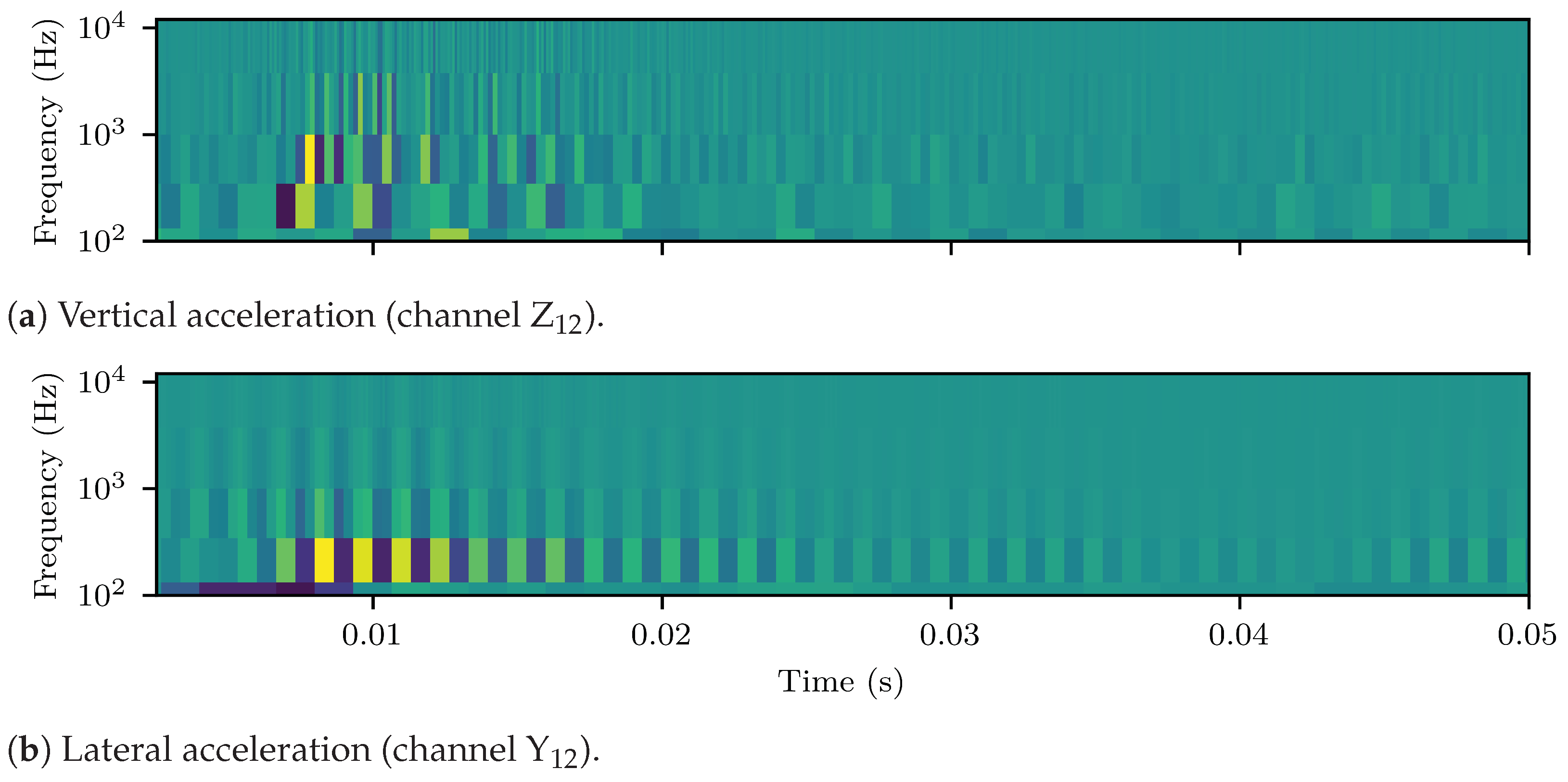
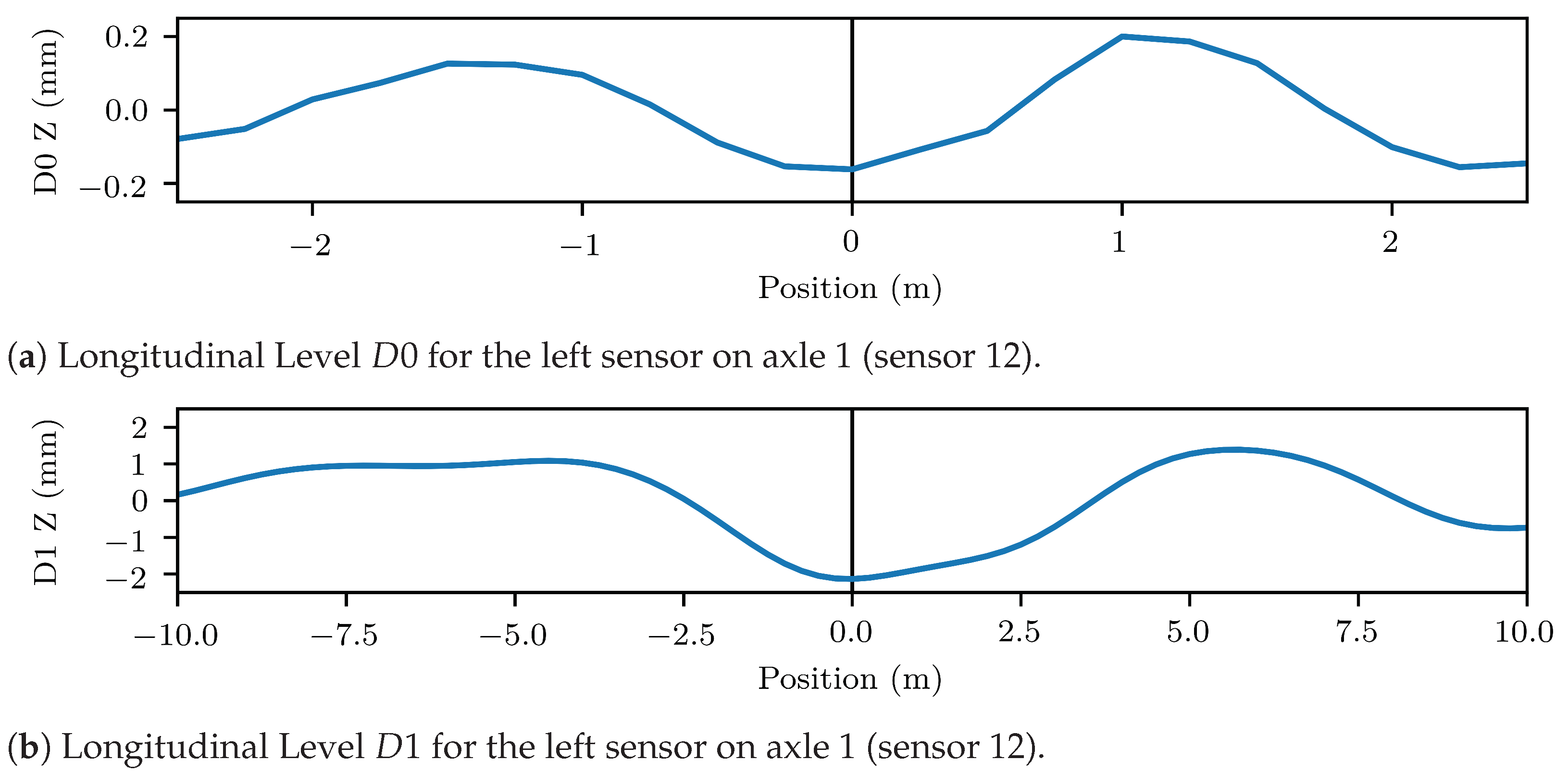
3.1. Feature Extraction
3.2. Time Series Analysis
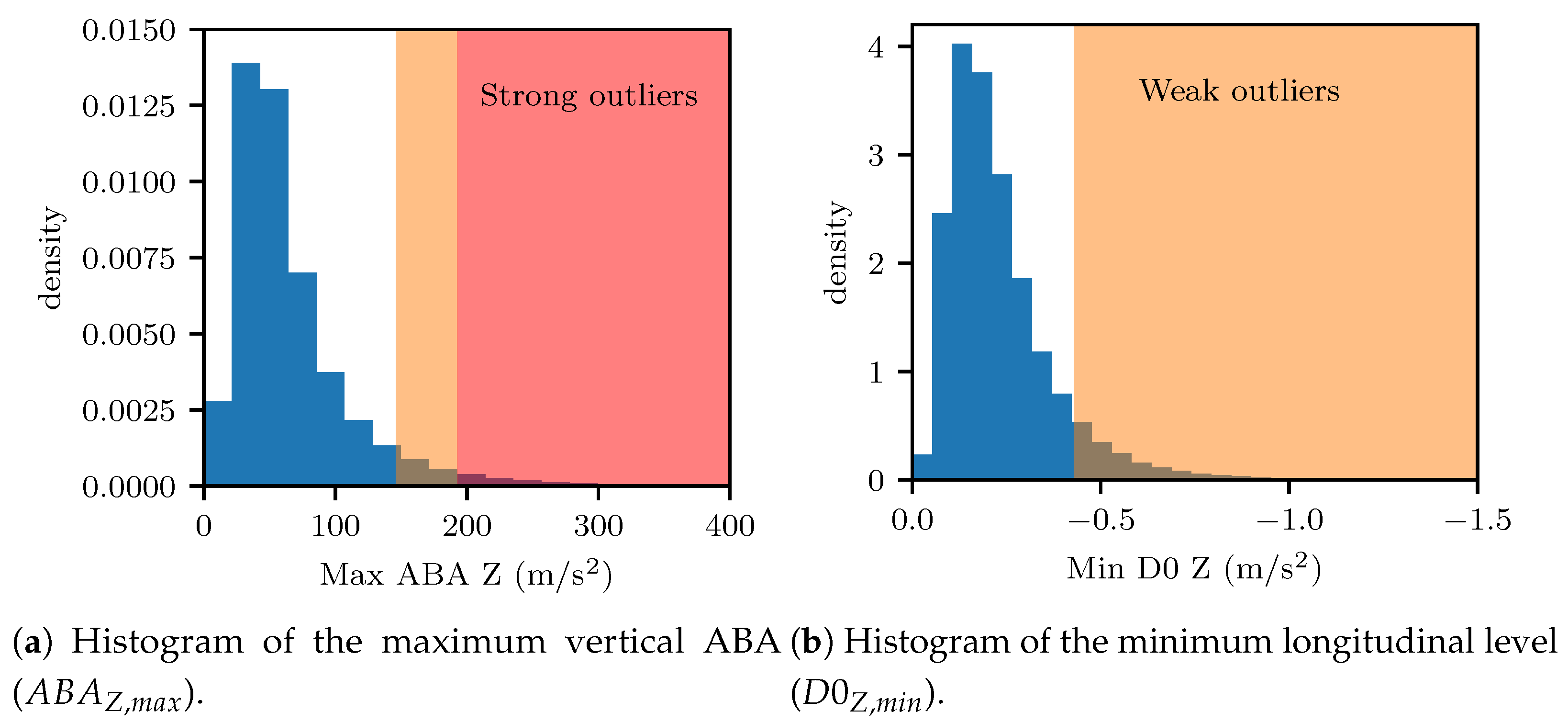
3.3. Extreme Value Analysis for Outlier Identification and Expert Labeling
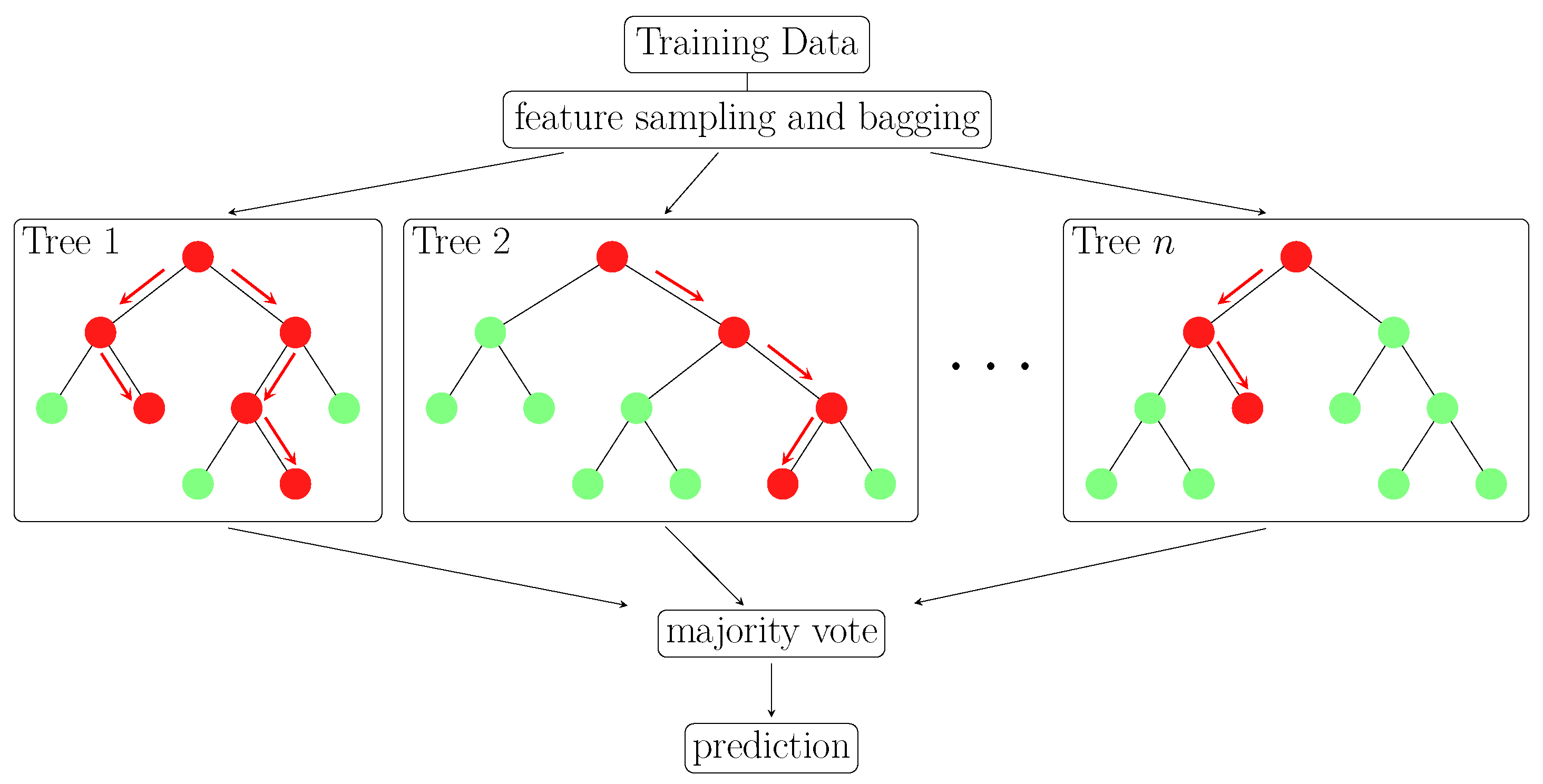
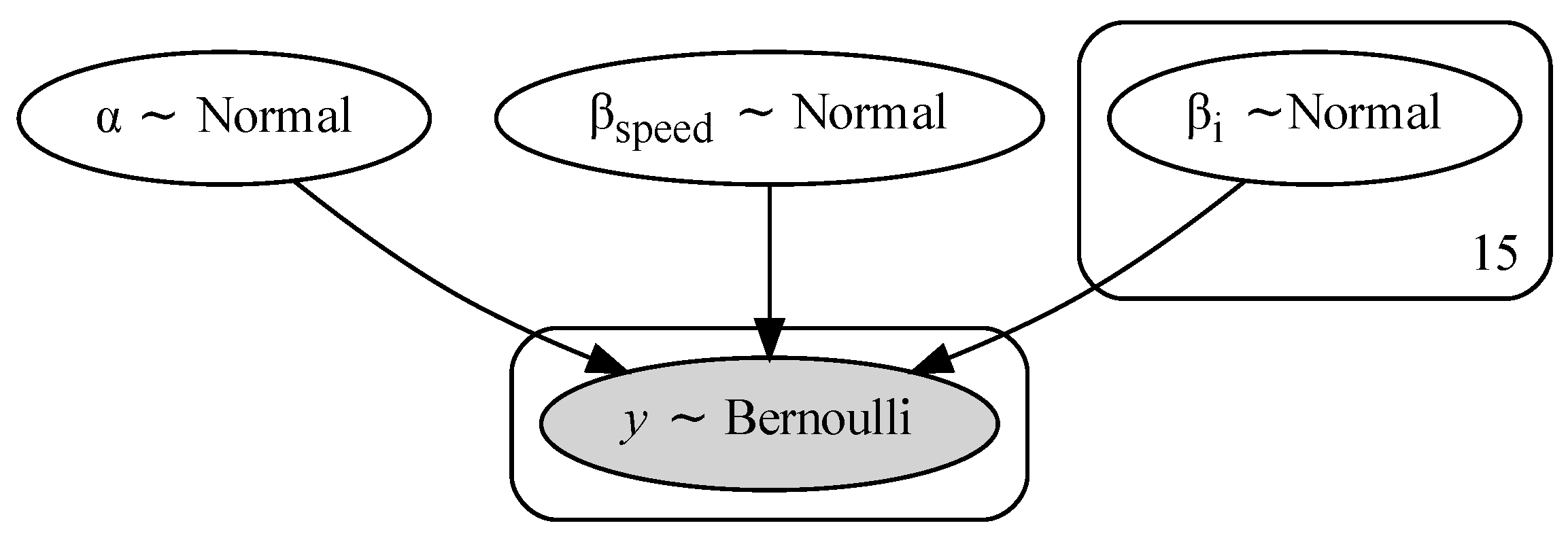
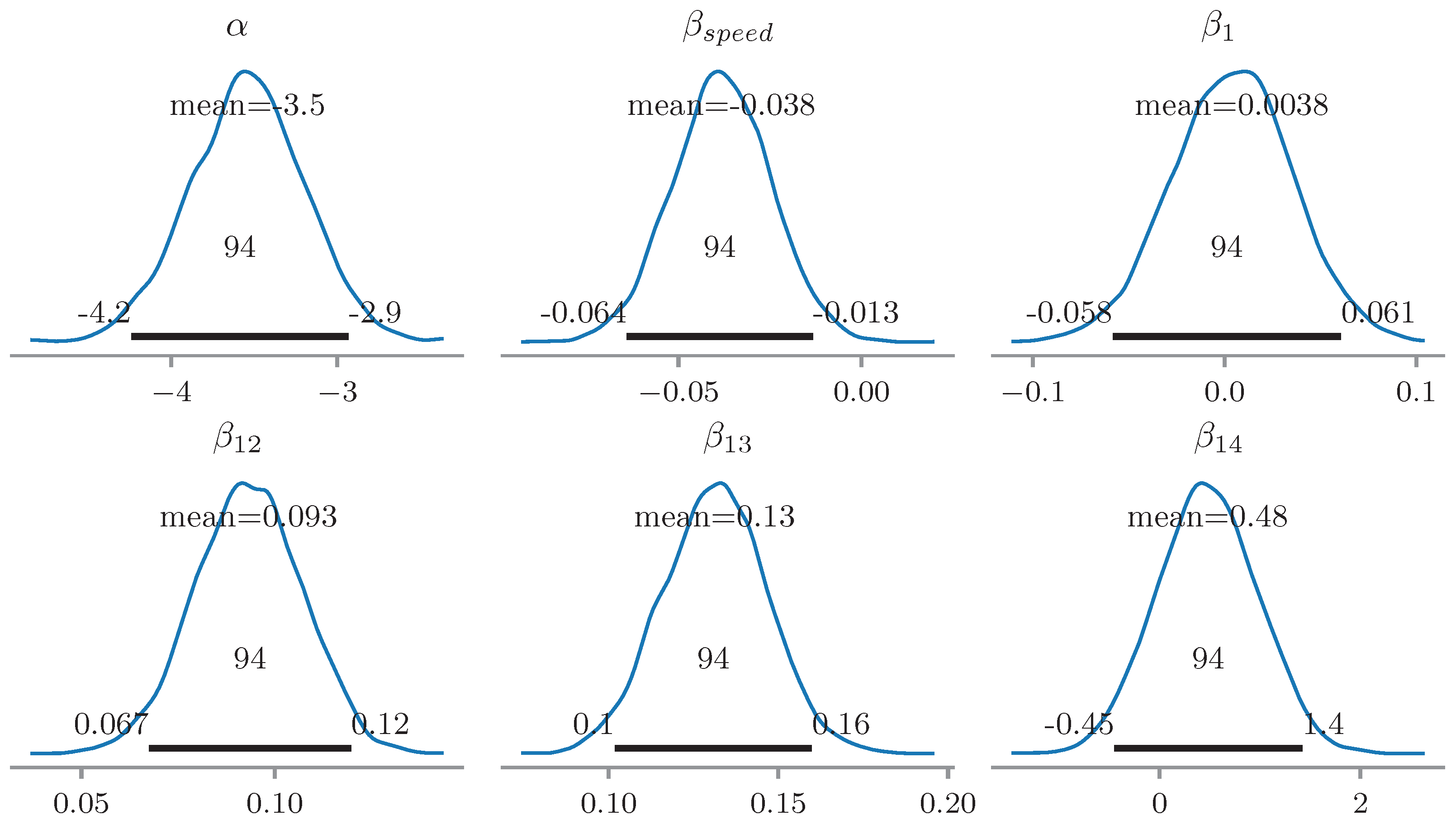
3.4. Expert-Informed Classification Models
4. Results and Discussion
4.1. Expert-Based Evaluation of Outlier Welds
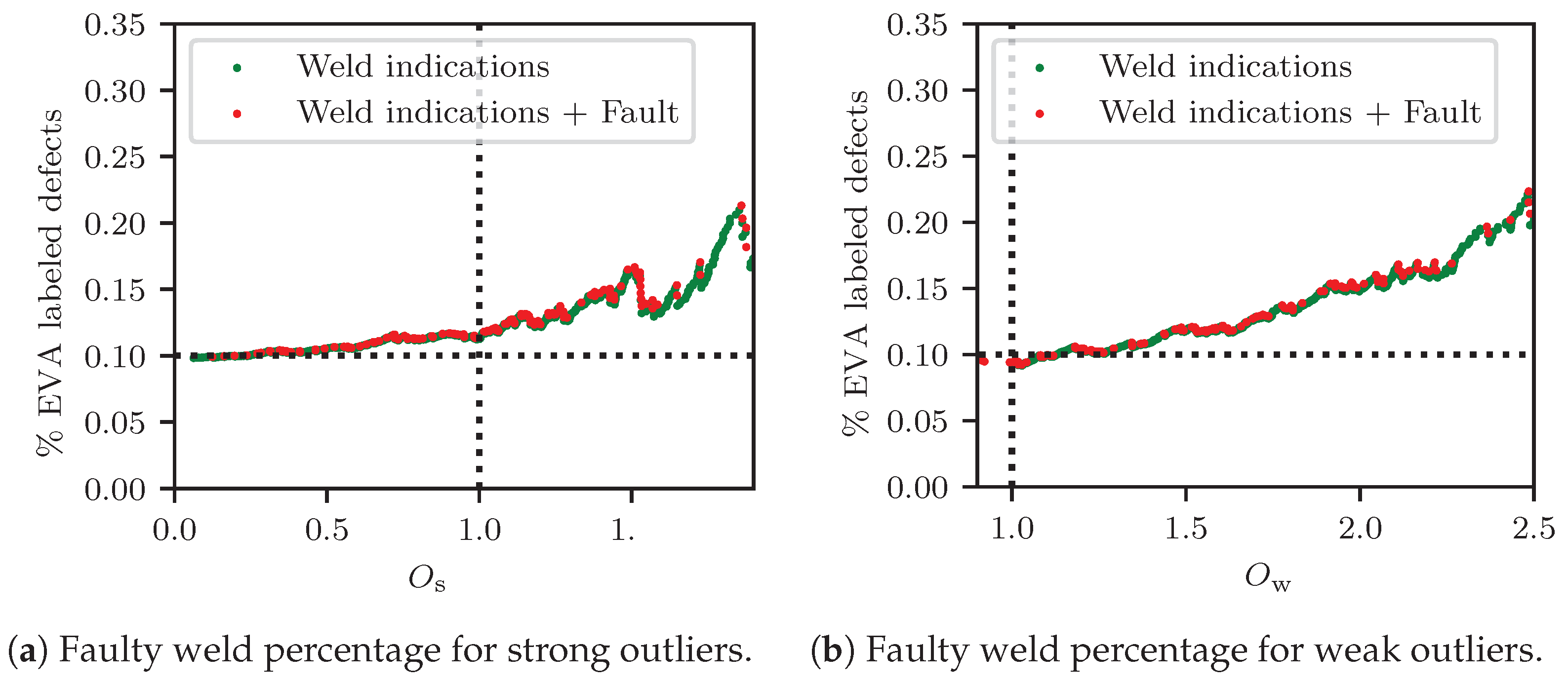
4.1.1. Definition of Capacity-Based Thresholds
4.1.2. Expert Assessment
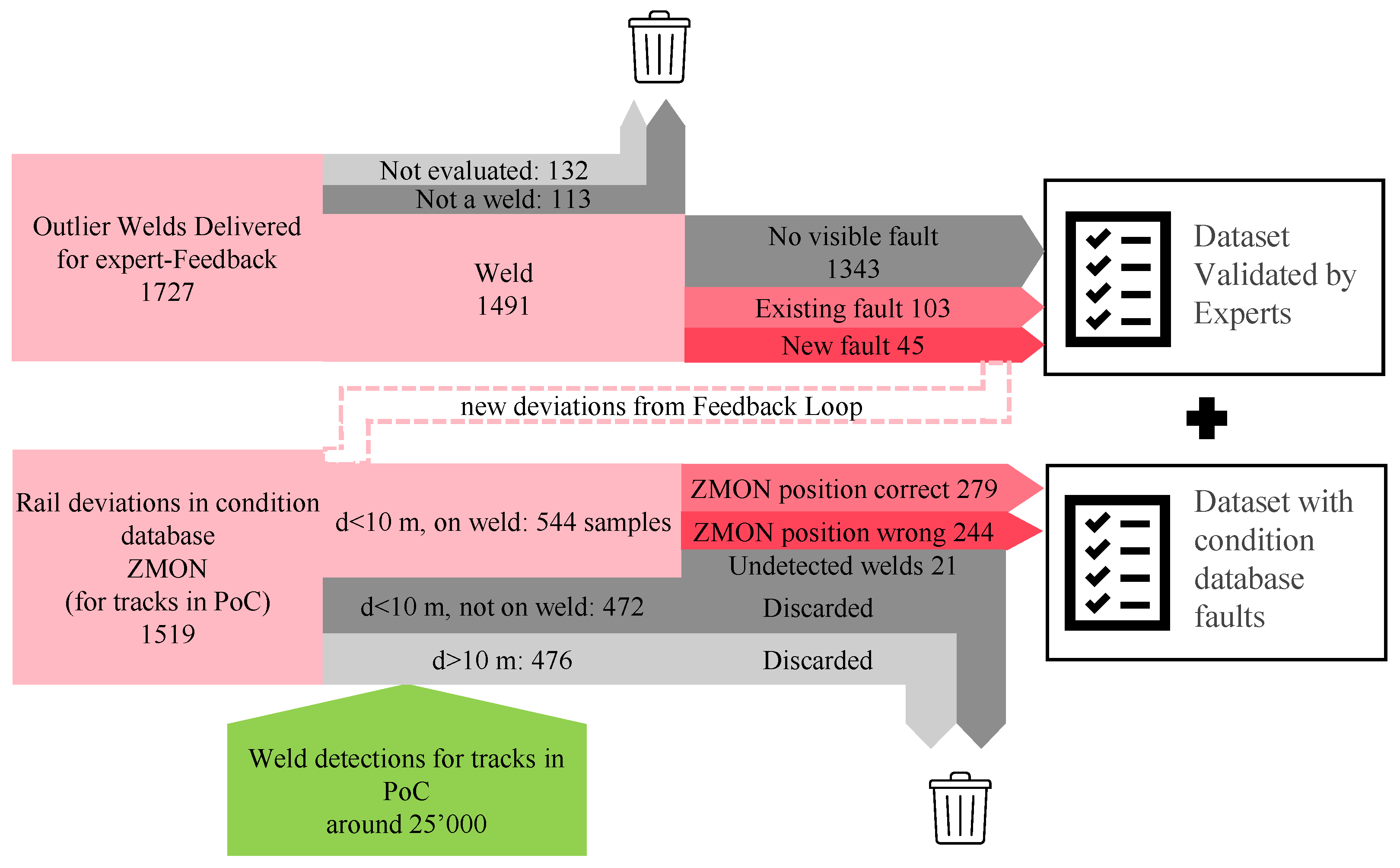
4.1.3. Fusion of Data from the Standard Condition Monitoring Database (ZMON)
4.2. Classification of Weld Condition
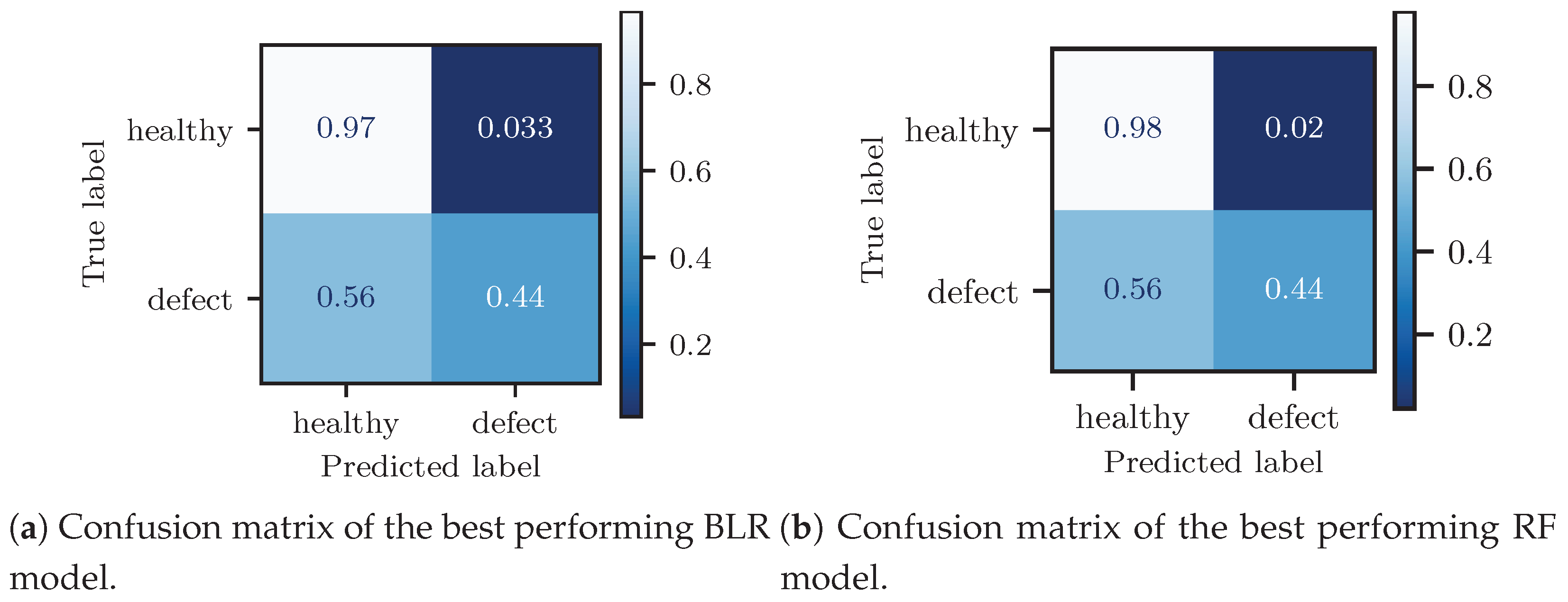
- The assumption that all welds not linked to a fault (from the ZMON database or the PoC expert-based evaluation) are healthy is inaccurate. Figure 14b illustrates that some samples assumed as healthy, but classified as defective (categorized as False positives), were indeed defective as they were not recorded in the ZMON database at the time of the inspection.
- Additionally, errors can occur when matching the potentially outdated time and inaccurate location of defects recorded in the ZMON database with the weld observations. This can result in false negatives, where one can visually observe faults, as shown in Figure 14d.
- Finally, additional uncertainty arises from expert judgment, which tends to vary considerably as each expert can reach a differing conclusion on the same sample.
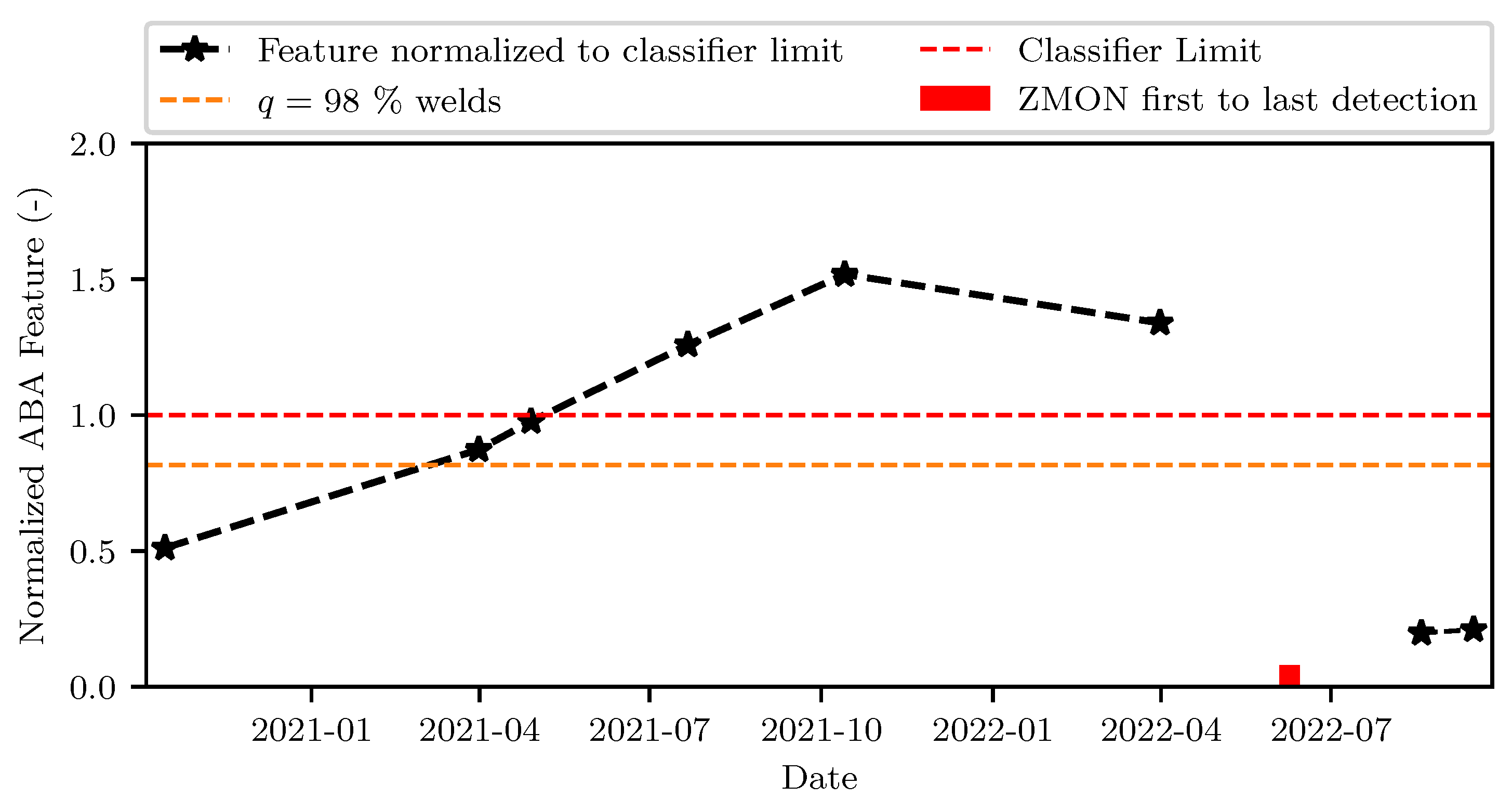
4.3. Continuous Tracking of Health Condition
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABA | Axle Box Accelerations |
| BC | Binary Choice model |
| BLR | Bayesian Logistic Regression model |
| CWT | Continuous Wavelet Transform |
| DWT | Discrete Wavelet Transform |
| EVA | Extreme Value Analysis |
| gDFZ | Diagnostic Monitoring Vehicle of the SBB |
| OBM | On Board Monitoring |
| PoC | Proof-of-Concept |
| STFT | Short Time Fourier Transform |
| RF | Random Forest model |
| SBB | Swiss Federal Railways |
| VCUBE | Rail-Head Imaging System on the gDFZ |
| ZMON | Database for Condition Monitoring & Logging |
References
- Linke, P.; Hoksch, D.I.V.; Wolter, K.; Werning, B.; Mösken, H.; Uebel, L. Monitoring und Zustandsorientierte Instandhaltung von Schienenfahrzeugen und -fahrweg mittels Mustererkennung in Ereignisdaten. Tag. Mod. Schienenfahrzeuge 2016, 140, 214–223. [Google Scholar]
- Mcmahon, P.; Zhang, T.; Dwight, R. Requirements for Big Data Adoption for Railway Asset Management. IEEE Access 2020, 8, 15543–15564. [Google Scholar] [CrossRef]
- Schweizerische Bundesbahnen AG. SBB Geschäftsbericht 2021. Press@SBB.ch. 2021, pp. 29–31. Available online: https://company.sbb.ch/content/dam/internet/corporate/de/medien/publikationen/geschaeftsbericht/SBB-Geschaeftsbericht-2021.pdf.sbbdownload.pdf (accessed on 17 January 2023).
- Hoelzl, C.; Dertimanis, V.; Landgraf, M.; Ancu, L.; Zurkirchen, M.; Chatzi, E. On-board monitoring for smart assessment of railway infrastructure: A systematic review. In The Rise of Smart Cities; Elsevier: Amsterdam, The Netherlands, 2022; pp. 223–259. [Google Scholar] [CrossRef]
- Barke, D.; Chiu, W.K. Structural Health Monitoring in the Railway Industry: A Review. Struct. Health Monit. 2005, 4, 81–93. [Google Scholar] [CrossRef]
- Artagan, S.S.; Ciampoli, L.B.; D’Amico, F.; Calvi, A.; Tosti, F. Non-destructive Assessment and Health Monitoring of Railway Infrastructures. Surv. Geophys. 2019, 41, 447–483. [Google Scholar] [CrossRef]
- Yan, T.H.; De Almeida Costa, M.; Corman, F. Developing and extending status prediction models for railway tracks based on on-board monitoring data. In Proceedings of the 102nd Annual Meeting of the Transportation Research Board (TRB 2023), Washington, DC, USA, 8–12 January 2023. OMISM (MI Mobility Initiative Project). [Google Scholar]
- Xie, J.; Huang, J.; Zeng, C.; Jiang, S.H.; Podlich, N. Systematic literature review on data-driven models for predictive maintenance of railway track: Implications in geotechnical engineering. Geosciences 2020, 10, 425. [Google Scholar] [CrossRef]
- Guo, Y.; Xie, J.; Fan, Z.; Markine, V.; Connolly, D.P.; Jing, G. Railway ballast material selection and evaluation: A review. Constr. Build. Mater. 2022, 344, 128218. [Google Scholar] [CrossRef]
- Group VöV. Schweissarbeiten an Schienen und Weichenbauteilen; VöV: Bern, Switzerland, 2006. [Google Scholar]
- Yao, N.; Jia, Y.; Tao, K. Rail Weld Defect Prediction and Related Condition-Based Maintenance. IEEE Access 2020, 8, 103746–103758. [Google Scholar] [CrossRef]
- Gerum, P.C.L.; Altay, A.; Baykal-Gürsoy, M. Data-driven predictive maintenance scheduling policies for railways. Transp. Res. Part C Emerg. Technol. 2019, 107, 137–154. [Google Scholar] [CrossRef]
- Nejad, R.M.; Berto, F. Fatigue fracture and fatigue life assessment of railway wheel using non-linear model for fatigue crack growth. Int. J. Fatigue 2021, 153, 106516. [Google Scholar] [CrossRef]
- Rail Defects, 4th ed.; UIC Code 712; International Union of Railways: Paris, France, 2002; pp. 106–107.
- Zhu, H.; Li, H.; Al-Juboori, A.; Wexler, D.; Lu, C.; McCusker, A.; McLeod, J.; Pannila, S.; Barnes, J. Understanding and treatment of squat defects in a railway network. Wear 2020, 442–443, 203139. [Google Scholar] [CrossRef]
- Królicka, A.; Lesiuk, G.; Radwański, K.; Kuziak, R.; Janik, A.; Mech, R.; Zygmunt, T. Comparison of fatigue crack growth rate: Pearlitic rail versus bainitic rail. Int. J. Fatigue 2021, 149, 106280. [Google Scholar] [CrossRef]
- Schmid, P.; Casutt, J.; Zurkirchen, M. Künstliche Intelligenz auf Schienen. Bulletin 2019, 9, 42–46. [Google Scholar]
- Liu, Y.; Wei, X. Track Surface Defect Detection Based on Image Processing. In Lecture Notes in Electrical Engineering; Springer: Singapore, 2018; pp. 225–232. [Google Scholar] [CrossRef]
- Paixão, A.; Fortunato, E.; Calçada, R. Smartphone’s Sensing Capabilities for On-Board Railway Track Monitoring: Structural Performance and Geometrical Degradation Assessment. Adv. Civ. Eng. 2019, 2019, 1–13. [Google Scholar] [CrossRef]
- Malekjafarian, A.; OBrien, E.; Quirke, P.; Bowe, C. Railway Track Monitoring Using Train Measurements: An Experimental Case Study. Appl. Sci. 2019, 9, 4859. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Chen, S.; Lederman, G.; Kramer, D.B.; Noh, H.Y.; Bielak, J.; Garrett, J.H.; Kovačević, J.; Bergés, M. Dynamic responses, GPS positions and environmental conditions of two light rail vehicles in Pittsburgh. Sci. Data 2019, 6, 146. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bernal, E.; Spiryagin, M.; Cole, C. Ultra-Low Power Sensor Node for On-Board Railway Wagon Monitoring. IEEE Sensors J. 2020, 20, 15185–15192. [Google Scholar] [CrossRef]
- Cii, S.; Tomasini, G.; Bacci, M.L.; Tarsitano, D. Solar Wireless Sensor Nodes for Condition Monitoring of Freight Trains. IEEE Trans. Intell. Transp. Syst. 2022, 23, 3995–4007. [Google Scholar] [CrossRef]
- Qin, Y.; Liu, M.; Fu, H. Small excitation self-powered sensing energy harvester for rail traffic condition monitoring. J. Phys. Conf. Ser. 2022, 2369, 012087. [Google Scholar] [CrossRef]
- SBB/CFF/FFS. Einbau, Kontrollen und Unterhalt von Gleisen. In Regelwerk Technik Eisenbahn RTE; SBB: Bern, Switzerland, 2022. [Google Scholar]
- Hoelzl, C.A.; Dertimanis, V.; Ancu, L.; Kollros, A.; Chatzi, E. Vold-Kalman Filter Order tracking of Axle Box Accelerations for Railway Stiffness Assessment. arXiv 2022, arXiv:2209.12899. [Google Scholar]
- Dertimanis, V.K.; Zimmermann, M.; Corman, F.; Chatzi, E.N. On-Board monitoring of rail roughness via axle box accelerations of revenue trains with uncertain dynamics. Model Valid. Uncertain. Quantif. 2019, 3, 167–171. [Google Scholar] [CrossRef]
- Tsunashima, H.; Hirose, R. Condition monitoring of railway track from car-body vibration using time–frequency analysis. Veh. Syst. Dyn. 2020, 60, 1170–1187. [Google Scholar] [CrossRef]
- Li, Z.; Molodova, M.; Dollevoet, R. An investigation of the possibility to use axle box acceleration for condition monitoring of welds. In Proceedings of the 2008 International Conference on Noise and Vibration Engineering, ISMA 2008, Leuven, Belgium, 15–17 September 2008; Sas, P., Bergen, B., Eds.; Katholieke Universiteit Leuven: Leuven, Belgium, 2008; pp. 2879–2886. [Google Scholar]
- An, B.; Wang, P.; Xu, J.; Chen, R.; Cui, D. Observation and Simulation of Axle Box Acceleration in the Presence of Rail Weld in High-Speed Railway. Appl. Sci. 2017, 7, 1259. [Google Scholar] [CrossRef] [Green Version]
- Esveld, C.; Steenbergen, M. Force-based assessment of weld geometry. In Proceedings of the 8th International Heavy Haul Conference, Rio de Janeiro, Brazil, 14–16 June 2005. [Google Scholar]
- Steenbergen, M.J.M.M.; Esveld, C. Rail weld geometry and assessment concepts. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2006, 220, 257–271. [Google Scholar] [CrossRef]
- Li, Z.; Molodova, M.; Nunez, A.; Dollevoet, R. Improvements in Axle Box Acceleration Measurements for the Detection of Light Squats in Railway Infrastructure. IEEE Trans. Ind. Electron. 2015, 62, 4385–4397. [Google Scholar] [CrossRef]
- Li, S.; Núñez, A.; Li, Z.; Dollevoet, R. Automatic detection of corrugation: Preliminary results in the Dutch network using axle box acceleration measurements. In ASME/IEEE Joint Rail Conference; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Cho, H.; Park, J. Study of Rail Squat Characteristics through Analysis of Train Axle Box Acceleration Frequency. Appl. Sci. 2021, 11, 7022. [Google Scholar] [CrossRef]
- Ng, A.K.; Martua, L.; Sun, G. Dynamic Modelling and Acceleration Signal Analysis of Rail Surface Defects for Enhanced Rail Condition Monitoring and Diagnosis. In Proceedings of the 2019 4th International Conference on Intelligent Transportation Engineering (ICITE), Singapore, 5–7 September 2019; pp. 69–73. [Google Scholar] [CrossRef]
- Zuo, Y.; Thiery, F.; Chandran, P.; Odelius, J.; Rantatalo, M. Squat Detection of Railway Switches and Crossings Using Wavelets and Isolation Forest. Sensors 2022, 22, 6357. [Google Scholar] [CrossRef] [PubMed]
- Wei, X.; Yin, X.; Hu, Y.; He, Y.; Jia, L. Squats and corrugation detection of railway track based on time-frequency analysis by using bogie acceleration measurements. Veh. Syst. Dyn. 2019, 58, 1167–1188. [Google Scholar] [CrossRef]
- Bergquist, B.; Söderholm, P. Data Analysis for Condition-Based Railway Infrastructure Maintenance. Qual. Reliab. Eng. Int. 2014, 31, 773–781. [Google Scholar] [CrossRef]
- Falamarzi, A.; Moridpour, S.; Nazem, M. Development of a tram track degradation prediction model based on the acceleration data. Struct. Infrastruct. Eng. 2019, 15, 1308–1318. [Google Scholar] [CrossRef]
- Sresakoolchai, J.; Kaewunruen, S. Railway defect detection based on track geometry using supervised and unsupervised machine learning. Struct. Health Monit. 2022, 21, 1757–1767. [Google Scholar] [CrossRef]
- Yang, C.; Sun, Y.; Ladubec, C.; Liu, Y. Developing Machine Learning-Based Models for Railway Inspection. Appl. Sci. 2021, 11, 13. [Google Scholar] [CrossRef]
- Tsunashima, H.; Takikawa, M. Monitoring the Condition of Railway Tracks Using a Convolutional Neural Network. In Recent Advances in Wavelet Transforms and Their Applications; Bulnes, F., Ed.; IntechOpen: Rijeka, Croatia, 2022; Chapter 6. [Google Scholar] [CrossRef]
- Shadfar, M.; Molatefi, H.; Nasr, A. An Index for Rail Weld Health Assessment in Urban Metro Using In-Service Train. Math. Probl. Eng. 2022, 2022, 1–10. [Google Scholar] [CrossRef]
- Xiao, B.; Mao, X.; Liu, J.; Niu, L.; Xu, X.; Zhang, M. An Improved Marginal Index Method to Diagnose Poor Welded Joints of Heavy-haul Railway. In Proceedings of the 2021 Global Reliability and Prognostics and Health Management (PHM-Nanjing), Nanjing, China, 15–17 October 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Ji, Y.; Zeng, J.; Sun, W. Research on Wheel-Rail Local Impact Identification Based on Axle Box Acceleration. Shock Vib. 2022, 2022, 1–17. [Google Scholar] [CrossRef]
- Pappaterra, M.J.; Flammini, F.; Vittorini, V.; Bešinović, N. A Systematic Review of Artificial Intelligence Public Datasets for Railway Applications. Infrastructures 2021, 6, 136. [Google Scholar] [CrossRef]
- Liu, J.; Chen, S.; Lederman, G.; Kramer, D.B.; Noh, H.Y.; Bielak, J.; Garrett, J.H.; Kovacevic, J.; Berges, M. The DR-Train Dataset: Dynamic Responses, GPS Positions and Environmental Conditions of Two Light Rail Vehicles in Pittsburgh; Technologies for Safe and Efficient Transportation University Transportation Center: Pittsburgh, PA, USA, 2018. [Google Scholar] [CrossRef]
- Lasisi, A.; Attoh-Okine, N. Machine Learning Ensembles and Rail Defects Prediction: Multilayer Stacking Methodology. Asce-Asme J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2019, 5, 04019016. [Google Scholar] [CrossRef]
- Oh, K.; Yoo, M.; Jin, N.; Ko, J.; Seo, J.; Joo, H.; Ko, M. A Review of Deep Learning Applications for Railway Safety. Appl. Sci. 2022, 12, 10572. [Google Scholar] [CrossRef]
- Hoelzl, C.; Ancu, L.; Grossmann, H.; Ferrari, D.; Dertimanis, V.; Chatzi, E. Classification of Rail Irregularities from Axle Box Accelerations Using Random Forests and Convolutional Neural Networks. In Data Science in Engineering; Springer International Publishing: Cham, Switzerland, 2022; Volume 9, pp. 91–97. [Google Scholar]
- Yuan, Z.; Zhu, S.; Yuan, X.; Zhai, W. Vibration-based damage detection of rail fastener clip using convolutional neural network: Experiment and simulation. Eng. Fail. Anal. 2021, 119, 104906. [Google Scholar] [CrossRef]
- Sresakoolchai, J.; Kaewunruen, S. Detection and Severity Evaluation of Combined Rail Defects Using Deep Learning. Vibration 2021, 4, 341–356. [Google Scholar] [CrossRef]
- Peng, L.; Zheng, S.; Li, P.; Wang, Y.; Zhong, Q. A Comprehensive Detection System for Track Geometry Using Fused Vision and Inertia. IEEE Trans. Instrum. Meas. 2021, 70, 1–15. [Google Scholar] [CrossRef]
- Hoelzl, C.A.; Dertimanis, V.; Kollros, A.; Ancu, L.; Chatzi, E. Weld Condition Monitoring Using Expert Informed Extreme Value Analysis. In European Workshop on Structural Health Monitoring; Springer International Publishing: Cham, Switzerland, 2023; pp. 711–720. [Google Scholar] [CrossRef]
- Pieringer, A.; Kropp, W. Model-based estimation of rail roughness from axle box acceleration. Appl. Acoust. 2022, 193, 108760. [Google Scholar] [CrossRef]
- Martakis, P.; Movsessian, A.; Reuland, Y.; Pai, S.G.S.; Quqa, S.; Garcia Cava, D.; Tcherniak, D.; Chatzi, E. A semi-supervised interpretable machine learning framework for Sensor Fault detection. Smart Struct. Syst. Int. J. 2021, 29, 251–266. [Google Scholar]
- Rees, D. Summarizing Data by Numerical Measures. In Essential Statistics; Springer: Boston, MA, USA, 2020. [Google Scholar] [CrossRef]
- Maes, J.; Sol, H. A double tuned rail damper—Increased damping at the two first pinned–pinned frequencies. J. Sound Vib. 2003, 267, 721–737. [Google Scholar] [CrossRef]
- Blanco, B.; Alonso, A.; Kari, L.; Gil-Negrete, N.; Giménez, J.G. Implementation of Timoshenko element local deflection for vertical track modelling. Veh. Syst. Dyn. 2019, 57, 1421–1444. [Google Scholar] [CrossRef] [Green Version]
- Goswami, J.C.; Chan, A.K. Fundamentals of Wavelets: Theory, Algorithms, and Applications, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Gonzalez, R.C. Digital Image Processing; Pearson Education: London, UK, 2009. [Google Scholar]
- Wang, H.; Berkers, J.; Hurk, N.; Farsad Layegh, N. Study of loaded versus unloaded measurements in railway track inspection. Measurement 2020, 169, 108556. [Google Scholar] [CrossRef]
- CEN. EN 13848-1, Railway Applications. Track. Track Geometry Quality. Characterization of Track Geometry; BSI: London, UK, 2019. [Google Scholar]
- Chudzikiewicz, A.; Bogacz, R.; Kostrzewski, M.; Konowrocki, R. Condition monitoring of railway track systems by using acceleration signals on wheelset axle-boxes. Transport 2017, 33, 555–566. [Google Scholar] [CrossRef] [Green Version]
- Saussine, G.; Cholet, C.; Gautier, P.E.; Dubois, F.; Bohatier, C.; Moreau, J.J. Modelling ballast behaviour under dynamic loading. Part 1: A 2D polygonal discrete element method approach. Comput. Methods Appl. Mech. Eng. 2006, 195, 2841–2859. [Google Scholar] [CrossRef] [Green Version]
- Dahlberg, T. Railway track stiffness variations—Consequences and countermeasures. Int. J. Civ. Eng. 2010, 8, 1–12. [Google Scholar]
- Hansen, A. The Three Extreme Value Distributions: An Introductory Review. Front. Phys. 2020, 8, 604053. [Google Scholar] [CrossRef]
- van der Wiel, K.; Wanders, N.; Selten, F.M.; Bierkens, M.F. Added Value of Large Ensemble Simulations for Assessing Extreme River Discharge in a 2 °C Warmer World. Geophys. Res. Lett. 2019, 46, 2093–2102. [Google Scholar] [CrossRef] [Green Version]
- Coles, S. Basics of Statistical Modeling. In An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001; pp. 18–44. [Google Scholar] [CrossRef]
- Chatzi, E.; Abdallah, I.; Tatsis, K.; Osmani, S.; Robles, I. Using interpretable machine learning for data-driven decision support for infrastructure operation & maintenance. In Bridge Safety, Maintenance, Management, Life-Cycle, Resilience and Sustainability; CRC Press: Boca Raton, FL, USA, 2022; pp. 837–845. [Google Scholar] [CrossRef]
- Abdallah, I.; Dertimanis, V.; Mylonas, H.; Tatsis, K.; Chatzi, E.; Dervili, N.; Worden, K.; Maguire, E. Fault diagnosis of wind turbine structures using decision tree learning algorithms with big data. In Safety and Reliability–Safe Societies in a Changing World; CRC Press: Boca Raton, FL, USA, 2018; pp. 3053–3061. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef] [Green Version]
- Avendaño-Valencia, L.D.; Chatzi, E.N.; Tcherniak, D. Gaussian process models for mitigation of operational variability in the structural health monitoring of wind turbines. Mech. Syst. Signal Process. 2020, 142, 106686. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: Berlin, Germany, 2006; Volume 4. [Google Scholar]
- Hoffman, M.D.; Gelman, A. The No-U-Turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 2014, 15, 1593–1623. [Google Scholar]
- Salvatier, J.; Wiecki, T.; Fonnesbeck, C. Probabilistic Programming in Python using PyMC. arXiv 2015, arXiv:1507.08050. [Google Scholar]
- Molodova, M.; Li, Z.; Núñez, A.; Dollevoet, R. Parametric study of axle box acceleration at squats. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2015, 229, 841–851. [Google Scholar] [CrossRef]
- SBB. Catalog of deviations for track inspectors. In Surveillance of Installations, ZMON; SBB: Bern, Switzerland, 2019. [Google Scholar]
- Gong, W.; Akbar, M.F.; Jawad, G.N.; Mohamed, M.F.P.; Wahab, M.N.A. Nondestructive Testing Technologies for Rail Inspection: A Review. Coatings 2022, 12, 1790. [Google Scholar] [CrossRef]
- Maharana, K.; Mondal, S.; Nemade, B. A review: Data pre-processing and data augmentation techniques. Glob. Transitions Proc. 2022, 3, 91–99. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Hossin, M.; Sulaiman, M.N. A Review on Evaluation Metrics for Data Classification Evaluations. Int. J. Data Min. Knowl. Manag. Process 2015, 5, 1–11. [Google Scholar] [CrossRef]
- McElreath, R. Statistical Rethinking: A Bayesian Course with Examples in R and Stan; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the International Conference on Machine Learning, PMLR, New York, NY, USA, 20–22 June 2016; pp. 1050–1059. [Google Scholar]
- Kendall, A.; Gal, Y. What uncertainties do we need in bayesian deep learning for computer vision? Adv. Neural Inf. Process. Syst. 2017, 30, 5580–5590. [Google Scholar]
- Nerlich, I.; Holzfeind, J.; Wilczek, K. SwissTAMP—Big data in proactive track asset management. Eur. Railw. Rev. 2016, 2, 41–44. [Google Scholar]
- Northcutt, C.; Jiang, L.; Chuang, I. Confident Learning: Estimating Uncertainty in Dataset Labels. J. Artif. Int. Res. 2021, 70, 1373–1411. [Google Scholar] [CrossRef]
- Arcieri, G.; Hoelzl, C.; Schwery, O.; Straub, D.; Papakonstantinou, K.G.; Chatzi, E. Bridging POMDPs and Bayesian decision making for robust maintenance planning under model uncertainty: An application to railway systems. arXiv 2022, arXiv:2212.07933. [Google Scholar]



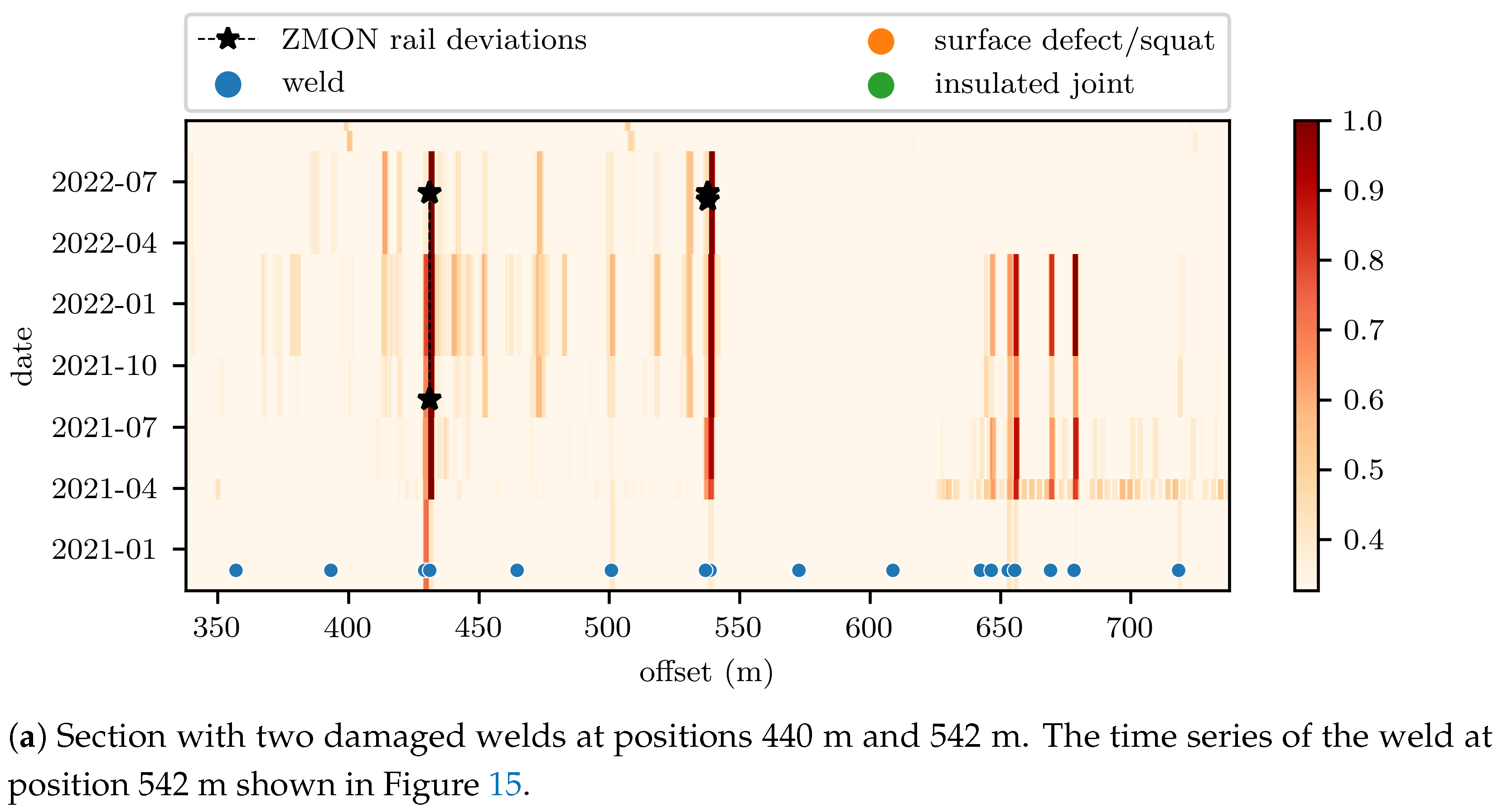
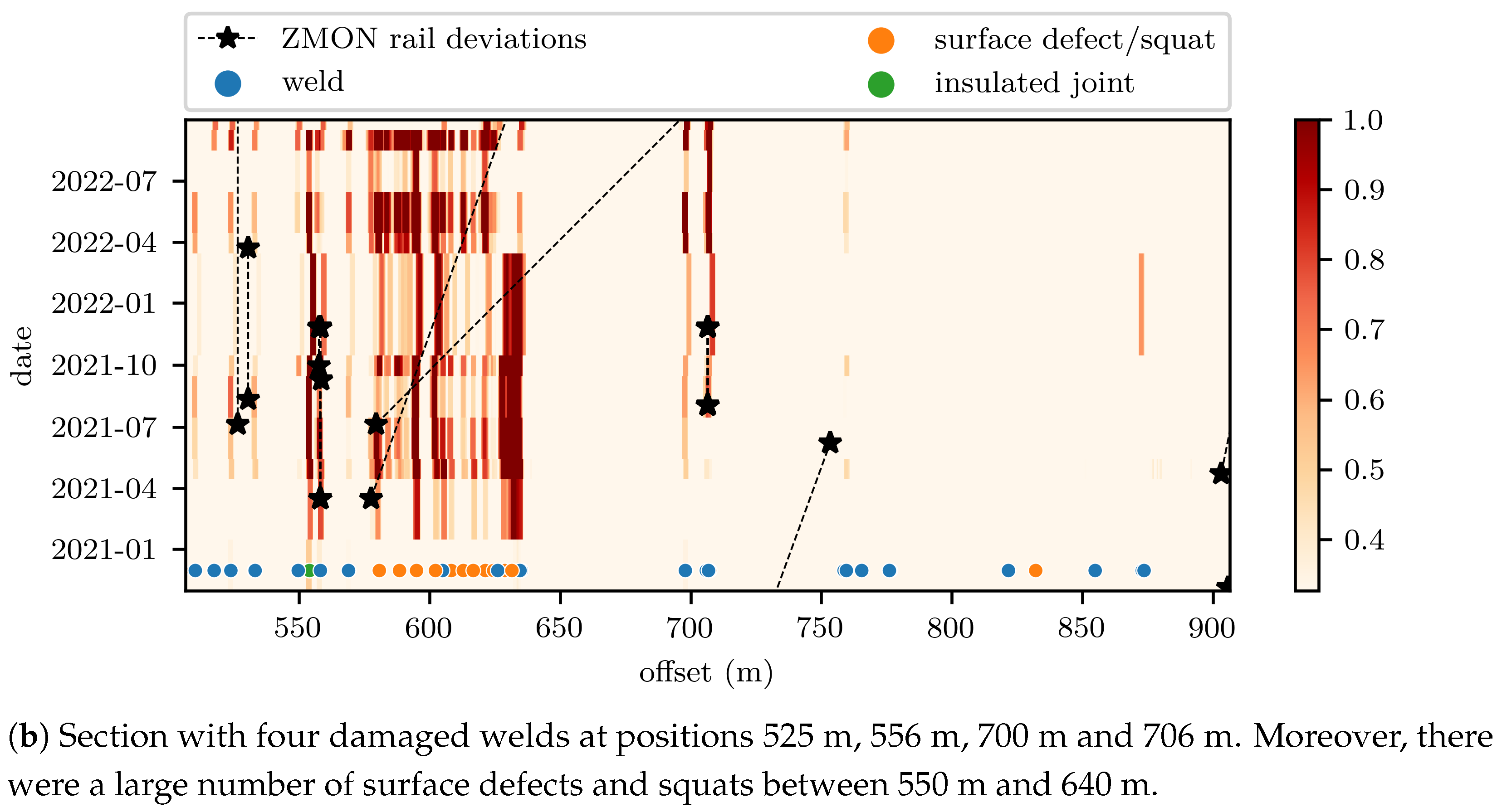
| Proposed Approach | Research Findings | Limitations |
|---|---|---|
| Time-frequency analysis via Continuous Wavelet Transform (CWT) | Demonstrated identification of rail faults using the Scale-Averaged Wavelet Power of the CWT of ABA [33,34,35,36,37] or bogie measurements [38]. | While the methodology can be extended to other components, these studies are limited to the assessment of squats. |
| Principal Component Analysis (PCA) on FFT coefficients. | Threshold for evaluating the condition of welds for the prioritization of inspection schedules [44]. | Definition of linear weighting on the vehicle speed. The authors note that further studies are necessary to substantiate this indicator. |
| Wavelet Packet Decomposition (WPD) and Adaptive Synchro-squeezed Short Time Fourier Transform. | The authors identify the 300∼800 Hz frequency range to be indicative for poorly welded joints [45]. | Empirical definition of a fixed damage threshold. |
| Hilbert-Huang Transform (HHT). | Rail joints were detected as impact points and outliers in the ABA signal with the HHT [46] | The methodology does not differentiate between components and only is demonstrated on a couple of samples. |
| Deep Learning architectures. | Classification of rail faults using Random Forests, Support Vector Machine, Artificial Neural Networks or Convolutional Neural Networks [40,50,51,52,53]. | Requires large training datasets, especially when using acceleration time series instead of features as an input. Complex models require special care since they have a higher risk of overfitting. |
| Model & simulation based approaches. | Diagnostic thresholds were defined for faulty welds on the basis of ABA or force response simulations [30,31,36,56]. | No generalization to generic geometries and track types; simulation may not fully reflect complex site conditions and noisy data. |
| Current Work: Fusion of ABA-derived indicator with expert feedback. | Statistical methods applied on essential indicators for the identification of weld condition [55]. | Uncertainties in the expert assessment cause noise in the input labels for classification algorithms. |
| Letter | Explanation | Possible Entries |
|---|---|---|
| D | direction | Y for lateral, Z for vertical |
| A | axle number | 1 to 4, starting from the front (leading) axle |
| S | vehicle side | 1 for right, 2 for left (w.r.t vehicle’s top view) |
| Feature | Quantity | Signal Length |
|---|---|---|
| RAW ABA | Raw accelerations | 2 m, 3 m |
| VS ABA | Vector sum of Y and Z axes | 2 m |
| BP ABA | Band Pass filtered accelerations | 3 m |
| STFT | Short Time Fourier Transform | 2 m |
| DWT | Discrete Wavelet Transform | 0.625 s |
| & | Longitudinal level and lateral displacement | 5 m, 20 m |
| Index | Feature |
|---|---|
| vehicle velocity |
| Condition | No Defect | Defect | No Defect | |
|---|---|---|---|---|
| Label Source | EL-EVA 1 | EL-EVA 1 | ZMON 2 | Unlabeled Condition 3 |
| Low Outliers | 0 | 0 | 368 | 19668 |
| Weak Outlier | 656 | 42 | 141 | 2242 |
| Strong Outlier | 710 | 83 | 54 | 285 |
| Letter | Explanation | Possible Entries |
|---|---|---|
| Summary statistic computed over all (Y/Z) sensor channels | mean , standard deviation , min, max… | |
| Summary statistic computed over time series where the subscript denotes the window size | mean , standard deviation , min, max… | |
| M | Applied method and parameters | STFT, Longitudinal Level , DWT… |
| C | Sensor channel | Z for vertical, Y for lateral |
| Classifier | Features | F1 | Roc-Auc | Accuracy | Recall | Precision |
|---|---|---|---|---|---|---|
| BC | 0.109 | 0.553 | 0.290 | 0.846 | 0.058 | |
| BC | 0.111 | 0.555 | 0.371 | 0.761 | 0.060 | |
| BC | 0.116 | 0.542 | 0.799 | 0.256 | 0.075 | |
| BC | 0.119 | 0.543 | 0.822 | 0.233 | 0.079 | |
| BC | 0.250 | 0.610 | 0.921 | 0.265 | 0.236 | |
| BC | 0.259 | 0.647 | 0.893 | 0.373 | 0.198 | |
| BC | 0.263 | 0.634 | 0.908 | 0.329 | 0.219 | |
| BC | 0.264 | 0.645 | 0.898 | 0.364 | 0.207 | |
| BC | 0.270 | 0.635 | 0.912 | 0.327 | 0.230 | |
| BC | 0.293 | 0.668 | 0.902 | 0.408 | 0.229 | |
| BC | 0.307 | 0.641 | 0.927 | 0.322 | 0.293 | |
| BC | 0.307 | 0.654 | 0.919 | 0.360 | 0.268 | |
| BC | 0.308 | 0.638 | 0.930 | 0.313 | 0.303 | |
| BC | 0.315 | 0.650 | 0.925 | 0.344 | 0.291 | |
| BC | 0.323 | 0.655 | 0.926 | 0.355 | 0.295 | |
| BLR | 15 indicators with highest -score 1 and cross-feature correlation under 0.8 | 0.422 | 0.696 | 0.937 | 0.426 | 0.417 |
| BLR | 15 indicators with highest -score 1 and cross-feature correlation under 0.8 & speed | 0.431 | 0.701 | 0.938 | 0.432 | 0.427 |
| RF | 15 indicators with highest -score 1 and cross-feature correlation under 0.8 | 0.479 | 0.711 | 0.948 | 0.446 | 0.517 |
| RF | 15 indicators with highest -score 1 and cross-feature correlation under 0.8 & speed | 0.486 | 0.708 | 0.950 | 0.436 | 0.550 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoelzl, C.; Arcieri, G.; Ancu, L.; Banaszak, S.; Kollros, A.; Dertimanis, V.; Chatzi, E. Fusing Expert Knowledge with Monitoring Data for Condition Assessment of Railway Welds. Sensors 2023, 23, 2672. https://doi.org/10.3390/s23052672
Hoelzl C, Arcieri G, Ancu L, Banaszak S, Kollros A, Dertimanis V, Chatzi E. Fusing Expert Knowledge with Monitoring Data for Condition Assessment of Railway Welds. Sensors. 2023; 23(5):2672. https://doi.org/10.3390/s23052672
Chicago/Turabian StyleHoelzl, Cyprien, Giacomo Arcieri, Lucian Ancu, Stanislaw Banaszak, Aurelia Kollros, Vasilis Dertimanis, and Eleni Chatzi. 2023. "Fusing Expert Knowledge with Monitoring Data for Condition Assessment of Railway Welds" Sensors 23, no. 5: 2672. https://doi.org/10.3390/s23052672
APA StyleHoelzl, C., Arcieri, G., Ancu, L., Banaszak, S., Kollros, A., Dertimanis, V., & Chatzi, E. (2023). Fusing Expert Knowledge with Monitoring Data for Condition Assessment of Railway Welds. Sensors, 23(5), 2672. https://doi.org/10.3390/s23052672








