Dual-Band Frequency Selective Surface with Different Polarization Selectivity for Wireless Communication Application
Abstract
:1. Introduction
- Current designs feature a frequency ratio that is notably high, making the design of the feeding networks and signal processing modules in frequency division duplex (FDD) systems more difficult and costly, particularly in satellite communication and base station applications. In addition, despite the widespread use of circuit analysis in the literature, the relationship between circuit components, physical structure, achievable performance, and the general design process applicable to different frequency bands has not been thoroughly explored;
- There are few studies on the in-band flatness and out-of-band rejection in the current research on polarization and frequency selective surfaces of duplex systems. It is rarely addressed how to introduce one or more transmission zeros (TZs) at the cross-polarized frequency to improve polarization isolation, particularly when the two orthogonal polarizations operate at close frequencies.
- By grounding the U-shaped resonant structure, a small frequency ratio between the two orthogonal polarizations can be achieved. By adjusting the substrate thickness, the radius of the grounded via, and the dimensions of the U-shaped resonator, the frequency ratio achievable at X-band ranges between 1.05 and 1.4;
- A general framework is provided. In addition, full-wave simulations and equivalent circuits are analyzed and were found to agree well, which would be of great assistance in comprehending the mechanism of our structure and optimizing its parameters during design. Followed by step-by-step explanations and design examples for the S-, X-, and K-bands, the most significant contribution is a summary of the general design flow diagram. The proposed designs have significant application potential in modern wireless communication and multiple-input, multiple-output (MIMO) systems due to their high selectivity, small frequency ratio, low profile, and stable performance under oblique incidence.
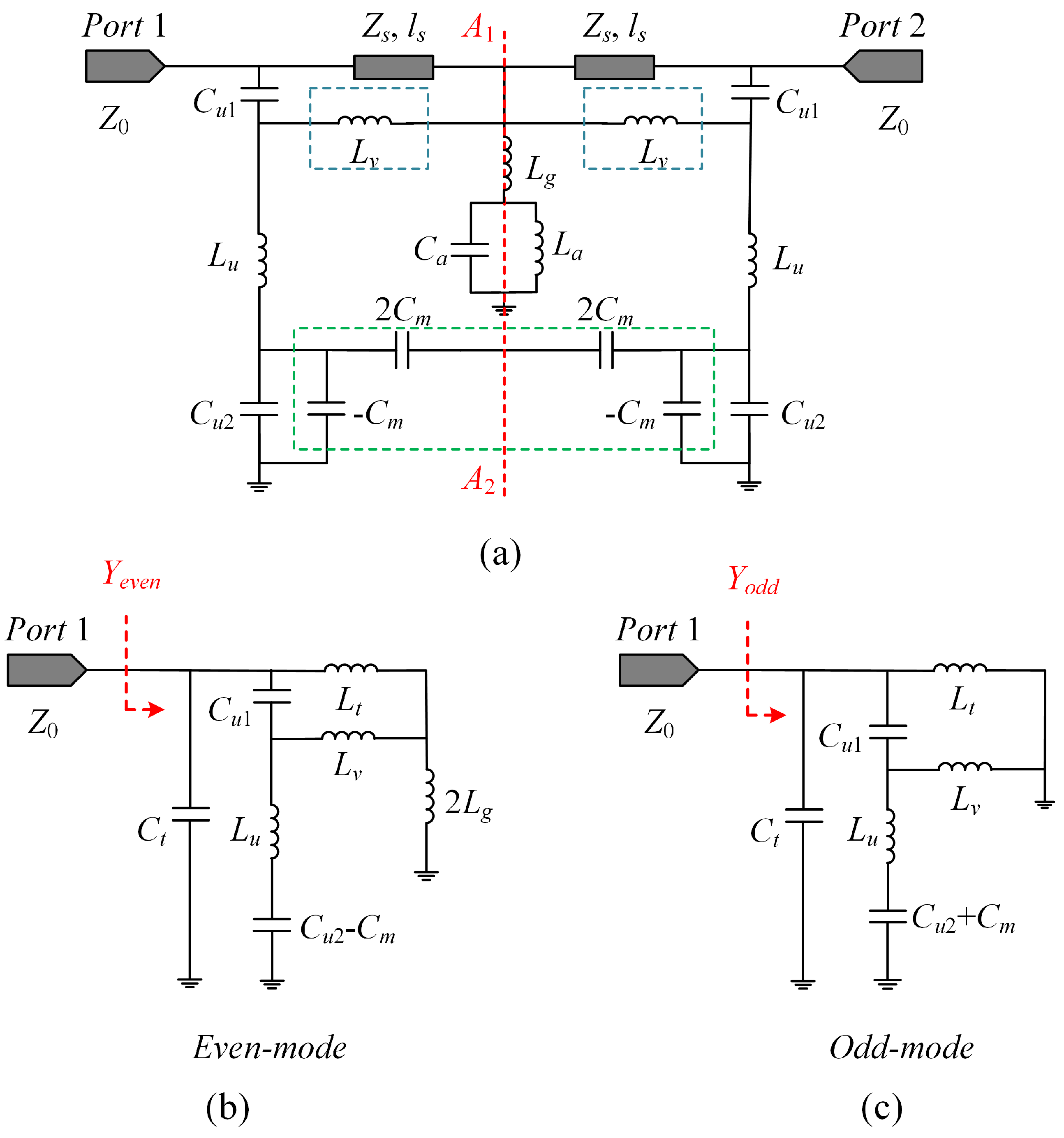
2. Operation Principles and Analysis Methods
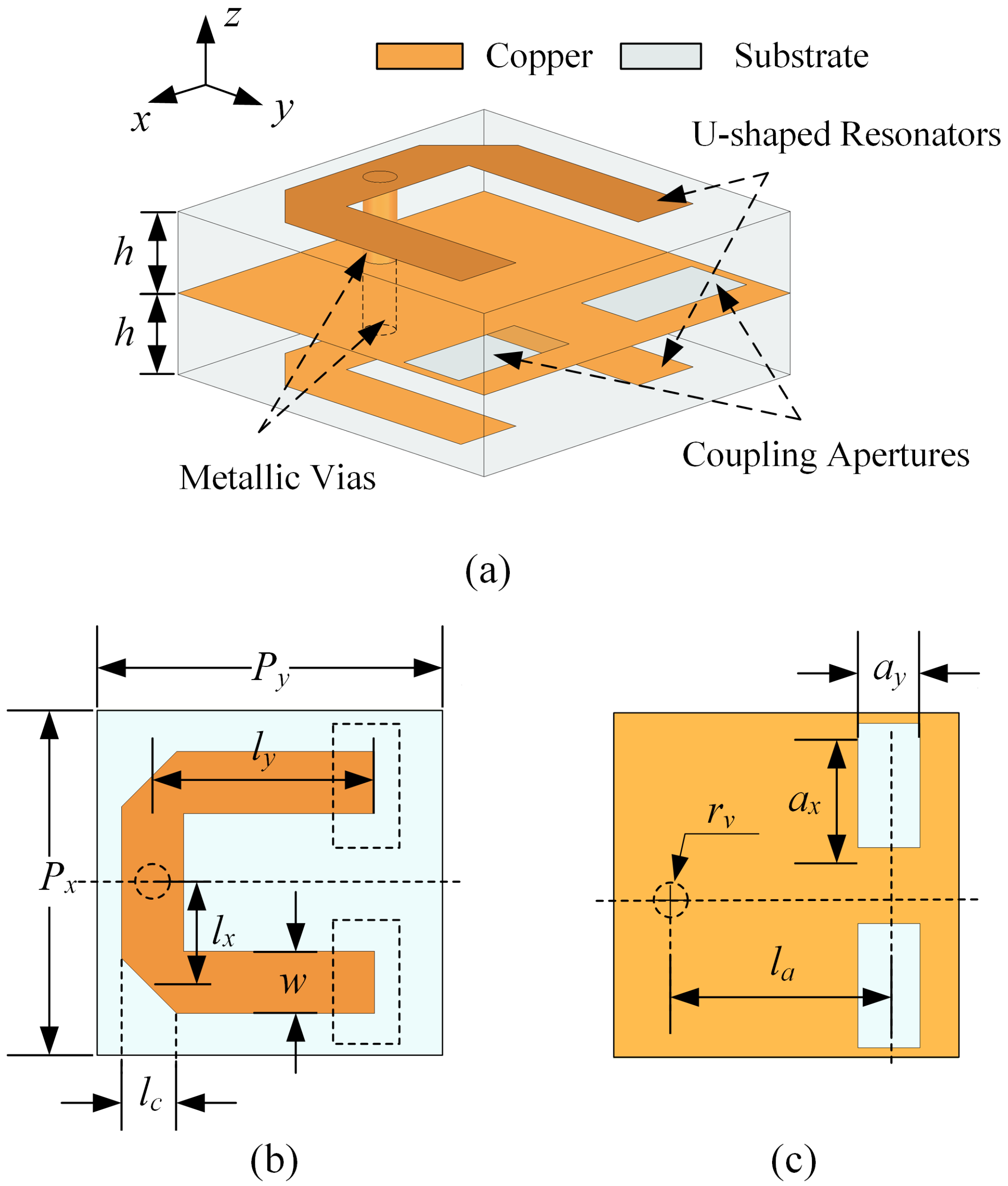
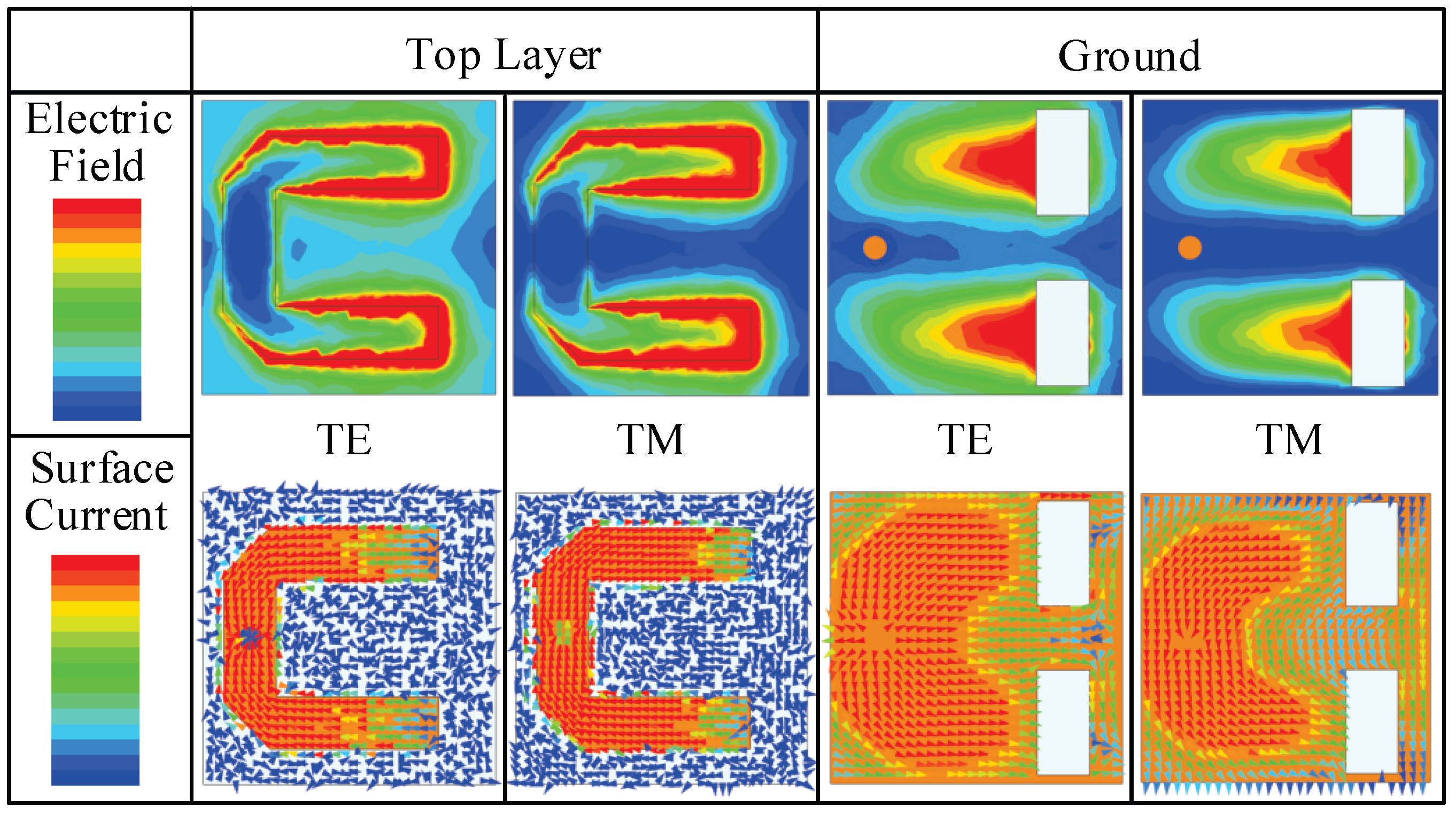
2.1. Dual Modes U-Shaped Resonator with One Grounded Metallic Via
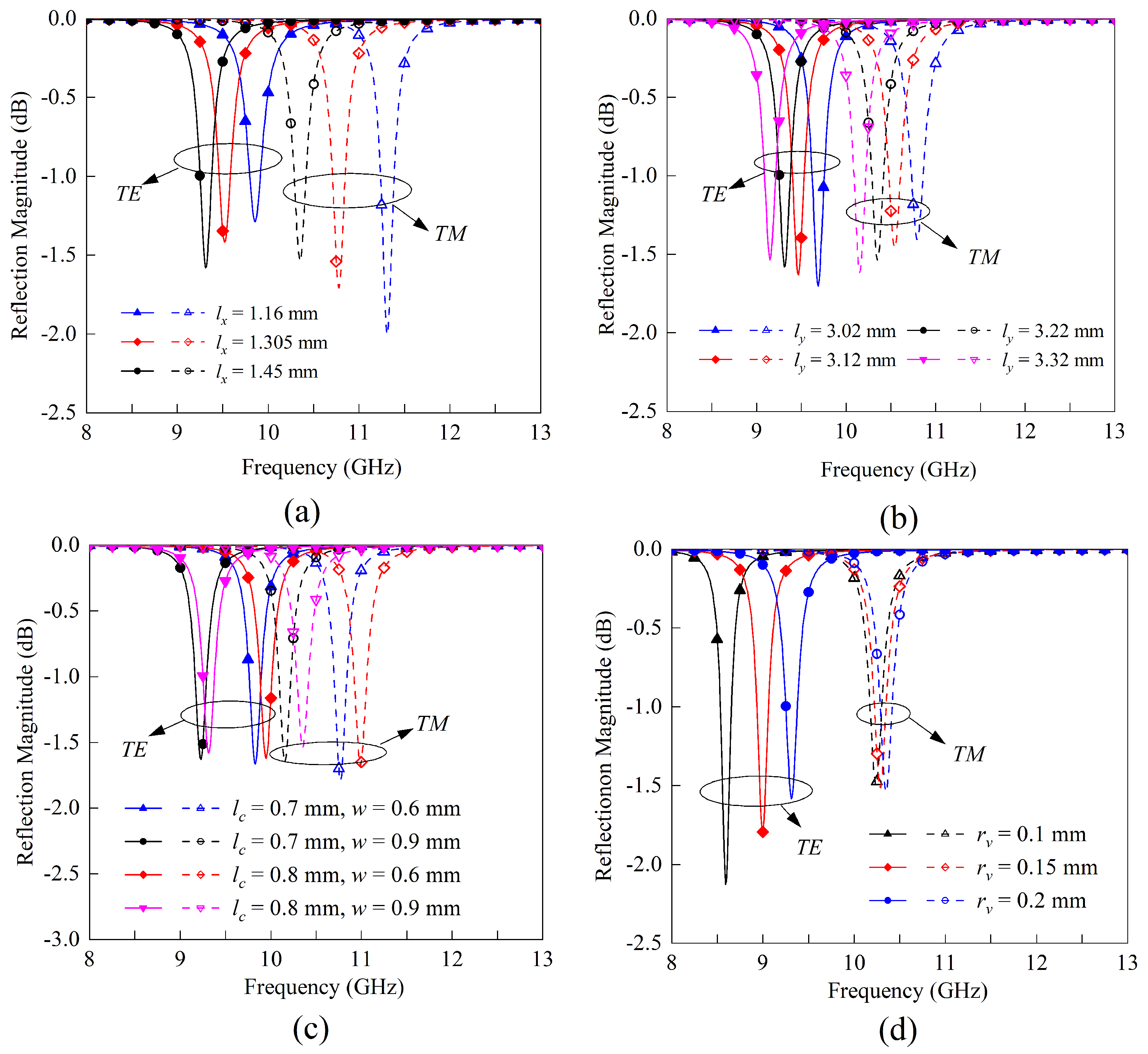
2.2. Parametric Study of the Grounded U-Shaped Resonator
- and : Lengths of the stub and arm have a strong effect on the resonant frequencies. Typically, when the widths of the stub and the arm are comparable, resonance occurs when the sum of the electrical lengths of the stub and the arm is approximately half a wavelength. The resonant frequencies are then estimated to be:where, to simplify the calculation, the equivalent permittivity expression without regard to the strip width and substrate height, , is used here to estimate the operating wavelength of the microstrip line. Equation (3) shows that when or increases, the resonant frequency will decrease. For further validation, the full-wave simulation results of and parameter sweeping are given in Figure 5a,b, respectively.
- and w: The width of the stub and arms primarily affects the characteristic impedance and propagation constant of their respective transmission lines, which have substantial effects on the resonance frequencies and input coupling bandwidth, i.e. the loaded quality factor. In addition, the ratio of to w influences the frequency ratio between TE and TM resonances. In general, as shown in Figure 5c, the loaded quality factor increases as the width increases. The closer the ratio of to w approaches 1, the closer the resonant frequencies of the two modes become.
- : This parameter primarily affects the equivalent inductance introduced by the grounded metallic via, which in turn influences the tuning effect on the TE resonance frequency. As shown in Figure 5d, the impact of this parameter on TM resonance is minimal due to the presence of an equivalent magnetic wall. Consequently, the ratio of resonant frequency can also be tuned by adjusting the radium of the grounded via.
2.3. Frequency Selection and Cross-Polarization Suppression Introduced by Coupling Apertures
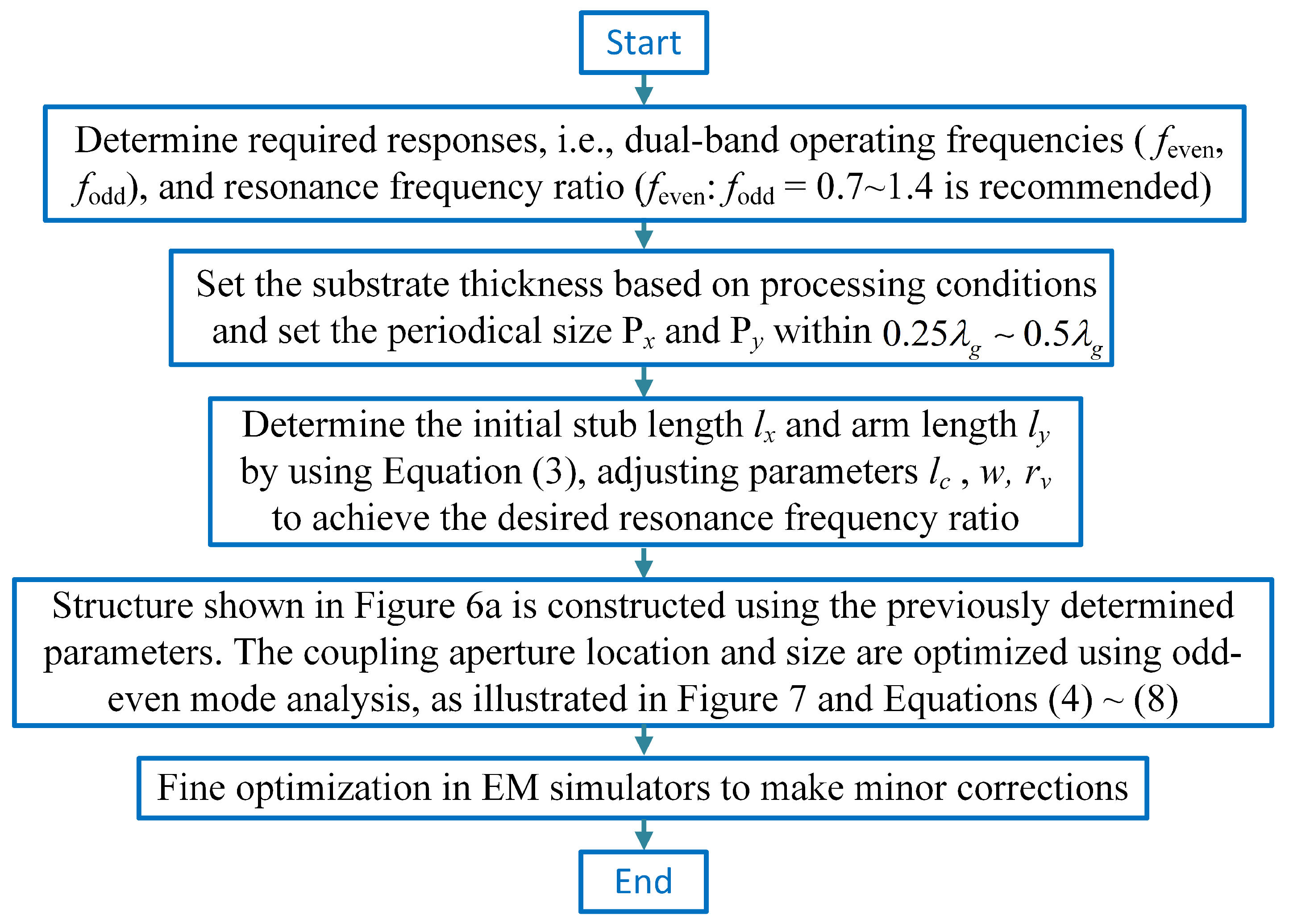
2.4. Sensitivity Analysis and General Design Flowchart
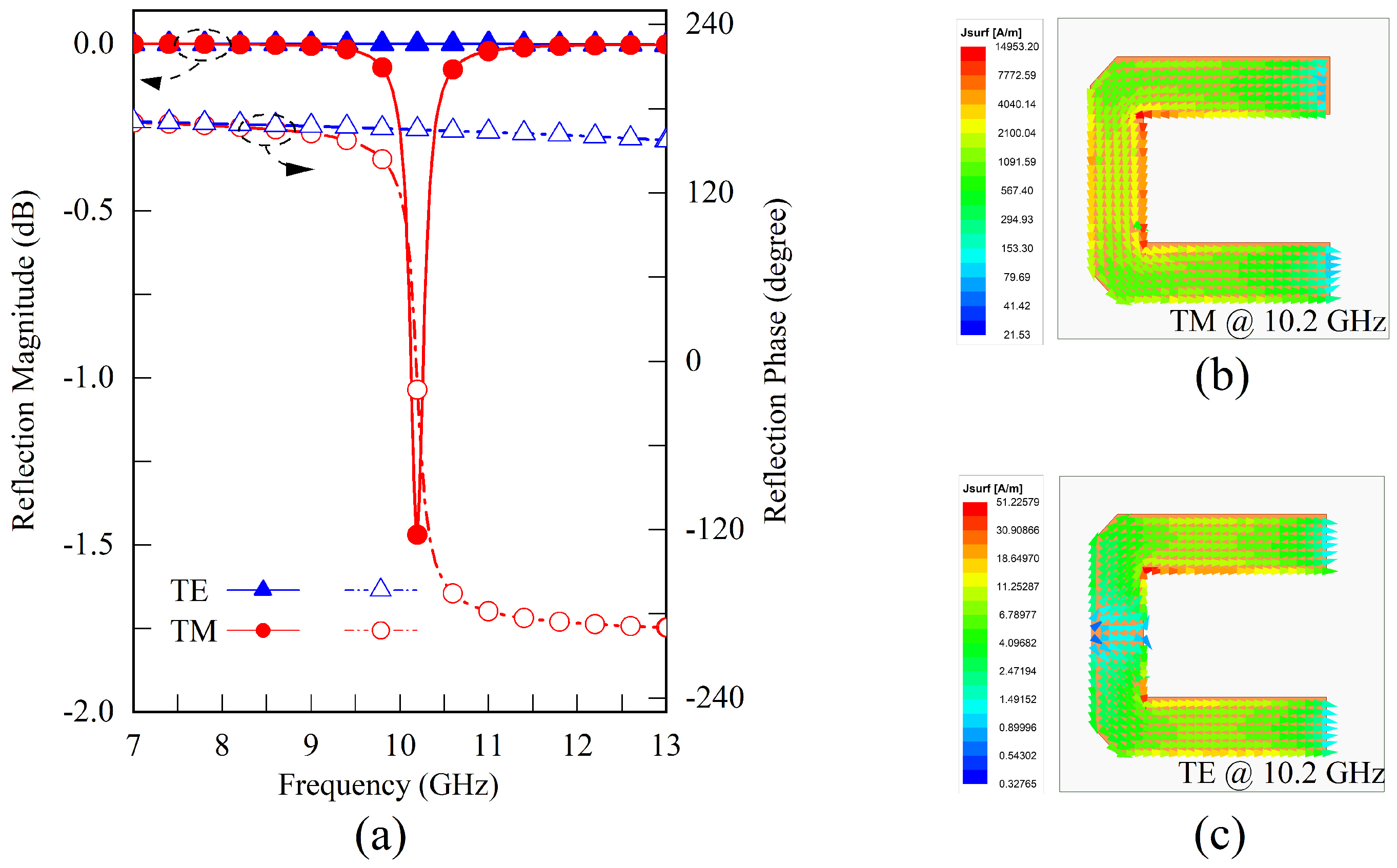
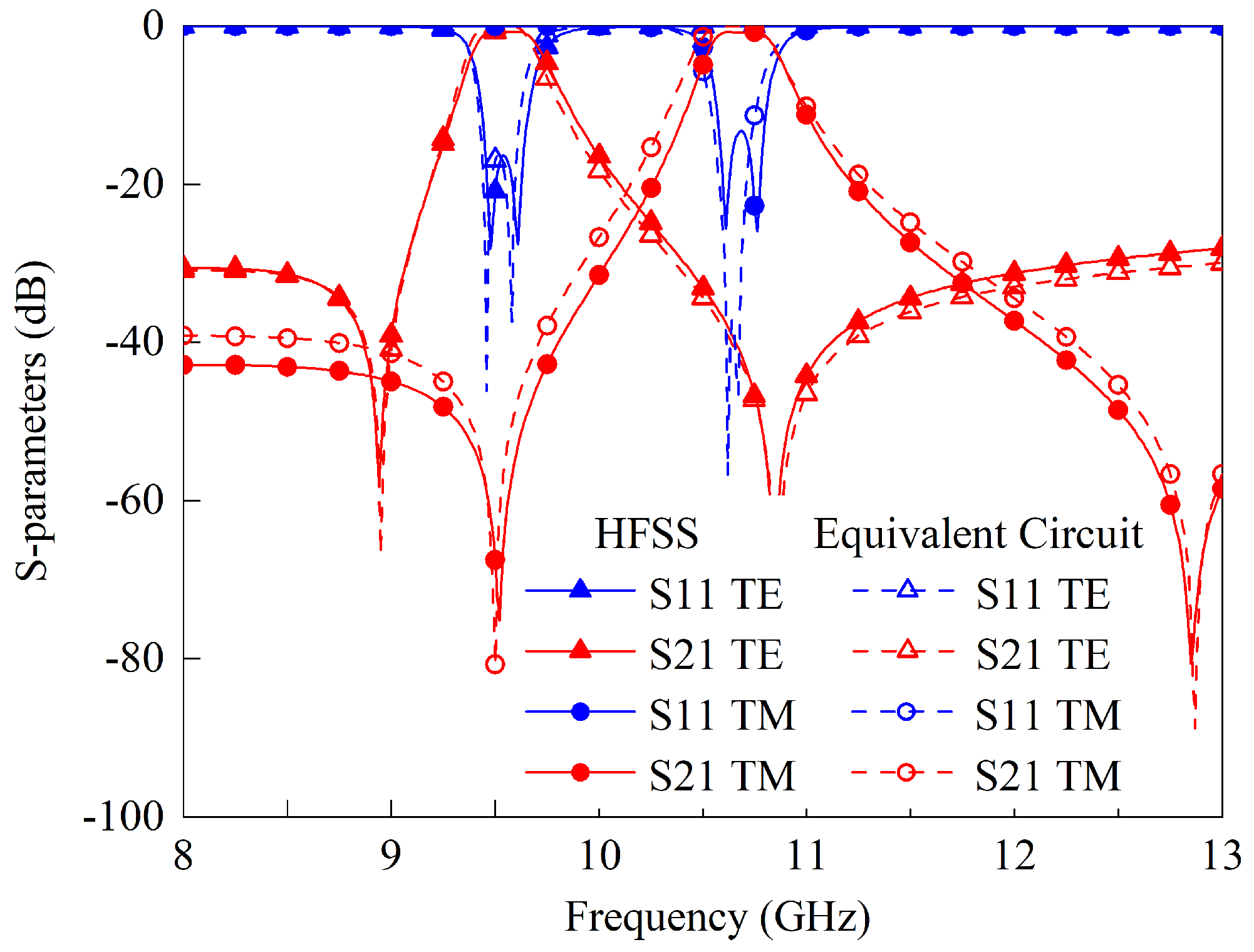
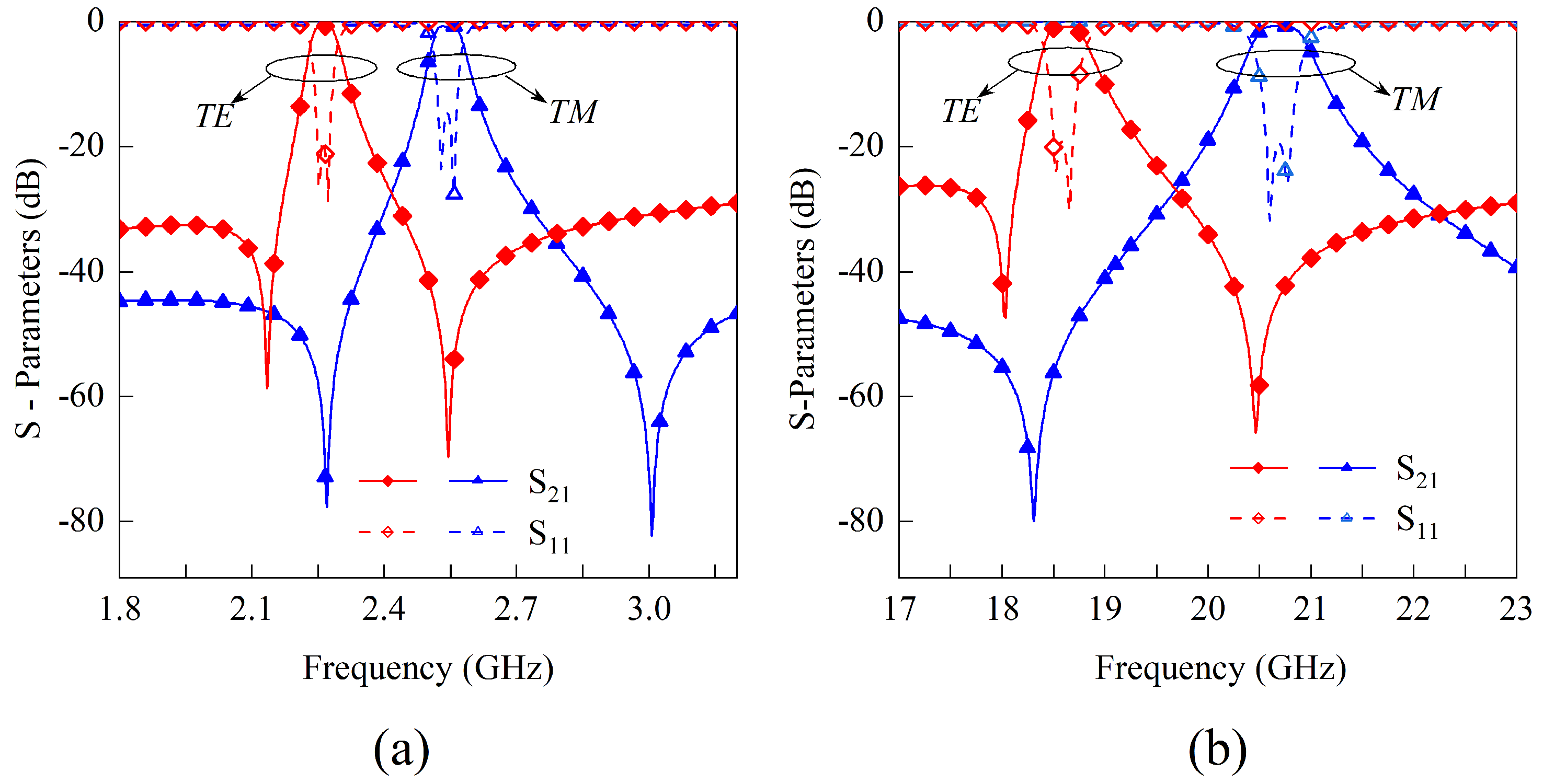
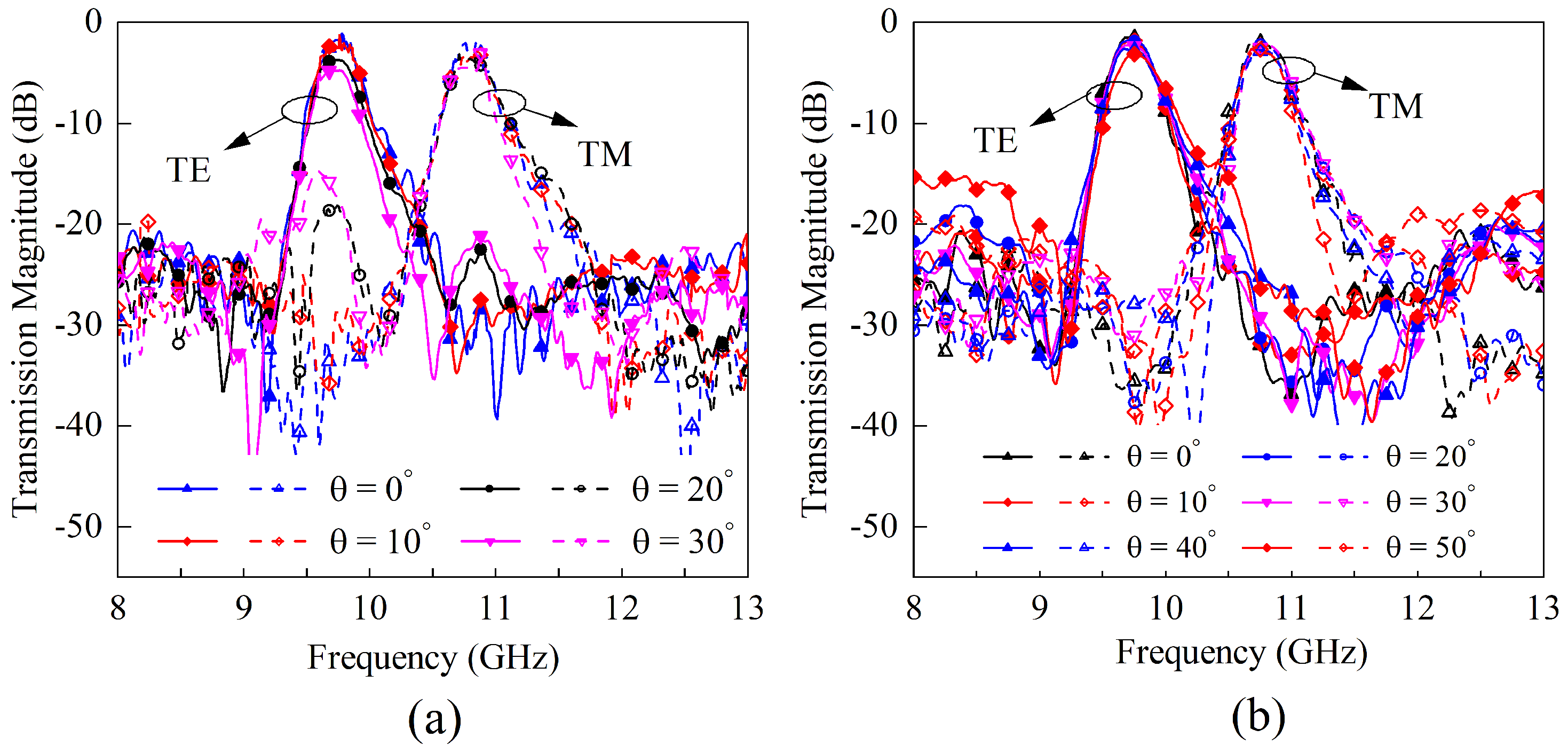
3. Fabrication and Measurement Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, Y.; Li, Y. Compact Co-Linearly Polarized Microstrip Antenna With Fence-Strip Resonator Loading for In-Band Full-Duplex Systems. IEEE Trans. Antennas Propag. 2021, 69, 7125–7133. [Google Scholar] [CrossRef]
- Adhikary, A.; Nam, J.; Ahn, J.Y.; Caire, G. Joint Spatial Division and Multiplexing—The Large-Scale Array Regime. IEEE Trans. Inf. Theory 2013, 59, 6441–6463. [Google Scholar] [CrossRef]
- Ranjbar Nikkhah, M.; Wu, J.; Luyen, H.; Behdad, N. A Concurrently Dual-Polarized, Simultaneous Transmit and Receive (STAR) Antenna. IEEE Trans. Antennas Propag. 2020, 68, 5935–5944. [Google Scholar] [CrossRef]
- Ji, H.; Kim, Y.; Muhammad, K.; Tarver, C.; Tonnemacher, M.; Kim, T.; Oh, J.; Yu, B.; Xu, G.; Lee, J. Extending 5G TDD Coverage With XDD: Cross Division Duplex. IEEE Access 2021, 9, 51380–51392. [Google Scholar] [CrossRef]
- Ericsson, A.; Sjöberg, D.; Gerini, G.; Cappellin, C.; Jensen, F.; Balling, P.; Fonseca, N.J.G.; de Maagt, P. A Contoured-Beam Reflector Satellite Antenna Using Two Doubly Curved Circular Polarization Selective Surfaces. IEEE Trans. Antennas Propag. 2021, 69, 658–671. [Google Scholar] [CrossRef]
- Zhu, Z.b.; Hu, W.D.; Qin, T.; Li, S.; Li, X.j.; Zeng, J.j.; Lin, X.q.; Ligthart, L. A high-precision terahertz retrodirective antenna array with navigation signal at a different frequency. Front. Inf. Technol. Electron. Eng. 2020, 21, 377–383. [Google Scholar] [CrossRef]
- Li, J.F.; Wu, D.L.; Zhang, G.; Wu, Y.J.; Mao, C.X. Compact Dual-Polarized Antenna for Dual-Band Full-Duplex Base Station Applications. IEEE Access 2019, 7, 72761–72769. [Google Scholar] [CrossRef]
- Xie, H.; Gao, F.; Zhang, S.; Jin, S. A Unified Transmission Strategy for TDD/FDD Massive MIMO Systems With Spatial Basis Expansion Model. IEEE Trans. Veh. Technol. 2017, 66, 3170–3184. [Google Scholar] [CrossRef]
- Albattah, W.; Habib, S.; Alsharekh, M.F.; Islam, M.; Albahli, S.; Dewi, D.A. An Overview of the Current Challenges, Trends, and Protocols in the Field of Vehicular Communication. Electronics 2022, 11, 3581. [Google Scholar] [CrossRef]
- Kuo, N.C.; Niknejad, A.M. Single-Antenna FDD Reader Design and Communication to a Commercial UHF RFID Tag. IEEE Microw. Wirel. Components Lett. 2018, 28, 630–632. [Google Scholar] [CrossRef]
- Liu, X.; Fang, S.; Liu, H. A Compact Dual-Band Circularly Polarized RFID Reader/WLAN Antenna. In Proceedings of the 2021 9th International Conference on Communications and Broadband Networking; Association for Computing Machinery: New York, NY, USA, 2021; pp. 269–273. [Google Scholar] [CrossRef]
- Chen, Z.; Shen, Z. Dual-Polarized Angle-Selective Surface Based on Three-Layer Frequency Selective Surfaces. In Proceedings of the 2022 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting (AP-S/URSI), Denver, CO, USA, 10–15 July 2022; pp. 910–911. [Google Scholar] [CrossRef]
- Zhu, X.C.; Zhang, P.P.; Zhang, Y.X.; Ge, J.X.; Gao, Z.H. A High-Gain Filtering Antenna Based on Folded Reflectarray Antenna and Polarization-Sensitive Frequency Selective Surface. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1462–1465. [Google Scholar] [CrossRef]
- Costa, F.; Monorchio, A. A Frequency Selective Radome With Wideband Absorbing Properties. IEEE Trans. Antennas Propag. 2012, 60, 2740–2747. [Google Scholar] [CrossRef]
- Yan, X.; Kong, X.; Wang, Q.; Xing, L.; Xue, F.; Xu, Y.; Jiang, S.; Liu, X. Water-Based Reconfigurable Frequency Selective Rasorber With Thermally Tunable Absorption Band. IEEE Trans. Antennas Propag. 2020, 68, 6162–6171. [Google Scholar] [CrossRef]
- Wang, S.Y.; Bi, J.D.; Liu, W.; Geyi, W.; Gao, S. Polarization-Insensitive Cross-Polarization Converter. IEEE Trans. Antennas Propag. 2021, 69, 4670–4680. [Google Scholar] [CrossRef]
- Qin, T.; Lin, X.Q.; Yao, Y.; Liu, Y.; Liu, H.; Hao, P.; Mei, P. Efficient Synthesis of Angular Selective Surfaces Based on Accurate Equivalent Circuit Analysis. IEEE Trans. Microw. Theory Tech. 2023, 1–14. [Google Scholar] [CrossRef]
- Bouslama, M.; Traii, M.; Denidni, T.A.; Gharsallah, A. Beam-Switching Antenna With a New Reconfigurable Frequency Selective Surface. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1159–1162. [Google Scholar] [CrossRef]
- Edalati, A.; Denidni, T.A. Frequency Selective Surfaces for Beam-Switching Applications. IEEE Trans. Antennas Propag. 2013, 61, 195–200. [Google Scholar] [CrossRef]
- Al-Joumayly, M.; Behdad, N. A New Technique for Design of Low-Profile, Second-Order, Bandpass Frequency Selective Surfaces. IEEE Trans. Antennas Propag. 2009, 57, 452–459. [Google Scholar] [CrossRef]
- Yan, M.; Wang, J.; Ma, H.; Feng, M.; Pang, Y.; Qu, S.; Zhang, J.; Zheng, L. A Tri-Band, Highly Selective, Bandpass FSS Using Cascaded Multilayer Loop Arrays. IEEE Trans. Antennas Propag. 2016, 64, 2046–2049. [Google Scholar] [CrossRef]
- Yan, M.; Qu, S.; Wang, J.; Zhang, A.; Zheng, L.; Pang, Y.; Zhou, H. A Miniaturized Dual-Band FSS With Second-Order Response and Large Band Separation. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 1602–1605. [Google Scholar] [CrossRef]
- Döken, B.; Kartal, M. Easily Optimizable Dual-Band Frequency-Selective Surface Design. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2979–2982. [Google Scholar] [CrossRef]
- Gianvittorio, J.; Romeu, J.; Blanch, S.; Rahmat-Samii, Y. Self-similar prefractal frequency selective surfaces for multiband and dual-polarized applications. IEEE Trans. Antennas Propag. 2003, 51, 3088–3096. [Google Scholar] [CrossRef]
- Romeu, J.; Rahmat-Samii, Y. Fractal FSS: A novel dual-band frequency selective surface. IEEE Trans. Antennas Propag. 2000, 48, 1097–1105. [Google Scholar] [CrossRef]
- Rahmat-Samii, Y.; Tulintseff, A. Diffraction analysis of frequency selective reflector antennas. IEEE Trans. Antennas Propag. 1993, 41, 476–487. [Google Scholar] [CrossRef]
- Ünaldı, S.; Çimen, S.; Çakır, G.; Ayten, U.E. A Novel Dual-Band Ultrathin FSS with Closely Settled Frequency Response. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 1381–1384. [Google Scholar] [CrossRef]
- Li, B.; Shen, Z. Dual-Band Bandpass Frequency-Selective Structures with Arbitrary Band Ratios. IEEE Trans. Antennas Propag. 2014, 62, 5504–5512. [Google Scholar] [CrossRef]
- Zhang, B.; Jin, C.; Ye, X.; Mittra, R. Dual-Band Dual-Polarized Quasi-Elliptic Frequency Selective Surfaces. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 298–302. [Google Scholar] [CrossRef]
- Tan, M.T.; Wang, B.Z. A Compact Dual-Band Dual-Polarized Loop-Slot Planar Antenna. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 1742–1745. [Google Scholar] [CrossRef]
- Silaghi, A.M.; De Sabata, A.; Matekovits, L. Single-Layered Frequency Selective Surface for Polarization Processing by Transmission Through Elementary Simple Structure Unit Cell Array. IEEE Access 2021, 9, 30615–30625. [Google Scholar] [CrossRef]
- Montori, S.; Vincenti Gatti, R.; Sorrentino, R.; Dieter, S.; Menzel, W. Reconfigurable and dual-polarization folded reflectarray antenna. In Proceedings of the 2012 42nd European Microwave Conference, Amsterdam, The Netherlands, 1 October–2 November 2012; pp. 735–738. [Google Scholar] [CrossRef]
- Wang, H.; Zheng, L.; Yan, M.; Wang, J.; Qu, S.; Luo, R. Design and Analysis of Miniaturized Low Profile and Second-Order Multi-Band Polarization Selective Surface for Multipath Communicatio Application. IEEE Access 2019, 7, 13455–13467. [Google Scholar] [CrossRef]
- Li, W.; Xia, S.; Shi, H.; Li, J.; Zhang, A.; Li, Z.; Xu, Z. Design of a Dual-Band Dual-Polarization Transparent Frequency Selective Surface. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 3172–3175. [Google Scholar] [CrossRef]
- Bakır, M.; Delihacioğlu, K.; Karaaslan, M.; Dinçer, F.; Sabah, C. U-shaped frequency selective surfaces for single- and dual-band applications together with absorber and sensor configurations. Iet Microwaves Antennas Propag. 2016, 10, 293–300. [Google Scholar] [CrossRef]
- Wong, S.W.; Sun, G.H.; Zhu, L.; Chu, Q.X. Broadband Dual-Polarization and Stable-Beamwidth Slot Antenna Fed by U-Shape Microstrip Line. IEEE Trans. Antennas Propag. 2016, 64, 4477–4481. [Google Scholar] [CrossRef]
- Liu, W.; Yan, Z.; Wang, J.; Yan, X.; Fan, J. An Ultrawideband Electric Probe Based on U-Shaped Structure for Near-Field Measurement From 9 kHz to 40 GHz. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1283–1287. [Google Scholar] [CrossRef]
- Erman, F.; Hanafi, E.; Lim, E.H.; Mahyiddin, W.A.W.M.; Harun, S.W.; Umair, H.; Soboh, R. U-Shaped Inductively Coupled Feed UHF RFID Tag Antenna With DMS for Metal Objects. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 907–911. [Google Scholar] [CrossRef]
- Djouimaa, A.; Titaouine, M.; Saidi, R.; Adoui, I.; de Sousa, T.R.; Neto, A.G.; Baudrand, H. Characterization of dual band and double polarized notched metallic ring FSS and their equivalent parallel metallic strip structures. J. Electromagn. Waves Appl. 2019, 33, 41–56. [Google Scholar] [CrossRef]
- Mekaoussi, A.; Titaouine, M. Analysis of the U-shaped geometry of a frequency selective surface using the WCIP. In Proceedings of the 2022 7th International Conference on Image and Signal Processing and their Applications (ISPA), Mostaganem, Algeria, 8–9 May 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Pozar, D. Microwave Engineering, 4th ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Hong, J. Basic Concepts and Theories of Filters. Microstrip Filters for RF/Microwave Applications, 2nd ed.; Wiley: Hoboken, NJ, USA, 2011; pp. 28–74. [Google Scholar] [CrossRef]
- Goldfarb, M.; Pucel, R. Modeling via hole grounds in microstrip. IEEE Microw. Guid. Wave Lett. 1991, 1, 135–137. [Google Scholar] [CrossRef]
- Swanson, D. Grounding microstrip lines with via holes. IEEE Trans. Microw. Theory Tech. 1992, 40, 1719–1721. [Google Scholar] [CrossRef]
- Sorrentino, R.; Alessandri, F.; Mongiardo, M.; Avitabile, G.; Roselli, L. Full-wave modeling of via hole grounds in microstrip by three-dimensional mode matching technique. IEEE Trans. Microw. Theory Tech. 1992, 40, 2228–2234. [Google Scholar] [CrossRef]
- Xie, J.M.; Li, B.; Lyu, Y.P.; Zhu, L. Dual-Band Frequency Selective Surface on Aperture-Coupled Patch Resonators With Different Polarization Rotation. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 2632–2636. [Google Scholar] [CrossRef]
- Jiang, B.; Hu, H.; Tian, J.; Lei, S.; Chen, M.; Chen, B. A Polarization-Insensitive Dual-Band FSS With High Selectivity and Independently Switchable Characteristics. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 14–18. [Google Scholar] [CrossRef]
- Yu, Q.; Liu, S.; Kong, X.; Wen, Y. A Dual-Band, Highly Selective Bandpass Frequency Selective Surface Using Coupling Resonance. In Proceedings of the 2018 International Applied Computational Electromagnetics Society Symposium—China (ACES), Beijing, China, 29 July–1 August 2018; pp. 1–2. [Google Scholar] [CrossRef]
- Jia, Y.; Wu, A.; Liu, Y.; Zhang, W.; Zhou, Z. Dual-Polarization Frequency-Selective Rasorber With Independently Controlled Dual-Band Transmission Response. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 831–835. [Google Scholar] [CrossRef]





| Parameter | h | w | ||||||
|---|---|---|---|---|---|---|---|---|
| Value (mm) | 1.45 | 3.22 | 0.8 | 5.0 | 5.0 | 0.508 | 0.9 | 0.2 |
| Parameter | w | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Value (mm) | 1.45 | 3.22 | 0.8 | 5.0 | 5.0 | 0.9 | 0.2 | 3.19 | 1.8 | 0.9 |
| TE Polarization | C/L 1 | ||||||||
| Value (pF/nH) | 0.093 | 0.511 | 0.008 | 0.38 | 0.125 | 0.638 | 8.91 | 3.44 | |
| TM Polarization | C/L | ||||||||
| Value (pF/nH) | 0.061 | 0.170 | 0.008 | 0.05 | 0.028 | 0.638 | 8.04 | 3.44 |
| C.F. 2 | h | w | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Figure 11a | 2.25/2.55 | 2.5 | 6 | 4 | 3 | 25 | 25 | 4 | 1 | 6.5 | 8 | 4 |
| Figure 11b | 18.7/20.7 | 0.3 | 0.8 | 1.5 | 0.3 | 3 | 3 | 0.4 | 0.1 | 0.68 | 1.15 | 0.42 |
| Reference | Technology | C.F. (GHz) | FBW (%) | Worst IL 1 (dB) | Pol. Iso. 2 (dB) | Profile (mm, ) | Order | TZ |
|---|---|---|---|---|---|---|---|---|
| [29] | Cylindrical dielectric resonators | 7.4&11 (TE) 9.2 (TM) | 17.5&14.5 (TE) 21 (TM) | 0.9 | 30 | 4 / | 2 | 2 |
| [33] | Jerusalem cross | 7.3&26.9 (TE) 11.4 (TM) | 21.5&11.3 (TE) 26.1 (TM) | 1.2 | 13.7 | / | 2 | 0 |
| [34] | Patch with twisted slot | 8.2/13.58 | 16/4.5 | 2.4 | 14.2 | / | 2 | 0 |
| [46] | Patch resonator | 3.34/4.41 | 9/4.5 | 2 | / | 2 | 0/2 | |
| [47] | Multi-mode patch | 3.03/4.33 | 2.44/2.46 3 | 12 | / | 2 | 1 | |
| [48] | Cross-dipole, loop | 15/23 (Sim. 4) | 10.7/11.7 (Sim.) | - | >12 | / | 2 | 4 |
| [49] | Cross-dipole, loop | 16/28 (Sim.) | 35/45 (Sim.) | (Sim.) | >20 | / | 2 | 0 |
| This work | Grounded U-shaped resonator | 9.68/10.73 | 3.45/3.48 | 1.1 | 30 | 1.07 / | 2 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, T.; Huang, C.; Cai, Y.; Lin, X. Dual-Band Frequency Selective Surface with Different Polarization Selectivity for Wireless Communication Application. Sensors 2023, 23, 4264. https://doi.org/10.3390/s23094264
Qin T, Huang C, Cai Y, Lin X. Dual-Band Frequency Selective Surface with Different Polarization Selectivity for Wireless Communication Application. Sensors. 2023; 23(9):4264. https://doi.org/10.3390/s23094264
Chicago/Turabian StyleQin, Tao, Chenlu Huang, Yang Cai, and Xianqi Lin. 2023. "Dual-Band Frequency Selective Surface with Different Polarization Selectivity for Wireless Communication Application" Sensors 23, no. 9: 4264. https://doi.org/10.3390/s23094264
APA StyleQin, T., Huang, C., Cai, Y., & Lin, X. (2023). Dual-Band Frequency Selective Surface with Different Polarization Selectivity for Wireless Communication Application. Sensors, 23(9), 4264. https://doi.org/10.3390/s23094264






