Damage Localization on Composite Structures Based on the Delay-and-Sum Algorithm Using Simulation and Experimental Methods
Abstract
:1. Introduction
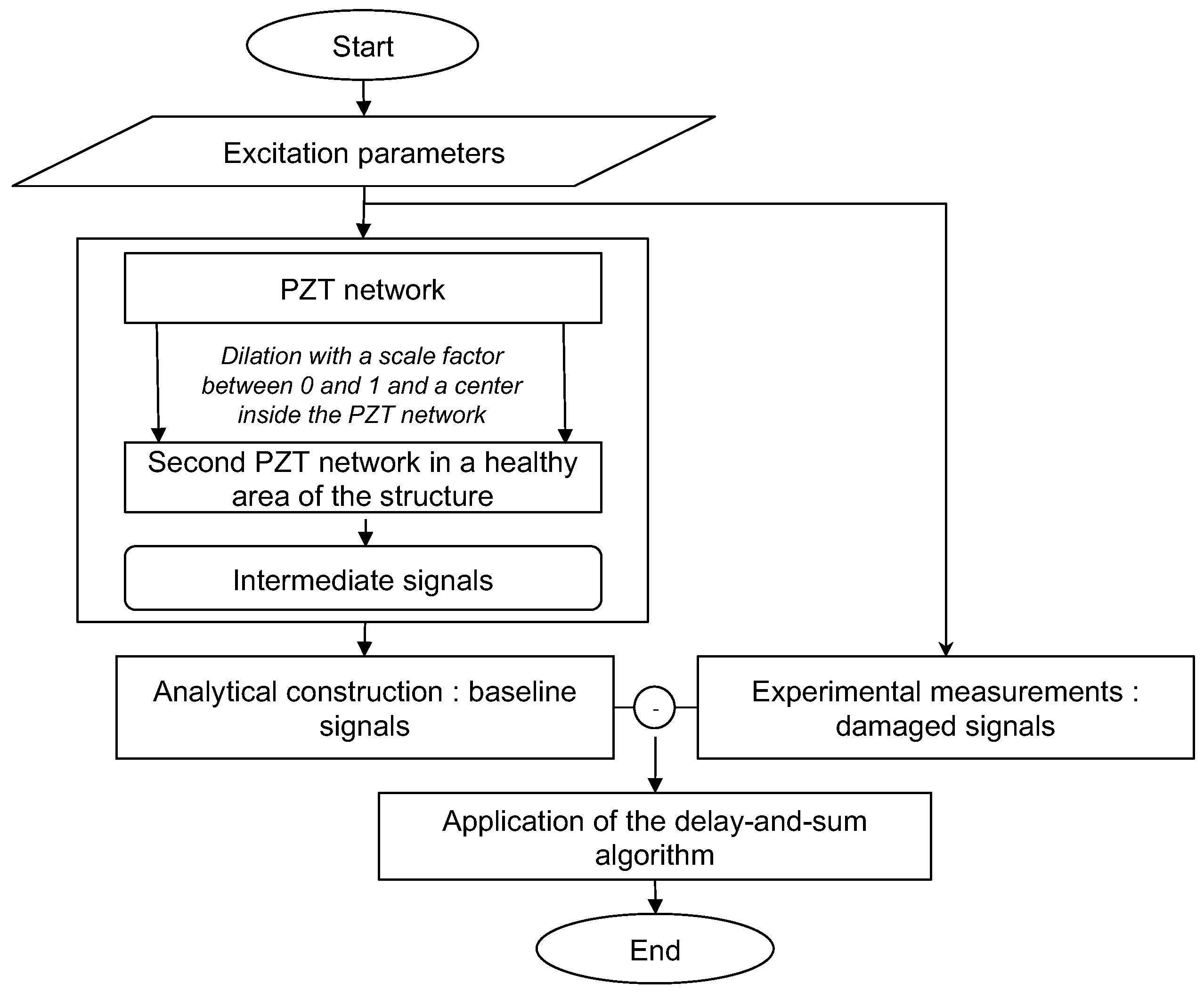
2. Damage Localization Methods Based on Delay-and-Sum Algorithm
2.1. Simulation Method
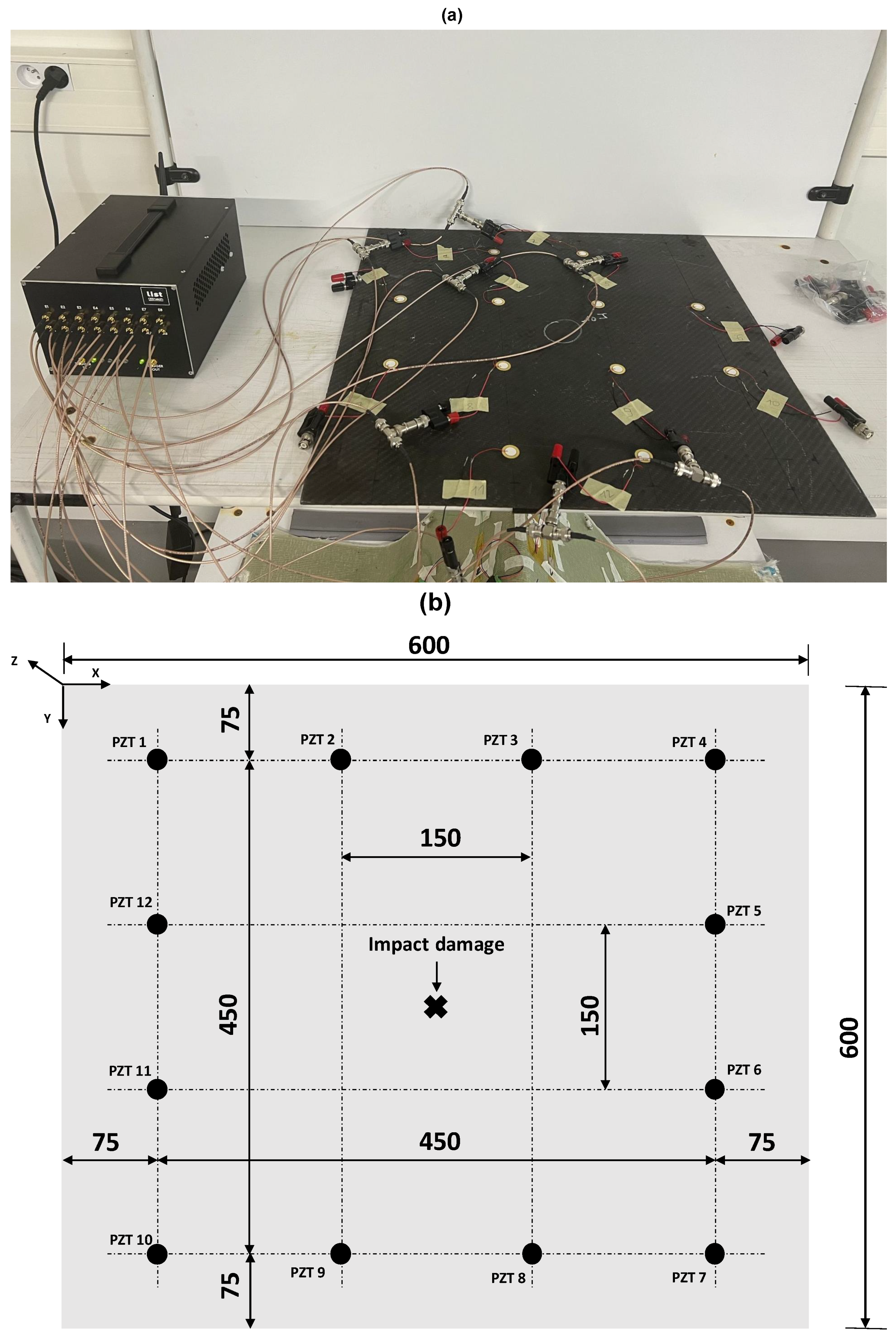
2.2. Experimental Method
2.3. Delay-and-Sum Algorithm Applied to Anisotropic Materials
3. Transverse Isotropic Composite Plate
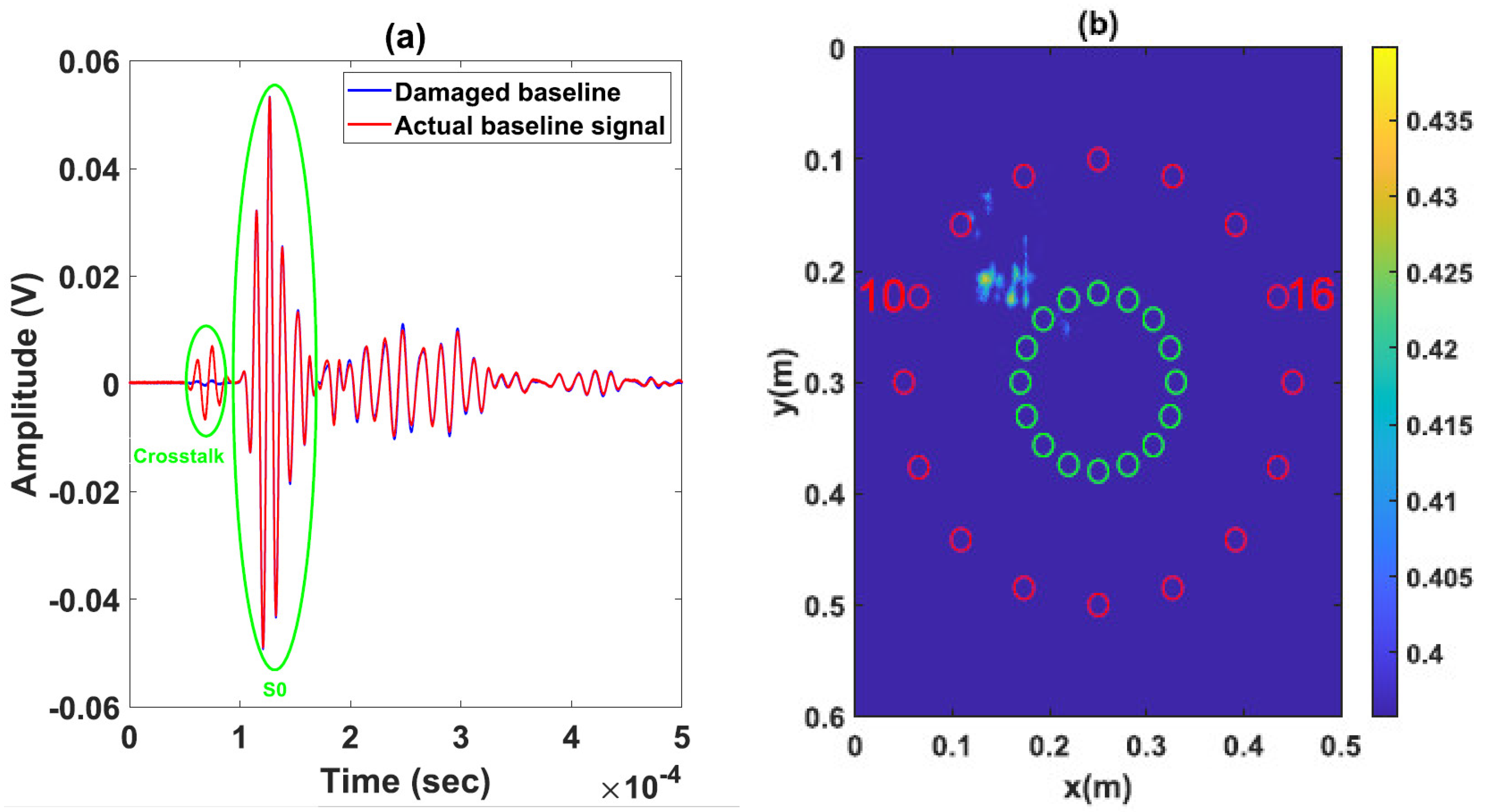
3.1. Acquisitions at the Damaged State
3.2. CIVA Modelling for the Creation of the Baseline State
- The geometry and mechanical properties of the plate (elasticity tensor, density). The plate is considered as homogeneous.
- The positions and size of the PZTs and the excitation signal are taken to be exactly the same as the experimental configuration.
- The duration of signals, i.e., 500 µs, and the sampling frequency are identical to those used in experiments.
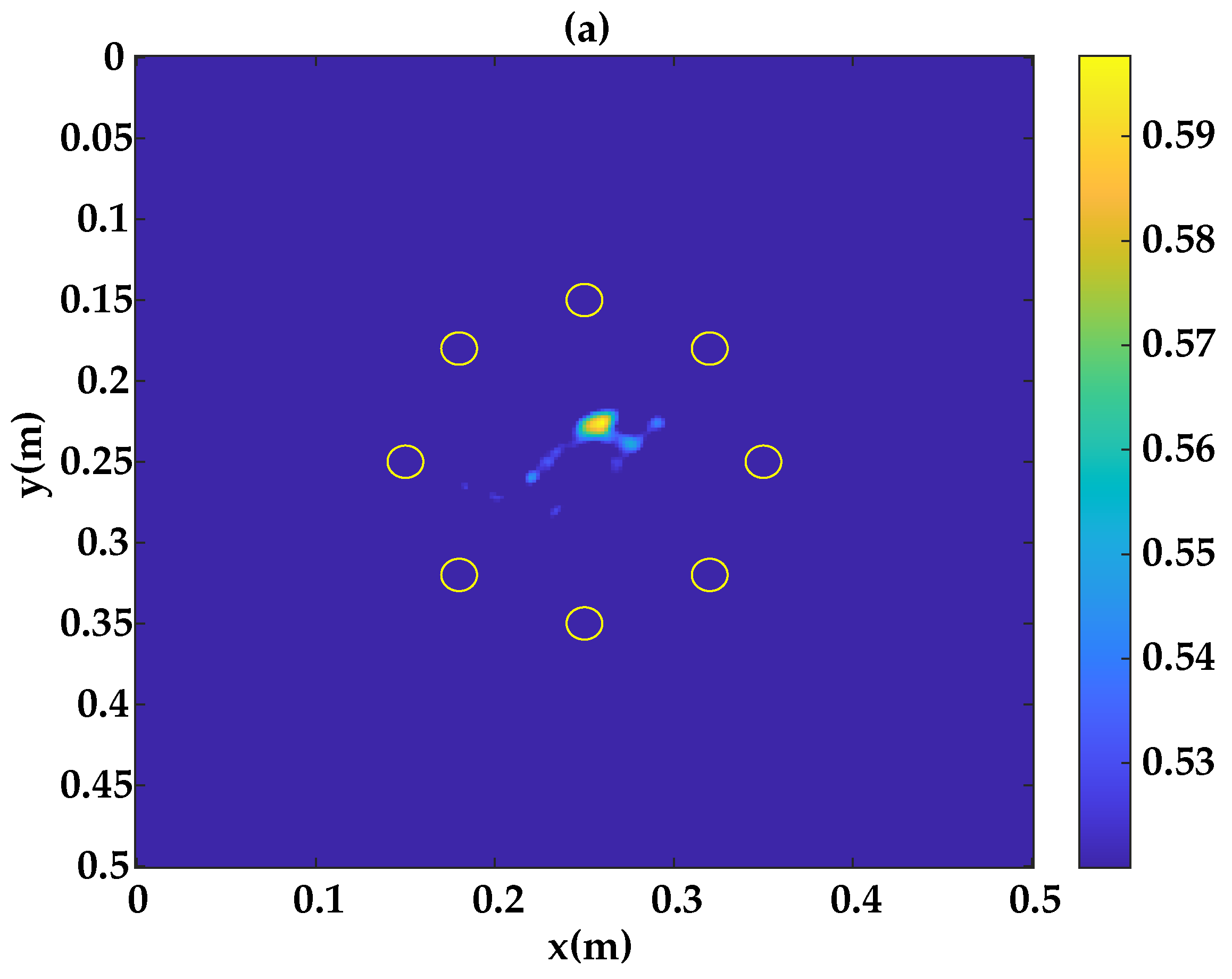
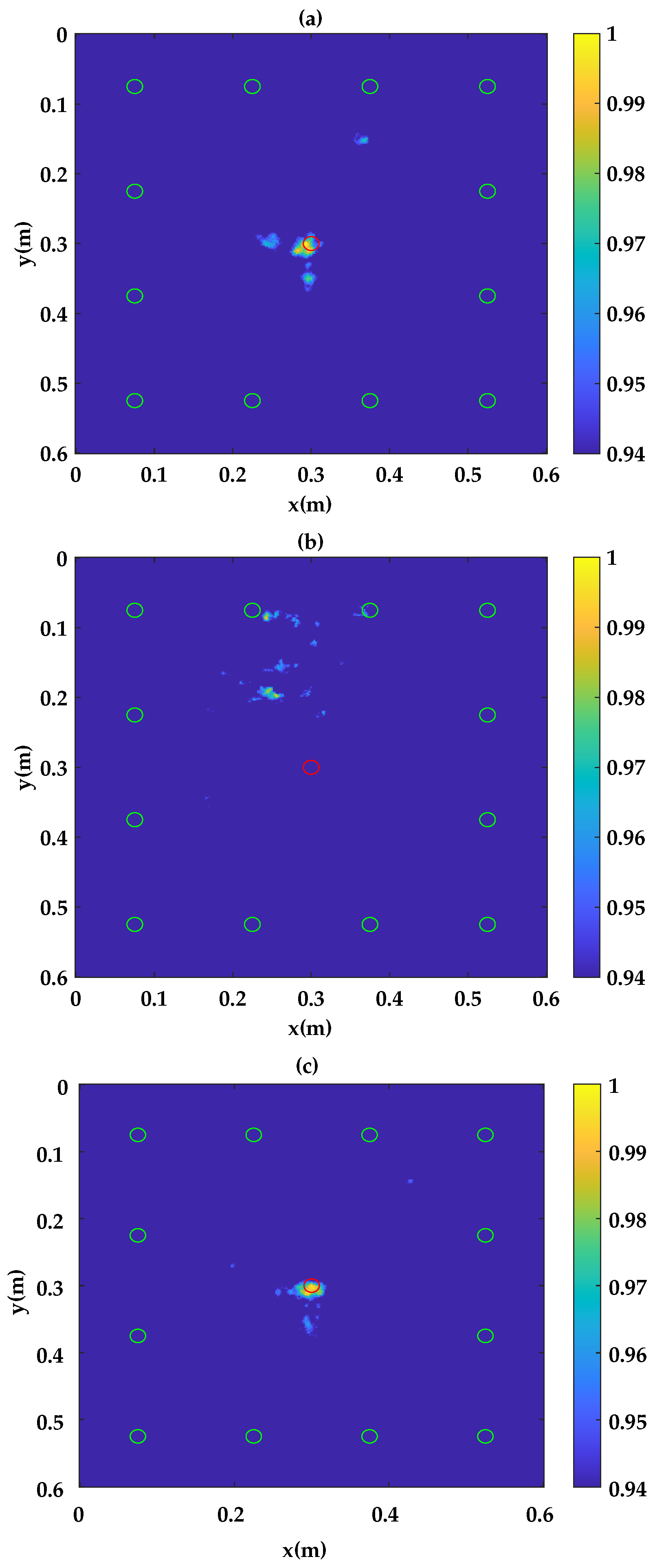
3.3. Results and Discussion
4. Curved Wind Turbine Blade Sample
4.1. Characterization of the Wind Turbine Sample
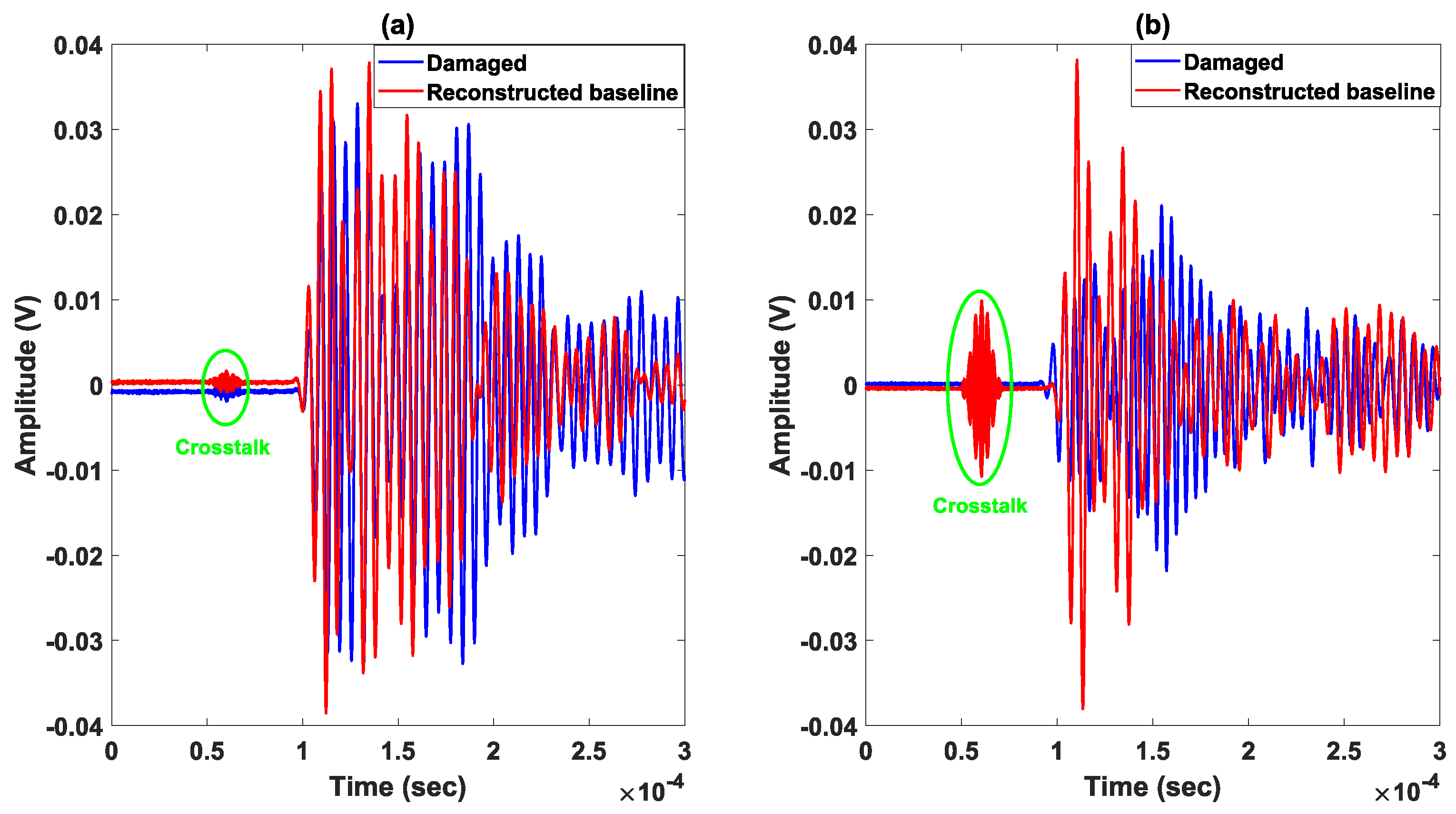
4.2. Measurements and Reconstruction of Baseline Signals
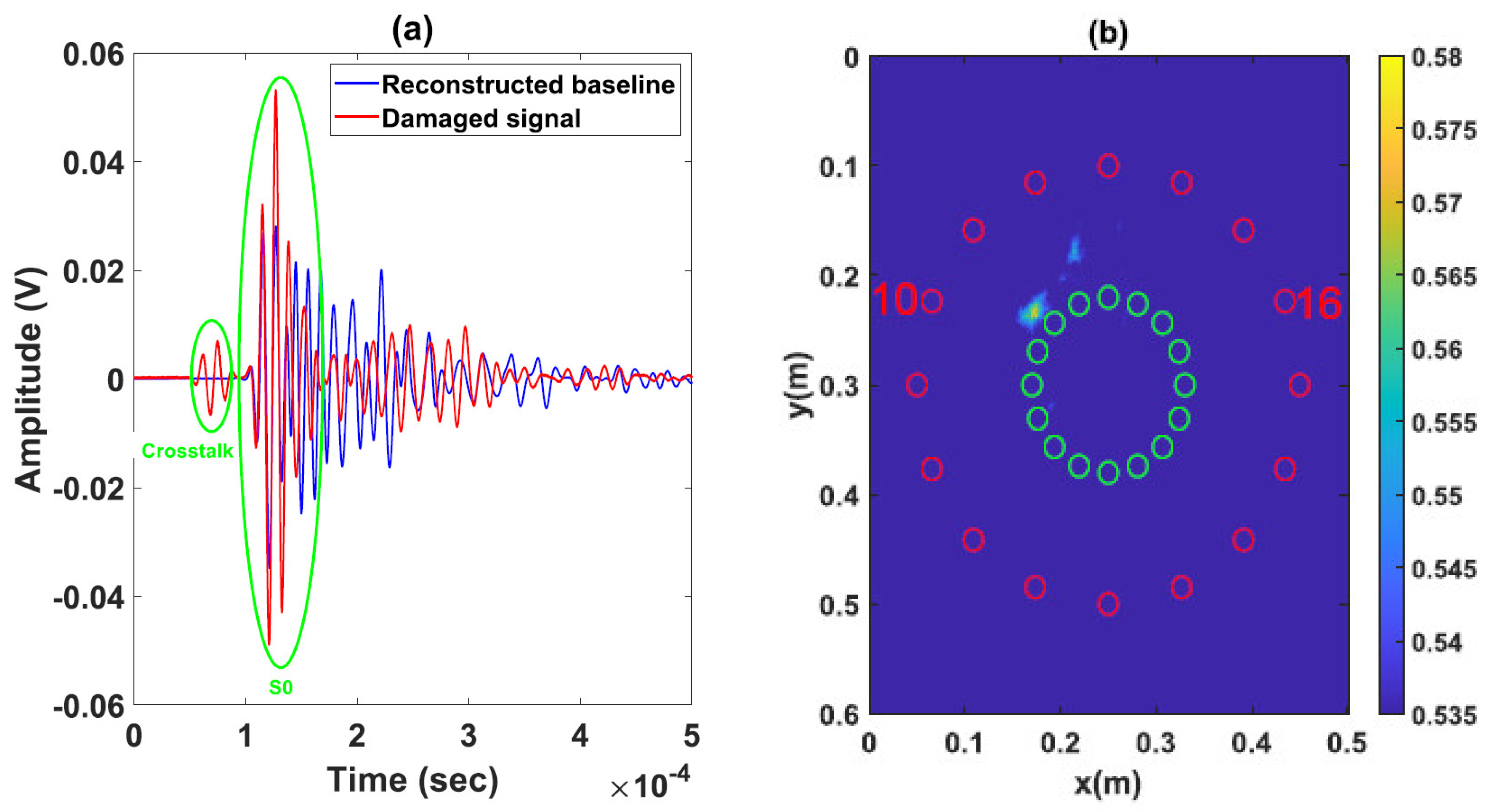
4.3. Results and Discussion
5. Anisotropic Carbon Fiber Composite Plate
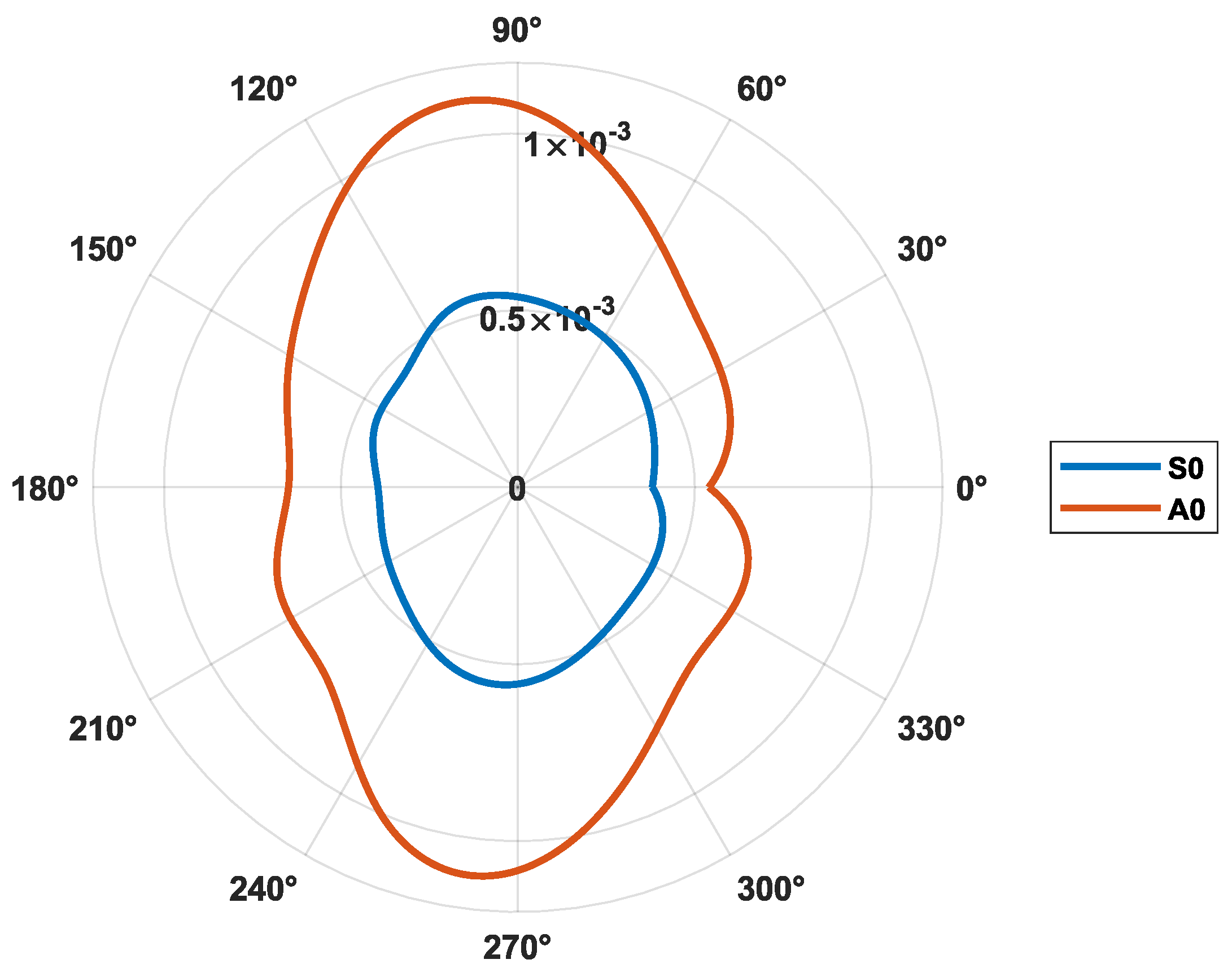
5.1. Characterisation of the Composite Symmetry
5.2. Damaged State and Baseline Signals
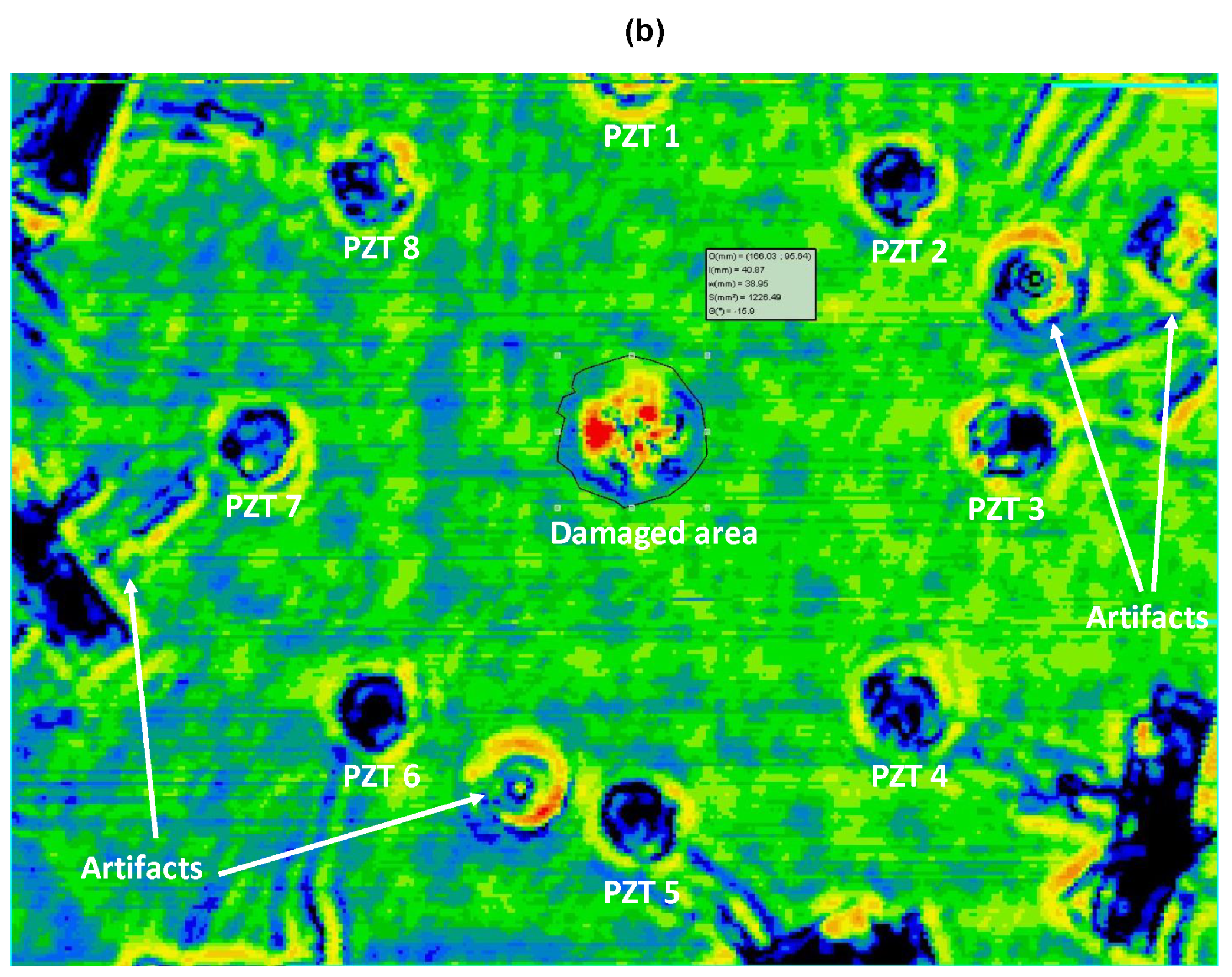
5.3. Results and Discussion
6. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chang, F.K. Structural Health Monitoring: A Summary Report on the First Stanford Workshop on Structural Health Monitoring. In Report on the First Stanford Workshop on Structural; Stanford University: Stanford, CA, USA, 1997; p. 12. [Google Scholar]
- Raghavan, A.; Cesnik, C.E. Review of Guided-wave Structural Health Monitoring. SAGE Publ. 2007, 39, 91–114. [Google Scholar] [CrossRef]
- Royer, D.; Dieulesaint, E. Ondes éLastiques Dans les Solides, masson ed.; Elsevier Masson: Issy Les Moulineaux, France, 1996; Volume 1. [Google Scholar]
- Su, Z.; Ye, L. Identification of Damages Using Lamb Waves; Lecture Notes in Applied and Computational Mechanics; Springer: London, UK, 2009; Volume 48. [Google Scholar]
- Giurgiutiu, V.; Soutis, C. Enhanced Composites Integrity Through Structural Health Monitoring. Appl. Compos. Mater. 2012, 19, 813–829. [Google Scholar] [CrossRef]
- Lize, E. Détection D’endommagement sans État de Référence et Estimation de la Température Pour le Contrôle Santé Intégré de Structures Composites par Ondes Guidées. Ph.D. Thesis, Ecole nationale supérieure d’arts et métiers-ENSAM, Paris, France, 2018. [Google Scholar]
- Diamanti, K.; Soutis, C.; Hodgkinson, J. Piezoelectric transducer arrangement for the inspection of large composite structures. Compos. Part A-Appl. Sci. Manuf. 2007, 38, 1121–1130. [Google Scholar] [CrossRef]
- Kessler, S.S. Piezoelectric-Based In-Situ Damage Detection of Composite Materials for Structural Health Monitoring Systems. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2002. [Google Scholar]
- Masurkar, F.; Yelve, N. Optimizing location of damage within an enclosed area defined by an algorithm based on the Lamb wave response data. Appl. Acoust. 2017, 120, 98–110. [Google Scholar] [CrossRef]
- Saravanos, D.A.; Hopkins, D.A.; Birman, V. Detection of delaminations in composite beams using piezoelectric sensors. In Proceedings of the 35th Structures, Structural Dymimics, and Materials Conference, Hilton Head, SC, USA, 18–20 April 1994. [Google Scholar]
- Kessler, S.S.; Spearing, S.M. Damage Detection in Composite Materials Using Lamb Wave Methods. Smart Mater. Struct. 2002, 11, 269. [Google Scholar] [CrossRef] [Green Version]
- Sharif Khodaei, Z.; Aliabadi, M.H.F. Damage Detection and Characterization with Piezoelectric Transducers: Active Sensing. In Structural Health Monitoring for Advanced Composite Structures; Computational and Experimental Methods in Structures, Ed.; World Scientific Publishing: Singapore, 2018; Volume 8, p. 288. [Google Scholar]
- Wang, D.; Zhang, W.; Wang, X.; Sun, B. Lamb-Wave-Based Tomographic Imaging Techniques for Hole-Edge Corrosion Monitoring in Plate Structures. Materials 2016, 9, 916. [Google Scholar] [CrossRef] [Green Version]
- Leonard, K.R.; Malyarenko, E.R.; Hinders, M.K. Ultrasonic Lamb wave tomography. Inverse Probl. 2002, 18, 15. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, S.; Ning, H.; Yan, C.; Hu, N. An Inverse Approach of Damage Identification Using Lamb Wave Tomography. Sensors 2019, 19, 2180. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Royer, R.L.; Owens, S.E.; Joseph, L.R. Ultrasonic Lamb wave tomography in structural health monitoring. Smart Mater. Struct. 2011, 20, 105002. [Google Scholar] [CrossRef]
- Zhao, X.; Rose, J.L. Ultrasonic guided wave tomography for ice detection. Ultrasonics 2015, 67, 212–219. [Google Scholar] [CrossRef]
- Wang, S.; Wu, W.; Shen, Y.; Liu, Y.; Jiang, S. Influence of the PZT Sensor Array Configuration on Lamb Wave Tomography Imaging with the RAPID Algorithm for Hole and Crack Detection. Sensors 2020, 20, 260. [Google Scholar] [CrossRef] [Green Version]
- Dziendzikowski, M.; Dragan, K.; Katunin, A. Localizing impact damage of composite structures with modified RAPID algorithm and non-circular PZT arrays. Arch. Civ. Mech. Eng. 2016, 17, 178–187. [Google Scholar] [CrossRef]
- Sheen, B.; Cho, Y. A study on quantitative Lamb Waves Tomogram via modified RAPID Algorithm with shape factor optimisation. Int. J. Precis. Eng. Manuf. 2012, 13, 671–677. [Google Scholar] [CrossRef]
- Hua, J.; Lin, J.; Zeng, L. High-resolution damage detection based on local signal difference coefficient model. Struct. Health Monit. 2014, 14, 20–34. [Google Scholar] [CrossRef]
- Levine, R.M. Ultrasonic Guided Wave Imaging via Sparse Reconstruction. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2014. [Google Scholar]
- Levine, R.M.; Michaels, J.E. Model-based imaging of damage with Lamb waves via sparse reconstruction. Acoust. Soc. Am. 2013, 133, 1525–1534. [Google Scholar] [CrossRef]
- Sharif-Khodaei, Z.; Aliabadi, M.H. Assessment of delay-and-sum algorithms for damage detection in aluminium and composite plates. Smart Mater. Struct. 2014, 23, 075007. [Google Scholar] [CrossRef]
- Michaels, J.E. Detection, localization and characterization of damage in plates with an in situ array of spatially distributed ultrasonic sensors. Smart Mater. Struct. 2008, 17, 035035. [Google Scholar] [CrossRef] [Green Version]
- Shan, S.; Qiu, J.; Zhang, C.; Ji, H.; Cheng, L. Multi-damage localization on large complex structures through an extended delay-and-sum based method. Struct. Health Monit. 2016, 15, 50–64. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, X.; Wang, Y.; Wang, Y.; Qing, X. Lamb wave-based damage imaging of CFRP composite structures using autoencoder and delay-and-sum. Compos. Struct. 2022, 303, 116263. [Google Scholar] [CrossRef]
- Salmanpour, M.; Khodaei, Z.S.; Aliabadi, M. Guided wave temperature correction methods in structural health monitoring. J. Intell. Mater. Syst. Struct. 2017, 28, 604–618. [Google Scholar] [CrossRef] [Green Version]
- Park, H.W.; Sohn, H.; Law, K.H.; Farrar, C.R. Time reversal active sensing for health monitoring of a composite plate. J. Sound Vib. 2007, 302, 50–66. [Google Scholar] [CrossRef]
- Park, H.W.; Kim, S.B.; Sohn, H. Understanding a time reversal process in Lamb wave propagation. Wave Motion 2009, 46, 451–467. [Google Scholar] [CrossRef]
- Salmanpour, M.S.; Khodaei, Z.S.; Aliabadi, M.H. Instantaneous Baseline Damage Localization Using Sensor Mapping. IEEE Sens. J. 2017, 17, 295–301. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Zhang, A.; Wang, Y.; Qing, X. Baseline-free damage imaging for metal and composite plate-type structures based on similar paths. Int. J. Distrib. Sens. Netw. 2019, 15. [Google Scholar] [CrossRef]
- Hettler, J.; Tabatabateipour, M.; Delrue, S.; Van Den Abeele, K. Application of Probabilistic Algorithm for Ultrasonic Guided Wave Imaging of Carbon Composites. Phys. Procedia 2015, 70, 664–667. [Google Scholar] [CrossRef] [Green Version]
- Singh, D.; Mechri, C.; El Guerjouma, R.; Bentahar, M. 3D Modelling of the Scattering of the Fundamental Anti-Symmetric Lamb Mode (A0) Propagating within a Point-Impacted Transverse-Isotropic Composite Plate. Appl. Sci. 2021, 11, 7276. [Google Scholar] [CrossRef]
- Mesnil, O.; Imperiale, A.; Demaldent, E.; Chapuis, B. Validation of spectral finite element simulation tools dedicated to guided wave based structure health monitoring. AIP Conf. Proc. 2019, 38, 050018. [Google Scholar]
- CIVA SHM. Available online: https://www.extende.com/files/extende/download_files/Discover_CIVA_SHM.pdf (accessed on 9 March 2023).
- Han Orta, A.; Segers, J.; Vandendriessche, J.; Bernardus Roozen, N.; Van Paepegem, W.; Kersemans, M.; Van Den Abeele, K. Characterization of orthotropic elastic tensor using lamb waves. Proc. Forum Acusticum 2020, 3319–3326. [Google Scholar] [CrossRef]
- Kudela, P.; Radzienski, M.; Fiborek, P.; Wandowski, T. Elastic constants identification of fibre-reinforced composites by using guided wave dispersion curves and genetic algorithm for improved simulations. Compos. Struct. 2021, 272, 114178. [Google Scholar] [CrossRef]
- Wang, W.; Bao, Y.; Zhou, W.; Li, H. Sparse representation for Lamb-wave-based damage detection using a dictionary algorithm. Ultrasonics 2018, 87, 48–58. [Google Scholar] [CrossRef]
- Xu, C.; Yang, Z.; Tian, S.; Chen, X. Lamb wave inspection for composite laminates using a combined method of sparse reconstruction and delay-and-sum. Compos. Struct. 2019, 223, 110973. [Google Scholar] [CrossRef]
- Abbas, S.; Jianxi, Q.; Li, F. A Review on SHM Techniques and Current Challenges for Characteristic Investigation of Damage in Composite Material Components of Aviation Industry. ASTM 2018, 7, 224–258. [Google Scholar] [CrossRef]
- Castaings, M.; Singh, D.; Philippe, V. Sizing of impact damages in composite materials using ultrasonic guided waves. NDT&E Int. 2011, 46, 22–31. [Google Scholar]
- Le Cam, V.; Döhler, M.; Mathieu, L.P.; Guéguen, I.; Mevel, L. Embedded subspace-based modal analysis and uncertainty quantification on wireless sensor platform PEGASE. In Proceedings of the EWSHM-8th European Workshop on Structural Health Monitoring, Bilbao, Spain, 5–8 July 2016. [Google Scholar]
- De Luca, A.; Caputo, F.; Sharif Khodaei, Z.; Aliabadi, M. Damage characterization of composite plates under low velocity impact using ultrasonic guided waves. Compos. Part B 2018, 138, 168–180. [Google Scholar] [CrossRef]
- Li, X.; Yang, Z.; Chen, X. Quantitative Damage Detection and Sparse Sensor Array Optimization of Carbon Fiber Reinforced Resin Composite Laminates for Wind Turbine Blade Structural Health Monitoring. Sensors 2014, 14, 7312–7331. [Google Scholar] [CrossRef] [Green Version]
- Li, F.; Meng, G.; Ye, L.; Lu, Y.; Kageyama, K. Dispersion analysis of Lamb waves and damage detection for aluminum structures using ridge in the time-scale domain. Meas. Sci. Technol. 2009, 20, 095704. [Google Scholar] [CrossRef]
- Zhao, X.; Gao, H.; Zhang, G.; Ayhan, B.; Yan, F.; Kwan, C.; Rose, J.L. Active health monitoring of an aircraft wing with embedded piezoelectric sensor/actuator network: I. Defect detection, localization and growth monitoring. Smart Mater. Struct. 2007, 16, 1208–1217. [Google Scholar] [CrossRef]
- Chevalier, Y. Comportements élastique et viscoélastique des composites. Techniques de l’Ingénieur 1988, 5. [Google Scholar]
- Lammering, R.; Gabbert, U.; Sinapius, M.; Schuster, T.; Wierach, P. Lamb-Wave Based Structural Health Monitoring in Polymer Composites; Springer International Publishing AG: Cham, Switzerland, 2018. [Google Scholar]
- Jia, H.; Liu, H.; Zhang, Z.; Dai, F.; Liu, Y.; Leng, J. A baseline-free approach of locating defect based on mode conversion and the reciprocity principle of Lamb waves. Ultrasonics 2020, 102, 106063. [Google Scholar] [CrossRef]
- Kubrusly, A.C.; Tovar, P.; von der Weid, J.P.; Dixon, S. Mode conversion of SH guided waves with symmetry inversion in plates. Ultrasonics 2021, 112, 106334. [Google Scholar] [CrossRef]
- Ramadas, C.; Balasubramaniam, K.; Joshi, M.; Krishnamurthy, C.V. Numerical and experimental studies on propagation of A0 mode in a composite plate containing semi-infinite delamination: Observation of turning modes. Compos. Struct. 2011, 93, 1929–1938. [Google Scholar] [CrossRef]
- Ramadas, C.; Balasubramaniam, K.; Hood, A.; Joshi, M.; Krishnamurthy, C.V. Modelling of attenuation of Lamb waves using Rayleigh damping: Numerical and experimental studies. Compos. Struct. 2011, 93, 2020–2025. [Google Scholar] [CrossRef]
- Kubrusly, A.C.; Freitas, M.A.; von der Weid, J.P.; Dixon, S. Interaction of SH guided waves with wall thinning. NDT&E Int. 2018. [Google Scholar] [CrossRef] [Green Version]
- Nurmalia; Nakamura, N.; Ogi, H.; Hirao, M.; Nakahata, K. Mode conversion behavior of SH guided wave in a tapered plate. NDT&E Int. 2012, 45, 156–161. [Google Scholar] [CrossRef]











| 1.55 ± 0.05 | 52.4 ± 2% | 52.4 ± 2% | 12.6 ± 2% | 17.8 ± 2% | 3.1 ± 2% | 3.1 ± 2% | 3.7 ± 2% | 3.7 ± 2% | 17.3 ± 2% |
| Positions | PZT1 | PZT2 | PZT3 | PZT4 | PZT5 | PZT6 | PZT7 | PZT8 |
|---|---|---|---|---|---|---|---|---|
| X (mm) | 250 | 320 | 350 | 320 | 250 | 180 | 150 | 180 |
| Y (mm) | 150 | 180 | 250 | 320 | 350 | 320 | 250 | 180 |
| PZT | X(mm) | Y(mm) |
|---|---|---|
| 1 | 450 | 300 |
| 2 | 434.8 | 376.5 |
| 3 | 391.4 | 441.4 |
| 4 | 326.5 | 484.8 |
| 5 | 250 | 500 |
| 6 | 173.5 | 484.8 |
| 7 | 108.6 | 441.4 |
| 8 | 65.2 | 376.5 |
| 9 | 500 | 300 |
| 10 | 65.2 | 223.5 |
| 11 | 108.6 | 158.6 |
| 12 | 173.5 | 115.2 |
| 13 | 250 | 100 |
| 14 | 326.5 | 115.2 |
| 15 | 391.4 | 158.6 |
| 16 | 434.8 | 223.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nzouatchoua, C.B.; Bentahar, M.; Montresor, S.; Colin, N.; Le Cam, V.; Trottier, C.; Terrien, N. Damage Localization on Composite Structures Based on the Delay-and-Sum Algorithm Using Simulation and Experimental Methods. Sensors 2023, 23, 4368. https://doi.org/10.3390/s23094368
Nzouatchoua CB, Bentahar M, Montresor S, Colin N, Le Cam V, Trottier C, Terrien N. Damage Localization on Composite Structures Based on the Delay-and-Sum Algorithm Using Simulation and Experimental Methods. Sensors. 2023; 23(9):4368. https://doi.org/10.3390/s23094368
Chicago/Turabian StyleNzouatchoua, Cedric Bertolt, Mourad Bentahar, Silvio Montresor, Nicolas Colin, Vincent Le Cam, Camille Trottier, and Nicolas Terrien. 2023. "Damage Localization on Composite Structures Based on the Delay-and-Sum Algorithm Using Simulation and Experimental Methods" Sensors 23, no. 9: 4368. https://doi.org/10.3390/s23094368






