Small-Signal Stability Analysis and MOSMA-Based Optimization Control Strategy of OWF with MMC-HVDC Grid Connection
Abstract
:1. Introduction
- (1)
- The distributed parameter model is developed to accurately analyze the submarine cable capacitance effect and the equivalent impedance model of the wind farm is established considering wideband influence factors. The wideband impedance model of MMC is also established considering the multi-harmonic characteristics, control dynamics and delay effect based on HSS theory.
- (2)
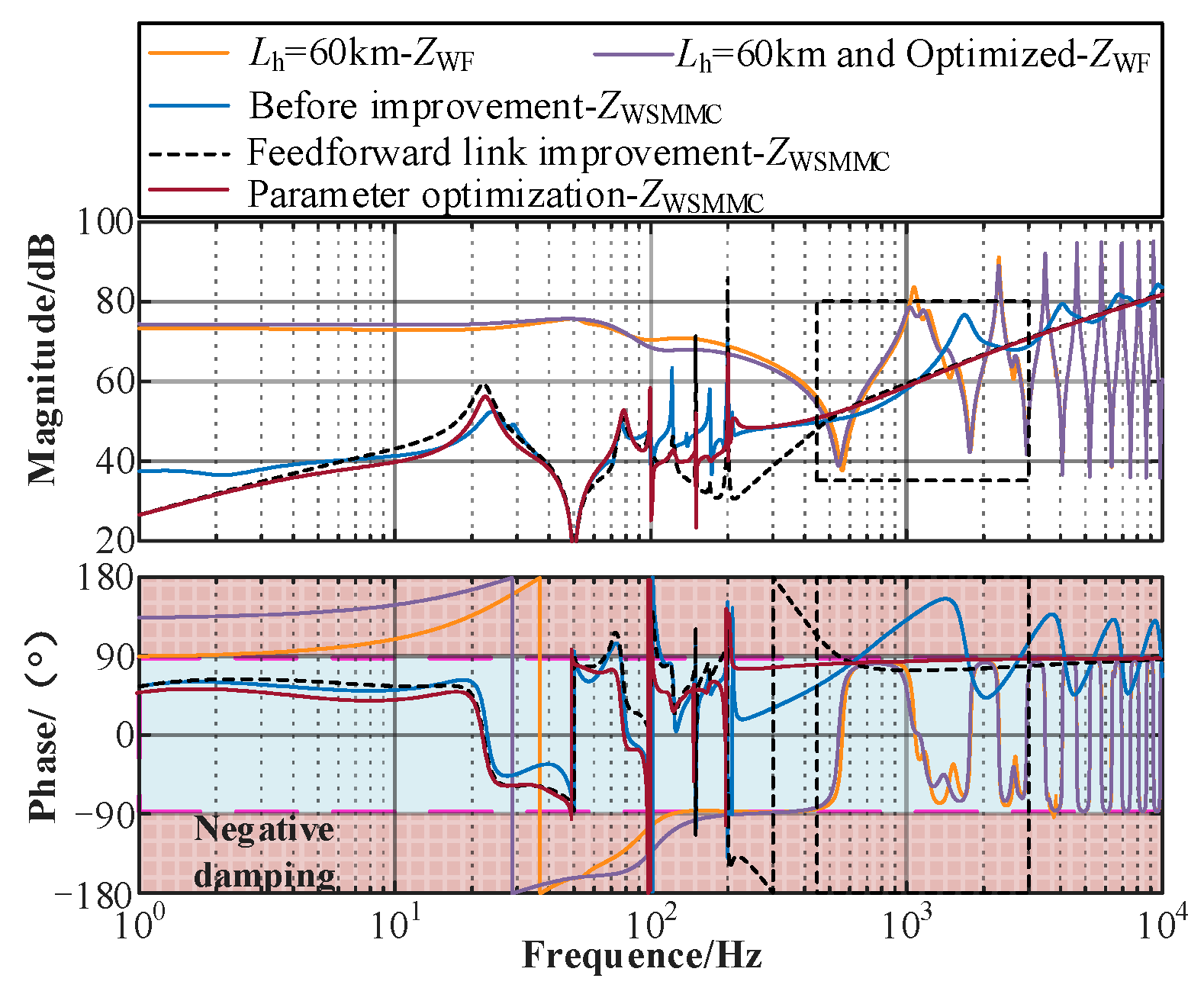
- The capacitance effect of long submarine cable and the delay effect of MMC will weaken the high-frequency damping of the system, and the control system dynamics will increase the risk of sub/super-synchronous resonance. The influence of the MHFRs’ suppression strategy on the wideband dynamic performance of the system is investigated, and the wideband stability constraints for the optimized controller parameter design are evaluated.
- (3)
- Considering the design principle of wideband dominant factors, an improved MOSMA (IMOSMA) algorithm is advanced to assist the controller parameter design for both the wind farm and the MMC system, and improve the wideband damping ability of the grid-connected system with a greater comprehensive optimization performance.
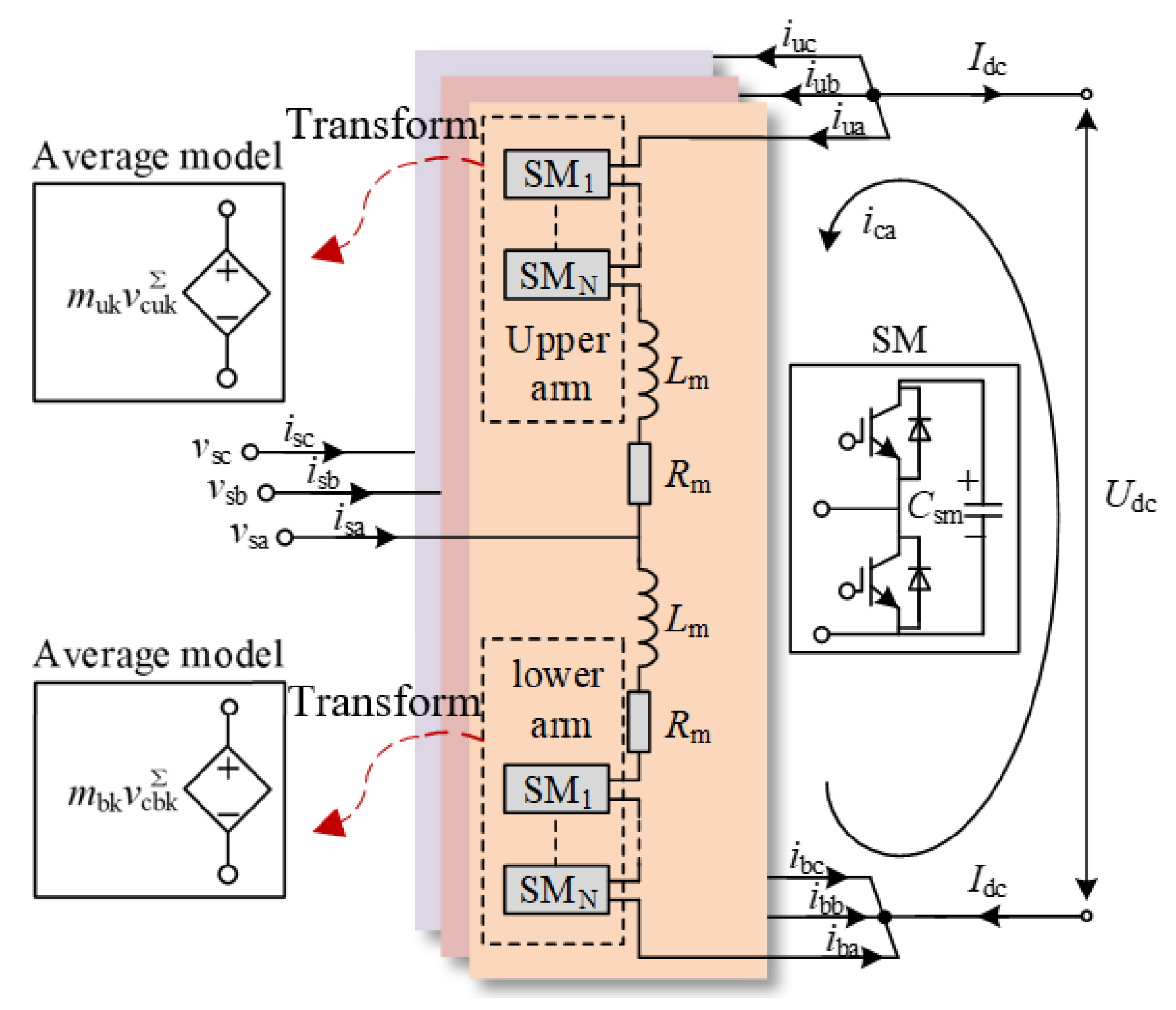
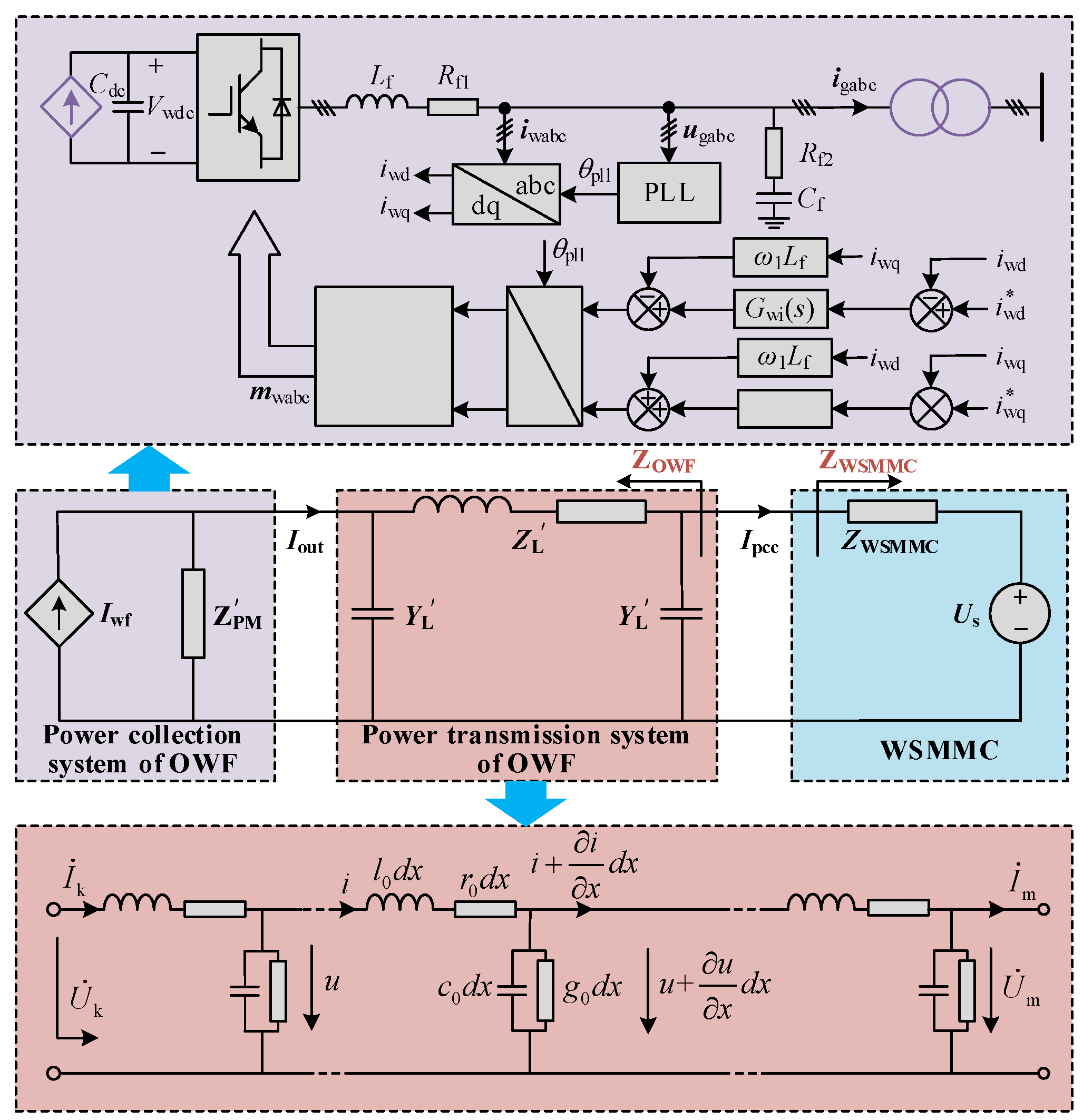
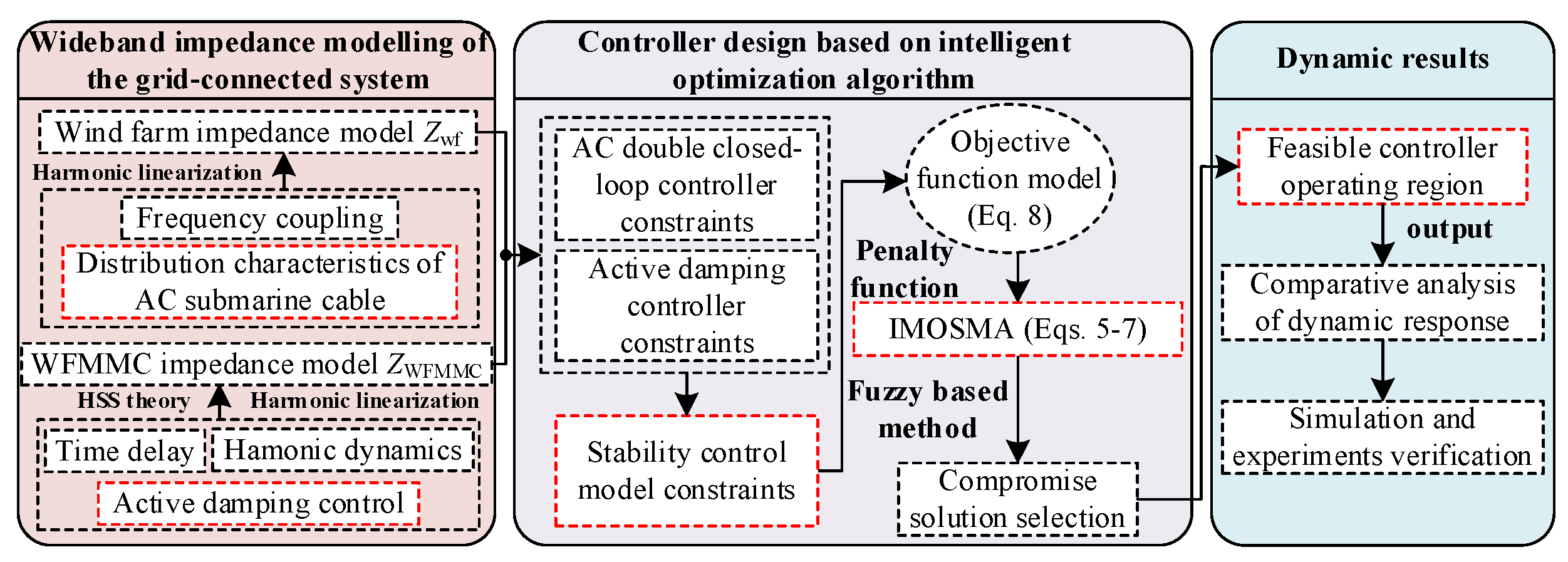
2. Wideband Impedance Modeling of MMC-HVDC-Connected OWF
2.1. System Configuration
2.2. MMC Impedance Modeling
2.3. Equivalent Impedance Modeling of OWF
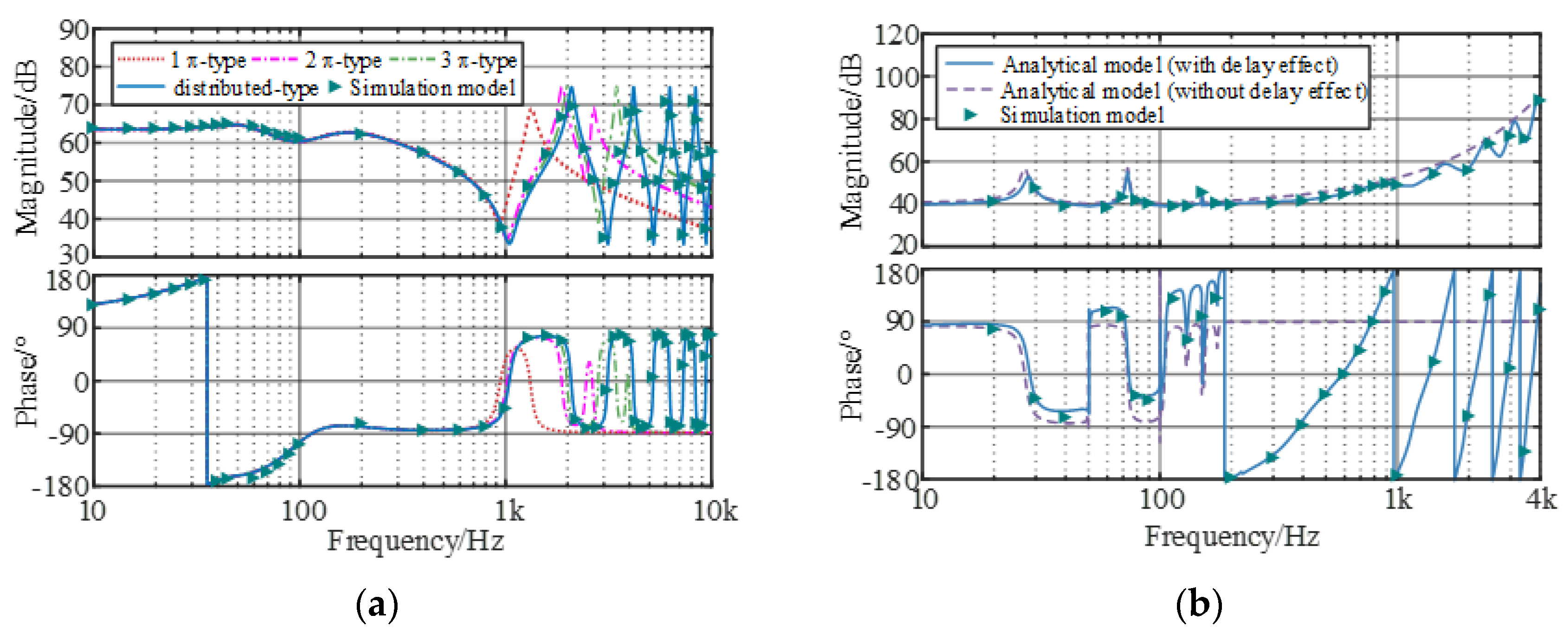
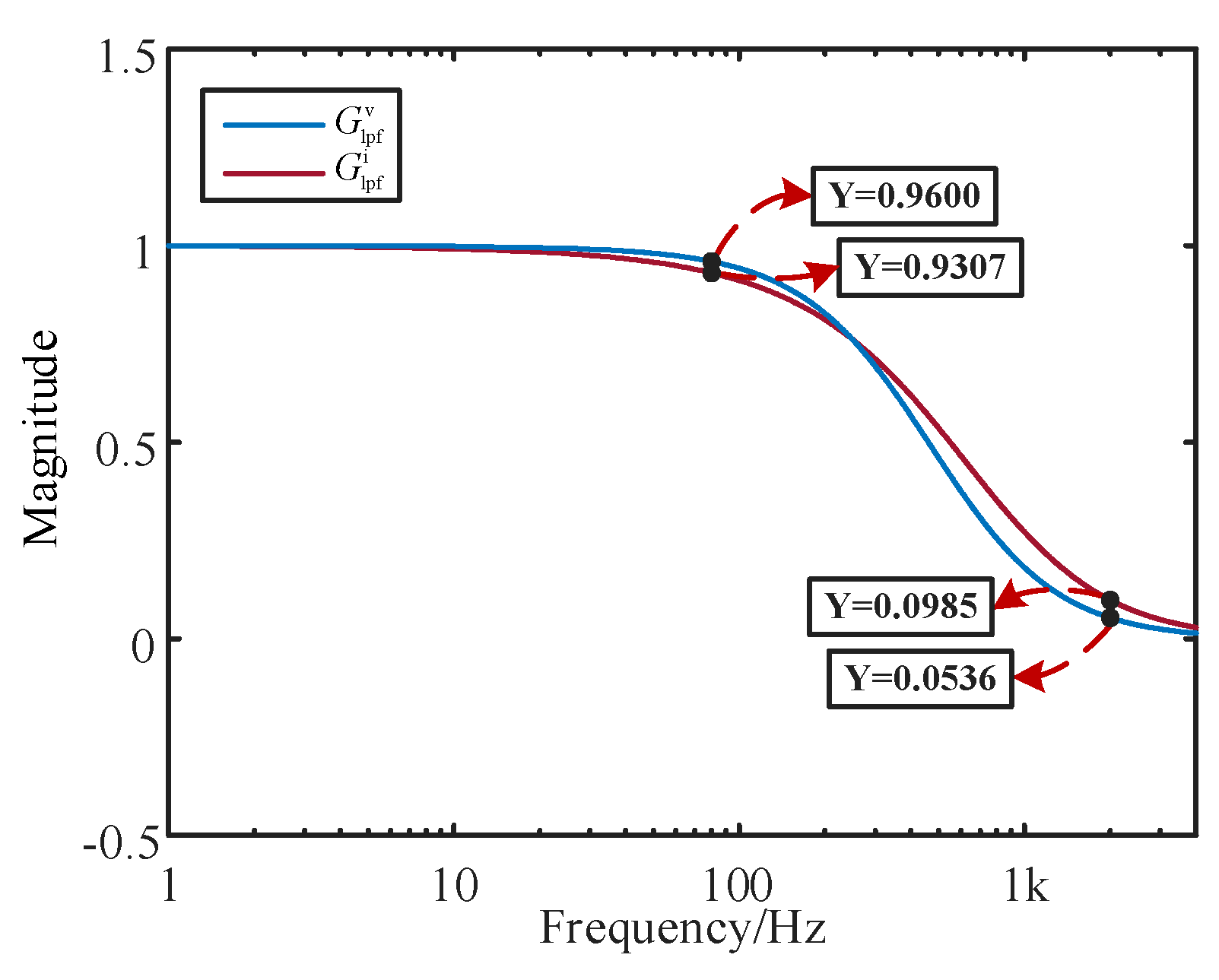
2.4. Model Validation
3. Wideband Small-Signal Stability Mechanism and Constraints Analysis
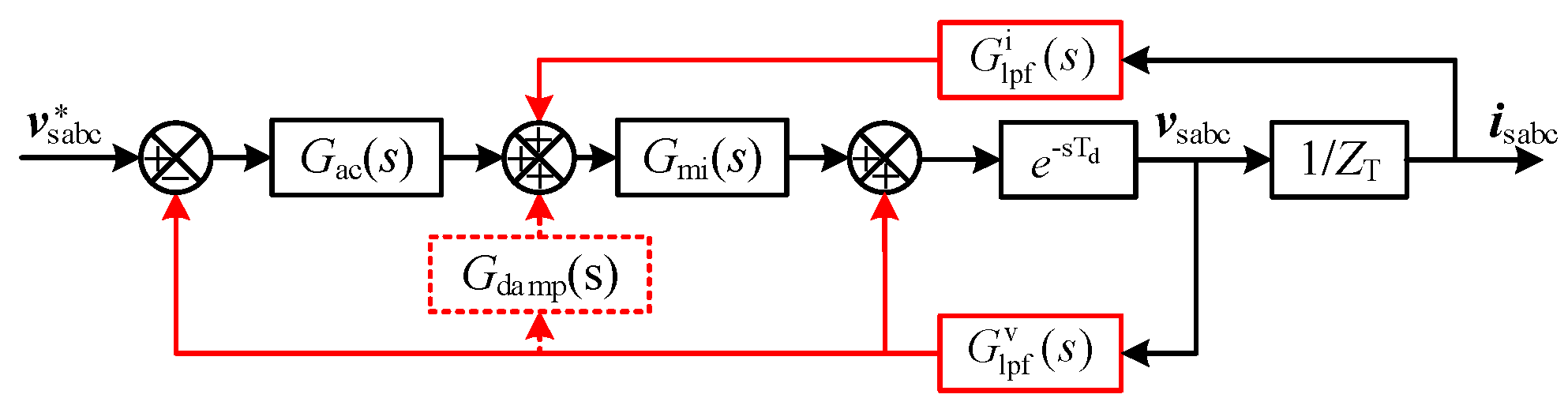
3.1. Active Damping Controller Design
3.2. Wideband Small-Signal Stability Analysis
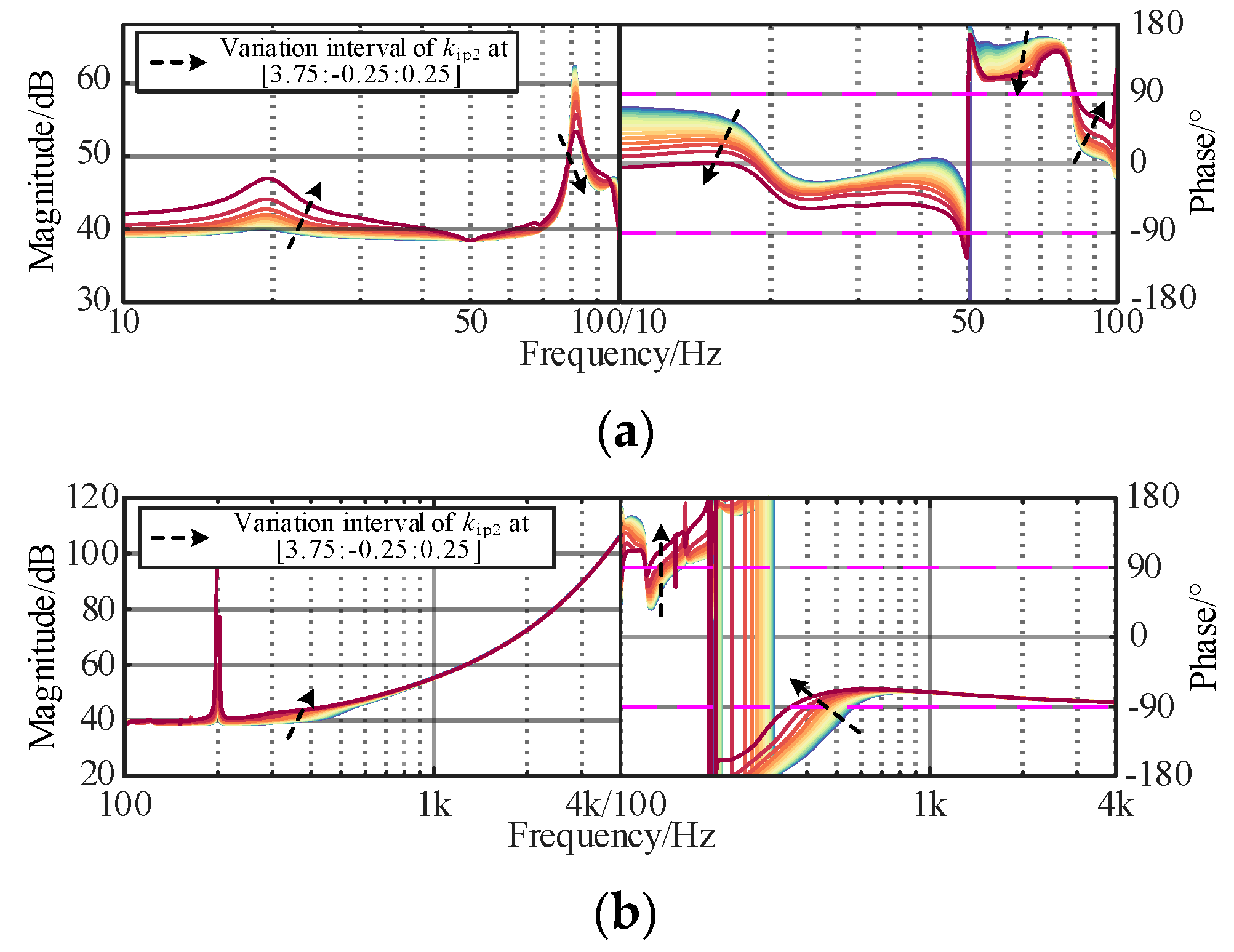
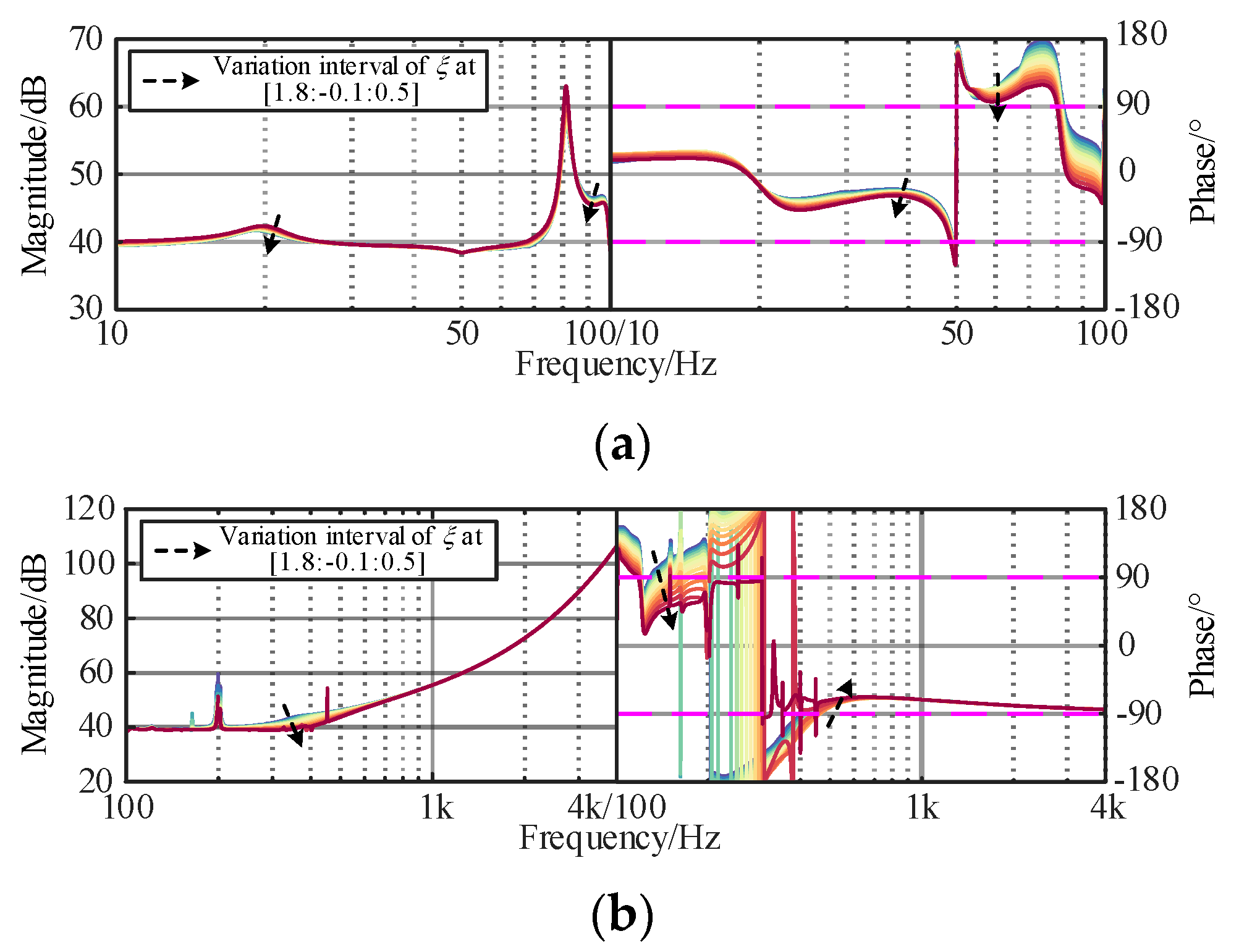
3.3. Original Controller Parameter Constraints
3.4. Active Damping Controller Parameter Constraints
4. Parameter Optimization Control Strategy Based on IMOSMA
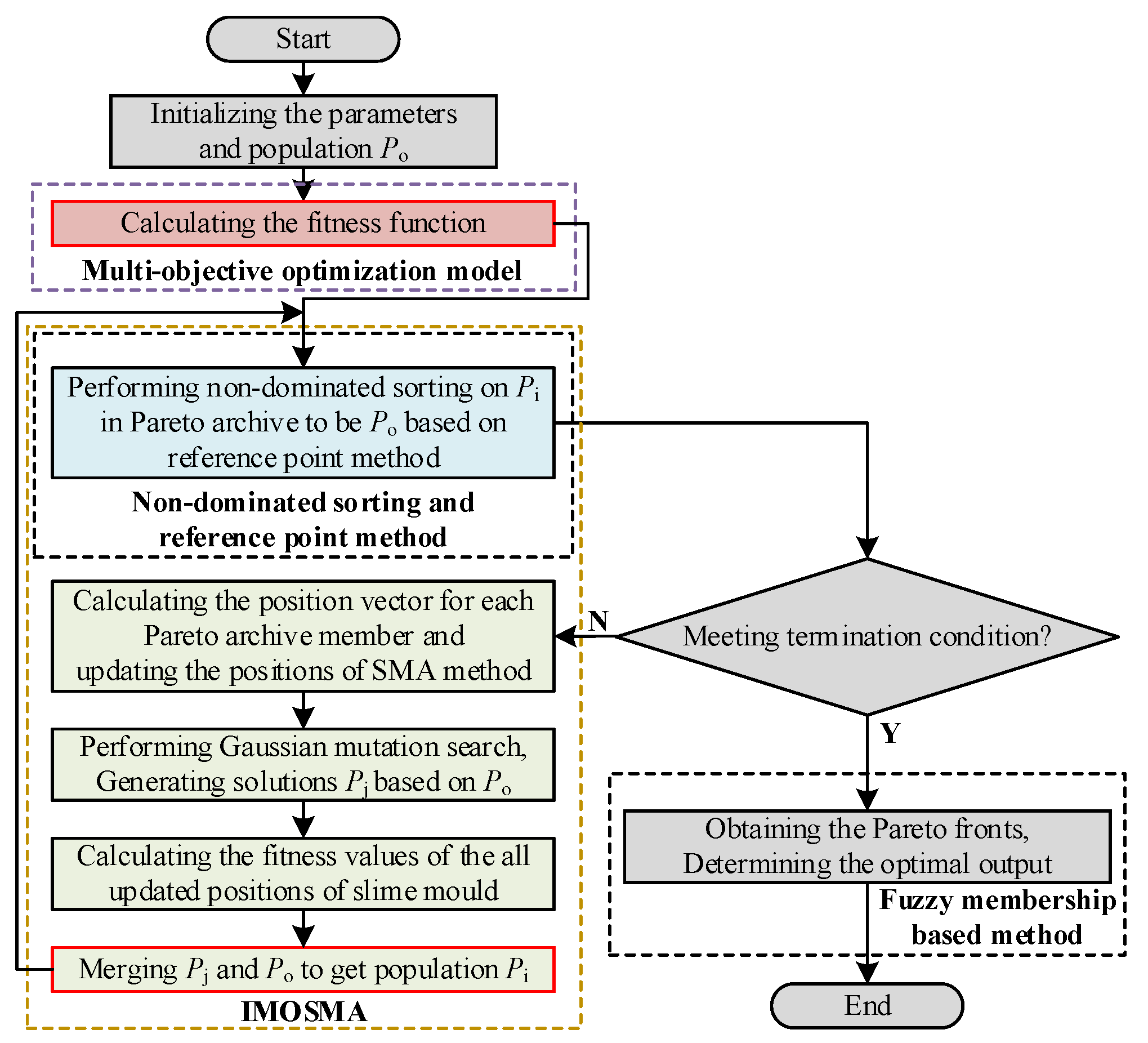
4.1. Principle of Improved MOSMA Algorithm
- (1)
- A single-dimensional Gaussian mutation strategy is proposed by combining the elite strategy to enhance the global search ability of the SMA, allowing the algorithm to obtain greater convergence and search capabilities. It can be written as follows:where δ is a row vector that obeys the standard normal distribution, whose one random position is a non-zero element.
- (2)
- The reference point method [21] is introduced to obtain the next generation of the candidate population for enhancing the diversity of the population. Furthermore, it requires no additional parameters to be set, which is beneficial for solving different problems.
- (3)
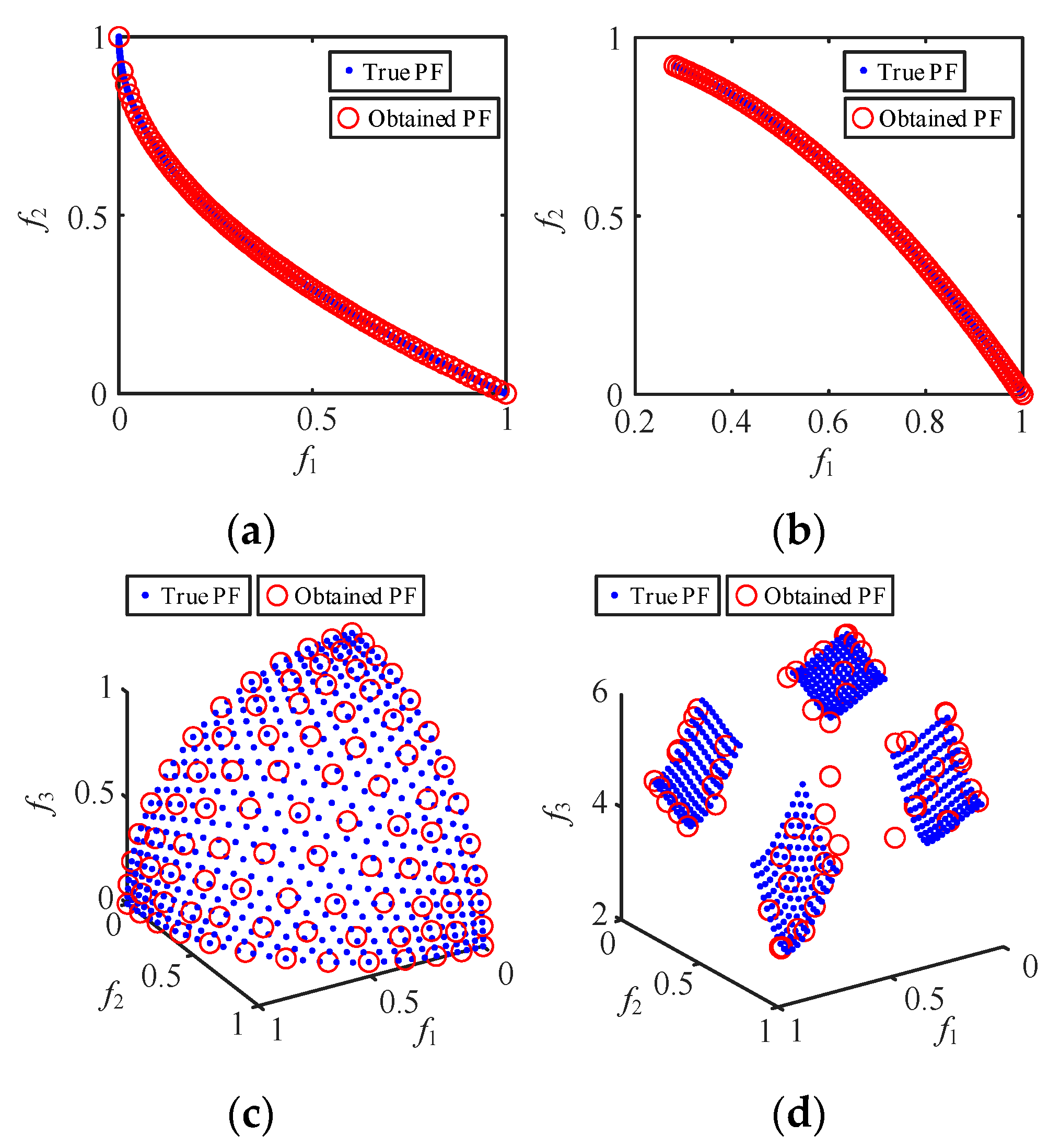
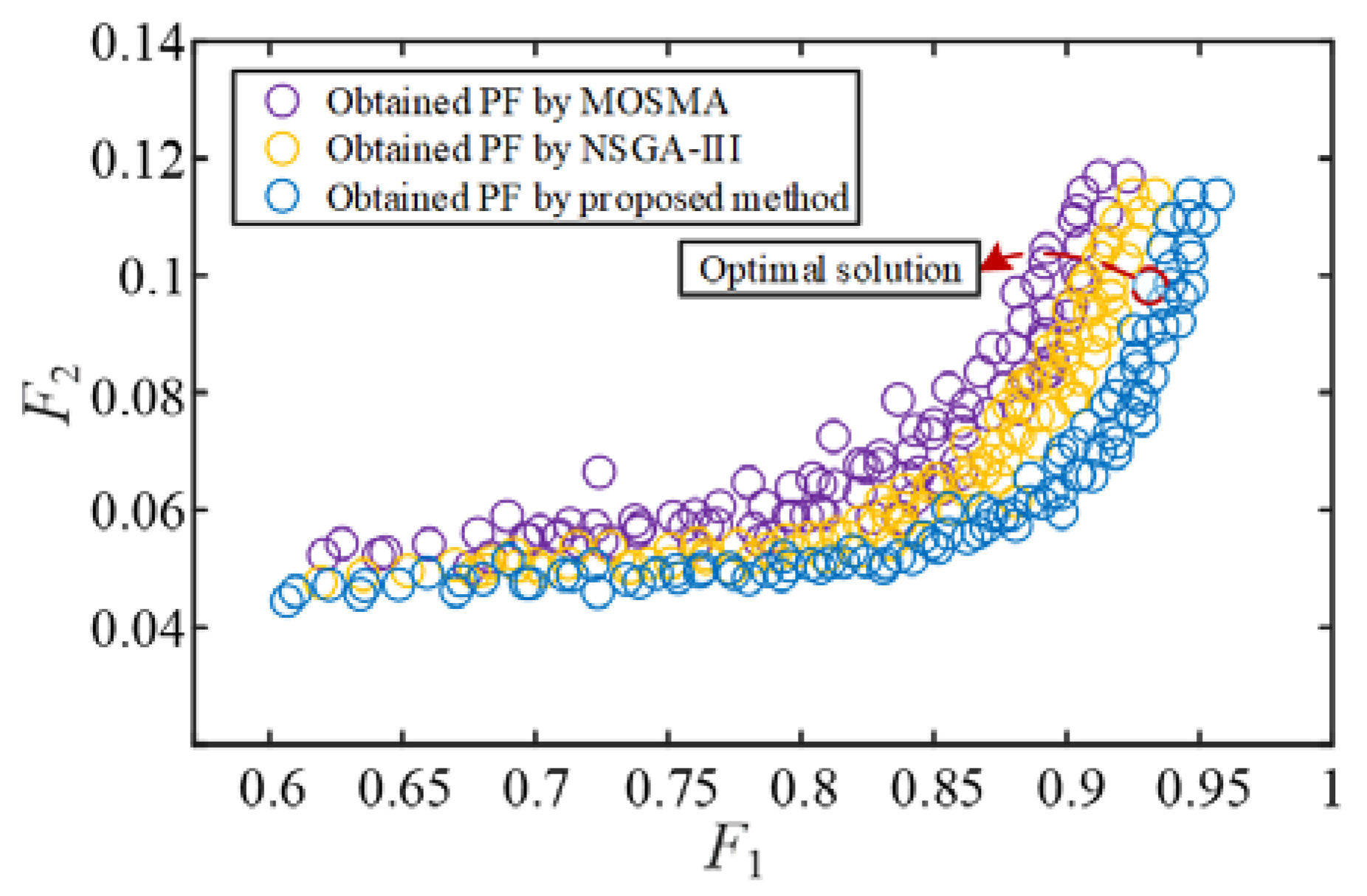
- The Pareto fronts (PFs) and optimal output solution can be calculated under different practical conditions, implying it is an adaptive algorithm that can be applied to the model of the MMC-HVDC-connected OWF.
4.2. Parameter Optimization Design Based on IMOSMA
5. Simulation and Experimental Verification
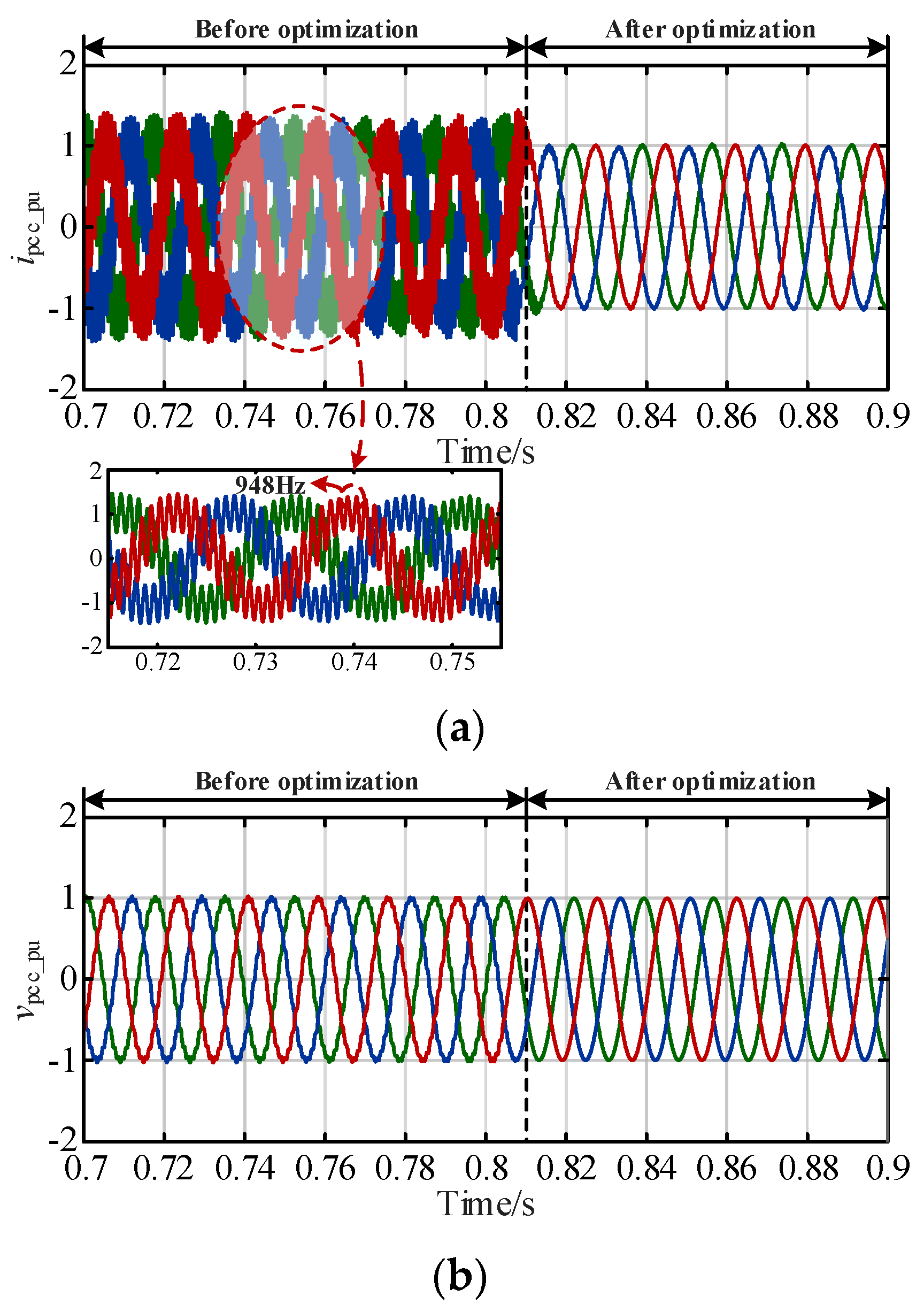
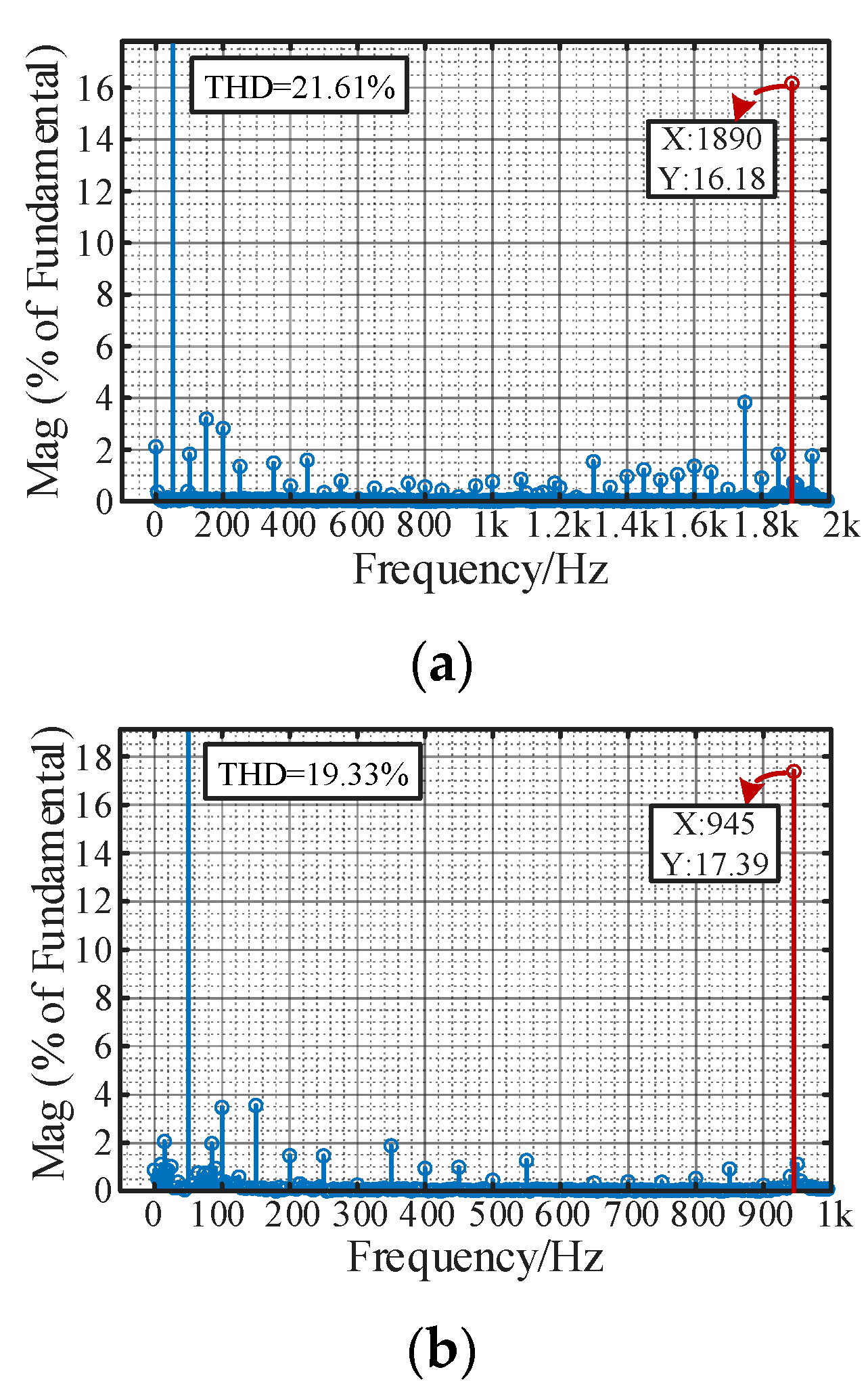
5.1. Simulation Results
5.2. Experimental Results
6. Conclusions
- (1)
- The established distribution parameter model is applicable to the long submarine cable network and reflects the periodic negative damping dynamics in the medium/high response, and the control delay effect has a similar influence in MMC. This solves the problem of the analysis of medium- and high-frequency oscillation characteristics being inaccurate due to ignoring the dynamic characteristics of medium and high frequencies in the existing methods.
- (2)
- The proportional coefficient of fundamental frequency voltage and current controllers in MMC and the phase current controller in the wind power converter, and the active damping controllers are the dominant factors of the wideband stability. The parallel virtual admittance control strategy could eliminate the negative damping behaviors in the medium/high-frequency band while deteriorating the sub/super-synchronous damping performance and intensifying the risk of super-synchronous resonances. The elucidated mechanism of medium- and high-frequency dynamic stability provides theoretical support for research on the strategy of improving the dynamic stability of medium and high frequency.
- (3)
- The proposed IMOSMA optimization algorithm outperforms the others, improving the population quality and global search ability of the algorithm, and the coordinated control strategy could enhance the adaptability of controller parameters and the wideband damping ability of the grid-connected system for meeting the wideband stability demand. The applicable regions of the controller parameters were also derived. The simulation and experimental results verify the correctness of the stability analysis conclusion and feasibility of the proposed control strategy.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Beza, M.; Bongjorno, M. Identification of resonance interactions in offshore-wind farms connected to the main grid by MMC-based HVDC system. Int. J. Electr. Power Energy Syst. 2019, 111, 101–113. [Google Scholar] [CrossRef]
- Ji, K.; Liu, S.; Pang, H.; Yang, J.; Xu, Z.G.; He, Z.Y.; Tang, G.F. Generalized Impedance Analysis and New Sight at Damping Controls for Wind Farm Connected MMC–HVdc. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 7278–7295. [Google Scholar] [CrossRef]
- Man, J.F.; Xie, X.R.; Xu, S.K.; Zou, C.Y.; Yin, C.Q. Frequency-coupling impedance model based analysis of a high-frequency resonance incident in an actual MMC-HVDC system. IEEE Trans. Power Deliv. 2020, 35, 2963–2971. [Google Scholar] [CrossRef]
- Amin, M.; Molinas, M. Understanding the origin of oscillatory phenomena observed between wind farms and HVdc systems. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 378–392. [Google Scholar] [CrossRef]
- Li, Y.; Fan, L.L.; Miao, Z.X. Wind in weak grids: Low-frequency oscillations, subsynchronous oscillations, and torsional interactions. IEEE Trans. Power Syst. 2020, 35, 109–118. [Google Scholar] [CrossRef]
- Wang, Y.F.; Zhao, C.Y.; Guo, C.Y.; Rehman, A.U. Dynamics and small signal stability analysis of PMSG-based wind farm with an MMC-HVDC system. CSEE J. Power Energy Syst. 2020, 6, 226–235. [Google Scholar]
- Liu, H.C.; Sun, J. Voltage stability and control of OWFs with AC collection and HVDC transmission. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 1181–1189. [Google Scholar]
- Lyu, J.; Cai, X.; Molinas, M. Frequency domain stability analysis of MMC-based HVDC for wind farm integration. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 141–151. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X.F.; Kocewiak, L.H. Impedance-based stability analysis of voltage-controlled MMCs feeding linear AC systems. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 4060–4074. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, X.; Gao, B.; Xiao, X.Y. Harmonic impedance model of DFIG considering dynamic coupling effect of DC link. Power Syst. Technol. 2022, 46, 558–567. [Google Scholar]
- Zhu, S.; Liu, K.P.; Wang, Q.; Li, Y.Y.; Qin, L.; Ji, K.; Cheng, F.; Wang, F.Z. Sub-synchronous oscillation suppression of modular multilevel converter based on capacitance energy and its impedance analysis. Proc. CSEE 2021, 41, 2230–2244. [Google Scholar]
- Zou, C.Y.; Rao, H.; Xu, S.K.; Li, Y.; Li, W.W.; Chen, J.; Zhao, X.B.; Yang, Y.; Lei, B. Analysis of resonance between a VSC-HVDC converter and the AC grid. IEEE Trans. Power Electron. 2018, 33, 10157–10168. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Luo, A.; Kuang, H.M.; Zhou, L.M.; Chen, Y.D.; Huang, Y. Harmonic resonance characteristics of large-scale distributed power plant in wideband frequency domain. Electr. Power Syst. Res. 2017, 143, 53–65. [Google Scholar] [CrossRef]
- Song, Y.P.; Ebrahimzadeh, E.; Blaabjerg, F. Analysis of high-frequency resonance in DFIG-based OWF via long transmission cable. IEEE Trans. Energy Convers. 2018, 33, 1036–1046. [Google Scholar] [CrossRef]
- Qin, Y.; Wang, H.; Zhuang, S.L.; Cai, X.; Lyu, J.; Huo, Q.T. Analysis on high frequency resonance of collector network in OWF. Proc. CSEE 2021, 42, 5169–5182. [Google Scholar]
- Ren, Y.N.; Wang, X.H.; Chen, L.; Min, Y.; Li, G.; Wang, L.K.; Zhang, Y.W. A strictly sufficient stability criterion for grid-connected converters based on impedance models and Gershgorin’s theorem. IEEE Trans. Power Deliv. 2020, 35, 1606–1609. [Google Scholar] [CrossRef]
- Nian, H.; Zhu, M.W.; Xu, Y.Y.; Chen, L.; Zou, C.Y.; Xu, S.K. Impedance modeling and system stability analysis of MMC with double closed-loop AC voltage control. Autom. Electr. Power Syst. 2020, 44, 81–90. [Google Scholar]
- Li, G.H.; Wang, W.S.; Guo, J.B.; Chen, X.; Liu, C.; He, G.Q. Broadband oscillation mechanism and analysis for wind farm integration through MMC-HVDC system. Proc. CSEE 2019, 39, 5281–5297. [Google Scholar]
- Huang, T.; Yang, F.; Zhang, D.H.; Chen, X. High-frequency stability analysis and impedance optimization for an MMC-HVDC integrated system considering delay effects. IEEE J. Emerg. Sel. Top. Circuits Syst. 2022, 12, 59–72. [Google Scholar] [CrossRef]
- Li, Y.F.; An, T.; Zhang, D.; Pei, X.Y.; Ji, K.; Tang, G.F. Analysis and suppression control of high frequency resonance for MMC-HVDC system. IEEE Trans. Power Deliv. 2021, 36, 3867–3881. [Google Scholar] [CrossRef]
- Bostani, Y.; Jalilzadeh, S.; Mobayen, S.; Rojsiraphisal, T.; Bartoszewicz, A. Damping of Subsynchronous Resonance in Utility DFIG-Based Wind Farms Using Wide-Area Fuzzy Control Approach. Energies 2022, 15, 1787. [Google Scholar] [CrossRef]
- Ji, K.; Pang, H.; He, Z.Y.; Li, Y.F.; Liu, D.; Tang, G.F. Active/passive method-based hybrid high-frequency damping design for MMCs. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 6086–6098. [Google Scholar] [CrossRef]
- Akbari, M.S.; Asemani, M.H.; Vafamand, N.; Mobayen, S.; Fekih, A. Observer-Based Predictive Control of Nonlinear Clutchless Automated Manual Transmission for Pure Electric Vehicles: An LPV Approach. IEEE Access 2021, 9, 20469–20480. [Google Scholar] [CrossRef]
- Lyu, J.; Cai, X.; Molinas, M. Optimal design of controller parameters for improving the stability of MMC-HVDC for wind farm integration. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 40–53. [Google Scholar] [CrossRef]
- Ji, K.; Chen, W.M.; Wu, X.G.; Pang, H.; Hu, J.; Liu, S.; Cheng, F.; Tang, G.F. High frequency stability constraints based MMC controller design applying NSGA-III algorithm. CSEE J. Power Energy Syst. 2021, 9, 623–633. [Google Scholar] [CrossRef]
- Premkumar, M.; Jangir, P.; Sowmya, R.; Alhelou, H.H.; Heidari, A.A.; Chen, H.L. MOSMA: Multi-objective slime mold algorithm based on elitist non-dominated sorting. IEEE Access 2021, 9, 3229–3248. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Abdulkareem, I.H.; Hashim, K.S.; Al-Bugharbee, H.; Ridha, H.M.; Gharghan, S.K.; Al-Qaim, F.F.; Muradov, M.; Kot, P.; Al-Khaddar, R. Hybridised artificial neural network model with slime mould algorithm: A novel methodology for prediction of urban stochastic water demand. Water 2020, 12, 2692. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]










| Model | Parameter | Value |
|---|---|---|
| OWF | Nominal power | Sbase1 = 400 MW |
| Nominal AC voltage | Vn = 0.69 kV | |
| Nominal DC voltage | Vwdc = 1.2 kV | |
| Phase current regulator | kip1 = 3.107, kii1 = 120 | |
| PLL regulator | kpp = 12.003, kpi = 180 | |
| AC cable collection network | 35 kV cable resistance | R35 = 0.365 Ω/km |
| 35 kV cable inductance | L35 = 0.503 mH/km | |
| 35 kV cable capacitance | C35 = 0.117 μF/km | |
| 220 kV cable resistance | R220 = 0.064 Ω/km | |
| 220 kV cable inductance | L220 = 0.427 mH/km | |
| 220 kV cable capacitance | C220 = 0.139 μF/km | |
| WSMMC | AC system line voltage | Vs = 370 kV |
| DC Nominal voltage | Vmdc = 640 kV | |
| Number of submodules | Ns = 200 | |
| Submodule capacitance | Csm = 8 mF | |
| Arm inductance | Larm = 80 mH | |
| Arm resistance | Rarm = 1 Ω | |
| Delay time | Td = 550 μs | |
| AC voltage regulator | kvp = 1.102, kvi = 30 | |
| Phase current regulator | kip2 = 2.816, kip2 = 50 | |
| CCSC | kcp = 38.805, kci = 1500 |
| Controllers | Parameters | Value |
|---|---|---|
| (900 Hz, 0.707, 1) | ||
| (900 Hz, 0.707, 1) | ||
| Gdamp(s) | (30 Hz, 400 Hz, 1) |
| MOPs | IMOSMA | NSGA-III | MOSMA | |||
|---|---|---|---|---|---|---|
| IGD (10−3) | HV (10−1) | IGD (10−3) | HV (10−1) | IGD (10−3) | HV (10−1) | |
| ZDT4 | 3.966 | 7.199 | 17.83 | 7.053 | 358.1 | 4.719 |
| ZDT6 | 3.023 | 3.889 | 3.689 | 3.873 | 29.36 | 3.600 |
| DTLZ2 | 52.92 | 5.591 | 152.0 | 5.148 | 109.8 | 4.910 |
| DTLZ7 | 84.75 | 2.686 | 79.48 | 2.658 | 151.1 | 2.300 |
| Performance | Optimized Controller Parameters | ||||
|---|---|---|---|---|---|
| kip1 | kvp | kip2 | |||
| Initial value | 3.107 | 1.102 | 2.812 | (900 Hz, 0.707) | (900 Hz, 0.707) |
| MOSMA in [24] | 6.306 | 4.780 | 0.791 | (480 Hz, 0.712) | (1378 Hz, 2.251) |
| NSGA-III in [23] | 4.889 | 5.331 | 0.384 | (338 Hz, 0.574) | (1038 Hz, 1.811) |
| Proposed method | 5.124 | 5.818 | 0.515 | (496 Hz, 0.531) | (1285 Hz, 1.529) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, J.; Li, H.; Zhang, B.; Li, Q. Small-Signal Stability Analysis and MOSMA-Based Optimization Control Strategy of OWF with MMC-HVDC Grid Connection. Sensors 2024, 24, 139. https://doi.org/10.3390/s24010139
Zheng J, Li H, Zhang B, Li Q. Small-Signal Stability Analysis and MOSMA-Based Optimization Control Strategy of OWF with MMC-HVDC Grid Connection. Sensors. 2024; 24(1):139. https://doi.org/10.3390/s24010139
Chicago/Turabian StyleZheng, Jie, Hui Li, Bo Zhang, and Qinghe Li. 2024. "Small-Signal Stability Analysis and MOSMA-Based Optimization Control Strategy of OWF with MMC-HVDC Grid Connection" Sensors 24, no. 1: 139. https://doi.org/10.3390/s24010139
APA StyleZheng, J., Li, H., Zhang, B., & Li, Q. (2024). Small-Signal Stability Analysis and MOSMA-Based Optimization Control Strategy of OWF with MMC-HVDC Grid Connection. Sensors, 24(1), 139. https://doi.org/10.3390/s24010139






