PVS-GEN: Systematic Approach for Universal Synthetic Data Generation Involving Parameterization, Verification, and Segmentation
Abstract
1. Introduction
2. Background and Related Works
2.1. Overview of Synthetic Time-Series Data Generation
- Frequency denotes the number of data inputs collected during a specific time frame. High-frequency data, characterized by more values per unit of time, typically display increased variability and regularity. Conversely, low-frequency data exhibit decreases in these traits.
- Variability measures the degree of change in sensor values over time. A high variability indicates rapid and frequent changes in the sensor values, whereas a low variability denotes slow and gradual shifts.
- Regularity refers to the uniformity of the recurring patterns in the data. High regularity suggests a consistent pattern, requiring fewer data samples to fully represent the data. Conversely, low regularity indicates less uniformity in the data patterns, requiring more data samples for a complete representation.
2.2. Related Works
- Statistical methods: Traditional statistical methods have been employed to generate time-series synthetic data by modeling sensor output results. Examples of statistical models include simple exponential smoothing (SES), autoregressive integrated moving average (ARIMA), and Gaussian mixture models (GMM).
- Machine learning methods: These techniques leverage machine learning algorithms to learn patterns and structures in the empirical data and generate synthetic data that resemble the original data. Examples of machine learning methods for synthetic data generation include deep learning techniques such as generative adversarial networks (GANs), variational autoencoders (VAEs), support vector regression (SVR), and recurrent neural networks (RNNs).
2.3. Challenges and Contributions
- A universal synthetic data-generation model independent of sensor data traits.
- An automated process for data generation that eliminates the need for parameter estimation or separate supervised learning.
- A universally applicable verification metric irrespective of sensors and generation methodologies.
- We introduce a modeling methodology for universal synthetic data generation that is independent of sensor data traits, thereby enabling adaptable data synthesis for diverse sensor types and a generation process with unparalleled scalability.
- We propose an automated process with its data frame for synthetic data generation, thereby reducing the intricacies of parameter tuning and supervised learning, which bolsters consistency, enhances reproducibility, and streamlines the qualitative overhead in the modeling process.
- We formulate a universally applicable verification metric that adeptly encapsulates the temporal dynamics of time-series data, facilitating precise differentiations between empirical and synthetic datasets, thereby augmenting both the consistency and reliability of data quality assessments across various research endeavors.
3. PVS-GEN: Automated Universial Synthetic Data Generation
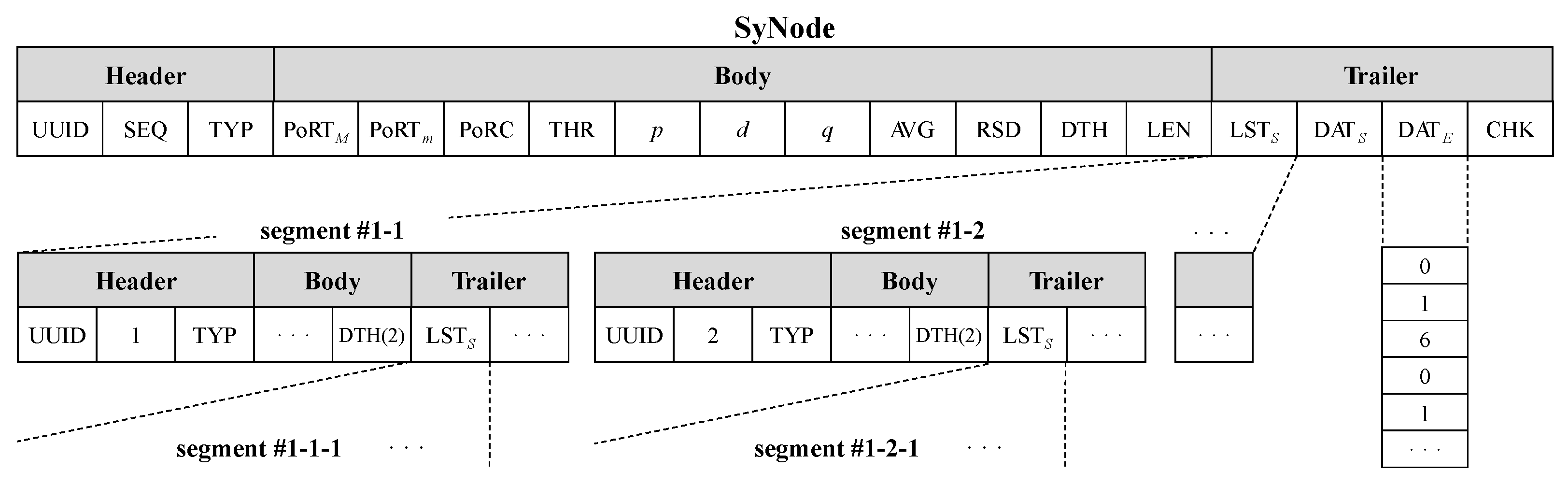
3.1. Parameterization: Configuring a SyNode for Synthetic Data Generation
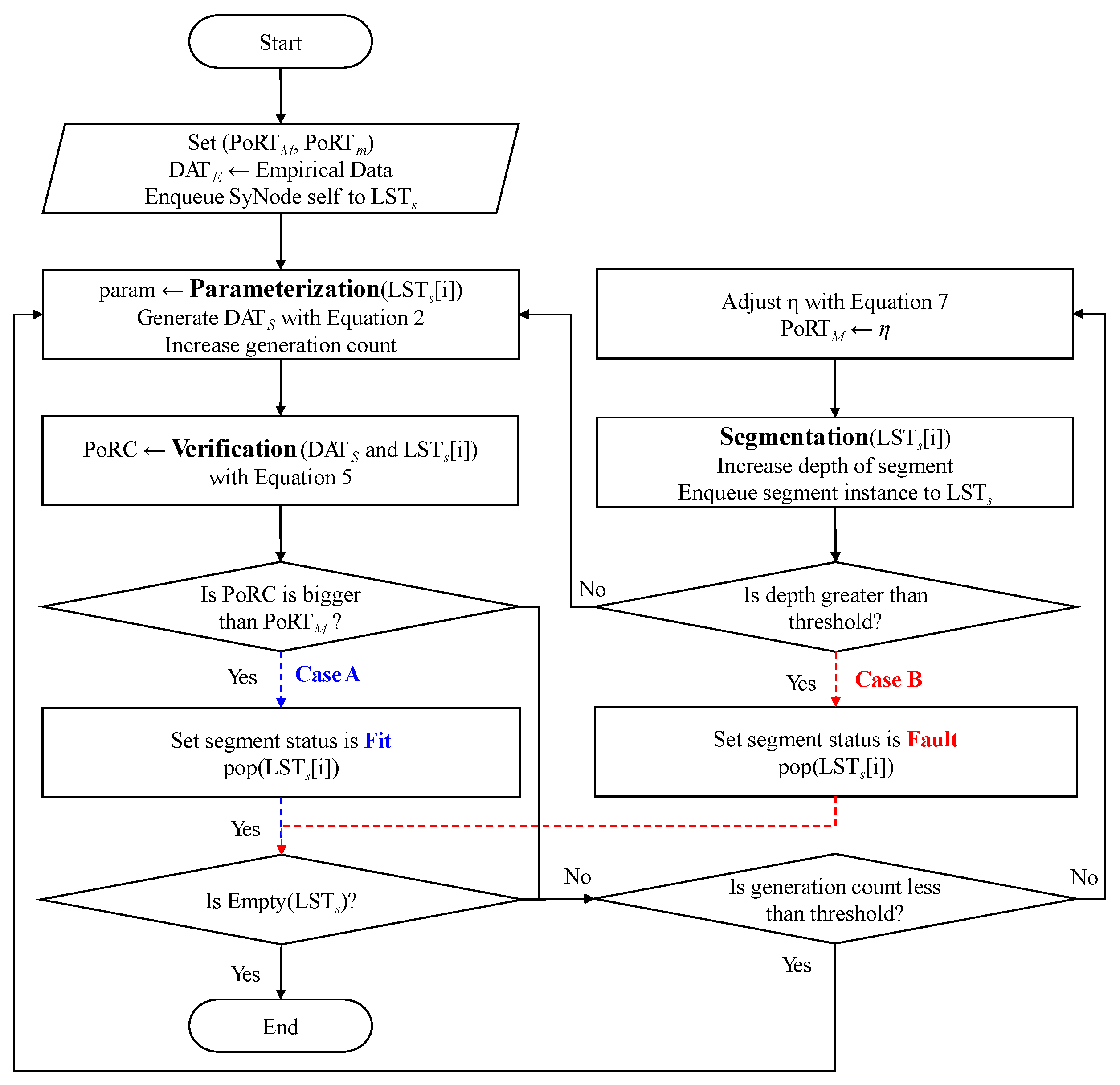
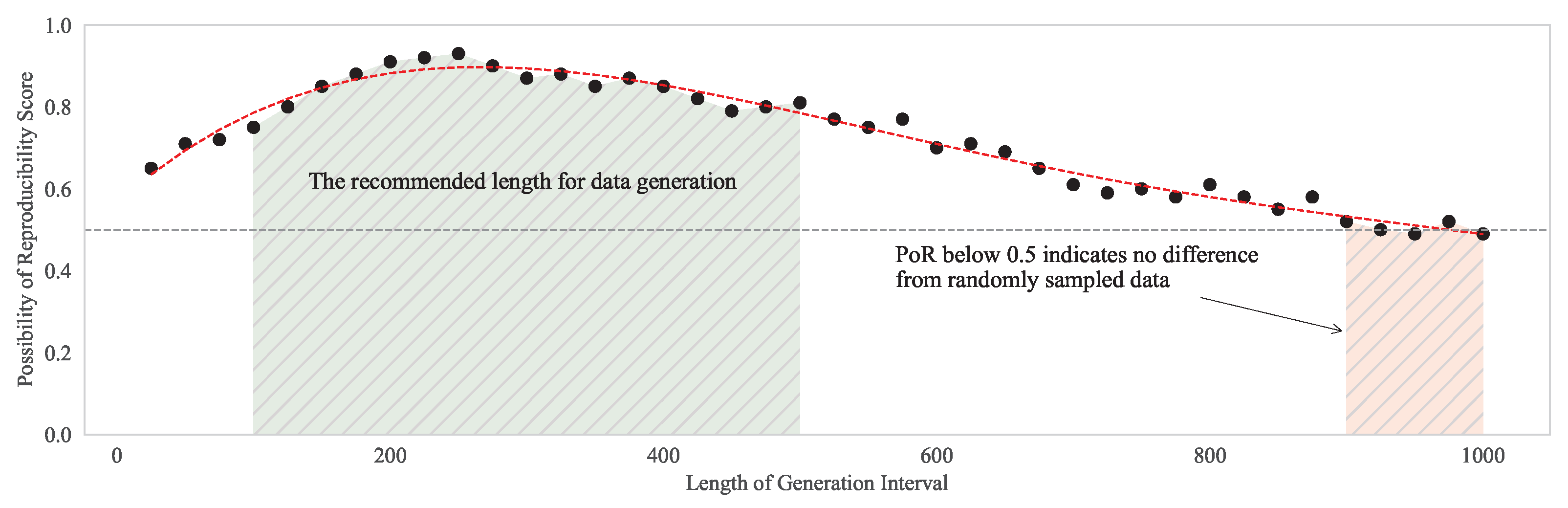
3.2. Verification: Assessing Model Reproducibility via Frequency Domain Analysis
| Algorithm 1 Obtain time-series similarity via the possibility of reproducibility |
 |
3.3. Segmentation: Data Partitioning with Change-Point Detection
| Algorithm 2 Divide a SyNode into SyNode segments with change-point detection |
 |
3.4. PVS-GEN Process
- Innovative methodology for synthetic data generation: PVS-GEN builds upon existing methods of synthetic data generation but refines and enhances them specifically for the challenges of time-series data generation. This approach has led to the development of a novel methodology capable of effectively generating synthetic data that mirror the empirical characteristics across various sensor data types.
- Automated synthetic data generation process: PVS-GEN introduces an automated process for data parameterization, significantly reducing human intervention. Simultaneously, it incorporates an efficient segmentation and parameter extraction process for empirical datasets. This approach allows for the effective handling of complex data and enhances the consistency and regularity of time-series data.
- Introduction of a new metric for time-series similarity evaluation: Our research proposes the PoR metric as a novel method for evaluating the quality of synthetic data. This metric assesses time-series characteristics in a manner different from existing models, offering a new standard for evaluating the quality of synthetic data. It enables researchers to compare the similarity between synthetic and empirical data more precisely.
4. Results and Discussion
4.1. Experiment Setup
- Gas Sensor Array Dataset: This dataset, generated from a small polytetrafluoroethylene (PTFE) test chamber exposed to dynamic mixtures of CO and humid synthetic air, provides the mixtures sourced from high-purity gases and delivered to the chamber through a mass flow-controlled piping system [54].
- Low-Energy House Dataset: This dataset contains data on the energy usage of appliances in a low-energy house. It features both temperature and humidity measurements, providing a comprehensive account of energy consumption patterns in relation to these environmental variables [55].
- EEG Alcoholism Dataset: This dataset is from a study investigating how EEG signals correlate to the genetic predisposition of alcoholism. The dataset features EEG recordings from 122 subjects, categorized as alcoholic or control. Subjects were exposed to visual stimuli under various conditions. Three versions of the dataset are available, differing in the number of subjects and trials included [56].
- Heterogeneity Activity Recognition Dataset: This dataset includes readings from two motion sensors (Accelerometer and Gyroscope) in smartphones and smartwatches, used to investigate sensor heterogeneities’ impacts on human activity recognition algorithms. Data were collected from nine users executing six activities, capturing data at the highest frequency allowed [57].
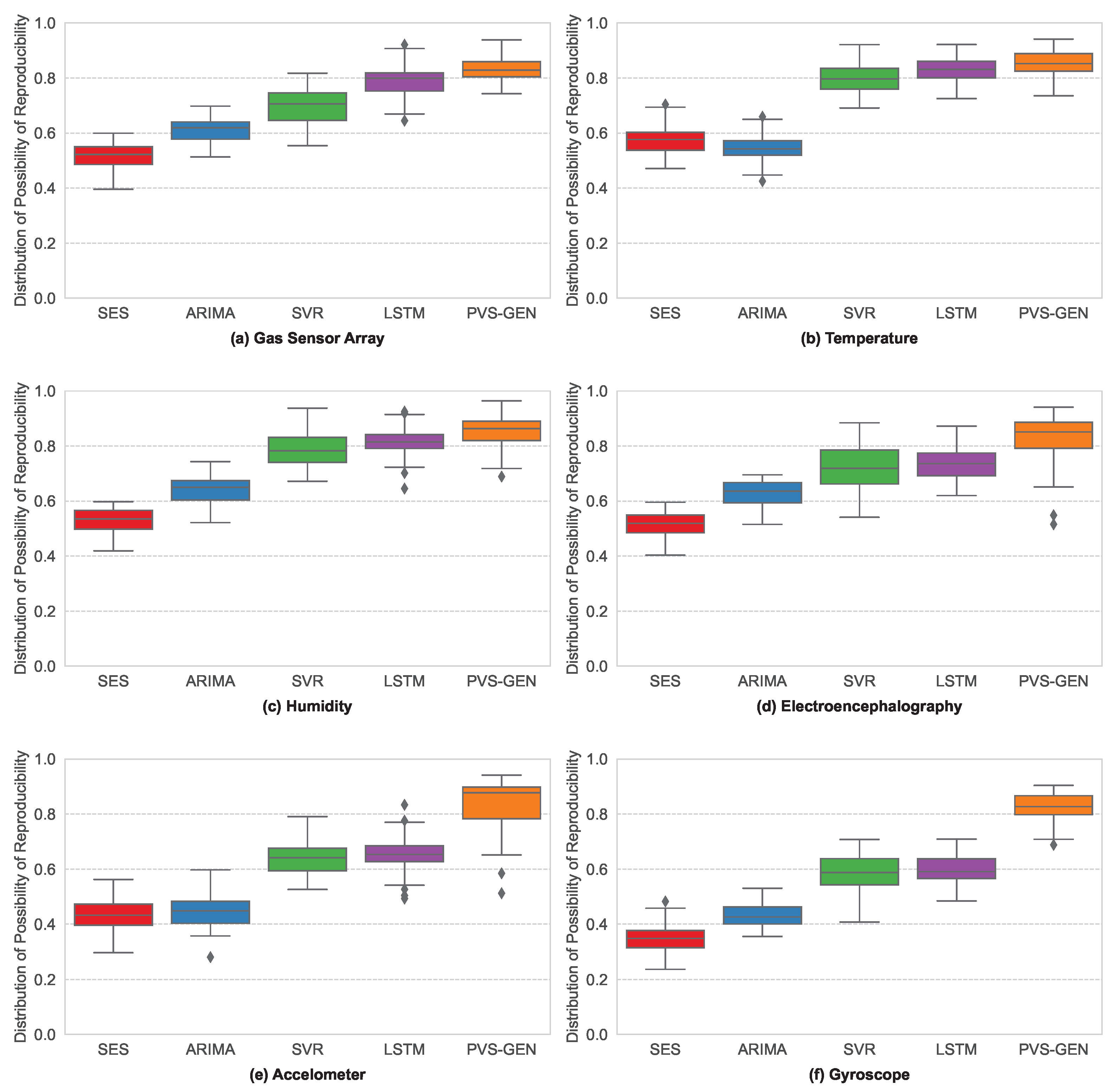
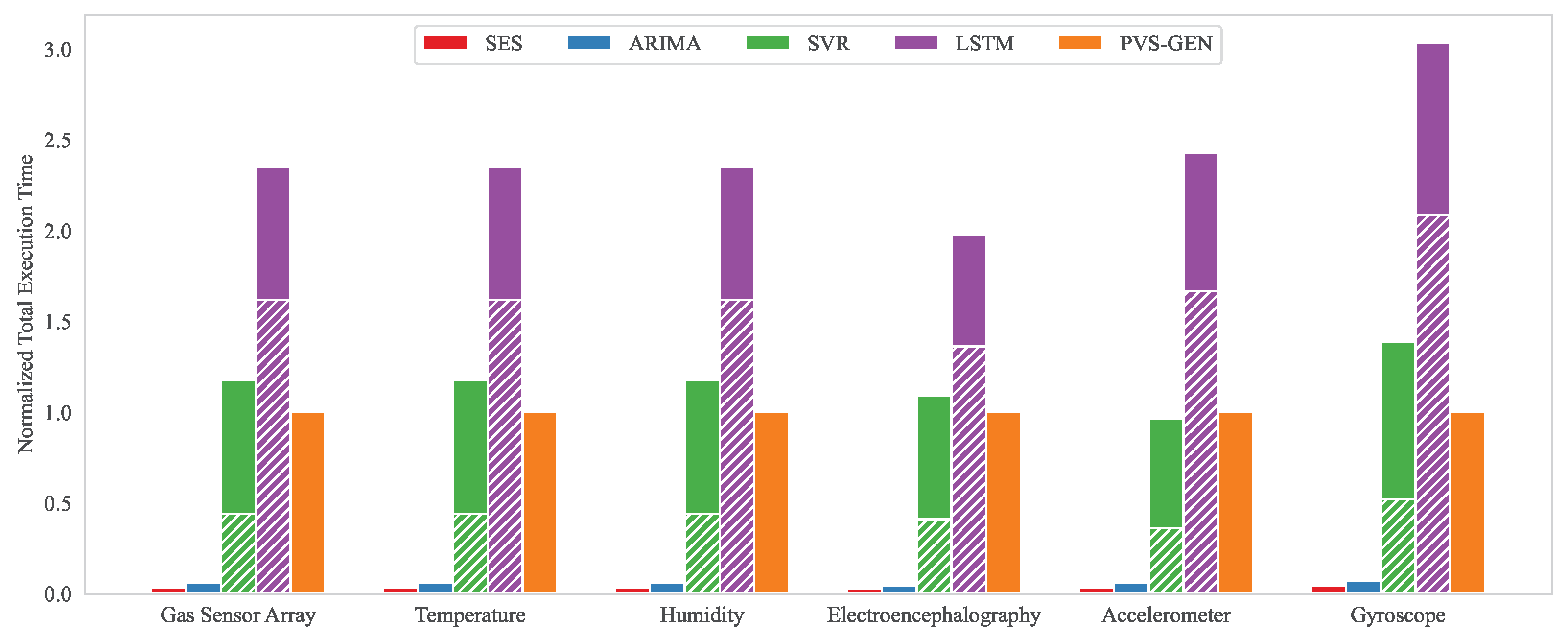
4.2. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Al Khalil, Y.; Amirrajab, S.; Lorenz, C.; Weese, J.; Pluim, J.; Breeuwer, M. On the usability of synthetic data for improving the robustness of deep learning-based segmentation of cardiac magnetic resonance images. Med. Image Anal. 2023, 84, 102688. [Google Scholar] [CrossRef] [PubMed]
- Luotsinen, L.J.; Kamrani, F.; Lundmark, L.; Sabel, J.; Stiff, H.; Sandström, V. Deep Learning with Limited Data: A Synthetic Approach; Totalförsvarets Forskningsinstitut: Stockholm, Sweden, 2021. [Google Scholar]
- Lu, Y.; Wang, H.; Wei, W. Machine Learning for Synthetic Data Generation: A Review. arXiv 2023, arXiv:2302.04062. [Google Scholar]
- Pérez-Porras, F.J.; Triviño-Tarradas, P.; Cima-Rodríguez, C.; Meroño-de Larriva, J.E.; García-Ferrer, A.; Mesas-Carrascosa, F.J. Machine learning methods and synthetic data generation to predict large wildfires. Sensors 2021, 21, 3694. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Panagiotakos, D. Real-world data: A brief review of the methods, applications, challenges and opportunities. BMC Med. Res. Methodol. 2022, 22, 287. [Google Scholar] [CrossRef] [PubMed]
- Wen, Q.; Zhang, Z.; Li, Y.; Sun, L. Fast RobustSTL: Efficient and robust seasonal-trend decomposition for time series with complex patterns. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery &Data Mining, Virtual, 6–10 July 2020; pp. 2203–2213. [Google Scholar]
- Kotelnikov, A.; Baranchuk, D.; Rubachev, I.; Babenko, A. Tabddpm: Modelling tabular data with diffusion models. In Proceedings of the International Conference on Machine Learning, PMLR, Honolulu, HI, USA, 23–29 July 2023; pp. 17564–17579. [Google Scholar]
- Dargan, S.; Kumar, M.; Ayyagari, M.R.; Kumar, G. A survey of deep learning and its applications: A new paradigm to machine learning. Arch. Comput. Methods Eng. 2020, 27, 1071–1092. [Google Scholar] [CrossRef]
- Lee, I.; Shin, Y.J. Machine learning for enterprises: Applications, algorithm selection, and challenges. Bus. Horizons 2020, 63, 157–170. [Google Scholar] [CrossRef]
- Sarker, I.H. Machine learning: Algorithms, real-world applications and research directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar] [CrossRef]
- Parmezan, A.R.S.; Souza, V.M.; Batista, G.E. Evaluation of statistical and machine learning models for time series prediction: Identifying the state-of-the-art and the best conditions for the use of each model. Inf. Sci. 2019, 484, 302–337. [Google Scholar] [CrossRef]
- Palomero, L.; García, V.; Sánchez, J.S. Fuzzy-Based Time Series Forecasting and Modelling: A Bibliometric Analysis. Appl. Sci. 2022, 12, 6894. [Google Scholar] [CrossRef]
- Assefa, S.A.; Dervovic, D.; Mahfouz, M.; Tillman, R.E.; Reddy, P.; Veloso, M. Generating synthetic data in finance: Opportunities, challenges and pitfalls. In Proceedings of the First ACM International Conference on AI in Finance, New York, NY, USA, 15–16 October 2020; pp. 1–8. [Google Scholar]
- El Emam, K.; Mosquera, L.; Hoptroff, R. Practical Synthetic Data Generation: Balancing Privacy and the Broad Availability of Data; O’Reilly Media: Sebastopol, CA, USA, 2020. [Google Scholar]
- Joshi, I.; Grimmer, M.; Rathgeb, C.; Busch, C.; Bremond, F.; Dantcheva, A. Synthetic data in human analysis: A survey. arXiv 2022, arXiv:2208.09191. [Google Scholar]
- Tucker, A.; Wang, Z.; Rotalinti, Y.; Myles, P. Generating high-fidelity synthetic patient data for assessing machine learning healthcare software. NPJ Digit. Med. 2020, 3, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Kaggle. Kaggle Dataset Public Cloud. 2023. Available online: https://www.kaggle.com/datasets (accessed on 22 February 2023).
- Google Dataset Search. Available online: https://datasetsearch.research.google.com/ (accessed on 21 February 2023).
- Dua, D.; Graff, C. UCI Machine Learning Repository. 2019. Available online: http://archive.ics.uci.edu/ml (accessed on 21 July 2023).
- Kuppa, A.; Aouad, L.; Le-Khac, N.A. Towards improving privacy of synthetic datasets. In Proceedings of the Annual Privacy Forum, Oslo, Norway, 17–18 June 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 106–119. [Google Scholar]
- Khan, M.S.N.; Reje, N.; Buchegger, S. Utility assessment of synthetic data generation methods. arXiv 2022, arXiv:2211.14428. [Google Scholar]
- Yu, D.; Zhang, H.; Chen, W.; Yin, J.; Liu, T.Y. How does data augmentation affect privacy in machine learning? In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 10746–10753. [Google Scholar] [CrossRef]
- Triastcyn, A.; Faltings, B. Generating Higher-Fidelity Synthetic Datasets with Privacy Guarantees. Algorithms 2022, 15, 232. [Google Scholar] [CrossRef]
- Soufleri, E.; Saha, G.; Roy, K. Synthetic Dataset Generation for Privacy-Preserving Machine Learning. arXiv 2022, arXiv:2210.03205. [Google Scholar]
- Rankin, D.; Black, M.; Bond, R.; Wallace, J.; Mulvenna, M.; Epelde, G. Reliability of supervised machine learning using synthetic data in health care: Model to preserve privacy for data sharing. JMIR Med. Inform. 2020, 8, e18910. [Google Scholar] [CrossRef]
- Shiau, Y.H.; Yang, S.F.; Adha, R.; Muzayyanah, S. Modeling industrial energy demand in relation to subsector manufacturing output and climate change: Artificial neural network insights. Sustainability 2022, 14, 2896. [Google Scholar] [CrossRef]
- Mahia, F.; Dey, A.R.; Masud, M.A.; Mahmud, M.S. Forecasting electricity consumption using ARIMA model. In Proceedings of the 2019 International Conference on Sustainable Technologies for Industry 4.0 (STI), Dhaka, Banglades, 24–25 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Yan, B.; Mu, R.; Guo, J.; Liu, Y.; Tang, J.; Wang, H. Flood risk analysis of reservoirs based on full-series ARIMA model under climate change. J. Hydrol. 2022, 610, 127979. [Google Scholar] [CrossRef]
- Dahmen, J.; Cook, D. SynSys: A synthetic data generation system for healthcare applications. Sensors 2019, 19, 1181. [Google Scholar] [CrossRef]
- Kim, K.H.; Sohn, M.J.; Lee, S.; Koo, H.W.; Yoon, S.W.; Madadi, A.K. Descriptive time series analysis for downtime prediction using the maintenance data of a medical linear accelerator. Appl. Sci. 2022, 12, 5431. [Google Scholar] [CrossRef]
- Kim, K.; Song, J.; Kwak, J.W. PRIGM: Partial-Regression-Integrated Generic Model for Synthetic Benchmarks Robust to Sensor Characteristics. IEICE Trans. Inf. Syst. 2022, E105.D, 1330–1334. [Google Scholar] [CrossRef]
- Khan, F.M.; Gupta, R. ARIMA and NAR based prediction model for time series analysis of COVID-19 cases in India. J. Saf. Sci. Resil. 2020, 1, 12–18. [Google Scholar] [CrossRef]
- Satrio, C.B.A.; Darmawan, W.; Nadia, B.U.; Hanafiah, N. Time series analysis and forecasting of coronavirus disease in Indonesia using ARIMA model and PROPHET. Procedia Comput. Sci. 2021, 179, 524–532. [Google Scholar] [CrossRef]
- Castán-Lascorz, M.; Jiménez-Herrera, P.; Troncoso, A.; Asencio-Cortés, G. A new hybrid method for predicting univariate and multivariate time series based on pattern forecasting. Inf. Sci. 2022, 586, 611–627. [Google Scholar] [CrossRef]
- Rabbani, M.B.A.; Musarat, M.A.; Alaloul, W.S.; Rabbani, M.S.; Maqsoom, A.; Ayub, S.; Bukhari, H.; Altaf, M. a comparison between seasonal autoregressive integrated moving average (SARIMA) and exponential smoothing (ES) based on time series model for forecasting road accidents. Arab. J. Sci. Eng. 2021, 46, 11113–11138. [Google Scholar] [CrossRef]
- Wang, Z.; Olivier, J. Synthetic High-Resolution Wind Data Generation Based on Markov Model. In Proceedings of the 2021 13th IEEE PES Asia Pacific Power & Energy Engineering Conference (APPEEC), Trivandrum, India, 21–23 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Chen, Y.; Rao, M.; Feng, K.; Niu, G. Modified Varying Index Coefficient Autoregression Model for Representation of the Nonstationary Vibration From a Planetary Gearbox. IEEE Trans. Instrum. Meas. 2023, 72, 1–12. [Google Scholar]
- Shaukat, M.A.; Shaukat, H.R.; Qadir, Z.; Munawar, H.S.; Kouzani, A.Z.; Mahmud, M.P. Cluster analysis and model comparison using smart meter data. Sensors 2021, 21, 3157. [Google Scholar] [CrossRef]
- Rajagukguk, R.A.; Ramadhan, R.A.; Lee, H.J. A review on deep learning models for forecasting time series data of solar irradiance and photovoltaic power. Energies 2020, 13, 6623. [Google Scholar] [CrossRef]
- Boikov, A.; Payor, V.; Savelev, R.; Kolesnikov, A. Synthetic data generation for steel defect detection and classification using deep learning. Symmetry 2021, 13, 1176. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Chimmula, V.K.R.; Zhang, L. Time series forecasting of COVID-19 transmission in Canada using LSTM networks. Chaos Solitons Fractals 2020, 135, 109864. [Google Scholar] [CrossRef] [PubMed]
- Esteva, A.; Chou, K.; Yeung, S.; Naik, N.; Madani, A.; Mottaghi, A.; Liu, Y.; Topol, E.; Dean, J.; Socher, R. Deep learning-enabled medical computer vision. NPJ Digit. Med. 2021, 4, 5. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Zheng, X.; Li, J.; Zhu, B. Prediction of epidemic trends in COVID-19 with logistic model and machine learning technics. Chaos Solitons Fractals 2020, 139, 110058. [Google Scholar] [CrossRef] [PubMed]
- Sharadga, H.; Hajimirza, S.; Balog, R.S. Time series forecasting of solar power generation for large-scale photovoltaic plants. Renew. Energy 2020, 150, 797–807. [Google Scholar] [CrossRef]
- Yilmaz, B.; Korn, R. Synthetic demand data generation for individual electricity consumers: Generative Adversarial Networks (GANs). Energy AI 2022, 9, 100161. [Google Scholar] [CrossRef]
- Lee, M.; Yu, Y.; Cheon, Y.; Baek, S.; Kim, Y.; Kim, K.; Jung, H.; Lim, D.; Byun, H.; Lee, C.; et al. Machine Learning-Based Prediction of Controlled Variables of APC Systems Using Time-Series Data in the Petrochemical Industry. Processes 2023, 11, 2091. [Google Scholar] [CrossRef]
- Dudek, G. Pattern-based local linear regression models for short-term load forecasting. Electr. Power Syst. Res. 2016, 130, 139–147. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Khandakar, Y. Automatic Time Series Forecasting: The forecast Package for R. J. Stat. Softw. 2008, 27, 1–22. [Google Scholar] [CrossRef]
- Ospina, R.; Gondim, J.A.M.; Leiva, V.; Castro, C. An Overview of Forecast Analysis with ARIMA Models during the COVID-19 Pandemic: Methodology and Case Study in Brazil. Mathematics 2023, 11, 3069. [Google Scholar] [CrossRef]
- Killick, R.; Fearnhead, P.; Eckley, I.A. Optimal detection of changepoints with a linear computational cost. J. Am. Stat. Assoc. 2012, 107, 1590–1598. [Google Scholar] [CrossRef]
- Militino, A.F.; Moradi, M.; Ugarte, M.D. On the performances of trend and change-point detection methods for remote sensing data. Remote Sens. 2020, 12, 1008. [Google Scholar] [CrossRef]
- Fonollosa, J. Gas Sensor Array Exposed to Turbulent Gas Mixtures. UCI Machine Learning Repository. 2014. Available online: https://archive.ics.uci.edu/dataset/309/gas+sensor+array+exposed+to+turbulent+gas+mixtures. (accessed on 21 July 2023).
- Candanedo, L. Appliances Energy Prediction. UCI Machine Learning Repository. 2017. Available online: https://archive.ics.uci.edu/dataset/374/appliances+energy+prediction (accessed on 21 July 2023).
- Begleiter, H. EEG Database. UCI Machine Learning Repository. 1999. Available online: https://archive.ics.uci.edu/dataset/121/eeg+database (accessed on 21 July 2023).
- Stisen, A.; Blunck, H.; Bhattacharya, S.; Prentow, T.S.; Kjærgaard, M.B.; Dey, A.; Sonne, T.; Jensen, M.M. Smart devices are different: Assessing and mitigatingmobile sensing heterogeneities for activity recognition. In Proceedings of the 13th ACM Conference on Embedded Networked Sensor Systems, Seoul, Republic of Korea, 1–4 November 2015; pp. 127–140. [Google Scholar]
- Garza, F.; Canseco, M.M.; Challú, C.; Olivares, K.G. StatsForecast: Lightning Fast Forecasting with Statistical and Econometric Models; PyCon: Salt Lake City, UT, USA, 2022. [Google Scholar]
- Arlitt, M.; Marwah, M.; Bellala, G.; Shah, A.; Healey, J.; Vandiver, B. IoTAbench: An Internet of Things Analytics Benchmark. In Proceedings of the 6th ACM/SPEC International Conference on Performance Engineering, ICPE ’15, Austin, TX, USA, 28 January–4 February 2015; pp. 133–144. [Google Scholar] [CrossRef]
- Burgués, J.; Marco, S. Multivariate estimation of the limit of detection by orthogonal partial least squares in temperature-modulated MOX sensors. Anal. Chim. Acta 2018, 1019, 49–64. [Google Scholar] [CrossRef] [PubMed]
- Burgués, J.; Jiménez-Soto, J.M.; Marco, S. Estimation of the limit of detection in semiconductor gas sensors through linearized calibration models. Anal. Chim. Acta 2018, 1013, 13–25. [Google Scholar] [CrossRef] [PubMed]
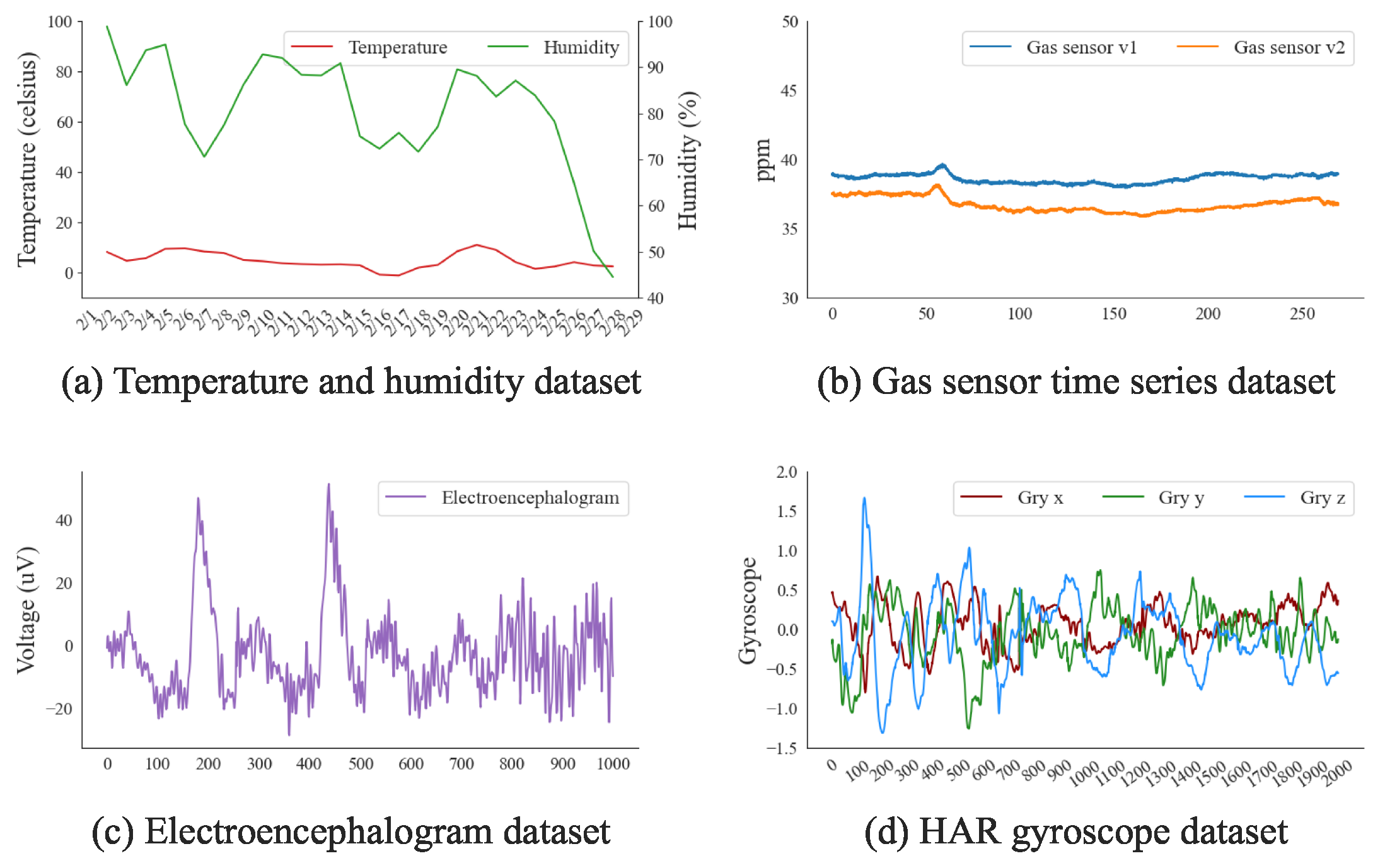
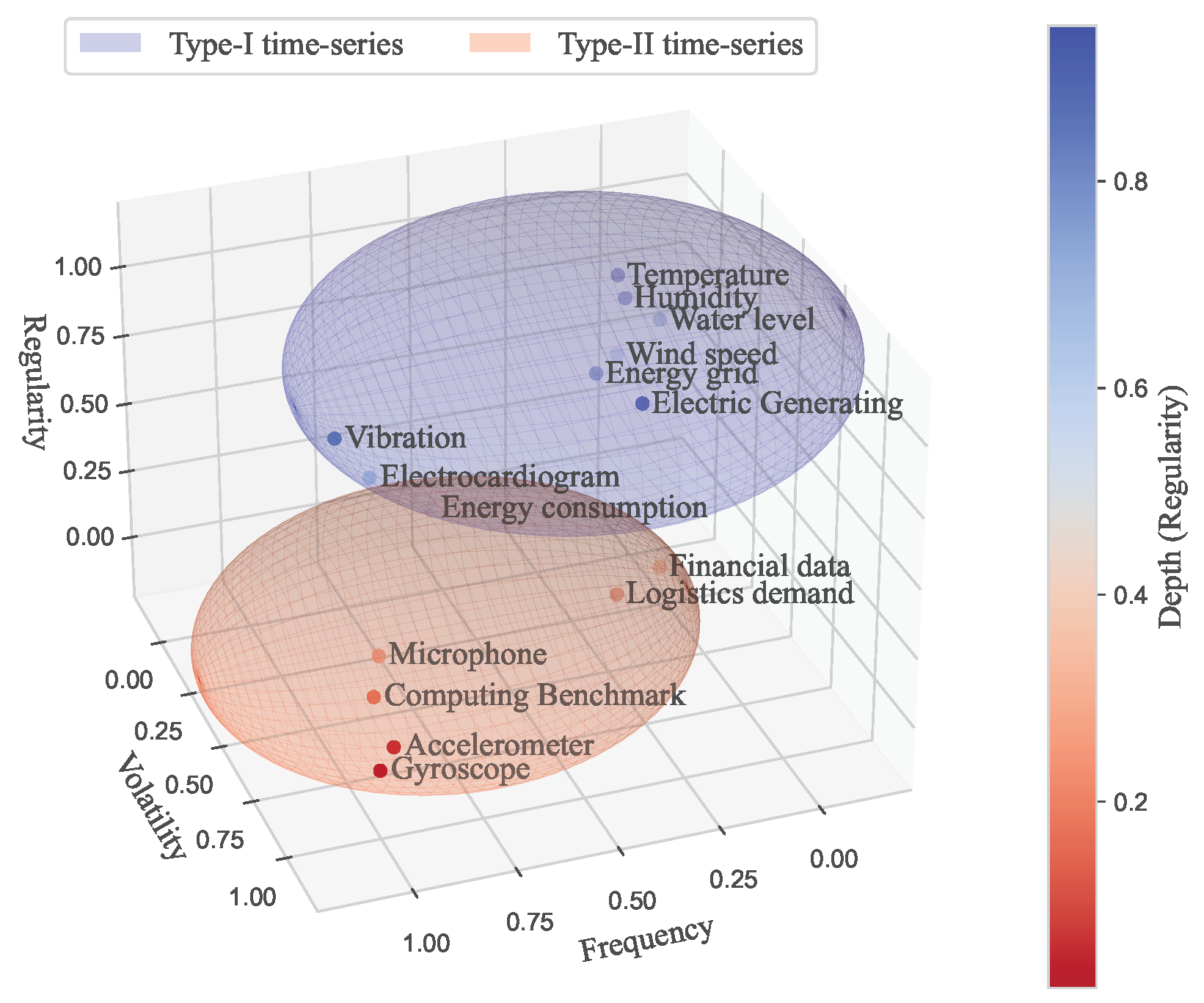


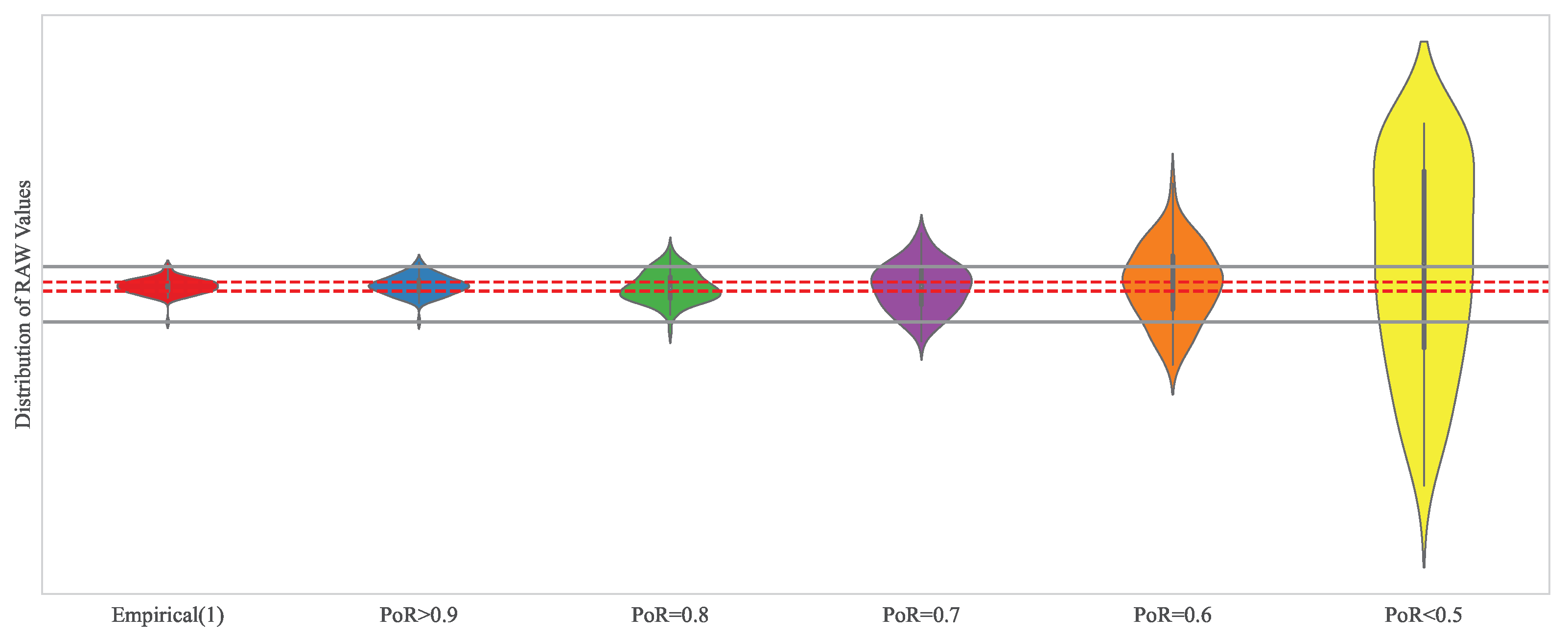
| Frequency | Variance * | Regularity | |
|---|---|---|---|
| Type-I time series (low volatility) | Low | Low | High |
| Type-II time series (high volatility) | High | High | Low |
| Category | Proposal | Base Methodology | Target Data | Features |
|---|---|---|---|---|
| Statistical Based Model | ARIMA Model for predict Flood Risk [28] | Full-Series ARIMA, BMA method | Yalong River Basin Flood | Utilizes ARIMA for synthesizing future flood series, integrating past and predicted data. |
| Duplex Markov Models [36] | Markov Chain | Wind Speed | Applies three Markov models for accurate high-resolution wind speed data generation. | |
| Modified VICAR [37] | VICAR | Gearbox Vibration Signals | Produces synthetic signals for improved detection of faults in gearboxes using VICAR | |
| Machine Learning Based Model | Deep Learning Model for Solar Energy Prediction [39] | CNN-LSTM | Solar Irradiance, PV Power | Creates predictive synthetic data for solar energy using CNN-LSTM Model |
| LSTM Model for COVID-19 Forecasting [45] | LSTM | COVID-19 Case Data in Canada | Generates forecasted synthetic data for spread of COVID-19 and their intervention impact | |
| GAN model for Electricity Consumption [47] | RCGAN, TimeGAN, CWGAN, RCWGAN | Electricity Consumption | Synthesizes electricity consumption data for smart grids using various GANs. |
| Dataset | Sensor Type | Data Range | Unit | Dataset Size |
|---|---|---|---|---|
| Gas Sensor Array | Gas Sensor Array | 0∼ | ppm | 284.58 MB |
| Low-Energy House | Temperature | ∼ | °C | 11.42 MB |
| Humidity | 0∼ | %R.H. | ||
| EEG Alcoholism | Electroencephalography | ∼ | mV | 762.2 MB |
| Heterogeneity Activity Recognition | Accelerometer | ∼ | g | 3.07 GB |
| Gyroscope | ∼ | rad/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.-M.; Kwak, J.W. PVS-GEN: Systematic Approach for Universal Synthetic Data Generation Involving Parameterization, Verification, and Segmentation. Sensors 2024, 24, 266. https://doi.org/10.3390/s24010266
Kim K-M, Kwak JW. PVS-GEN: Systematic Approach for Universal Synthetic Data Generation Involving Parameterization, Verification, and Segmentation. Sensors. 2024; 24(1):266. https://doi.org/10.3390/s24010266
Chicago/Turabian StyleKim, Kyung-Min, and Jong Wook Kwak. 2024. "PVS-GEN: Systematic Approach for Universal Synthetic Data Generation Involving Parameterization, Verification, and Segmentation" Sensors 24, no. 1: 266. https://doi.org/10.3390/s24010266
APA StyleKim, K.-M., & Kwak, J. W. (2024). PVS-GEN: Systematic Approach for Universal Synthetic Data Generation Involving Parameterization, Verification, and Segmentation. Sensors, 24(1), 266. https://doi.org/10.3390/s24010266





