Improvement in Multi-Angle Plane Wave Image Quality Using Minimum Variance Beamforming with Adaptive Signal Coherence
Abstract
1. Introduction
2. Theory
2.1. CPWC Beamforming
2.2. MV Beamforming for PW Imaging
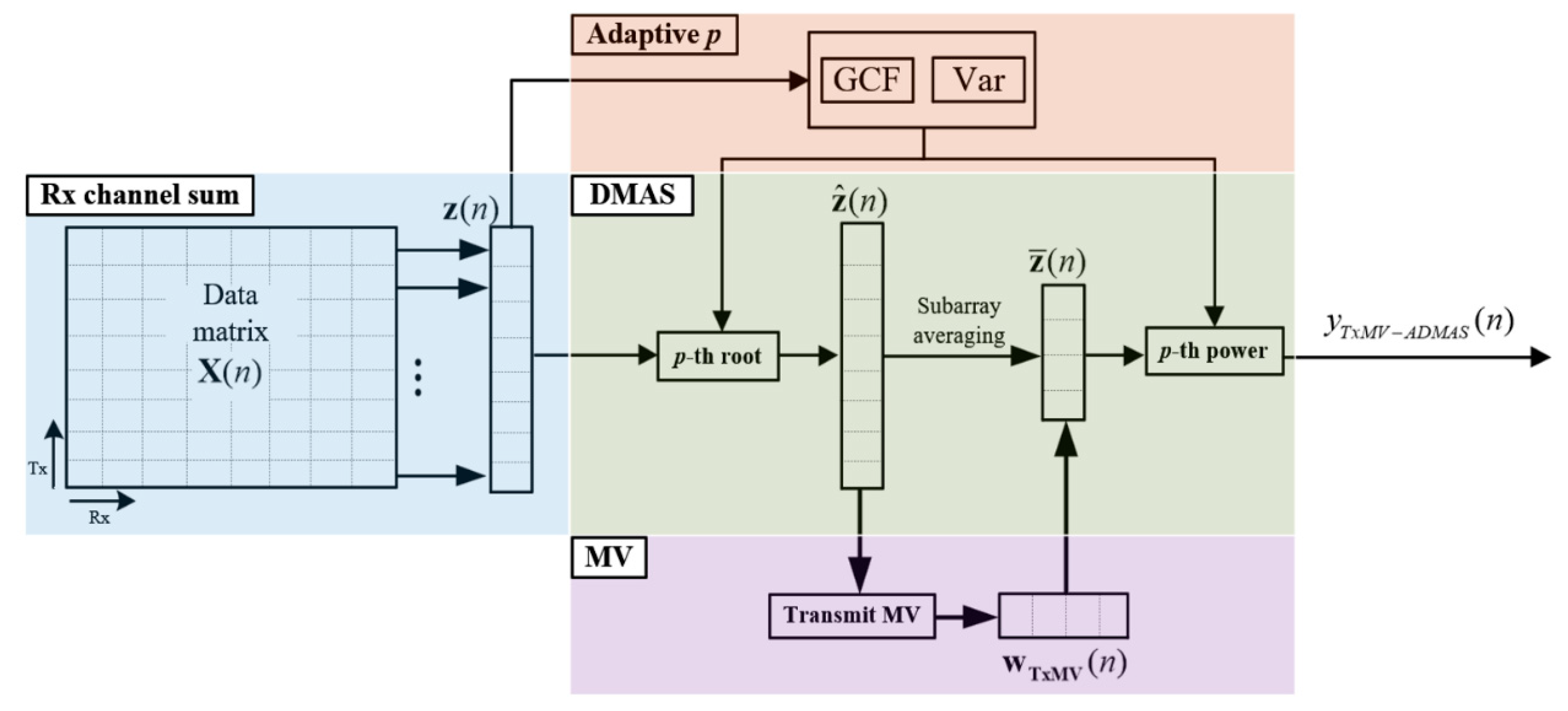
2.3. TxMV-DMAS Beamforming for PW Imaging
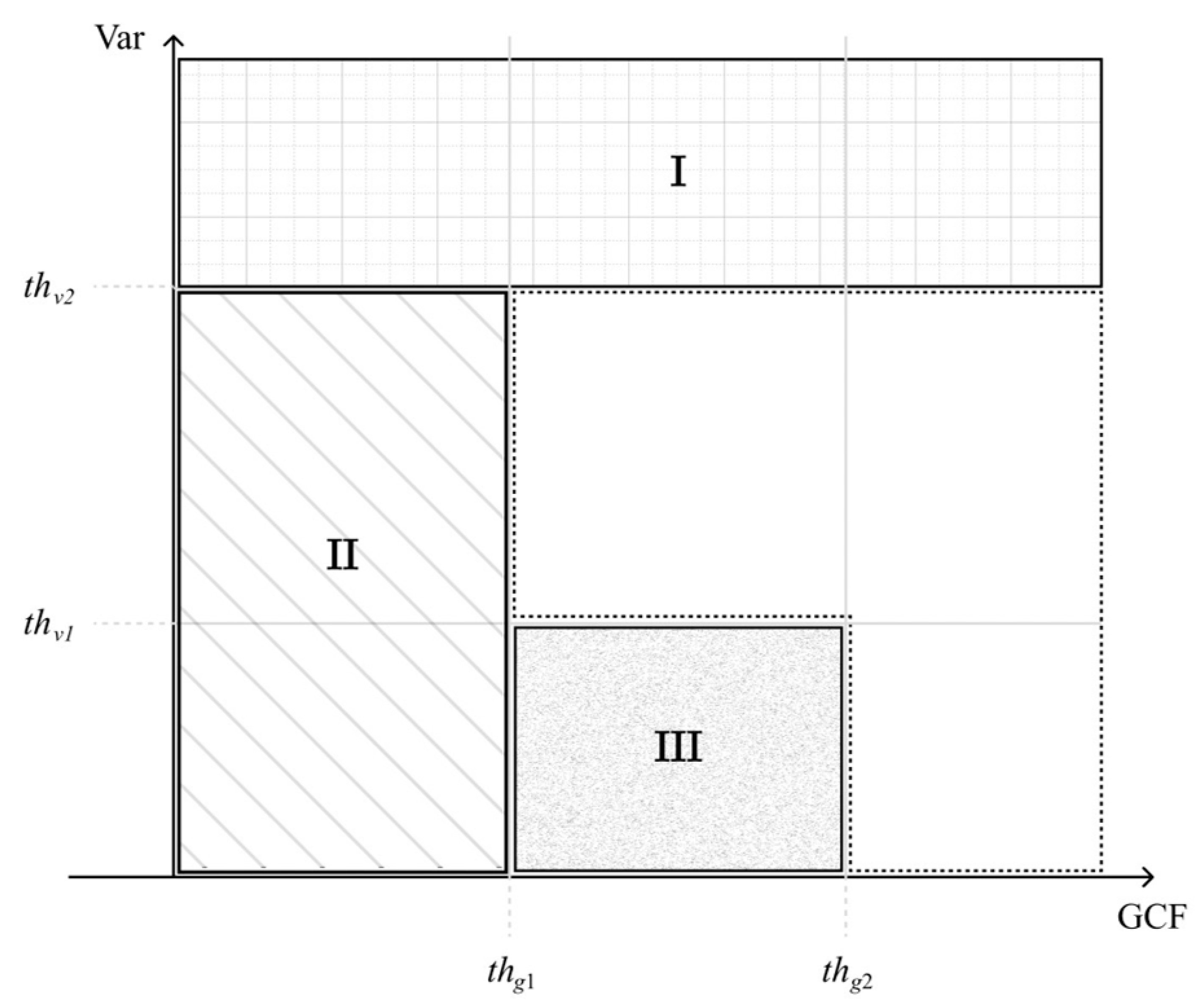
2.4. Adaptive DMAS Beamforming
3. Research Methods
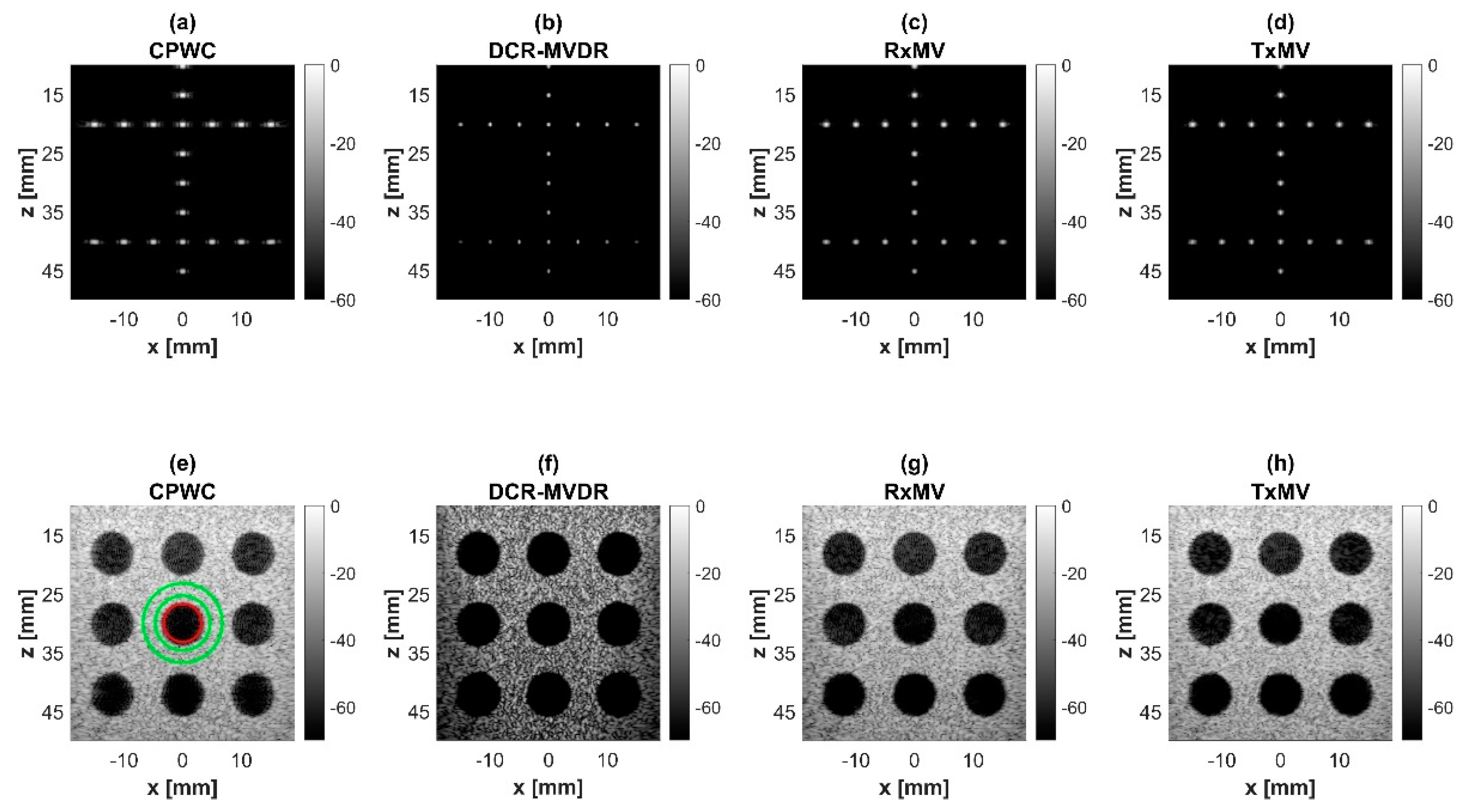
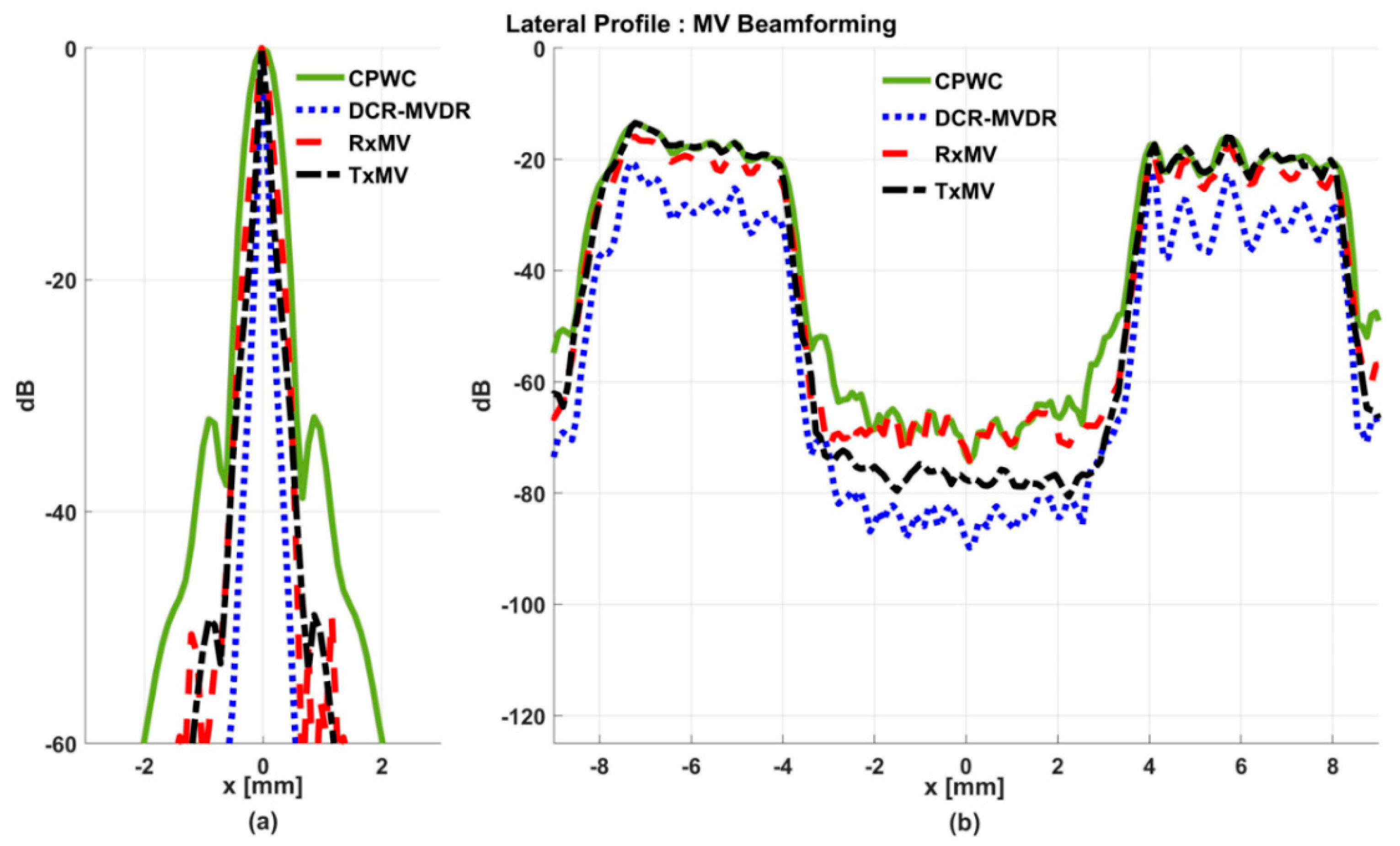
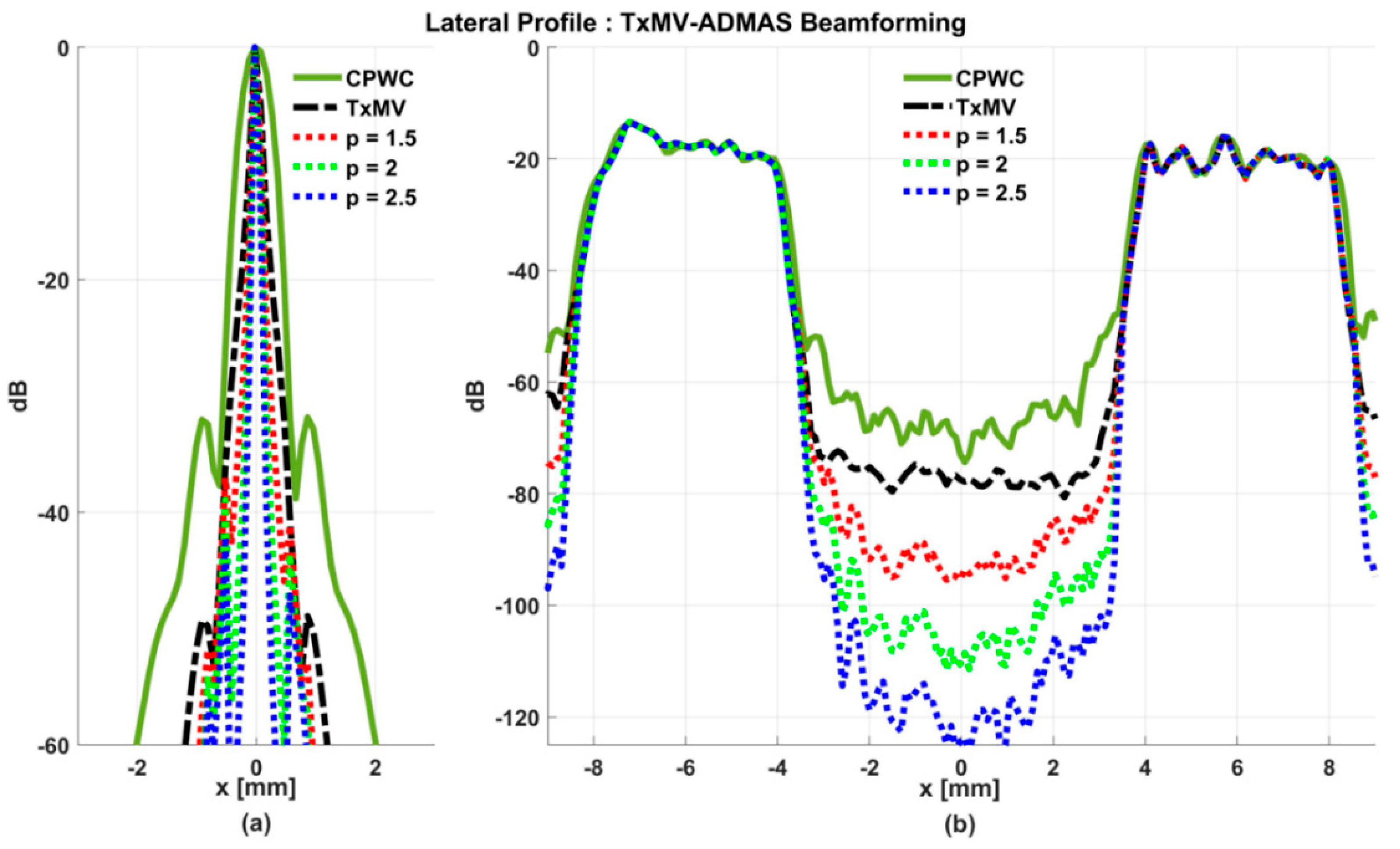
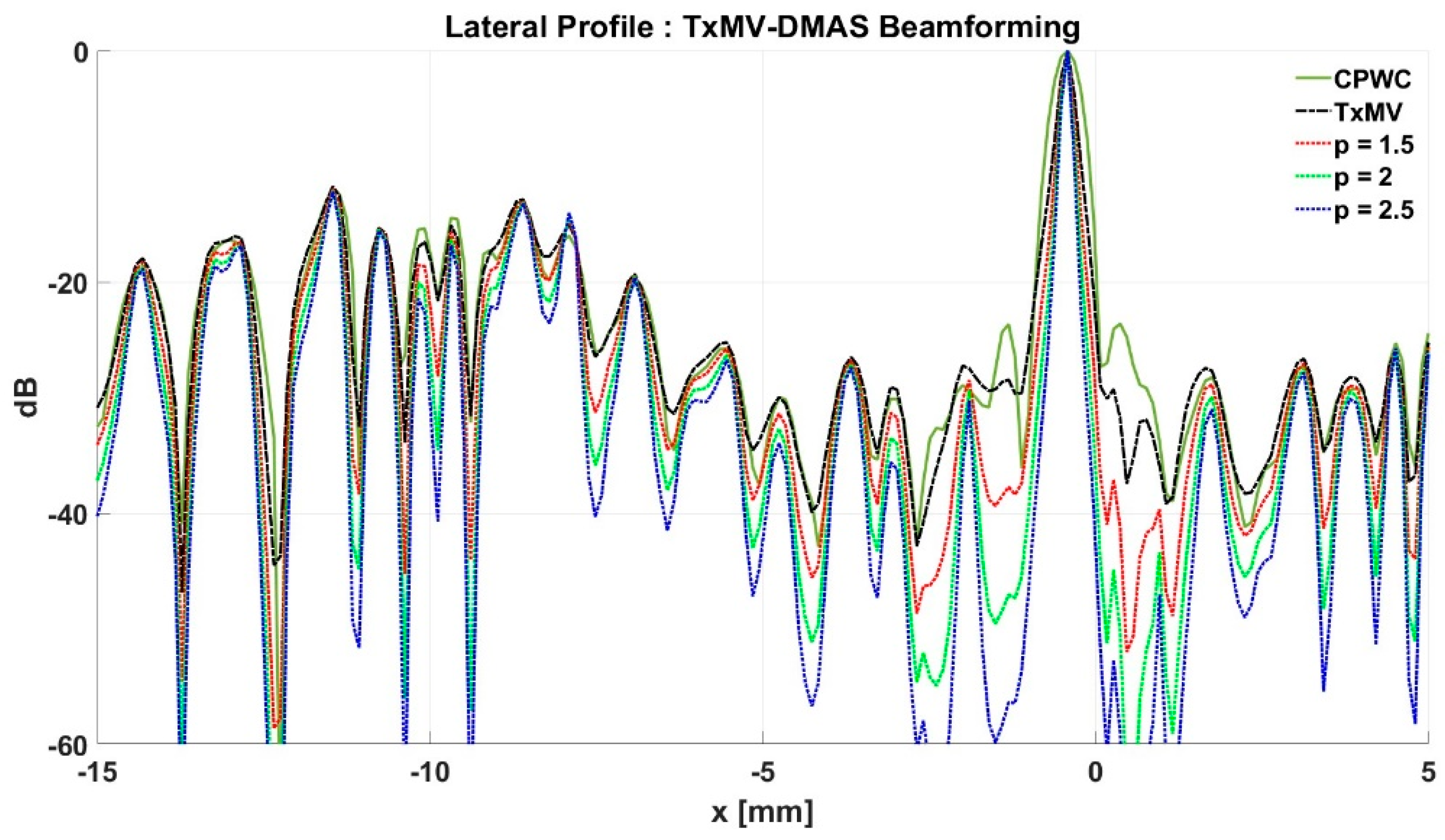
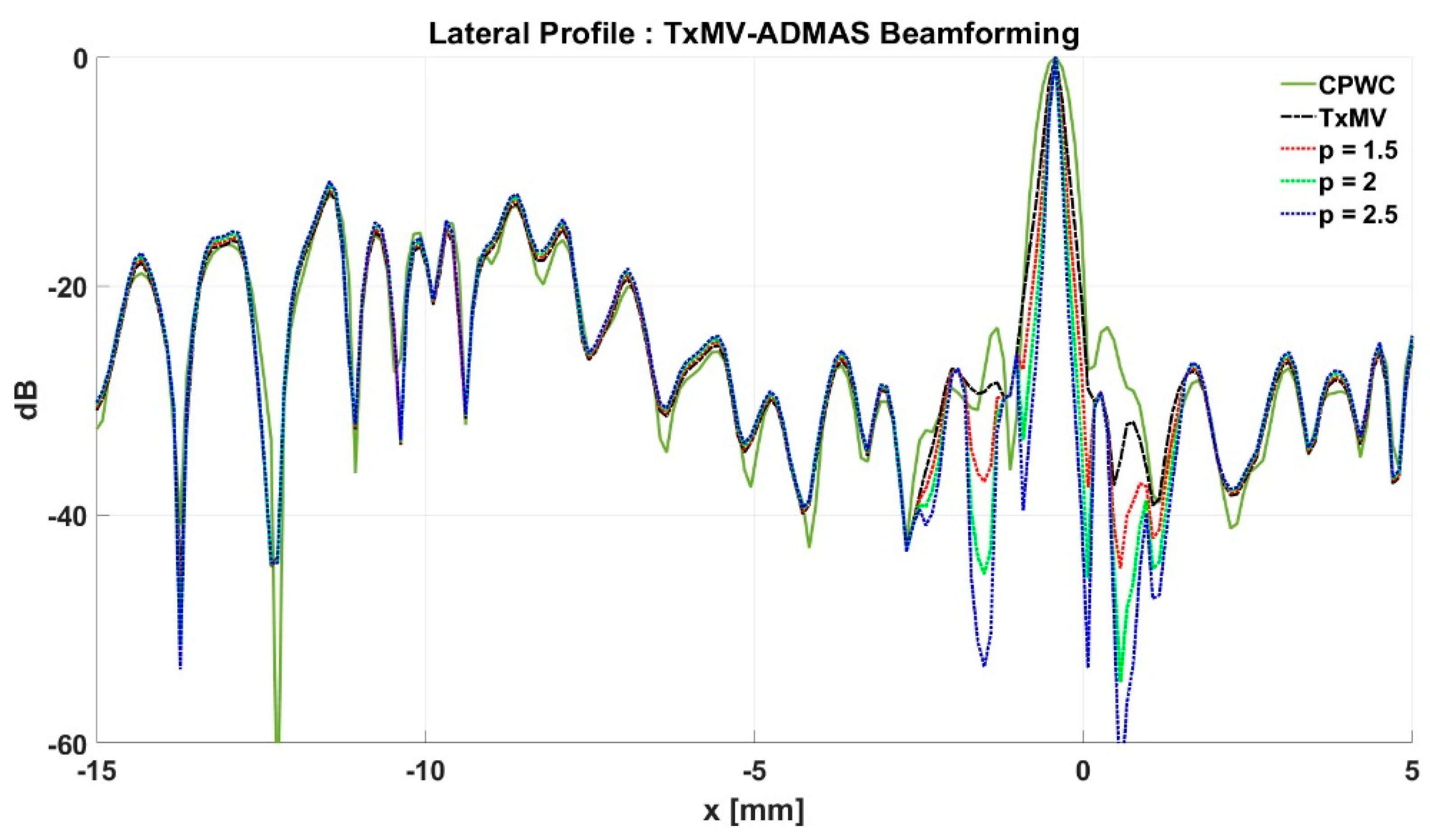
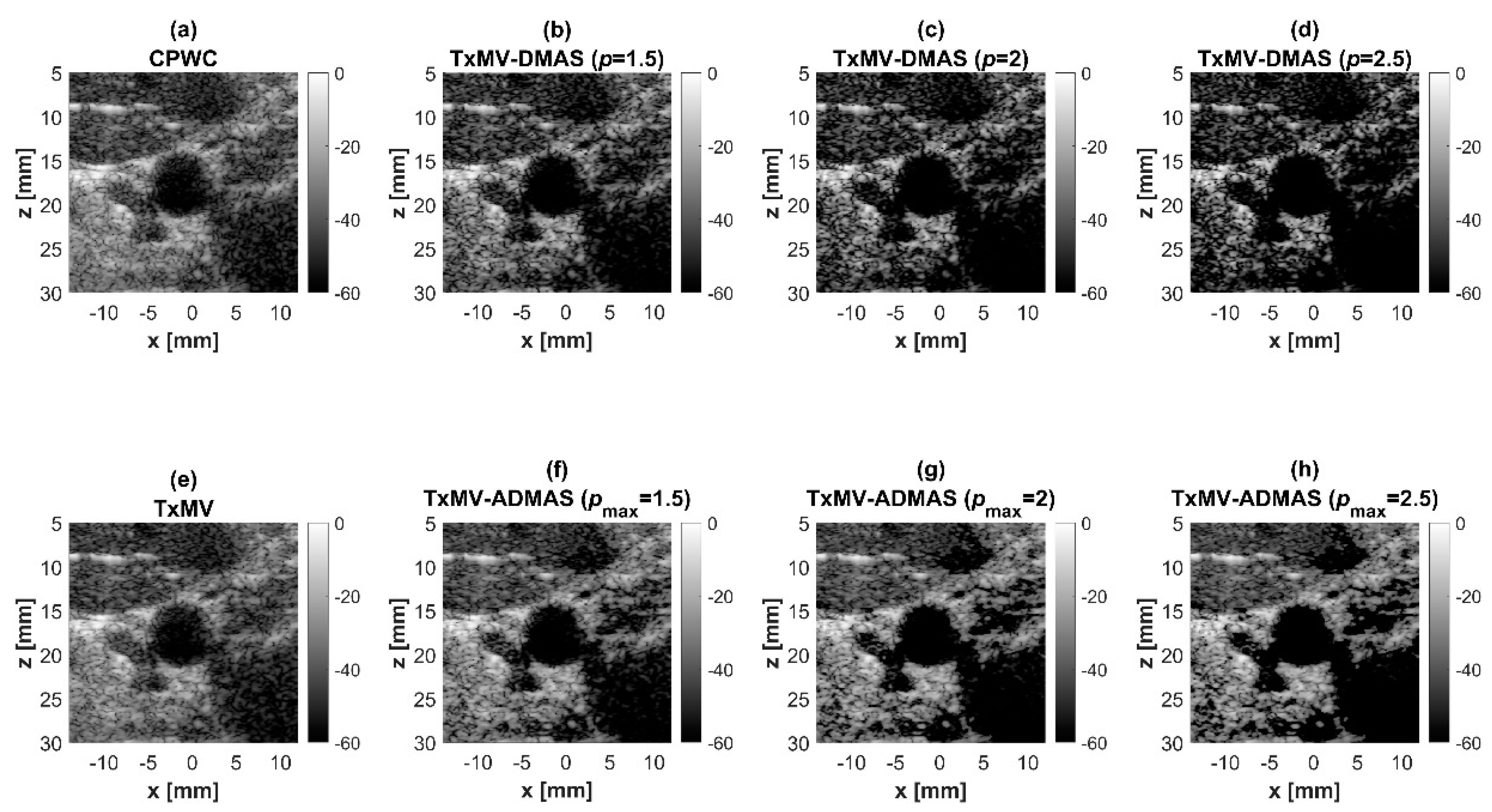
4. Results
4.1. MV Beamforming without DMAS Algorithm (Simulation)
4.2. MV Beamforming with DMAS Algorithm (Simulation)
4.3. MV Beamforming with DMAS Algorithm (Experiments)
5. Discussions and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sandrin, L.; Catheline, S.; Tanter, M.; Hennequin, X.; Fink, M. Time-resolved pulsed elastography with ultrafast ultrasonic imaging. Ultrason. Imaging 1999, 21, 259–272. [Google Scholar] [CrossRef] [PubMed]
- So, H.; Chen, J.; Yiu, B.; Yu, A. Medical ultrasound imaging: To GPU or not to GPU? IEEE Micro 2011, 31, 54–65. [Google Scholar] [CrossRef]
- Tanter, M.; Fink, M. Ultrafast imaging in biomedical ultrasound. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2014, 61, 102–119. [Google Scholar] [CrossRef]
- Montaldo, G.; Tanter, M.; Bercoff, J.; Benech, N.; Fink, M. Coherent plane-wave compounding for very high frame rate ultrasonography and transient elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2009, 56, 489–506. [Google Scholar] [CrossRef] [PubMed]
- Foiret, J.; Cai, X.; Bendjador, H.; Park, E.Y.; Kamaya, A.; Ferrara, K.W. Improving plane wave ultrasound imaging through real-time beamformation across multiple arrays. Sci. Rep. 2022, 12, 13386. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Wang, Y.; Yu, J.; Guo, Y.; Guo, W.; Qi, Y. High spatial–temporal resolution reconstruction of plane-wave ultrasound images with a multichannel multiscale convolutional neural network. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2018, 65, 1983–1996. [Google Scholar] [CrossRef] [PubMed]
- Luchies, A.C.; Byram, B.C. Deep neural networks for ultrasound beamforming. IEEE Trans. Med. Imag. 2018, 37, 2010–2021. [Google Scholar] [CrossRef]
- Tang, J.; Zou, B.; Li, C.; Feng, S.; Peng, H. Plane-wave image reconstruction via generative adversarial network and attention mechanism. IEEE Trans. Instrum. Meas. 2021, 70, 1–15. [Google Scholar] [CrossRef]
- Lu, J.; Millioz, F.; Garcia, D.; Salles, S.; Ye, D.; Friboulet, D. Complex convolutional neural networks for ultrafast ultrasound imaging reconstruction from in-phase/quadrature signal. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2022, 69, 592–603. [Google Scholar] [CrossRef]
- Lu, J.Y.; Lee, P.Y.; Huang, C.C. Improving image quality for single-angle plane wave ultrasound imaging with convolutional neural network beamformer. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2022, 69, 1326–1336. [Google Scholar] [CrossRef]
- Synnevag, J.F.; Austeng, A.; Holm, S. Adaptive beamforming applied to medical ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2007, 54, 1606–1613. [Google Scholar] [CrossRef]
- Synnevag, J.F.; Austeng, A.; Holm, S. Benefits of minimum-variance beamforming in medical ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2009, 56, 1868–1879. [Google Scholar] [CrossRef] [PubMed]
- Nilsen, C.I.C.; Hafizovic, I. Beamspace adaptive beamforming for ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2009, 56, 2187–2197. [Google Scholar] [CrossRef] [PubMed]
- Asl, B.M.; Mahloojifar, A. Eigenspace-based minimum variance beamforming applied to medical ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2010, 57, 2381–2390. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.; Chen, C.; Wang, Y. Eigenspace-based minimum variance beamformer combined with Wiener postfilter for medical ultrasound imaging. Ultrasonics. 2012, 52, 996–1004. [Google Scholar] [CrossRef] [PubMed]
- Mehdizadeh, S.; Austeng, A.; Johansen, T.F.; Holm, S. Eigenspace based minimum variance beamforming applied to ultrasound imaging of acoustically hard tissues. IEEE Trans. Med. Imag. 2012, 31, 1912–1921. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Wang, Y.; Zeng, X.; Yu, J.; Yiu, B.Y.S.; Yu, A.C.H. Plane wave compounding based on a joint transmitting-receiving adaptive beamformer. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2015, 62, 1440–1452. [Google Scholar] [CrossRef]
- Rindal, O.M.H.; Austeng, A. Double adaptive plane-wave imaging. In Proceedings of the 2016 IEEE International Ultrasonics Symposium, Tours, France, 18–21 September 2016; pp. 1–4. [Google Scholar]
- Nguyen, N.Q.; Prager, R.W. A spatial coherence approach to minimum variance beamforming for plane-wave compounding. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2018, 65, 522–534. [Google Scholar] [CrossRef]
- Wang, S.L.; Li, P.C. MVDR-based coherence weighting for high-frame-rate adaptive imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2009, 56, 2097–2110. [Google Scholar] [CrossRef]
- Asl, B.M.; Mahloojifar, A. Minimum variance beamforming combined with adaptive coherence weighting applied to medical ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2009, 56, 1923–1931. [Google Scholar] [CrossRef]
- Qi, Y.; Wang, Y.; Guo, W. Joint subarray coherence and minimum variance beamformer for multitransmission ultrasound imaging modalities. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2018, 65, 1600–1617. [Google Scholar] [CrossRef] [PubMed]
- Nilsen, C.I.; Holm, S. Wiener beamforming and the coherence factor in ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2010, 57, 1329–1346. [Google Scholar] [CrossRef] [PubMed]
- Paridar, R.; Asl, B.M. Plane wave ultrasound imaging using compressive sensing and minimum variance beamforming. Ultrasonics. 2023, 127, 106838. [Google Scholar] [CrossRef] [PubMed]
- Hollman, K.W.; Rigby, K.W.; Donnell, M.O. Coherence factor of speckle from a multi-row probe. In Proceedings of the 1999 IEEE Ultrasonics Symposium, Tahoe, NV, USA, 17–20 October 1999; pp. 1257–1260. [Google Scholar]
- Li, P.C.; Li, M.L. Adaptive imaging using the generalized coherence factor. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2003, 50, 128–141. [Google Scholar]
- Lediju, M.A.; Trahey, G.E.; Byram, B.C.; Dahl, J.J. Short-lag spatial coherence of backscattered echoes: Imaging characteristics. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2011, 58, 1377–1388. [Google Scholar] [CrossRef]
- Pinton, G.; Trahey, G.E.; Dahl, J.J. Spatial coherence in human tissue: Implications for imaging and measurement. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2014, 61, 1976–1987. [Google Scholar] [CrossRef][Green Version]
- Matrone, G.; Savoia, A.S.; Caliano, G.; Magenes, G. The delay multiply and sum beamforming algorithm in ultrasound B-mode medical imaging. IEEE Trans. Med. Imag. 2015, 34, 940–949. [Google Scholar] [CrossRef]
- Matrone, G.; Ramalli, A. Spatial coherence of backscattered signals in multi-line transmit ultrasound imaging and its effect on short-lag filtered-delay multiply and sum beamforming. Appl. Sci. 2018, 8, 486. [Google Scholar] [CrossRef]
- Shen, C.C.; Hsieh, P.Y. Ultrasound baseband delay-multiply-and-sum (BB-DMAS) nonlinear beamforming. Ultrasonics 2019, 96, 165–174. [Google Scholar] [CrossRef]
- Polichetti, M.; Varray, F.; Béra, J.C.; Cachard, C.; Nicolas, B. A nonlinear beamformer based on p-th root compression—Application to plane wave ultrasound imaging. Appl. Sci. 2018, 8, 599. [Google Scholar] [CrossRef]
- Prieur, F.; Rindal, O.M.H.; Austeng, A. Signal coherence and image amplitude with the filtered delay multiply and sum beamformer. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2018, 65, 1133–1140. [Google Scholar] [CrossRef] [PubMed]
- Shen, C.C. Computationally efficient minimum-variance baseband delay-multiply-and-sum beamforming for adjustable enhancement of ultrasound image resolution. Ultrasonics 2021, 112, 106345. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.L.; Shen, C.C. Delay-multiply-and-sum beamforming with transmit minimum-variance estimation in multi-angle plane-wave imaging. In Proceedings of the 2022 IEEE International Ultrasonics Symposium, Venice, Italy, 10–13 October 2022; pp. 1–4. [Google Scholar]
- Shen, C.C.; Hsieh, P.Y. Two-dimensional spatial coherence for ultrasonic DMAS beamforming in multi-angle plane-wave imaging. Appl. Sci. 2019, 9, 3973. [Google Scholar] [CrossRef]
- Liebgott, H.; Rodriguez-Molares, A.; Cervenansky, F.; Jensen, J.A.; Bernard, O. Plane-wave imaging challenge in medical ultrasound. In Proceedings of the 2016 IEEE International Ultrasonics Symposium, Tours, France, 18–21 September 2016; pp. 1–4. [Google Scholar]
- Rodriguez-Molares, A.; Rindal, O.M.H.; D’Hooge, J.; Måsøy, S.E.; Austeng, A.; Lediju Bell, M.A.; Torp, H. The generalized contrast-to-noise ratio: A formal definition for lesion detectability. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2020, 67, 745–759. [Google Scholar] [CrossRef]
- Synnevåg, J.F.; Nilsen, C.I.C.; Holm, S. Speckle statistics in adaptive beamforming. In Proceedings of the 2007 IEEE International Ultrasonics Symposium, New York, NY, USA, 28–31 October 2007; pp. 1545–1548. [Google Scholar]
- Ziksari, M.S.; Asl, B.M. Minimum variance combined with modified delay multiply-and-sum beamforming for plane-wave compounding. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2021, 68, 1641–1652. [Google Scholar] [CrossRef]
- Hashemseresht, M.; Afrakhteh, S.; Behnam, H. High-resolution and high-contrast ultrafast ultrasound imaging using coherent plane wave adaptive compounding. Biomed. Signal Process. Control 2022, 73, 103446. [Google Scholar] [CrossRef]






| Beamformer | FWHM (mm) | CR (dB) | CNR |
|---|---|---|---|
| CPWC | 0.57 | 40.1 | 16.0 |
| DCR-MVDR | 0.16 | 47.4 | 14.5 |
| RxMV | 0.28 | 43.4 | 16.6 |
| TxMV | 0.17 | 47.8 | 17.7 |
| p Value | Beamformer | FWHM (mm) | CR (dB) | CNR |
|---|---|---|---|---|
| 1 | CPWC | 0.57 | 40.1 | 16.0 |
| TxMV | 0.17 | 47.8 | 17.7 | |
| 1.5 | TxMV-DMAS | 0.12 | 58.3 | 16.8 |
| TxMV-ADMAS | 0.11 | 59.6 | 17.9 | |
| 2 | TxMV-DMAS | 0.09 | 67.2 | 16.0 |
| TxMV-ADMAS | 0.09 | 69.0 | 17.7 | |
| 2.5 | TxMV-DMAS | 0.07 | 75.8 | 15.4 |
| TxMV-ADMAS | 0.09 | 77.6 | 17.5 |
| p Value | Beamformer | FWHM (mm) | CR (dB) | CNR | gCNR |
|---|---|---|---|---|---|
| 1 | CPWC | 0.57 | 27.0 | 12.8 | 0.97 |
| TxMV | 0.36 | 27.4 | 13.0 | 0.97 | |
| 1.5 | TxMV-DMAS | 0.28 | 33.2 | 11.9 | 0.94 |
| TxMV-ADMAS | 0.28 | 33.4 | 13.0 | 0.97 | |
| 2 | TxMV-DMAS | 0.24 | 38.0 | 11.3 | 0.92 |
| TxMV-ADMAS | 0.23 | 37.3 | 12.8 | 0.97 | |
| 2.5 | TxMV-DMAS | 0.21 | 42.1 | 10.9 | 0.91 |
| TxMV-ADMAS | 0.20 | 39.6 | 12.5 | 0.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, C.-C.; Huang, C.-L. Improvement in Multi-Angle Plane Wave Image Quality Using Minimum Variance Beamforming with Adaptive Signal Coherence. Sensors 2024, 24, 262. https://doi.org/10.3390/s24010262
Shen C-C, Huang C-L. Improvement in Multi-Angle Plane Wave Image Quality Using Minimum Variance Beamforming with Adaptive Signal Coherence. Sensors. 2024; 24(1):262. https://doi.org/10.3390/s24010262
Chicago/Turabian StyleShen, Che-Chou, and Chun-Lin Huang. 2024. "Improvement in Multi-Angle Plane Wave Image Quality Using Minimum Variance Beamforming with Adaptive Signal Coherence" Sensors 24, no. 1: 262. https://doi.org/10.3390/s24010262
APA StyleShen, C.-C., & Huang, C.-L. (2024). Improvement in Multi-Angle Plane Wave Image Quality Using Minimum Variance Beamforming with Adaptive Signal Coherence. Sensors, 24(1), 262. https://doi.org/10.3390/s24010262





