Combining Different Wearable Devices to Assess Gait Speed in Real-World Settings
Abstract
:1. Introduction
2. Materials and Methods
2.1. Instrumentation
2.1.1. Wearable Devices
2.1.2. Reference System
2.2. Experimental Protocol
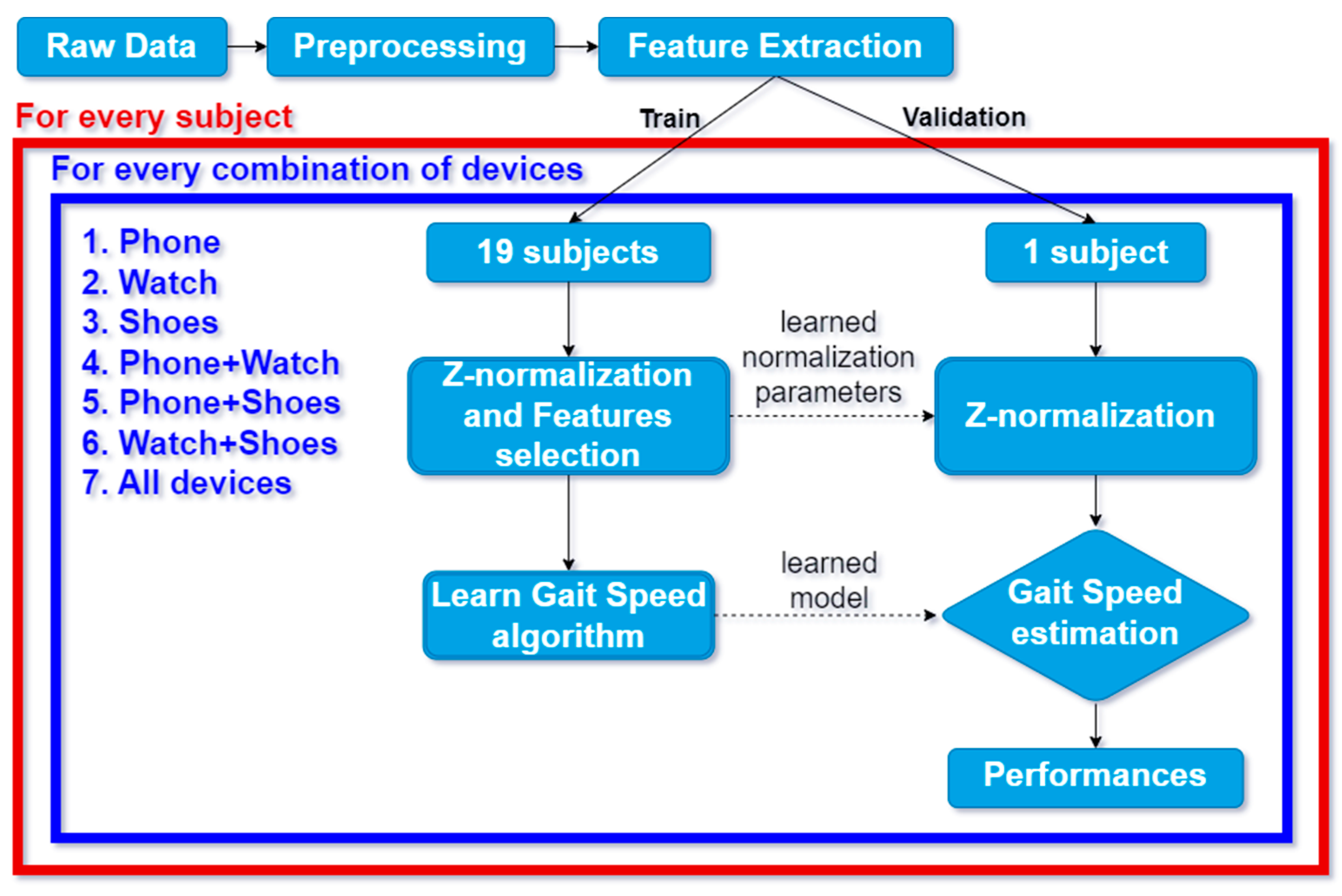
2.3. Algorithm for Gait Speed Estimation
2.4. Algorithm Evaluation
2.4.1. Error Metrics
2.4.2. Feature Interpretability
- Selection of significant features: we select features found to have been chosen in at least one model and found to be significant (p-value < 0.001);
- First drop-out stage: for each combination, we drop out the features selected in less than half of the folds of the validation, i.e., 10 folds;
- Second drop-out stage: through observing that each device can appear in 4 of the 7 combinations, we will select, for each device, those that appear in more than half of the possible combinations, i.e., 2 combinations.
3. Results
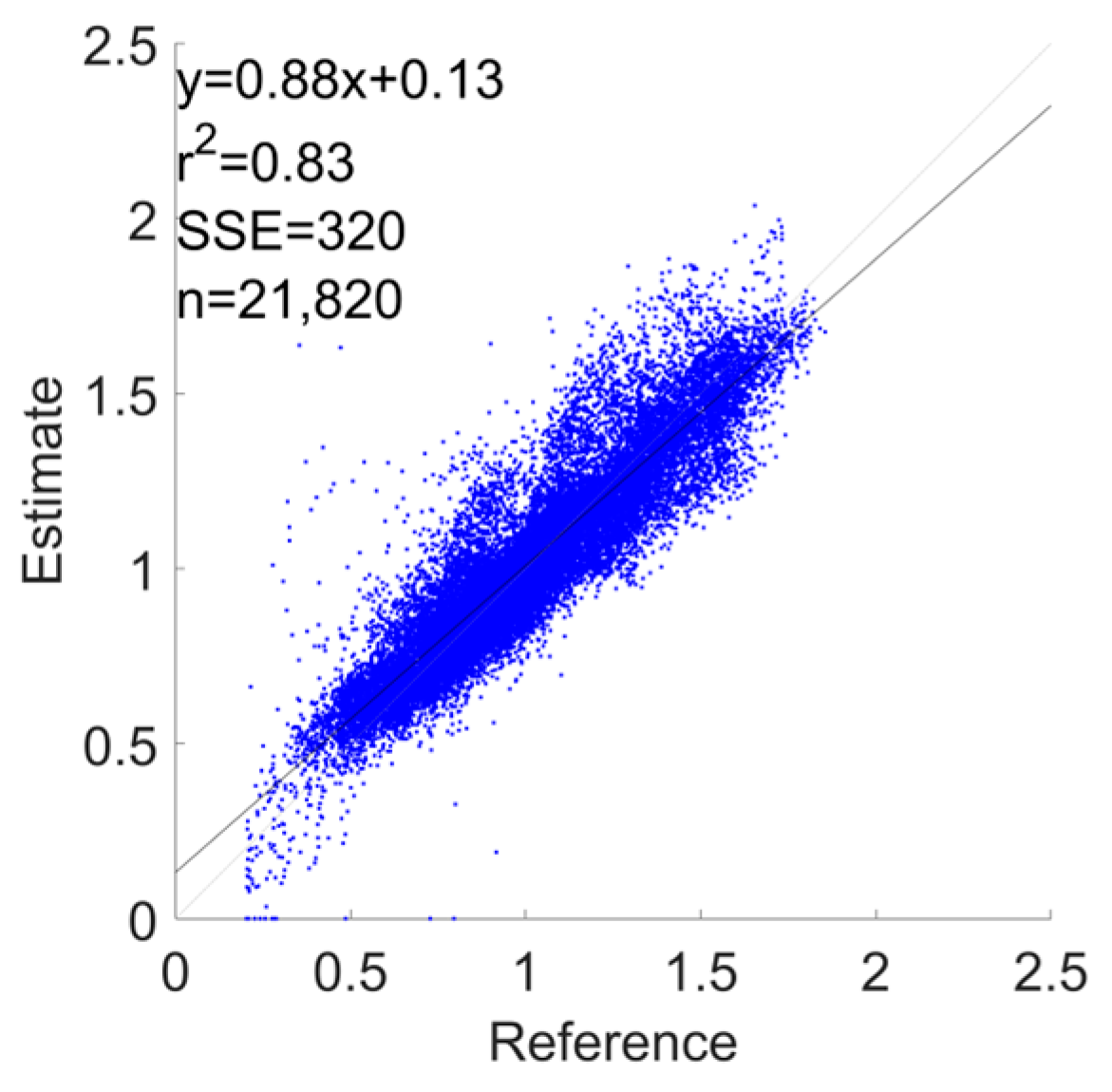
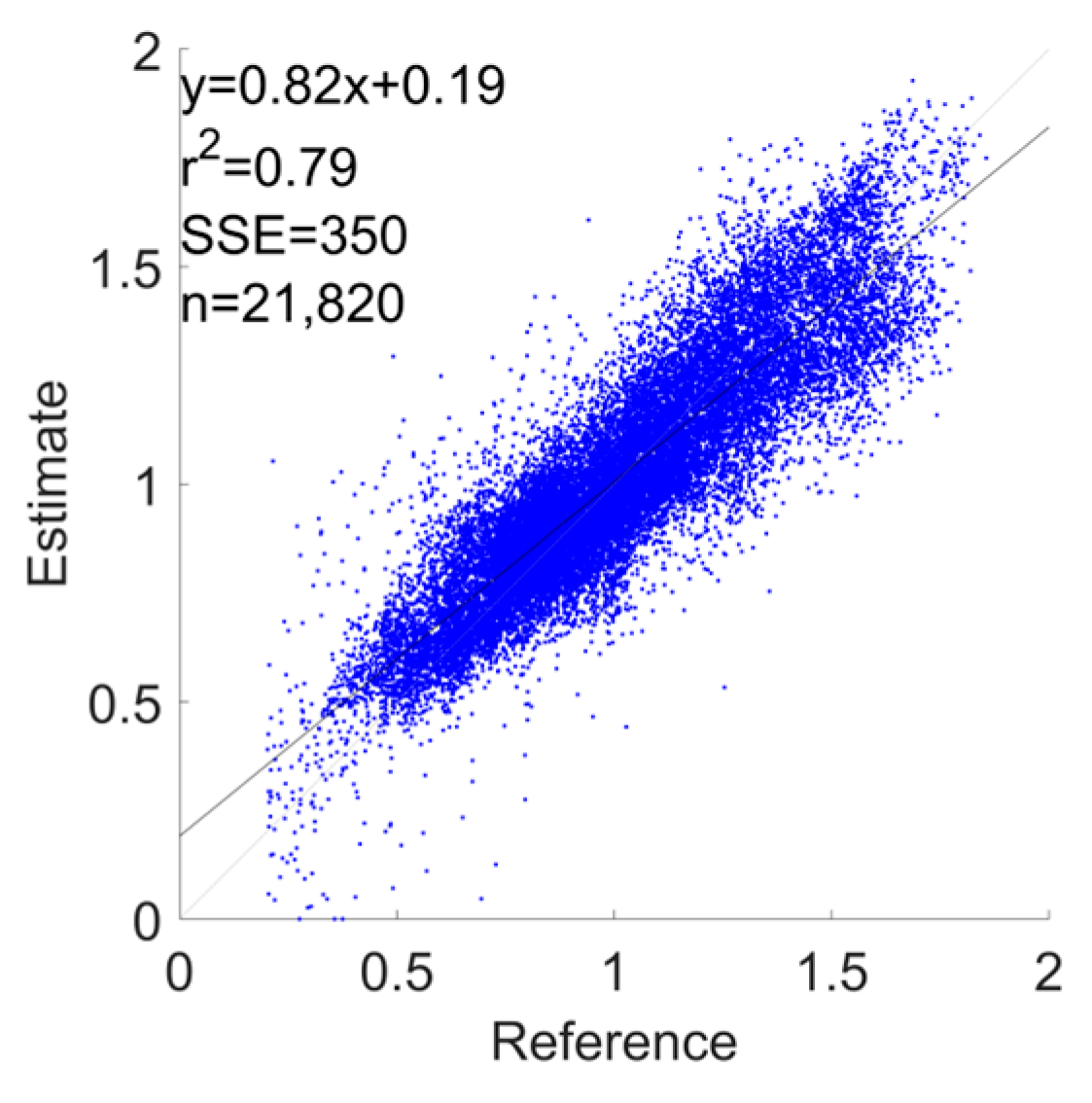
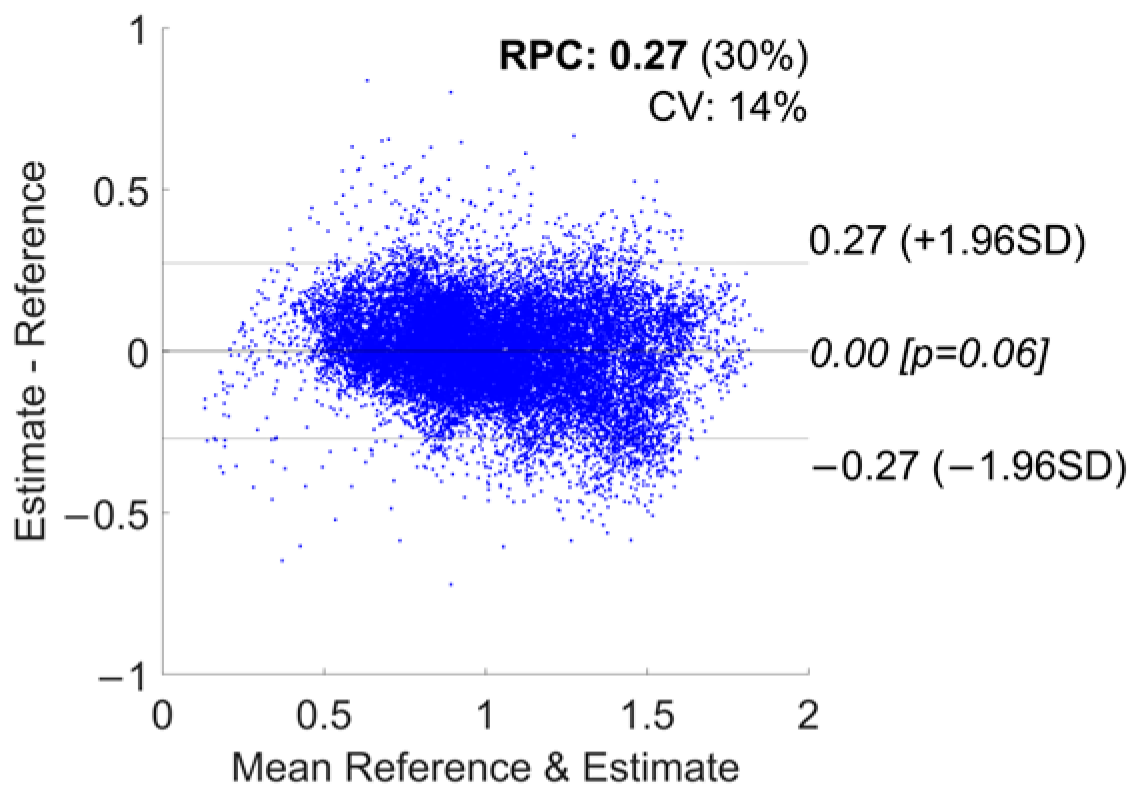
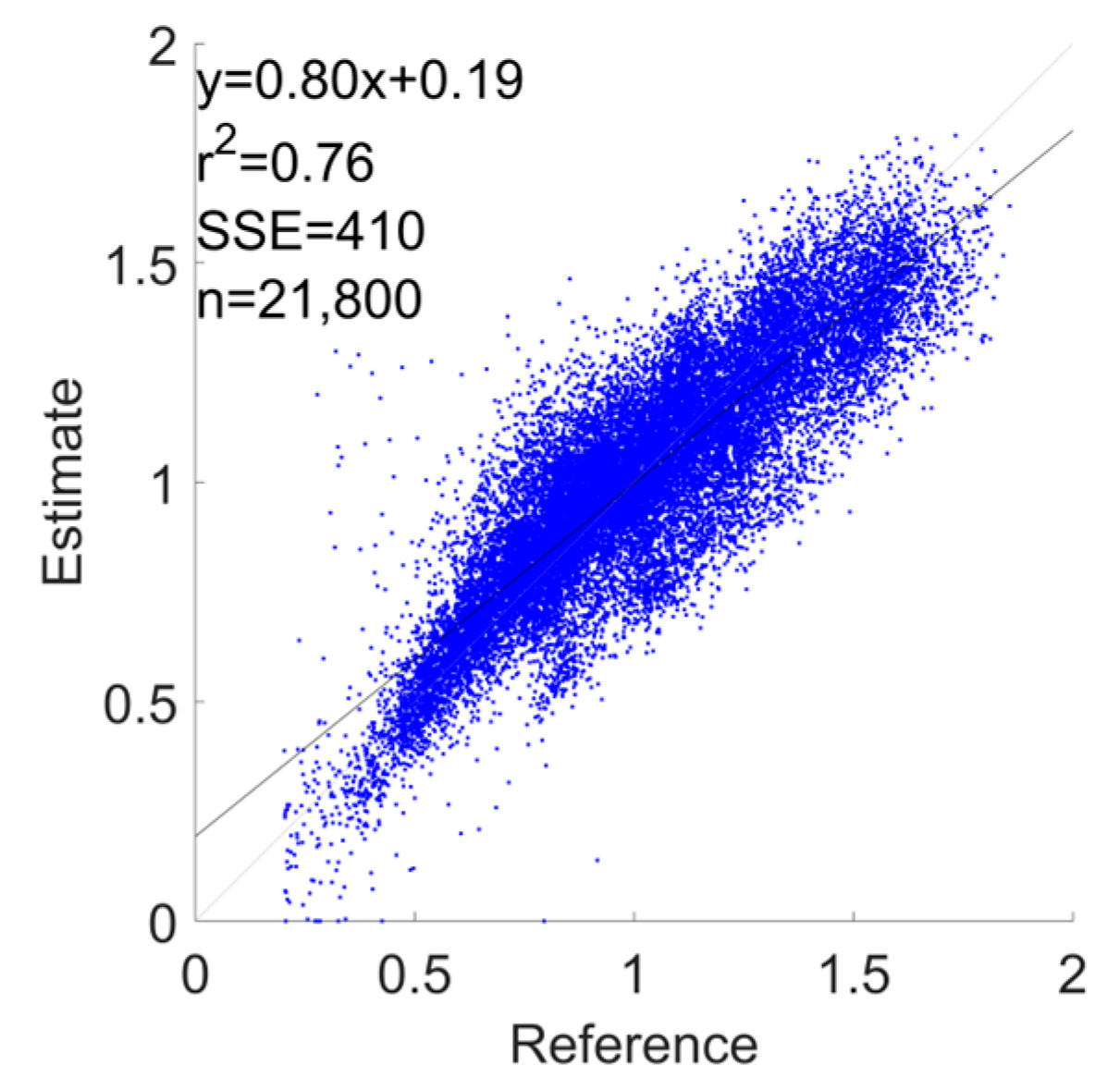
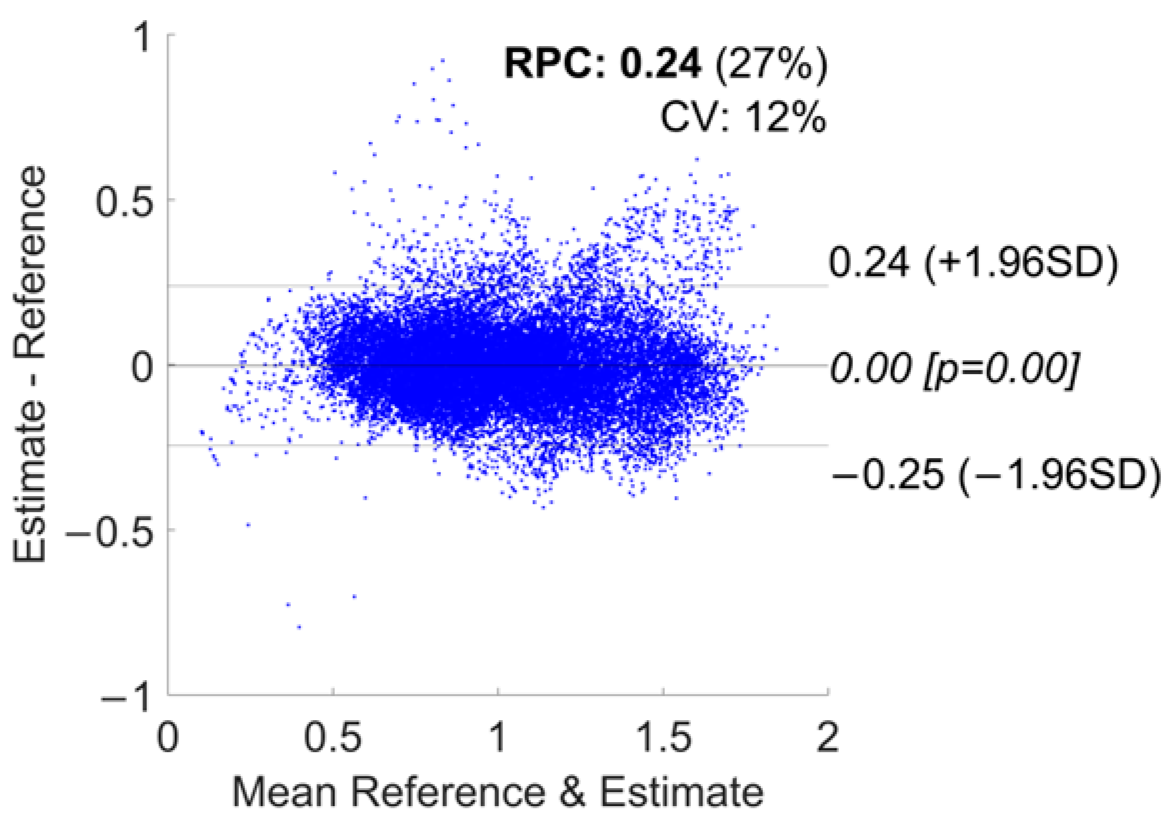
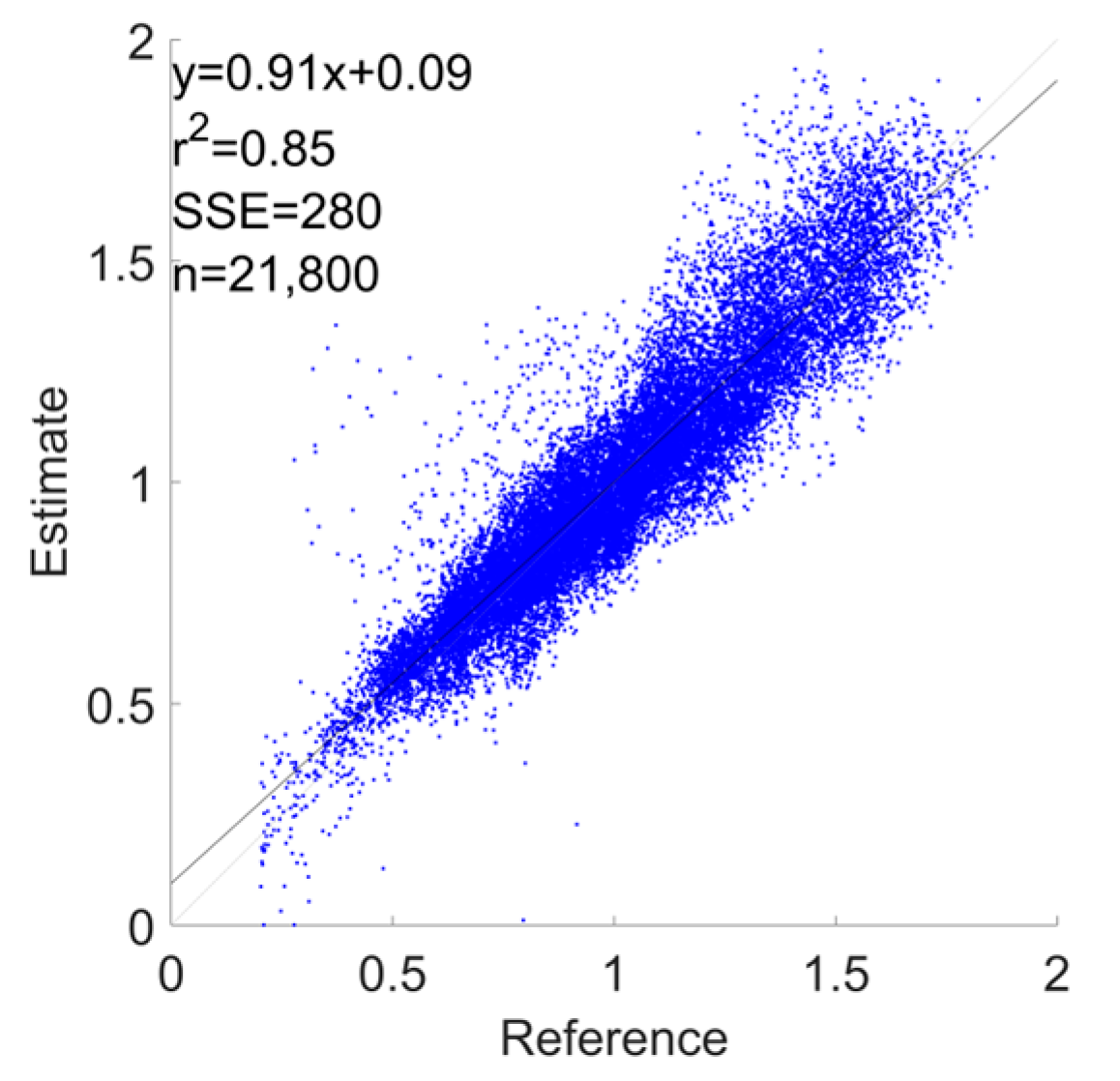
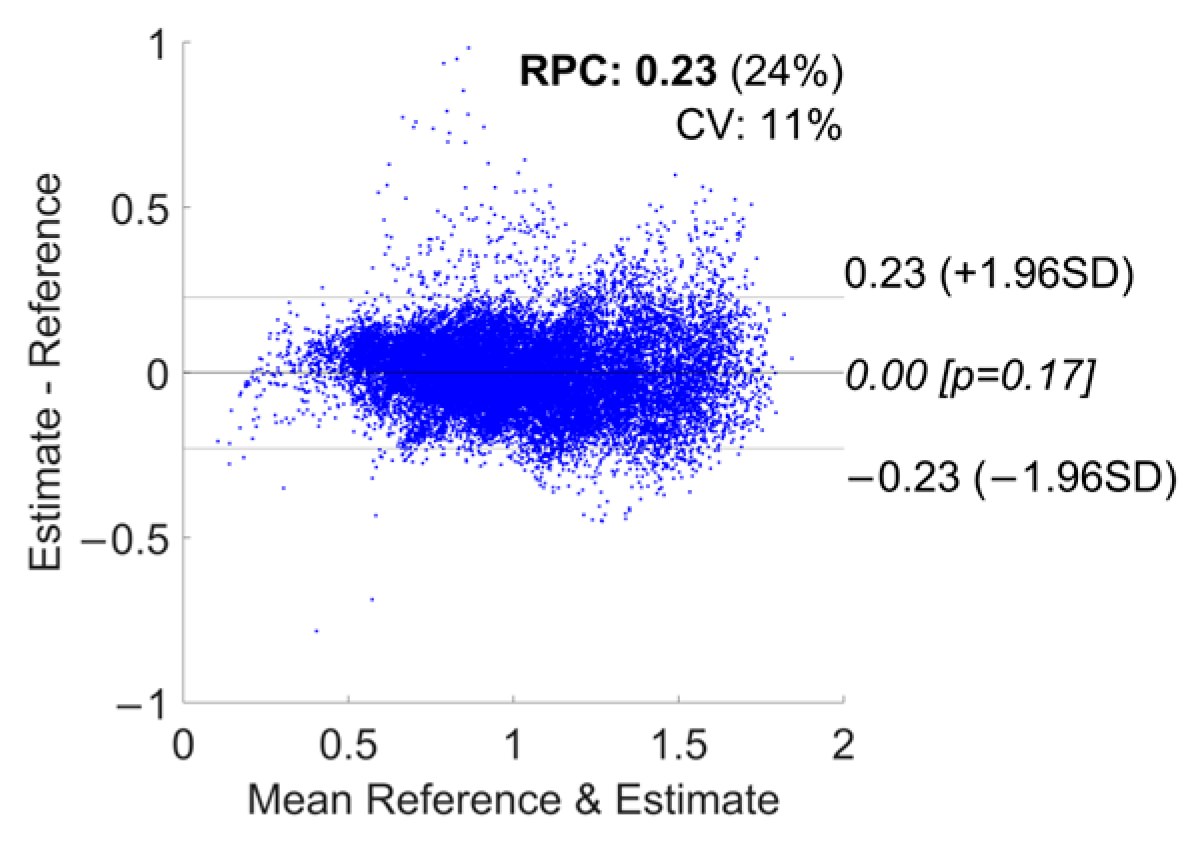
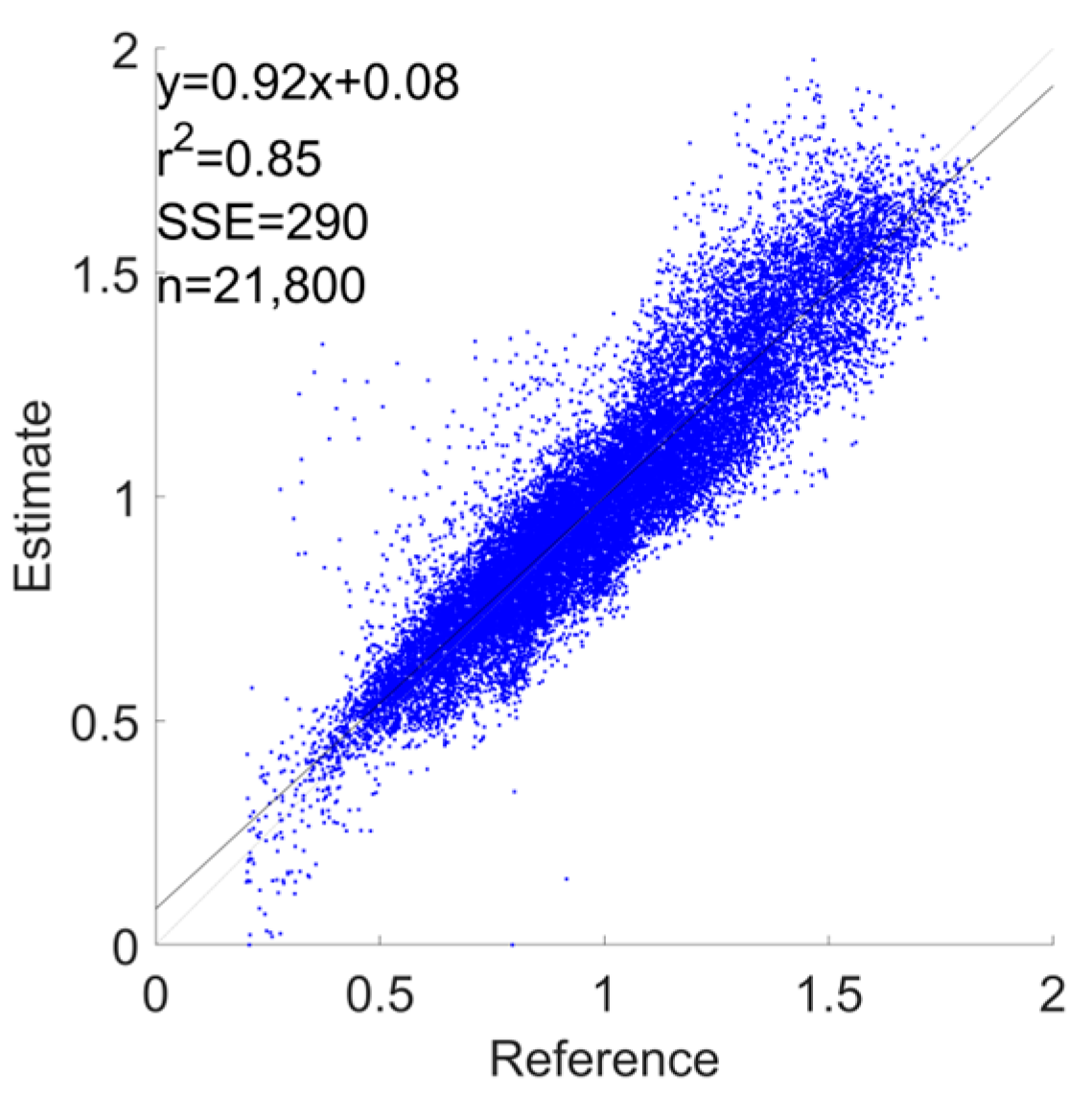
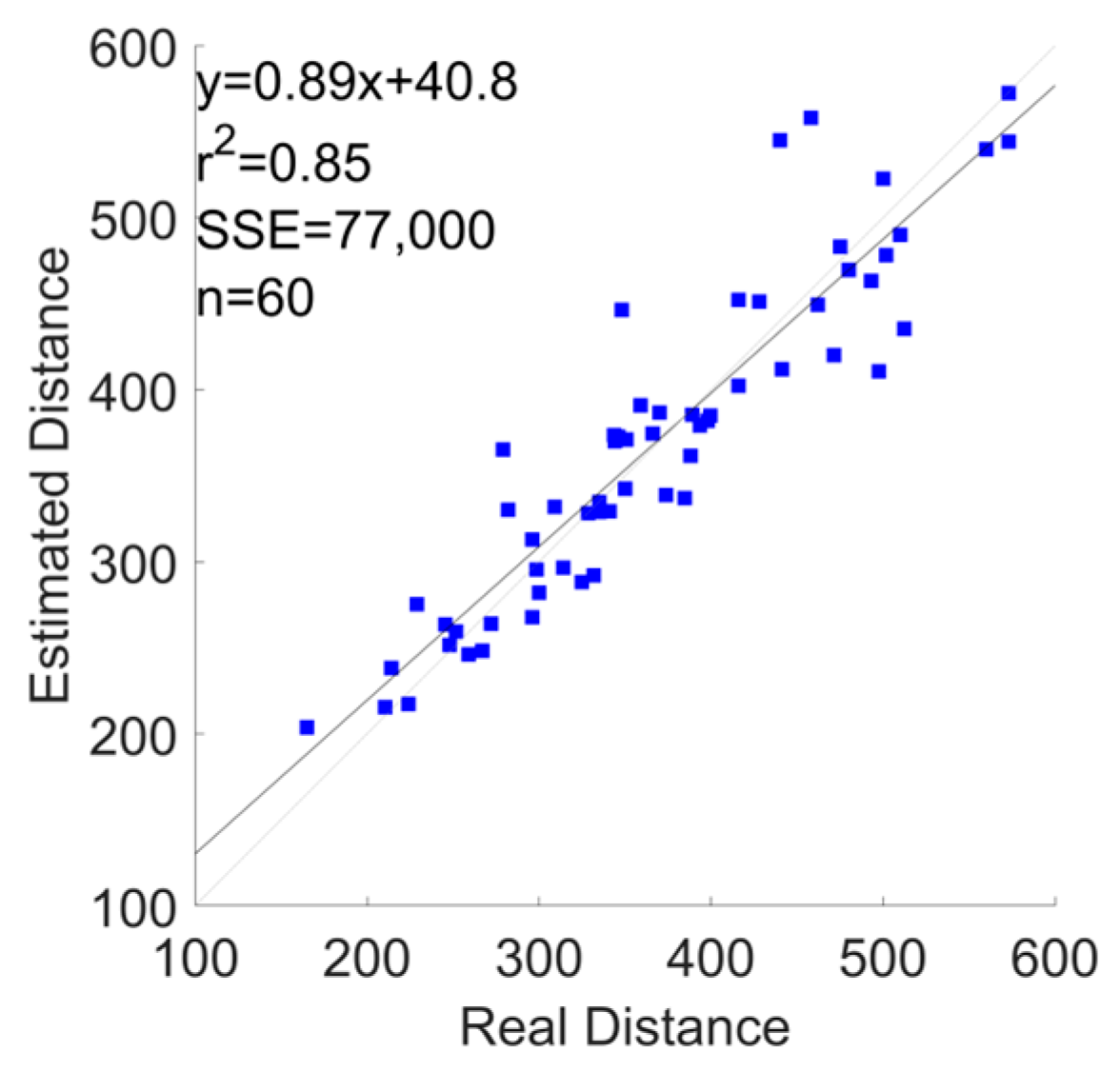
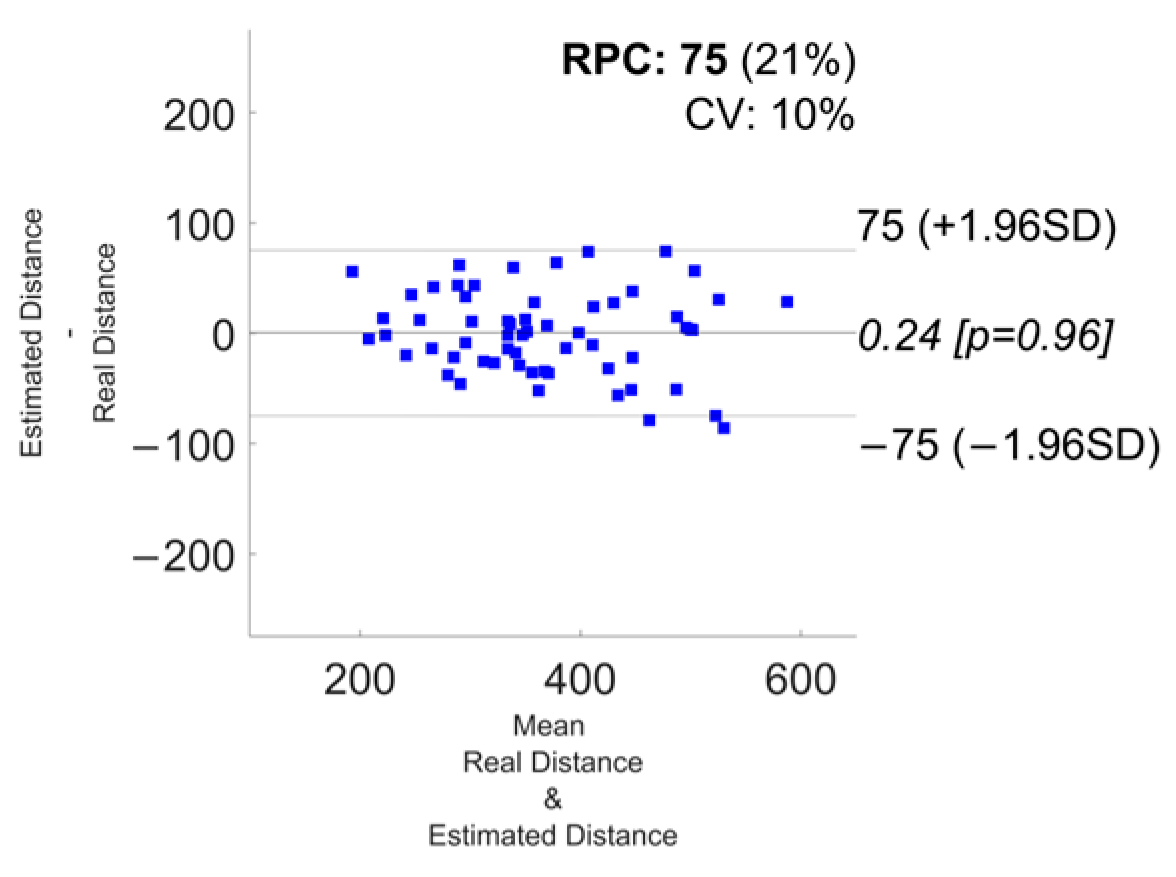
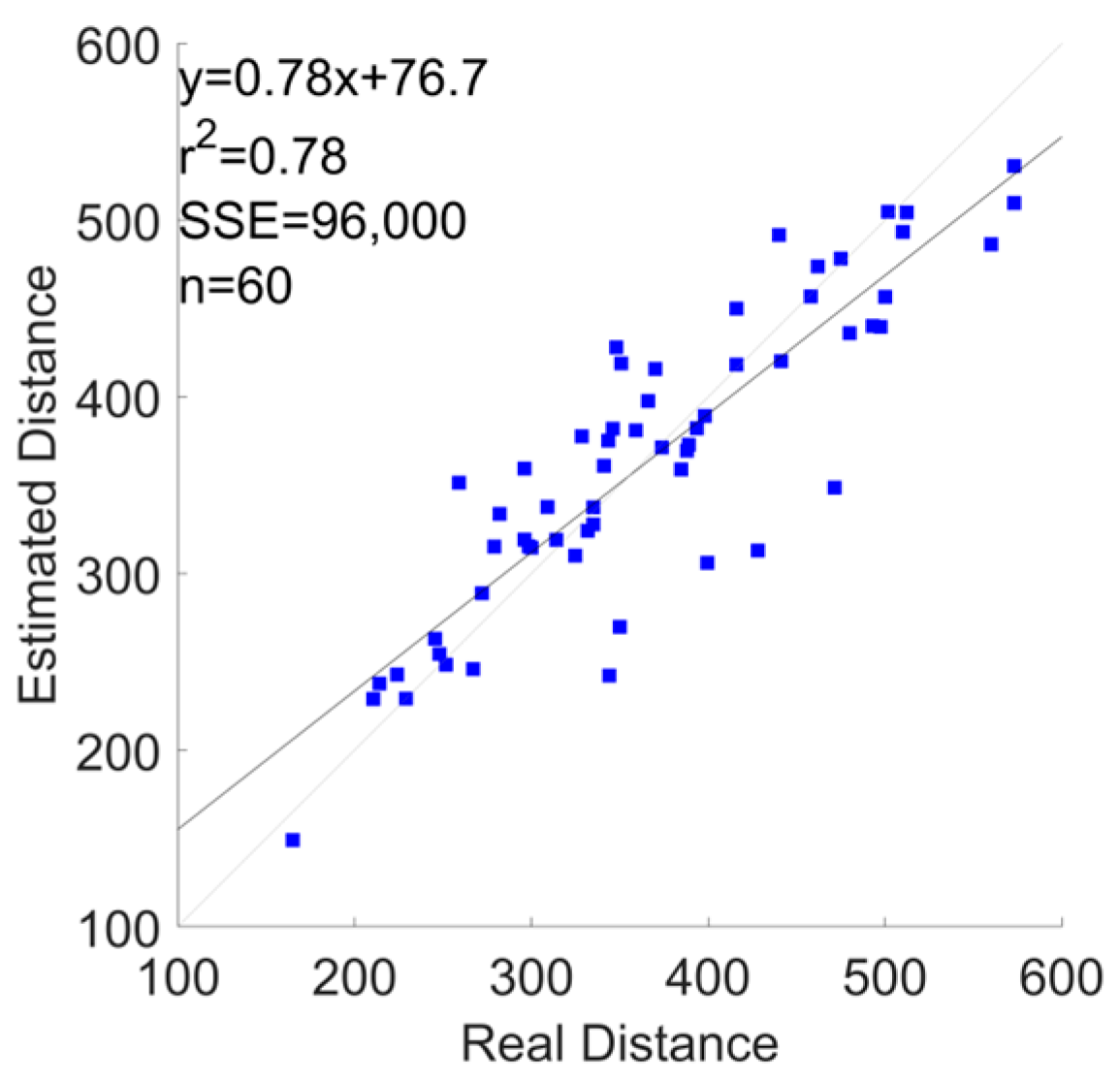
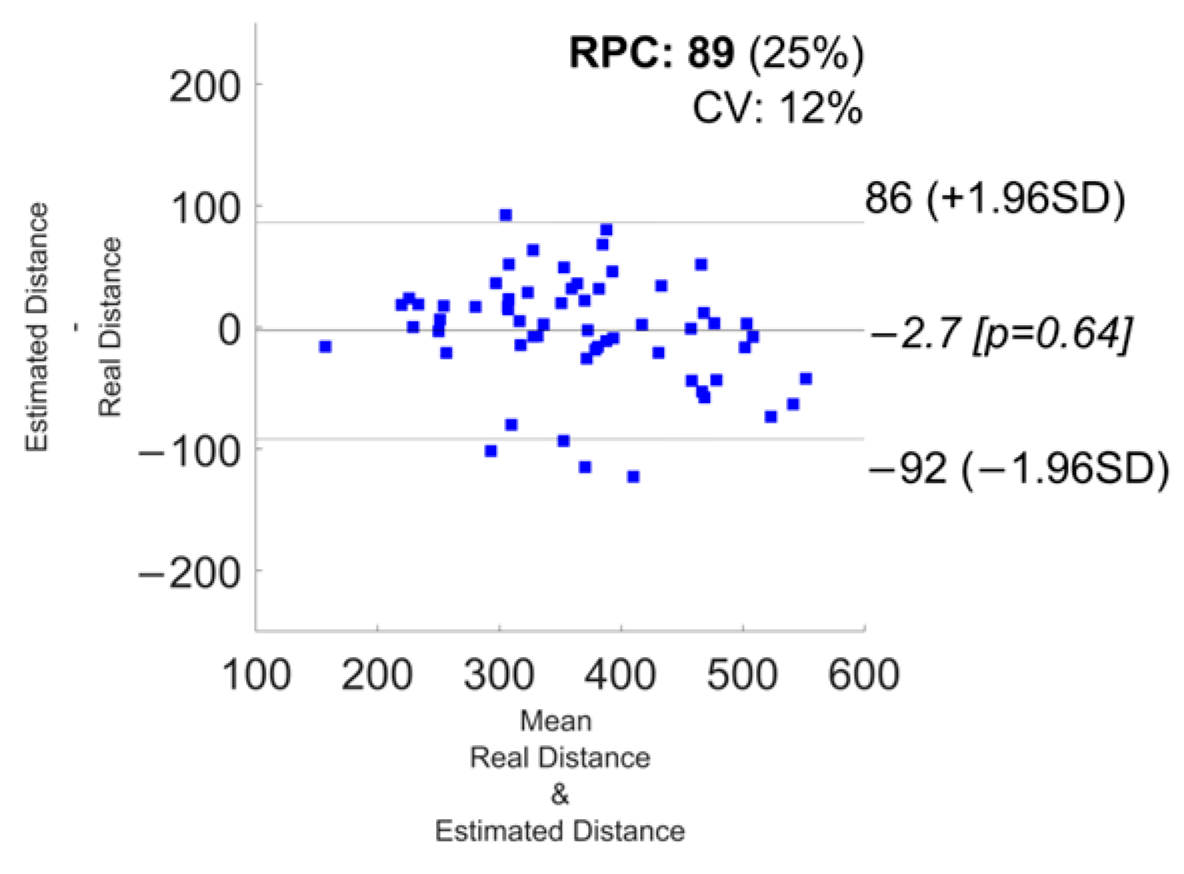
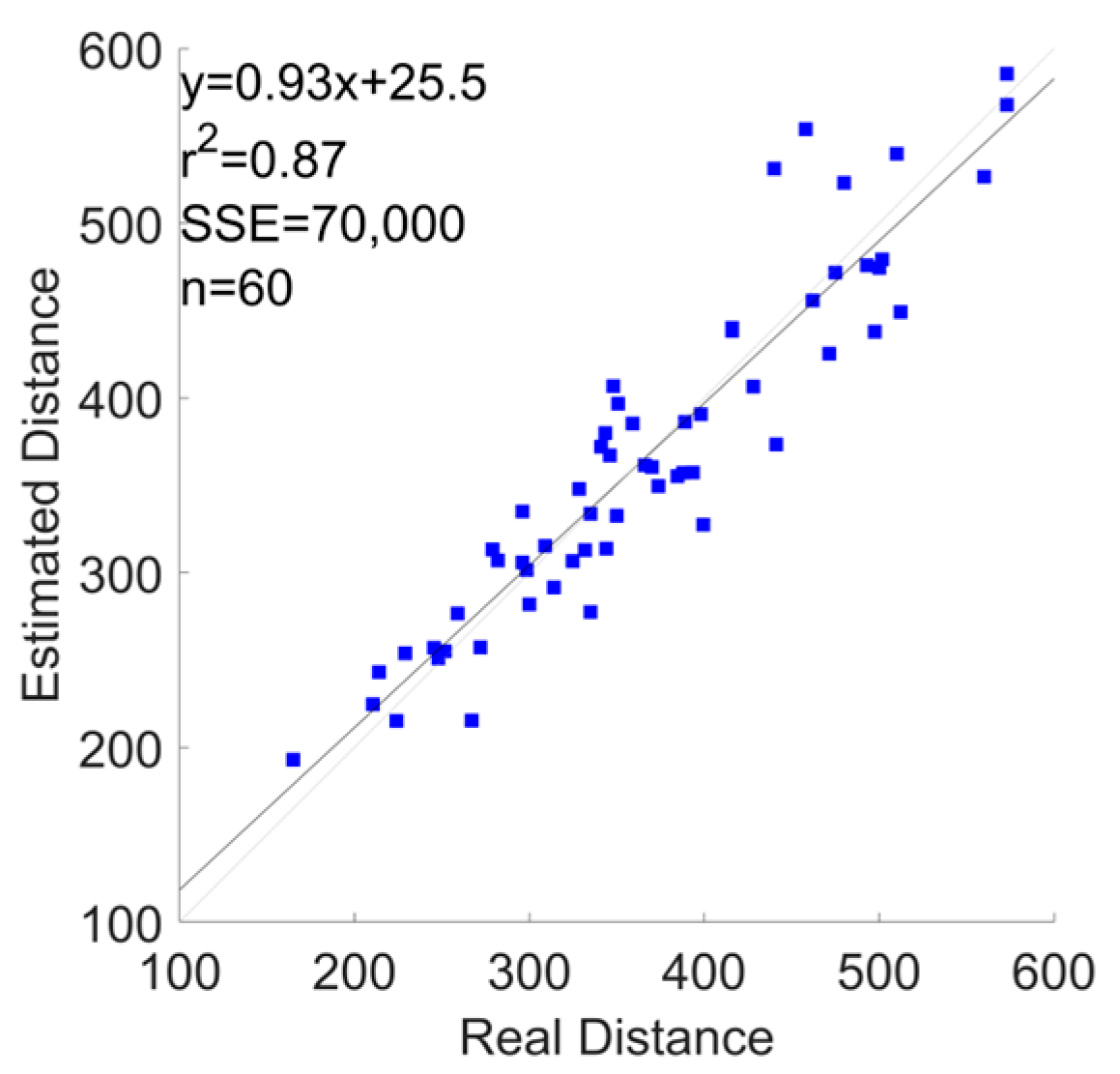
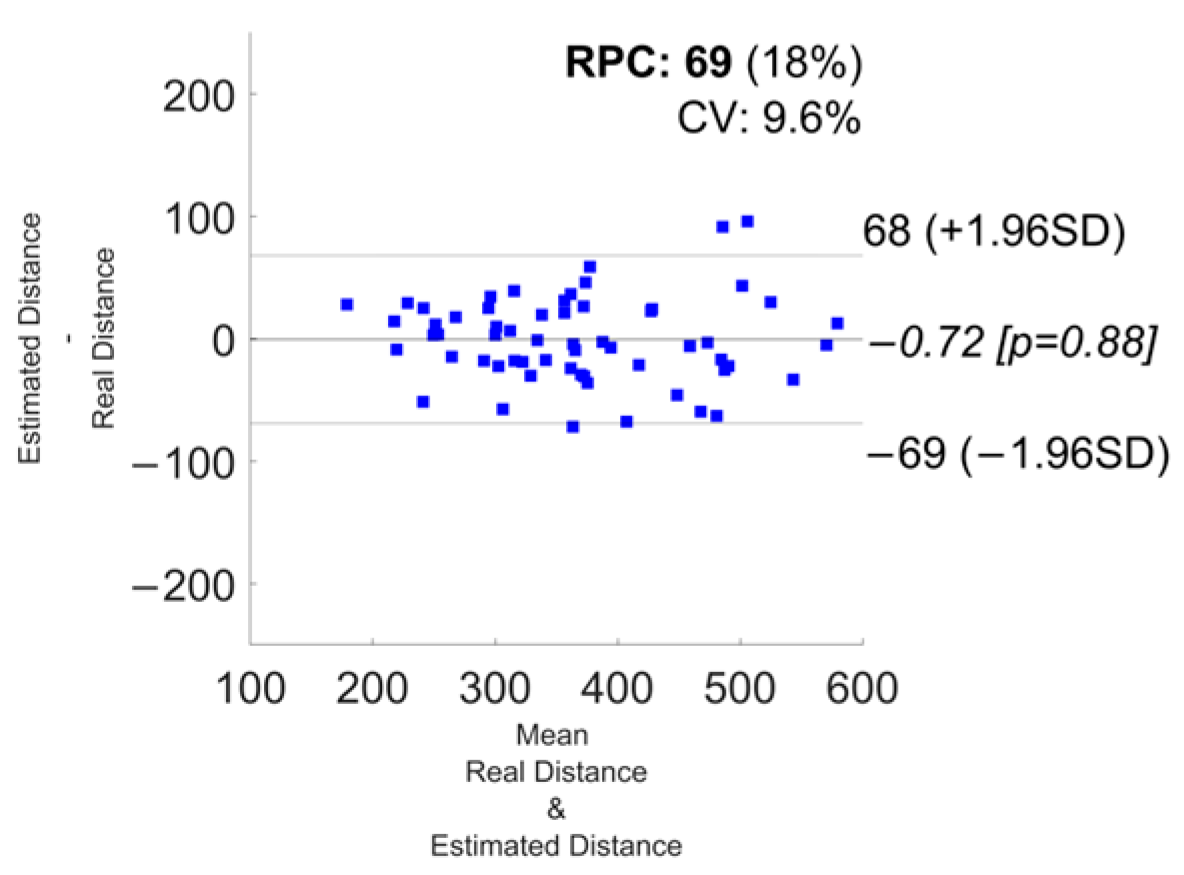
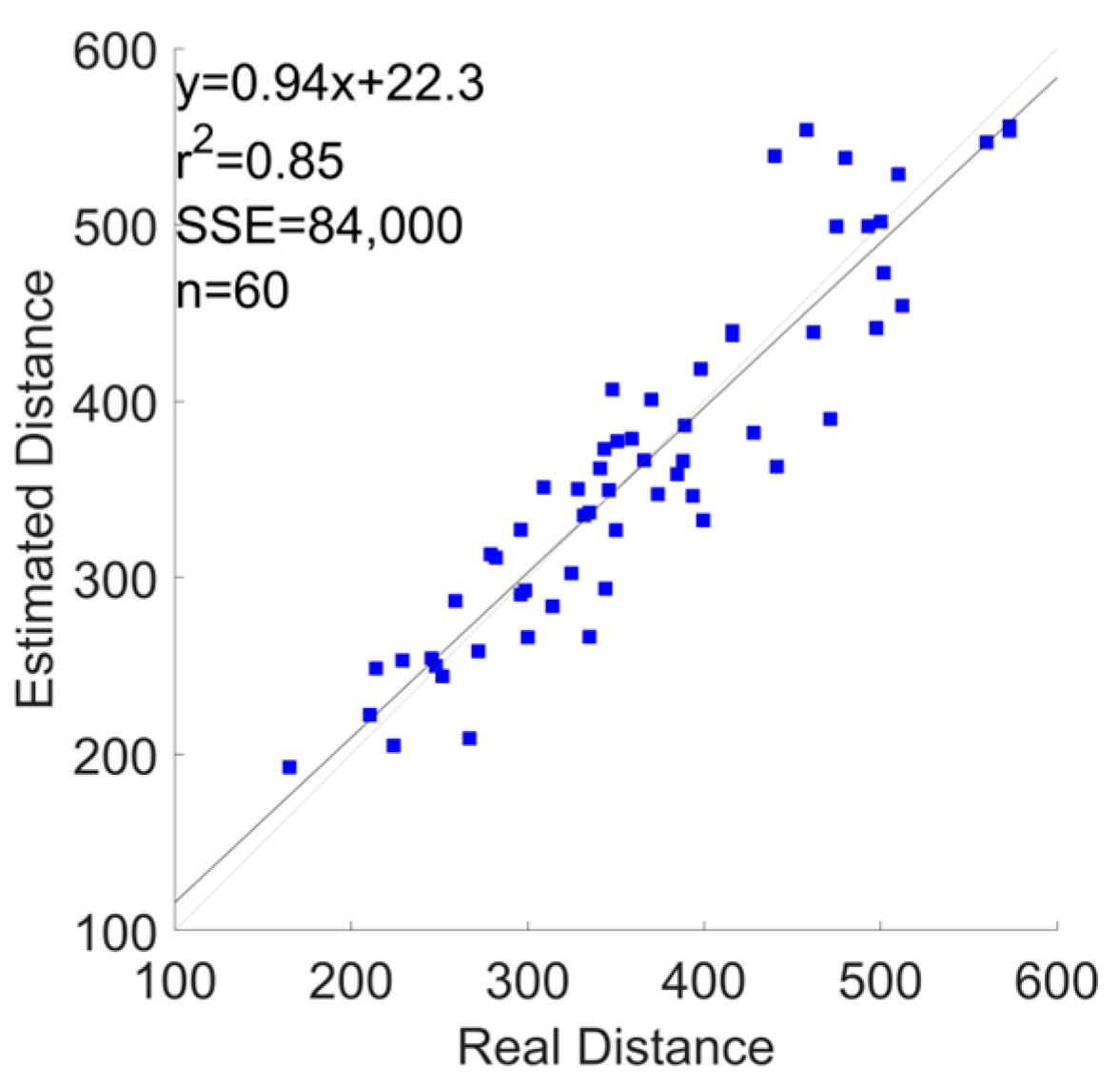
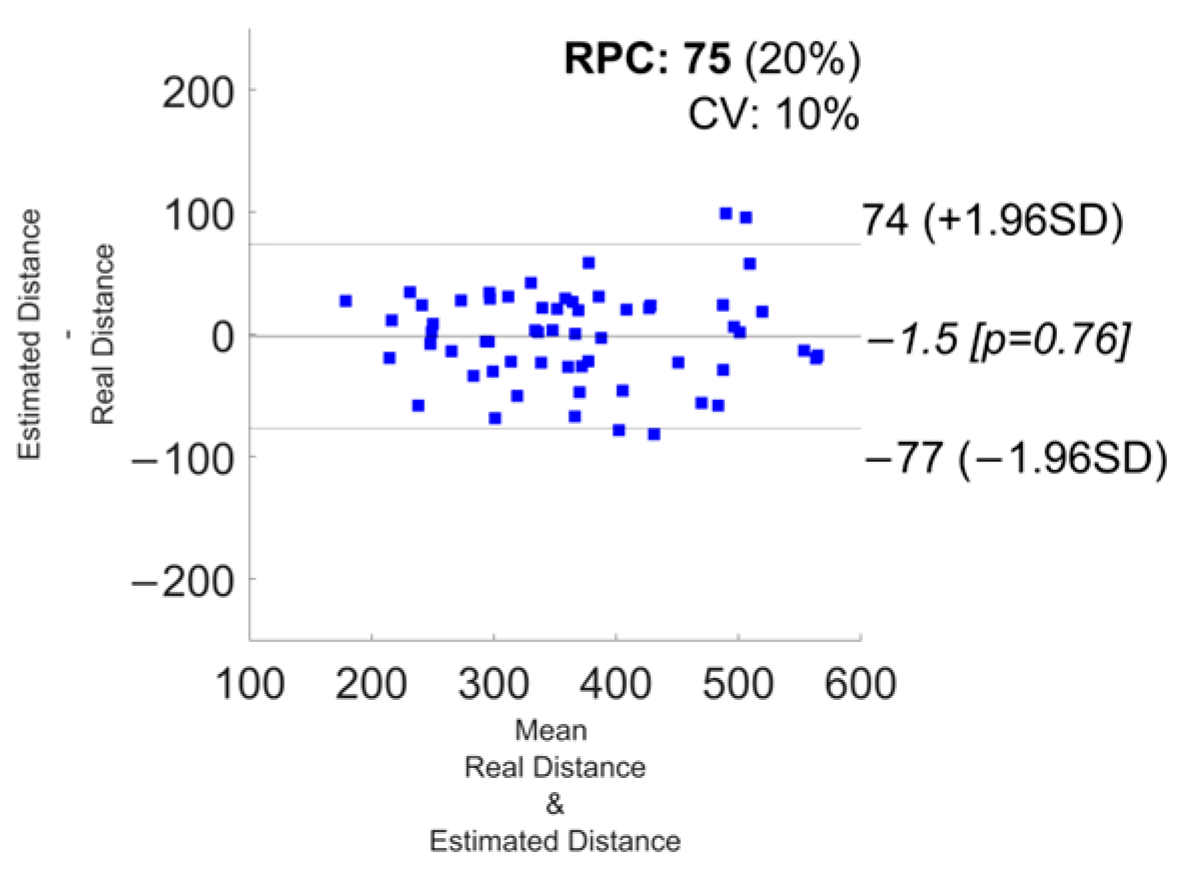
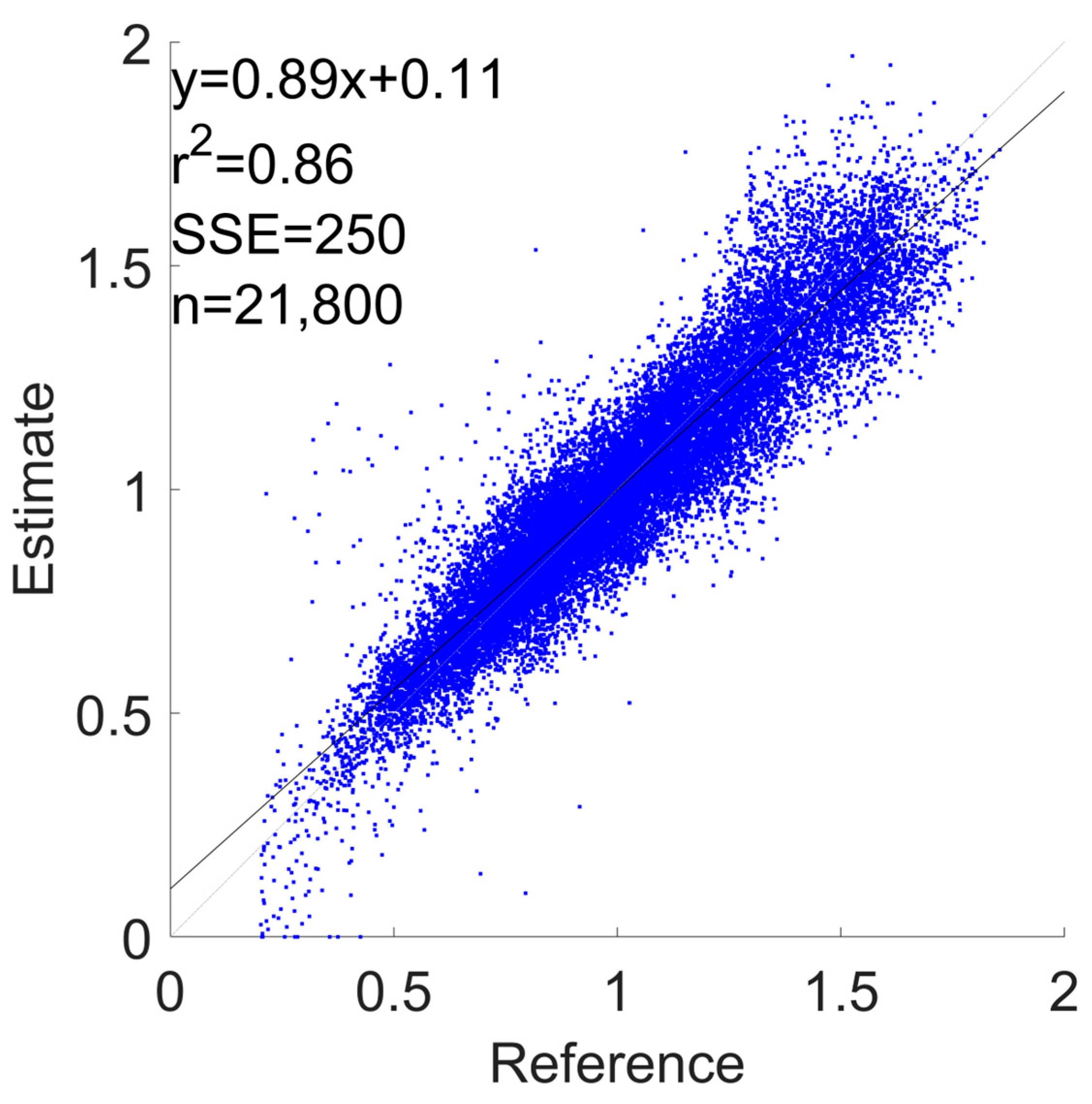
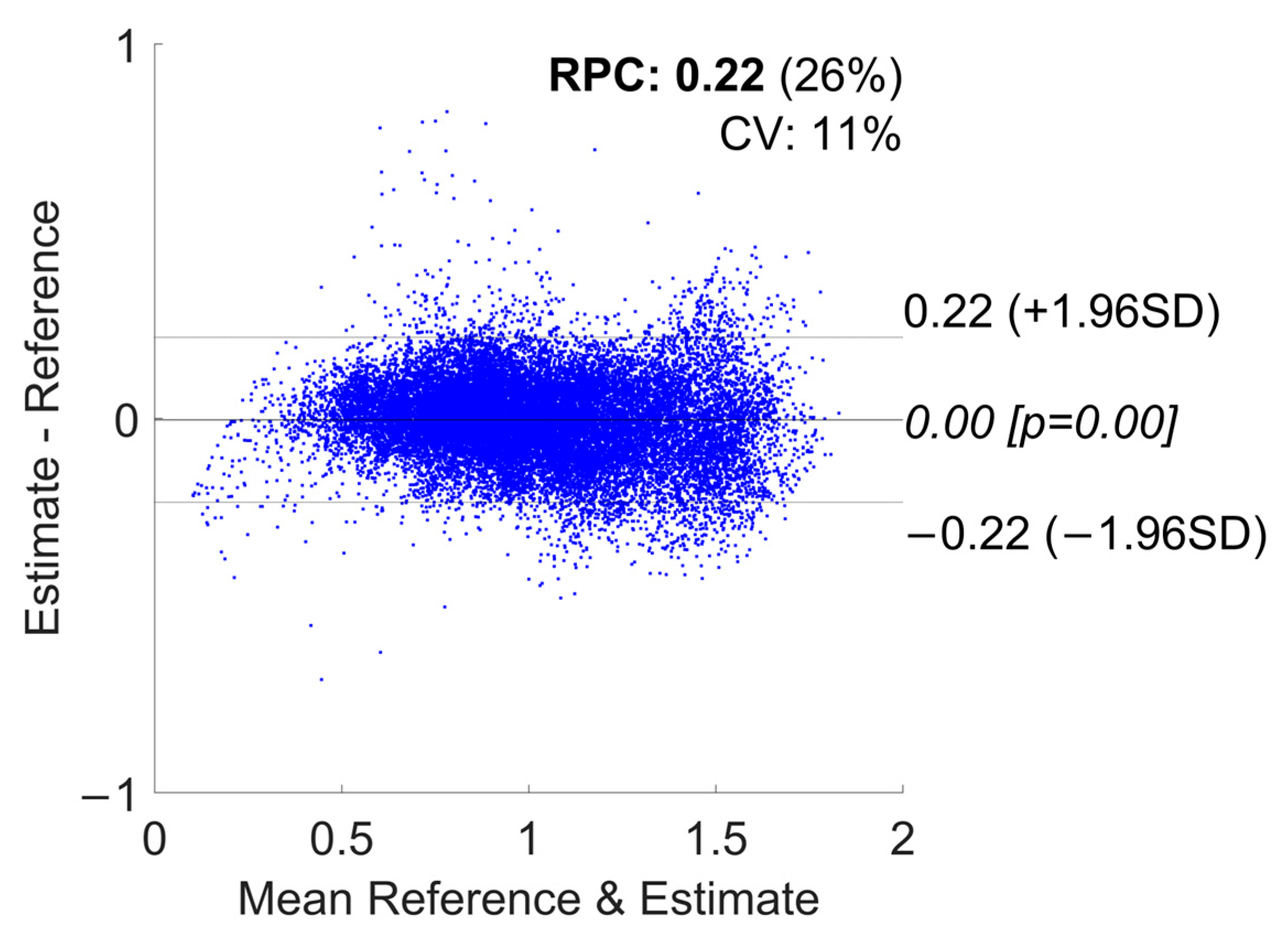
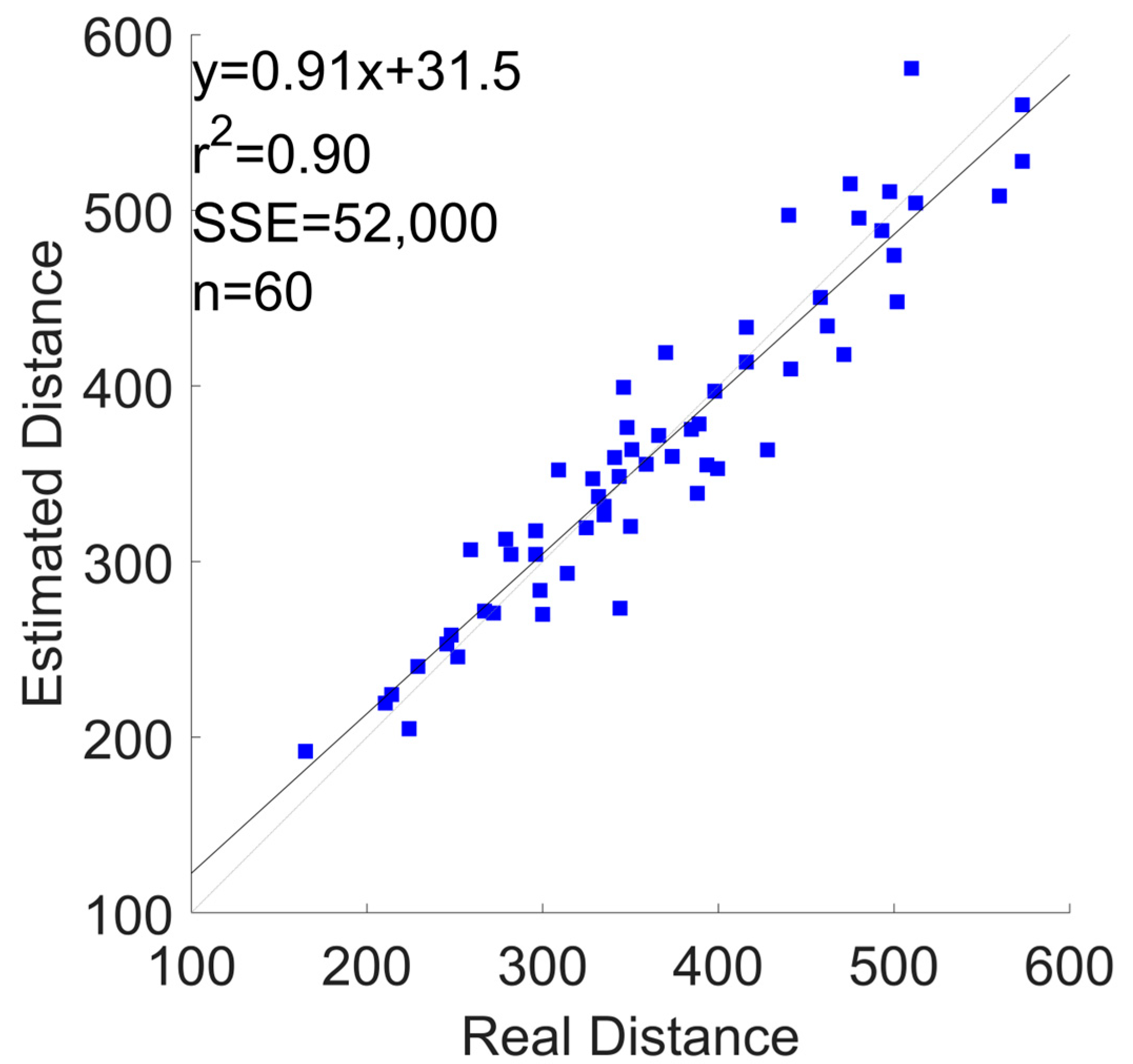
3.1. Error Metrics
3.2. Feature Interpretability
- Significant features: starting from 518 (148 from phones, 148 from watches, 222 from shoes), we obtained 123 features;
- First drop-out stage: from 123, we dropped to 32;
- Second drop-out stage: out of the thirty-two, only six were retained.
- A.
- Smartphone:
- The Shannon entropy of the modulus of the accelerometer when low-pass filtered (β = 0.0527 ± 0.0162, tStat = 45.57 ± 12.57);
- The mean crossing rate of the modulus of the orientation sensor when low-pass filtered (β = 0.0279 ± 0.0048, tStat = 36.70 ± 7.37);
- The range of the y (vertical) component of the accelerometer when low-pass filtered (β = −0.1469 ± 0.0234, tStat = −54.20 ± 11.21);
- The standard deviation of the y (vertical) component of the accelerometer when low-pass filtered (β = 0.255 ± 0.1159, tStat = 77.38 ± 40.48).
- B.
- Smartwatch:
- The root mean square of the modulus of the accelerometer when low-pass filtered (β = −0.279 ± 0.4715, tStat = 29.19 ± 47.73).
- C.
- Smart shoes:
- The mean of the z (vertical) component of the accelerometer of the left shoe when low-pass filtered (β = −0.0487 ± 0.0163, tStat = −39.58 ± 11.81).
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A








References
- Ma, R.; Zhào, H.; Wei, W.; Liu, Y.; Huang, Y. Gait characteristics under single-/dual-task walking conditions in elderly patients with cerebral small vessel disease: Analysis of gait variability, gait asymmetry and bilateral coordination of gait. Gait Posture 2022, 92, 65–70. [Google Scholar] [CrossRef] [PubMed]
- Onder, H.; Dinc, E.; Yucesan, K.; Comoglu, S. The gait parameters in patients with Parkinson’s Disease under STN-DBS therapy and associated clinical features. Neurol. Res. 2023, 45, 779–785. [Google Scholar] [CrossRef]
- Sabo, A.; Iaboni, A.; Taati, B.; Fasano, A.; Gorodetsky, C. Evaluating the ability of a predictive vision-based machine learning model to measure changes in gait in response to medication and DBS within individuals with Parkinson’s disease. Biomed. Eng. Online 2023, 22, 120. [Google Scholar] [CrossRef] [PubMed]
- Bufano, P.; Laurino, M.; Said, S.; Tognetti, A.; Menicucci, D. Digital Phenotyping for Monitoring Mental Disorders: Systematic Review. J. Med. Internet Res. 2023, 25, e46778. [Google Scholar] [CrossRef] [PubMed]
- Jehn, M.; Schmidt-Trucksäss, A.; Meyer, A.; Schindler, C.; Tamm, M.; Stolz, D. Association of daily physical activity volume and intensity with COPD severity. Respir. Med. 2011, 105, 1846–1852. [Google Scholar] [CrossRef] [PubMed]
- Sarkar, P.; Dey, A.; Bhattacharya, S.; Chakrabarti, R. Correlation of six minute walk test with spirometry in COPD patients. Eur. Respir. J. 2021, 58, PA1068. [Google Scholar]
- Middleton, A.; Fritz, S.L.; Lusardi, M. Walking Speed: The Functional Vital Sign. J. Aging Phys. Act. 2015, 23, 314–322. [Google Scholar] [CrossRef] [PubMed]
- Fritz, S.; Lusardi, M. White paper: “walking speed: The sixth vital sign”. J. Geriatr. Phys. Ther. 2009, 32, 46–49. [Google Scholar] [CrossRef]
- Studenski, S. Bradypedia: Is gait speed ready for clinical use? J. Nutr. Health Aging 2009, 13, 878–880. [Google Scholar] [CrossRef] [PubMed]
- Soltani, A.; Dejnabadi, H.; Savary, M.; Aminian, K. Real-World Gait Speed Estimation Using Wrist Sensor: A Personalized Approach. IEEE J. Biomed. Health Inform. 2020, 24, 658–668. [Google Scholar] [CrossRef] [PubMed]
- Soltani, A.; Aminian, K.; Mazza, C.; Cereatti, A.; Palmerini, L.; Bonci, T.; Paraschiv-Ionescu, A. Algorithms for Walking Speed Estimation Using a Lower-Back-Worn Inertial Sensor: A Cross-Validation on Speed Ranges. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 1955–1964. [Google Scholar] [CrossRef]
- Shrestha, A.; Won, M. DeepWalking: Enabling Smartphone-Based Walking Speed Estimation Using Deep Learning. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Nemati, E.; Suh, Y.S.; Motamed, B.; Sarrafzadeh, M. Gait velocity estimation for a smartwatch platform using Kalman filter peak recovery. In Proceedings of the 2016 IEEE 13th International Conference on Wearable and Implantable Body Sensor Networks (BSN), San Fransisco, CA, USA, 14–17 June 2016; pp. 230–235. [Google Scholar]
- McGinnis, R.S.; Mahadevan, N.; Moon, Y.; Seagers, K.; Sheth, N.; Wright, J.A.; DiCristofaro, S.; Silva, I.; Jortberg, E.; Ceruolo, M.; et al. A machine learning approach for gait speed estimation using skin-mounted wearable sensors: From healthy controls to individuals with multiple sclerosis. PLoS ONE 2017, 12, e0178366. [Google Scholar] [CrossRef] [PubMed]
- «TOLIFE | AI and Smart Sensing for COPD | Horizon Europe Project», Tolife Project. Consultato: 20 Febbraio 2024. Available online: https://www.tolife-project.eu/ (accessed on 29 April 2024).
- Carbonaro, N.; Laurino, M.; Greco, A.; Marinai, C.; Giannetti, F.; Righetti, F.; Di Rienzo, F.; Rho, G.; Arcarisi, L.; Zanoletti, M.; et al. Smart Sensors for Daily-Life Data Collection Toward Precision and Personalized Medicine: The TOLIFE Project Approach. In MEDICON’23 and CMBEBIH’23; Badnjević, A., Gurbeta Pokvić, L., Eds.; MEDICON CMBEBIH 2023 2023; IFMBE Proceedings; Springer: Cham, Switzerland, 2024; Volume 93. [Google Scholar] [CrossRef]
- Buttery, S.C.; Williams, P.J.; Alghamdi, S.M.; Philip, K.E.; Perkins, A.; Kallis, C.; Quint, J.K.; Polkey, M.I.; Breuls, S.; Buekers, J.; et al. Investigating the prognostic value of digital mobility outcomes in patients with chronic obstructive pulmonary disease: A systematic literature review and meta-analysis. Eur. Respir. Rev. 2023, 32, 230134. [Google Scholar] [CrossRef] [PubMed]
- Xsens—MVN Gait Report White Paper. Available online: https://www.xsens.com/hubfs/Downloads/Whitepapers/Xsens%20-%20MVN%20Gait%20report%20white%20paper.pdf (accessed on 29 April 2024).
- Annegarn, J.; Spruit, M.A.; Savelberg, H.H.C.M.; Willems, P.J.B.; van de Bool, C.; Schols, A.M.W.J.; Wouters, E.F.M.; Meijer, K. Differences in Walking Pattern during 6-Min Walk Test between Patients with COPD and Healthy Subjects. PLoS ONE 2012, 7, e37329. [Google Scholar] [CrossRef] [PubMed]
- Rienzo, F.D.; Righetti, F.; Laurino, M.; Greco, A.; Marinai, C.; Di Mambro, I.; Melissa, E.; Carbonaro, N.; Bossi, F.; Rho, G.; et al. Using Multiple Devices for Patient Monitoring in Clinical Studies: The TOLIFE Experience. In Proceedings of the 2024 IEEE In-ternational Conference on Pervasive Computing and Communications Workshops and other Affiliated Events, Biarritz, France, 11–15 March 2024. [Google Scholar]
- Carbonaro, N.; Lorussi, F.; Tognetti, A. Assessment of a Smart Sensing Shoe for Gait Phase Detection in Level Walking. Electronics 2016, 5, 78. [Google Scholar] [CrossRef]
- Avvenuti, M.; Carbonaro, N.; Cimino, M.G.C.A.; Cola, G.; Tognetti, A.; Vaglini, G. Smart Shoe-Assisted Evaluation of Using a Single Trunk/Pocket-Worn Accelerometer to Detect Gait Phases. Sensors 2018, 18, 3811. [Google Scholar] [CrossRef]
- Storm, F.A.; Cesareo, A.; Reni, G.; Biffi, E. Wearable Inertial Sensors to Assess Gait during the 6-Minute Walk Test: A Systematic Review. Sensors 2020, 20, 2660. [Google Scholar] [CrossRef] [PubMed]
- ATS Statement: Guidelines for the Six-Minute Walk Test. Available online: https://www.thoracic.org/statements/resources/pfet/sixminute.pdf (accessed on 29 April 2024).
- Schubert, C.; Archer, G.; Zelis, J.M.; Nordmeyer, S.; Runte, K.; Hennemuth, A.; Berger, F.; Falk, V.; Tonino, P.A.L.; Hose, R.; et al. Wearable devices can predict the outcome of standardized 6-minute walk tests in heart disease. NPJ Digit. Med. 2020, 3, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Q.; Juen, J.; Li, Y.; Prieto-Centurion, V.; Krishnan, J.A.; Schatz, B.R. GaitTrack: Health Monitoring of Body Motion from Spatio-Temporal Parameters of Simple Smart Phones. In Proceedings of the International Conference on Bioinformatics, Computational Biology and Biomedical Informatics, Washington, DC, USA, 22–25 September 2013; ACM: New York, NY, USA, 2013; pp. 897–906. [Google Scholar] [CrossRef]
- Mannini, A.; Sabatini, A.M. On-Line Classification of Human Activity and Estimation of Walk-Run Speed from Acceleration Data Using Support Vector Machines. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 3302–3305. [Google Scholar]
- Karpman, C.; Benzo, R. Gait speed as a measure of functional status in COPD patients. Int. J. Chronic Obstr. Pulm. Dis. 2014, 9, 1315–1320. [Google Scholar]
- Ozalevli, S.; Kilinc, O.; Sevinc, C.; Cimrin, A.H.; Ucan, E.S.; Ilgin, D. Gait speed as a functional capacity indicator in patients with chronic obstructive pulmonary disease. Ann. Thorac. Med. 2011, 6, 141–146. [Google Scholar] [CrossRef]
- Waschki, B.; Kirsten, A.; Holz, O.; Müller, K.C.; Meyer, T.; Watz, H.; Magnussen, H. Physical activity is the strongest predictor of all-cause mortality in patients with COPD: A prospective cohort study. Chest 2011, 140, 331–342. [Google Scholar] [CrossRef] [PubMed]
- Peel, N.M.; Kuys, S.S.; Klein, K. Gait Speed as a Measure in Geriatric Assessment in Clinical Settings: A Systematic Review. J. Gerontol. Ser. 2013, 68, 39–46. [Google Scholar] [CrossRef] [PubMed]
- Buracchio, T.; Dodge, H.H.; Howieson, D.; Wasserman, D.; Kaye, J. The Trajectory of Gait Speed Preceding Mild Cognitive Impairment. Arch. Neurol. 2010, 67, 980–986. [Google Scholar] [CrossRef] [PubMed]
- Mirelman, A.; Bonato, P.; Camicioli, R.; Ellis, T.D.; Giladi, P.N.; Hamilton, J.L.; Hass, C.J.; Hausdorff, J.M.; Pelosin, E.; Almeida, Q.J. Gait impairments in Parkinson’s disease. Lancet Neurol. 2019, 18, 697–708. [Google Scholar] [CrossRef] [PubMed]


| Sensor | Units | Sampling Frequency (Hz) | Phone | Watch | Shoes |
|---|---|---|---|---|---|
| Accelerometer | m/s2 | 50 | X, Y, Z | X, Y, Z | X, Y, Z |
| Gyroscope | rad/s | 50 | - | X, Y, Z | X, Y, Z |
| Orientation | deg | 50 | Azimuth-Pitch-Roll | - | - |
| Pressure | mV | 50 | - | - | X, Y, Z |
| Devices Combination | RMSE [m/s] | Lower Limit of Agreement [−1.96 SD] | Upper Limit of Agreement [+1.96 SD] | Bias | R2 |
|---|---|---|---|---|---|
| Phone | 0.114 ± 0.055 | −0.24 | 0.25 | 0.01 | 0.83 |
| Watch | 0.135 ± 0.033 | −0.27 | 0.27 | 0.00 | 0.79 |
| Shoes | 0.141 ± 0.05 | −0.3 | 0.29 | −0.01 | 0.76 |
| Phone + Watch | 0.113 ± 0.051 | −0.25 | 0.24 | −0.00 | 0.84 |
| Phone + Shoes | 0.11 ± 0.04 | −0.23 | 0.23 | 0.00 | 0.85 |
| Watch + Shoes | 0.109 ± 0.029 | −0.22 | 0.22 | 0.00 | 0.86 |
| All Devices | 0.111 ± 0.043 | −0.24 | 0.23 | −0.00 | 0.85 |
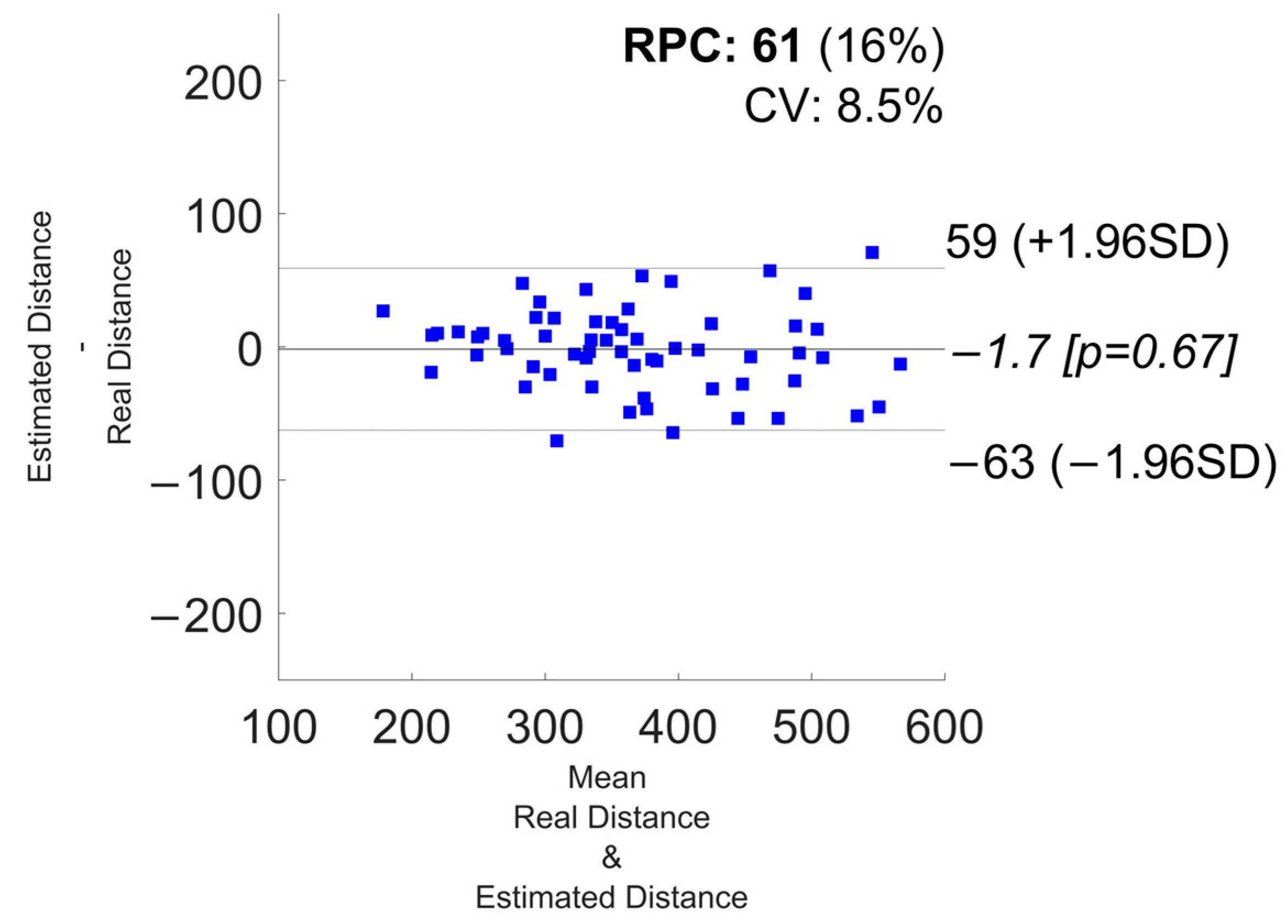
| Devices Combination | εr | Lower Limit of Agreement [−1.96SD] | Upper Limit of Agreement [+1.96SD] | Bias | R2 |
|---|---|---|---|---|---|
| Phone | 7.2 ± 7.1 | −72 | 75 | 1.6 | 0.85 |
| Watch | 8.6 ± 6.7 | −75 | 75 | 0.24 | 0.85 |
| Shoes | 9.3 ± 8.1 | −92 | 86 | −2.7 | 0.78 |
| Phone + Watch | 7.8 ± 6.6 | −73 | 70 | −1.6 | 0.86 |
| Phone + Shoes | 7.6 ± 5.5 | −69 | 68 | −0.72 | 0.87 |
| Watch + Shoes | 6.6 ± 5.1 | −63 | 59 | −1.7 | 0.9 |
| All Devices | 8.4 ± 6 | −77 | 74 | −1.5 | 0.85 |
| 2.5 s | 5 s | 10 s | 20 s | |||||
|---|---|---|---|---|---|---|---|---|
| Devices Combination | GS (RMSE [m/s]) | 6MWD (εr) | GS (RMSE [m/s]) | 6MWD (εr) | GS (RMSE [m/s]) | 6MWD (εr) | GS (RMSE [m/s]) | 6MWD (εr) |
| Phone | 0.145 ± 0.053 | 8 ± 7.6 | 0.114 ± 0.055 | 7.2 ± 7.1 | 0.108 ± 0.06 | 8.2 ± 7.1 | 0.101 ± 0.064 | 8.6 ± 6.7 |
| Watch | 0.179 ± 0.042 | 9.3 ± 8.2 | 0.135 ± 0.033 | 8.6 ± 6.7 | 0.122 ± 0.036 | 9.4 ± 7.0 | 0.116 ± 0.036 | 9.1 ± 6.5 |
| Shoes | 0.17 ± 0.038 | 9.6 ± 6.7 | 0.141 ± 0.05 | 9.3 ± 8.1 | 0.112 ± 0.047 | 7.5 ± 6.5 | 0.112 ± 0.05 | 8.5 ± 6.7 |
| Phone + Watch | 0.135 ± 0.038 | 7.2 ± 6.1 | 0.113 ± 0.051 | 7.8 ± 6.6 | 0.109 ± 0.058 | 8.5 ± 7 | 0.094 ± 0.051 | 7.6 ± 5.9 |
| Phone + Shoes | 0.134 ± 0.043 | 8.3 ± 6.5 | 0.11 ± 0.04 | 7.6 ± 5.5 | 0.095 ± 0.046 | 7.2 ± 5.1 | 0.1 ± 0.044 | 8.5 ± 6.2 |
| Watch + Shoes | 0.152 ± 0.035 | 8.5 ± 6.7 | 0.109 ± 0.029 | 6.6 ± 5.1 | 0.093 ± 0.041 | 6.4 ± 5.4 | 0.091 ± 0.043 | 6.9 ± 5.8 |
| All Devices | 0.124 ± 0.031 | 7.9 ± 5.4 | 0.111 ± 0.043 | 8.4 ± 6 | 0.098 ± 0.036 | 7.8 ± 4.9 | 0.088 ± 0.041 | 7.2 ± 6 |
| Phone | Watch | Shoes | Phone + Watch | Phone + Shoes | Watch + Shoes | All Devices | |
|---|---|---|---|---|---|---|---|
| Intercept | 0.951 +/− 0.001 | 0.945 +/− 0.001 | 0.971 +/− 0.001 | 0.954 +/− 0.001 | 1.375 +/− 0.011 | 0.963 +/− 0.001 | 0.955 +/− 0.001 |
| Feat. 1 | ENT_acc_lp_mod_dev_1: 0.062 +/− 0.001 | RNG_acc_lp_mod_dev_2: −0.114 +/− 0.004 | MEAN_acc_lp_mod_dev_3: 0.14 +/− 0.002 | STD_acc_lp_mod_dev_1: 0.373 +/− 0.006 | ENT_acc_lp_mod_dev_1: 0.032 +/− 0.001 | RMS_acc_lp_mod_dev_2: 0.079 +/− 0.001 | MCR_acc_lp_mod_dev_1: −0.03 +/− 0.001 |
| Feat. 2 | RNG_acc_lp_y_dev_1: −0.143 +/− 0.003 | RMS_acc_lp_mod_dev_2: −0.9 +/− 0.028 | MEAN_acc_lp_z_dev_3: −0.02 +/− 0.002 | MCR_acc_lp_mod_dev_1: −0.035 +/− 0.001 | RNG_acc_lp_y_dev_1: −0.122 +/− 0.003 | STD_acc_lp_mod_dev_2: 0.086 +/− 0.001 | ENT_acc_lp_mod_dev_1: 0.03 +/− 0.001 |
| Feat. 3 | MEAN_acc_lp_y_dev_1: −0.021 +/− 0.001 | MEAN_acc_lp_mod_dev_2: 0.908 +/− 0.025 | ENT_acc_lp-hp_y_dev_3: 0.048 +/− 0.001 | ENT_acc_lp_mod_dev_1: 0.065 +/− 0.001 | STD_acc_lp_y_dev_1: 0.291 +/− 0.003 | ENT_acc_lp_mod_dev_2: 0.037 +/− 0.001 | RNG_acc_lp_y_dev_1: −0.128 +/− 0.003 |
| Feat. 4 | STD_acc_lp_y_dev_1: 0.374 +/− 0.004 | STD_acc_lp_mod_dev_2: 0.437 +/− 0.008 | MCR_pre_lp_mod_dev_3: 0.043 +/− 0.001 | MAX_acc_lp_y_dev_1: −0.09 +/− 0.002 | MCR_gyr_lp_x_dev_1: 0.031 +/− 0.001 | CV_gyr_lp-hp_mod_dev_2: 0.025 +/− 0.001 | STD_acc_lp_y_dev_1: 0.292 +/− 0.003 |
| Feat. 5 | MCR_acc_lp_y_dev_1: −0.035 +/− 0.001 | ENT_acc_lp_mod_dev_2: 0.028 +/− 0.002 | PF_pre_lp_z_dev_3: 0.053 +/− 0.001 | STD_acc_lp_y_dev_1: 0.019 +/− 0.006 | PF_gyr_lp_y_dev_1: 0.022 +/− 0.001 | MEAN_acc_lp_z_dev_3: −0.063 +/− 0.001 | MCR_gyr_lp_mod_dev_1: 0.03 +/− 0.001 |
| Feat. 6 | MCR_acc_lp-hp_mod_dev_1: 0.039 +/− 0.001 | MEAN_acc_lp_y_dev_2: 0.028 +/− 0.001 | MAX_pre_lp-hp_x_dev_3: 0.032 +/− 0.001 | PF_acc_lp_z_dev_1: 0.028 +/− 0.001 | PF_gyr_lp-hp_z_dev_1: 0.019 +/− 0.001 | ENT_gyr_lp_z_dev_3: 0.044 +/− 0.001 | SMA_gyr_lp-hp_dev_2: 0.058 +/− 0.001 |
| Feat. 7 | PF_acc_lp-hp_mod_dev_1: 0.02 +/− 0.001 | SMA_acc_lp-hp_dev_2: 0.054 +/− 0.003 | ENT_acc_lp_x_dev_4: 0.025 +/− 0.001 | SMA_acc_lp-hp_dev_1: 0.068 +/− 0.003 | MEAN_acc_lp_z_dev_3: −0.047 +/− 0.001 | RMS_acc_lp_z_dev_4: 0.071 +/− 0.00 | MEAN_acc_lp_z_dev_3: −0.045 +/− 0.001 |
| Feat. 8 | PF_acc_lp-hp_z_dev_1: 0.028 +/− 0.001 | MCR_acc_lp-hp_mod_dev_2: 0.051 +/− 0.002 | RMS_acc_lp_z_dev_4: 0.117 +/− 0.002 | STD_acc_lp-hp_mod_dev_1: −0.165 +/− 0.004 | CV_gyr_lp_mod_dev_3: 1.922 +/− 0.051 | RMS_gyr_lp_z_dev_4: −0.047 +/− 0.001 | MEAN_acc_lp_z_dev_4: −0.045 +/− 0.001 |
| Feat. 9 | MCR_gyr_lp_mod_dev_1: 0.025 +/− 0.001 | CV_gyr_lp_mod_dev_2: 0.039 +/− 0.001 | MCR_gyr_lp-hp_z_dev_4: 0.041 +/− 0.001 | MCR_gyr_lp_mod_dev_1: 0.032 +/− 0.001 | MAX_pre_lp_z_dev_3: 0.023 +/− 0.001 | MEAN_gyr_lp-hp_mod_dev_4: 0.05 +/− 0.002 | RMS_gyr_lp_x_dev_4: 0.032 +/− 0.001 |
| Feat. 10 | PF_gyr_lp-hp_z_dev_1: 0.024 +/− 0.001 | RNG_gyr_lp_y_dev_2: −0.046 +/− 0.002 | ENT_pre_lp-hp_y_dev_4: 0.036 +/− 0.001 | RMS_acc_lp_mod_dev_2: 0.074 +/− 0.001 | MEAN_acc_lp_z_dev_4: −0.069 +/− 0.001 | ENT_pre_lp_z_dev_4: 0.031 +/− 0.001 | ENT_gyr_lp-hp_x_dev_4: 0.032 +/− 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zanoletti, M.; Bufano, P.; Bossi, F.; Di Rienzo, F.; Marinai, C.; Rho, G.; Vallati, C.; Carbonaro, N.; Greco, A.; Laurino, M.; et al. Combining Different Wearable Devices to Assess Gait Speed in Real-World Settings. Sensors 2024, 24, 3205. https://doi.org/10.3390/s24103205
Zanoletti M, Bufano P, Bossi F, Di Rienzo F, Marinai C, Rho G, Vallati C, Carbonaro N, Greco A, Laurino M, et al. Combining Different Wearable Devices to Assess Gait Speed in Real-World Settings. Sensors. 2024; 24(10):3205. https://doi.org/10.3390/s24103205
Chicago/Turabian StyleZanoletti, Michele, Pasquale Bufano, Francesco Bossi, Francesco Di Rienzo, Carlotta Marinai, Gianluca Rho, Carlo Vallati, Nicola Carbonaro, Alberto Greco, Marco Laurino, and et al. 2024. "Combining Different Wearable Devices to Assess Gait Speed in Real-World Settings" Sensors 24, no. 10: 3205. https://doi.org/10.3390/s24103205
APA StyleZanoletti, M., Bufano, P., Bossi, F., Di Rienzo, F., Marinai, C., Rho, G., Vallati, C., Carbonaro, N., Greco, A., Laurino, M., & Tognetti, A. (2024). Combining Different Wearable Devices to Assess Gait Speed in Real-World Settings. Sensors, 24(10), 3205. https://doi.org/10.3390/s24103205










