Sensor Fault Reconstruction Using Robustly Adaptive Unknown-Input Observers
Abstract
:1. Introduction
- (i)
- A novel sensor fault estimation approach is proposed by integrating unknown input observer and adaptive observer techniques, which is named as adaptive unknown input observer (UIO) approach.
- (ii)
- An unknown input observer is used to decouple partial input uncertainties, and the linear matrix inequality approach is employed to attenuate un-decoupled unknown input uncertainty and the differential of the sensor fault. As a result, a robust reconstruction of the sensor fault is achieved.
- (iii)
- Without the aid of the well-known augmented system technique, the proposed adaptive observer technique can achieve a direct reconstruction of the sensor fault, which provides a novel way for sensor fault reconstruction.
- (iv)
- The observer gains are solved by using strict linear matrix inequalities without equality constraints, which are more convenient for calculation.
- (v)
- The proposed sensor fault estimation approaches are developed for both linear systems and Lipschitz nonlinear systems, which have a wide applicability.
- (vi)
- The effectiveness of the proposed sensor fault algorithms is validated by two engineering-oriented examples, and comparison studies are carried out to demonstrate the tracing performance of the proposed technique.
2. Robustly Adaptive Sensor Fault Estimation for Linear System
2.1. System Description
2.2. Adaptive UIO Design for Sensor Fault Reconstruction
- (i)
- (a) in Assumption 1 can ensure the disturbance can be completely decoupled, and one can calculate a special solution by .
- (ii)
- (b) and (c) in Assumption 1 can ensure one can find an observer gain to make the matrix stable.
3. Adaptive UIO for Sensor Fault Estimation in Lipschitz Nonlinear System
4. Design Procedures for Sensor Fault Estimation
4.1. Procedure 1. Sensor Fault Estimation for Linear Dynamic Systems
- a.
- Select a matrix as follows:
- b.
- Select the adaptive learning rate which is a positive definite matrix.
- c.
- Solve the LMI (15) in Theorem 1 to obtain appropriate matrices , and , and calculate the estimator gain by .
- d.
- Calculate the other estimator gain matrices:
- e.
- Implement the robust adaptive estimator in the form of (2) and (6), and the real-time estimate of state and sensor fault can be obtained.
4.2. Procedure 2. Sensor Fault Estimation for Lipschitz Nonlinear Dynamic Systems
- a.
- Select a matrix as follows:
- b.
- Select the adaptive learning rate which is a positive definite matrix.
- c.
- Solve the LMI (30) in Theorem 2 to obtain appropriate matrices , and , and calculate the estimator gain by .
- d.
- Calculate the other estimator gain matrices:
- e.
- Implement the nonlinear adaptive estimator in the form of (6) and (26), and the real-time estimate of state and sensor fault can be obtained.
5. Simulation Studies
5.1. Civil Aircraft
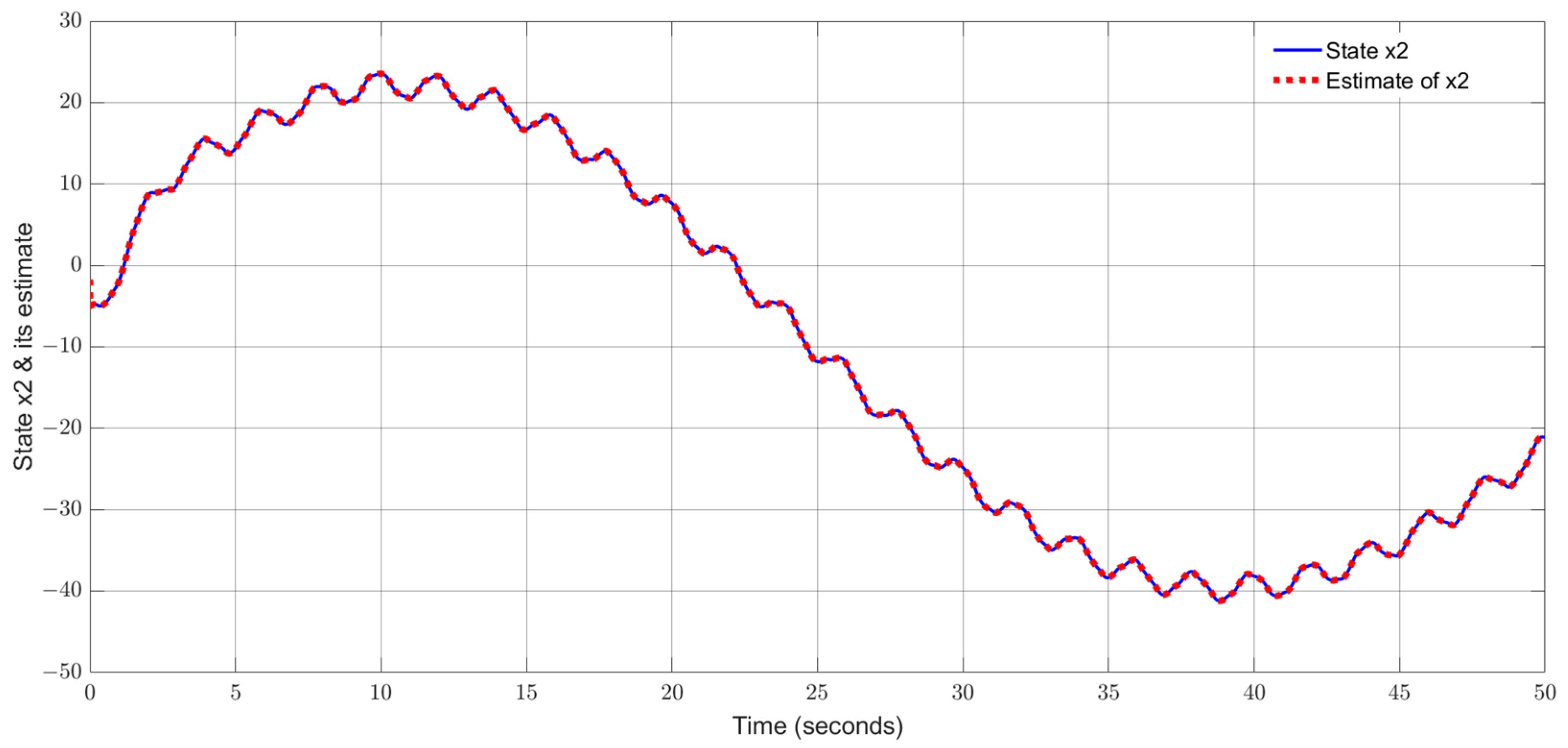
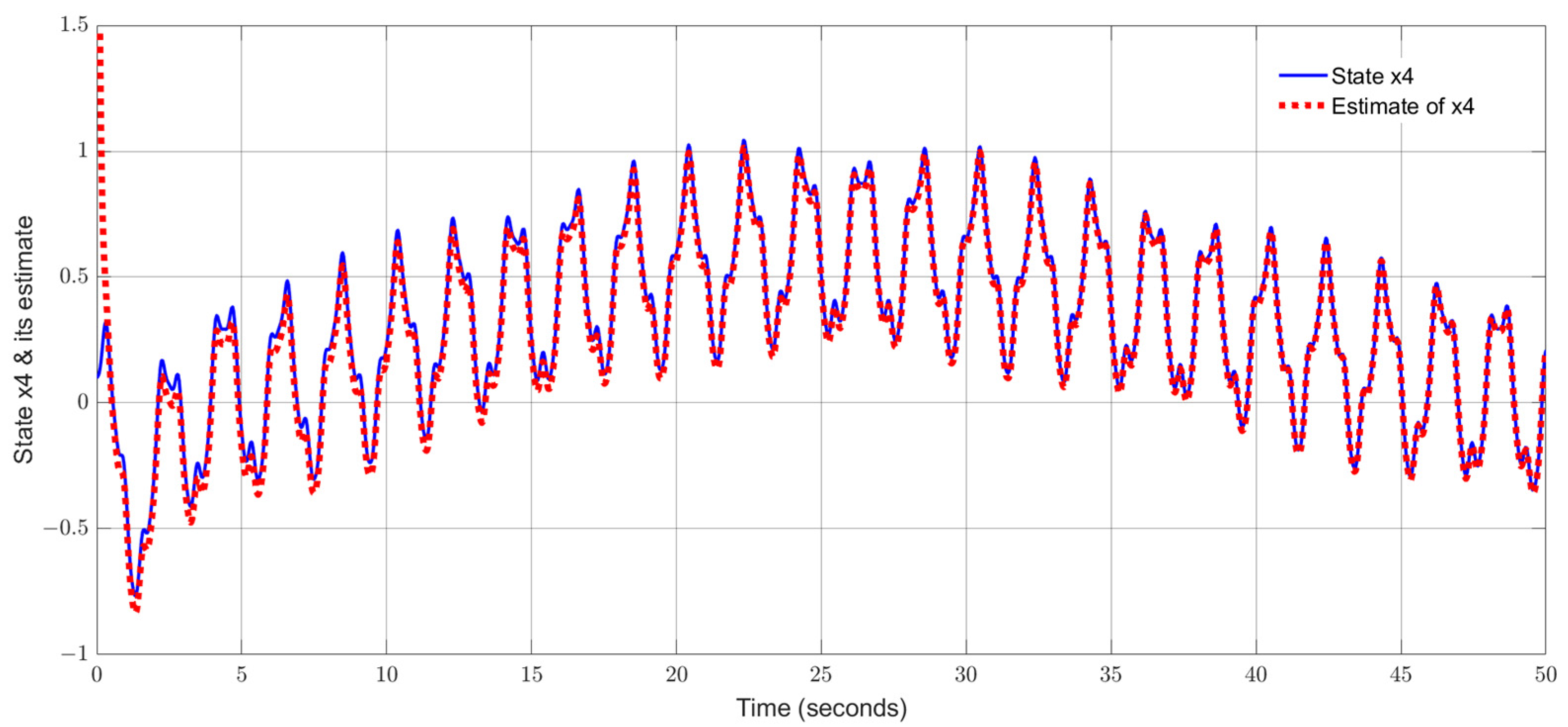
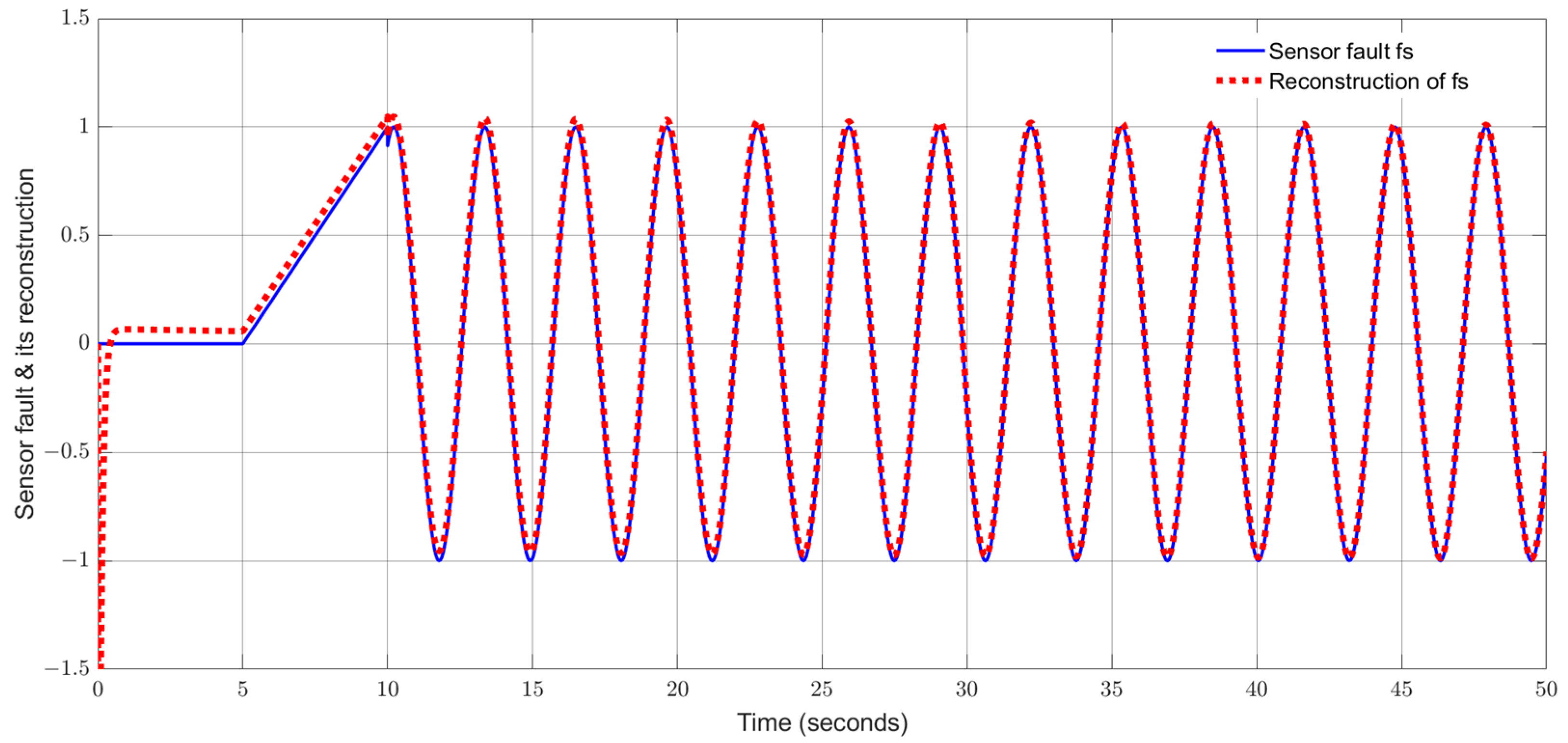
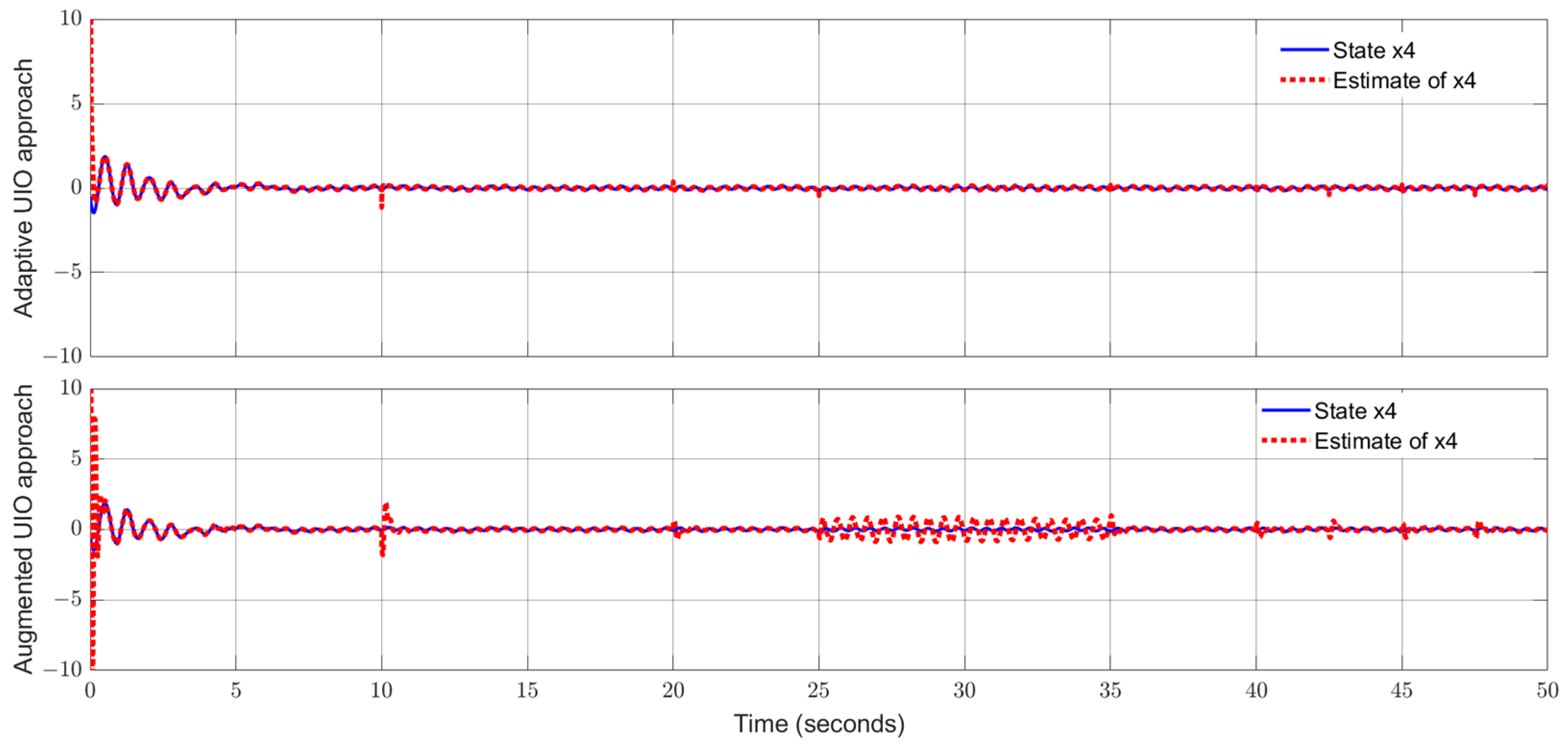
5.2. Single-Link Flexible Joint Robot
- (i)
- The proposed adaptive UIO estimation technique
- (ii)
- The augmented UIO estimation technique [17]
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, W.; Xie, C.; Zhuang, M.; Shou, Y.; Tang, Y.J. Sensor data fusion with z-numbers and its application in fault diagnosis. Sensors 2016, 16, 1509. [Google Scholar] [CrossRef]
- Sohaib, M.; Kim, C.-H.; Kim, J. A hybrid feature model and deep-learning-based bearing fault diagnosis. Sensors 2017, 17, 2876. [Google Scholar] [CrossRef]
- Xu, J.; Wang, J.; Li, S.; Cao, B. A method to simultaneously detect the current sensor fault and estimate the state of energy for batteries in electric vehicles. Sensors 2016, 16, 1328. [Google Scholar] [CrossRef] [PubMed]
- Yan, R.; Shen, F.; Sun, C.; Chen, X. Knowledge transfer for rotary machine fault diagnosis. IEEE Sens. J. 2019, 20, 8374–8393. [Google Scholar] [CrossRef]
- Yin, S.; Ding, S.X.; Xie, X.; Luo, H.J.I.T.o.I.e. A review on basic data-driven approaches for industrial process monitoring. IEEE Trans. Ind. Electron. 2014, 61, 6418–6428. [Google Scholar] [CrossRef]
- Lan, T.; Gao, Z.-W.; Yin, H.; Liu, Y. A Sensor-Fault-Estimation Method for Lithium-Ion Batteries in Electric Vehicles. Sensors 2023, 23, 7737. [Google Scholar] [CrossRef]
- Li, B.; Zhao, Y.-P.; Chen, Y.-B. Technology. Unilateral alignment transfer neural network for fault diagnosis of aircraft engine. Aerosp. Sci. Technol. 2021, 118, 107031. [Google Scholar] [CrossRef]
- Gao, Z.; Breikin, T.; Wang, H. High-gain estimator and fault-tolerant design with application to a gas turbine dynamic system. IEEE Trans. Control Syst. Technol. 2017, 21, 861–868. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, L.; Decastro, J. Robust fault diagnosis of aircraft engines: A nonlinear adaptive estimation-based approach. IEEE Trans. Control Syst. Technol. 2013, 21, 861–868. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A survey of fault diagnosis and fault-tolerant techniques—Part I: Fault diagnosis with model-based and signal-based approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Witczak, M.; Buciakowski, M.; Puig, V.; Rotondo, D.; Nejjari, F. An LMI approach to robust fault estimation for a class of nonlinear systems. Int. J. Robust Nonlinear Control 2016, 26, 1530–1548. [Google Scholar] [CrossRef]
- Yin, X.; Chen, J.; Li, Z.; Li, S. Robust fault diagnosis of stochastic discrete event systems. IEEE Trans. Autom. Control 2019, 64, 4237–4244. [Google Scholar] [CrossRef]
- Castaldi, P.; Mimmo, N.; Simani, S. Fault diagnosis and fault-tolerant control techniques for aircraft systems. In Fault Diagnosis and Fault-Tolerant Control of Robotic and Autonomous Systems; IET: London, UK, 2020; pp. 197–212. [Google Scholar]
- Castaldi, P.; Mimmo, N.; Simani, S. Differential geometry based active fault tolerant control for aircraft. Control Eng. Pract. 2014, 32, 227–235. [Google Scholar] [CrossRef]
- Du, D.; Cocquempot, V.; Jiang, B. Robust fault estimation observer design for switched systems with unknown input. Appl. Math. Comput. 2019, 348, 70–83. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, S.; Shi, J.; Li, T.; Wang, X. Fault diagnosis of an intelligent hydraulic pump based on a nonlinear unknown input observer. Chin. J. Aeronaut. 2018, 31, 385–394. [Google Scholar] [CrossRef]
- Gao, Z.; Liu, X.; Chen, M. Unknown input observer-based robust fault estimation for systems corrupted by partially decoupled disturbances. IEEE Trans. Ind. Electron. 2016, 63, 2537–2547. [Google Scholar] [CrossRef]
- Gao, Z.; Wang, H. Descriptor observer approaches for multivariable systems with measurement noises and application in fault detection and diagnosis. Syst. Control Lett. 2006, 55, 304–313. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, F.; Wang, X.; Bu, X. Robust sliding-mode observer-based sensor fault estimation, actuator fault detection and isolation for uncertain nonlinear systems. Control Theory 2015, 13, 1037–1046. [Google Scholar] [CrossRef]
- Liu, M.; Shi, P. Sensor fault estimation and tolerant control for Itô stochastic systems with a descriptor sliding mode approach. Automatica 2013, 49, 1242–1250. [Google Scholar] [CrossRef]
- Gao, Z.; Ding, S. Fault reconstruction for Lipschitz nonlinear descriptor systems via linear matrix inequality approach. Circuits Syst. Signal Process. 2008, 27, 295–308. [Google Scholar] [CrossRef]
- Chang, J. Applying discrete-time proportional integral observers for state and disturbance estimations. IEEE Trans. Autom. Control 2006, 51, 814–818. [Google Scholar] [CrossRef]
- Do, M.; Koenig, D.; Theilliol, D. Robust H∞ proportional-integral observer for fault diagnosis: Application to vehicle suspension. IFAC-Pap. 2018, 51, 536–543. [Google Scholar] [CrossRef]
- Gao, Z.; Breikin, T.; Wang, H. Discrete-time proportional and integral observer and observer-based controller for systems both with unknown input and output disturbances. Optim. Control. Appl. Methods 2008, 29, 171–189. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, G. Fault-estimation-based output-feedback adaptive FTC for uncertain nonlinear systems with actuator faults. IEEE Trans. Ind. Electron. 2019, 67, 3065–3075. [Google Scholar] [CrossRef]
- Zhang, K.; Jiang, B.; Cocquempot, V. Adaptive observer-based fast fault estimation. Int. J. Control Automaition Syst. 2008, 6, 320–326. [Google Scholar]
- Gao, S.; Ma, G.; Guo, Y.; Zhang, W. Fast actuator and sensor fault estimation based on adaptive unknown input observer. ISA Trans. 2022, 129, 305–323. [Google Scholar] [CrossRef] [PubMed]
- Defoort, M.; Veluvolu, K.C.; Rath, J.; Djemai, M. Adaptive sensor and actuator fault estimation for a class of uncertain Lipschitz nonlinear systems. Int. J. Adapt. Control Signal Process. 2016, 30, 271–283. [Google Scholar] [CrossRef]
- Chen, J.; Patton, R. Robust Model-Based Fault Diagnosis for Dynamic Systems; Kluwer: Boston, MA, USA, 1999. [Google Scholar]
- Li, L.; Jia, Y.; Du, J.; Yuan, S. Robust L2–L∞ control for uncertain singular systems with time-varying delay. Prog. Nat. Sci. 2008, 18, 1015–1021. [Google Scholar] [CrossRef]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 1994. [Google Scholar]
- Alwi, H.; Edwards, C. Robust sensor fault estimation for tolerant control of a civil aircraft using sliding modes. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 5704–5709. [Google Scholar]
- Rajamani, R.; Cho, Y. Existence and design of observers for nonlinear systems: Relation to distance to unobservability. Int. J. Control 1998, 69, 717–731. [Google Scholar] [CrossRef]






|
|
|
|
|
|
| Sensor Fault Type | Proposed Adaptive UIO | Existing Augmented UIO |
|---|---|---|
| Biased fault | Track well | Track well |
| Incipient fault | Track well | Track well |
| Measurement effectiveness loss | Work well with a quicker tracking | Track well |
| Low-frequency sinusoidal signal fault | Work well with a quicker tracking | Track well |
| High-frequency sinusoidal signal fault | Better tracking performance compared with the augmented UIO | Tracking performance is reduced with a high-frequency sensor fault signal |
| Intermittent square wave fault | Work well with a quicker tracking | Track well |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Q.; Gao, Z.-W.; Liu, Y. Sensor Fault Reconstruction Using Robustly Adaptive Unknown-Input Observers. Sensors 2024, 24, 3224. https://doi.org/10.3390/s24103224
Huang Q, Gao Z-W, Liu Y. Sensor Fault Reconstruction Using Robustly Adaptive Unknown-Input Observers. Sensors. 2024; 24(10):3224. https://doi.org/10.3390/s24103224
Chicago/Turabian StyleHuang, Qiang, Zhi-Wei Gao, and Yuanhong Liu. 2024. "Sensor Fault Reconstruction Using Robustly Adaptive Unknown-Input Observers" Sensors 24, no. 10: 3224. https://doi.org/10.3390/s24103224
APA StyleHuang, Q., Gao, Z.-W., & Liu, Y. (2024). Sensor Fault Reconstruction Using Robustly Adaptive Unknown-Input Observers. Sensors, 24(10), 3224. https://doi.org/10.3390/s24103224






