Ultra-Wideband Vertical Transition in Coplanar Stripline for Ultra-High-Speed Digital Interfaces
Abstract
:1. Introduction
2. Design of a Conventional DL-Based via Structure
3. Design of a CPS-Based Vertical Transition
3.1. Electric Field Distributions
3.2. Cross-Sectional Models and Analytical Formulas
3.3. Characteristic Line Impedance
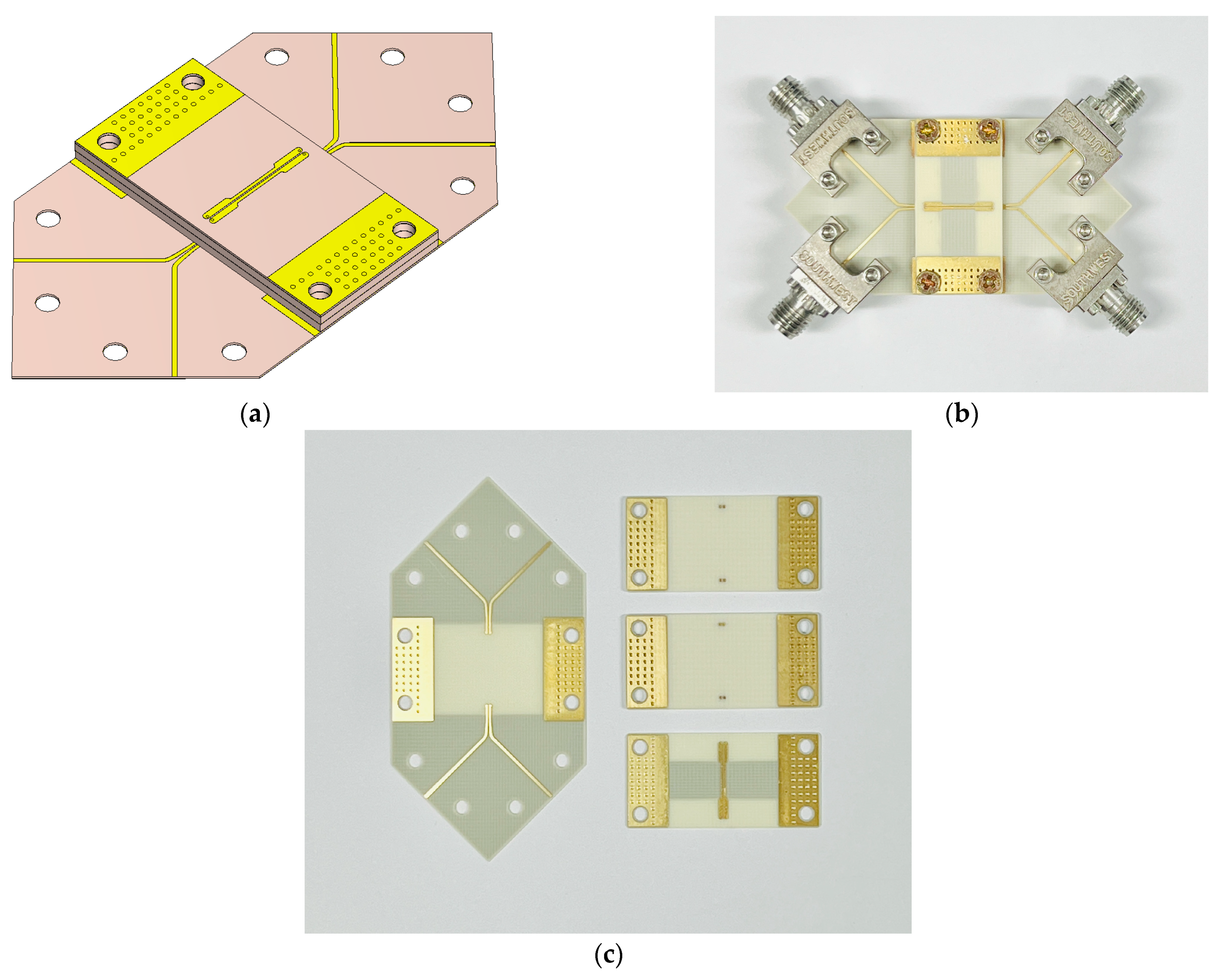
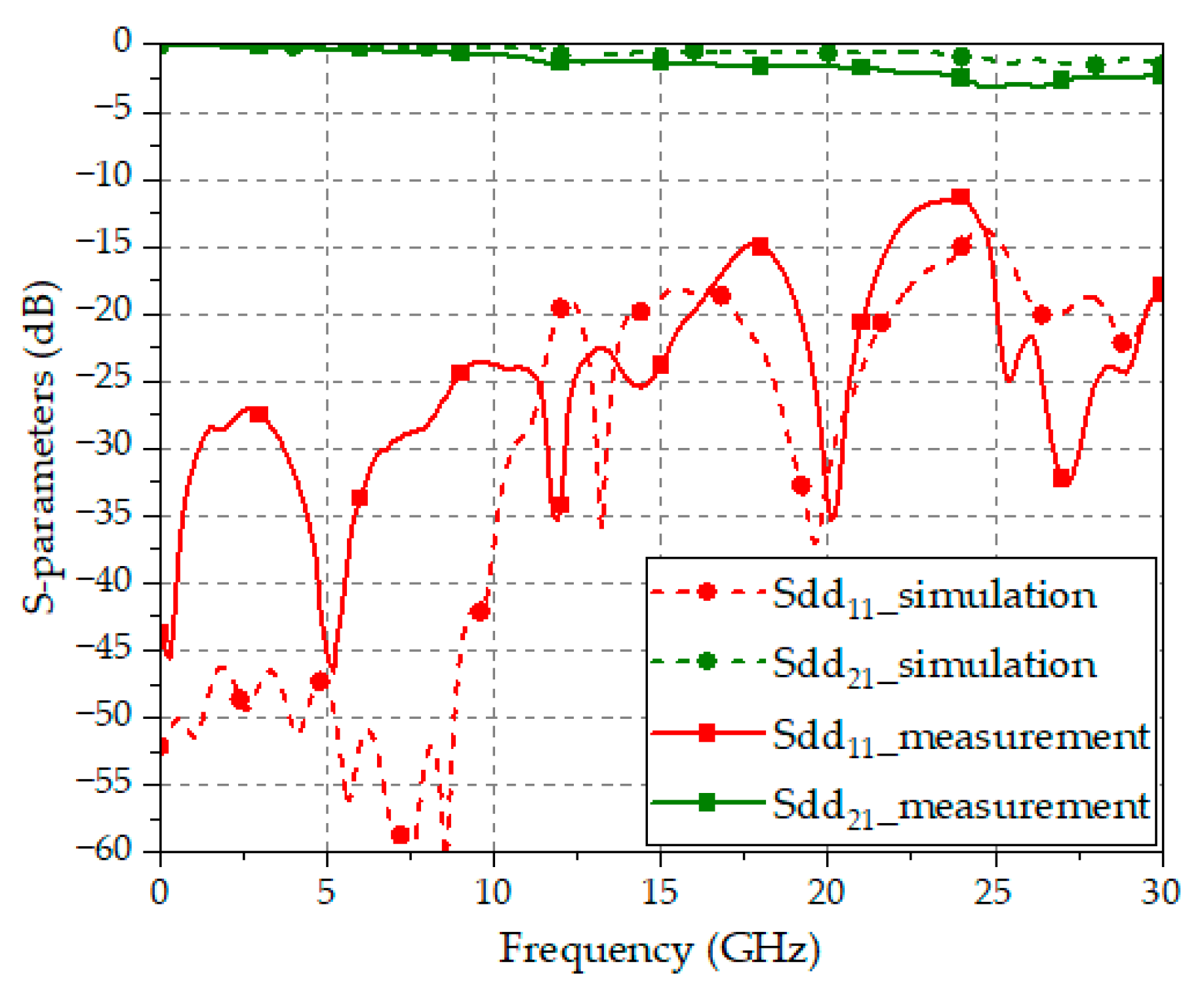
4. Fabrication and Measurements
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Kang, K.; Huang, Y.; Shafi, M.; Molisch, A.F. Millimeter and THz wave for 5G and beyond. China Commun. 2019, 16, iii–vi. [Google Scholar]
- You, X.H. Towards 6G wireless communication networks: Vision, enabling technologies, and new paradigm shifts. Sci. China Inf. Sci. 2021, 64, i–iii. [Google Scholar] [CrossRef]
- Bogatin, E. Signal and Power Integrity–Simplified, 2nd ed.; Pearson Education: Boston, MA, USA, 2010; pp. 5–8, 475–480. [Google Scholar]
- Shashikanth, R. How PCB Vias Interconnect Circuit Board Layers. Available online: https://www.protoexpress.com/blog/via-the-tiny-conductive-tunnel-that-interconnects-the-pcb-layers/ (accessed on 29 February 2024).
- Intel. AN 672: Transceiver Link Design Guidelines for High-Gbps Data Rate Transmission. Available online: https://www.intel.com/content/www/us/en/docs/programmable/683624/current/an-672-transceiver-link-design-guidelines.html (accessed on 14 March 2024).
- Simonovich, B. Controlling Electromagnetic Emissions from PCB Edges in Backplanes. Available online: https://www.signalintegrityjournal.com/articles/292-controlling-electromagnetic-emissions-from-pcb-edges-in-backplanes (accessed on 12 January 2024).
- Texas Instruments. High-Speed Layout Guidelines for Signal Conditioners and USB Hubs. Available online: https://www.ti.com/lit/an/slla414/slla414.pdf?ts=1687054366645 (accessed on 16 January 2024).
- Beyene, W.; Hahm, Y.C.; Secker, D.; Mullen, D.; Shlepnev, Y. Design, Modeling, and Characterization of Passive Channels for Data Rates of 50 Gbps and Beyond. In Proceedings of the 2014 IEEE 64th Electronic Components and Technology Conference (ECTC), Orlando, FL, USA, 15 September 2014. [Google Scholar]
- Vardapetyan, A.; Ong, C.J. Via Design Optimization for High Speed Differential Interconnects on Circuit Boards. In Proceedings of the 2020 IEEE 29th Conference on Electrical Performance of Electronic Packaging and Systems (EPEPS), San Jose, CA, USA, 5–7 October 2020. [Google Scholar]
- Cho, C.; Kim, K.; Lee, M.; Shin, J.; Yoon, S.; Lee, Y.; Song, C.; Choi, W.; Kwak, M.; Choi, Y.; et al. Novel Optimization Methodology of Design Parameters in High-Speed Differential Via for PCIe Gen5 Channels Based on Particle Swarm Optimization Algorithm. IEEE Trans. Compon. Packag. Manuf. Technol. 2023, 13, 1545–1552. [Google Scholar] [CrossRef]
- Deng, Y.; Li, Z.; Yu, Y.; Li, B.; Wang, X.; Wu, Z. S Parameters Optimization of High-Speed Differential Vias Model on A Multilayer PCB. In Proceedings of the 2022 23rd International Conference on Electronic Packaging Technology (ICEPT), Dalian, China, 10–13 August 2022. [Google Scholar]
- Ye, C.; Ye, X.; Miralrio, E.L. Via Pattern Design and Optimization for Differential Signaling 25Gbps and Above. In Proceedings of the 2016 IEEE International Symposium on Electromagnetic Compatibility (EMC), Ottawa, ON, Canada, 25–29 July 2016. [Google Scholar]
- Chen, S.; Chen, C.; Liao, C.-L.; Chen, J.; Wu, T.-L.; Mutnury, B. Via Optimization for Next Generation Speeds. In Proceedings of the 2017 IEEE 26th Conference on Electrical Performance of Electronic Packaging and Systems (EPEPS), San Jose, CA, USA, 15–18 October 2017. [Google Scholar]
- Seo, D.; Lee, H.; Park, M.; Nah, W. Enhancement of Differential Signal Integrity by Employing a Novel Face Via Structure. IEEE Trans. Electromagn. Compat. 2017, 60, 26–33. [Google Scholar] [CrossRef]
- Park, H.H.; Hwang, C.; Jung, K.Y.; Park, Y.B. Mode Matching Analysis of via-Plate Capacitance in Multilayer Structures with Finite Plate Thickness. IEEE Trans. Electromagn. Compat. 2015, 57, 1188–1196. [Google Scholar] [CrossRef]
- Gao, S.P.; De Paulis, F.; Liu, E.X.; Guo, Y.X. Transmission Line Representation of the Capacitive via-Plate Interaction toward a Capacitor-Free Via Model. IEEE Trans. Compon. Packag. Manuf. Technol. 2019, 9, 2248–2256. [Google Scholar] [CrossRef]
- Min, B.C.; Lee, G.H.; Lee, J.S.; Nashuha, S.H.; Choi, H.C.; Kim, K.W. Ultra-Wideband Differential Line-to-Balanced Line Transitions for Super-High-Speed Digital Transmission. Sensors 2022, 22, 6873. [Google Scholar] [CrossRef] [PubMed]
- Lee, G.H.; Kim, D.H.; Mohyuddin, W.; Kumar, S.; Choi, H.C.; Kim, K.W. Wideband bended CPS-to-microstrip transition for millimeter-wave antenna-detector module. Microw. Opt. Technol. Lett. 2020, 62, 1991–1996. [Google Scholar] [CrossRef]
- Lee, G.H.; Kumar, S.; Mohyuddin, W.; Choi, H.C.; Kim, K.W. Generalized Design Technique of Ultra-Wideband Transitions for Quasi-TEM Planar Transmission Lines Based on Analytical Models. IEEE Access 2021, 9, 52619–52633. [Google Scholar] [CrossRef]
- Wang, Q.X. Interaction of two circular cylinders in inviscid fluid. Phys. Fluids 2004, 16, 4412–4425. [Google Scholar] [CrossRef]
- Chen, Y. De-Embedding Method Comparisons and Physics Based Circuit Model for High Frequency D-Probe. Master’s Thesis, Department of Electrical and Computer Engineering, Missouri University of Science and Technology, Rolla, MO, USA, 2018. [Google Scholar]
- Liu, C. 224 Gb/s Per Lane: Options and Challenges. Available online: https://www.signalintegrityjournal.com/articles/2018-gbs-per-lane-options-and-challenges (accessed on 19 March 2024).

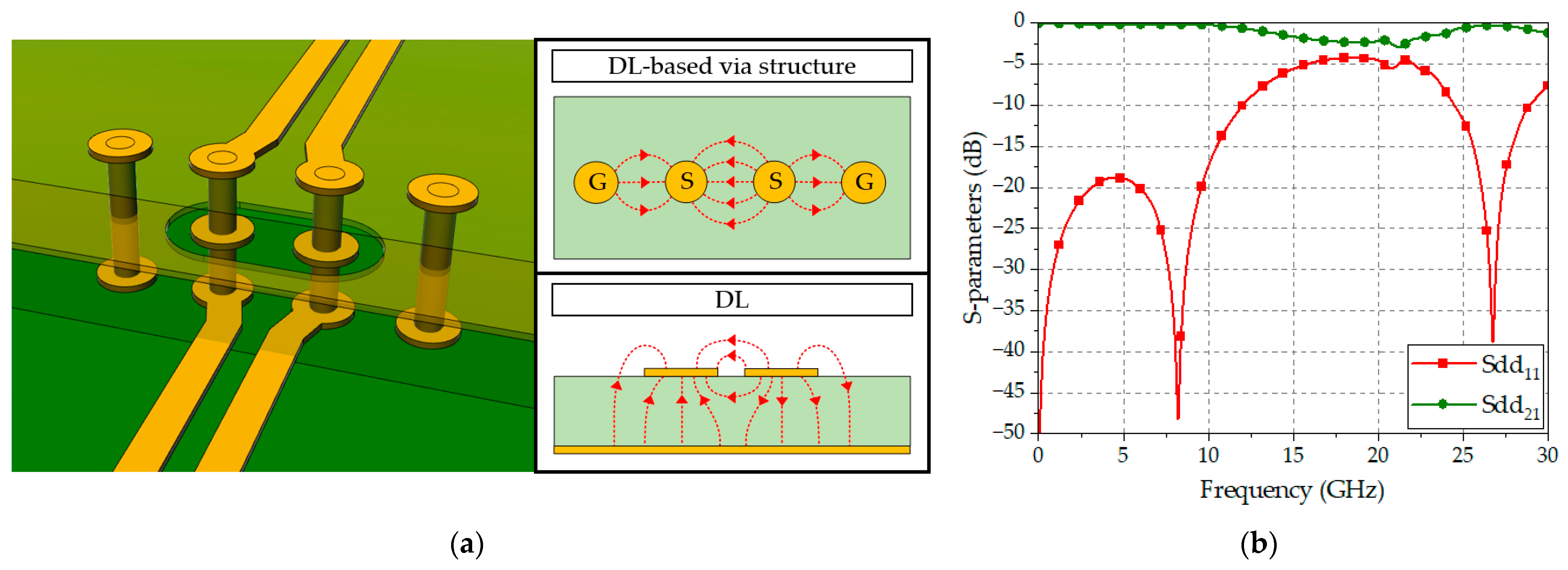
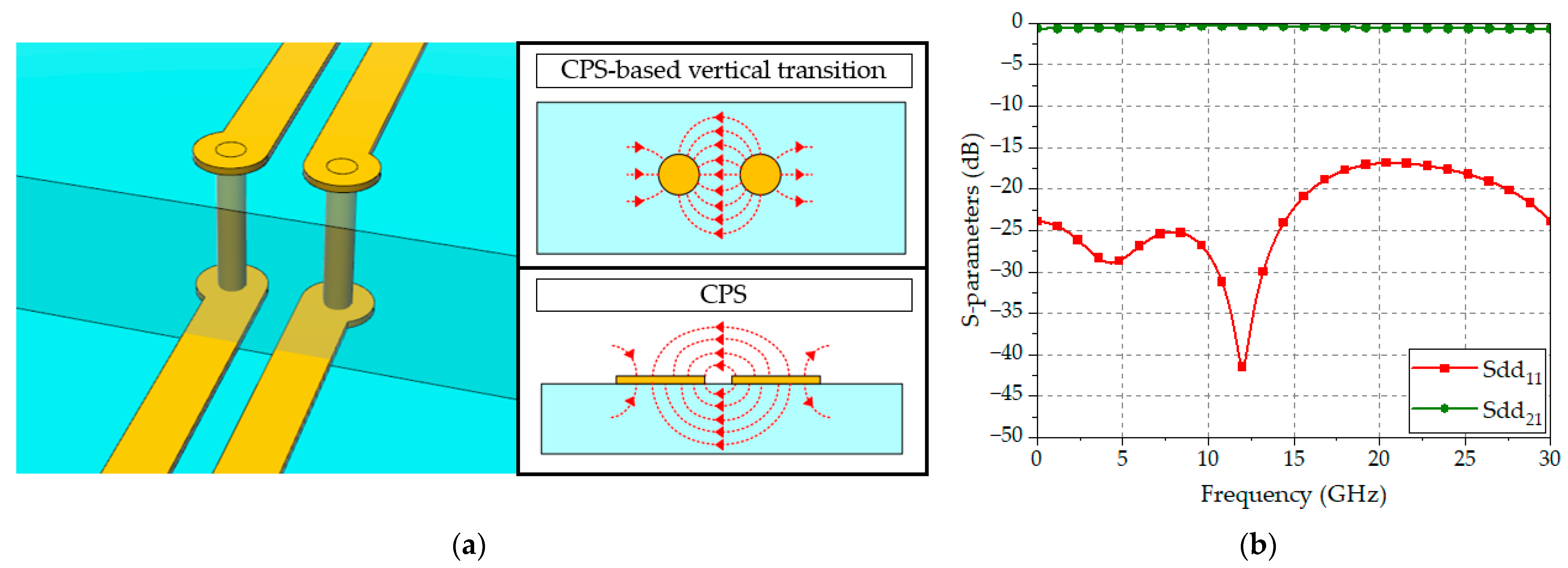



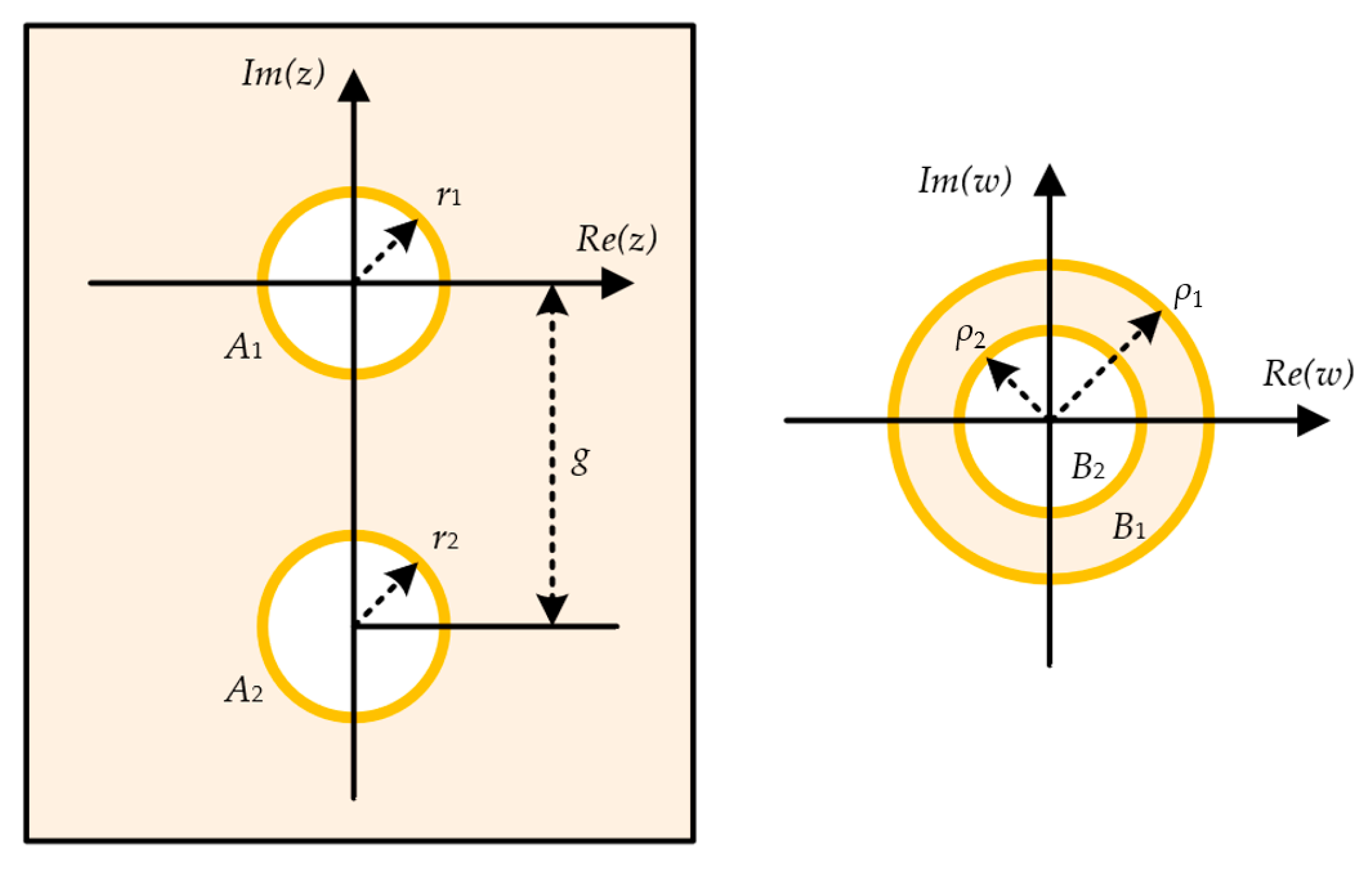
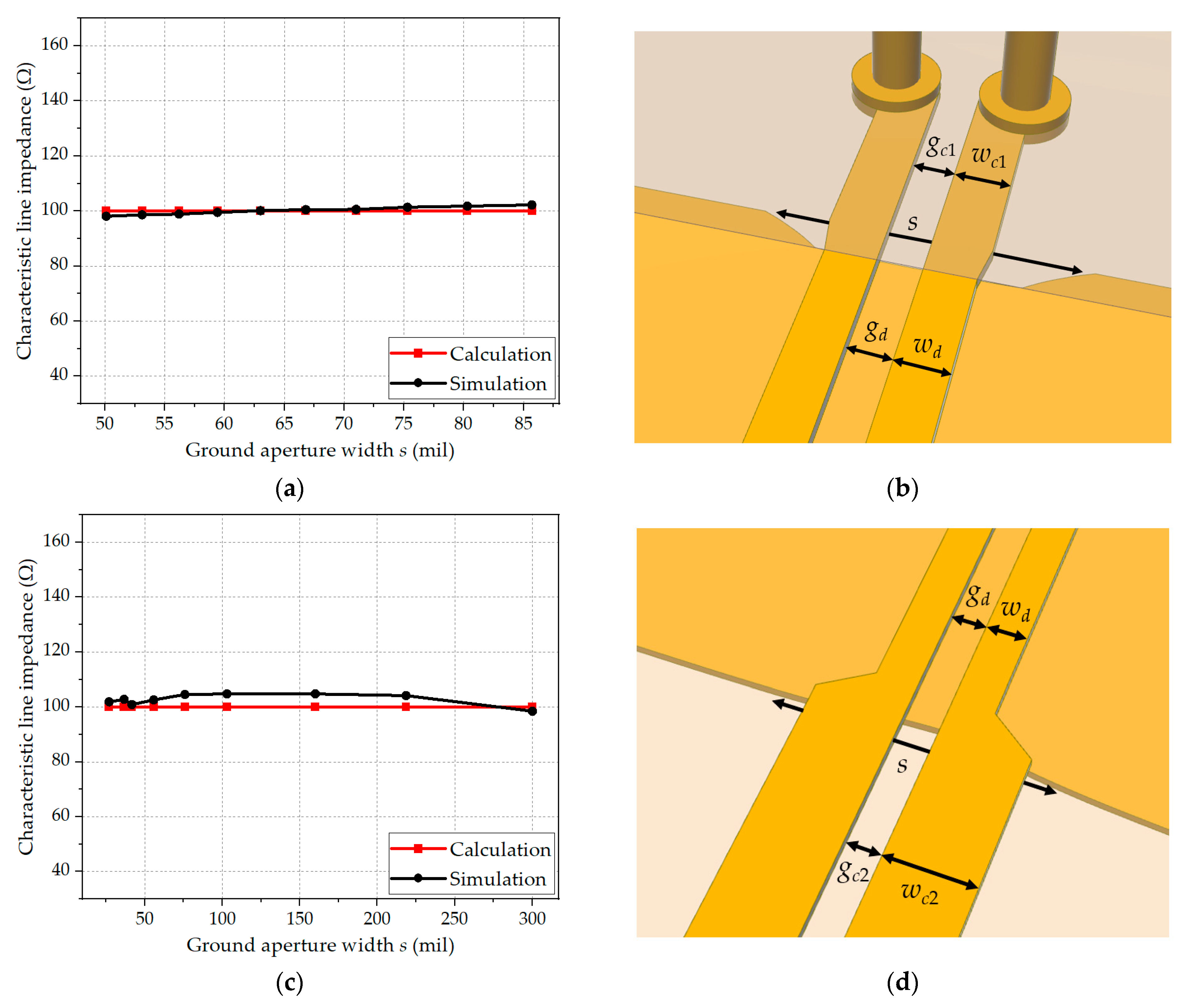

| Reference | Configuration | Frequency Range [GHz] | Number of Vias |
|---|---|---|---|
| [10] | DL-based vias | DC-16 | 4 |
| [13] | DL-based vias | DC-20 | 8 |
| [14] | DL-based vias | DC-7 | 4 |
| This work | CPS-based vias | DC-30 | 2 |
| Region | Capacitance (BB′-CC′) | Capacitance (FF′-GG′) |
|---|---|---|
| I | ||
| II | ||
| III | ||
| IV | ||
| Parameters | wd | gd | wc1 | gc1 |
| Size in mil | 11.4 | 5 | 13 | 5 |
| (mm) | 0.29 | 0.13 | 0.33 | 0.13 |
| Parameters | wc2 | gc2 | r | g |
| Size in mil | 24.5 | 5 | 6 | 29.1 |
| (mm) | 0.62 | 0.13 | 0.15 | 0.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.-J.; Lee, J.-S.; Min, B.-C.; Choi, J.-S.; Kumar, S.; Choi, H.-C.; Kim, K.-W. Ultra-Wideband Vertical Transition in Coplanar Stripline for Ultra-High-Speed Digital Interfaces. Sensors 2024, 24, 3233. https://doi.org/10.3390/s24103233
Kim M-J, Lee J-S, Min B-C, Choi J-S, Kumar S, Choi H-C, Kim K-W. Ultra-Wideband Vertical Transition in Coplanar Stripline for Ultra-High-Speed Digital Interfaces. Sensors. 2024; 24(10):3233. https://doi.org/10.3390/s24103233
Chicago/Turabian StyleKim, Mun-Ju, Jung-Seok Lee, Byung-Cheol Min, Jeong-Sik Choi, Sachin Kumar, Hyun-Chul Choi, and Kang-Wook Kim. 2024. "Ultra-Wideband Vertical Transition in Coplanar Stripline for Ultra-High-Speed Digital Interfaces" Sensors 24, no. 10: 3233. https://doi.org/10.3390/s24103233
APA StyleKim, M.-J., Lee, J.-S., Min, B.-C., Choi, J.-S., Kumar, S., Choi, H.-C., & Kim, K.-W. (2024). Ultra-Wideband Vertical Transition in Coplanar Stripline for Ultra-High-Speed Digital Interfaces. Sensors, 24(10), 3233. https://doi.org/10.3390/s24103233








