Optimizing Capacitive Pressure Sensor Geometry: A Design of Experiments Approach with a Computer-Generated Model
Abstract
1. Introduction
2. Methodology
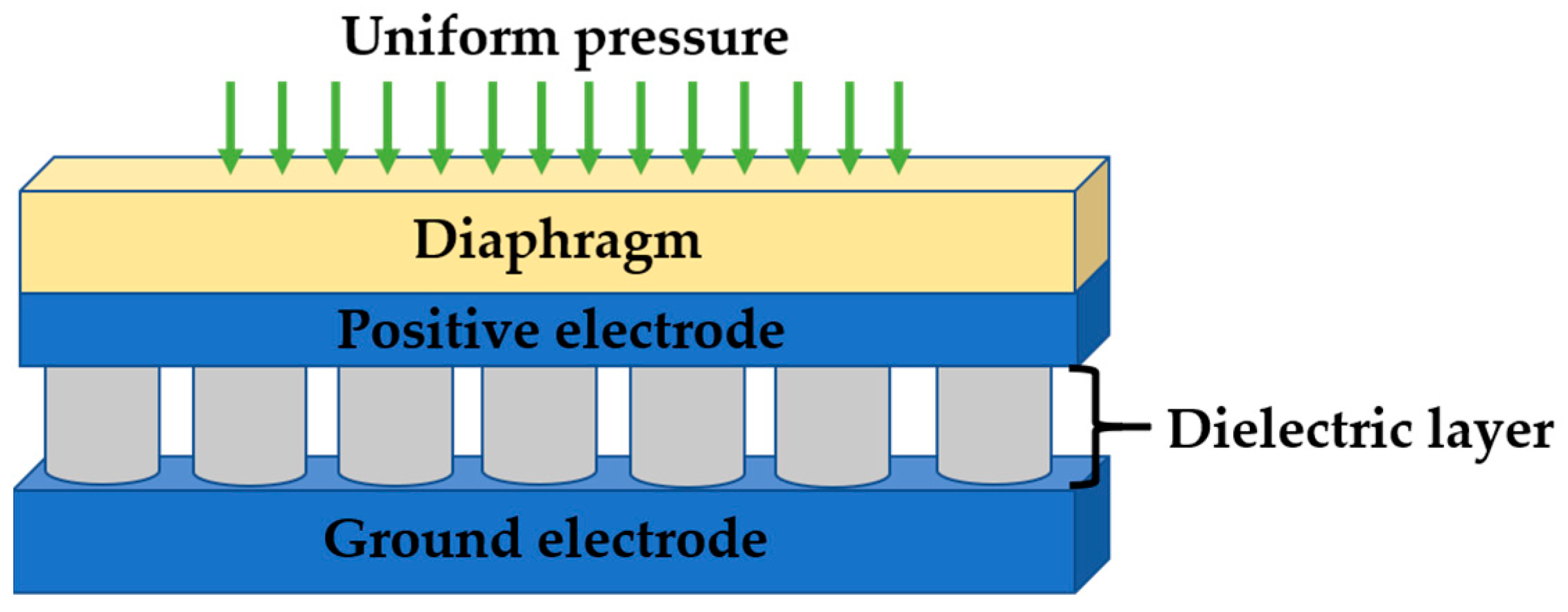
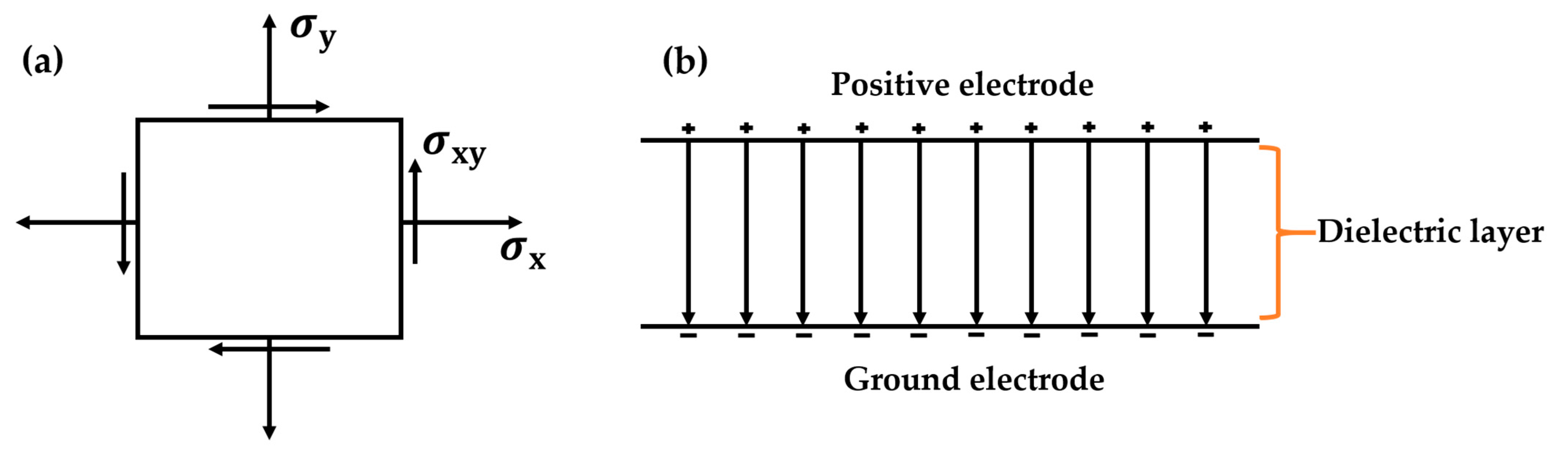
2.1. Change in the Capacitance under Compression
2.2. Displacement of the Diaphragm
2.3. Stress Level upon External Load
2.4. Energy Storage in the Capacitive Model
2.5. Sensitivity
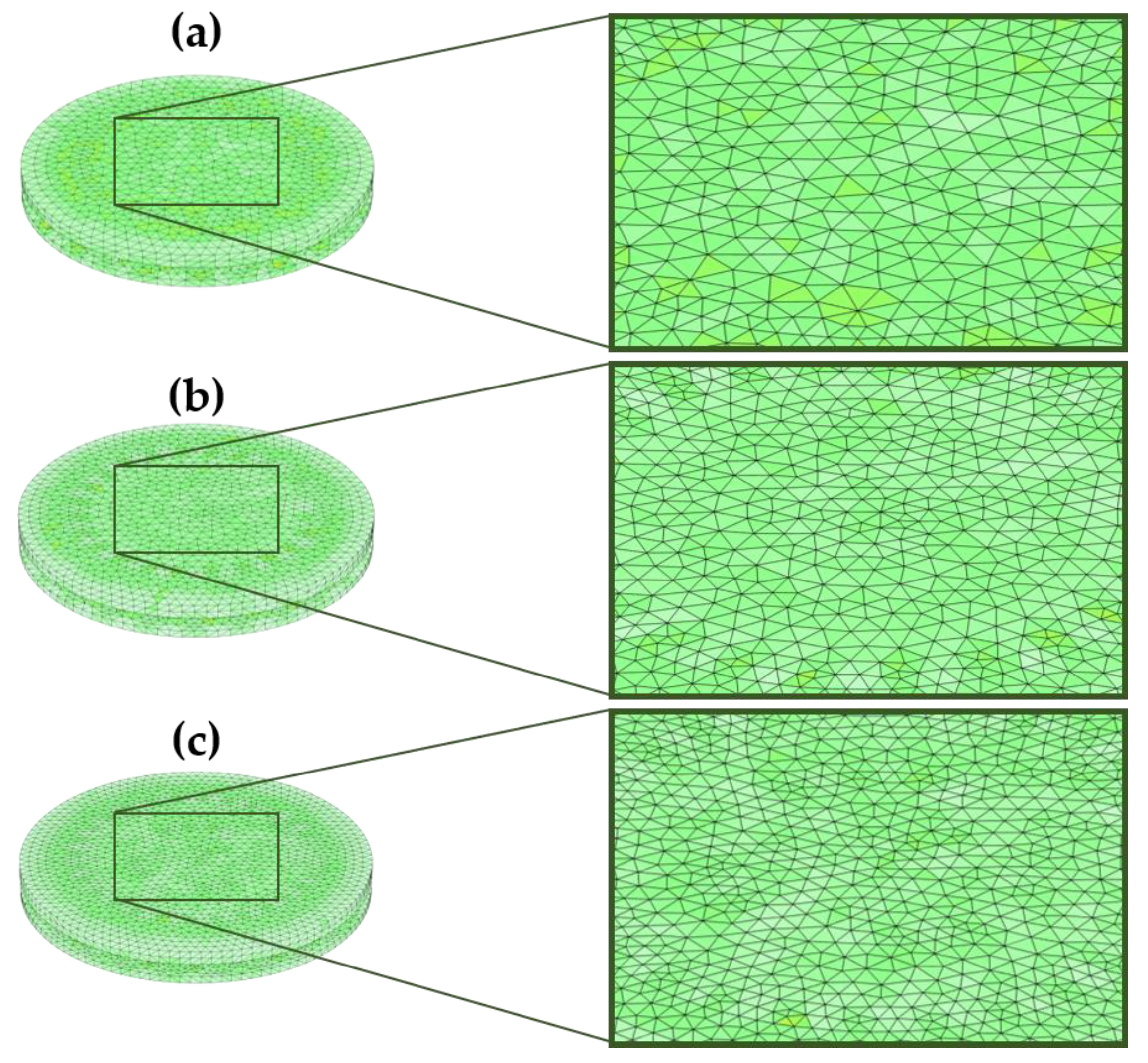
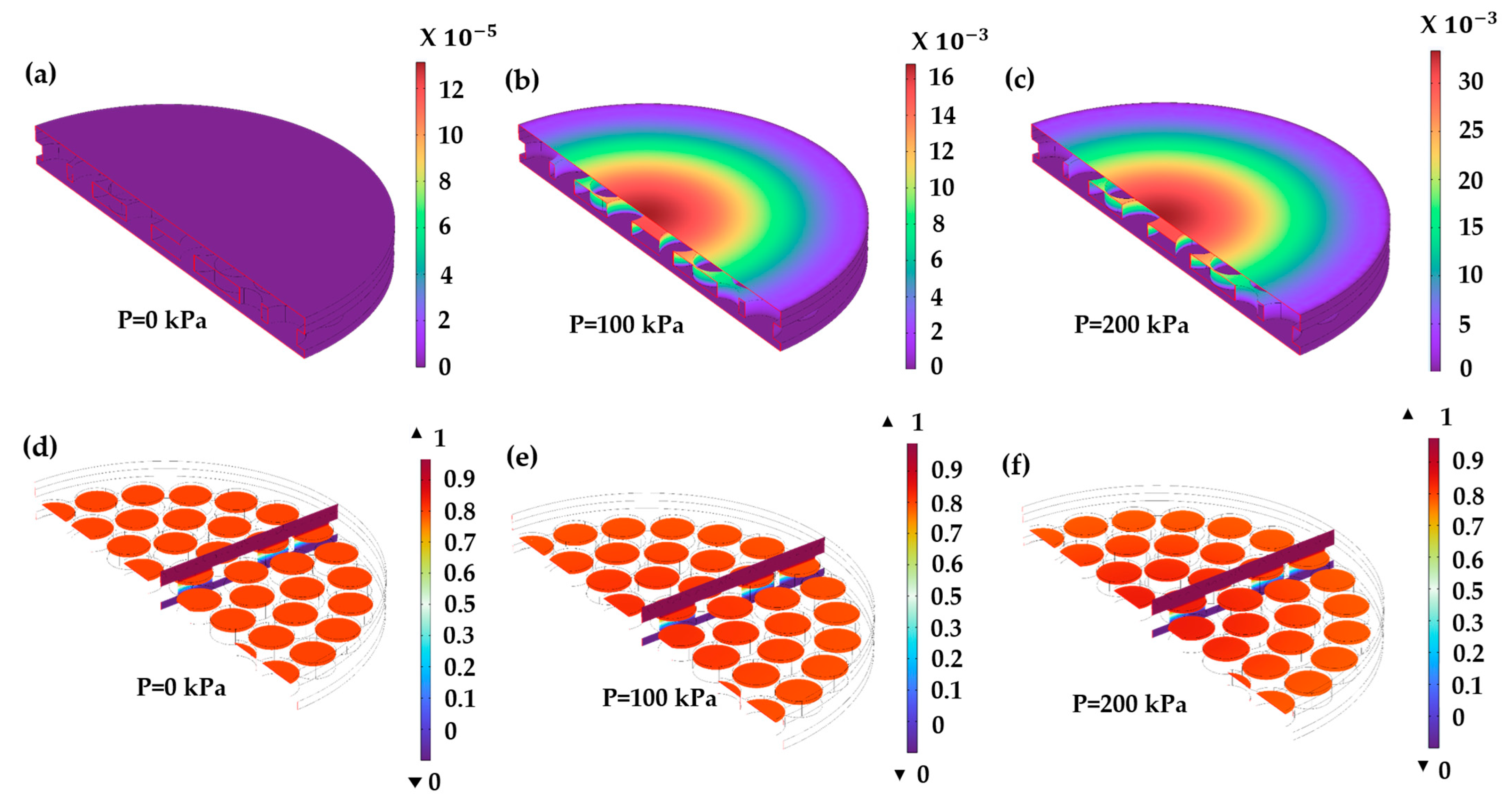
2.6. FE Analysis
2.7. Material Properties and Dimensions
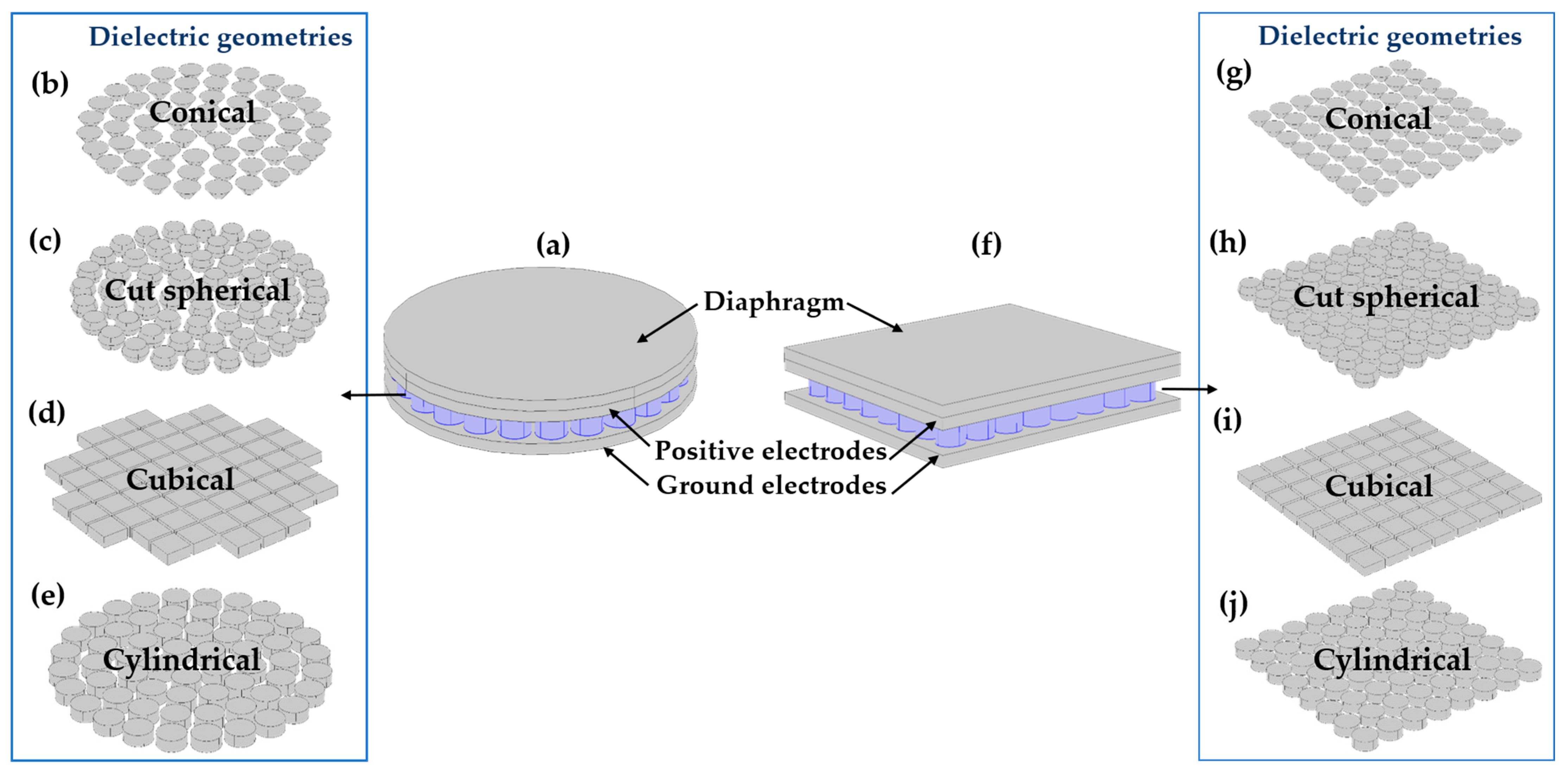
2.8. Geometry of the Diaphragm
2.9. Geometry of the Dielectric Medium
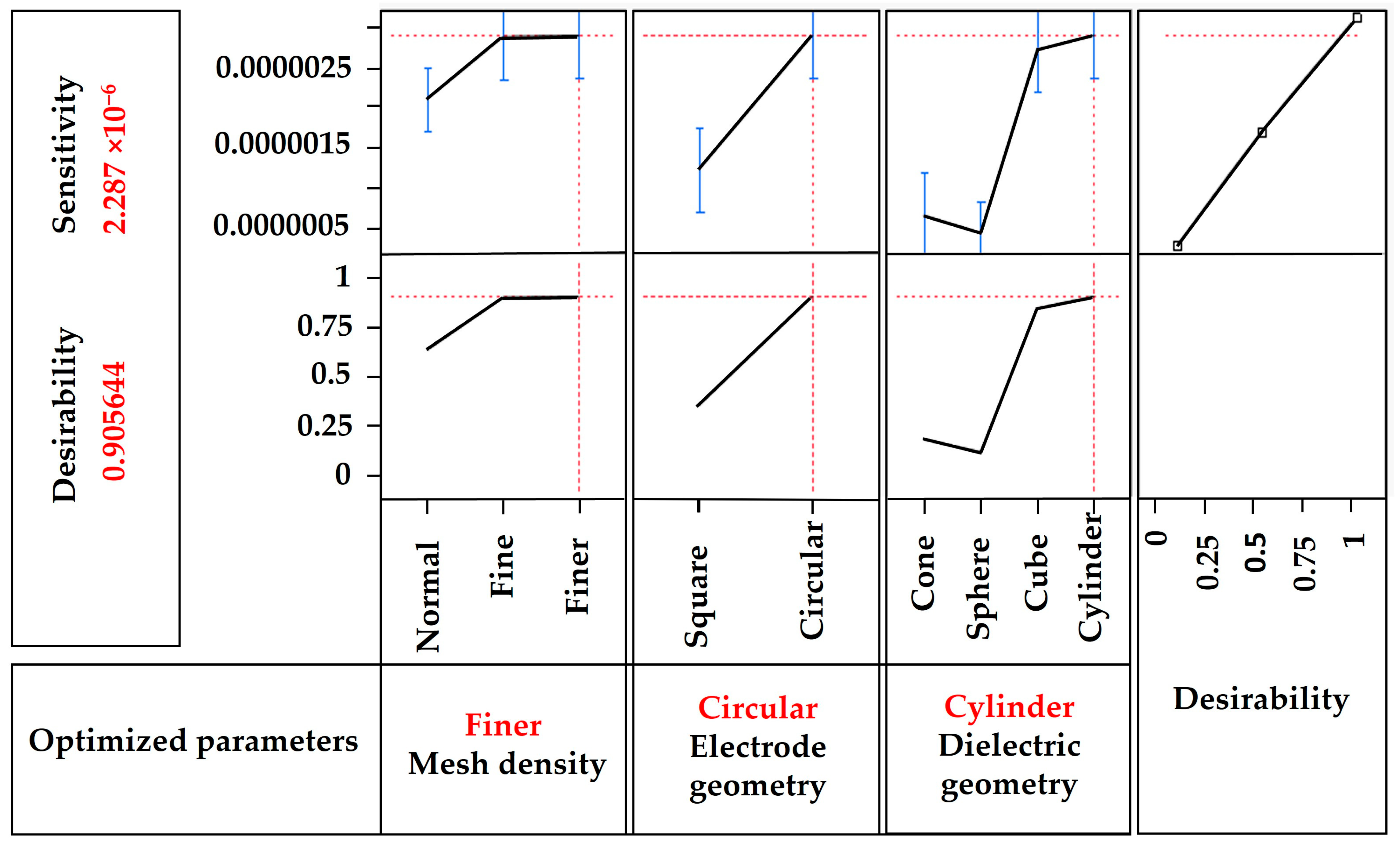
2.10. Optimization of the CPS Geometry Using DoE
3. Result and Discussion
3.1. Analysis of Variance (ANOVA)
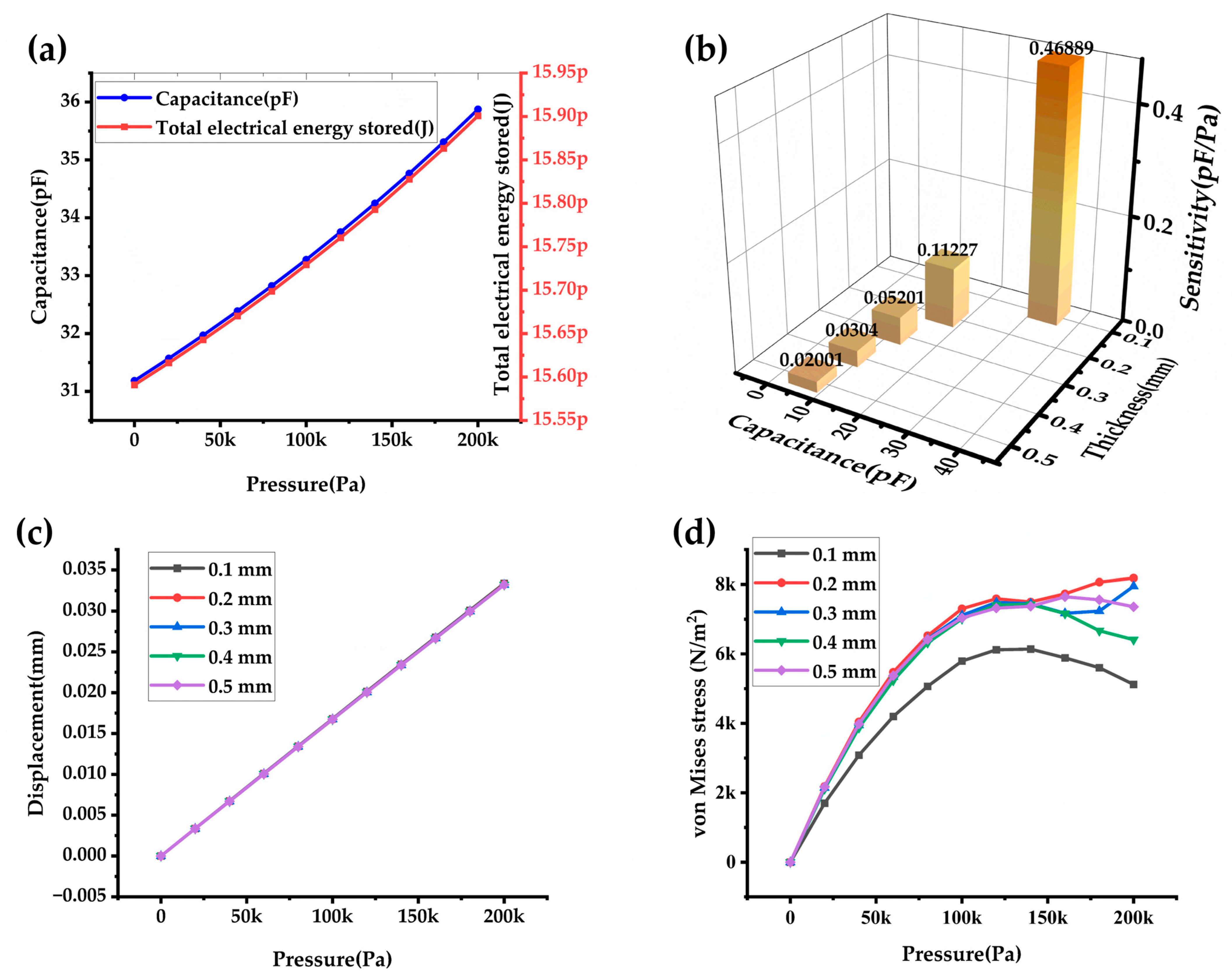
3.2. Electrical Parameter Analysis
3.3. Mechanical Parameter Analysis
3.4. Sensitivity
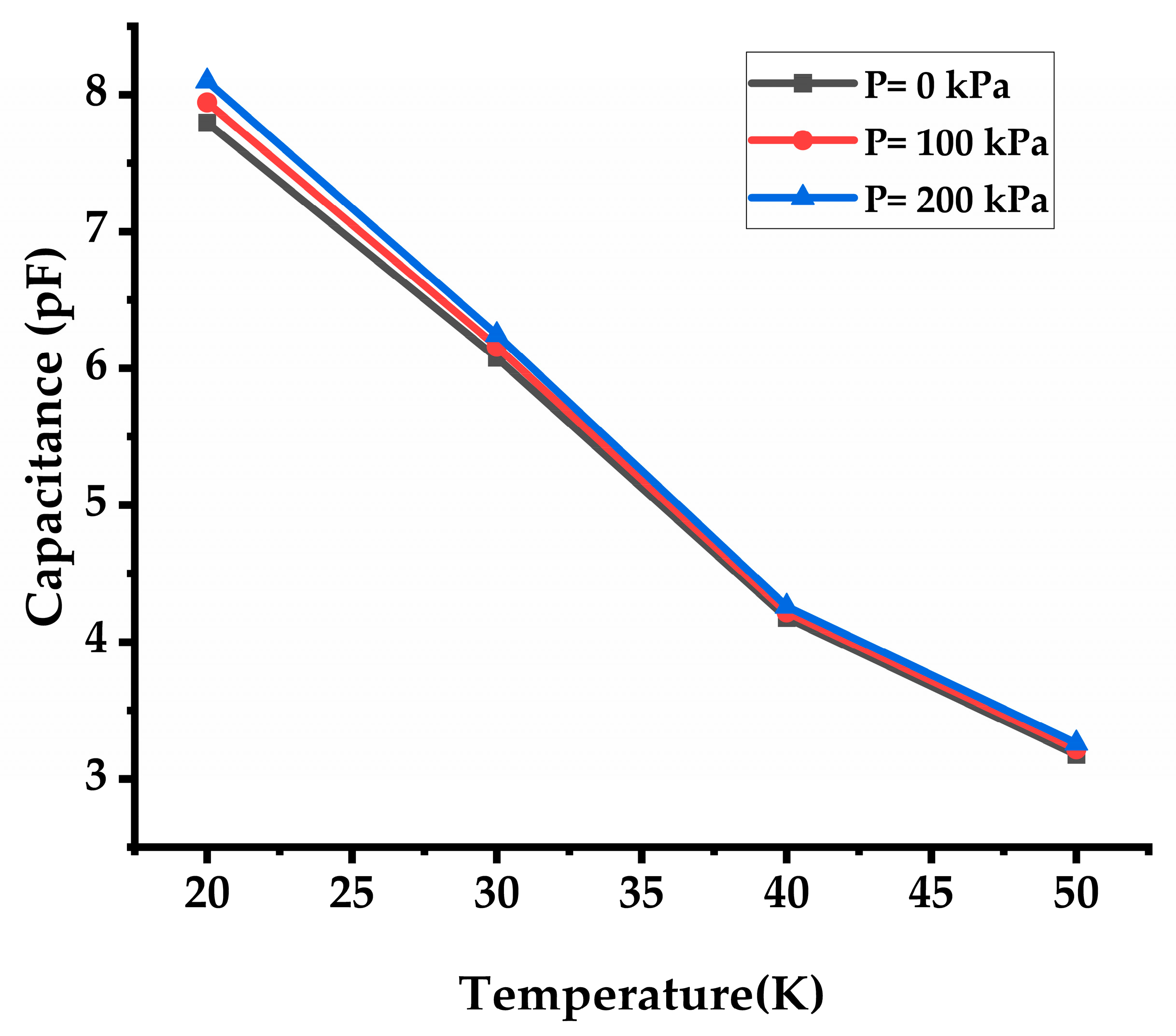
3.5. Temperature Effect on Capacitance of CPS
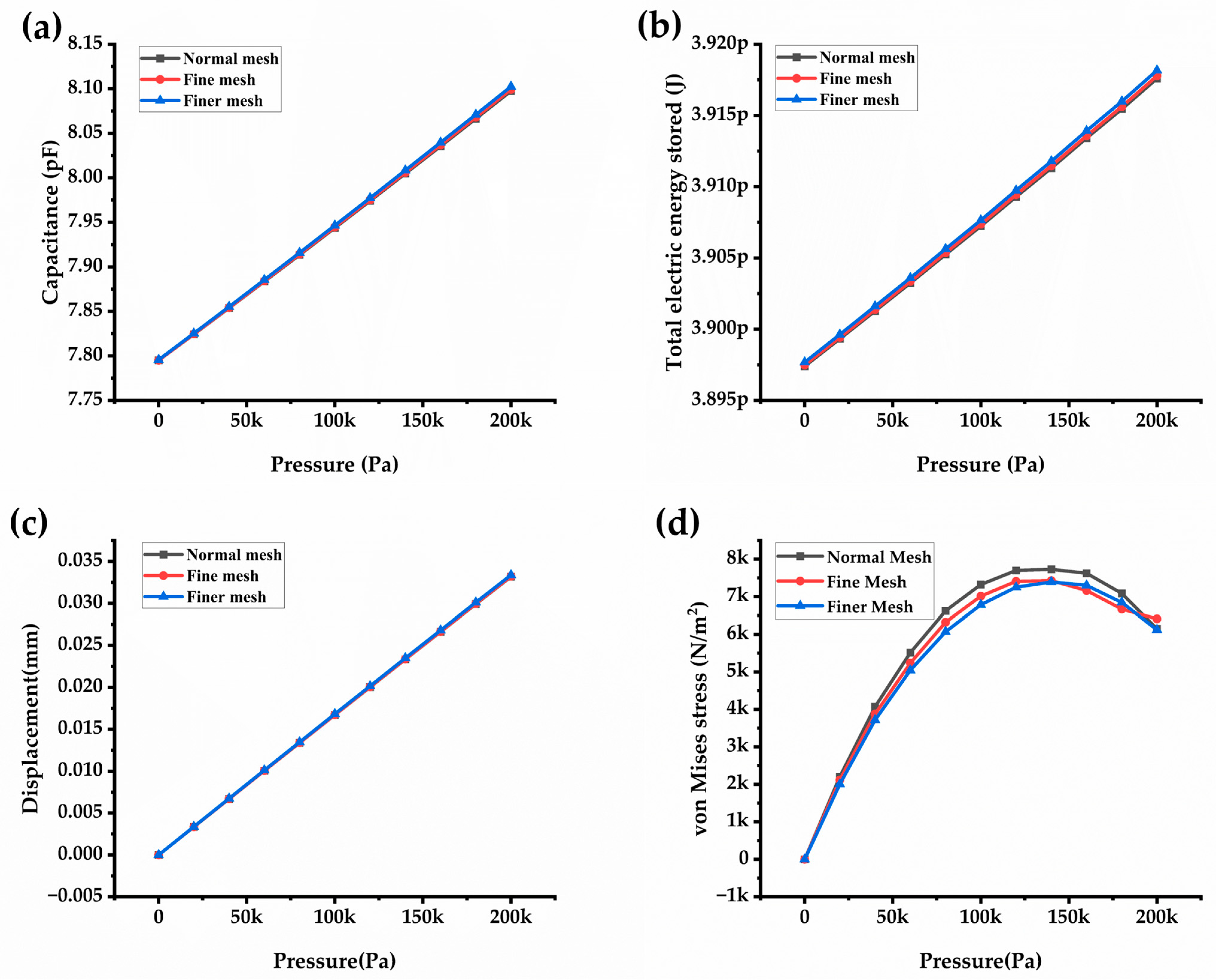
3.6. Comparative Study of Mesh Optimization
3.7. A Comparative Study on the Existing Geometry of Capacitive Sensors
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CPS | Capacitive Pressure Sensor |
| FEM or FEA | Finite Element Method or Finite Element Analysis |
| DoE | Design of Experiments |
| ANOVA | Analysis of Variance |
| RSM | response surface methodology |
| IoT | Internet of things |
| 2D | Two-Dimensional |
| 3D | Three-Dimensional |
References
- Dong, C.; Bai, Y.; Zou, J.; Cheng, J.; An, Y.; Zhang, Z.; Li, Z.; Lin, S.; Zhao, S.; Li, N. Flexible capacitive pressure sensor: Material, structure, fabrication and application. In Nondestructive Testing and Evaluation; Taylor and Francis Ltd.: Oxford, UK, 2024. [Google Scholar] [CrossRef]
- Hu, Z.; Chu, Z.; Chen, G.; Cui, J. Design of Capacitive Pressure Sensors Integrated with Anisotropic Wedge Microstructure-Based Dielectric Layer. IEEE Sensors J. 2023, 23, 21040–21049. [Google Scholar] [CrossRef]
- Khan, S.M.; Mishra, R.B.; Qaiser, N.; Hussain, A.M.; Hussain, M.M. Diaphragm shape effect on the performance of foil-based capacitive pressure sensors. AIP Adv. 2020, 10, 015009. [Google Scholar] [CrossRef]
- Singh, V.; Singh, B. PDMS/PVDF-MoS2 based flexible triboelectric nanogenerator for mechanical energy harvesting. Polymer 2023, 274, 125910. [Google Scholar] [CrossRef]
- Chen, J.; Zheng, J.; Gao, Q.; Zhang, J.; Zhang, J.; Omisore, O.M.; Wang, L.; Li, H. Polydimethylsiloxane (PDMS)-based flexible resistive strain sensors for wearable applications. Appl. Sci. 2018, 8, 345. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, C.; Li, B.; Shen, Y.; Wang, H.; Ji, K.; Mao, X.; Wei, L.; Sun, R.; Zhou, F. Electrospun PVDF-based piezoelectric nanofibers: Materials, structures, and applications. Nanoscale Adv. 2023, 5, 1043–1059. [Google Scholar] [CrossRef] [PubMed]
- Hiremath, S.; Kim, T.-W. Detection of physical signal and time-frequency analysis owing to the impact on rubber material using a piezoelectric sensor. J. Mech. Sci. Technol. 2024, 1–9. [Google Scholar] [CrossRef]
- Padurariu, L.; Brunengo, E.; Canu, G.; Curecheriu, L.P.; Conzatti, L.; Buscaglia, M.T.; Stagnaro, P.; Mitoseriu, L.; Buscaglia, V. Role of Microstructures in the Dielectric Properties of PVDF-Based Nanocomposites Containing High-Permittivity Fillers for Energy Storage. ACS Appl. Mater. Interfaces 2022, 15, 13535–13544. [Google Scholar] [CrossRef]
- Rao, K.S.; Reddy, B.M.; Teja, V.B.; Krishnateja, G.V.S.; Kumar, P.A.; Ramesh, K.S. Design and simulation of MEMS based capacitive pressure sensor for harsh environment. Microsyst. Technol. 2020, 26, 1875–1880. [Google Scholar] [CrossRef]
- Chittibabu, S.K.; Chintagumpala, K.; Chandrasekhar, A. Porous dielectric materials based wearable capacitance pressure sensors for vital signs monitoring: A review. In Materials Science in Semiconductor Processing; Elsevier Ltd.: Amsterdam, The Netherlands, 2022; Volume 151. [Google Scholar] [CrossRef]
- Huang, Y.; Yuan, H.; Kan, W.; Guo, X.; Liu, C.; Liu, P. A flexible three-axial capacitive tactile sensor with multilayered dielectric for artificial skin applications. Microsyst. Technol. 2017, 23, 1847–1852. [Google Scholar] [CrossRef]
- Marsi, N.; Majlis, B.Y.; Hamzah, A.A.; Mohd-Yasin, F. The Mechanical and Electrical Effects of MEMS Capacitive Pressure Sensor Based 3C-SiC for Extreme Temperature. J. Eng. 2014, 2014, 715167. [Google Scholar] [CrossRef]
- Masihi, S.; Panahi, M.; Maddipatla, D.; Hanson, A.J.; Bose, A.K.; Hajian, S.; Palaniappan, V.; Narakathu, B.B.; Bazuin, B.J.; Atashbar, M.Z. Highly Sensitive Porous PDMS-Based Capacitive Pressure Sensors Fabricated on Fabric Platform for Wearable Applications. ACS Sensors 2021, 6, 938–949. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Dong, K.; Li, R.; Huang, X.; Chen, T.; Xiao, X. Capacitive pressure sensor inlaid a porous dielectric layer of superelastic polydimethylsiloxane in conductive fabrics for detection of human motions. Sens. Actuators A Phys. 2020, 312, 112106. [Google Scholar] [CrossRef]
- Mishra, R.B.; El-Atab, N.; Hussain, A.M.; Hussain, M.M. Recent Progress on Flexible Capacitive Pressure Sensors: From Design and Materials to Applications. Adv. Mater. Technol. 2021, 6, 2001023. [Google Scholar] [CrossRef]
- Dagamseh, A.; Al-Bataineh, Q.; Al-Bataineh, Z.; Daoud, N.S.; Alsaad, A.; Omari, A. Modeling of a square-shape ZnO, ZnS and AlN membrane for mems capacitive pressure-sensor applications. Int. J. Simul. Multidiscip. Des. Optim. 2020, 11, 14. [Google Scholar] [CrossRef]
- Park, S.-H.; Kareem, A.B.; Joo, W.J.; Hur, J.-W. FEA Assessment of Contact Pressure and Von Mises Stress in Gasket Material Suitability for PEMFCs in Electric Vehicles. Inventions 2023, 8, 116. [Google Scholar] [CrossRef]
- Keshyagol, K.; Hiremath, S.; M., V.H.; Hiremath, P. Estimation of Energy Storage Capability of the Parallel Plate Capacitor Filled with Distinct Dielectric Materials. Eng. Proc. 2023, 59, 95. [Google Scholar] [CrossRef]
- Keum, K.; Heo, J.S.; Eom, J.; Lee, K.W.; Park, S.K.; Kim, Y.-H. Highly sensitive textile-based capacitive pressure sensors using PVDF-HFP/ionic liquid composite films. Sensors 2021, 21, 442. [Google Scholar] [CrossRef] [PubMed]
- Lei, K.F.; Lee, K.-F.; Lee, M.-Y. Development of a flexible PDMS capacitive pressure sensor for plantar pressure measurement. Microelectron. Eng. 2012, 99, 1–5. [Google Scholar] [CrossRef]
- Xiong, Y.; Shen, Y.; Tian, L.; Hu, Y.; Zhu, P.; Sun, R.; Wong, C.-P. A flexible, ultra-highly sensitive and stable capacitive pressure sensor with convex microarrays for motion and health monitoring. Nano Energy 2020, 70, 104436. [Google Scholar] [CrossRef]
- Liu, Z.; Liang, T.; Xin, Y.; Huang, J.; Liang, J.; He, X.; Zhang, C.; Yang, W.; He, X. Natural bamboo leaves as dielectric layers for flexible capacitive pressure sensors with adjustable sensitivity and a broad detection range. RSC Adv. 2021, 11, 17291–17300. [Google Scholar] [CrossRef]
- Qi, L.; Lee, B.I.; Chen, S.; Samuels, W.D.; Exarhos, G.J. High-dielectric-constant silver–epoxy composites as embedded dielectrics. Adv. Mater. 2005, 17, 1777–1781. [Google Scholar] [CrossRef]
- Oliveira, A.E.F.; Pereira, A.C.; de Resende, M.A.C. Fabrication of Low-cost Screen-printed Electrode in Paper Using Conductive Inks of Graphite and Silver/Silver Chloride. Electroanalysis 2023, 35, e202200093. [Google Scholar] [CrossRef]
- Thimmaiah, P.G.; Mudinepalli, V.R.; Thota, S.R.; Obireddy, S.R.; Lai, W.-F. Preparation, Characterization and Dielectric Properties of Alginate-Based Composite Films Containing Lithium Silver Oxide Nanoparticles. Front. Chem. 2022, 9, 777079. [Google Scholar] [CrossRef]
- Silakaew, K.; Thongbai, P. Silver nanoparticles–deposited sub-micro sized BaTiO3/PVDF composites: Greatly increased enhanced constant and effectively suppressed dielectric loss. Nanocomposites 2022, 8, 125–135. [Google Scholar] [CrossRef]
- Zhou, J.; Hou, D.; Cheng, S.; Zhang, J.; Chen, W.; Zhou, L.; Zhang, P. Recent advances in dispersion and alignment of fillers in PVDF-based composites for high-performance dielectric energy storage. In Materials Today Energy; Elsevier Ltd.: Amsterdam, The Netherlands, 2023; Volume 31. [Google Scholar] [CrossRef]
- Bai, N.; Wang, L.; Wang, Q.; Deng, J.; Wang, Y.; Lu, P.; Huang, J.; Li, G.; Zhang, Y.; Yang, J.; et al. Graded intrafillable architecture-based iontronic pressure sensor with ultra-broad-range high sensitivity. Nat. Commun. 2020, 11, 209. [Google Scholar] [CrossRef]
- Balavalad, K.B.; Balavalad, P.B.; Pidashetti, S. Optimization of Nano Capacitive Pressure Sensor for Medical Applications. In IOP Conference Series: Materials Science and Engineering; IOP Publishing Ltd.: Bristol, UK, 2021. [Google Scholar] [CrossRef]
- Stebel, M.; Kubiczek, K.; Rodriguez, G.R.; Palacz, M.; Garelli, L.; Melka, B.; Haida, M.; Bodys, J.; Nowak, A.J.; Lasek, P.; et al. Thermal analysis of 8.5 MVA disk-type power transformer cooled by biodegradable ester oil working in ONAN mode by using advanced EMAG–CFD–CFD coupling. Int. J. Electr. Power Energy Syst. 2022, 136, 107737. [Google Scholar] [CrossRef]
- Baek, S.; Jang, H.; Kim, S.Y.; Jeong, H.; Han, S.; Jang, Y.; Kim, D.H.; Lee, H.S. Flexible piezocapacitive sensors based on wrinkled microstructures: Toward low-cost fabrication of pressure sensors over large areas. RSC Adv. 2017, 7, 39420–39426. [Google Scholar] [CrossRef]
- Choi, J.; Kwon, D.; Kim, K.; Park, J.; Del Orbe, D.; Gu, J.; Ahn, J.; Cho, I.; Jeong, Y.; Oh, Y.S.; et al. Synergetic Effect of Porous Elastomer and Percolation of Carbon Nanotube Filler toward High Performance Capacitive Pressure Sensors. ACS Appl. Mater. Interfaces 2020, 12, 1698–1706. [Google Scholar] [CrossRef]
- Mahata, C.; Algadi, H.; Lee, J.; Kim, S.; Lee, T. Biomimetic-inspired micro-nano hierarchical structures for capacitive pressure sensor applications. Measurement 2020, 151, 107095. [Google Scholar] [CrossRef]
- Parthasarathy, E.; S, M. Modeling and analysis of MEMS capacitive differential pressure sensor structure for altimeter application. Microsyst. Technol. 2017, 23, 1343–1349. [Google Scholar] [CrossRef]
- Ruth, S.R.A.; Bao, Z. Designing Tunable Capacitive Pressure Sensors Based on Material Properties and Microstructure Geometry. ACS Appl. Mater. Interfaces 2020, 12, 58301–58316. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Ran, W.; Wang, D.; Yin, R.; Yan, Y.; Jiang, K.; Lou, Z.; Shen, G. 3D Dielectric Layer Enabled Highly Sensitive Capacitive Pressure Sensors for Wearable Electronics. ACS Appl. Mater. Interfaces 2020, 12, 32023–32030. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Yang, H.; Oh, J.H. Simple fabrication of highly sensitive capacitive pressure sensors using a porous dielectric layer with cone-shaped patterns. Mater. Des. 2021, 197, 109203. [Google Scholar] [CrossRef]
- Kim, S.-W.; Oh, G.-Y.; Lee, K.-I.; Yang, Y.-J.; Ko, J.-B.; Kim, Y.-W.; Hong, Y.-S. A Highly Sensitive and Flexible Capacitive Pressure Sensor Based on Alignment Airgap Dielectric. Sensors 2022, 22, 7390. [Google Scholar] [CrossRef] [PubMed]
- Park, S.W.; Das, P.S.; Park, J.Y. Development of wearable and flexible insole type capacitive pressure sensor for continuous gait signal analysis. Org. Electron. 2018, 53, 213–220. [Google Scholar] [CrossRef]
- Wu, J.; Yao, Y.; Zhang, Y.; Shao, T.; Wu, H.; Liu, S.; Li, Z.; Wu, L. Rational design of flexible capacitive sensors with highly linear response over a broad pressure sensing range. Nanoscale 2020, 12, 21198–21206. [Google Scholar] [CrossRef] [PubMed]
- Bijender; Kumar, A. One-Rupee Ultrasensitive Wearable Flexible Low-Pressure Sensor. ACS Omega 2020, 5, 16944–16950. [Google Scholar] [CrossRef]
- Li, W.; Jin, X.; Zheng, Y.; Chang, X.; Wang, W.; Lin, T.; Zheng, F.; Onyilagha, O.; Zhu, Z. A porous and air gap elastomeric dielectric layer for wearable capacitive pressure sensor with high sensitivity and a wide detection range. J. Mater. Chem. C 2020, 8, 11468–11476. [Google Scholar] [CrossRef]
- Jung, Y.; Lee, W.; Jung, K.; Park, B.; Park, J.; Ko, J.; Cho, H. A highly sensitive and flexible capacitive pressure sensor based on a porous three-dimensional PDMS/microsphere composite. Polymers 2020, 12, 1412. [Google Scholar] [CrossRef]
- Lei, K.F.; Lee, K.-F.; Lee, M.-Y. A flexible PDMS capacitive tactile sensor with adjustable measurement range for plantar pressure measurement. Microsyst. Technol. 2014, 20, 1351–1358. [Google Scholar] [CrossRef]

| Parameters | Materials | Dielectric Constant (ε) | Young’s Modulus(E) [GPa] | Poisson’s Ratio (ν) | Density (ρ) [kg/m3] |
|---|---|---|---|---|---|
| Diaphragm | PDMS | 2.4–2.7 | 0.00075–0.00090 | 0.49 | 970 |
| Dielectric | PVDF | 10–12 | 2.17 | 0.40 | 1.78 |
| Electrodes | Silver | 0.188–1.971 | 83 | 0.37 | 10.8 |
| Square Electrode Setup | Circular Electrode Setup |
|---|---|
| Diaphragm/Electrodes | Diaphragm/Electrodes |
| Area-10 × 10 mm2 | Radius—5 mm |
| Height—0.2 mm | Height—0.2 mm |
| Conical | Cubical | Cut-Sphere | Cylindrical |
|---|---|---|---|
| Upper radius—0.5 mm | Width = 0.5 mm | Radius—0.5 mm (Cut on both sides and kept height 0.2 mm) | Radius—0.5 mm Height—Variable |
| Lower radius—0.3 mm | Length = 0.5 mm | ||
| Height—0.2 mm | Hight = 0.2 mm |
| Factors | Description | Level 1 | Level 2 | Level 3 | Level 4 |
|---|---|---|---|---|---|
| X | Mesh density | 0.1–1.5 mm | 0.1–0.8 mm | 0.04–0.55 mm | |
| (normal) | (fine) | (finer) | - | ||
| Y | Dielectric geometry | Conical shape | Cut-spherical | Cubical | Cylindrical shape |
| Z | Diaphragm geometry/Electrode geometry | Square form | Circular form | - | - |
| Treatments | Factor Assigned | Response (Sensitivity pF/Pa) | ||
|---|---|---|---|---|
| Mesh Density | Dielectric Geometry | Electrode Geometry | ||
| 1 | Normal | Cone | Square | 0.9380 |
| 2 | Finer | Cylinder | Circular | 2.9945 |
| 3 | Normal | Sphere | Circular | 0.4040 |
| 4 | Normal | Cube | Square | 1.3683 |
| 5 | Fine | Cylinder | Circular | 2.9801 |
| 6 | Fine | Sphere | Square | 0.6848 |
| 7 | Normal | Cone | Circular | 0.5503 |
| 8 | Fine | Sphere | Circular | 0.4052 |
| 9 | Finer | Cone | Circular | 0.5611 |
| 10 | Fine | Cone | Square | 0.9531 |
| 11 | Finer | Cube | Circular | 2.7738 |
| 12 | Normal | Cylinder | Square | 1.1300 |
| 13 | Finer | Cylinder | Square | 1.1090 |
| 14 | Fine | Cone | Circular | 0.5578 |
| 15 | Normal | Sphere | Square | 0.6806 |
| 16 | Normal | Cube | Circular | 2.0147 |
| 17 | Finer | Sphere | Circular | 0.3962 |
| 18 | Fine | Cylinder | Square | 0.1108 |
| 19 | Finer | Sphere | Circular | 0.3962 |
| 20 | Fine | Cube | Square | 0.1343 |
| 21 | Finer | Cone | Square | 0.9624 |
| 22 | Normal | Cylinder | Circular | 2.4421 |
| 23 | Fine | Cube | Square | 1.3432 |
| 24 | Fine | Cube | Circular | 2.6648 |
| 25 | Normal | Cone | Square | 0.9380 |
| 26 | Normal | Cylinder | Circular | 1.5121 |
| 27 | Finer | Cube | Square | 1.3314 |
| 28 | Finer | Sphere | Square | 0.6680 |
| Source | DF | Sum of Squares | Mean Square | F Ratio | Prob > F |
|---|---|---|---|---|---|
| Model | 17 | 1.745 × 10−11 | 1.026 × 10−12 | 13.6232 | <0.0001 |
| Error | 10 | 7.5349 × 10−13 | 7.535 × 10−14 | - | - |
| Corrected total | 27 | 1.8204 × 10−11 | - | - | - |
| Authors | Geometry | Dielectric Material | Electrode Material | Sensitivity | Application |
|---|---|---|---|---|---|
| Baek et al., 2017 [31] | Wrinkled dielectric layer | PDMS | Gold | 4.8 × 10−6 to 5.2 × 10−6 kPa−1 | Bio-medical devices |
| Choi et al., 2020 [32] | Porous composite | Porous eco flex-Multiwalled CNT | Conductive fabric | 1.72 kPa−1 | Electronic devices |
| Mahata et al., 2020 [33] | Scrubber composite | Rose petal-PMMA-double-layer PDMS | ITO/PET | 0.055 kPa−1 | e-skin |
| Parthasarathy and S, 2017 [34] | Flat square | Silicon/Silicon carbide | - | 0.574 kPa−1 | Altimeter |
| Ruth and Bao, 2020 [35] | Microstructure | PDMS | - | 0.1 to 1 kPa−1 | Robotics |
| Zhao et al., 2020 [36] | 3D dielectric layer | Silver nanowire | Gold plated PDMS | 1.21 kPa−1 | Wearable electronics |
| Y. Kim et al., 2021 [37] | Cone shape dielectric | Porous PDMS | Aluminum | 5 kPa−1 | Sensor array and skin at touched sensors |
| S. Li et al., 2020 [14] | Super elastic dielectric | Porous PDMS Film | Conductive cloth tape | 0.023 kPa−1 | Detection of human motions |
| Bai et al., 2020 [28] | Graphene based Architecture | PVA/H3PO4 Ionic film | PI–Au | 220 kPa−1 to 3300 kPa−1 | e-skin |
| Xiong et al., 2020 [21] | Convex microarrays | PVDF | PDMS—PS—Au | 30.2 kPa−1 | Motion and health monitoring |
| S. W. Kim et al., 2022 [38] | Microarray | Barium titanate—PVDF | PDMS | 4.9 kPa−1 | e-skin and wearable medical assistive devices |
| S. W. Park et al., 2018 [39] | Elastomer dielectric | Porous PDMS | MWCNT/PEDOT: PSS | 1.12 × 103 kPa−1 | Gait signal analysis |
| Wu et al., 2020 [40] | Microstructure dielectric | Spiky Ni/PDMS | Silver flakes/PDMS | 0.0046 kPa−1 | e-skin |
| Liu et al., 2021 [22] | Microstructure dielectric | Natural bamboo leaves | Ag NW/MXene | 2.08 kPa−1 | Breath/wrist pulse/speech, joint bending detecting sensors |
| Keum et al., 2021 [19] | Textile array | PVDF—HFP/IL | Ag-plated fibers on polyester | 9.51 kPa−1 | e-textile |
| Bijender and Kumar, 2020 [41] | Microstructure | Porous-PDMS scrubber composite | ITO/PET | 0.0083 kPa−1 | Wearable application |
| W. Li et al., 2020 [42] | Elastomer | Airgap-PDMS | PPy/Filter paper | 0.0040 kPa−1 | Wearable devices |
| Jung et al., 2020 [43] | 3D | PDMS/MS Composite | ITO/PET | 0.124 kPa−1 | Detecting moments in fingers |
| Lei et al., 2014 [44] | Flat square | PDMS | indium-zinc-oxide | 2.24 and 0.28 × 103 Pa−1 | Bio-Medical devices |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keshyagol, K.; Hiremath, S.; H. M., V.; Kini U., A.; Naik, N.; Hiremath, P. Optimizing Capacitive Pressure Sensor Geometry: A Design of Experiments Approach with a Computer-Generated Model. Sensors 2024, 24, 3504. https://doi.org/10.3390/s24113504
Keshyagol K, Hiremath S, H. M. V, Kini U. A, Naik N, Hiremath P. Optimizing Capacitive Pressure Sensor Geometry: A Design of Experiments Approach with a Computer-Generated Model. Sensors. 2024; 24(11):3504. https://doi.org/10.3390/s24113504
Chicago/Turabian StyleKeshyagol, Kiran, Shivashankarayya Hiremath, Vishwanatha H. M., Achutha Kini U., Nithesh Naik, and Pavan Hiremath. 2024. "Optimizing Capacitive Pressure Sensor Geometry: A Design of Experiments Approach with a Computer-Generated Model" Sensors 24, no. 11: 3504. https://doi.org/10.3390/s24113504
APA StyleKeshyagol, K., Hiremath, S., H. M., V., Kini U., A., Naik, N., & Hiremath, P. (2024). Optimizing Capacitive Pressure Sensor Geometry: A Design of Experiments Approach with a Computer-Generated Model. Sensors, 24(11), 3504. https://doi.org/10.3390/s24113504








