Autonomous Navigation by Mobile Robot with Sensor Fusion Based on Deep Reinforcement Learning
Abstract
1. Introduction
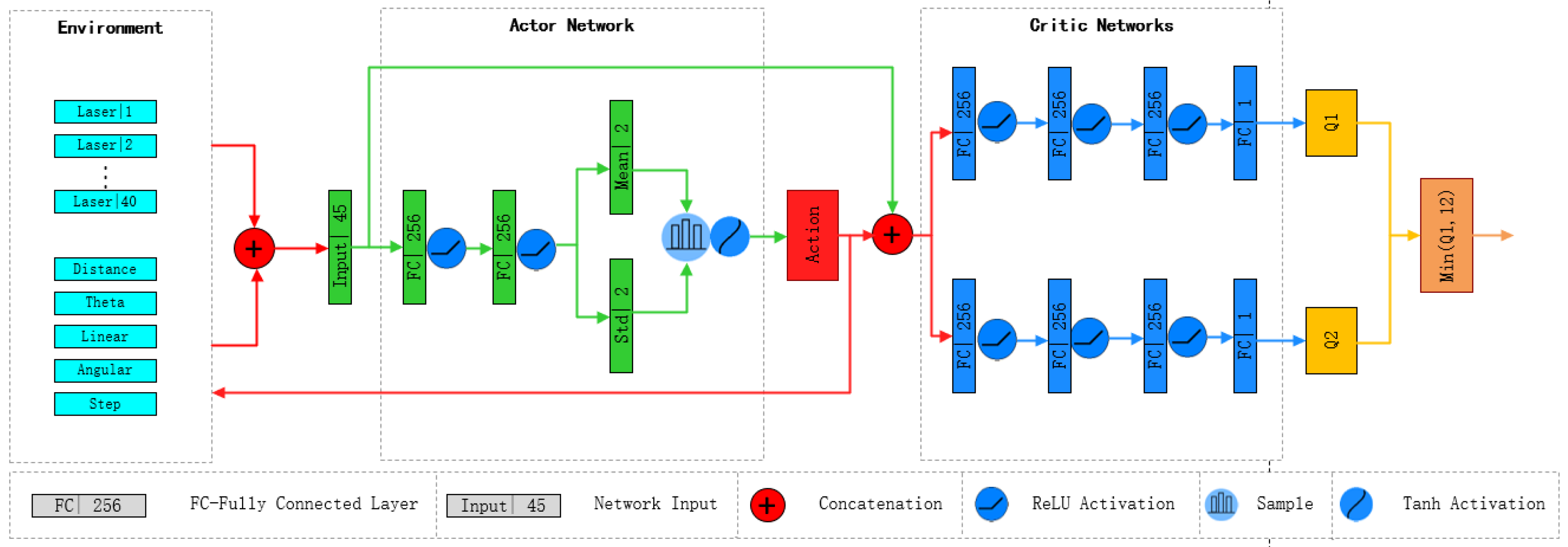
- Designed and implemented an algorithm based on the Soft Actor–Critic (SAC) network architecture, providing continuous action outputs for a four-wheeled mobile robot to navigate toward local goals.
- Proposed a Candidate Point-Target Distance (CPTD) method, an improved heuristic algorithm that integrates a heuristic evaluation function into the navigation system of a four-wheeled mobile robot. This function is used to assess navigation path points and guide the robot toward the global target point.
- Introduced a Bird’s-Eye View (BEV) mapping and data-level fusion approach, integrating a 2D lidar sensor with a camera to identify obstacles at different heights in the environment, thereby enhancing the robot’s environmental perception capabilities.
2. Related Work
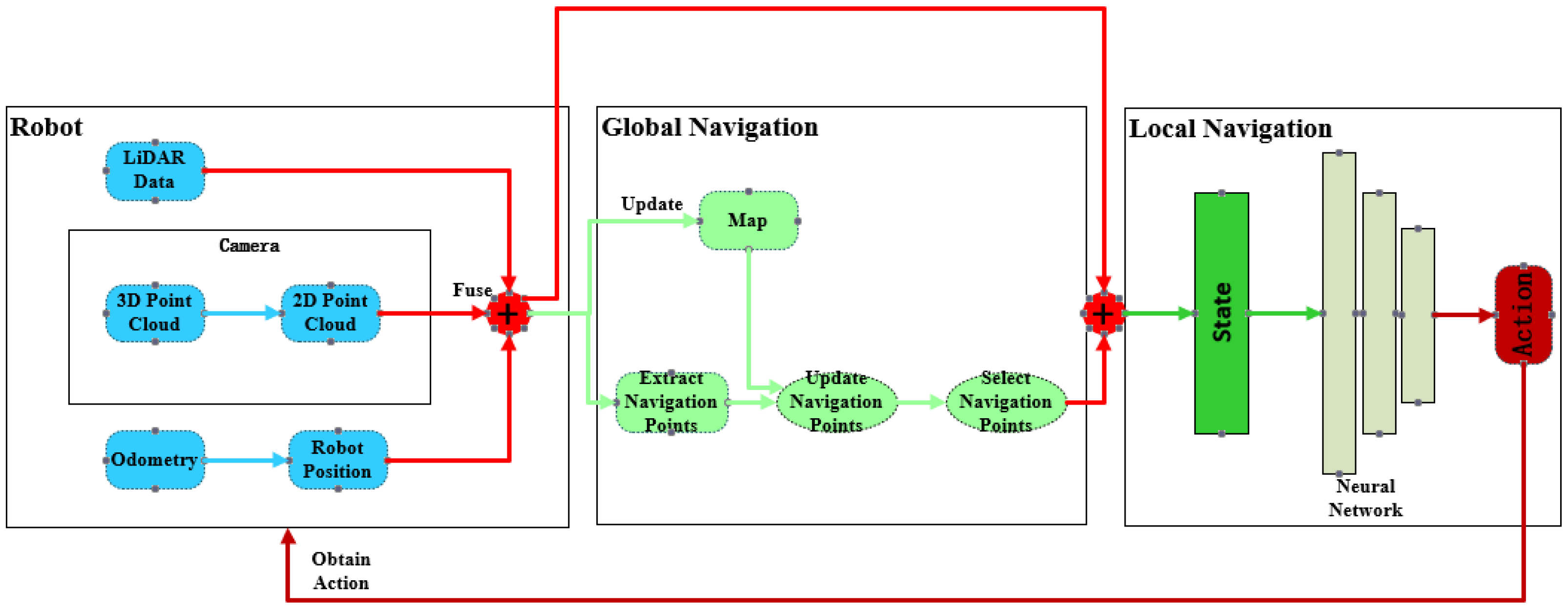
3. Heuristic SAC Autonomous Navigation System
3.1. Local Navigation
3.2. Global Navigation
- (1)
- When the distance between obstacles measured by two consecutive lidar readings exceeds the width of the robot, and the continuous lidar readings between these two readings are all greater than the values of these two readings, a navigation point is generated at the midpoint between these two lidar readings.
- (2)
- In environments with fewer obstacles, if continuous lidar readings indicate a larger free space, navigation points can be generated at a certain interval.
- (3)
- Considering that the detection range of sensors is limited, when the lidar detection values return a non-numeric type (NaN), it indicates that the obstacles have exceeded the sensor’s detection threshold, thus indicating the presence of a relatively spacious area. In this case, if there are non-numeric detection values between two lidar readings, a navigation point is generated at the midpoint between these two readings.
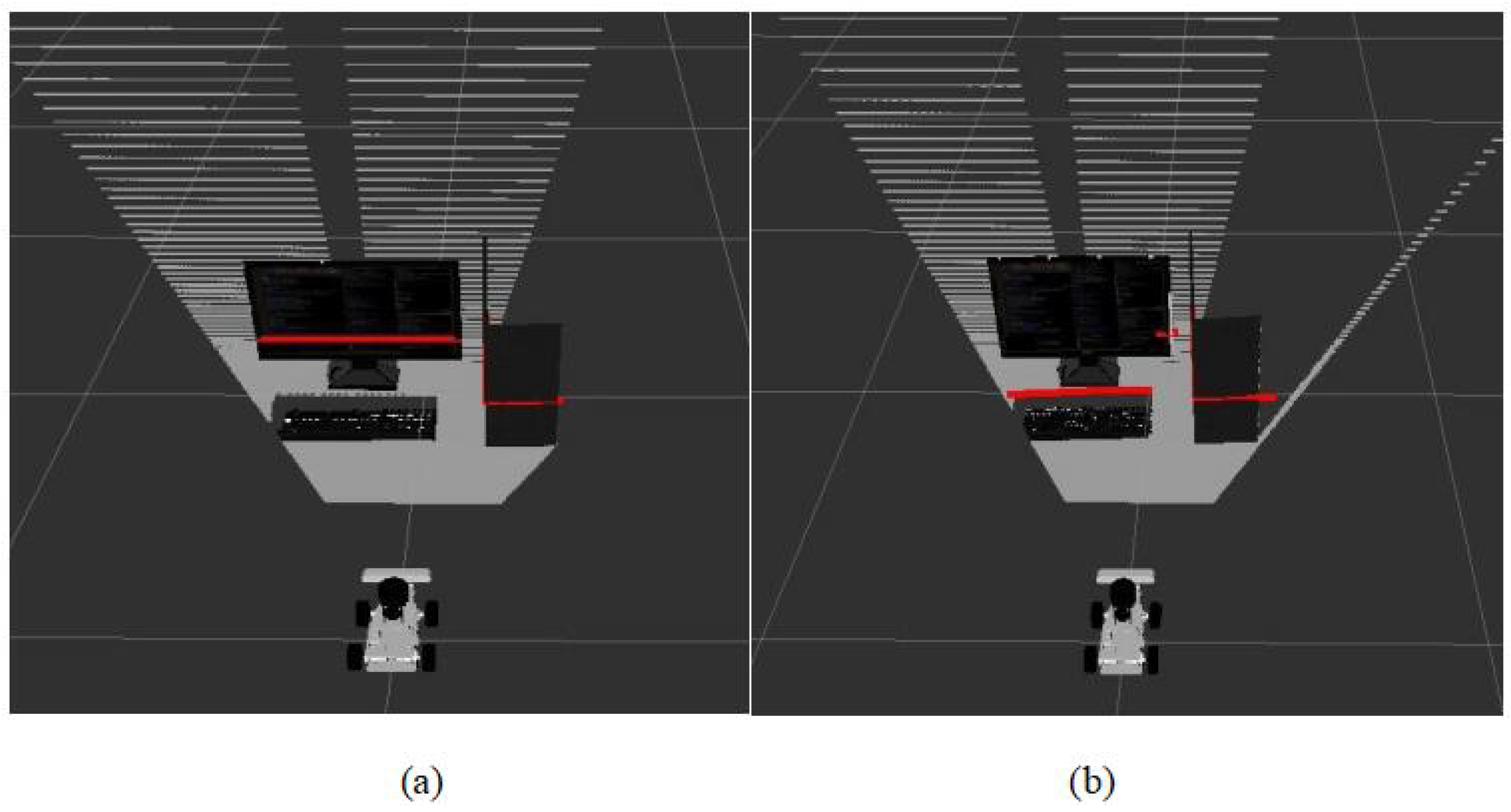
3.3. Sensor Data Fusion
| Algorithm 1 Sensor data fusion |
|
4. Experiments and Results
4.1. Device and Parameter Settings
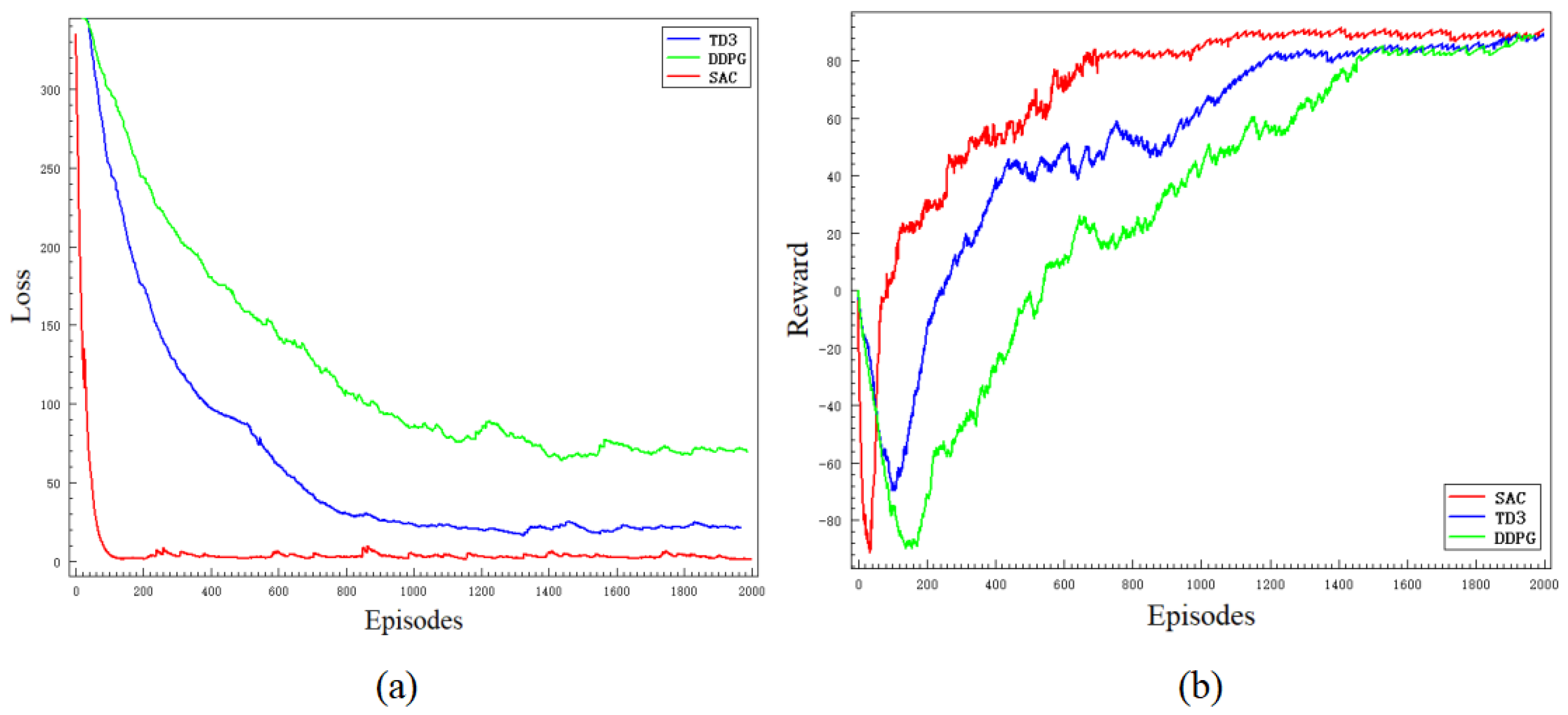
4.2. Network Training
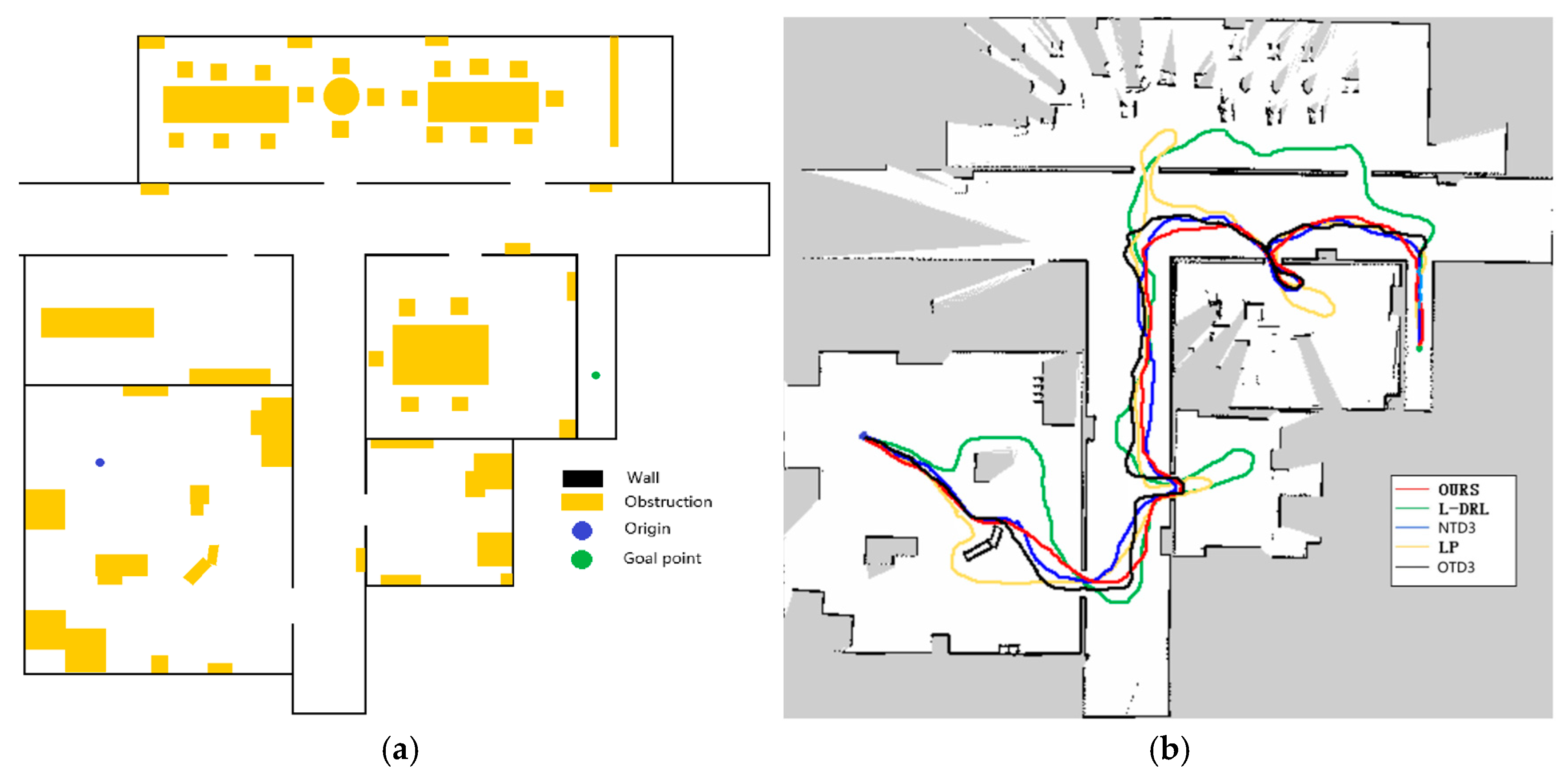
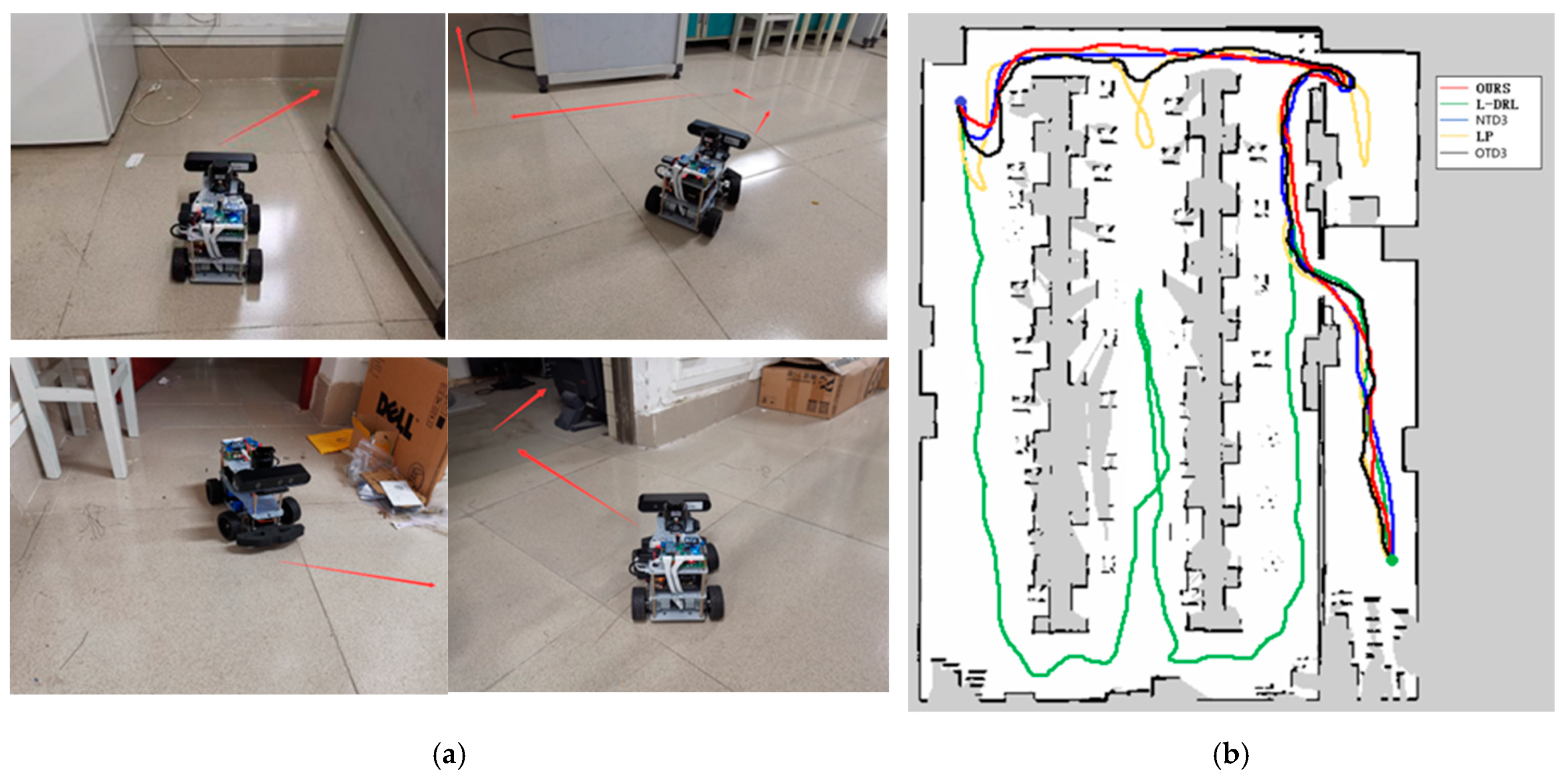
4.3. Autonomous Exploration and Navigation
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Singandhupe, A.; La, H.M. A review of slam techniques and security in autonomous driving. In Proceedings of the 2019 Third IEEE International Conference on Robotic Computing (IRC), Naples, Italy, 25–27 February 2019; pp. 602–607. [Google Scholar]
- Aggarwal, S.; Kumar, N. Path planning techniques for unmanned aerial vehicles: A review, solutions, and challenges. Comput. Commun. 2020, 149, 270–299. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, Z. A multiple mobile robots path planning algorithm based on A-star and Dijkstra algorithm. Int. J. Smart Home 2014, 8, 75–86. [Google Scholar] [CrossRef]
- Naderi, K.; Rajamäki, J.; Hämäläinen, P. RT-RRT* a real-time path planning algorithm based on RRT. In Proceedings of the 8th ACM SIGGRAPH Conference on Motion in Games, Paris, France, 16–18 November 2015; pp. 113–118. [Google Scholar]
- Patle, B.; Pandey, A.; Parhi, D.; Jagadeesh, A. A review: On path planning strategies for navigation of mobile robot. Def. Technol. 2019, 15, 582–606. [Google Scholar] [CrossRef]
- Shi, F.; Zhou, F.; Liu, H.; Chen, L.; Ning, H. Survey and Tutorial on Hybrid Human-Artificial Intelligence. Tsinghua Sci. Technol. 2022, 28, 486–499. [Google Scholar] [CrossRef]
- Hao, X.; Xu, C.; Xie, L.; Li, H. Optimizing the perceptual quality of time-domain speech enhancement with reinforcement learning. Tsinghua Sci. Technol. 2022, 27, 939–947. [Google Scholar] [CrossRef]
- Bouhamed, O.; Ghazzai, H.; Besbes, H.; Massoud, Y. Autonomous UAV navigation: A DDPG-based deep reinforcement learning approach. In Proceedings of the 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 12–14 October 2020; pp. 1–5. [Google Scholar]
- Gao, J.; Ye, W.; Guo, J.; Li, Z. Deep reinforcement learning for indoor mobile robot path planning. Sensors 2020, 20, 5493. [Google Scholar] [CrossRef]
- Cimurs, R.; Suh, I.H.; Lee, J.H. Goal-driven autonomous exploration through deep reinforcement learning. IEEE Robot. Autom. Lett. 2021, 7, 730–737. [Google Scholar] [CrossRef]
- Yang, L.; Bi, J.; Yuan, H. Intelligent Path Planning for Mobile Robots Based on SAC Algorithm. J. Syst. Simul. 2023, 35, 1726–1736. [Google Scholar]
- Morales, E.F.; Murrieta-Cid, R.; Becerra, I.; Esquivel-Basaldua, M.A. A survey on deep learning and deep reinforcement learning in robotics with a tutorial on deep reinforcement learning. Intell. Serv. Robot. 2021, 14, 773–805. [Google Scholar] [CrossRef]
- Cimurs, R.; Suh, I.H.; Lee, J.H. Information-based heuristics for learned goal-driven exploration and mapping. In Proceedings of the 2021 18th International Conference on Ubiquitous Robots (UR), Gangneung, Republic of Korea, 12–14 July 2021; pp. 571–578. [Google Scholar]
- Jiang, S.; Wang, S.; Yi, Z.; Zhang, M.; Lv, X. Autonomous navigation system of greenhouse mobile robot based on 3D lidar and 2D lidar SLAM. Front. Plant Sci. 2022, 13, 815218. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Sun, P.; Xu, Z.; Min, H.; Yu, H. Fusion of 3D LIDAR and camera data for object detection in autonomous vehicle applications. IEEE Sens. J. 2020, 20, 4901–4913. [Google Scholar] [CrossRef]
- Gatesichapakorn, S.; Takamatsu, J.; Ruchanurucks, M. ROS based autonomous mobile robot navigation using 2D LiDAR and RGB-D camera. In Proceedings of the 2019 First International Symposium on Instrumentation, Control, Artificial Intelligence, and Robotics (ICA-SYMP), Bangkok, Thailand, 16–18 January 2019; pp. 151–154. [Google Scholar]
- Kontoudis, G.P.; Vamvoudakis, K.G. Kinodynamic motion planning with continuous-time Q-learning: An online, model-free, and safe navigation framework. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3803–3817. [Google Scholar] [CrossRef] [PubMed]
- Marchesini, E.; Farinelli, A. Discrete deep reinforcement learning for mapless navigation. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 10688–10694. [Google Scholar]
- Dong, Y.; Zou, X. Mobile robot path planning based on improved DDPG reinforcement learning algorithm. In Proceedings of the 2020 IEEE 11th International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 16–18 October 2020; pp. 52–56. [Google Scholar]
- Li, P.; Wang, Y.; Gao, Z. Path planning of mobile robot based on improved td3 algorithm. In Proceedings of the 2022 IEEE International Conference on Mechatronics and Automation (ICMA), Guilin, China, 7–10 August 2022; pp. 715–720. [Google Scholar]
- Aman, M.S.; Mahmud, M.A.; Jiang, H.; Abdelgawad, A.; Yelamarthi, K. A sensor fusion methodology for obstacle avoidance robot. In Proceedings of the 2016 IEEE International Conference on Electro Information Technology (EIT), Grand Forks, ND, USA, 19–21 May 2016; pp. 0458–0463. [Google Scholar]
- Forouher, D.; Besselmann, M.G.; Maehle, E. Sensor fusion of depth camera and ultrasound data for obstacle detection and robot navigation. In Proceedings of the 2016 14th International Conference on Control, Automation, Robotics and vision (ICARCV), Phuket, Thailand, 13–15 November 2016; pp. 1–6. [Google Scholar]
- Zhang, B.; Zhang, J. Robot Mapping and Navigation System Based on Multi-sensor Fusion. In Proceedings of the 2021 4th International Conference on Artificial Intelligence and Big Data (ICAIBD), Chengdu, China, 28–31 May 2021; pp. 632–636. [Google Scholar]
- Theodoridou, C.; Antonopoulos, D.; Kargakos, A.; Kostavelis, I.; Giakoumis, D.; Tzovaras, D. Robot Navigation in Human Populated Unknown Environments based on Visual-Laser Sensor Fusion. In Proceedings of the 15th International Conference on PErvasive Technologies Related to Assistive Environments, Corfu, Greece, 29 June–1 July 2022; pp. 336–342. [Google Scholar]
- Surmann, H.; Jestel, C.; Marchel, R.; Musberg, F.; Elhadj, H.; Ardani, M. Deep reinforcement learning for real autonomous mobile robot navigation in indoor environments. arXiv 2020, arXiv:2005.13857. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P.; et al. Soft actor-critic algorithms and applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Sun, H.; Zhang, W.; Yu, R.; Zhang, Y. Motion planning for mobile robots—Focusing on deep reinforcement learning: A systematic review. IEEE Access 2021, 9, 69061–69081. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Icarte, R.T.; Klassen, T.Q.; Valenzano, R.; McIlraith, S.A. Reward machines: Exploiting reward function structure in reinforcement learning. J. Artif. Intell. Res. 2022, 73, 173–208. [Google Scholar] [CrossRef]
- Durrant-Whyte, H.; Henderson, T.C. Multisensor data fusion. In Springer Handbook of Robotics; Springer: Cham, Switzerland, 2016; pp. 867–896. [Google Scholar]
- Zhu, Z.; Zhang, Y.; Chen, H.; Dong, Y.; Zhao, S.; Ding, W.; Zhong, J.; Zheng, S. Understanding the Robustness of 3D Object Detection With Bird’s-Eye-View Representations in Autonomous Driving. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 21600–21610. [Google Scholar]

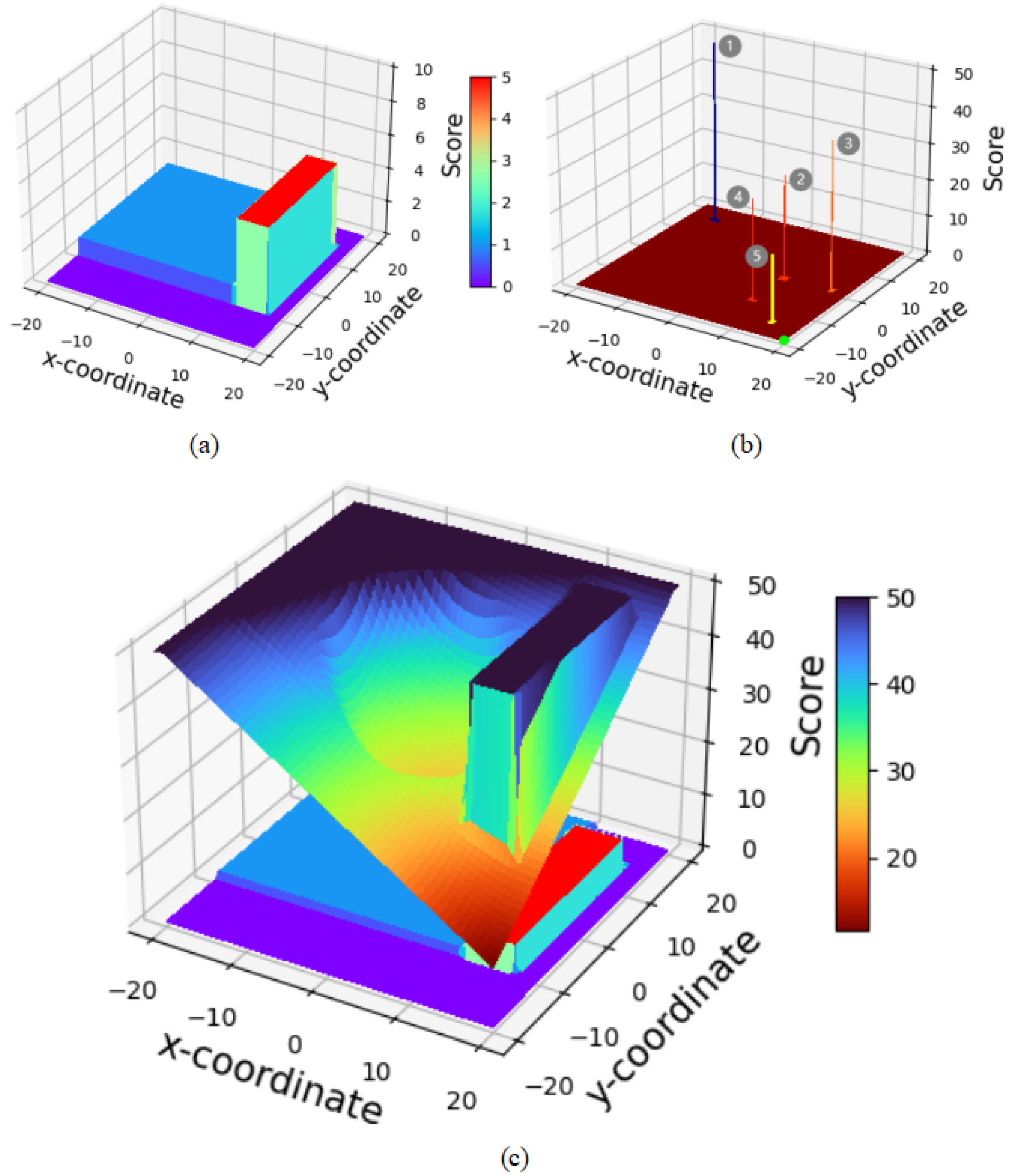
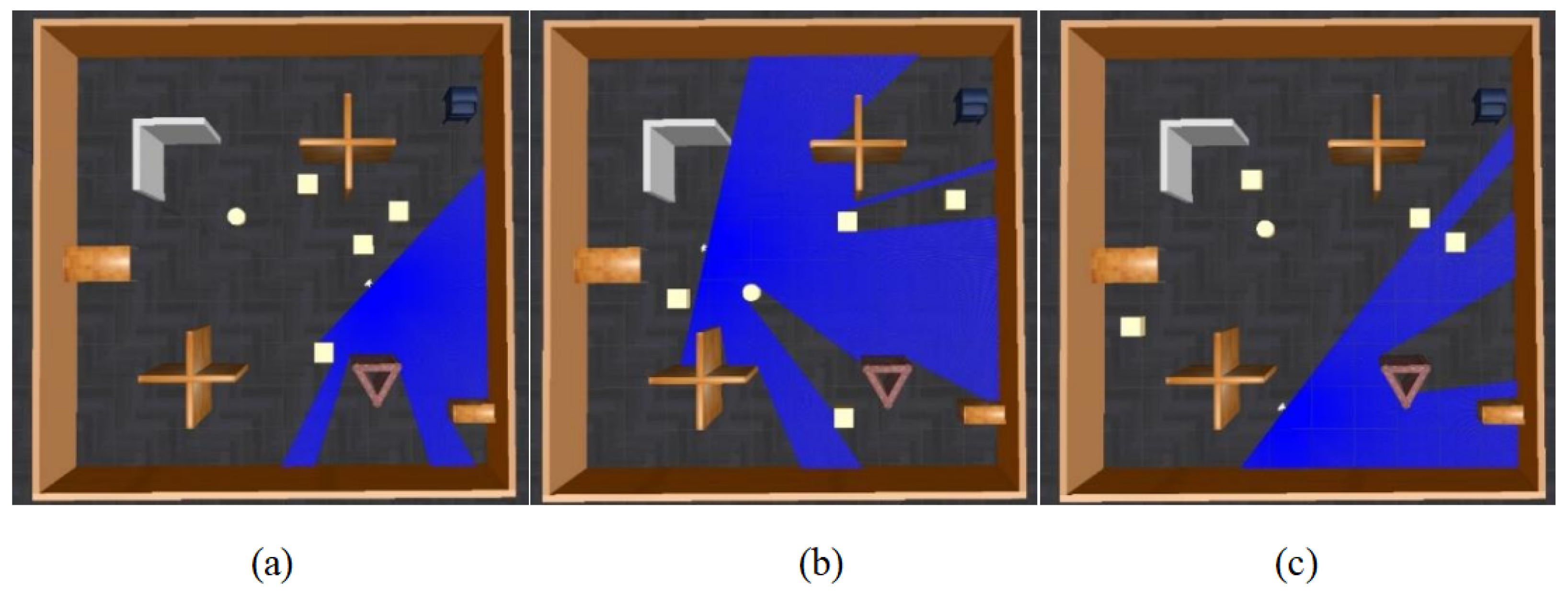

| Candidate Point | Point 1 | Point 2 | Point 3 | Point 4 | Point 5 |
|---|---|---|---|---|---|
| Score | 62.20 | 28.36 | 40.41 | 27.32 | 18.07 |
| Min.D (m) | Max.D (m) | Av.D (m) | Min.T (s) | Max.T (s) | Av.T (s) | Arrive | |
|---|---|---|---|---|---|---|---|
| OURS | 53.47 | 98.77 | 74.26 | 83.41 | 163.16 | 120.03 | 5/5 |
| L-DRL | 79.82 | 147.13 | 110.57 | 175.83 | 338.96 | 249.54 | 3/5 |
| NTD3 | 55.24 | 99.16 | 75.21 | 97.64 | 180.29 | 134.82 | 5/5 |
| OTD3 | 59.63 | 102.53 | 81.49 | 107.42 | 188.03 | 149.51 | 5/5 |
| LP | 69.53 | 122.06 | 94.59 | 150.12 | 273.41 | 211.98 | 5/5 |
| Dijkstra | 48.34 | 49.13 | 48.66 | 72.07 | 75.25 | 73.75 | 5/5 |
| Min.D (m) | Max.D (m) | Av.D (m) | Min.T (s) | Max.T (s) | Av.T (s) | Arrive | |
|---|---|---|---|---|---|---|---|
| OURS | 44.57 | 78.32 | 59.44 | 66.82 | 127.35 | 94.14 | 5/5 |
| L-DRL | 58.62 | 93.13 | 71.74 | 137.93 | 227.15 | 171.63 | 5/5 |
| NTD3 | 47.28 | 81.63 | 61.25 | 86.65 | 156.09 | 115.33 | 5/5 |
| OTD3 | 49.17 | 83.33 | 63.25 | 91.04 | 160.23 | 119.23 | 5/5 |
| LP | 50.58 | 86.91 | 65.57 | 120.13 | 208.93 | 156.84 | 5/5 |
| Dijkstra | 41.53 | 42.67 | 41.88 | 61.07 | 65.64 | 62.51 | 5/5 |
| Min.D (m) | Max.D (m) | Av.D (m) | Min.T (s) | Max.T (s) | Av.T (s) | Arrive | |
|---|---|---|---|---|---|---|---|
| OURS | 36.14 | 65.67 | 44.93 | 60.26 | 112.42 | 78.52 | 5/5 |
| L-DRL | 87.08 | 103.71 | 97.33 | 215.70 | 269.29 | 230.58 | 3/5 |
| NTD3 | 39.27 | 66.24 | 45.71 | 72.04 | 121.84 | 84.84 | 5/5 |
| OTD3 | 41.81 | 68.95 | 51.02 | 77.35 | 127.58 | 95.48 | 5/5 |
| LP | 49.34 | 90.59 | 64.56 | 115.51 | 210.92 | 152.46 | 5/5 |
| Dijkstra | 31.30 | 34.64 | 32.16 | 47.96 | 54.24 | 50.76 | 5/5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, Y.; Cai, Y.; Sun, Y.; Qin, T. Autonomous Navigation by Mobile Robot with Sensor Fusion Based on Deep Reinforcement Learning. Sensors 2024, 24, 3895. https://doi.org/10.3390/s24123895
Ou Y, Cai Y, Sun Y, Qin T. Autonomous Navigation by Mobile Robot with Sensor Fusion Based on Deep Reinforcement Learning. Sensors. 2024; 24(12):3895. https://doi.org/10.3390/s24123895
Chicago/Turabian StyleOu, Yang, Yiyi Cai, Youming Sun, and Tuanfa Qin. 2024. "Autonomous Navigation by Mobile Robot with Sensor Fusion Based on Deep Reinforcement Learning" Sensors 24, no. 12: 3895. https://doi.org/10.3390/s24123895
APA StyleOu, Y., Cai, Y., Sun, Y., & Qin, T. (2024). Autonomous Navigation by Mobile Robot with Sensor Fusion Based on Deep Reinforcement Learning. Sensors, 24(12), 3895. https://doi.org/10.3390/s24123895






