Band-Stop Frequency-Selective Surface (FSS) with Elliptic Response Designed by the Extracted Pole Technique
Abstract
1. Introduction
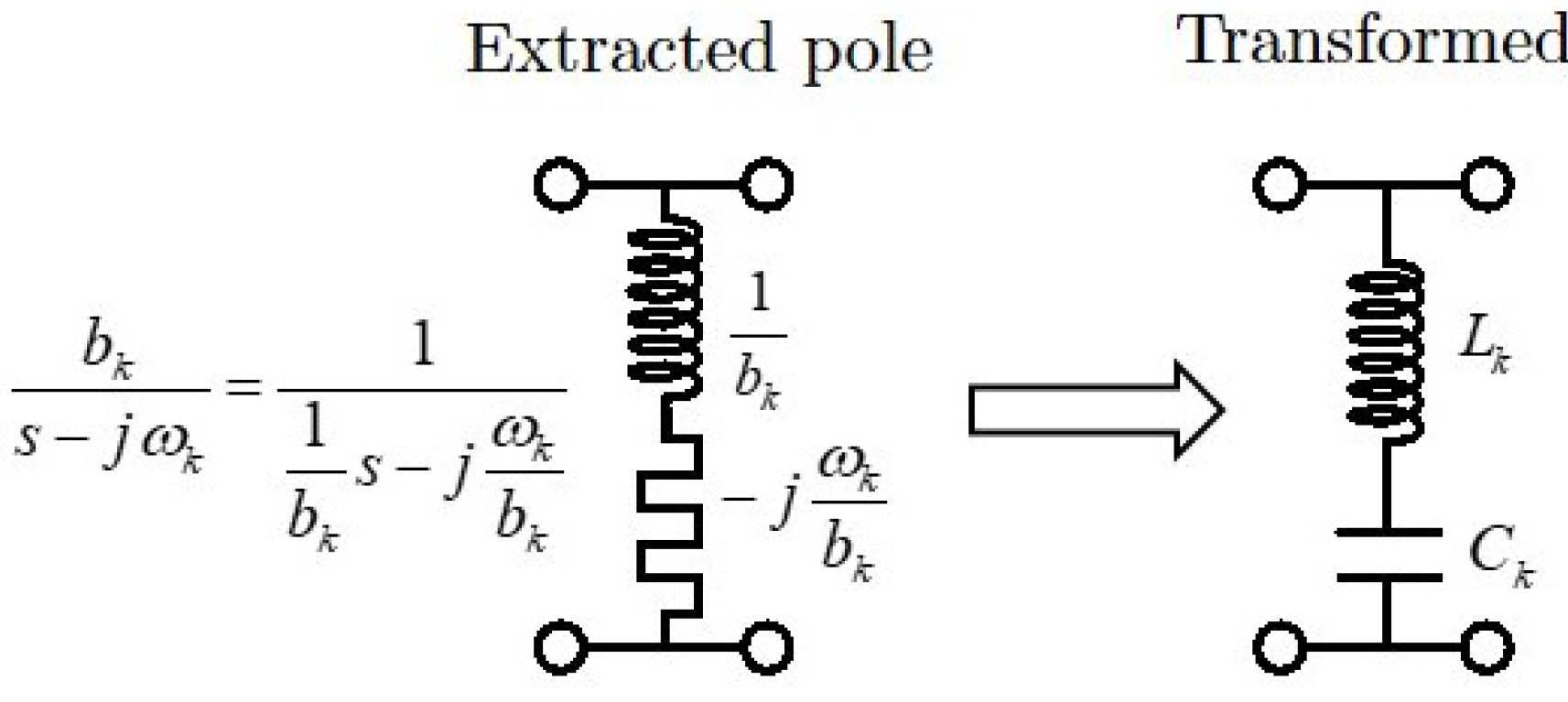
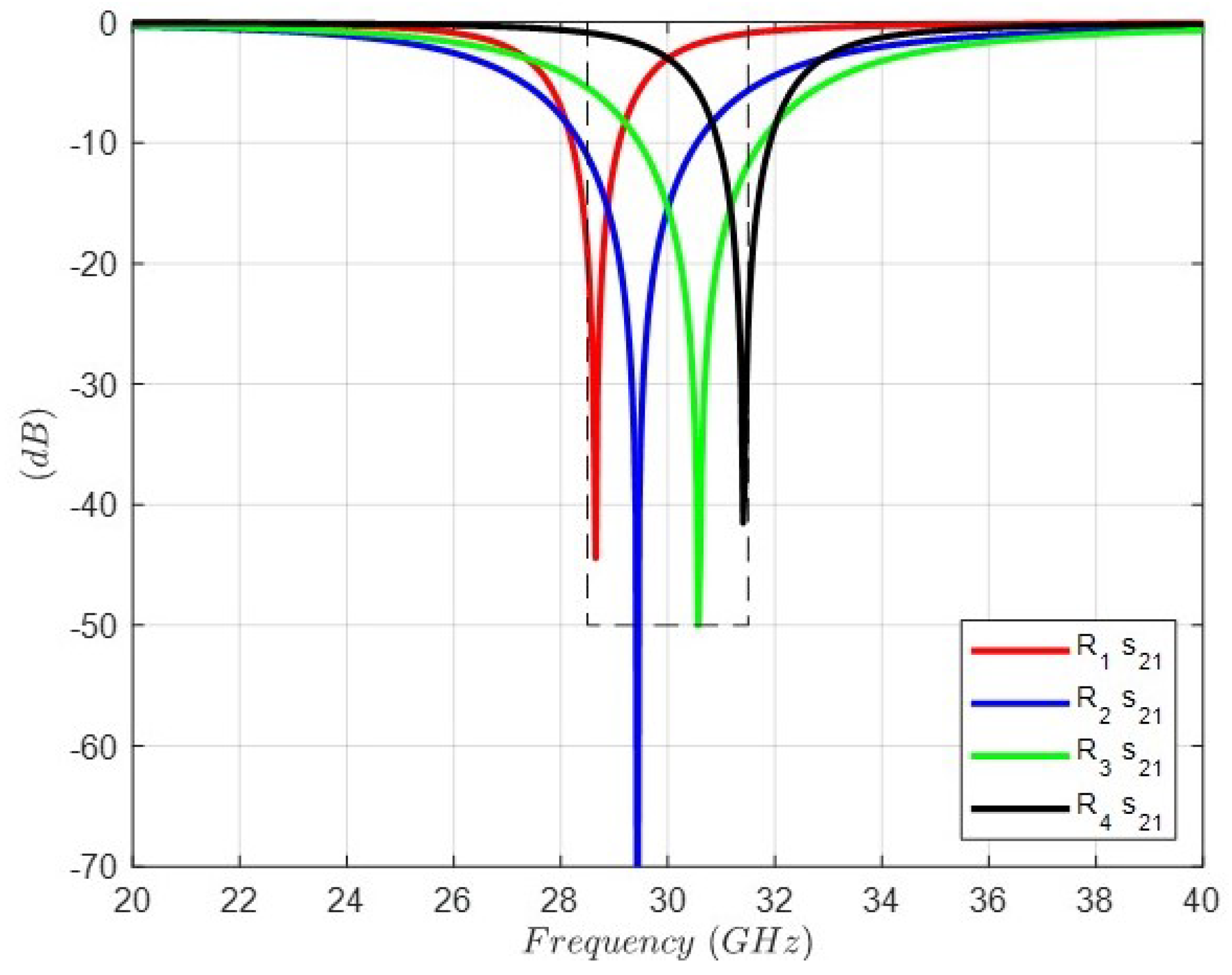
2. Theoretical Synthesis Procedure
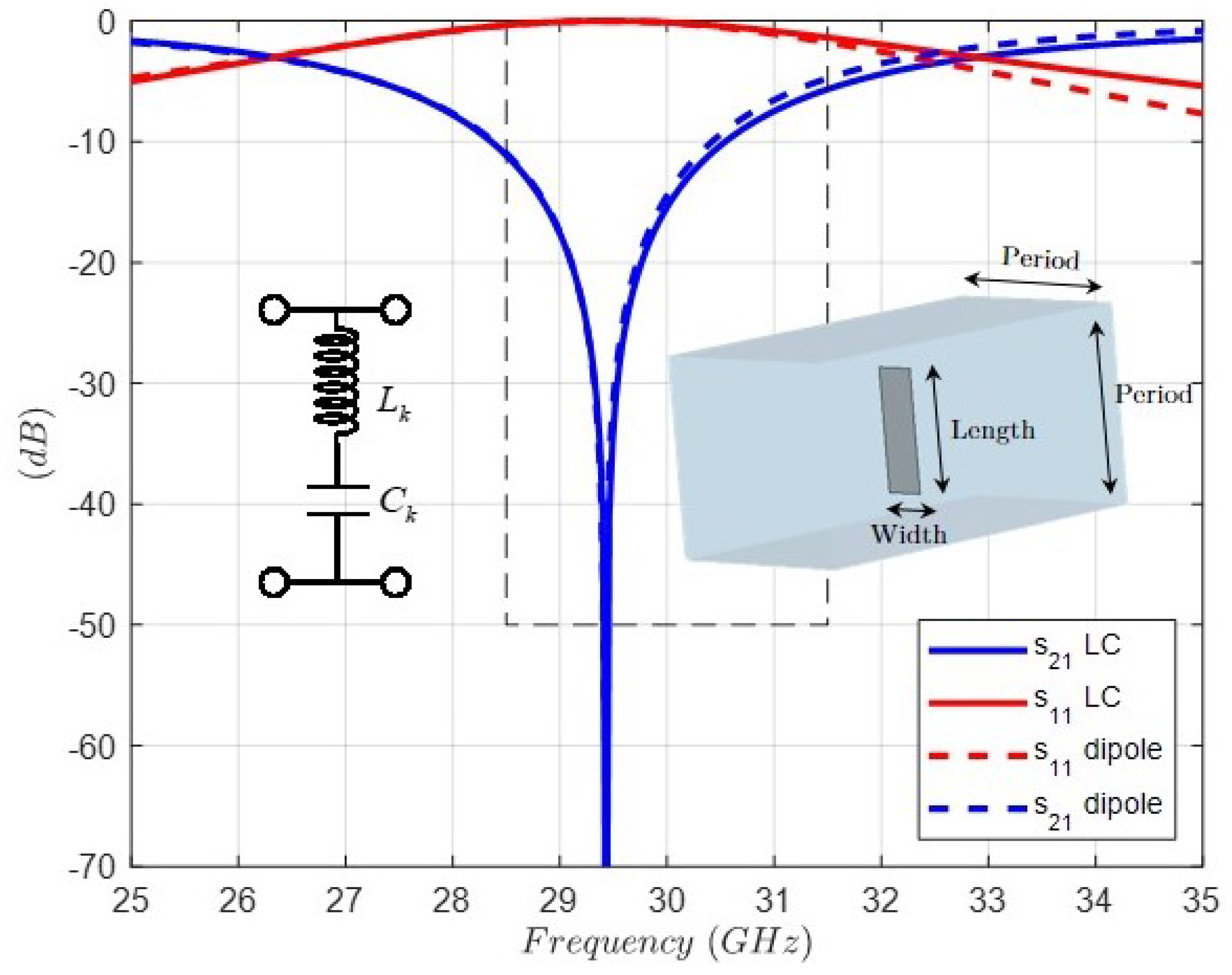
3. Unit Cell of the FSS and Equivalent Circuits
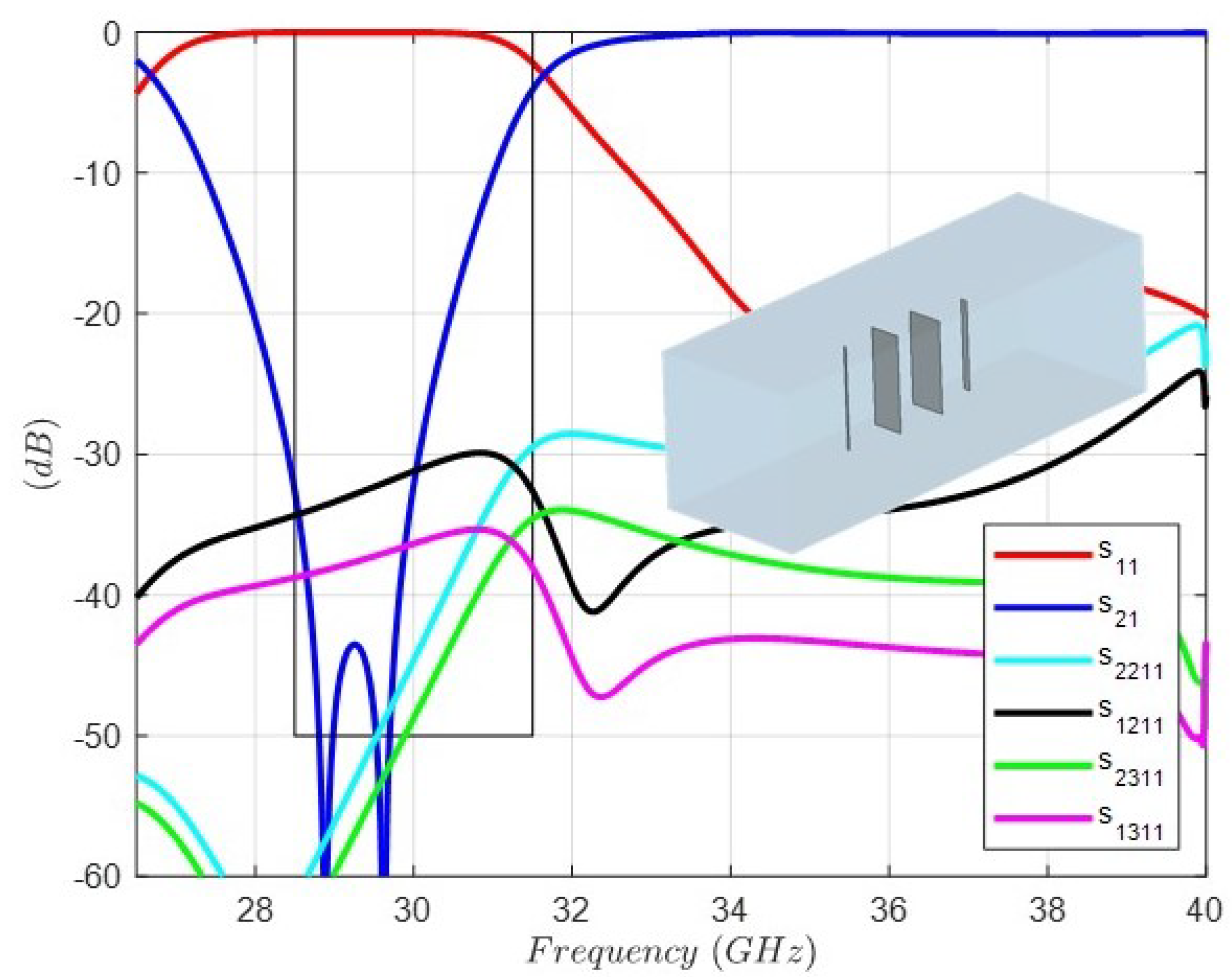
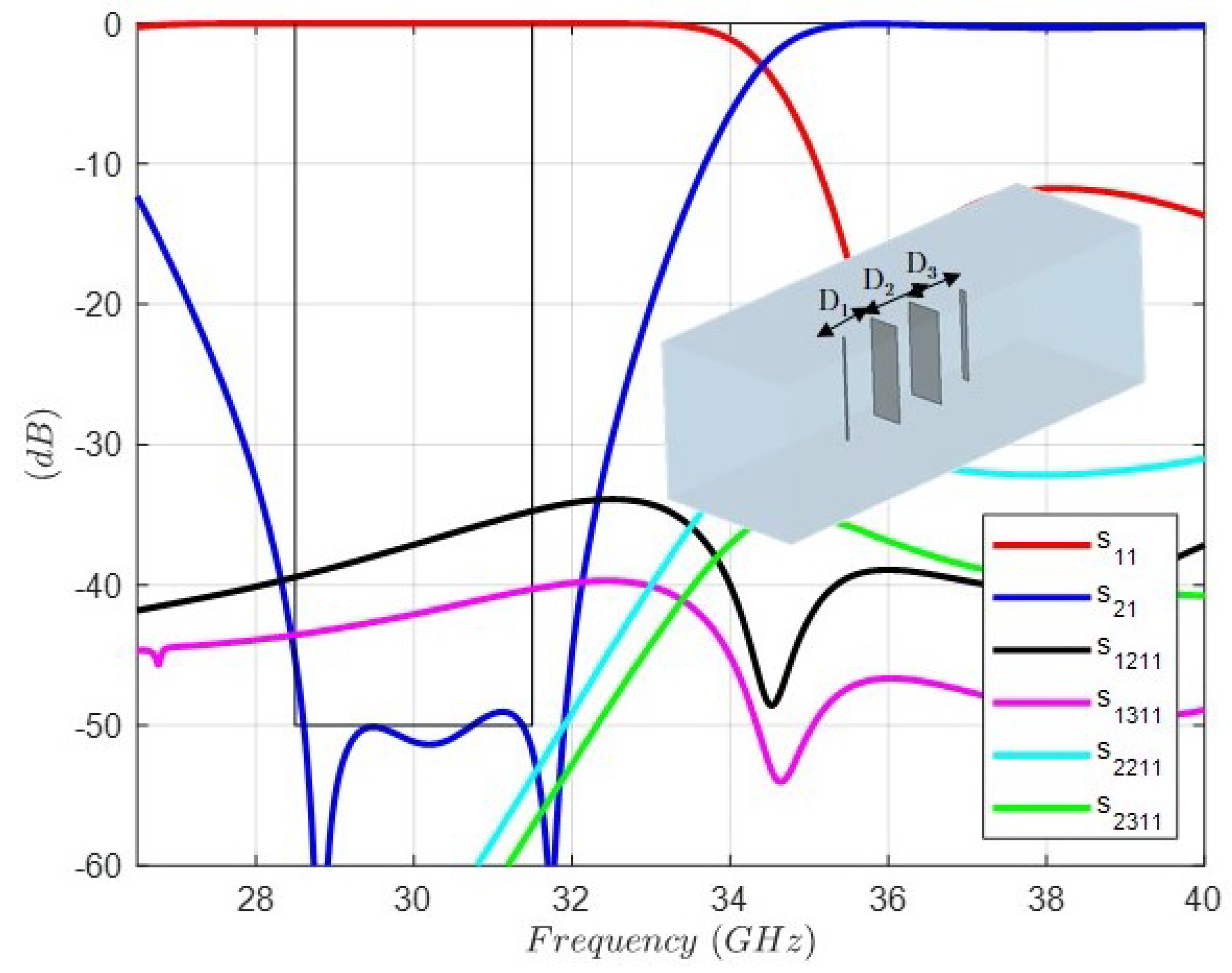
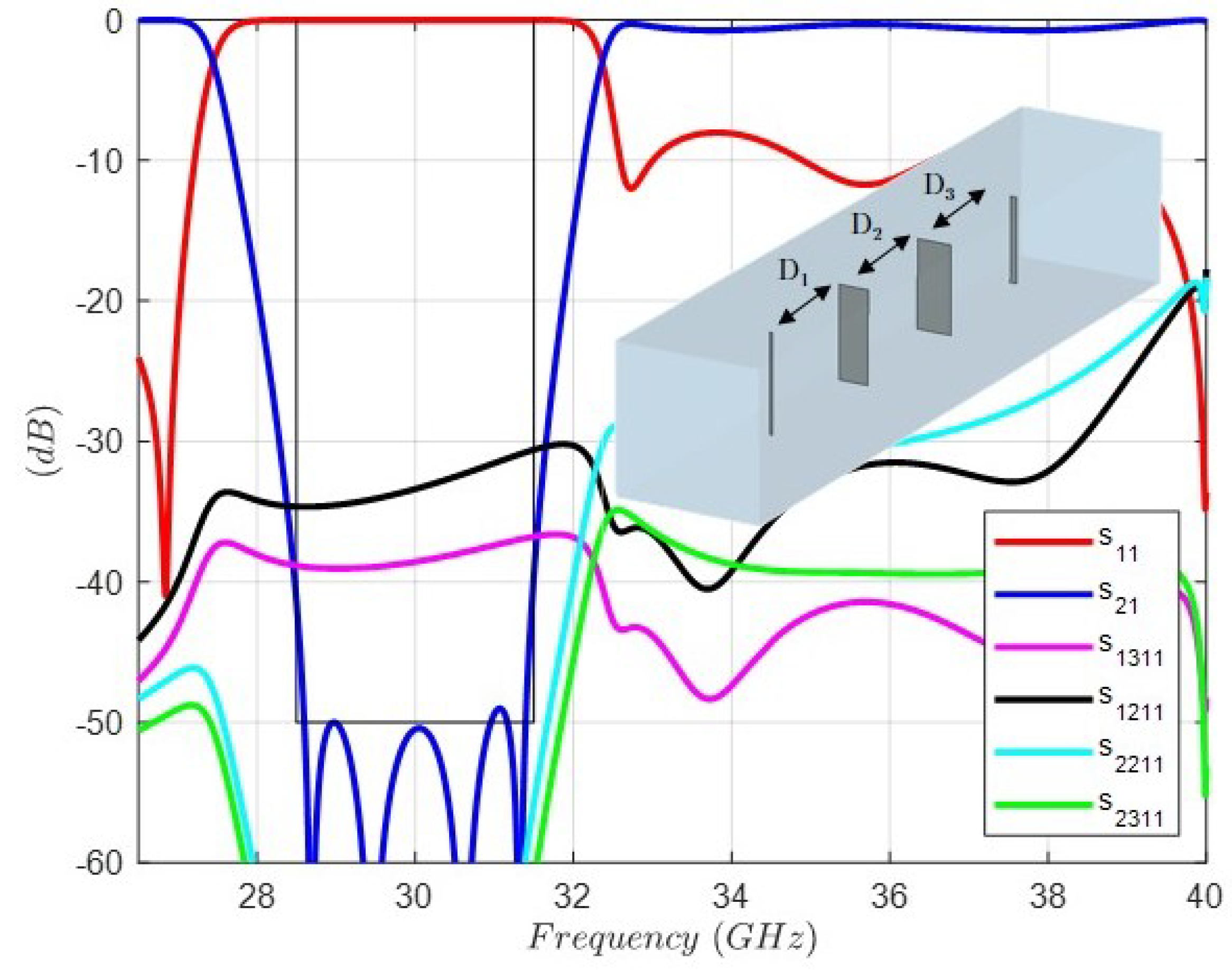
4. Full-Wave Design and Optimization
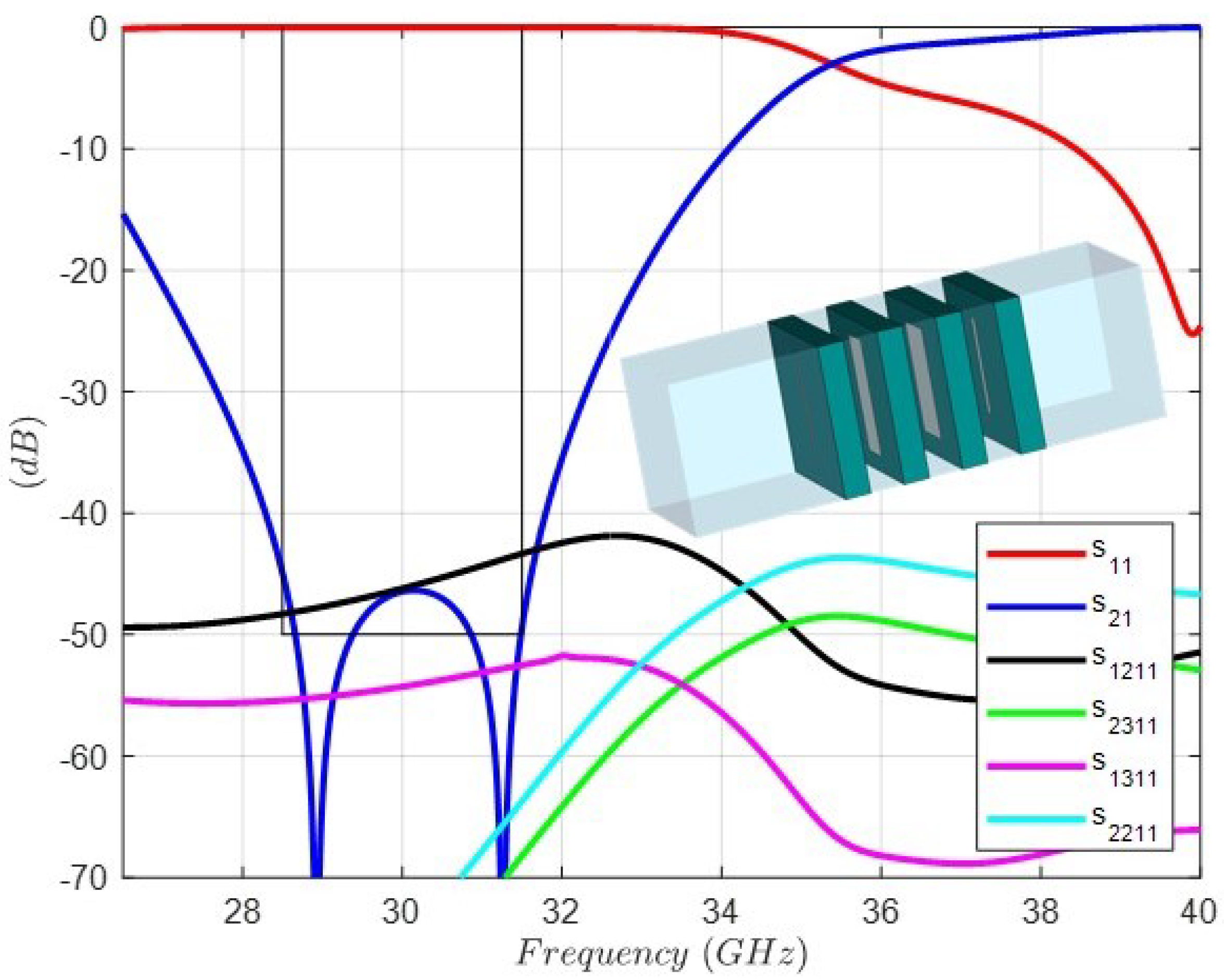
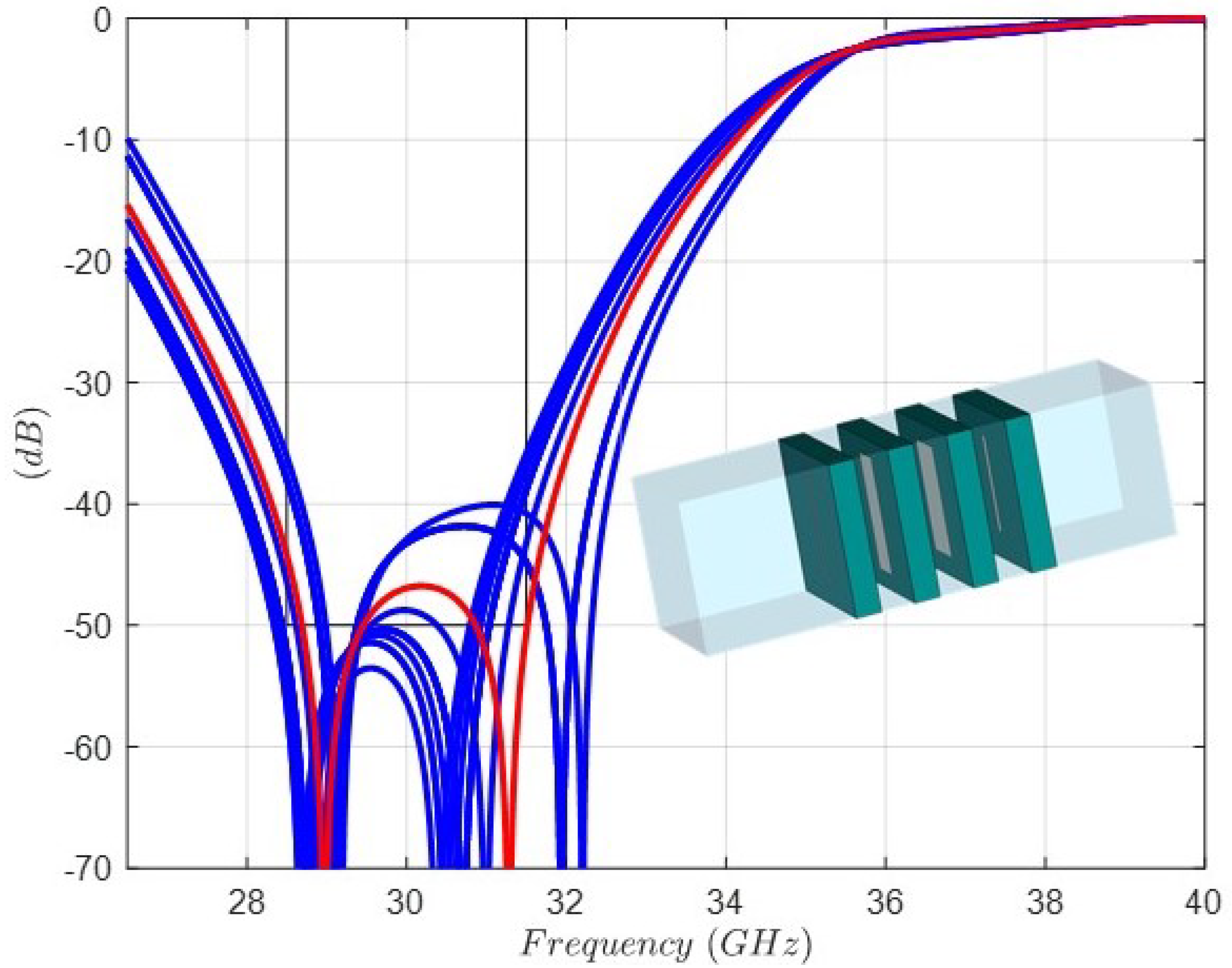
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Munk, B. Frequency Selective Surfaces: Theory and Design; John Wiley & Sons Interscience: Hoboken, NJ, USA, 2000. [Google Scholar]
- Li, L.; Chen, Q.; Yuan, Q.; Sawaya, K.; Maruyama, T.; Furuno, T.; Uebayashi, S. Frequency Selective Reflectarray Using Crossed-Dipole Elements with Square Loops for Wireless Communication Applications. IEEE Trans. Antennas Propag. 2011, 59, 89–99. [Google Scholar] [CrossRef]
- Lee, S.; Zimmerman, M.; Fujikawa, G.; Sharp, R. Designs for ATDRSS tri-band reflector antenna. In Proceedings of the Antennas and Propagation Society Symposium 1991 Digest, London, ON, Canada, 24–28 June 1991; Volume 2, pp. 666–669. [Google Scholar] [CrossRef]
- Ueno, K.; Itanami, T.; Kumazawa, H.; Ohtomo, I. Design and characteristics of a multiband communication satellite antenna system. IEEE Trans. Aerosp. Electron. Syst. 1995, 31, 600–607. [Google Scholar] [CrossRef]
- Matthaei, G.L.; Young, L.; Jones, E.M.T. Microwave Filters, Impedance-Matching Networks, and Coupling Strucures; Artech House: London, UK, 1980. [Google Scholar]
- Rashid, A.K.; Shen, Z. A Novel Band-Reject Frequency Selective Surface with Pseudo-Elliptic Response. IEEE Trans. Antennas Propag. 2010, 58, 1220–1226. [Google Scholar] [CrossRef]
- Ma, Y.; Yuan, Y.; Wang, D.; Shi, Q.; Yuan, N. A Way to Design the Miniaturized Dual-Stopbands FSS Based on the Topology Structure. IEEE Access 2019, 7, 156536–156543. [Google Scholar] [CrossRef]
- Ud Din, I.; Alibakhshikenari, M.; Virdee, B.S.; Jayanthi, R.K.R.; Ullah, S.; Khan, S.; See, C.H.; Golunski, L.; Koziel, S. Frequency-Selective Surface-Based MIMO Antenna Array for 5G Millimeter-Wave Applications. Sensors 2023, 23, 7009. [Google Scholar] [CrossRef] [PubMed]
- Tamoor, T.; Ahmed, F.; Qasim Ali Shah, S.M.; Hassan, T.; Shoaib, N. An FSS Based Stop Band Filter for EM Shielding Application. In Proceedings of the 2020 International Symposium on Electromagnetic Compatibility—EMC EUROPE, Rome, Italy, 23–25 September 2020; pp. 1–3. [Google Scholar] [CrossRef]
- Shengli, J.; Bingzheng, X.; Ting, Z. Design of A 3-D Band-Stop FSS with High Selectivity. In Proceedings of the 2020 IEEE 3rd International Conference on Electronics Technology (ICET), Chengdu, China, 8–12 May 2020; pp. 6–10. [Google Scholar] [CrossRef]
- Xie, X.; Fang, W.; Chen, P.; Poo, Y.; Wu, R. A Broadband and Wide-angle Band-stop Frequency Selective Surface (FSS) Based on Dual-layered Fractal Square Loops. In Proceedings of the 2018 IEEE Asia-Pacific Conference on Antennas and Propagation (APCAP), Auckland, New Zealand, 5–8 August 2018; pp. 278–280. [Google Scholar] [CrossRef]
- Yan, M.; Qu, S.; Wang, J.; Zhang, J.; Zhou, H.; Chen, H.; Zheng, L. A Miniaturized Dual-Band FSS with Stable Resonance Frequencies of 2.4 GHz/5 GHz for WLAN Applications. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 895–898. [Google Scholar] [CrossRef]
- Yin, W.; Zhang, H.; Zhong, T.; Min, X. A Novel Compact Dual-Band Frequency Selective Surface for GSM Shielding by Utilizing a 2.5-Dimensional Structure. IEEE Trans. Electromagn. Compat. 2018, 60, 2057–2060. [Google Scholar] [CrossRef]
- Khajevandi, S.; Oraizi, H.; Poordaraee, M. Design of Planar Dual-Bandstop FSS Using Square-Loop-Enclosing Superformula Curves. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 731–734. [Google Scholar] [CrossRef]
- Xu, C.; Qu, S.; Pang, Y.; Wang, J.; Yan, M.; Ma, H. A novel dual-stop-band FSS for infrared stealth application. In Proceedings of the 2017 International Applied Computational Electromagnetics Society Symposium (ACES), Firenze, Italy, 26–30 March 2017; pp. 1–2. [Google Scholar]
- Idrees, M.; He, Y.; Ullah, S.; Wong, S.W. A Dual-Band Polarization-Insensitive Frequency Selective Surface for Electromagnetic Shielding Applications. Sensors 2024, 24, 3333. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Sheng, X.; Zhang, C.; Fan, J.; Guo, D. A Design Method for Synthesizing Wideband Band-Stop FSS via Its Equivalent Circuit Model. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2721–2725. [Google Scholar] [CrossRef]
- Li, B.; Shen, Z. Three-Dimensional Bandpass Frequency-Selective Structures with Multiple Transmission Zeros. IEEE Trans. Microw. Theory Tech. 2013, 61, 3578–3589. [Google Scholar] [CrossRef]
- Omar, A.A.; Shen, Z. Multiband High-Order Bandstop 3-D Frequency-Selective Structures. IEEE Trans. Antennas Propag. 2016, 64, 2217–2226. [Google Scholar] [CrossRef]
- Al-Sheikh, A.; Shen, Z. Design of Wideband Bandstop Frequency-Selective Structures Using Stacked Parallel Strip Line Arrays. IEEE Trans. Antennas Propag. 2016, 64, 3401–3409. [Google Scholar] [CrossRef]
- Montejo-Garai, J.R.; Ruiz-Cruz, J.A.; Rebollar, J.M.; Estrada, T. In-Line Pure E-Plane Waveguide Band-Stop Filter with Wide Spurious-Free Response. IEEE Microw. Wirel. Components Lett. 2011, 21, 209–211. [Google Scholar] [CrossRef]
- Cameron, R.J.; Kudsia, C.M.; Mansour, R.R. Microwave Filters for Communication Systems: Fundamentals, Design and Applications; Wiley-Interscience: Hoboken, NJ, USA, 2007; 771p. [Google Scholar]
- Rhodes, J. Theory of Electrical Filters; John Wiley & Sons: Hoboken, NJ, USA, 1976. [Google Scholar]
- Perez-Palomino, G.; Page, J.E. Bimode Foster’s Equivalent Circuit of Arbitrary Planar Periodic Structures and Its Application to Design Polarization Controller Devices. IEEE Trans. Antennas Propag. 2020, 68, 5308–5321. [Google Scholar] [CrossRef]
- Conde-Pumpido, F.; Perez-Palomino, G.; Montejo-Garai, J.R.; Page, J.E. Generalized Bimode Equivalent Circuit of Arbitrary Planar Periodic Structures for Oblique Incidence. IEEE Trans. Antennas Propag. 2022, 70, 9435–9448. [Google Scholar] [CrossRef]
- Rohacell. Available online: https://www.thyssenkrupp-plastics.es/es/productos/rohacell (accessed on 24 October 2022).
- Coombs, C.F. Printed Circuit Handbook; McGraw-Hill USA: New York, NY, USA, 2008. [Google Scholar]
- Dey, S.; Dey, S.; Koul, S.K. Second-Order, Single-Band and Dual-Band Bandstop Frequency Selective Surfaces at Millimeter Wave Regime. IEEE Trans. Antennas Propag. 2022, 70, 7282–7287. [Google Scholar] [CrossRef]
- Mamedes, D.F.; Bornemann, J. Using an Equivalent-Circuit Model to Design Ultra-Wide Band-Stop Frequency-Selective Surface for 5G mm-Wave Applications. IEEE Open J. Antennas Propag. 2022, 3, 948–957. [Google Scholar] [CrossRef]
- Das, S.; Rajput, A.; Mukherjee, B. A Novel FSS-Based Bandstop Filter for TE/TM Polarization. IEEE Lett. Electromagn. Compat. Pract. Appl. 2024, 6, 11–15. [Google Scholar] [CrossRef]






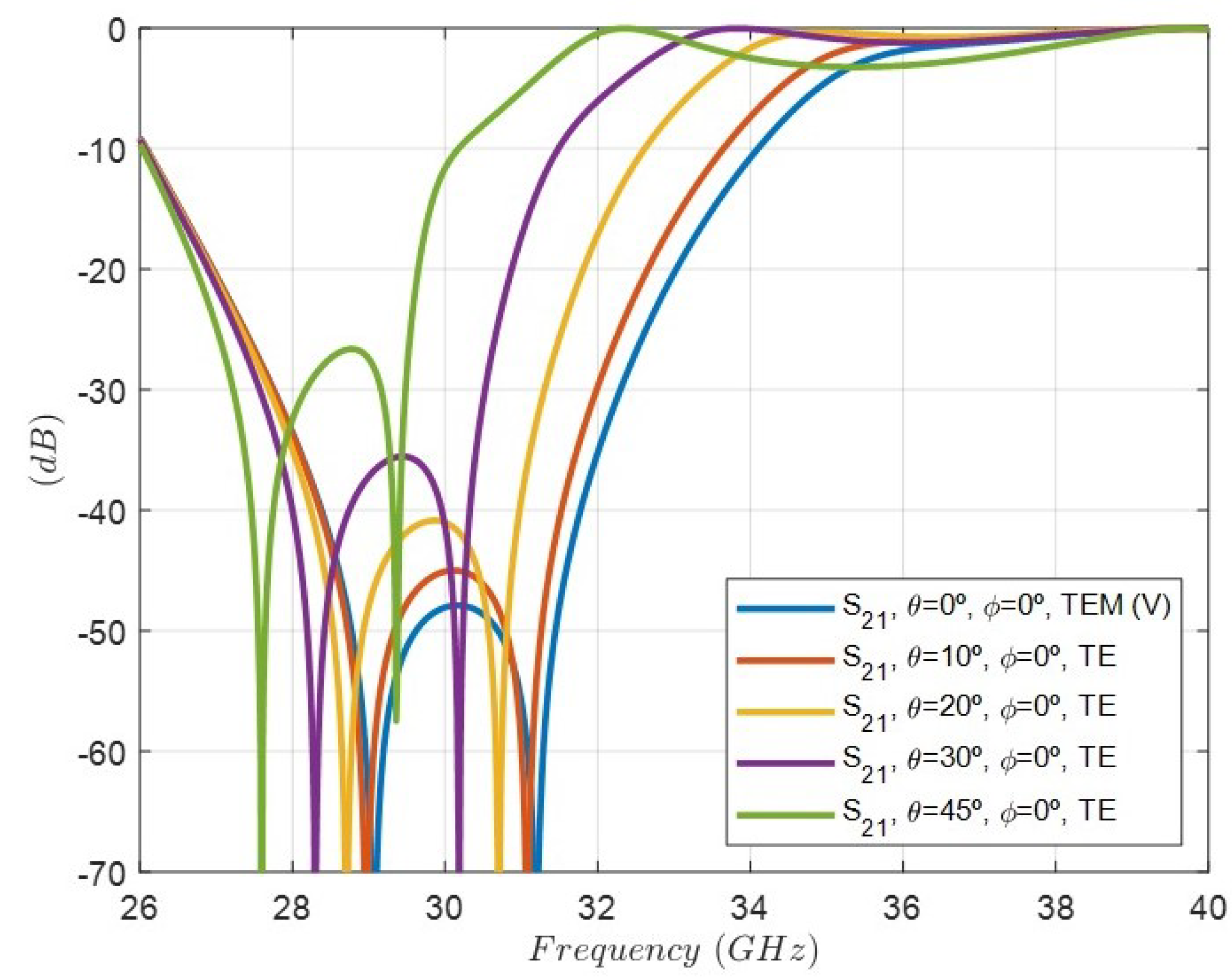



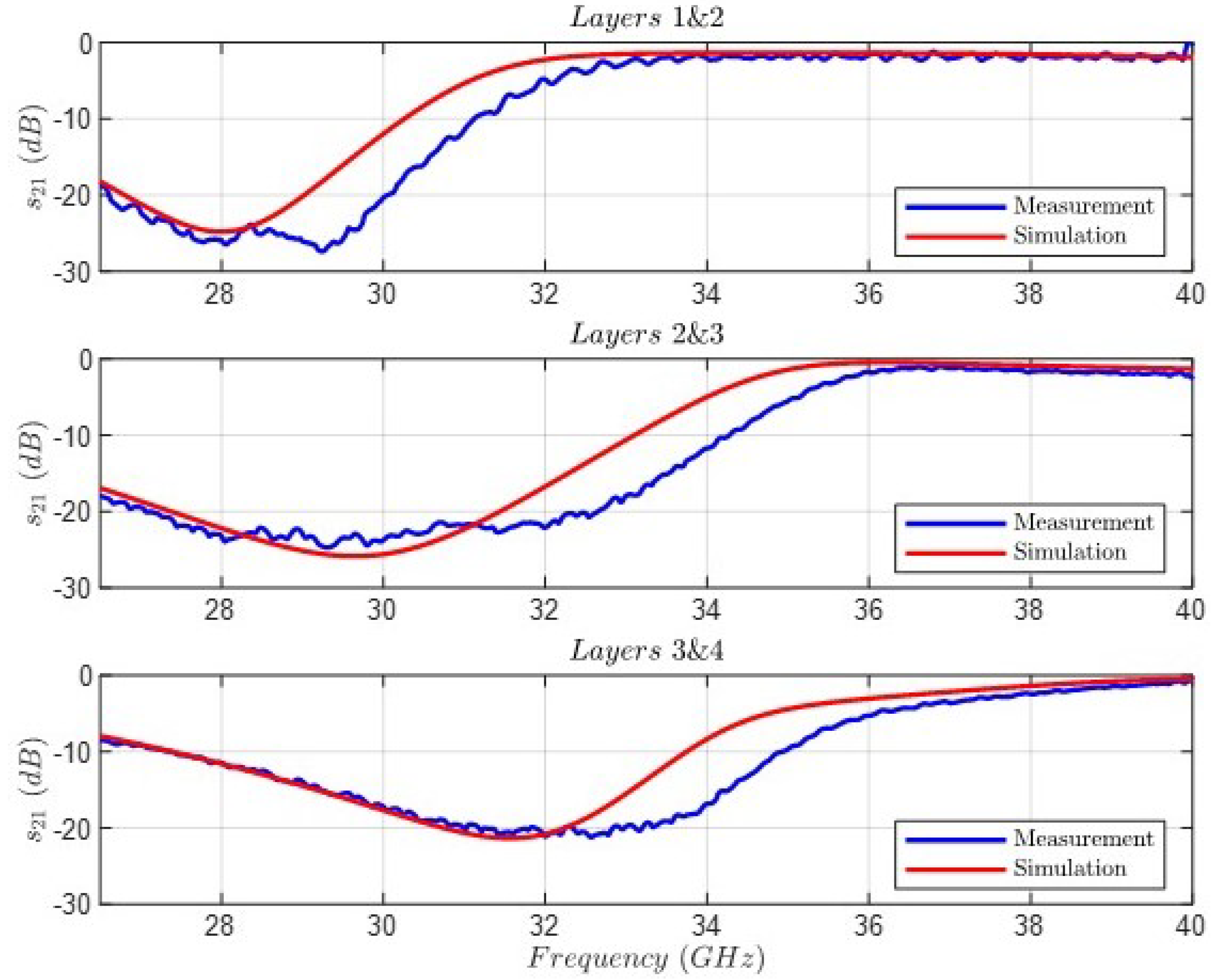
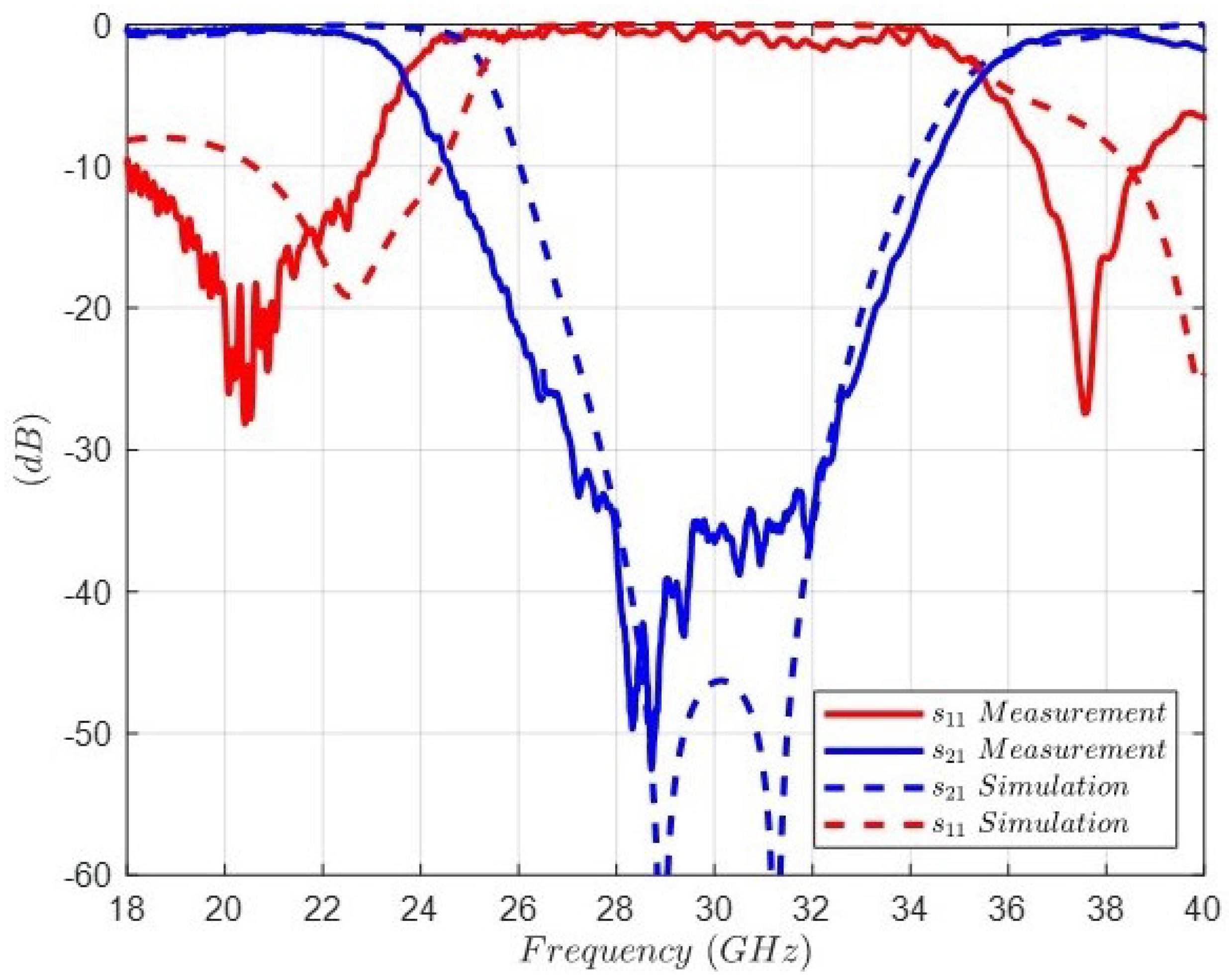
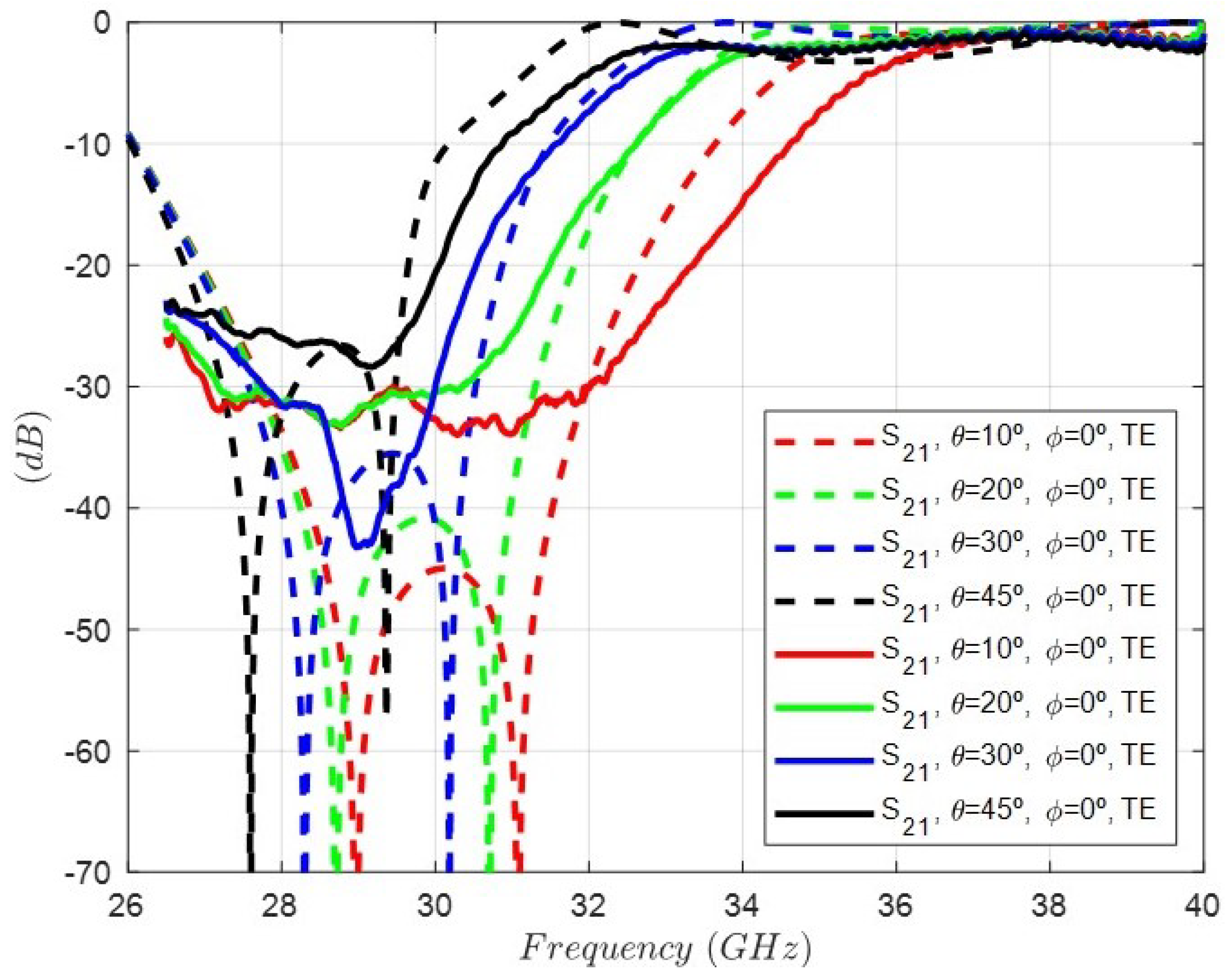

| Order N | 4 |
| Center Frequency | 30 GHz |
| Bandwidth BW | 3 GHz |
| Attenuation | 50 dB |
| Return Loss | 18 dB |
| Reference | Theoretical Synthesis | Transmission Zeros Control | Attenuation Level Control | Attenuation (dB) Sim./Meas. | Center Frequency (GHz) | Bandwidth (%) | Filter Order |
|---|---|---|---|---|---|---|---|
| [6]—2010 | NO | Heuristic | Heuristic | 10/8 | 10.25 | 44 | 2 |
| [20]—2016 | NO | Heuristic | Heuristic | 10/9 | 9.7 | 78 | 3 |
| [17]—2017 | NO | Heuristic | Heuristic | 30/29 | 13.75 | 55 | 2 |
| [11]—2018 | NO | Heuristic | Heuristic | 40/35 | 13 | 17 | 2 |
| [9]—2020 | NO | Heuristic | Heuristic | 10/- | 12 | 50 | 1 |
| [28]—2022 | NO | Heuristic | Heuristic | 10/10 | 27.2 | 27.6 | 2 |
| [29]—2022 | NO | Heuristic | Heuristic | 30/30 | 3.8 | 36 | 2 |
| [30]—2024 | NO | Heuristic | Heuristic | 10/10 | 3.96 | 40 | 1 |
| This work | YES | YES | YES | 48/35 | 30 | 10 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montejo-Garai, J.R.; Page, J.E.; Perez-Palomino, G.; Guirado, R. Band-Stop Frequency-Selective Surface (FSS) with Elliptic Response Designed by the Extracted Pole Technique. Sensors 2024, 24, 4452. https://doi.org/10.3390/s24144452
Montejo-Garai JR, Page JE, Perez-Palomino G, Guirado R. Band-Stop Frequency-Selective Surface (FSS) with Elliptic Response Designed by the Extracted Pole Technique. Sensors. 2024; 24(14):4452. https://doi.org/10.3390/s24144452
Chicago/Turabian StyleMontejo-Garai, José R., Juan E. Page, Gerardo Perez-Palomino, and Robert Guirado. 2024. "Band-Stop Frequency-Selective Surface (FSS) with Elliptic Response Designed by the Extracted Pole Technique" Sensors 24, no. 14: 4452. https://doi.org/10.3390/s24144452
APA StyleMontejo-Garai, J. R., Page, J. E., Perez-Palomino, G., & Guirado, R. (2024). Band-Stop Frequency-Selective Surface (FSS) with Elliptic Response Designed by the Extracted Pole Technique. Sensors, 24(14), 4452. https://doi.org/10.3390/s24144452






