A Remote Sensing Image Super-Resolution Reconstruction Model Combining Multiple Attention Mechanisms
Abstract
:1. Introduction
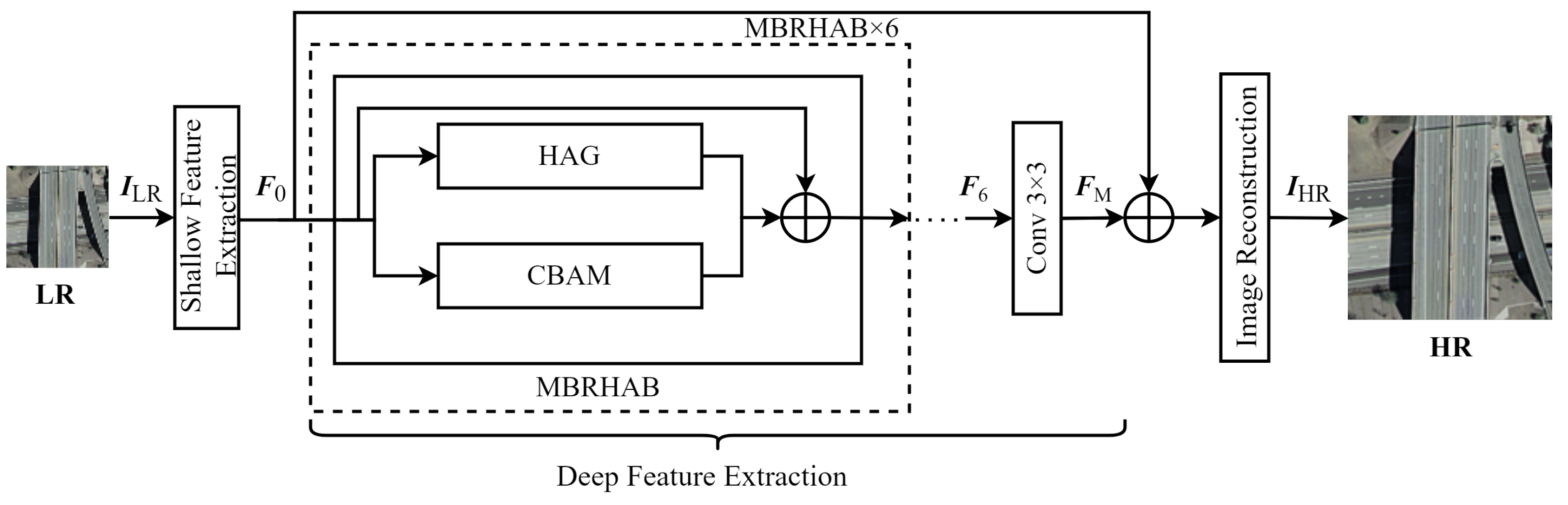
2. Model Architecture
2.1. Shallow Feature Extraction
2.2. Deep Feature Extraction
2.2.1. The Multi-Branch Residual Hybrid Attention Block (MBRHAB)
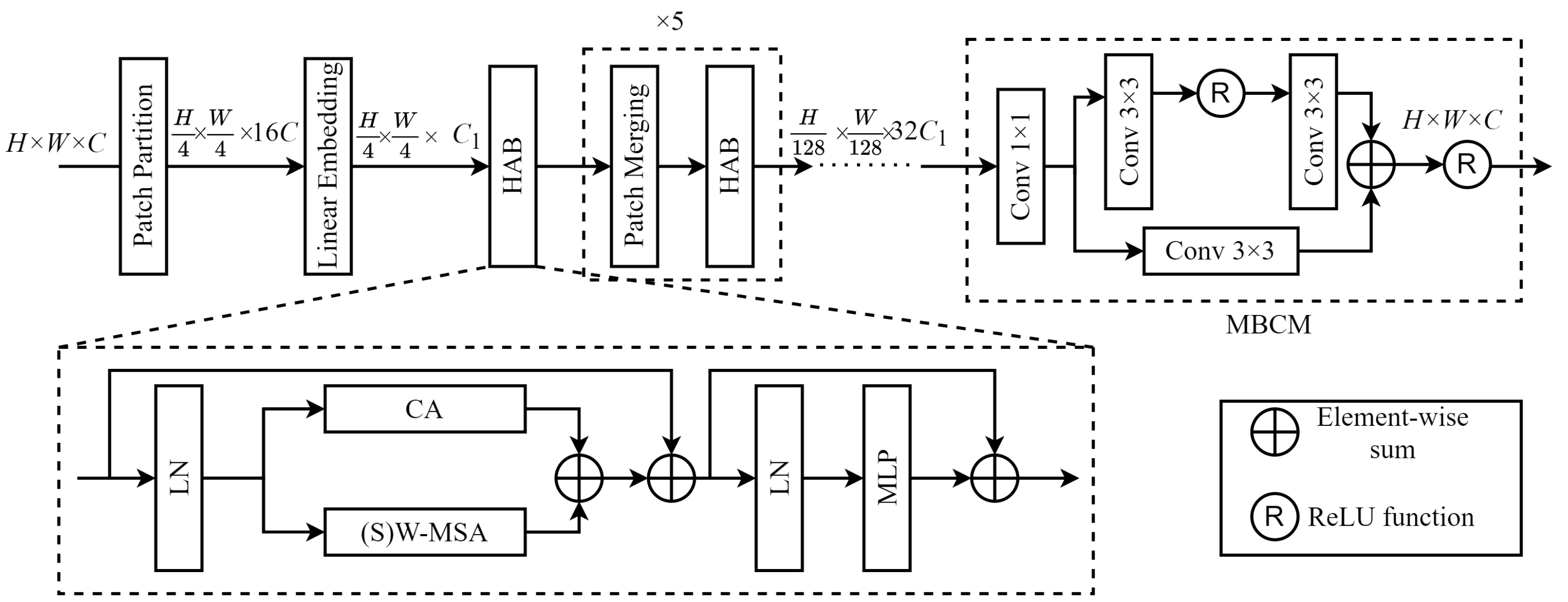
2.2.2. Hybrid Attention Group (HAG)
Window-Based Multi-Head Self-Attention
- The image is divided into uniformly sized windows through partitioning. Each window is then further subdivided into numerous patches of equal size.
- Within each window, a window-based MSA (W-MSA) step is applied to compute attention metrics among patches.
- Window shifting is then employed, thereby establishing a shift W-MSA (SW-MSA) to facilitate information exchange between the windows.
- Patch merging is applied after calculating attention values at specific scales. This involves combining smaller patches into larger ones and establishing a new window scale. Attention calculations are then repeated at the new scale to facilitate global modeling of image features across different hierarchical levels. The formula used for computing self-attention [17] can be expressed as follows:where Q, K, and V represent query, key, and value matrices, respectively; denotes the number of patches in a window; d is the dimension of the Q or K matrices; and B denotes learnable relative positional encoding.
Structure and Function of the HAG
- Patch Partitioning:Feature maps were first divided into patches of the same size, which were then grouped into the required window size. After shallow feature extraction, the feature map dimensions of were converted to after patch partitioning. An initial patch size of was employed, based on empirical results.
- Linear Embedding:Linear embedding transformed image dimensions after patch partitioning from to a value suitable for MSA (set to = 64 in this study).
- Hybrid Attention Block (HAB):Each HAB included W-MSA or SW-MSA (i.e., (S)W-MSA), CA, layer normalization (LN), and a multilayer perceptron (MLP). The parallel configuration of the (S)W-MSA and CA enabled the model to effectively capture long-range dependencies while simultaneously focusing on inter-channel feature correlations, thereby enhancing feature representation capabilities.
- (a)
- Taking X as input and using the HAB, combined with W-MSA, as a feature extraction unit. The output can then be described by the following expression:
- (b)
- Taking as input and using the HAB, combined with SW-MSA, as a feature extraction unit. The output can then be described by the following expression:where denotes layer normalization, is a multilayer perceptron, denotes channel attention, and and represent the W-MSA and SW-MSA operations, respectively. It should be noted the HAB itself does not change the size or dimensions of the image. However, after each HAB, the feature map length and width are reduced by half due to patch merging. The number of channels is also doubled and the image size becomes due to the HAB step.
- Patch Merging:The purpose of patch merging in the HAG is to construct a hierarchical framework, which allows each HAB to extract image features at various levels, effectively down-sampling the feature maps. This principle involves merging adjacent patches to form newly sized windows after computing attention values within the same scale windows. This process is then repeated in subsequent rounds of attention computation, enabling the acquisition of multi-scale features in remote sensing images. Figure 4 illustrates the patch merging process, in which a feature map of size is down-sampled by a factor of two after patch merging. In this process, patches of the same index are merged and then concatenated along the channel dimension. This changes the feature map dimensions to . A convolution was then used to reduce the number of channels to , resulting in a feature map of size .
- Multi-branch Convolutional Module (MBCM):A novel multi-branch convolutional module (MBCM) was included in the model to increase the size of the convolutional receptive field and integrate deep feature information extracted by the HAB. This enhancement aimed to improve feature representations for global information. The module simultaneously restored the feature map size to its original value of . The structure of the MBCM, which involved stacking convolutions of the same size but different depths across various branches, is depicted in the dashed box of the MBCM section in Figure 2. MBCM is first a convolution that is used to recover the channel dimension of the feature. Then the upper branch in the MBCM consisted of two consecutive convolutional layers with a ReLU activation function between them. The lower branch consisted of a single convolutional layer. Elements from both branches were added together and passed through a ReLU activation function before outputting the final feature information. The design of these two branches was intended to enrich the expression of feature information by using convolutional receptive fields of different sizes. Specifically, the upper branch employed two convolution layers instead of a single layer. This choice not only increased model depth and reduced the number of parameters, it also enhanced the model’s nonlinear expressive capacity by using nonlinear activation functions in the convolution layers.
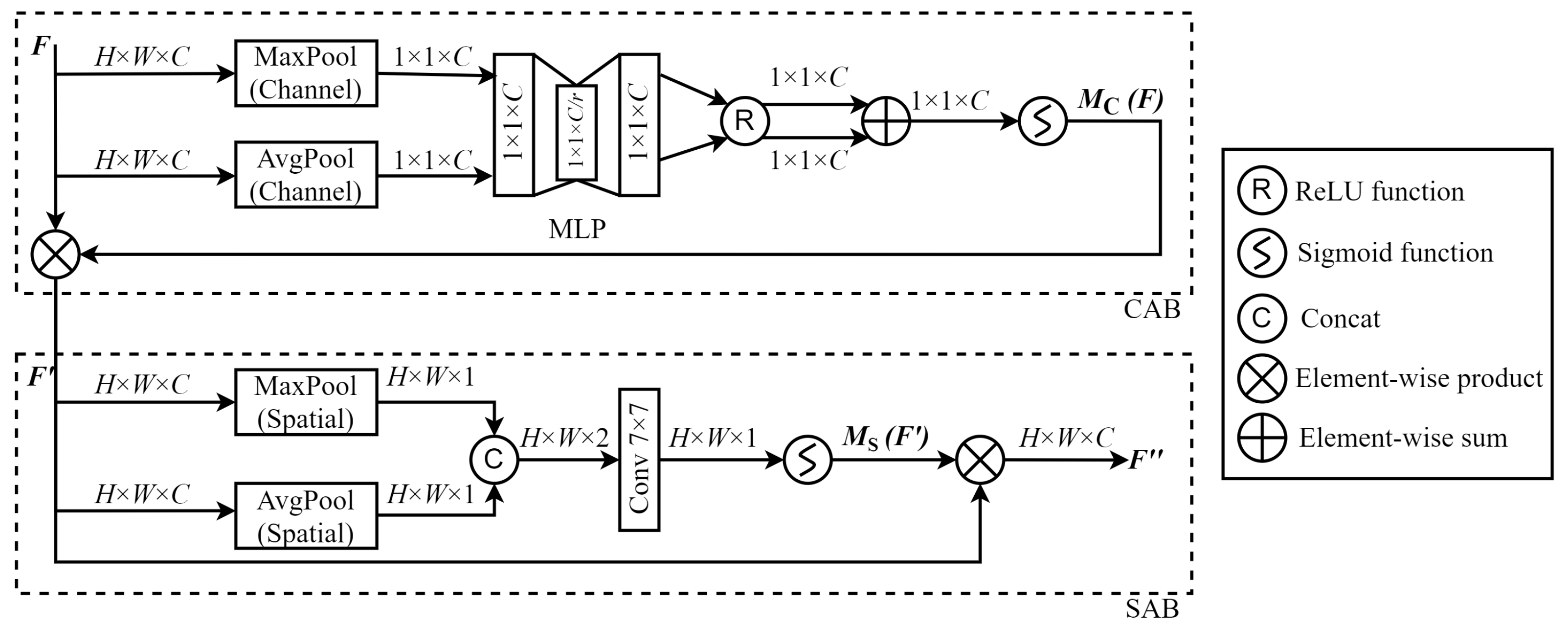
2.2.3. Convolutional Block Attention Module (CBAM)
- Channel Attention Block (CAB):The CAB processes channel dimensions and compresses feature maps in the spatial dimension, such that features in different channels are assigned various importance weights. This process can be described by the following steps.
- (a)
- A feature map F of size is processed through both channel max pooling and average pooling to obtain two feature maps of size .
- (b)
- These two feature maps are processed separately using a MLP. After processing, the maps are activated by a ReLU function and then combined by addition, resulting in a feature map of dimensions .
- (c)
- is the result of CA obtained using a sigmoid activation function. This result is then combined with the input feature F to produce , while the feature size remains unchanged .
- Spatial Attention Block (SAB):After acquiring importance differences between various channels, the feature map is then compressed in the channel dimension by the SAB, precisely extracting features at each spatial location. This process can be described by the following steps.
- (a)
- Spatial average pooling and maximum pooling are performed in the channel dimension for each feature map that has passed through CAB, producing two feature maps.
- (b)
- These maps are then concatenated to form a new feature map of size , and the combined map is then processed using a convolution to produce a map of dimensions .
- (c)
- is the result of SA obtained through the sigmoid activation function. This result is multiplied by the input feature to obtain , and the feature sizes of and are still .
2.3. Image Reconstruction
3. Experiments
3.1. Datasets for Experiments
3.2. Experimental Setup
3.3. Experimental Contents
4. Results
4.1. Objective Evaluation Metrics
4.1.1. Ablation Experiments
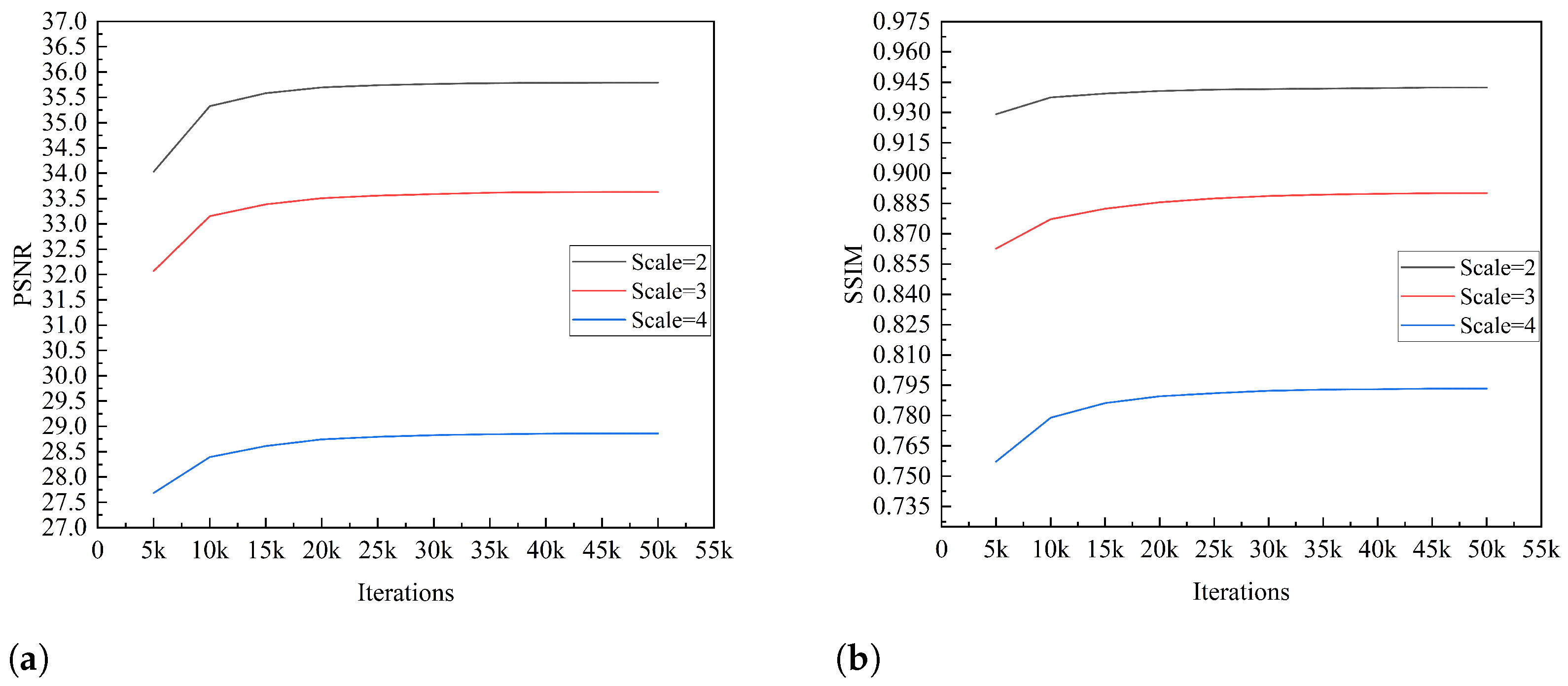
4.1.2. Model Feasibility Assessment
4.1.3. Comparative Experiments
4.1.4. Test Experiments for Different Categories
4.2. Subjective Visualization
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, P.; Bayram, B.; Sertel, E. A comprehensive review on deep learning based remote sensing image super-resolution methods. Earth-Sci. Rev. 2022, 232, 104–110. [Google Scholar] [CrossRef]
- Dixit, M.; Yadav, R.N. A Review of Single Image Super Resolution Techniques using Convolutional Neural Networks. Multimed. Tools Appl. 2024, 83, 29741–29775. [Google Scholar] [CrossRef]
- Yu, W.; Liang, X. A review of research on super-resolution image reconstruction based on deep learning. In Proceedings of the 8th International Conference on Intelligent Informatics and Biomedical Sciences (ICIIBMS), Okinawa, Japan, 23–25 November 2023. [Google Scholar]
- Yang, W.; Zhang, X.; Tian, Y.; Wang, W.; Xue, J.; Liao, Q. Deep learning for single image super-resolution: A brief review. IEEE Trans. Multimed 2019, 21, 3106–3121. [Google Scholar] [CrossRef]
- Chen, H.; He, X.; Qing, L.; Wang, W.; Wu, Y.; Ren, C.; Sheriff, R.E.; Zhu, C. Real-world single image super-resolution: A brief review. Inf. Fusion 2022, 79, 124–145. [Google Scholar] [CrossRef]
- Liebel, L.; Körner, M. Single-image super resolution for multispectral remote sensing data using convolutional neural networks. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 883–890. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the 13th European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- Lei, S.; Shi, Z.; Zou, Z. Super-resolution for remote sensing images via local–Global combined network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1243–1247. [Google Scholar] [CrossRef]
- Xie, H.; Jiang, H.; Liu, X.; Li, G.; Yang, H. Super Resolution for Remote Sensing Images via Improved Residual Network. In Proceedings of the 5th International Conference on Mechanical, Control and Computer Engineering (ICMCCE), Harbin, China, 25–27 December 2020. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27, 1–9. [Google Scholar]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Chen, C.L. Esrgan: Enhanced super-resolution generative adversarial networks. In Proceedings of the 15th European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Wang, X.; Xie, L.; Dong, C.; Shan, Y. Real-esrgan: Training real-world blind super-resolution with pure synthetic data. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021. [Google Scholar]
- Guo, D.; Xia, Y.; Xu, L.; Li, W.; Luo, X. Remote sensing image super-resolution using cascade generative adversarial nets. Neurocomputing 2021, 443, 117–130. [Google Scholar] [CrossRef]
- Jiang, K.; Wang, Z.; Yi, P.; Wang, G.; Lu, T.; Jiang, J. Edge-enhanced GAN for remote sensing image superresolution. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5799–5812. [Google Scholar] [CrossRef]
- Sustika, R.; Suksmono, A.B.; Danudirdjo, D.; Wikantika, K. Generative adversarial network with residual dense generator for remote sensing image super resolution. In Proceedings of the 2020 International Conference on Radar, Antenna, Microwave, Electronics, and Telecommunications (ICRAMET), Tangerang, Indonesia, 18–20 November 2020. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the 15th European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Dong, X.; Sun, X.; Jia, X.; Xi, Z.; Gao, L.; Zhang, B. Remote sensing image super-resolution using novel dense-sampling networks. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1618–1633. [Google Scholar] [CrossRef]
- Wang, P.; Bayram, B.; Sertel, E. Super-resolution of remotely sensed data using channel attention based deep learning approach. Int. J. Remote Sens. 2021, 42, 6048–6065. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the 15th European conference on computer vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Cheng, G.; Han, J.; Lu, X. Remote sensing image scene classification: Benchmark and state of the art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Zhou, W.; Newsam, S.; Li, C.; Shao, Z. PatternNet: A benchmark dataset for performance evaluation of remote sensing image retrieval. ISPRS J. Photogramm. Remote Sens. 2018, 145, 197–209. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S. Bag-of-visual-words and spatial extensions for land-use classification. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 3–5 November 20.
- Parsanta, P.; Virparia, P.V. A review: Image interpolation techniques for image scaling. Int. J. Innov. Res. Comput. Commun. Eng. 2014, 2, 7409–7414. [Google Scholar] [CrossRef]
- Dumitrescu, D.; Boiangiu, C.-A. A study of image upsampling and downsampling filters. Computers 2019, 8, 30. [Google Scholar] [CrossRef]
- Sara, U.; Akter, M.; Uddin, M.S. Image quality assessment through FSIM, SSIM, MSE and PSNR—A comparative study. J. Comput. Commun. 2019, 7, 8–18. [Google Scholar] [CrossRef]






| Baseline | MBCM | CBAM | Scale | PSNR/dB | SSIM |
|---|---|---|---|---|---|
| 1 | 0 | 0 | ×2 | 35.12 | 0.9306 |
| 1 | 1 | 0 | ×2 | 35.30 | 0.9336 |
| 1 | 1 | 1 | ×2 | 35.65 | 0.9388 |
| 1 | 0 | 0 | ×3 | 32.47 | 0.8755 |
| 1 | 1 | 0 | ×3 | 32.81 | 0.8802 |
| 1 | 1 | 1 | ×3 | 33.38 | 0.8860 |
| 1 | 0 | 0 | ×4 | 27.30 | 0.7729 |
| 1 | 1 | 0 | ×4 | 27.78 | 0.7780 |
| 1 | 1 | 1 | ×4 | 28.40 | 0.7850 |
| Model | Scale | Scale | Scale | |||
|---|---|---|---|---|---|---|
| PSNR/dB | SSIM | PSNR/dB | SSIM | PSNR/dB | SSIM | |
| Bicubic | 33.26 | 0.8677 | 32.23 | 0.8416 | 27.05 | 0.7708 |
| SRCNN | 34.50 | 0.9045 | 32.46 | 0.8578 | 27.47 | 0.7735 |
| ESRGAN | 34.83 | 0.9158 | 32.54 | 0.8627 | 27.58 | 0.7744 |
| Real-ESRGAN | 34.92 | 0.9217 | 32.70 | 0.8694 | 27.77 | 0.7772 |
| IRN | 35.21 | 0.9302 | 32.89 | 0.8742 | 27.93 | 0.7789 |
| DSSR | 35.48 | 0.9341 | 33.11 | 0.8809 | 28.12 | 0.7821 |
| Ours | 35.65 | 0.9388 | 33.38 | 0.8860 | 28.40 | 0.7850 |
| Category | Scale | Scale | Scale | |||
|---|---|---|---|---|---|---|
| PSNR/dB | SSIM | PSNR/dB | SSIM | PSNR/dB | SSIM | |
| agricultural | 36.9389 | 0.8897 | 35.1506 | 0.8141 | 30.1999 | 0.6503 |
| airplane | 36.6847 | 0.9419 | 34.3808 | 0.8925 | 28.6323 | 0.8104 |
| baseball-diamond | 41.1253 | 0.9638 | 39.0854 | 0.9376 | 33.2661 | 0.8575 |
| beach | 41.2185 | 0.9784 | 39.2264 | 0.9569 | 33.4048 | 0.8919 |
| buildings | 35.4007 | 0.9533 | 32.8697 | 0.9091 | 28.3992 | 0.8260 |
| chaparral | 33.4573 | 0.9252 | 31.2497 | 0.8584 | 26.5914 | 0.7333 |
| dense-residential | 37.7685 | 0.9679 | 34.4910 | 0.9364 | 31.5699 | 0.8564 |
| forest | 33.2402 | 0.9110 | 31.1615 | 0.8005 | 26.0286 | 0.6979 |
| freeway | 36.7079 | 0.9393 | 33.9108 | 0.8806 | 28.9242 | 0.8204 |
| golf-course | 38.7320 | 0.9494 | 37.8070 | 0.9226 | 32.1114 | 0.8522 |
| harbor | 32.6609 | 0.9746 | 30.3614 | 0.9357 | 24.5044 | 0.8249 |
| intersection | 33.5985 | 0.9410 | 31.3754 | 0.8700 | 25.8833 | 0.7562 |
| medium-density-residential | 31.2835 | 0.8682 | 28.9026 | 0.7825 | 23.5688 | 0.6322 |
| mobile-home-park | 36.8960 | 0.9759 | 34.0592 | 0.9510 | 29.5797 | 0.8603 |
| overpass | 32.8210 | 0.9316 | 30.7549 | 0.8670 | 24.6546 | 0.7451 |
| parking-lot | 32.1953 | 0.9514 | 29.5809 | 0.8991 | 24.4980 | 0.7826 |
| river | 35.4638 | 0.9332 | 33.1560 | 0.8686 | 28.4227 | 0.7588 |
| runway | 38.5161 | 0.9453 | 37.0427 | 0.9063 | 32.6700 | 0.8232 |
| sparse-residential | 33.5898 | 0.8915 | 31.3646 | 0.8526 | 26.8750 | 0.7045 |
| storage-tanks | 35.1514 | 0.9444 | 32.4735 | 0.8954 | 28.3216 | 0.8199 |
| tennis-courts | 35.2662 | 0.9386 | 32.6238 | 0.8695 | 28.3791 | 0.7821 |
| Average | 35.6532 | 0.9388 | 33.3823 | 0.8860 | 28.4041 | 0.7850 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Guo, T.; Wang, C. A Remote Sensing Image Super-Resolution Reconstruction Model Combining Multiple Attention Mechanisms. Sensors 2024, 24, 4492. https://doi.org/10.3390/s24144492
Xu Y, Guo T, Wang C. A Remote Sensing Image Super-Resolution Reconstruction Model Combining Multiple Attention Mechanisms. Sensors. 2024; 24(14):4492. https://doi.org/10.3390/s24144492
Chicago/Turabian StyleXu, Yamei, Tianbao Guo, and Chanfei Wang. 2024. "A Remote Sensing Image Super-Resolution Reconstruction Model Combining Multiple Attention Mechanisms" Sensors 24, no. 14: 4492. https://doi.org/10.3390/s24144492
APA StyleXu, Y., Guo, T., & Wang, C. (2024). A Remote Sensing Image Super-Resolution Reconstruction Model Combining Multiple Attention Mechanisms. Sensors, 24(14), 4492. https://doi.org/10.3390/s24144492






