Phase Noise Compensation Algorithm for Space-Borne Azimuth Multi-Channel SAR
Abstract
1. Introduction
2. Space-Borne Azimuth Multi-Channel SAR Imaging Principle
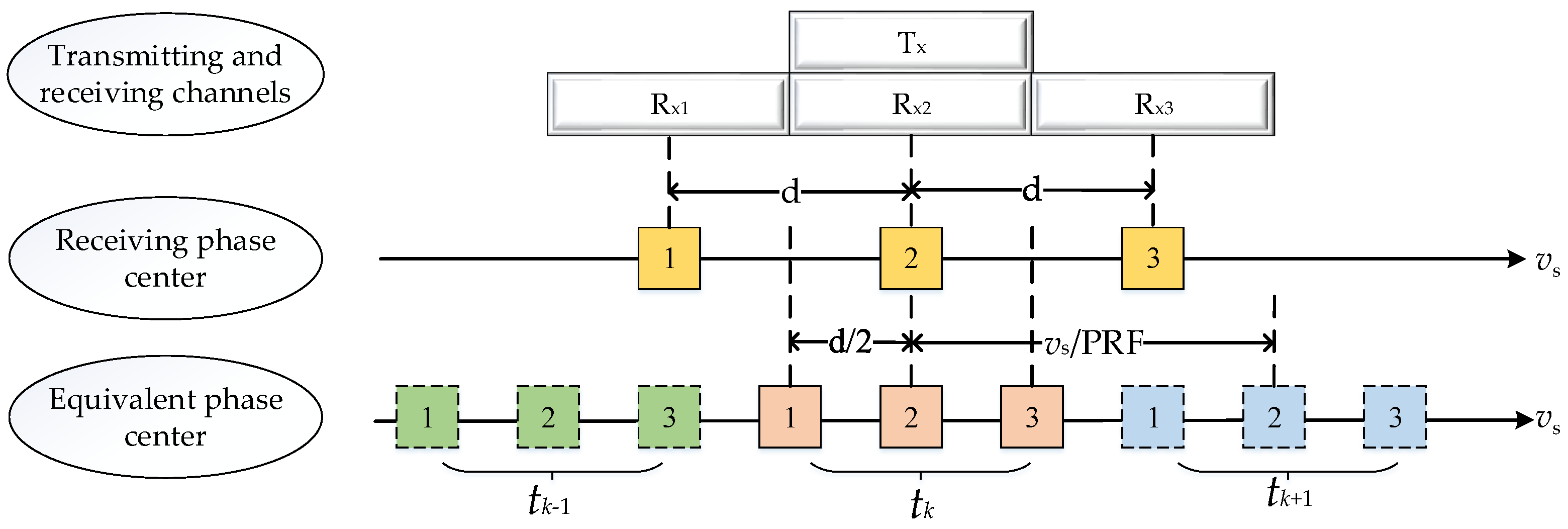
2.1. Imaging Geometry Model
2.2. Echo Signal Model
3. Doppler Aliasing and Phase Noise Effects
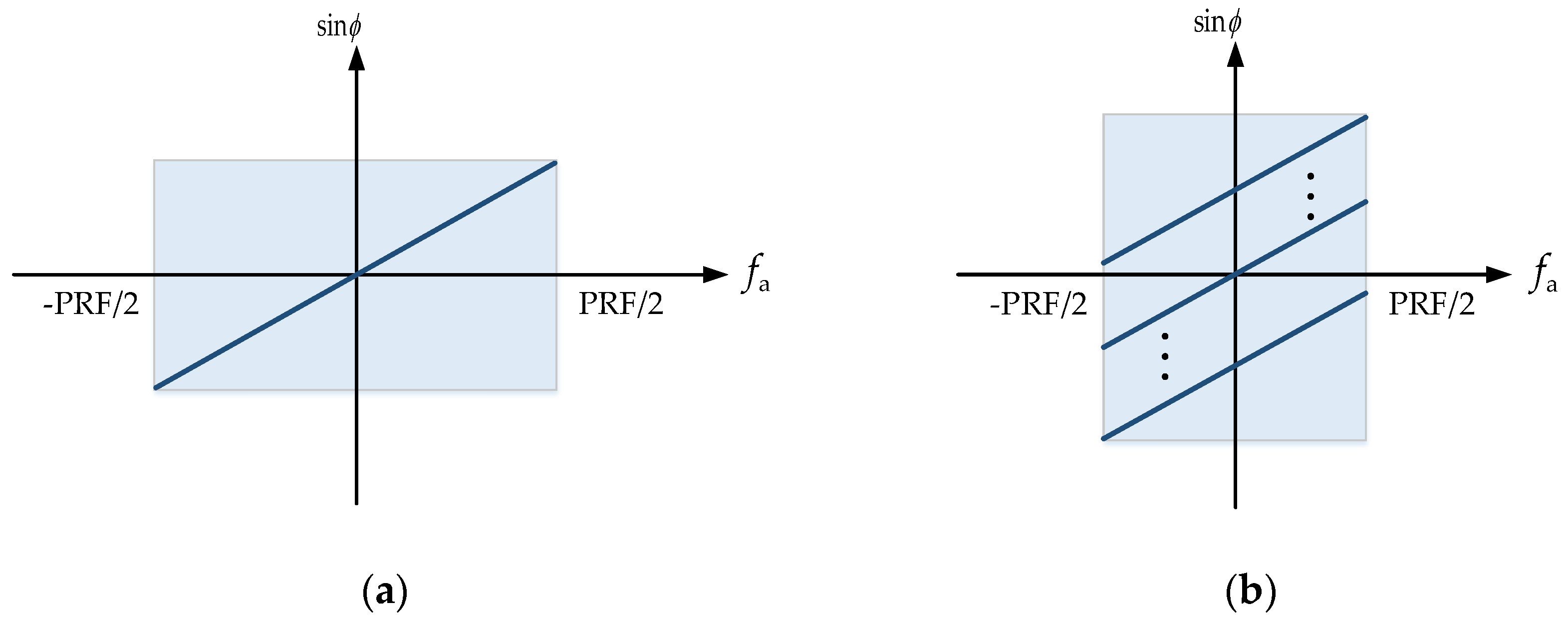
3.1. Doppler Aliasing
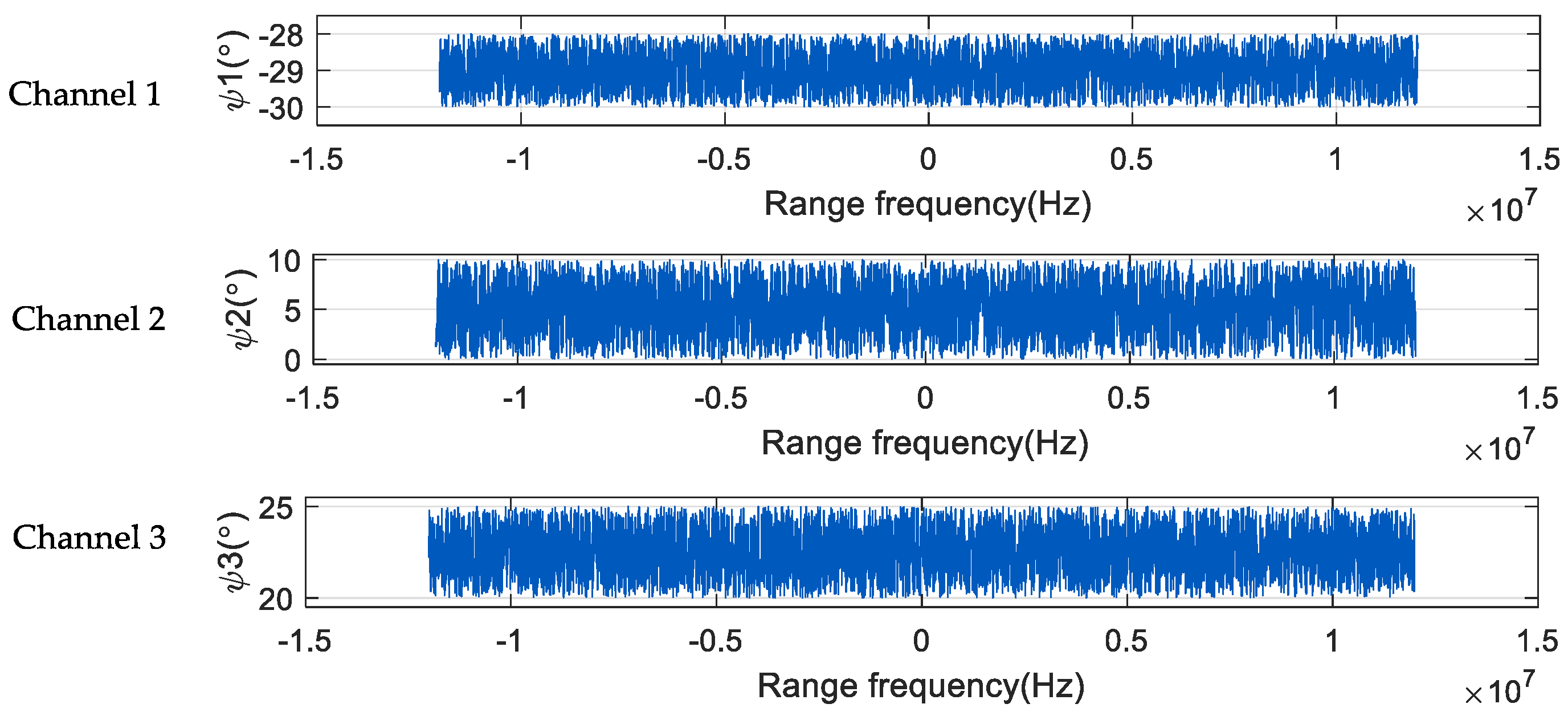
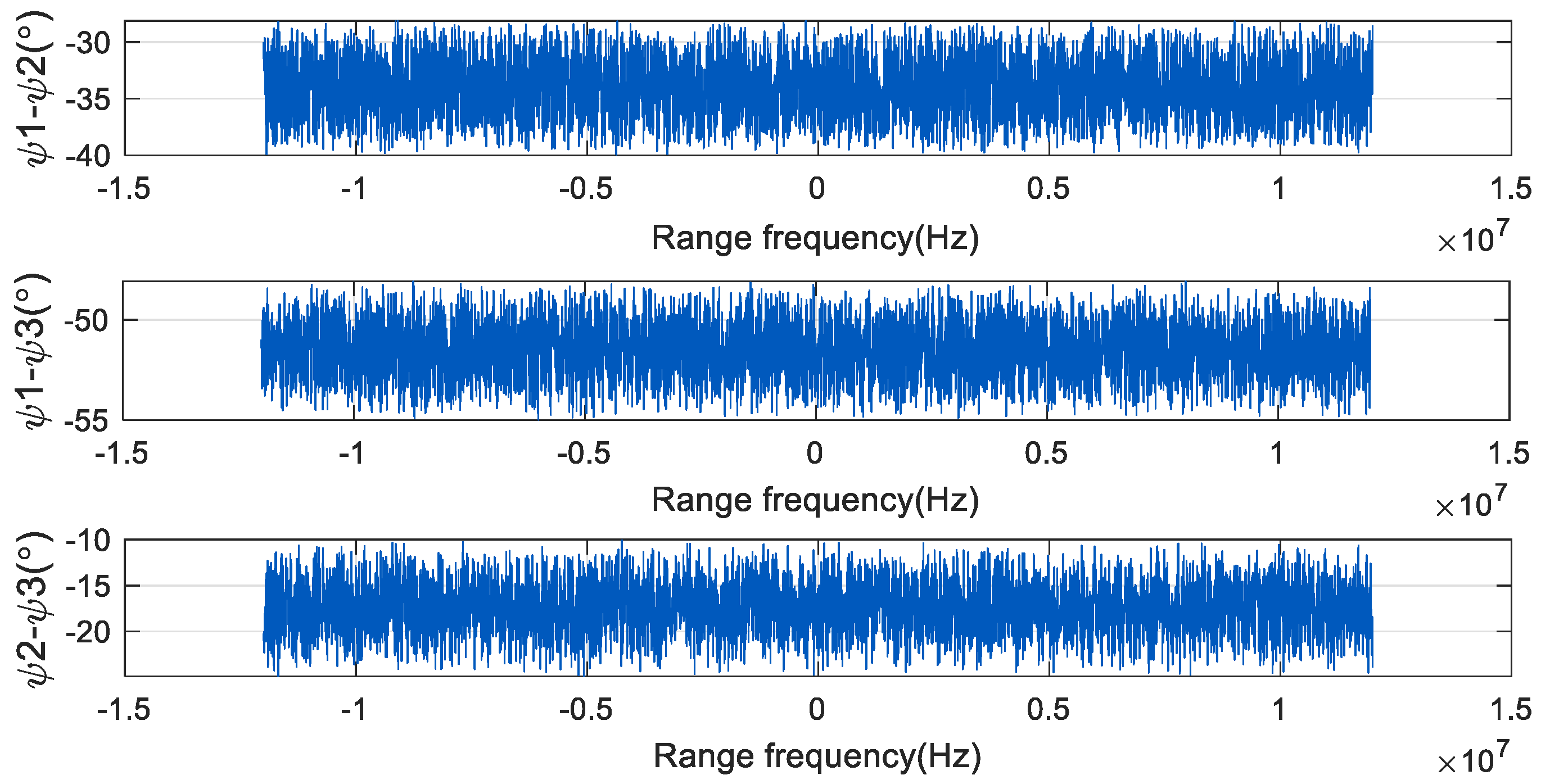
3.2. Phase-Noise Characteristics
3.3. Phase Noise Effect
4. Phase Noise Compensation Method
4.1. Phase Noise Compensation Idea
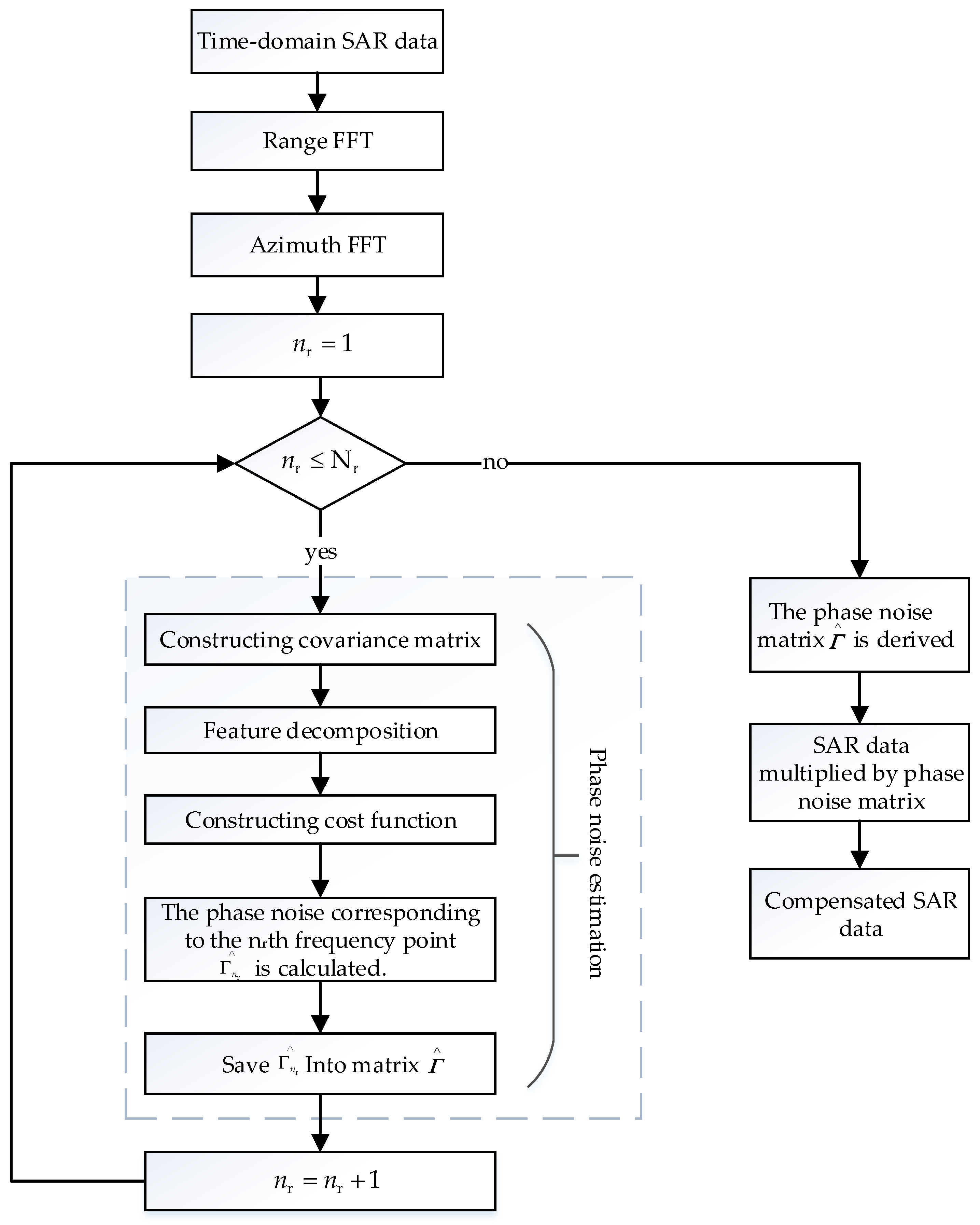
4.2. Phase-Noise-Compensation Steps
- The acquired 2D time-domain echo signal of each channel of SAR is transformed into the 2D frequency domain;
- 2.
- The covariance matrix is constructed based on the 2D frequency-domain signal and the signal subspace and noise subspace matrix are obtained by feature decomposition.
- 3.
- To determine the phase-noise estimate corresponding to each frequency point of each channel, the cost function is created.
- 4.
- Random phase noise compensation.
4.3. Phase Noise Compensation Algorithm Flow
4.4. Comparison of Computational Complexity
5. Simulation Verification
5.1. Simulation Environment Settings
- Hardware environment
- Software selection
- Phase-noise setting
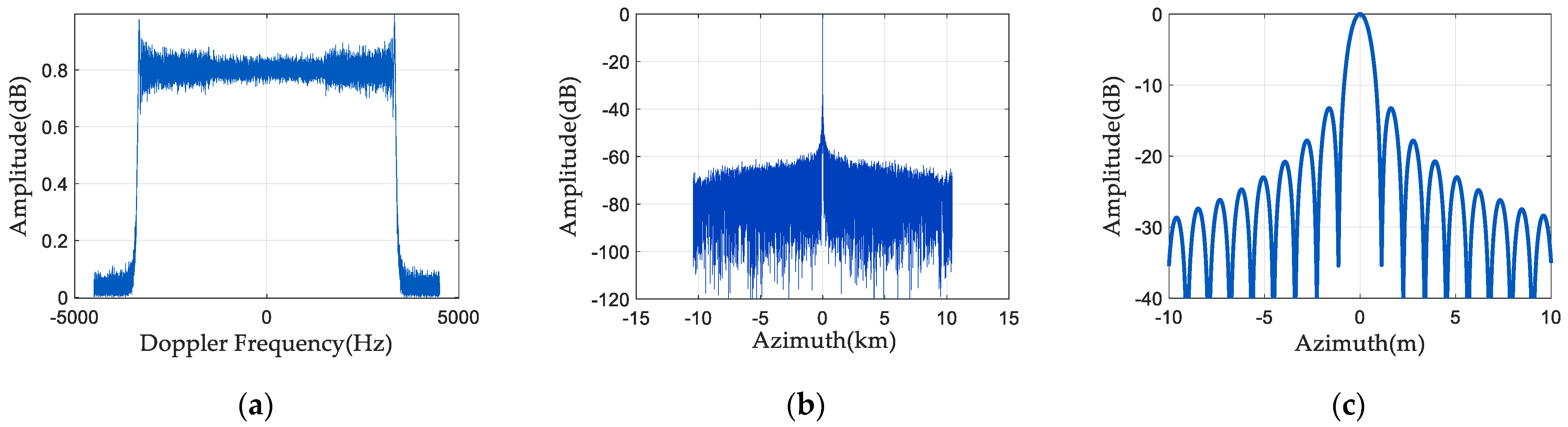
5.2. One-Dimensional Point Target Simulation
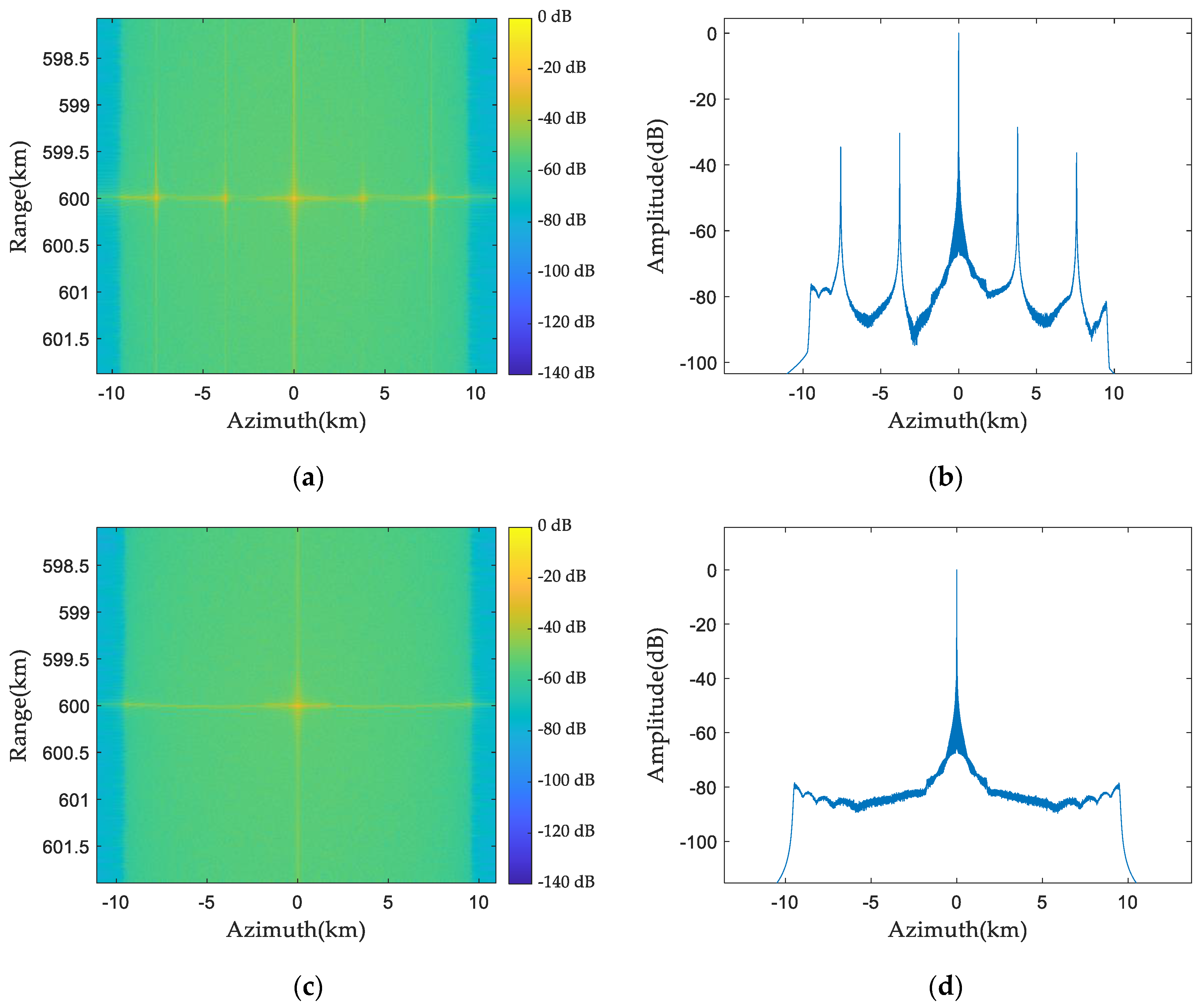
5.3. Two-Dimensional Point Target Simulation
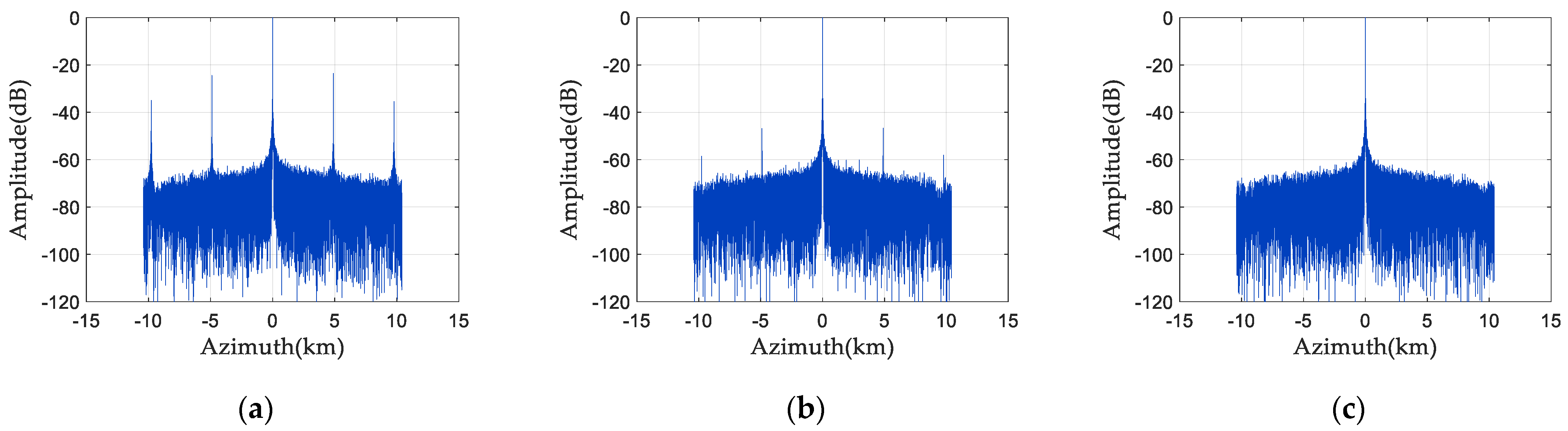
5.4. Comparison with Existing Methods
5.5. Distributed Target Simulation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, L. Research on Multi-Channel High-Resolution and Wide-Swath SAR Imaging and Motion Error Compensation Technology. Ph.D. Thesis, University of Electronic Science and Technology of China, Chengdu, China, June 2022. [Google Scholar]
- Liu, B.; He, Y. Improved DBF Algorithm for Multichannel High-Resolution Wide-Swath SAR. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1209–1225. [Google Scholar] [CrossRef]
- Almeida, F.; Younis, M.; Prats-Iraola, P.; Rodriguez-Cassola, M.; Krieger, G.; Moreira, A. Slow pulse repetition interval variation for high-resolution wide-swath SAR imaging. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5665–5686. [Google Scholar] [CrossRef]
- Zhang, L. Azimuth Multichannel High-Resolution and Wide-Swath SAR Imaging Processing Technique. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, May 2018. [Google Scholar]
- Zuo, S. Study on the Improved Methods for the Multichannel SAR Imaging. Ph.D. Thesis, Xi’an University of Electronic Technology, Xi’an, China, 2017. [Google Scholar]
- Zhang, L.; Gao, Y.; Liu, X. Robust channel phase error calibration algorithm for multichannel high-resolution and wide-swath SAR imaging. IEEE Geosci. Remote Sens. Lett. 2017, 14, 649–653. [Google Scholar] [CrossRef]
- Xu, H.; Liu, A.; Xia, X. Analysis of the effect of channel error on azimuth multi-channel SAR. Electron. Meas. Technol. 2017, 40, 152–156. [Google Scholar]
- Zhou, Y.; Wang, R.; Deng, Y.; Yu, W.; Fan, H.; Liang, D.; Zhang, Q. A novel approach to Doppler centroid and channel errors estimation in azimuth multi-channel SAR. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8430–8444. [Google Scholar] [CrossRef]
- Loria, E.; Prager, S.; Seker, I.; Ahmed, R.; Hawkins, B.; Lavalle, M. Modeling the effects of oscillator phase noise and synchronization on multistatic SAR tomography. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5204212. [Google Scholar] [CrossRef]
- Guo, X.; Gao, Y.; Wang, K.; Liu, X. Improved channel error calibration algorithm for azimuth multichannel SAR systems. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1022–1026. [Google Scholar] [CrossRef]
- Liang, D.; Wang, R.; Deng, Y.; Fan, H.; Zhang, H.; Zhang, L.; Wang, W.; Zhou, Y. A Channel Calibration Method Based on Weighted Backprojection Algorithm for Multichannel SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1254–1258. [Google Scholar] [CrossRef]
- Lu, H.; Zhang, H.; Fan, H.; Liu, D.; Wang, J.; Wan, X.; Zhao, L.; Deng, Y.; Zhao, F.; Wang, R. Forest height retrieval using P-band airborne multi-baseline SAR data: A novel phase compensation method. ISPRS J. Photogramm. Remote Sens. 2021, 175, 99–118. [Google Scholar] [CrossRef]
- Huang, H.; Huang, P.; Liu, X.; Xia, X.; Deng, Y.; Fan, H.; Liao, G. A novel channel errors calibration algorithm for multichannel high-resolution and wide-swath SAR imaging. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5201619. [Google Scholar] [CrossRef]
- Cai, Y.; Deng, Y.; Zhang, H.; Wang, R.; Wu, Y.; Cheng, S. An image-domain least L 1-norm method for channel error effect analysis and calibration of azimuth multi-channel SAR. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5222914. [Google Scholar] [CrossRef]
- Zhao, X.; Deng, Y.; Zhang, H.; Liu, X. A channel imbalance calibration scheme with distributed targets for circular quad-polarization SAR with reciprocal crosstalk. Remote Sens. 2023, 15, 1365. [Google Scholar] [CrossRef]
- Ding, Z.; Zheng, P.; Zhang, T.; Li, H.; Li, Z.; Long, T.; Zeng, T. Spaceborne multichannel SAR imaging algorithm for maritime moving targets. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5204815. [Google Scholar] [CrossRef]
- Cai, Y.; Lu, P.; Li, B.; Li, J.; Chen, Y.; Wang, Y.; Nan, Y.; Wang, R.; Wu, Y. An efficient phase error calibration method for azimuth multichannel SAR based on least spectrum difference. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5207213. [Google Scholar] [CrossRef]
- Bordbari, R.; Maghsoudi, Y. A new target detector based on subspace projections using polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2018, 57, 3025–3039. [Google Scholar] [CrossRef]
- Liang, Z.; Fu, X.; Lv, X. A Novel Channel Inconsistency Calibration Algorithm for Azimuth Multichannel SAR Based on Fourth-Order Cumulant. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 5561–5577. [Google Scholar] [CrossRef]
- Zuo, S.; Sun, G.; Xing, M. Improved channel error calibration method for the azimuth multichannel SAR. J. Xidian Univ. 2017, 44, 13–18. [Google Scholar]







| Parameter | Symbol | Value (Unit) |
|---|---|---|
| Carrier frequency | 9.6 (GHz) | |
| Signal bandwidth | 20 (MHz) | |
| Doppler bandwidth | 6245.4 (Hz) | |
| Pulse-repetition frequency | 3100 (Hz) | |
| Number of channels | K | 3 |
| Pulse width | 24 () | |
| Adjacent channel spacing | 1.65 (m) | |
| Number of azimuth samples | 15,650 | |
| Number of range samples | 6000 |
| Phase Noise Range | Before Compensation | The Existing Method | The Proposed Method |
|---|---|---|---|
| Channel 1: (−20°, −10°) Channel 3: (5°, 8°) | −24.48 dB | −47.27 dB | −66.89 dB |
| −35.02 dB | −58.54 dB | −79.77 dB | |
| Channel 1: (0°, 3°) Channel 3: (−12°, −5°) | −29.98 dB | −44.36 dB | −70.95 dB |
| −41.75 dB | −55.36 dB | −73.97 dB | |
| Channel 1: (−32°, −28°) Channel 3: (−30°, −25°) | −19.61 dB | −35.50 dB | −76.38 dB |
| −36.00 dB | −46.91 dB | −77.81 dB | |
| Channel 1: (15°, 28°) Channel 3: (−3°, 12°) | −23.45 dB | −36.62 dB | −64.92 dB |
| −36.12 dB | −52.12 dB | −77.81 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, L.; Xu, W.; Huang, P.; Tan, W.; Qi, Y.; Chen, Y.; Gao, Z. Phase Noise Compensation Algorithm for Space-Borne Azimuth Multi-Channel SAR. Sensors 2024, 24, 4494. https://doi.org/10.3390/s24144494
Bai L, Xu W, Huang P, Tan W, Qi Y, Chen Y, Gao Z. Phase Noise Compensation Algorithm for Space-Borne Azimuth Multi-Channel SAR. Sensors. 2024; 24(14):4494. https://doi.org/10.3390/s24144494
Chicago/Turabian StyleBai, Lu, Wei Xu, Pingping Huang, Weixian Tan, Yaolong Qi, Yuejuan Chen, and Zhiqi Gao. 2024. "Phase Noise Compensation Algorithm for Space-Borne Azimuth Multi-Channel SAR" Sensors 24, no. 14: 4494. https://doi.org/10.3390/s24144494
APA StyleBai, L., Xu, W., Huang, P., Tan, W., Qi, Y., Chen, Y., & Gao, Z. (2024). Phase Noise Compensation Algorithm for Space-Borne Azimuth Multi-Channel SAR. Sensors, 24(14), 4494. https://doi.org/10.3390/s24144494






