A Method for the Spatial Interpolation of EEG Signals Based on the Bidirectional Long Short-Term Memory Network
Abstract
1. Introduction
2. Materials and Methods
2.1. Interpolation Principle
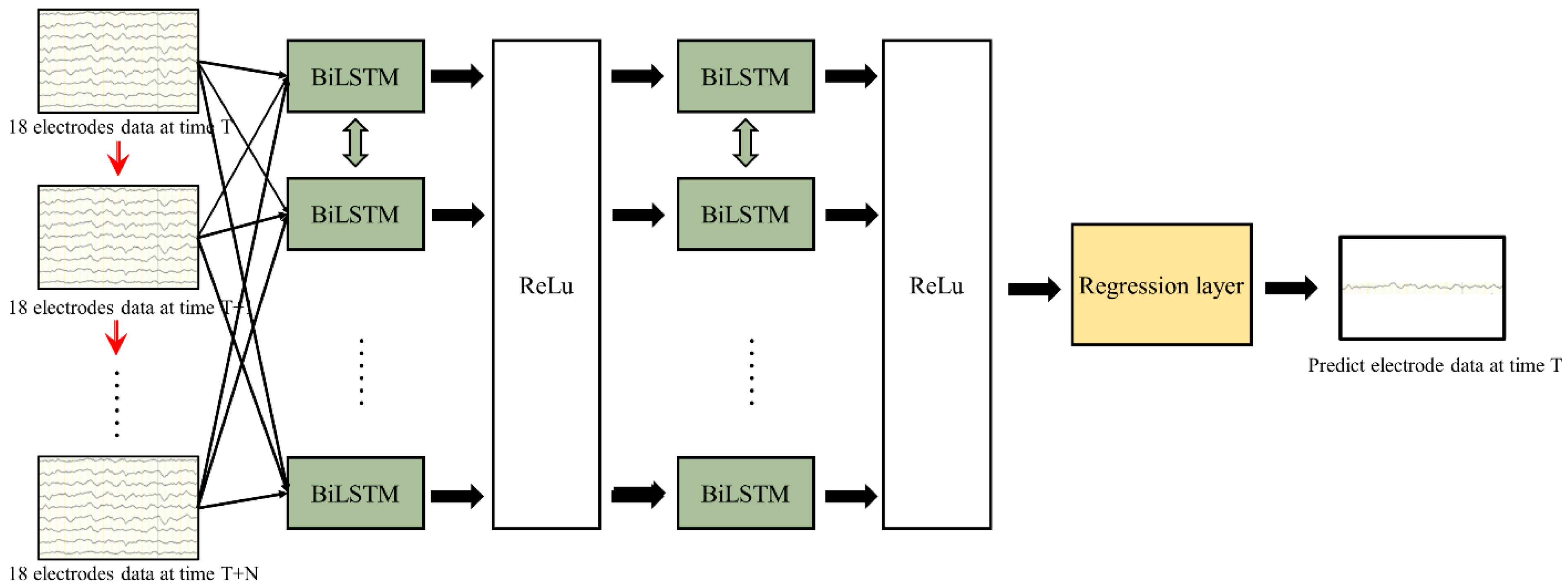
2.2. BiLSTM
- (1)
- Initially, we partitioned the EEG data into two feature dimensions: the temporal and spatial dimensions. The spatial dimension was segmented into distinct electrode data, while the temporal dimension was organized into different time points.
- (2)
- Spatial information was aggregated into comprehensive features, denoted as xt, enabling the processing of multiple electrode data with a single-time input.
- (3)
- The input data were sequenced chronologically along the time dimension (t/t + 1/t + 2), with each moment’s data features being multidimensional and inclusive of multiple electrode data.
2.3. Tools and Parameters
- (1)
- Batch Size: The batch size is a hyperparameter in deep learning that represents the number of samples processed in forward and backward propagation in the BiLSTM algorithm. Its size determines the generalization ability and training stability of the model, as well as the memory consumption requirement. Considering the sensitivity of EEG data processing and the computational efficiency of the hardware, we chose the batch size to be within the range of 80–120 in the dataset with a frequency of 250 Hz.
- (2)
- Hidden Units: Hidden units are another fundamental hyperparameter in neural networks, and their quantity also determines the model’s performance. Due to the unique gate mechanism of hidden units in BiLSTM, the more models there are, the better the fit to the data. However, there is also a risk of overfitting. Due to the bidirectional transmission effect, the number of selected hidden units is 120 and 128, respectively, and a double-layer BiLSTM is used for stacking.
- (3)
- Sequence Length: The sequence length determines the number of time steps processed by each forward and backward propagation. If this value is set too high, although it can capture long-range memory relationships, it increases the computational requirements and the risk of gradient vanishing. On the contrary, the computational requirements are small, but the utilization rate of time memory before and after is also meager. This article sets the sequence length to 120–180, which is about 0.5 s of time memory in the 250 Hz dataset.
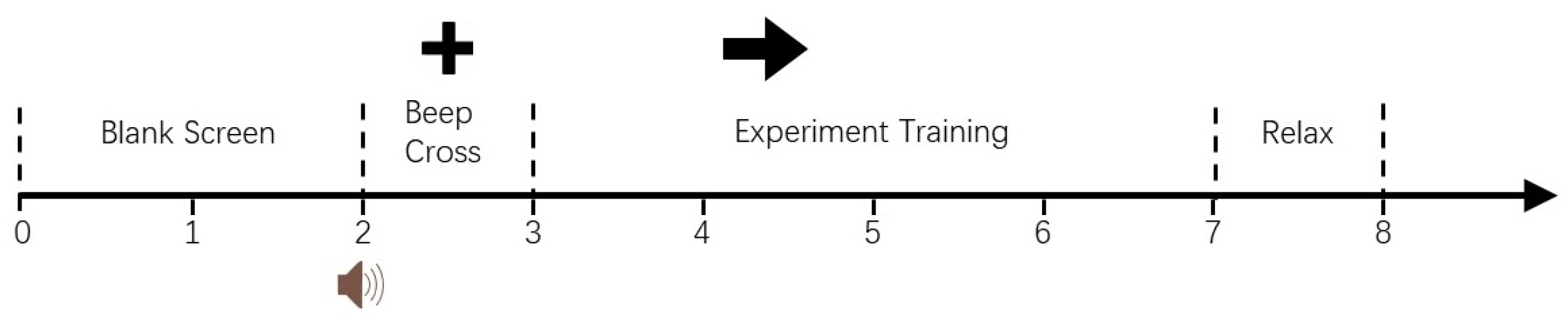
2.4. Data Preprocessing
- (1)
- Step 1—Identification of artifacts: Manually inspect the data and label the identified artifacts, or set a threshold through EEGLAB (v2023.0), so that signals outside the threshold are marked.
- (2)
- Step 2—Artifact removal: By checking the frequency components through the marked artifact parts and using a filter to filter out signals in specific frequency bands, the pure signal after removing the artifacts can be obtained. Alternatively, independent component analysis (ICA) can be used to decompose the EEG signals into independent components and identify and remove components related to artifacts.
- (3)
- Step 3—Choose baseline window: Usually, a time window before stimulation is chosen as the baseline period. For example, if the stimulus appears at 0 ms, a time period of [−200 ms, 0 ms] can be selected as the baseline window.
- (4)
- Step 4—Baseline correction: Calculate the average value of each signal within the baseline window and subtract the baseline mean of the corresponding channel from the recorded EEG signal.
- (5)
- Step 5—Dataset splitting: To ensure temporal data continuity, we performed 5-fold cross-validation on our dataset, using 8 out of 10 experimental rounds for training and the remaining 2 for testing.
2.5. Dataset
2.6. Locations of Electrodes
3. Results
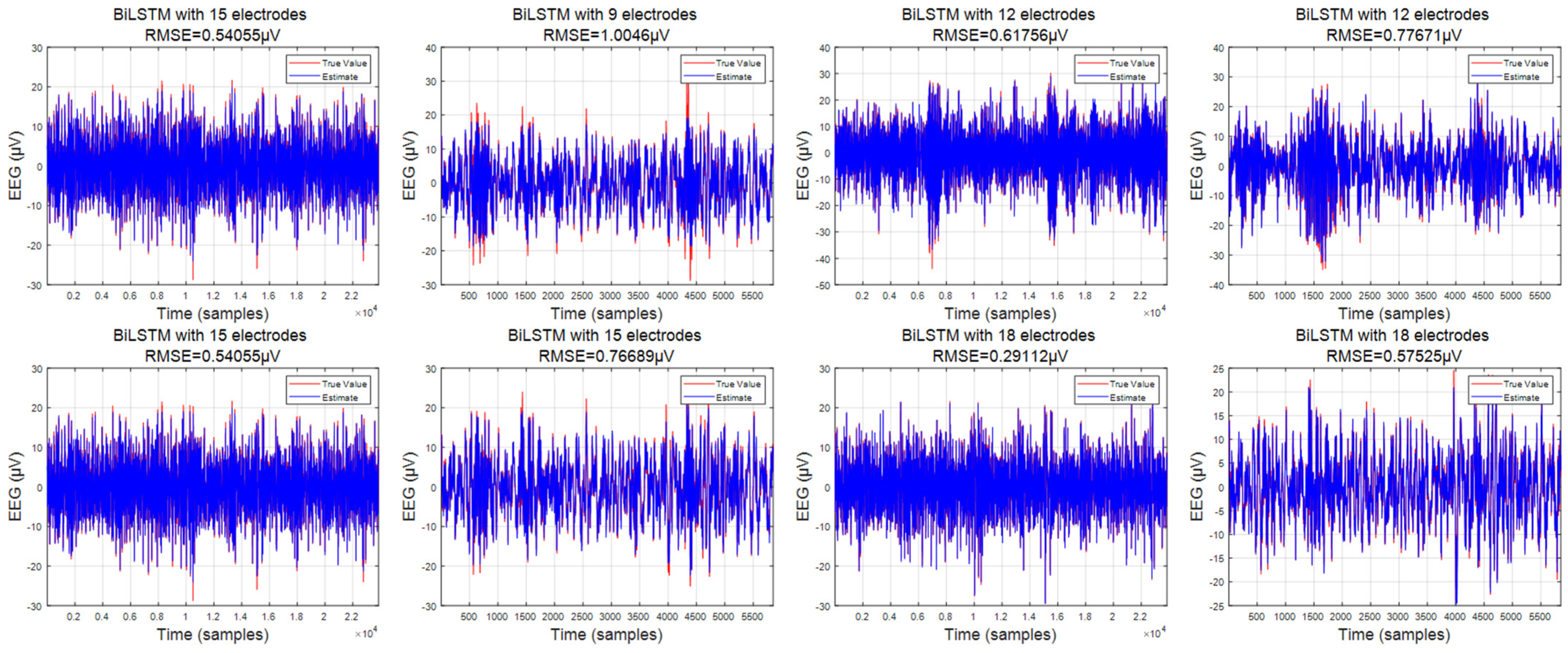
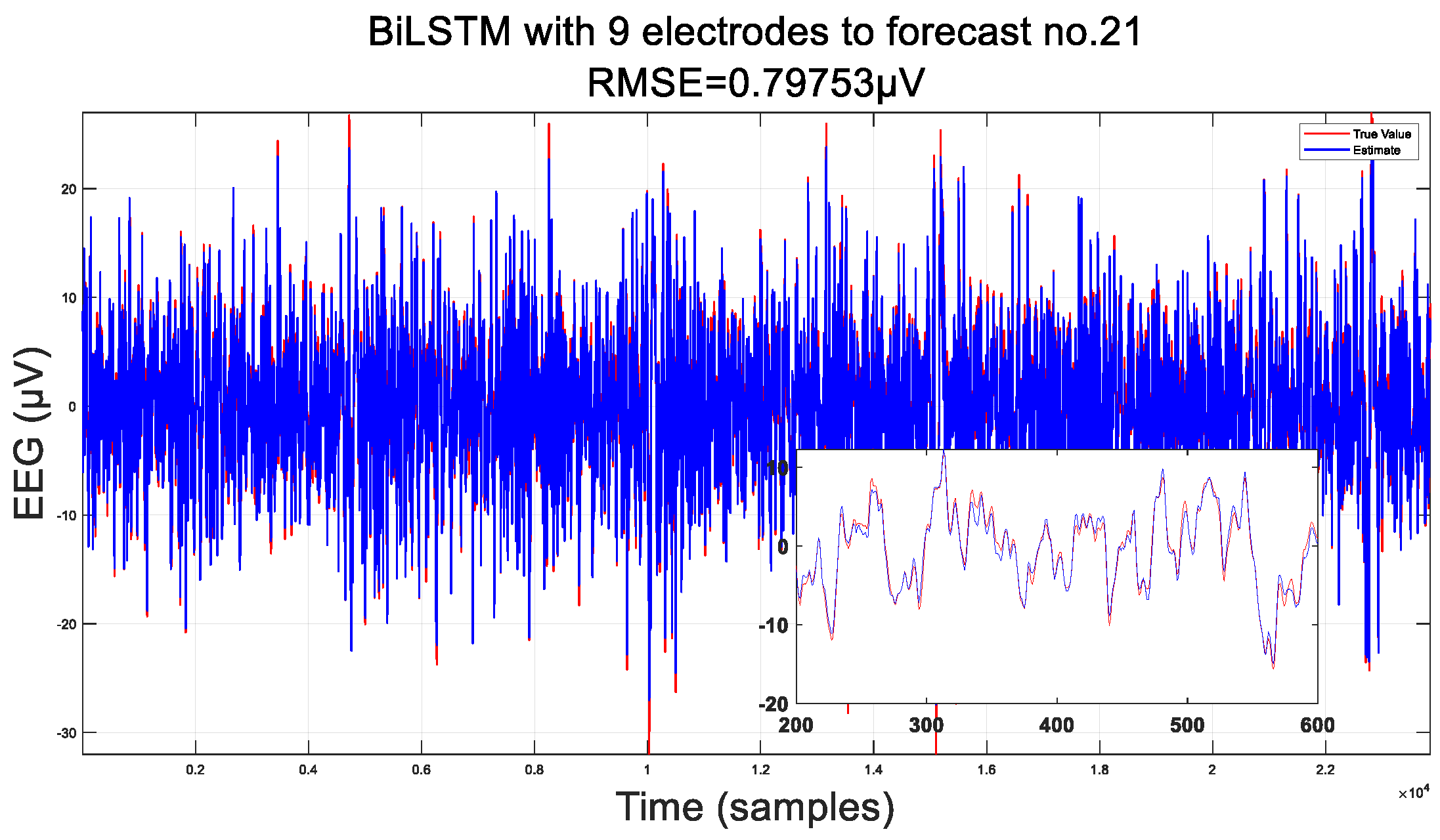
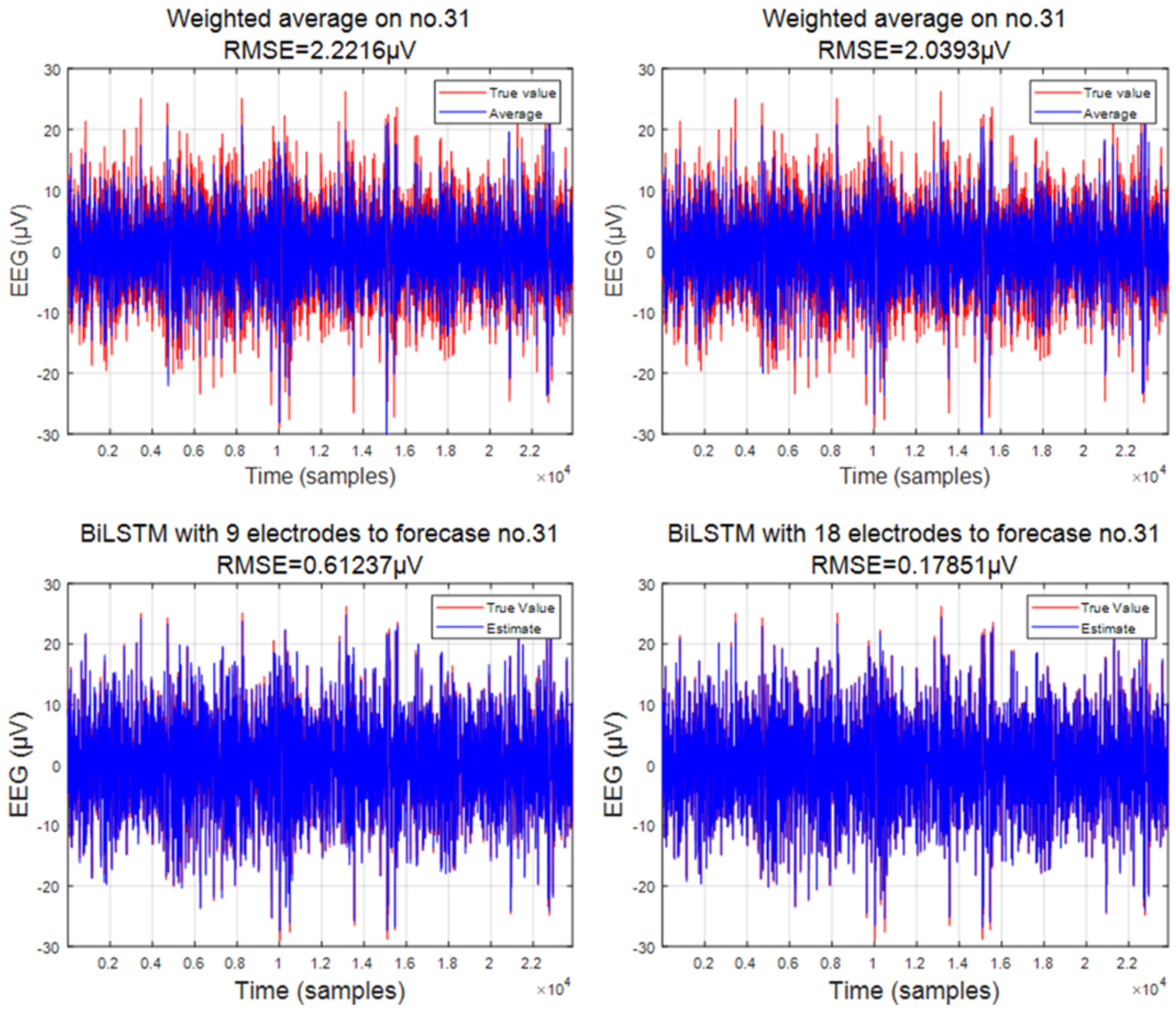
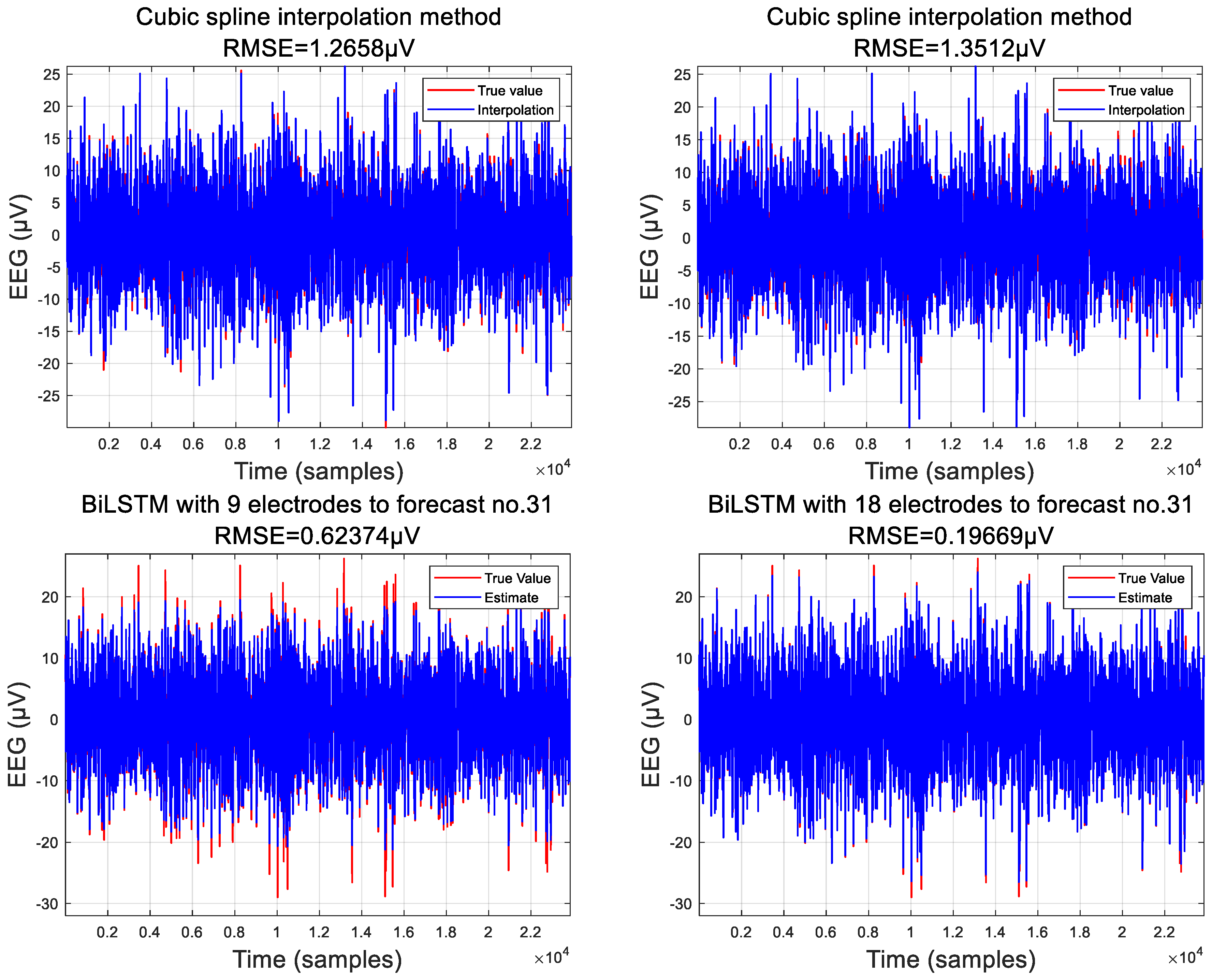
3.1. Predicted Data
3.2. Comparison of Interpolation Methods
3.3. Analysis of EEG Signals
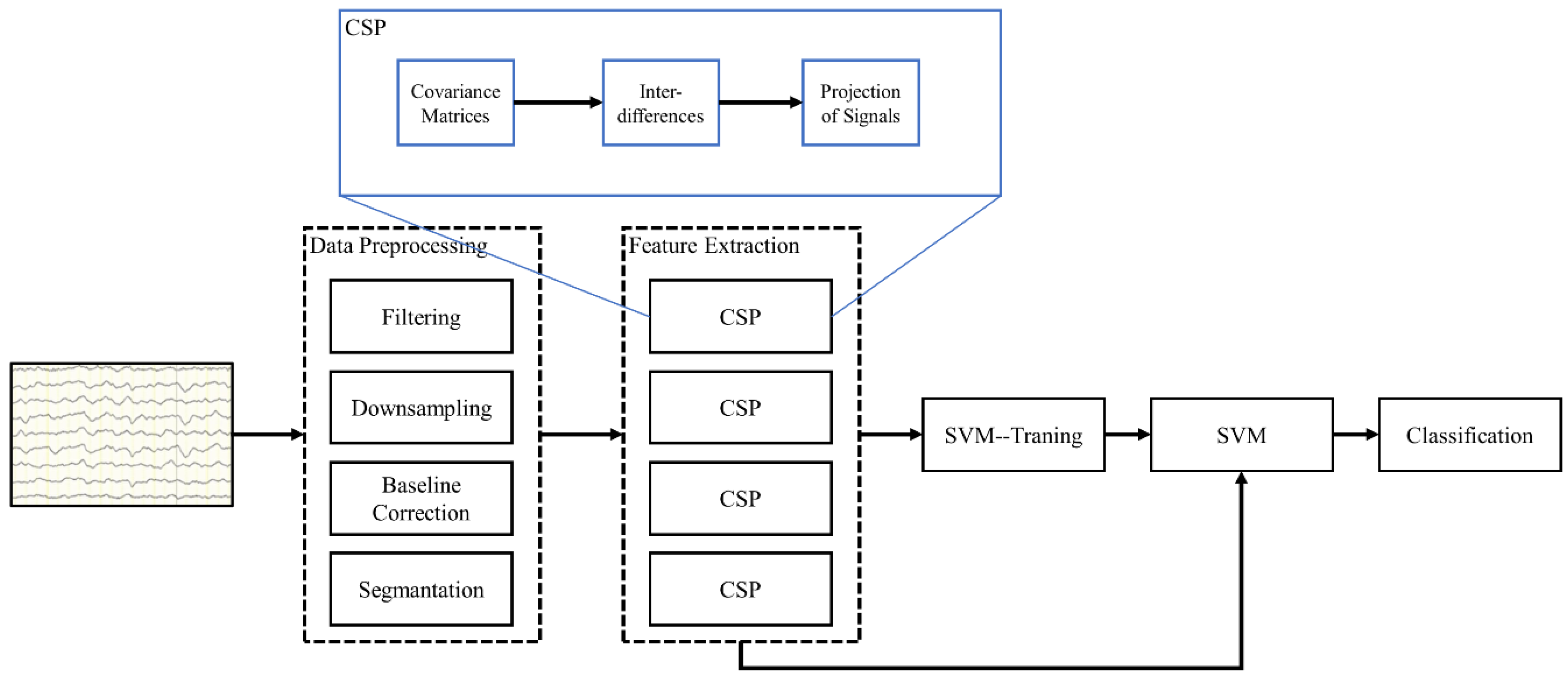
3.4. MI Task Evaluation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Orban, M.; Elsamanty, M.; Guo, K.; Zhang, S.; Yang, H. A Review of Brain Activity and EEG-Based Brain–Computer Interfaces for Rehabilitation Application. Bioengineering 2022, 9, 768. [Google Scholar] [CrossRef]
- Maiseli, B.; Abdalla, A.T.; Massawe, L.V.; Mbise, M.; Mkocha, K.; Nassor, N.A.; Ismail, M.; Michael, J.; Kimambo, S. Brain–computer interface: Trend, challenges, and threats. Brain Inform. 2023, 10, 20. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.; Hussain, A.A.; Lal, S.; Guesgen, H.W. A Comprehensive Review on Critical Issues and Possible Solutions of Motor Imagery Based Electroencephalography Brain-Computer Interface. Sensors 2021, 21, 2173. [Google Scholar] [CrossRef] [PubMed]
- Tai, P.; Ding, P.; Wang, F.; Gong, A.; Li, T.; Zhao, L.; Su, L.; Fu, Y. Brain-computer interface paradigms and neural coding. Front. Neurosci. 2024, 17, 1345961. [Google Scholar] [CrossRef] [PubMed]
- Ramantani, G.; Maillard, L.; Koessler, L. Correlation of invasive EEG and scalp EEG. Seizure 2016, 41, 196–200. [Google Scholar] [CrossRef] [PubMed]
- Casson, A.J. Wearable EEG and beyond. Biomed. Eng. Lett. 2019, 9, 53–71. [Google Scholar] [CrossRef]
- Lepola, P.; Myllymaa, S.; Töyräs, J.; Muraja-Murro, A.; Mervaala, E.; Lappalainen, R.; Myllymaa, K. Screen-printed EEG electrode set for emergency use. Sens. Actuators Phys. 2014, 213, 19–26. [Google Scholar] [CrossRef]
- Lin, B.-S.; Pan, J.-S.; Chu, T.-Y.; Lin, B.-S. Development of a Wearable Motor-Imagery-Based Brain–Computer Interface. J. Med. Syst. 2016, 40, 71. [Google Scholar] [CrossRef]
- Tseng, K.C.; Lin, B.-S.; Liao, L.-D.; Wang, Y.-T.; Wang, Y.-L. Development of a Wearable Mobile Electrocardiogram Monitoring System by Using Novel Dry Foam Electrodes. IEEE Syst. J. 2014, 8, 900–906. [Google Scholar] [CrossRef]
- Yu, Y.-H.; Lu, S.-W.; Liao, L.-D.; Lin, C.-T. Design, Fabrication, and Experimental Validation of Novel Flexible Silicon-Based Dry Sensors for Electroencephalography Signal Measurements. IEEE J. Transl. Eng. Health Med. 2014, 2, 2700307. [Google Scholar] [CrossRef]
- Lee, S.; Shin, Y.; Lee, H.-N. Design of active dry electrodes and its evaluation for EEG acquisition. In Proceedings of the 2015 International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Republic of Korea, 28–30 October 2015; pp. 560–562. [Google Scholar] [CrossRef]
- Parmigiani, S.; Mikulan, E.; Russo, S.; Sarasso, S.; Zauli, F.; Rubino, A.; Cattani, A.; Fecchio, M.; Giampiccolo, D.; Lanzone, J.; et al. Simultaneous stereo-EEG and high-density scalp EEG recordings to study the effects of intracerebral stimulation parameters. Brain Stimulat. 2022, 15, 664–675. [Google Scholar] [CrossRef]
- Buril, J.; Burilova, P.; Pokorna, A.; Balaz, M. Use of high-density EEG in patients with Parkinson’s disease treated with deep brain stimulation. Biomed. Pap. 2020, 164, 366–370. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Qiu, S.; He, H. Multi-channel EEG recording during motor imagery of different joints from the same limb. Sci. Data 2020, 7, 191. [Google Scholar] [CrossRef] [PubMed]
- Mohagheghian, F.; Khajehpour, H.; Samadzadehaghdam, N.; Eqlimi, E.; Jalilvand, H.; Makkiabadi, B.; Deevband, M.R. Altered effective brain network topology in tinnitus: An EEG source connectivity analysis. Biomed. Signal Process. Control 2021, 64, 102331. [Google Scholar] [CrossRef]
- Cottereau, B.R.; Ales, J.M.; Norcia, A.M. How to use fMRI functional localizers to improve EEG/MEG source estimation. J. Neurosci. Methods 2015, 250, 64–73. [Google Scholar] [CrossRef] [PubMed]
- Hassan, M.; Wendling, F. Electroencephalography Source Connectivity: Aiming for High Resolution of Brain Networks in Time and Space. IEEE Signal Process. Mag. 2018, 35, 81–96. [Google Scholar] [CrossRef]
- Khouaja, I.; Nouira, I.; Bedoui, M.H.; Akil, M. Enhancing EEG Surface Resolution by Using a Combination of Kalman Filter and Interpolation Method. In Proceedings of the 2016 13th International Conference on Computer Graphics, Imaging and Visualization (CGiV), Beni Mellal, Morocco, 29 March–1 April 2016; pp. 353–357. [Google Scholar] [CrossRef]
- Dimitrov, L.I. Texturing 3D-reconstructions of the human brain with EEG-activity maps. Hum. Brain Mapp. 1998, 6, 189–202. [Google Scholar] [CrossRef]
- Dong, L.; Zhao, L.; Zhang, Y.; Yu, X.; Li, F.; Li, J.; Lai, Y.; Liu, T.; Yao, D. Reference Electrode Standardization Interpolation Technique (RESIT): A Novel Interpolation Method for Scalp EEG. Brain Topogr. 2021, 34, 403–414. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Shafay, M.; Ahmad, R.W.; Salah, K.; Yaqoob, I.; Jayaraman, R.; Omar, M. Blockchain for deep learning: Review and open challenges. Clust. Comput. 2023, 26, 197–221. [Google Scholar] [CrossRef]
- Yang, J.; Gao, S.; Shen, T. A Two-Branch CNN Fusing Temporal and Frequency Features for Motor Imagery EEG Decoding. Entropy 2022, 24, 376. [Google Scholar] [CrossRef] [PubMed]
- Kumaravel, V.P.; Kartsch, V.; Benatti, S.; Vallortigara, G.; Farella, E.; Buiatti, M. Efficient Artifact Removal from Low-Density Wearable EEG using Artifacts Subspace Reconstruction. In Proceedings of the 2021 43rd Annual International Conference of the 2021 IEEE Engineering in Medicine & Biology Society (EMBC), Mexico, 1–5 November 2021; pp. 333–336. [Google Scholar] [CrossRef]
- Kaeseler, R.L.; Johansson, T.W.; Struijk, L.N.S.A.; Jochumsen, M. Feature and Classification Analysis for Detection and Classification of Tongue Movements from Single-Trial Pre-Movement EEG. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 678–687. [Google Scholar] [CrossRef] [PubMed]
- Tariq, M.; Trivailo, P.M.; Simic, M. Mu-Beta event-related (de)synchronization and EEG classification of left-right foot dorsiflexion kinaesthetic motor imagery for BCI. PLoS ONE 2020, 15, e0230184. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Yu, H.; Shen, T.; Song, Y.; Chen, Z. 4-Class MI-EEG Signal Generation and Recognition with CVAE-GAN. Appl. Sci. 2021, 11, 1798. [Google Scholar] [CrossRef]
- Altaheri, H.; Muhammad, G.; Alsulaiman, M. Physics-Informed Attention Temporal Convolutional Network for EEG-Based Motor Imagery Classification. IEEE Trans. Ind. Inform. 2023, 19, 2249–2258. [Google Scholar] [CrossRef]
- Singh, K.; Malhotra, J. Two-layer LSTM network-based prediction of epileptic seizures using EEG spectral features. Complex Intell. Syst. 2022, 8, 2405–2418. [Google Scholar] [CrossRef]
- Han, S.; Kwon, M.; Lee, S.; Jun, S.C. Feasibility Study of EEG Super-Density Using Deep Convolutional Networks. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 17 January 2018; pp. 1033–1038. [Google Scholar] [CrossRef]
- Gwon, D.; Won, K.; Song, M.; Nam, C.S.; Jun, S.C.; Ahn, M. Review of public motor imagery and execution datasets in brain-computer interfaces. Front. Hum. Neurosci. 2023, 17, 1134869. [Google Scholar] [CrossRef]
- Jeunet, C.; Glize, B.; McGonigal, A.; Batail, J.-M.; Micoulaud-Franchi, J.-A. Using EEG-based brain computer interface and neurofeedback targeting sensorimotor rhythms to improve motor skills: Theoretical background, applications and prospects. Neurophysiol. Clin. 2019, 49, 125–136. [Google Scholar] [CrossRef] [PubMed]
- Craik, A.; He, Y.; Contreras-Vidal, J.L. Deep learning for electroencephalogram (EEG) classification tasks: A review. J. Neural Eng. 2019, 16, 031001. [Google Scholar] [CrossRef]
- Karas, K.; Pozzi, L.; Pedrocchi, A.; Braghin, F.; Roveda, L. Brain-computer interface for robot control with eye artifacts for assistive applications. Sci. Rep. 2023, 13, 17512. [Google Scholar] [CrossRef]
- Li, T.; Zhang, J.; Xue, T.; Wang, B. Development of a Novel Motor Imagery Control Technique and Application in a Gaming Environment. Comput. Intell. Neurosci. 2017, 2017, 5863512. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Yang, B.; Xu, M.; Zan, P.; Chen, L.; Xia, X. Exploring quantitative assessment of cybersickness in virtual reality using EEG signals and a CNN-ECA-LSTM network. Displays 2024, 81, 102602. [Google Scholar] [CrossRef]
- Lin, B.-S.; Chen, J.-L.; Hsu, H.-C. Novel Upper-Limb Rehabilitation System Based on Attention Technology for Post-Stroke Patients: A Preliminary Study. IEEE Access 2018, 6, 2720–2731. [Google Scholar] [CrossRef]
- Arpaia, P.; Donnarumma, F.; Esposito, A.; Parvis, M. Channel Selection for Optimal EEG Measurement in Motor Imagery-Based Brain-Computer Interfaces. Int. J. Neural Syst. 2021, 31, 2150003. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhang, C.; Karkkainen, T.; Chang, Z.; Cong, F. Channel Increment Strategy-Based 1D Convolutional Neural Networks for Seizure Prediction Using Intracranial EEG. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 316–325. [Google Scholar] [CrossRef] [PubMed]
- Kwon, M.; Han, S.; Kim, K.; Jun, S.C. Super-Resolution for Improving EEG Spatial Resolution using Deep Convolutional Neural Network—Feasibility Study. Sensors 2019, 19, 5317. [Google Scholar] [CrossRef]
- Corley, I.A.; Huang, Y. Deep EEG super-resolution: Upsampling EEG spatial density with Generative Adversarial Networks. In Proceedings of the 2018 IEEE EMBS International Conference on Biomedical & Health Informatics (BHI), Las Vegas, NV, USA, 4–7 March 2018; pp. 100–103. [Google Scholar] [CrossRef]
- Wang, S.; Cao, J.; Yu, P.S. Deep Learning for Spatio-Temporal Data Mining: A Survey. arXiv 2019, arXiv:1906.04928. [Google Scholar] [CrossRef]








| 1:Nz | 2:Fp1 | 3:Fpz | 4:Fp2 | 5:AF7 | 6:AF3 | 7:AFz | 8:AF4 | 9:AF8 | 10:F7 |
| 11:F5 | 12:F3 | 13:Fz | 14:F4 | 15:F6 | 16:F8 | 17:FT7 | 18:FC5 | 19:FC3 | 20:FC1 |
| 21:FCz | 22:FC2 | 23:FC4 | 24:FC6 | 25:FT8 | 26:T9 | 27: T7 | 28:C5 | 29:C3 | 30:C1 |
| 31:Cz | 32:C2 | 33:C4 | 34:C6 | 35:T8 | 36:T10 | 37:TP7 | 38:CP5 | 39:CP3 | 40:CP1 |
| 41:CPz | 42:CP2 | 43:CP4 | 44CP6: | 45:TP8 | 46:P7 | 47:P5 | 48:P3 | 49:Pz | 50:P2 |
| 51:P4 | 52:P6 | 53:PO7 | 54:PO3 | 55:POz | 56:PO4 | 57:PO8 | 58:O1 | 59:Oz | 60:O2 |
| Left Hand | Right Hand | Tongue | Foot | Total | |
|---|---|---|---|---|---|
| K3B | 57.78% | 64.44% | 64.44% | 42.22% | 61.75% |
| K6B | 86.67% | 60% | 57.33% | 43.33% | 67.48% |
| L1B | 60% | 76.67% | 66.67% | 46.19% | 62.53% |
| Left Hand | Right Hand | Tongue | Foot | Total | |
|---|---|---|---|---|---|
| K3B | 88.89% | 84.44% | 82.22% | 73.33% | 82.22% |
| K6B | 84.44% | 84.44% | 86.66% | 77.78% | 83.33% |
| L1B | 86.67% | 80% | 90% | 73.3% | 82.5% |
| Left Hand | Right Hand | Tongue | Foot | Total | |
|---|---|---|---|---|---|
| K3B | 93.33% | 88.89% | 82.22% | 80% | 86.85% |
| K6B | 93.67% | 93.33% | 83.33% | 76.67% | 87.44% |
| L1B | 92.67% | 90% | 86.67% | 83.3% | 89.16% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, W.; Ji, B.; Gao, K. A Method for the Spatial Interpolation of EEG Signals Based on the Bidirectional Long Short-Term Memory Network. Sensors 2024, 24, 5215. https://doi.org/10.3390/s24165215
Hu W, Ji B, Gao K. A Method for the Spatial Interpolation of EEG Signals Based on the Bidirectional Long Short-Term Memory Network. Sensors. 2024; 24(16):5215. https://doi.org/10.3390/s24165215
Chicago/Turabian StyleHu, Wenlong, Bowen Ji, and Kunpeng Gao. 2024. "A Method for the Spatial Interpolation of EEG Signals Based on the Bidirectional Long Short-Term Memory Network" Sensors 24, no. 16: 5215. https://doi.org/10.3390/s24165215
APA StyleHu, W., Ji, B., & Gao, K. (2024). A Method for the Spatial Interpolation of EEG Signals Based on the Bidirectional Long Short-Term Memory Network. Sensors, 24(16), 5215. https://doi.org/10.3390/s24165215







