Fast-Activated Minimal Gated Unit: Lightweight Processing and Feature Recognition for Multiple Mechanical Impact Signals
Abstract
1. Introduction
2. Transfer Model for Multiple Impacts in Multibody Dynamical Systems
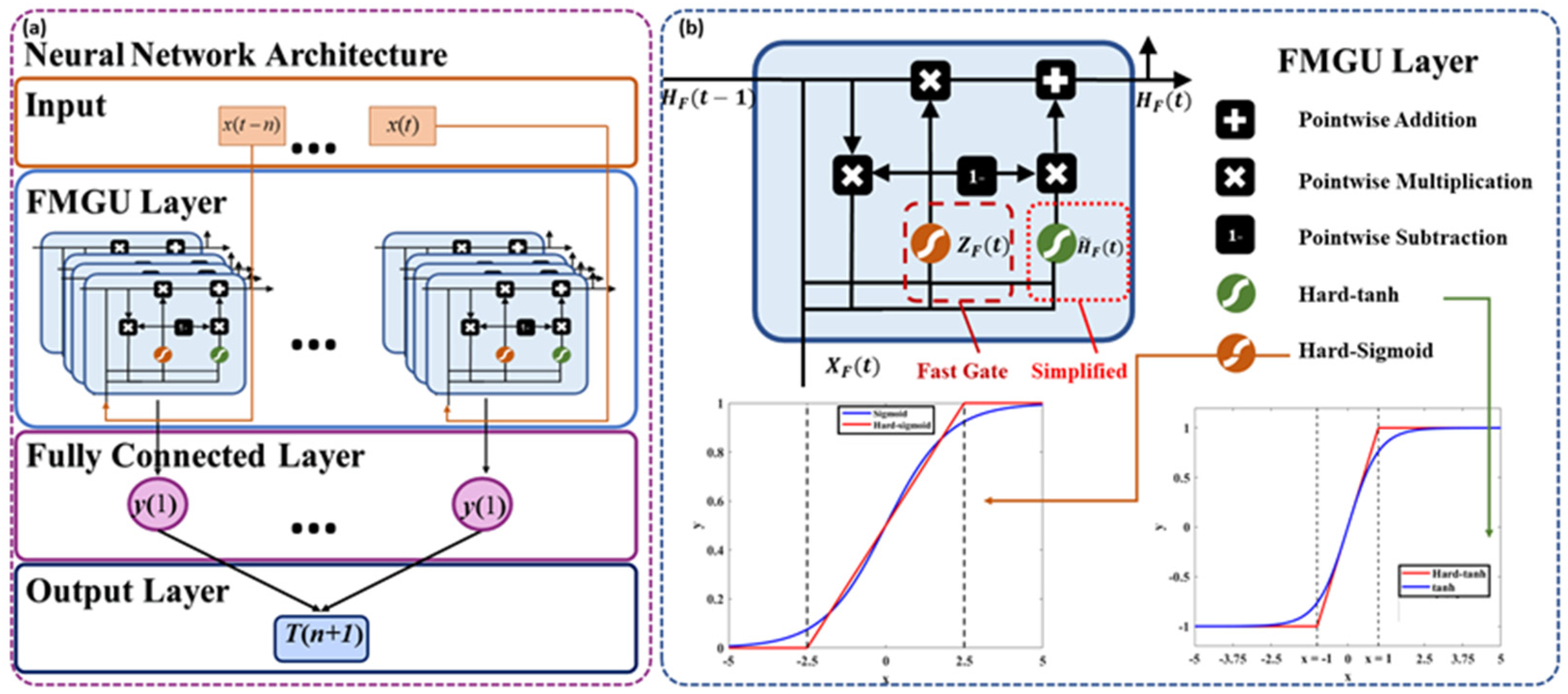
3. Combined Algorithm of Wavelet Transform Preprocess and FMGU Network
4. Results and Discussion
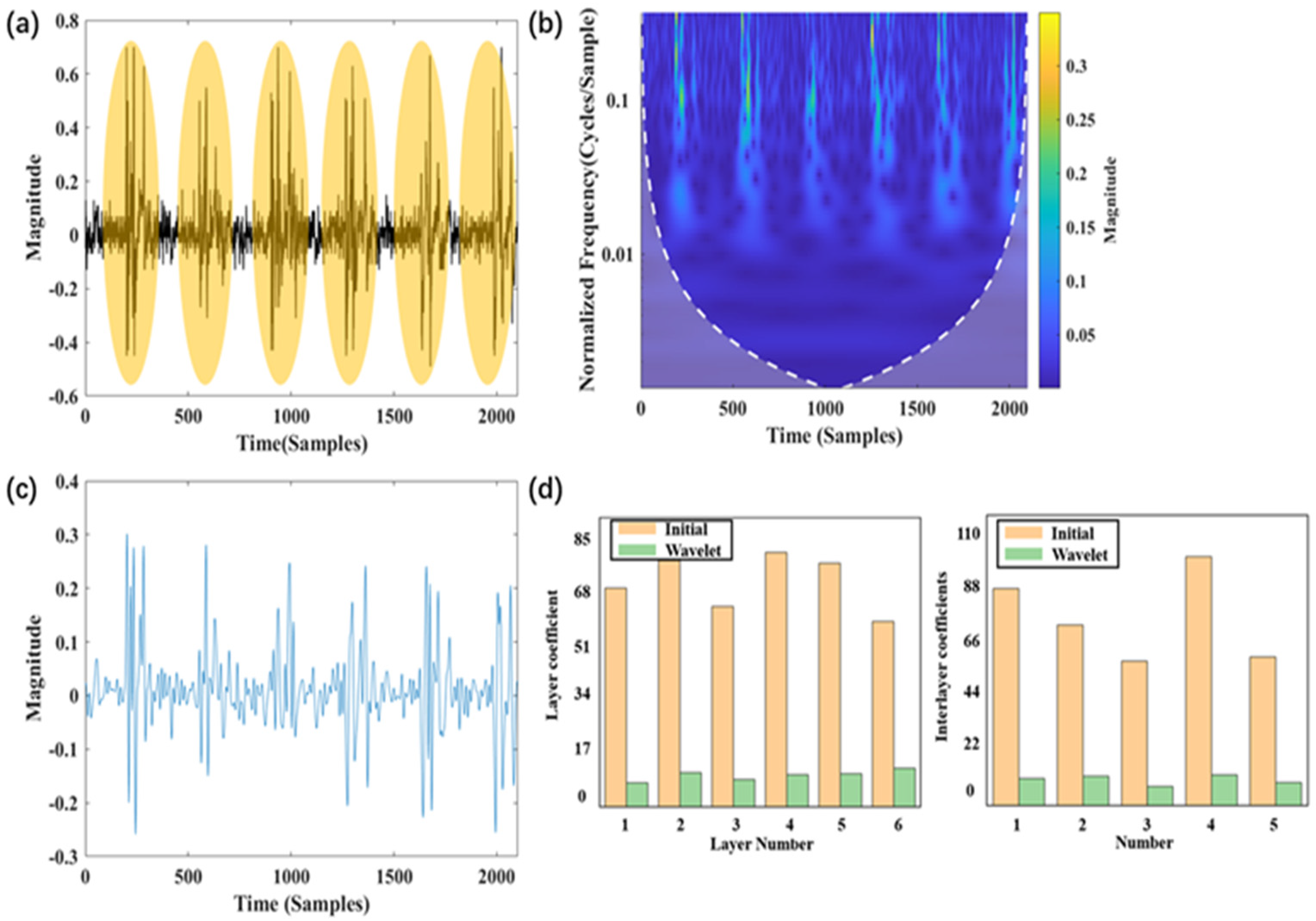
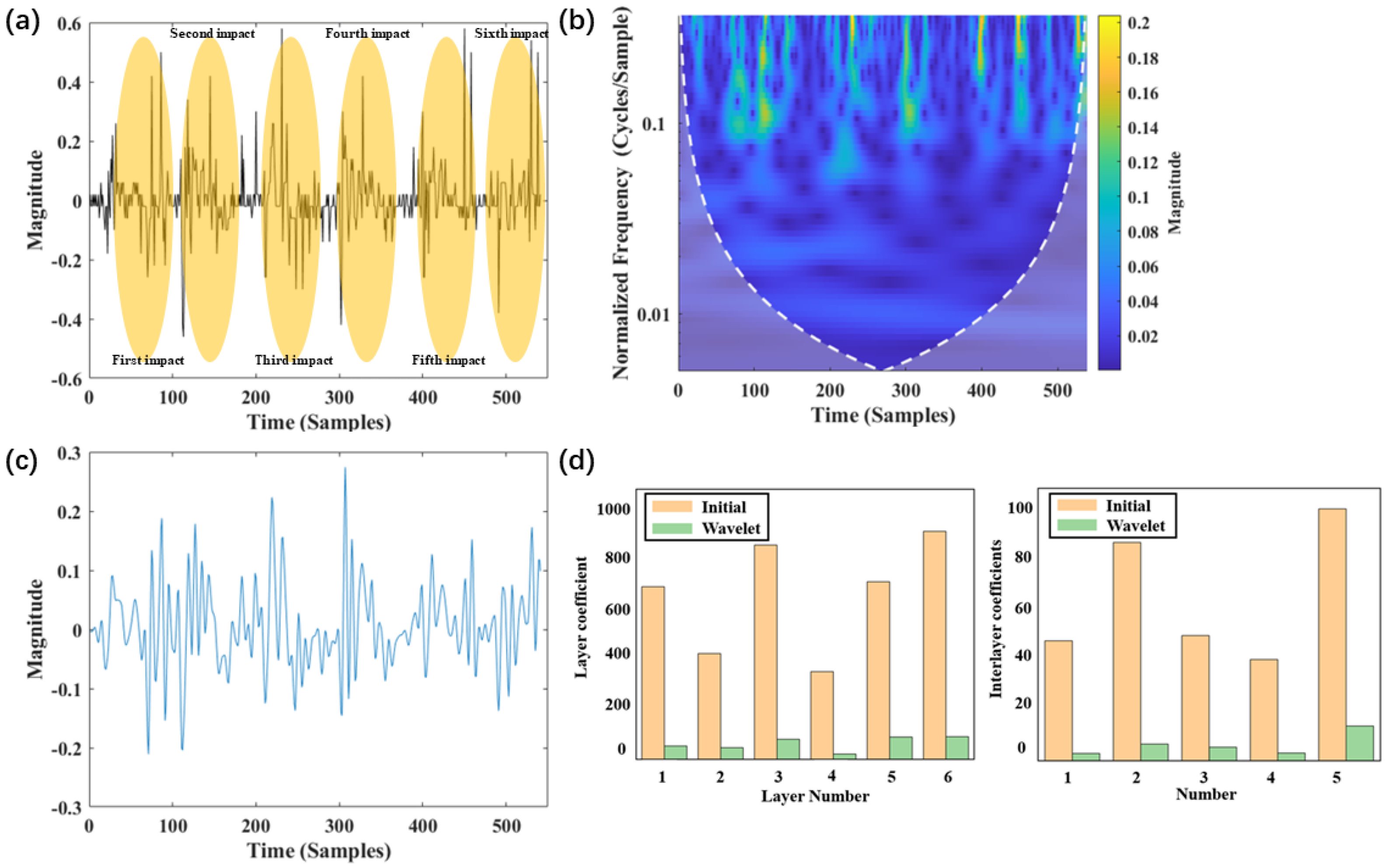
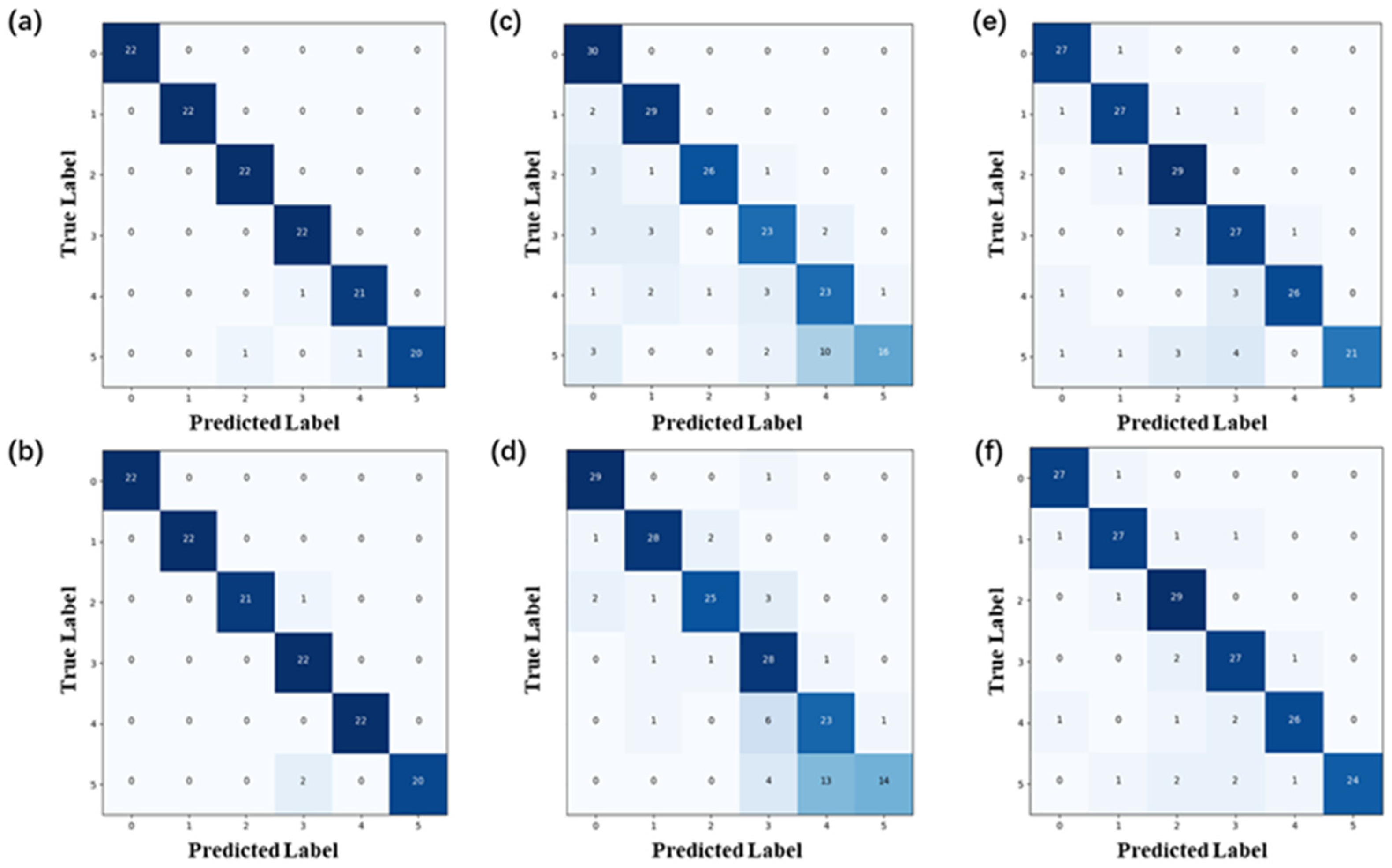
4.1. Contributions of Wavelet Preprocessing and FMGU Network
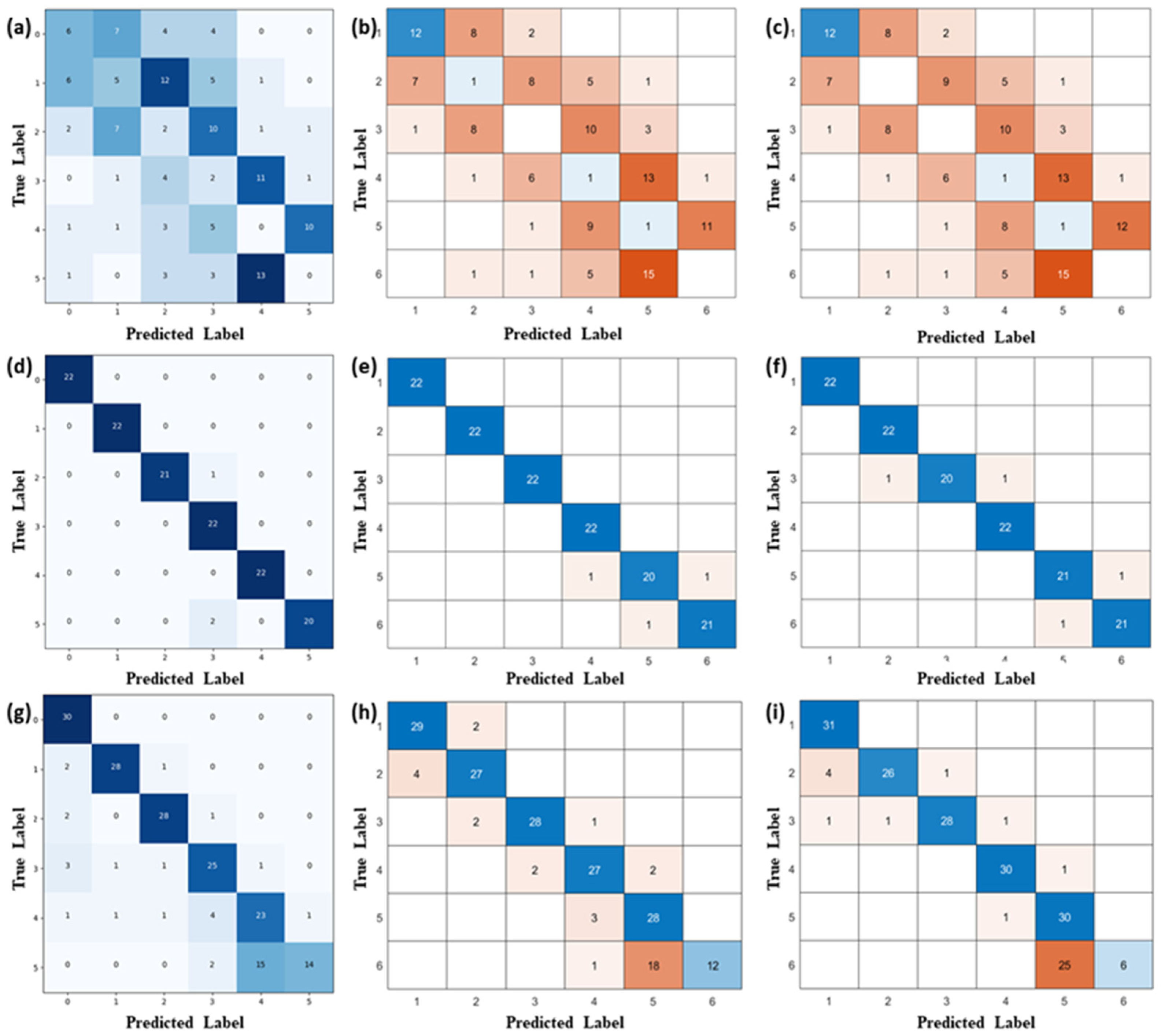
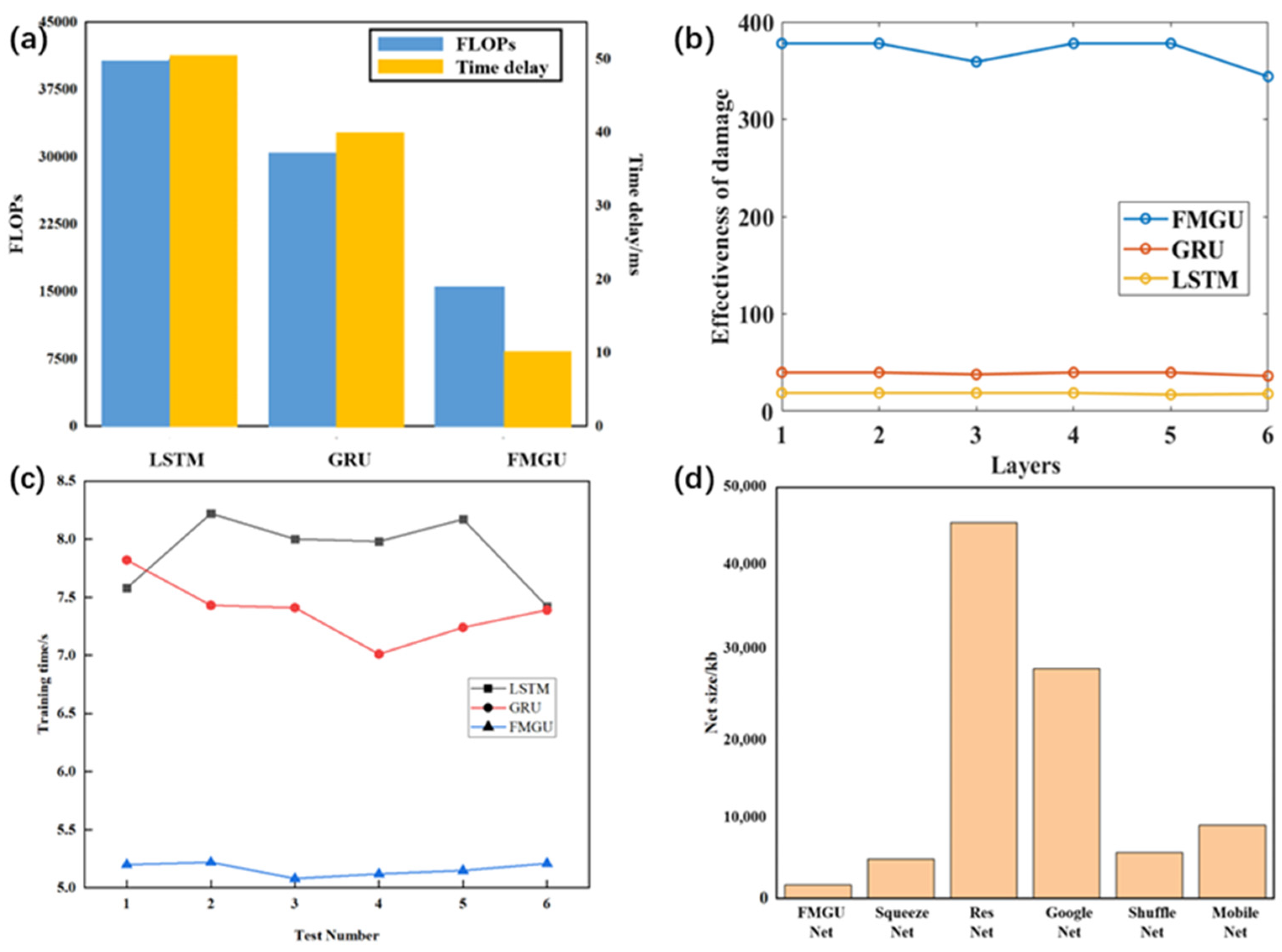
4.2. Robustness of FMGU Network Verification
4.3. Comparison of Real-Time Performance and Hardware Overhead Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Multiple Impact Signal Generation
Appendix A.2. Evaluation of Signal Adhesion
References
- Lv, Q. Damage Characteristics and Damage Tolerance of Fibre-Reinforced Composites under Multiple Low-Velocity Impacts. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2023. [Google Scholar]
- Zhao, N.; Zhang, J.; Ma, W.; Jiang, Z.; Mao, Z. Variational time-domain decomposition of reciprocating machine multi-impact vibration signals. Mech. Syst. Signal Process. 2022, 172, 108977. [Google Scholar] [CrossRef]
- Man, X. Research on Key Technology of Short Interval Multiple High Impact Experimental Device. Ph.D. Thesis, Nanjing University of Science and Technology, Nanjing, China, 2017. [Google Scholar] [CrossRef]
- Han, X.; Yu, D.; Chen, C.; Dai, K. Failure behavior of tantalum electrolytic capacitors under extreme dynamic impact: Mechanical–electrical model and microscale characterization. Nanotechnol. Precis. Eng. 2024, 7, 043004. [Google Scholar] [CrossRef]
- Yang, B.; Dai, K.; Li, C.; Yu, D.; Zhang, A.; Cheng, J. Zhang, H Lightweight recoverable mechanical metamaterials for efficient buffering of continuous multi extreme impacts. Sustain. Mater. Technol. 2024, 39, e00839. [Google Scholar]
- Huang, J.; Liu, P.; Wang, Y.; Dai, K.; Dou, Q.; Yin, Y.; Wang, X.; You, Z. Double-kill contribution of high-roughness high-density porous carbon electrodes to mechanically self-sensing supercapacitors. Nano Res. 2024, 17, 6157–6167. [Google Scholar] [CrossRef]
- Tong, X. Predictive Analysis of Future, U.S. Global Rapid Precision Strike System. Missile Space Deliv. Technol. 2008, 2008, 3–5. [Google Scholar] [CrossRef]
- Lai, J.; Zhou, J.; Yin, X.; Zheng, X. Dynamic behavior of functional graded cementitious composite under the coupling of high speed penetration and explosion. Compos. Struct. 2021, 274, 114326. [Google Scholar] [CrossRef]
- Liu, R.; Dobriban, E.; Hou, Z.; Qian, K. Dynamic load identification for mechanical systems: A review. Arch. Comput. Methods Eng. 2022, 29, 831–863. [Google Scholar] [CrossRef]
- Cen, J.; Yang, Z.; Wu, Y.; Hu, X.; Jiang, L.; Chen, H.; Si, W. A mask self-supervised learning-based transformer for bearing fault diagnosis with limited labeled samples. IEEE Sens. J. 2023, 23, 10359–10369. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y.; Shardt, Y.A.; Li, X.; Cui, J.; Tong, C. A KPI-based soft sensor development approach incorporating infrequent, variable time delayed measurements. IEEE Trans. Control. Syst. Technol. 2019, 28, 2523–2531. [Google Scholar] [CrossRef]
- Zhang, D.; Li, J.; Wei, X.; Feng, K.; Wang, Y.; Zhao, J. Signal measurement of projectile penetration overload based on charge sensor. IEEE Access 2019, 7, 178139–178152. [Google Scholar] [CrossRef]
- Yang, H.; Jiang, J.; Chen, G.; Zhao, J. Dynamic load identification based on deep convolution neural network. Mech. Syst. Signal Process. 2023, 185, 109757. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, L.; Jia, H.; Tong, X.; Li, F. A sequence-to-sequence deep learning architecture based on bidirectional GRU for type recognition and time location of combined power quality disturbance. IEEE Trans. Ind. Inform. 2019, 15, 4481–4493. [Google Scholar] [CrossRef]
- Iranmehr, E.; Böhnert, T.; Paz, E.; Martins, M.; Ferreira, R. Unsupervised extraction of shape-based signal patterns for incoming signal recognition. IEEE Sens. J. 2023, 23, 11992–12007. [Google Scholar] [CrossRef]
- Liu, X.; Wang, H.; Li, Z.; Qin, L. Deep learning in ECG diagnosis: A review. Knowl.-Based Syst. 2021, 227, 107187. [Google Scholar] [CrossRef]
- Ibrahim, S.K.; Ahmed, A.; Zeidan, M.A.E.; Ziedan, I.E. Machine learning methods for spacecraft telemetry mining. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 1816–1827. [Google Scholar] [CrossRef]
- Zhou, J.M.; Dong, L.; Guan, W.; Yan, J. Impact load identification of nonlinear structures using deep Recurrent Neural Network. Mech. Syst. Signal Process. 2019, 133, 106292. [Google Scholar] [CrossRef]
- Ma, X.; Shi, H.; Miao, X.; Li, Q.; Wang, X.; Ding, L.; Zhang, H.; Dai, K. Multiple dynamic impact signal identification method based on lightweight neural network with acceleration sensor. IEEE Sens. J. 2023, 23, 17289–17300. [Google Scholar] [CrossRef]
- Kong, X.Z.; Wu, H.; Fang, Q.; Zhang, W.; Xiao, Y.K. Projectile penetration into mortar targets with a broad range of striking velocities: Test and analyses. Int. J. Impact Eng. 2017, 106, 18–29. [Google Scholar] [CrossRef]
- Karimi, H.R.; Pawlus, W.; Robbersmyr, K.G. Signal reconstruction, modeling and simulation of a vehicle full-scale crash test based on Morlet wavelets. Neurocomputing 2012, 93, 88–99. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning Cambridge; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 12 December 2023).
- Computation, N. Long short-term memory. Neural Comput. 2016, 9, 1735–1780. [Google Scholar]
- Yu, D.; Yang, B.; Yan, K.; Li, C.; Ma, X.; Han, X.; Zhang, H.; Dai, K. Dynamic transfer model and applications of a penetrating projectile-fuze multibody system. Int. J. Mech. Syst. Dyn. 2023, 3, 360–372. [Google Scholar] [CrossRef]
- Zhou, G.B.; Wu, J.; Zhang, C.L.; Zhou, Z.H. Minimal gated unit for recurrent neural networks. Int. J. Autom. Comput. 2016, 13, 226–234. [Google Scholar] [CrossRef]
- Sak, H.; Senior, A.; Beaufays, F. Long short-term memory based recurrent neural network architectures for large vocabulary speech recognition. arXiv 2014, arXiv:1402.1128. [Google Scholar]
- Burrus, C.S.; Gopinath, R.A.; Guo, H. Wavelets and Wavelet Transforms; houston edition; Rice University: Houston, TX, USA, 1998; p. 98. [Google Scholar]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Chintala, S.; Killeen, T.; Lin, Z.; Gimelshein, N.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. {TensorFlow}: A system for {Large-Scale} machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Jouppi, N.P.; Young, C.; Patil, N.; Patterson, D.; Agrawal, G.; Bajwa, R.; Yoon, D.H.; Bhatia, S.; Boden, N.; Borchers, A.; et al. In-datacenter performance analysis of a tensor processing unit. In Proceedings of the 44th Annual International Symposium on Computer Architecture, Toronto, ON, Canada, 24–28 June 2017; pp. 1–12. [Google Scholar]
- Wang, C.; Gong, L.; Yu, Q.; Li, X.; Xie, Y.; Zhou, X. DLAU: A scalable deep learning accelerator unit on FPGA. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2016, 36, 513–517. [Google Scholar] [CrossRef]
- Chen, D. Epileptic EEG Signal Analysis Based on Wavelet Transform. Ph.D. Thesis, Southeast University, Nanjing, China, 2017. [Google Scholar]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Schuster, M.; Chen, Z.; Le, Q.V.; Norouzi, M.; Macherey, W.; Maxim, K.; Yuan, C.; Qin, G.; Klaus, M.; et al. Google’s neural machine translation system: Bridging the gap between human and machine translation. arXiv 2016, arXiv:1609.08144. [Google Scholar]
- Wang, S.; Jiang, J. Learning natural language inference with LSTM. arXiv 2015, arXiv:1512.08849. [Google Scholar]
- Li, X.; Wu, X. Constructing long short-term memory based deep recurrent neural networks for large vocabulary speech recognition. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, QLD, Australia, 19–24 April 2015; pp. 4520–4524. [Google Scholar]
- Schott, L.; Rauber, J.; Bethge, M.; Brendel, W. Towards the first adversarially robust neural network model on MNIST. arXiv 2018, arXiv:1805.09190. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. arXiv 2013, arXiv:1312.6199. [Google Scholar]
- Ebrahimi, J.; Rao, A.; Lowd, D.; Dou, D. Hotflip: White-box adversarial examples for text classification. arXiv 2017, arXiv:1712.06751. [Google Scholar]
- Wang, X.; Tian, W.; Tian, Y.; Liu, C.; Tian, G. Network delay analysis of ground unmanned system based on BO-LSTM neural network. Fire Command. Control. 2024, 49, 101–110. [Google Scholar] [CrossRef]
- Gao, Y.; Cao, Y.; Duan, P. A review of neural network model lightweighting methods. Comput. Sci. 2024, 51, 11–21. [Google Scholar]
- Lecysyn, N.; Dandrieux, A.; Heymes, F.; Aprin, L.; Slangen, P.; Munier, L.; Christian, L.; Dusserre, G. Ballistic impact on an industrial tank: Study and modeling of consequences. J. Hazard. Mater. 2009, 172, 587–594. [Google Scholar] [CrossRef]
- Li, F.; Ma, S. Analysis and experimental study of acceleration model for short interval and multiple impact equipment. Shock. Vib. 2019, 2019, 5139137. [Google Scholar] [CrossRef]
- Li, F.; Ma, S. Design of multiple rotating impact experiment system of high speed and heavy overload. In Proceedings of the 2017 3rd IEEE International Conference on Control Science and Systems Engineering (ICCSSE), Beijing, China, 17–19 August 2017; pp. 183–187. [Google Scholar]
- Li, F. Research on the theory and method of multiple short interval impact-vibration coupling mechanical experiment. Ph.D. Thesis, Nanjing University of Science and Technology, Nanjing, China, 2021. [Google Scholar]
- Ma, M.; Li, R.; Niu, L. Evaluation index of interference superposition degree in target signature of acceleration signal of intrusion fuze. J. Mil. Eng. 2022, 43, 20–28. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Han, D.; Duan, X.; Yong, Y.; Wu, Z.; Ma, X.; Zhang, H.; Dai, K. Fast-Activated Minimal Gated Unit: Lightweight Processing and Feature Recognition for Multiple Mechanical Impact Signals. Sensors 2024, 24, 5245. https://doi.org/10.3390/s24165245
Wang W, Han D, Duan X, Yong Y, Wu Z, Ma X, Zhang H, Dai K. Fast-Activated Minimal Gated Unit: Lightweight Processing and Feature Recognition for Multiple Mechanical Impact Signals. Sensors. 2024; 24(16):5245. https://doi.org/10.3390/s24165245
Chicago/Turabian StyleWang, Wenrui, Dong Han, Xinyi Duan, Yaxin Yong, Zhengqing Wu, Xiang Ma, He Zhang, and Keren Dai. 2024. "Fast-Activated Minimal Gated Unit: Lightweight Processing and Feature Recognition for Multiple Mechanical Impact Signals" Sensors 24, no. 16: 5245. https://doi.org/10.3390/s24165245
APA StyleWang, W., Han, D., Duan, X., Yong, Y., Wu, Z., Ma, X., Zhang, H., & Dai, K. (2024). Fast-Activated Minimal Gated Unit: Lightweight Processing and Feature Recognition for Multiple Mechanical Impact Signals. Sensors, 24(16), 5245. https://doi.org/10.3390/s24165245





