Quantification of the Uncertainty in Ultrasonic Wave Speed in Concrete: Application to Temperature Monitoring with Embedded Transducers
Abstract
:1. Introduction
2. Materials and Methods
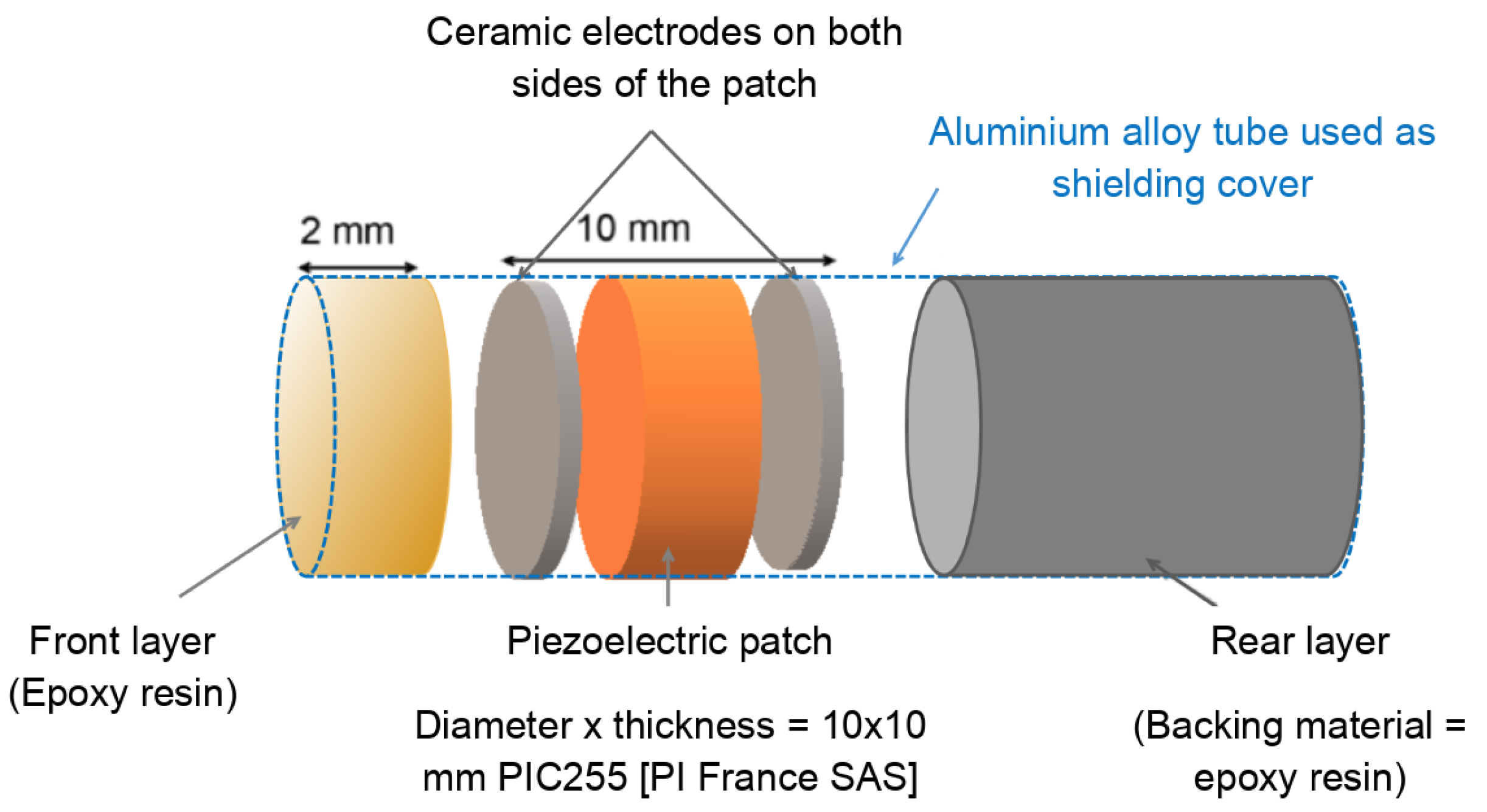
2.1. Fabrication of an Ultrasonic Transducer to Be Embedded in Concrete
2.2. Validation and Calibration of Piezoelectric Transducers
2.3. Concrete Specimens with Embedded Transducers
2.4. Conditioning Temperature and Monitoring System
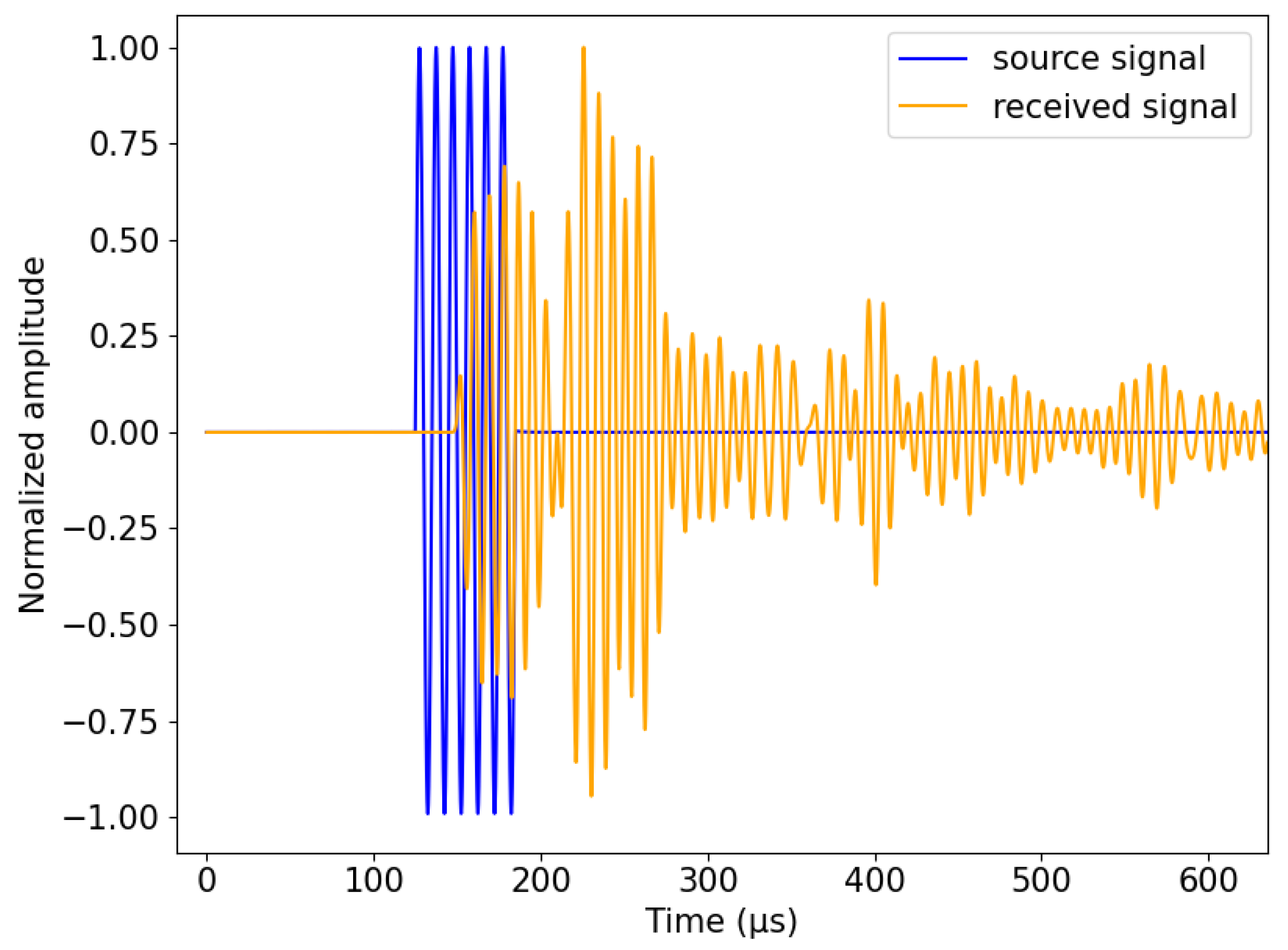
2.5. Signal Processing for Travel Time Estimation
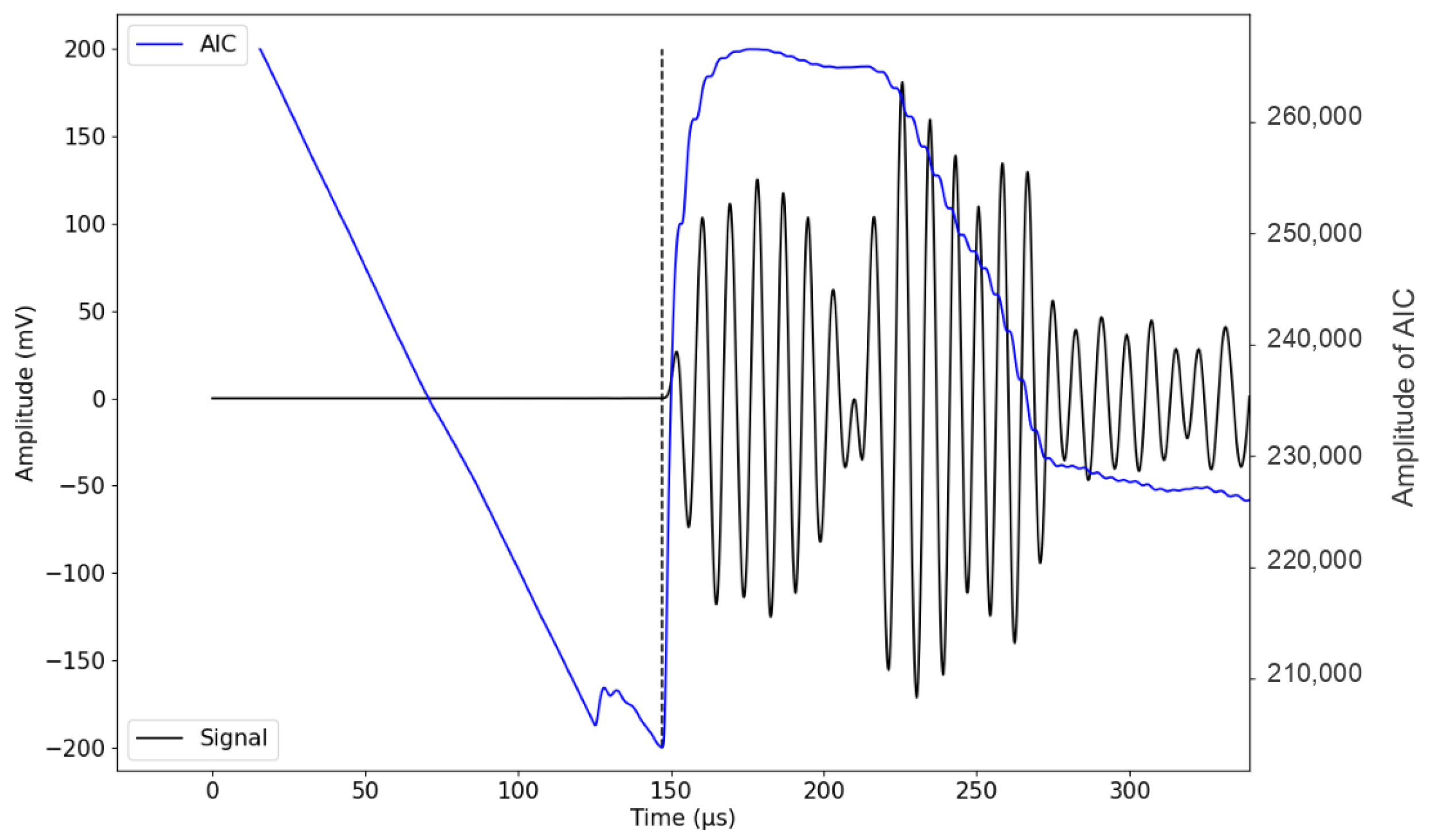
2.5.1. Determination of Onset Time
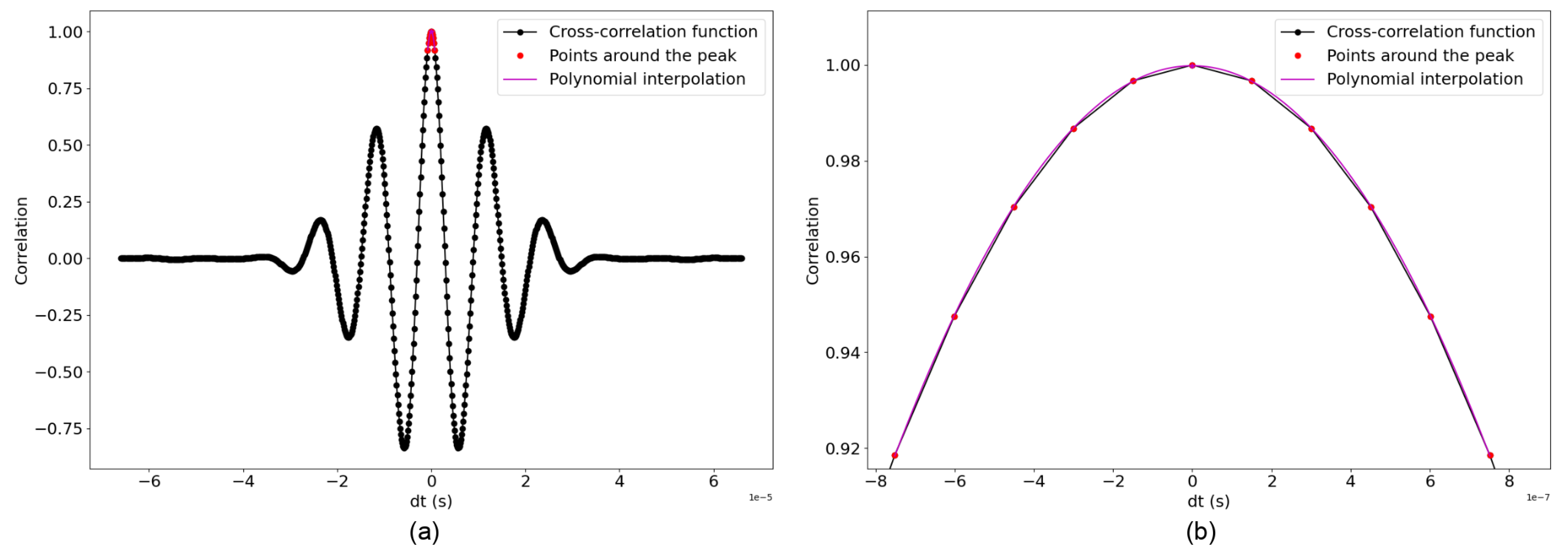
2.5.2. Determining the Relative Variation of Onset Time Using Cross-Correlation
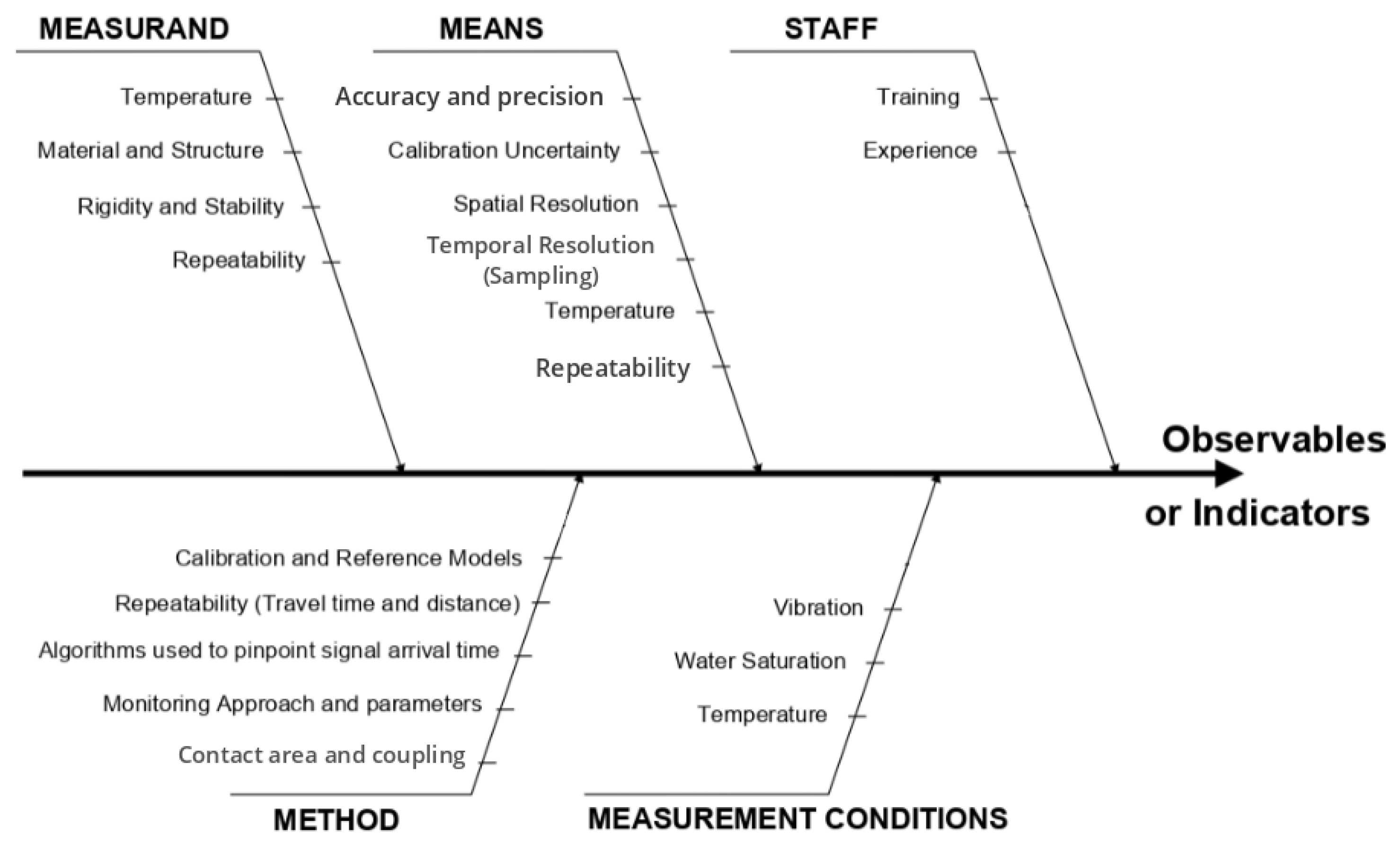
2.6. Measures and Uncertainties
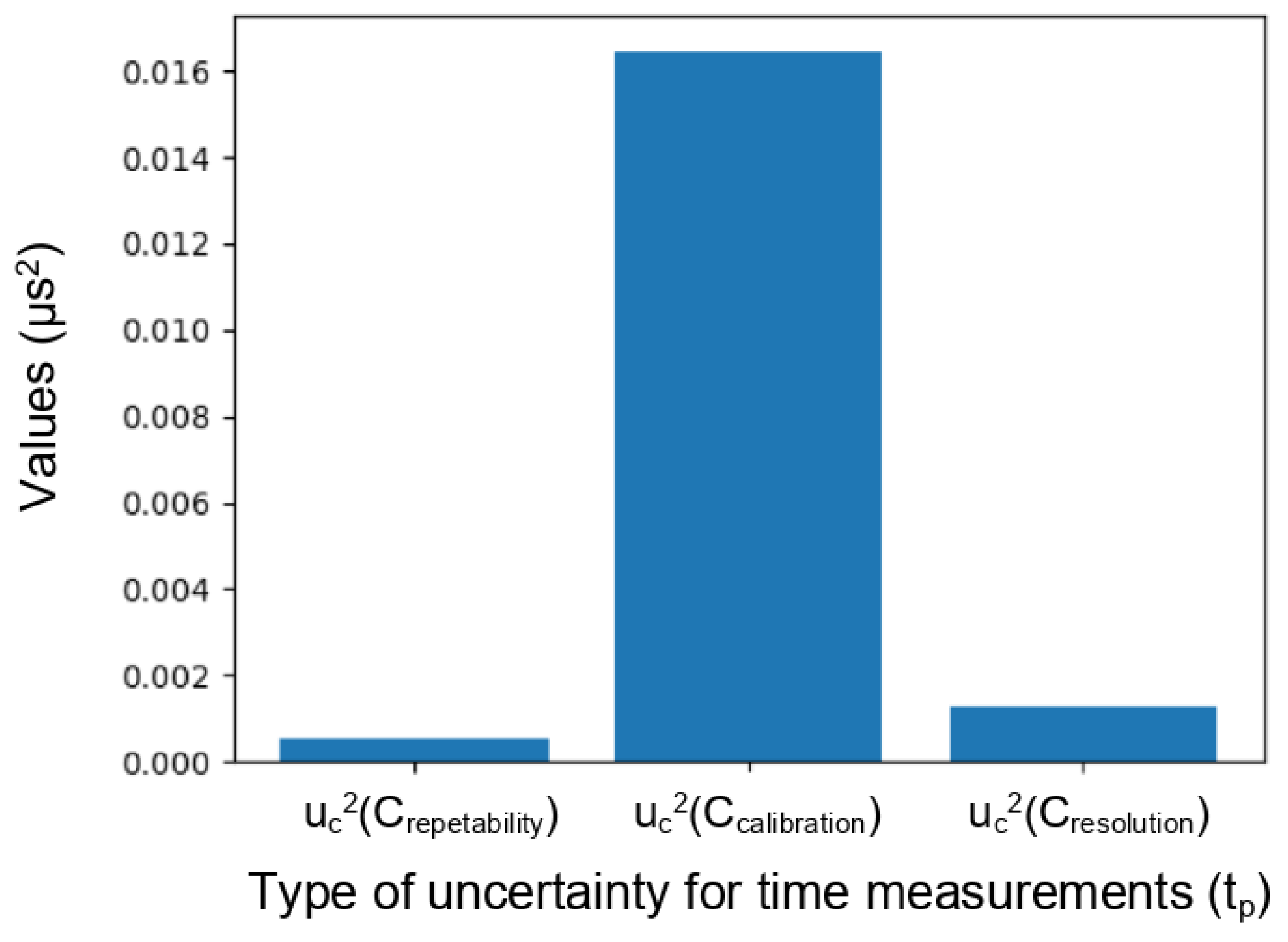
2.6.1. Uncertainty in Time
2.6.2. Uncertainty in Distance
2.6.3. Uncertainty in Absolute Velocity
2.6.4. Uncertainty in Relative Velocity
3. Results
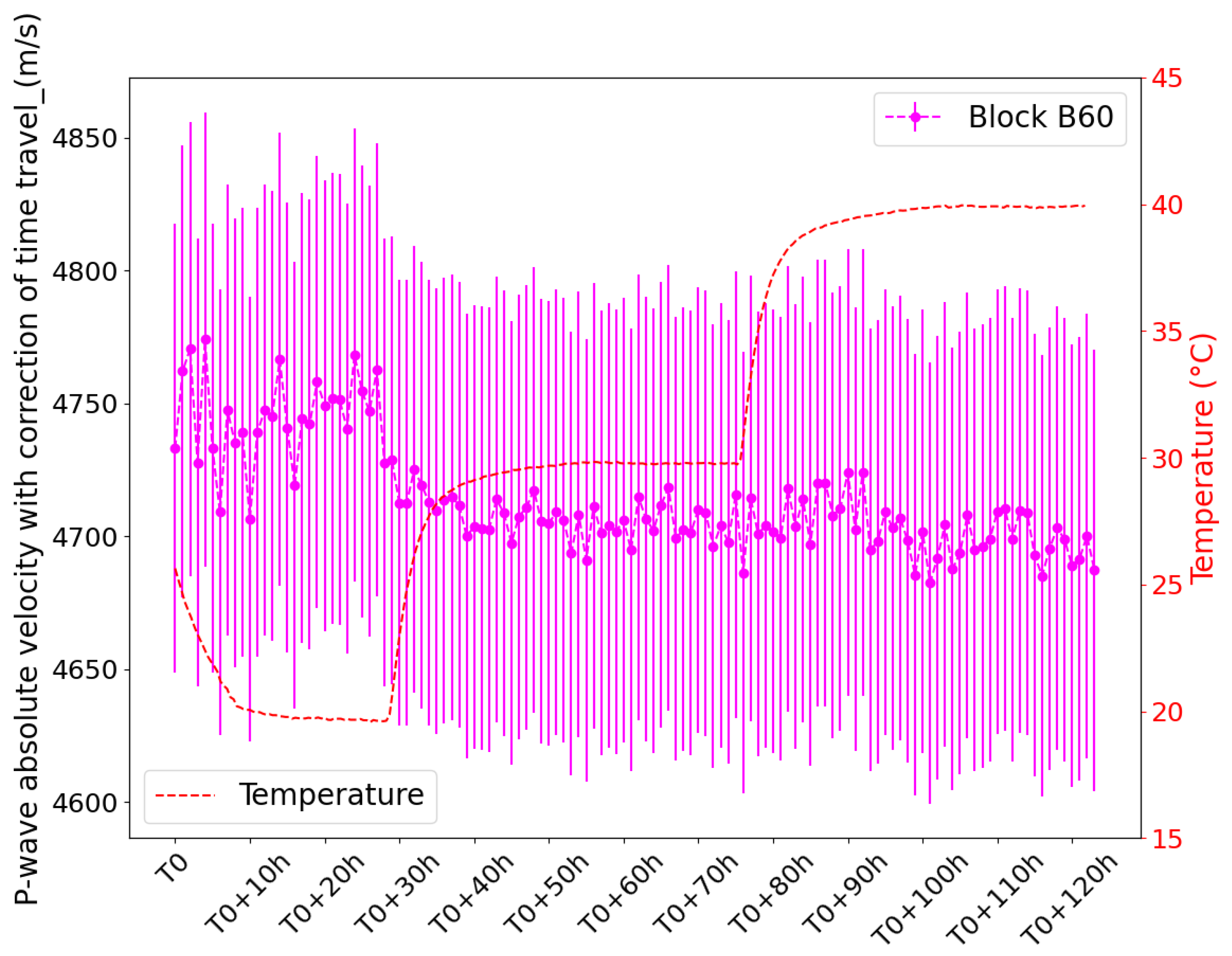
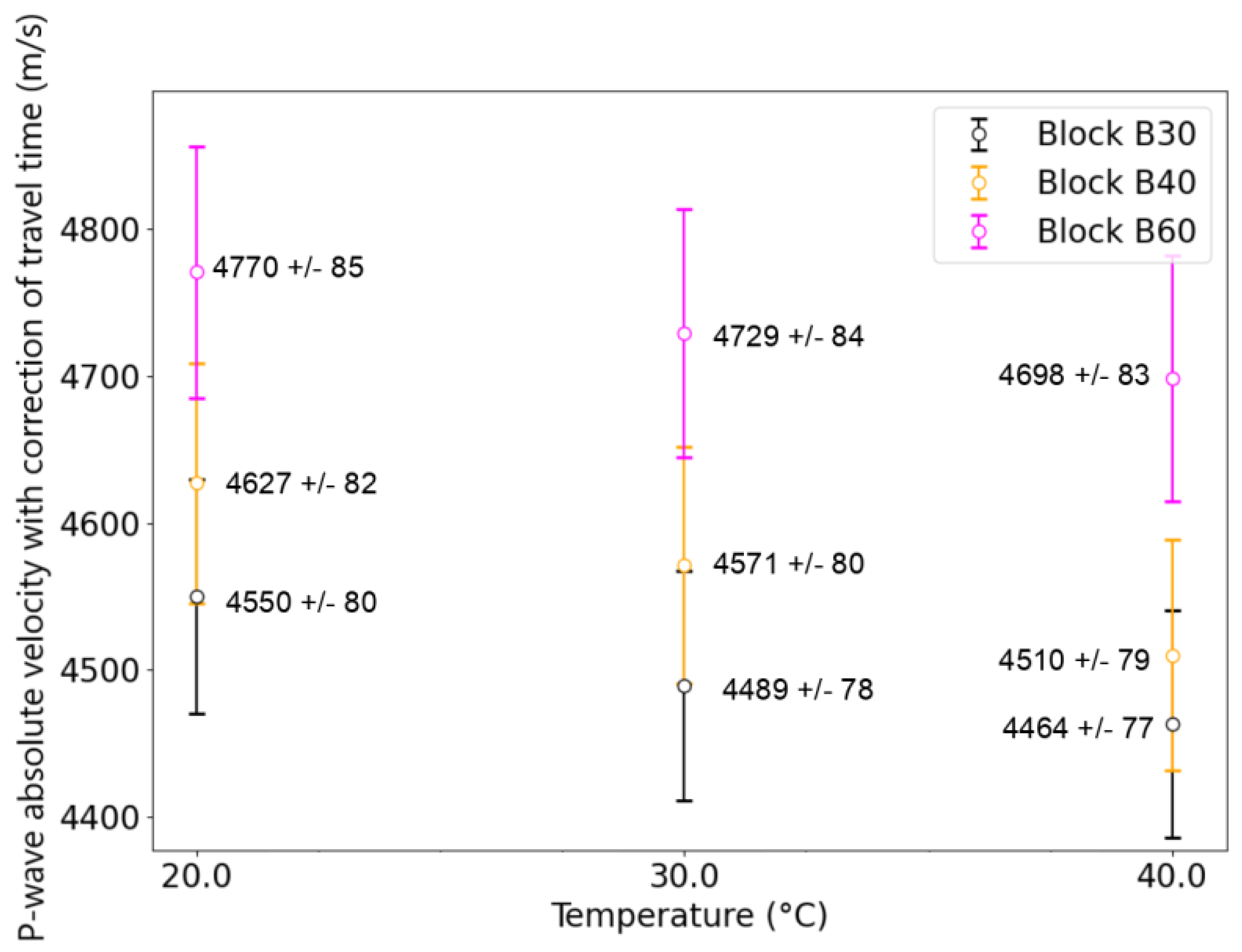
3.1. Influence of Temperature on the Absolute Vp Value
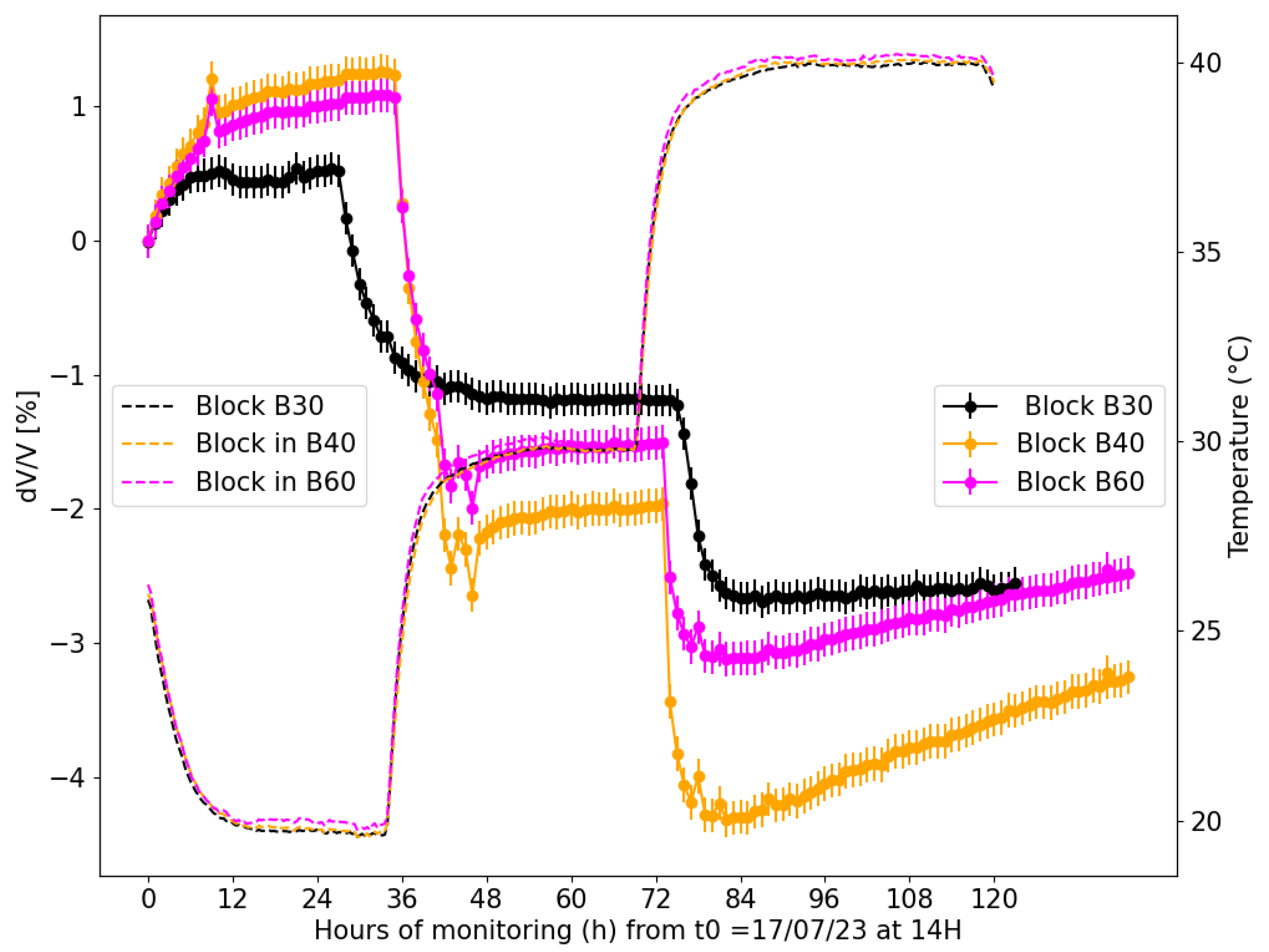
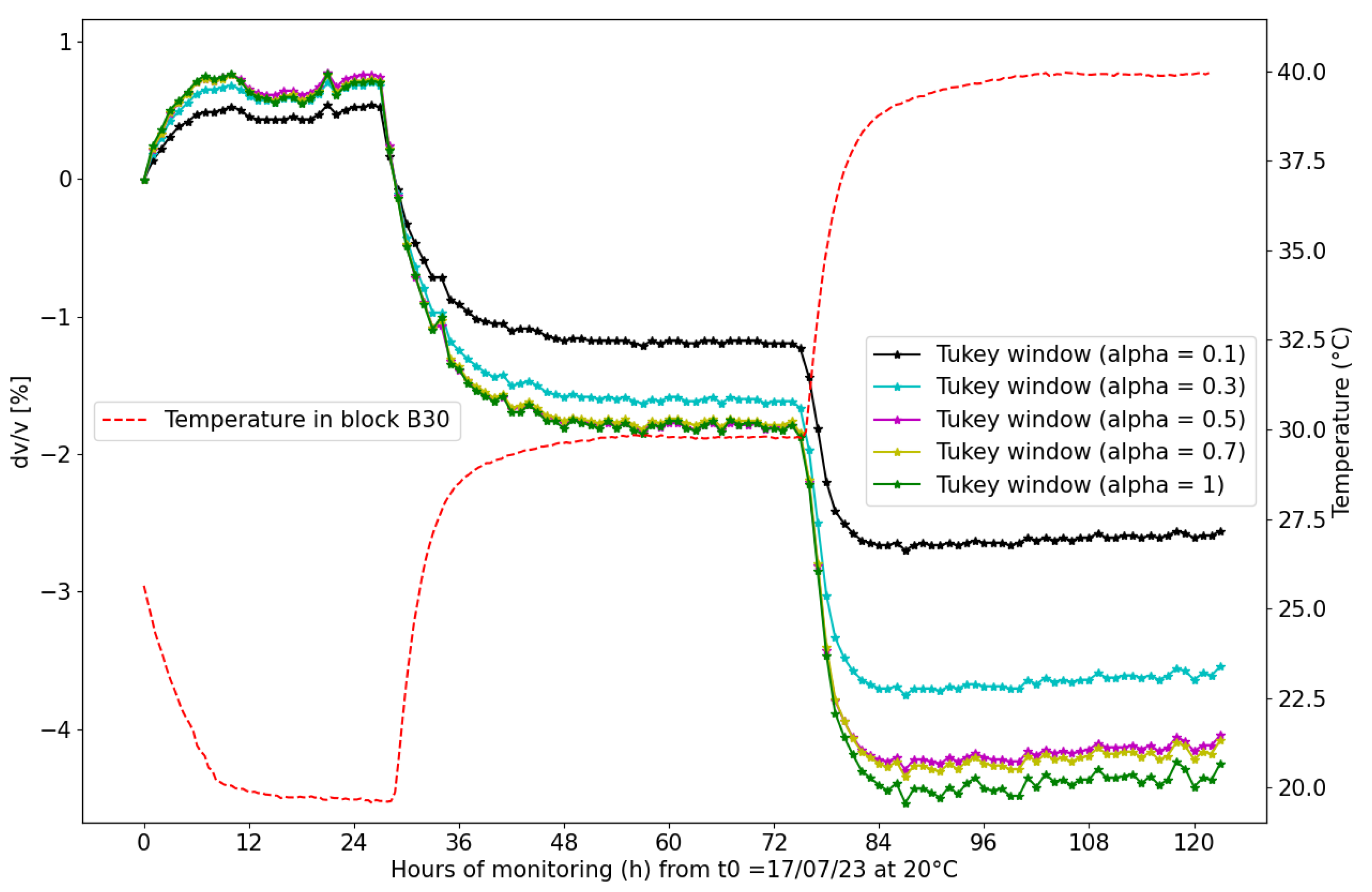
3.2. Influence of Temperature on the Relative Wave Velocity Change
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Greenwade, G.D. The Comprehensive Tex Archive Network (CTAN). TUGBoat 1993, 14, 342–351. [Google Scholar]
- Reddy, P.N.; Kavyateja, B.V.; Jindal, B.B. Structural health monitoring methods, dispersion of fibers, micro and macro structural properties, sensing, and mechanical properties of self-sensing concrete—A review. Struct. Concr. 2021, 22, 793–805. [Google Scholar] [CrossRef]
- Chen, M.; Gao, P.; Geng, F.; Zhang, L.; Liu, H. Mechanical and smart properties of carbon fiber and graphite conductive concrete for internal damage monitoring of structure. Constr. Build. Mater. 2017, 142, 320–327. [Google Scholar] [CrossRef]
- Granja, J.; Azenha, M. Continuous Monitoring of Concrete Mechanical Properties since an Early Age to Support Construction Phasing. In CONCREEP 10; American Society of Civil Engineers: Reston, VA, USA, 2014; pp. 1360–1370. [Google Scholar]
- Norris, A.; Saafi, M.; Romine, P. Temperature and moisture monitoring in concrete structures using embedded nanotechnology/microelectromechanical systems (MEMS) sensors. Constr. Build. Mater. 2008, 22, 111–120. [Google Scholar] [CrossRef]
- Tibaduiza Burgos, D.A.; Gomez Vargas, R.C.; Pedraza, C.; Agis, D.; Pozo, F. Damage identification in structural health monitoring: A brief review from its implementation to the use of data-driven applications. Sensors 2020, 20, 733. [Google Scholar] [CrossRef] [PubMed]
- Niederleithinger, E.; Wunderlich, C. Influence of small temperature variations on the ultrasonic velocity in concrete. AIP Conf. Proc. 2013, 1511, 390–397. [Google Scholar]
- Maierhofer, C.; Reinhardt, H.W.; Dobmann, G. Non-Destructive Evaluation of Reinforced Concrete Structures: Non-Destructive Testing Methods; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Monazami, M.; Sharma, A.; Gupta, R. Evaluating performance of carbon fiber-reinforced pavement with embedded sensors using destructive and non-destructive testing. Case Stud. Constr. Mater. 2022, 17, e01460. [Google Scholar] [CrossRef]
- Lawson, I.; Danso, K.; Odoi, H.; Adjei, C.; Quashie, F.; Mumuni, I.; Ibrahim, I. Non-destructive evaluation of concrete using ultrasonic pulse velocity. Res. J. Appl. Sci. Eng. Technol. 2011, 3, 499–504. [Google Scholar]
- Karaiskos, G.; Deraemaeker, A.; Aggelis, D.; Van Hemelrijck, D. Monitoring of concrete structures using the ultrasonic pulse velocity method. Smart Mater. Struct. 2015, 24, 113001. [Google Scholar] [CrossRef]
- Balayssac, J.P.; Garnier, V. Non-Destructive Testing and Evaluation of Civil Engineering Structures; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Yang, Y.; Hu, Y. Electromechanical impedance modeling of PZT transducers for health monitoring of cylindrical shell structures. Smart Mater. Struct. 2007, 17, 015005. [Google Scholar] [CrossRef]
- Luo, Z.; Deng, H.; Li, L.; Luo, M. A simple PZT transducer design for electromechanical impedance (EMI)-based multi-sensing interrogation. J. Civ. Struct. Health Monit. 2021, 11, 235–249. [Google Scholar] [CrossRef]
- Capineri, L.; Bulletti, A. Ultrasonic guided-waves sensors and integrated structural health monitoring systems for impact detection and localization: A review. Sensors 2021, 21, 2929. [Google Scholar] [CrossRef] [PubMed]
- Deraemaeker, A.; Dumoulin, C. Embedding ultrasonic transducers in concrete: A lifelong monitoring technology. Constr. Build. Mater. 2019, 194, 42–50. [Google Scholar] [CrossRef]
- Zhang, S.; Ma, W.; Xiong, Y.; Ma, J.; Chen, C.; Zhang, Y.; Li, Z. Ultrasonic monitoring of crack propagation of notched concretes using embedded piezo-electric transducers. J. Adv. Concr. Technol. 2019, 17, 449–461. [Google Scholar] [CrossRef]
- Ai, D.; Lin, C.; Zhu, H. Embedded piezoelectric transducers based early-age hydration monitoring of cement concrete added with accelerator/retarder admixtures. J. Intell. Mater. Syst. Struct. 2021, 32, 847–866. [Google Scholar] [CrossRef]
- Yoon, H.; Kim, Y.J.; Kim, H.S.; Kang, J.W.; Koh, H.M. Evaluation of early-age concrete compressive strength with ultrasonic sensors. Sensors 2017, 17, 1817. [Google Scholar] [CrossRef]
- Dumoulin, C.; Karaiskos, G.; Carette, J.; Staquet, S.; Deraemaeker, A. Monitoring of the ultrasonic P-wave velocity in early-age concrete with embedded piezoelectric transducers. Smart Mater. Struct. 2012, 21, 047001. [Google Scholar] [CrossRef]
- Teng, K.H.; Kot, P.; Muradov, M.; Shaw, A.; Hashim, K.; Gkantou, M.; Al-Shamma’a, A. Embedded smart antenna for non-destructive testing and evaluation (NDT&E) of moisture content and deterioration in concrete. Sensors 2019, 19, 547. [Google Scholar] [CrossRef]
- Chakraborty, J.; Katunin, A.; Klikowicz, P.; Salamak, M. Early crack detection of reinforced concrete structure using embedded sensors. Sensors 2019, 19, 3879. [Google Scholar] [CrossRef]
- Dumoulin, C.; Deraemaeker, A. Real-time fast ultrasonic monitoring of concrete cracking using embedded piezoelectric transducers. Smart Mater. Struct. 2017, 26, 104006. [Google Scholar] [CrossRef]
- Song, G.; Gu, H.; Mo, Y.L. Smart aggregates: Multi-functional sensors for concrete structures—A tutorial and a review. Smart Mater. Struct. 2008, 17, 033001. [Google Scholar] [CrossRef]
- Li, W.; Kong, Q.; Ho, S.C.M.; Mo, Y.; Song, G. Feasibility study of using smart aggregates as embedded acoustic emission sensors for health monitoring of concrete structures. Smart Mater. Struct. 2016, 25, 115031. [Google Scholar] [CrossRef]
- Jiang, S.F.; Wang, J.; Tong, S.Y.; Ma, S.L.; Tuo, M.B.; Li, W.J. Damage monitoring of concrete laminated interface using piezoelectric-based smart aggregate. Eng. Struct. 2021, 228, 111489. [Google Scholar] [CrossRef]
- Zhang, H.; Hou, S.; Ou, J. Smart aggregates for monitoring stress in structural lightweight concrete. Measurement 2018, 122, 257–263. [Google Scholar] [CrossRef]
- Saravanan, T.J.; Balamonica, K.; Priya, C.B.; Reddy, A.L.; Gopalakrishnan, N. Comparative performance of various smart aggregates during strength gain and damage states of concrete. Smart Mater. Struct. 2015, 24, 085016. [Google Scholar] [CrossRef]
- Garnier, V.; Piwakowski, B.; Abraham, O.; Villain, G.; Payan, C.; Chaix, J.F. Acoustic techniques for concrete evaluation: Improvements, comparisons and consistency. Constr. Build. Mater. 2013, 43, 598–613. [Google Scholar] [CrossRef]
- Zou, Z.; Meegoda, J.N. A validation of the ultrasound wave velocity method to predict porosity of dry and saturated cement paste. Adv. Civ. Eng. 2018, 2018, 3251206. [Google Scholar] [CrossRef]
- Métais, V.; Chekroun, M.; Le Marrec, L.; Le Duff, A.; Plantier, G.; Abraham, O. Influence of multiple scattering in heterogeneous concrete on results of the surface wave inverse problem. NDT&E Int. 2016, 79, 53–62. [Google Scholar]
- Thiery, M.; Baroghel-Bouny, V.; Bourneton, N.; Villain, G.; Stéfani, C. Modélisation du séchage des bétons: Analyse des différents modes de transfert hydrique. Rev. Eur. Génie Civ. 2007, 11, 541–577. [Google Scholar] [CrossRef]
- Metais, V. Auscultation Avec Les Ondes de Surface de Matériaux Très Hétérogènes. Ph.D. Thesis, Ecole centrale de Nantes, Nantes, France, 2016. [Google Scholar]
- Meyer, V.R. Measurement uncertainty. J. Chromatogr. A 2007, 1158, 15–24. [Google Scholar] [CrossRef]
- Li, Z.; Qin, L.; Huang, S. Embedded piezo-transducer in concrete for property diagnosis. J. Mater. Civ. Eng. 2009, 21, 643–647. [Google Scholar] [CrossRef]
- Hailu, B.; Hayward, G.; Gachagan, A.; McNab, A.; Farlow, R. Comparison of different piezoelectric materials for the design of embedded transducers for structural health monitoring applications. In Proceedings of the 2000 IEEE Ultrasonics Symposium. Proceedings. An International Symposium (Cat. No. 00CH37121), San Juan, PR, USA, 22–25 October 2000; Volume 2, pp. 1009–1012. [Google Scholar]
- Zhou, Q.; Lau, S.; Wu, D.; Shung, K.K. Piezoelectric films for high frequency ultrasonic transducers in biomedical applications. Prog. Mater. Sci. 2011, 56, 139–174. [Google Scholar] [CrossRef] [PubMed]
- Trnkoczy, A. Understanding and parameter setting of STA/LTA trigger algorithm. In New Manual of Seismological Observatory Practice (NMSOP); Deutsches GeoForschungsZentrum GFZ: Potsdam, Germany, 2009; pp. 1–20. [Google Scholar]
- Akaike, H. Markovian representation of stochastic processes and its application to the analysis of autoregressive moving average processes. Ann. Inst. Stat. Math. 1974, 26, 363–387. [Google Scholar] [CrossRef]
- Zhang, H.; Thurber, C.; Rowe, C. Automatic P-wave arrival detection and picking with multiscale wavelet analysis for single-component recordings. Bull. Seismol. Soc. Am. 2003, 93, 1904–1912. [Google Scholar] [CrossRef]
- Maeda, N. A method for reading and checking phase times in autoprocessing system of seismic wave data. Zisin 1985, 38, 365–379. [Google Scholar] [CrossRef]
- Kurz, J.H.; Grosse, C.U.; Reinhardt, H.W. Strategies for reliable automatic onset time picking of acoustic emissions and of ultrasound signals in concrete. Ultrasonics 2005, 43, 538–546. [Google Scholar] [CrossRef]
- Chaix, J.F.; Henault, J.M.; Garnier, V. Quality, Uncertainties and Variabilities. In Non-Destructive Testing and Evaluation of Civil Engineering Structures; Elsevier: Amsterdam, The Netherlands, 2018; pp. 199–229. [Google Scholar]







| Piezoelectric Transducers | PZT (Lead Zirconate Titanate) | PVDF (Polyvinylidene Fluoride) | Quartz (SiO2) | AlN (Aluminum Nitride) |
|---|---|---|---|---|
| Material | Lead zirconate titanate (PZT) | Polyvinylidene fluoride (PVDF) | Quartz (silicon dioxide) | Aluminum nitride |
| Design | Typically bare or with minimal protective coatings | Flexible polymer film | Rigid ceramic or crystal | Rigid ceramic |
| Interference Mitigation | Basic shielding, more susceptible to capacitive noise | Susceptible to electromagnetic interference | High resistance to interference | Good resistance to interference, can be sensitive to temperature |
| Calibration Requirement | Standard calibration, generally less complex | Requires careful calibration due to flexibility | Generally stable but needs calibration for precision | Calibration needed for specific applications, temperature-sensitive |
| Frequency Range | kHz to several MHz, depending on the design | 1 kHz to 100 MHz, typically used in lower-frequency applications | 1 kHz to several MHz, depending on the crystal cut | 100 kHz to several MHz, depending on the crystal cut |
| Sensitivity | High sensitivity, excellent for precise measurements | Lower sensitivity but flexible | High sensitivity, stable performance | High sensitivity and stable under varying conditions |
| Environmental Suitability | Robust but contains lead and may need additional protection for harsh environments | Flexible and suitable for dynamic surfaces but less durable | Very stable and suitable for harsh environments | Stable and durable but can be sensitive to temperature changes |
| Applications in SHM | Crack detection, delamination monitoring, and impact detection | Distributed strain sensing and vibration monitoring on flexible structures | Precision measurements and high-frequency applications | High-temperature environments and precision measurements |
| Description of the Blocks | B30 | B40 | B60 |
|---|---|---|---|
| Geometry of the blocks (L × l × h) (cm) | 30 × 30 × 30 | 30 × 30 × 30 | 30 × 30 × 30 |
| Distance between transducers (cm) | 10.01 | 9.98 | 10.03 |
| Density (kg/m3) | 2401 | 2408 | 2436 |
| Young’s Modulus E (MPa) | 35,719 | 37,321 | 43,279 |
| Compressive strength (MPa) | 34.4 | 46.9 | 64.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hariri, R.; Chaix, J.-F.; Shokouhi, P.; Garnier, V.; Saïdi-Muret, C.; Durand, O.; Abraham, O. Quantification of the Uncertainty in Ultrasonic Wave Speed in Concrete: Application to Temperature Monitoring with Embedded Transducers. Sensors 2024, 24, 5588. https://doi.org/10.3390/s24175588
Hariri R, Chaix J-F, Shokouhi P, Garnier V, Saïdi-Muret C, Durand O, Abraham O. Quantification of the Uncertainty in Ultrasonic Wave Speed in Concrete: Application to Temperature Monitoring with Embedded Transducers. Sensors. 2024; 24(17):5588. https://doi.org/10.3390/s24175588
Chicago/Turabian StyleHariri, Rouba, Jean-Francois Chaix, Parisa Shokouhi, Vincent Garnier, Cécile Saïdi-Muret, Olivier Durand, and Odile Abraham. 2024. "Quantification of the Uncertainty in Ultrasonic Wave Speed in Concrete: Application to Temperature Monitoring with Embedded Transducers" Sensors 24, no. 17: 5588. https://doi.org/10.3390/s24175588
APA StyleHariri, R., Chaix, J.-F., Shokouhi, P., Garnier, V., Saïdi-Muret, C., Durand, O., & Abraham, O. (2024). Quantification of the Uncertainty in Ultrasonic Wave Speed in Concrete: Application to Temperature Monitoring with Embedded Transducers. Sensors, 24(17), 5588. https://doi.org/10.3390/s24175588





