Fresnel Diffraction Model for Laser Dazzling Spots of Complementary Metal Oxide Semiconductor Cameras
Abstract
:1. Introduction
2. Experimental Set-Up
3. Experimental Results and Analysis
4. Simulation Methods and Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CMOS | Complementary Metal Oxide Semiconductor |
| CCD | Charge Coupled Device |
| WFOV | Wide Field of View |
| UAVs | Unmanned Aerial Vehicles |
| CW | Continuous Wave |
| FSI-CMOS | Front Side Illumination CMOS |
| BSI-CMOS | Back Side Illumination CMOS |
| OD | Optical Density |
| CDS | Correlated Double Sample |
References
- Zhu, Z.; Guo, K.; Wu, Y.; Liu, T.; Wu, M.; Lu, D. A CMOS 28 Gbps Low Power and High Jitter Tolerance CDR Circuit in Optical Communication Applications. J. Air Force Eng. Univ. 2022, 23, 77–82. [Google Scholar]
- Li, C.; Wang, S.; Chen, C. Design and implementation of lane deviation recognition system based on CMOS image acquisition. China Meas. Test 2022, 48, 106–110. [Google Scholar]
- Wang, X. Design of image processor for high-definition medical electronic endoscope based on CMOS. Biomed. Eng. Clin. Med. 2020, 24, 387–392. [Google Scholar]
- Lei, X.; Li, Y. The latest developments of CMOS sensors in digital industrial cameras. Sens. World 2017, 23, 7–11. [Google Scholar]
- Ye, W.; Xiao, K.; Kang, B.; Zhang, X. The application of CMOS sensors in aerial photogrammetry. Bull. Surv. Mapp. 2017, 8, 150–151. [Google Scholar]
- Li, F.; Yang, X.; Lu, X.; Xin, L.; Lu, M.; Zhang, N. A new hyper-temporal imaging mode for spaceborne CMOS cameras. Natl. Remote Sens. Bull. 2021, 5, 514–525. [Google Scholar] [CrossRef]
- Steinvall, O. Laser dazzling: An overview. In Proceedings of the Technologies for Optical Countermeasures XIX, Amsterdam, The Netherlands, 3–6 September 2023; Volume 12738, pp. 17–31. [Google Scholar]
- Wen, J.; Bian, J.; Li, X.; Kong, H.; Guo, L.; Lv, G. Research progress of laser dazzle and damage CMOS image sensor (invited). Infrared Laser Eng. 2023, 52, 379–393. [Google Scholar]
- Ni, X.; Shen, Z.; Lu, J. Study of Laser Destruction for Optoelectronic Device and Semiconductor Material. J. Optoelectron. Laser 1997, 8, 487. [Google Scholar]
- Qiu, W.; Wang, R.; Xu, Z.; Cheng, X. Study on the light response characteristics of PV HgCdTe linear array detector with CTIA circuit. Infrared Laser Eng. 2013, 42, 1394–1398. [Google Scholar]
- Jiang, T.; Cheng, X.A.; Zheng, X.; Jiang, H.; Lu, Q. The over-saturation phenomenon of a Hg0.46Cd0.54Te photovoltaic detector irradiated by a CW laser. Semicond. Sci. Technol. 2011, 26, 115004. [Google Scholar] [CrossRef]
- Jiang, T.; Zheng, X.; Cheng, X.; Xu, Z.; Jiang, H.; Lu, Q. The carrier transportation of photoconductive HgCdTe detector irradiated by CW bandoff laser. Infrared Millim Waves 2012, 31, 216–221. [Google Scholar] [CrossRef]
- Lavine, J.P.; Chang, W.C.; Anagnostopoulos, C.N.; Burkey, B.C.; Nelson, E. Monte Carlo simulation of the photoelectron crosstalk in silicon imaging devices. IEEE Trans. Electron Devices 1985, 32, 2087–2091. [Google Scholar] [CrossRef]
- Machet, N.; Kubert-Habart, C.; Baudinaud, V.; Fournier, D.; Forget, B. Study of the mechanism of electronic diffusion in a CCD camera subject to intense laser illumination. In Proceedings of the RADECS 97: Fourth European Conference on Radiation and its Effects on Components and Systems (Cat. No.97TH8294), Cannes, France, 15–19 September 1997; pp. 417–423. [Google Scholar]
- Liping, L.; Fu, L.; Rongzhu, Z. Research on electrical crosstalk of CMOS array. High Power Laser Part. Beams 2015, 27, 108–112. [Google Scholar]
- Sheng, L.; Zhang, Z.; Zhang, J.; Zuo, H. Pixel upset effect and mechanism of CW laser irradiated CMOS camera. Infrared Laser Eng. 2016, 45, 47–50. [Google Scholar]
- Wng, N.; Nie, J. Experimental study on supercontinuum laser irradiating a visible light CMOS imaging sensor. Infrared Laser Eng. 2017, 46, 128–133. [Google Scholar]
- Lin, J.; Shu, R.; Huang, G.; Fang, K.; Yan, Z. Study on Threshold of Laser Damage to CCD and CMOS Image Sensors. J. Infrared Millim. Waves 2008, 27, 475–478. [Google Scholar]
- Christopher, W.; David, J. Visible-Band Nanosecond Pulsed Laser Damage Thresholds of Silicon 2D Imaging Arrays. Sensors 2022, 22, 2526. [Google Scholar] [CrossRef]
- Bastian, S.; Gunnar, R.; Bernd, E. Impact of threshold assessment methods in laser-induced damage measurements using the examples of CCD, CMOS, and DMD. Appl. Opt. 2021, 60, F39–F49. [Google Scholar]
- Schleijpen, R.H.M.A.; van den Heuvel, J.C.; Mieremet, A.L.; Mellier, B.; van Putten, F.J.M. Laser dazzling of focal plane array cameras. In Proceedings of the Infrared Imaging Systems: Design, Analysis, Modeling, and Testing XVIII, Orlando, FL, USA, 11–13 April 2007. [Google Scholar]
- Jiang, T.; Cheng, X. Saturation interference to three-channel CCD camera by CW laser. High Power Laser Part. Beams 2010, 22, 2571–2574. [Google Scholar] [CrossRef]
- Han, K.; Xu, X. Study on Saturation Area of Detector Based on Envelope of Airy Function. Chin. J. Lasers 2010, 37, 94. [Google Scholar]
- Yang, H.; Guan, S.; Shao, M.; Liu, X. Study of saturation effect on electro-optical imaging system induced by intense light. Electro-Opt. Technol. Appl. 2018, 33, 21. [Google Scholar]
- Sun, K.; Jiang, H.; Cheng, X. Distribution of In-field Stray Light Due to Surface Scattering from Primary Mirror Illuminated by Intense Light. Opt. Precis. Eng. 2011, 19, 493–499. [Google Scholar] [CrossRef]
- Wang, A.; Guo, F.; Zhu, Z.; Xu, Z.; Cheng, X. Comparative study of hard CMOS damage irradiated by CW laser and single-pulse ns laser. High Power Laser Part. Beams 2014, 26, 49–53. [Google Scholar]
- Benoist, K.W.; Schleijpen, R.H. Modeling of the over-exposed pixel area of CCD cameras caused by laser dazzling. In Proceedings of the Technologies for Optical Countermeasures XI; and High-Power Lasers 2014: Technology and Systems, Amsterdam, The Netherlands, 24–25 September 2014; Volume 9251, pp. 105–113. [Google Scholar]
- Niu, S.; Yin, J.; Cao, W.; Yang, Y.; Wang, X.; Minmin, S. Simulation modeling of laser jamming spot in infrared imaging system. Infrared Laser Eng. 2017, 46, 19–23. [Google Scholar]
- Lewis, G.D.; Struyve, R.; Boeckx, C.; Vandewal, M. The effectiveness of amplitude modulation on the laser dazzling of a mid-infrared imager. In Proceedings of the High-Power Lasers and Technologies for Optical Countermeasures, Berlin, Germany, 5–7 September 2022; Volume 12273, pp. 120–137. [Google Scholar]
- Santos, C.N.; Chrétien, S.; Merella, L.; Vandewal, M. Visible and near-infrared laser dazzling of CCD and CMOS cameras. In Proceedings of the Technologies for Optical Countermeasures XV, Berlin, Germany, 10–12 September 2018; Volume 10797, pp. 179–187. [Google Scholar]
- Özbilgin, T.; Yeniay, A. Laser dazzling analysis of camera sensors. In Proceedings of the Technologies for Optical Countermeasures XV, Berlin, Germany, 10–12 September 2018; Volume 10797, pp. 156–165. [Google Scholar]
- Shapiro, J.H.; Boyd, R.W. The physics of ghost imaging. Quantum Inf. Process. 2012, 11, 949–993. [Google Scholar] [CrossRef]
- Tiwari, A.; Talwekar, R. Analysis and mathematical modelling of charge injection effect for efficient performance of CMOS imagers and CDS circuit. IET Circuits Devices Syst. 2020, 14, 1038–1048. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
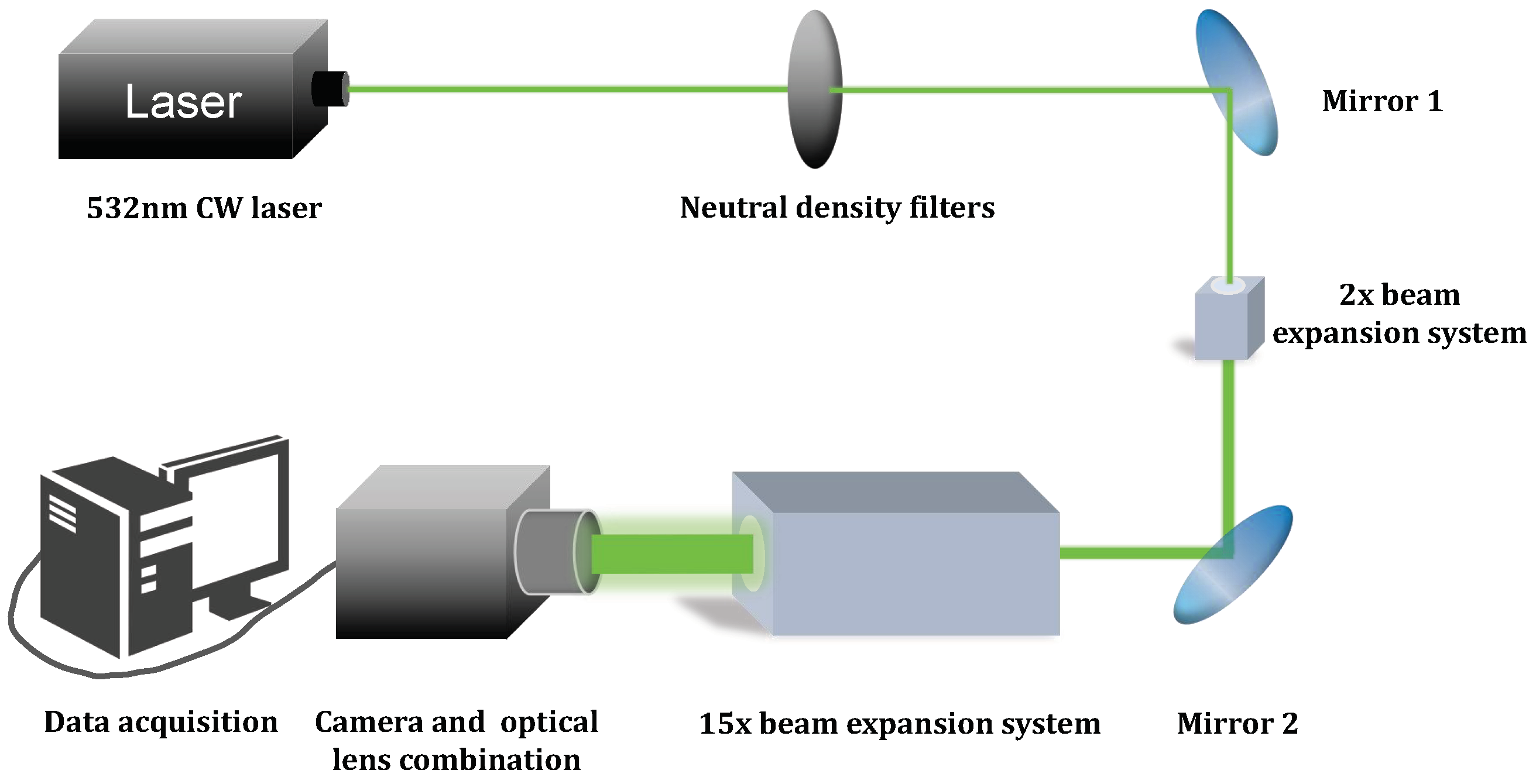
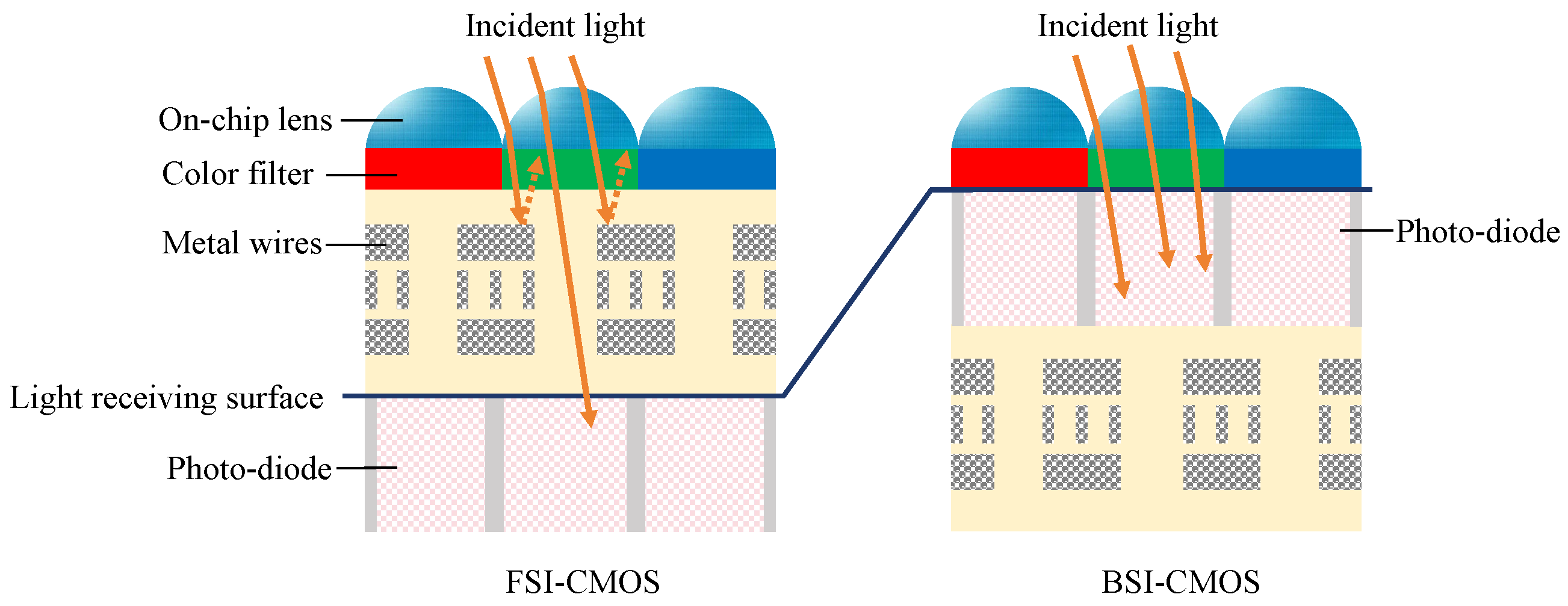

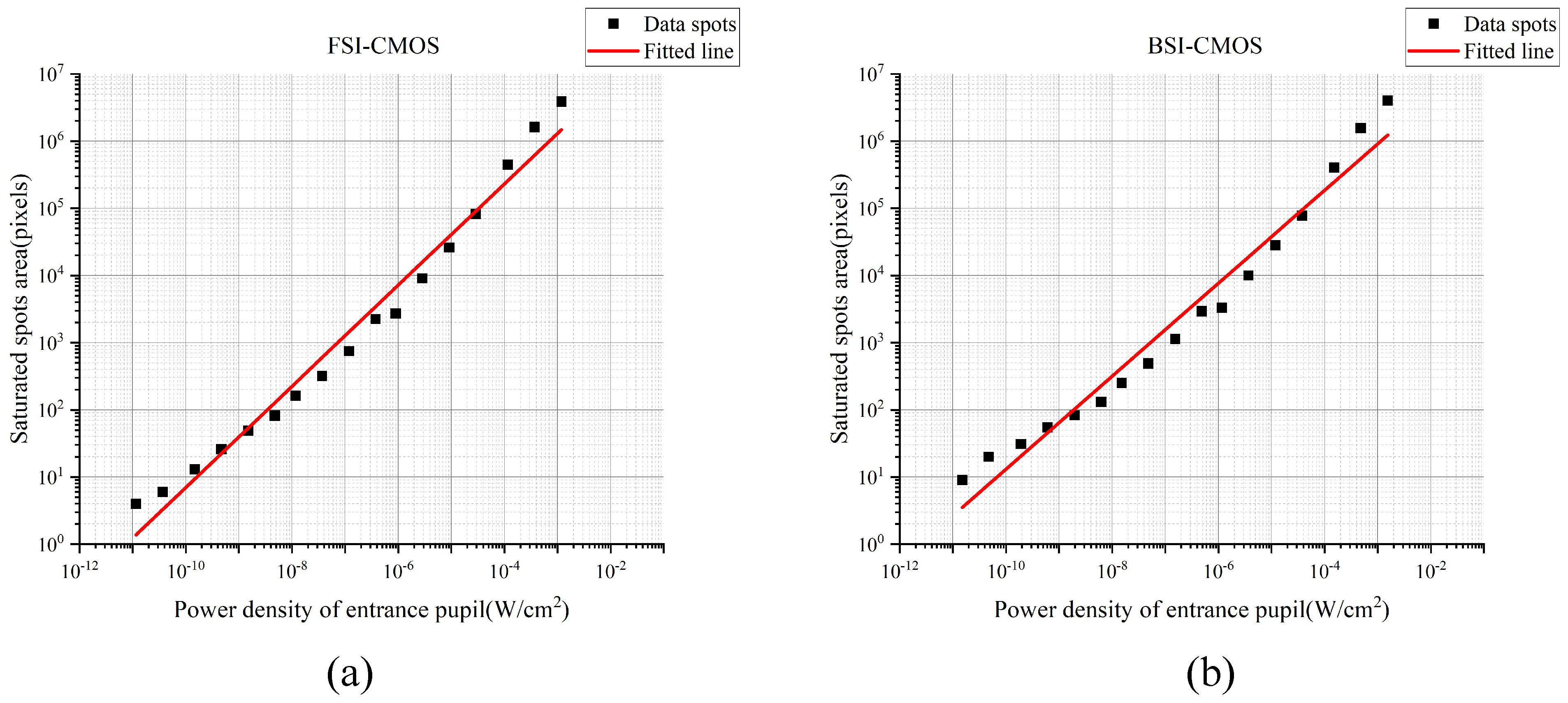
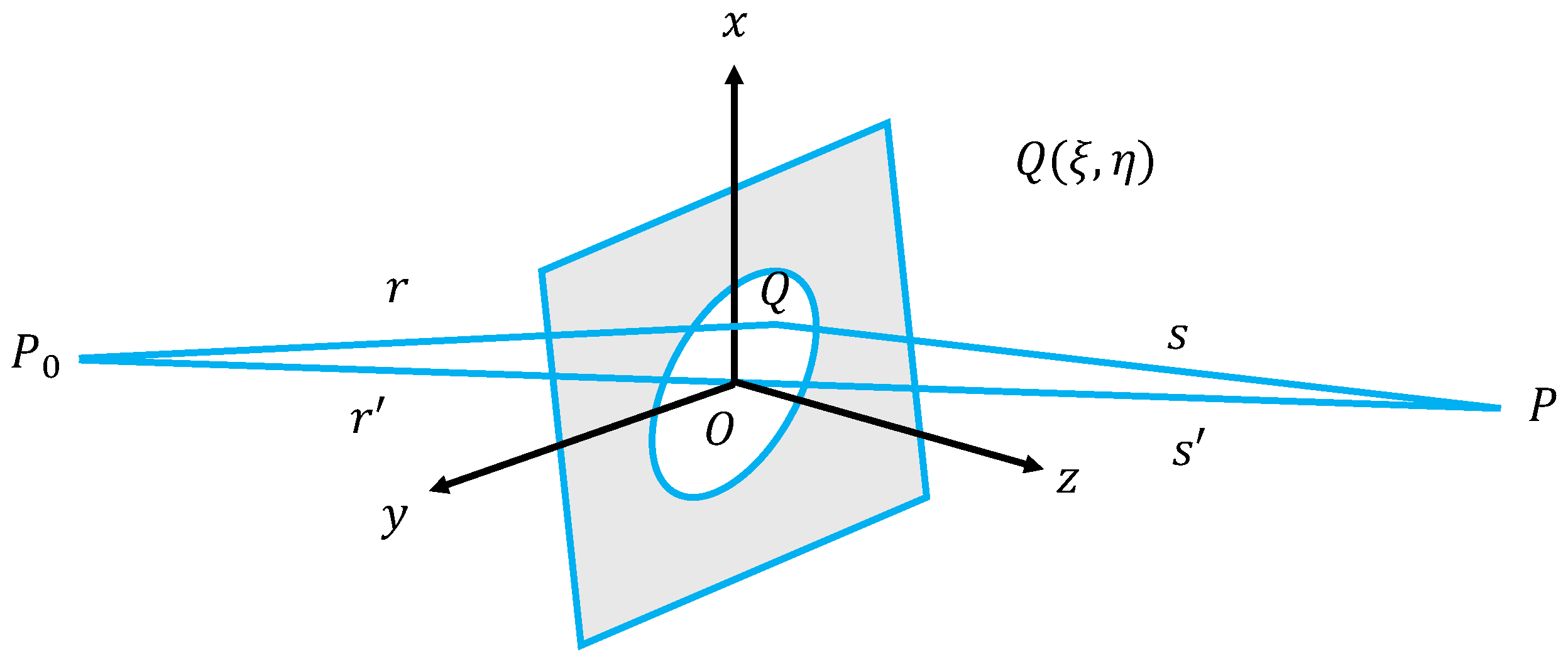
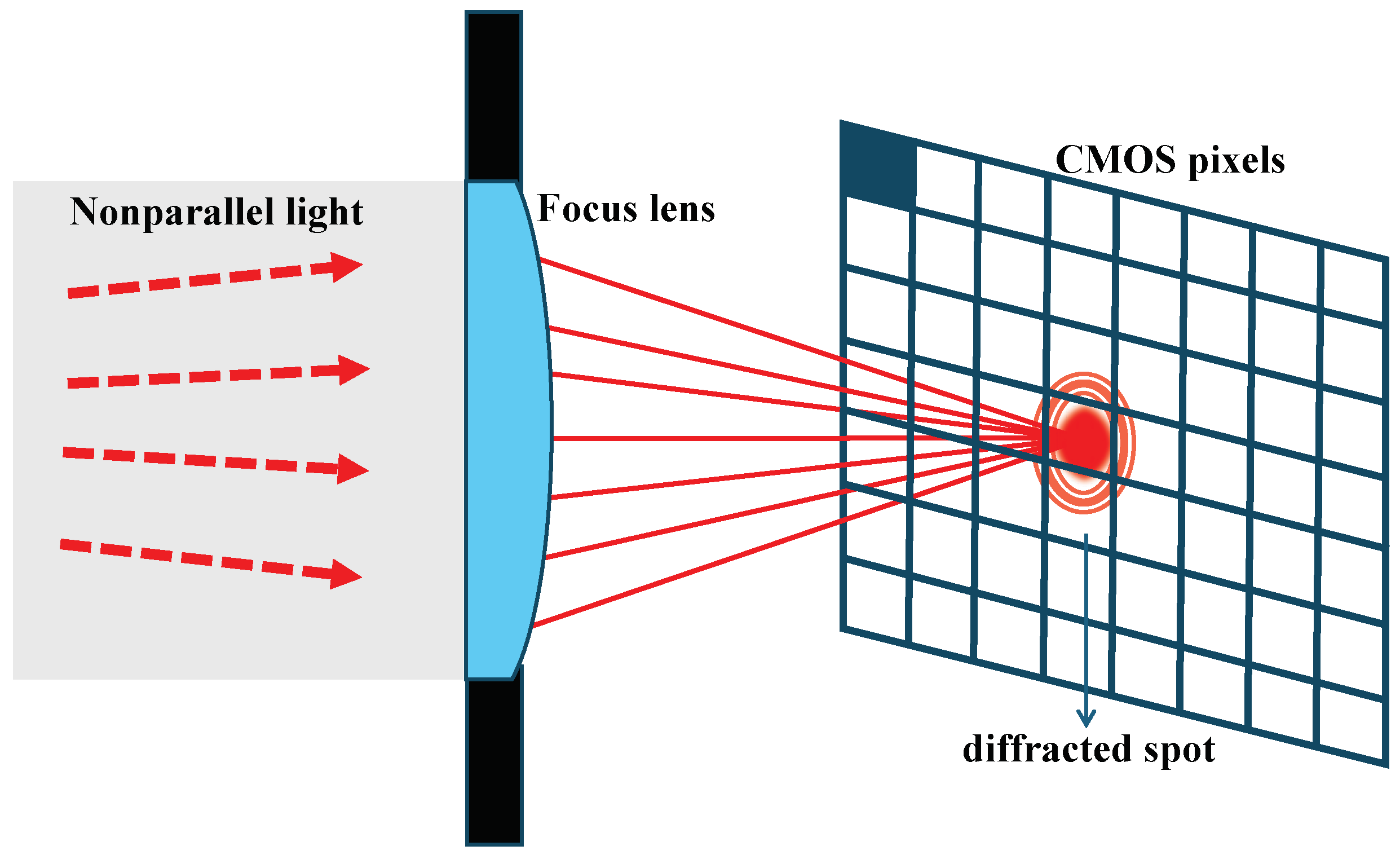
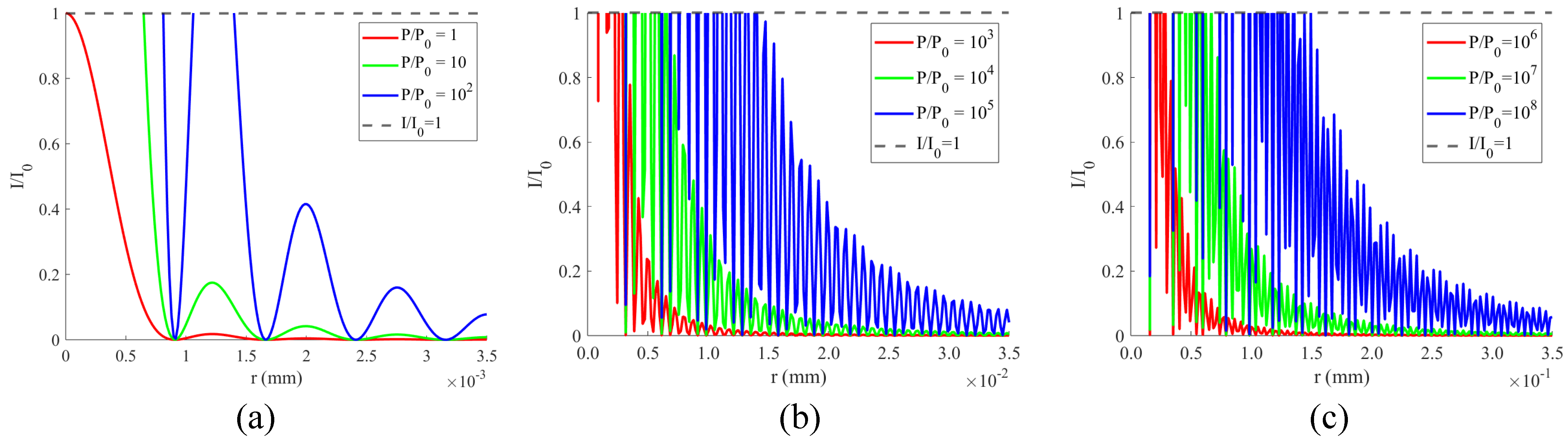
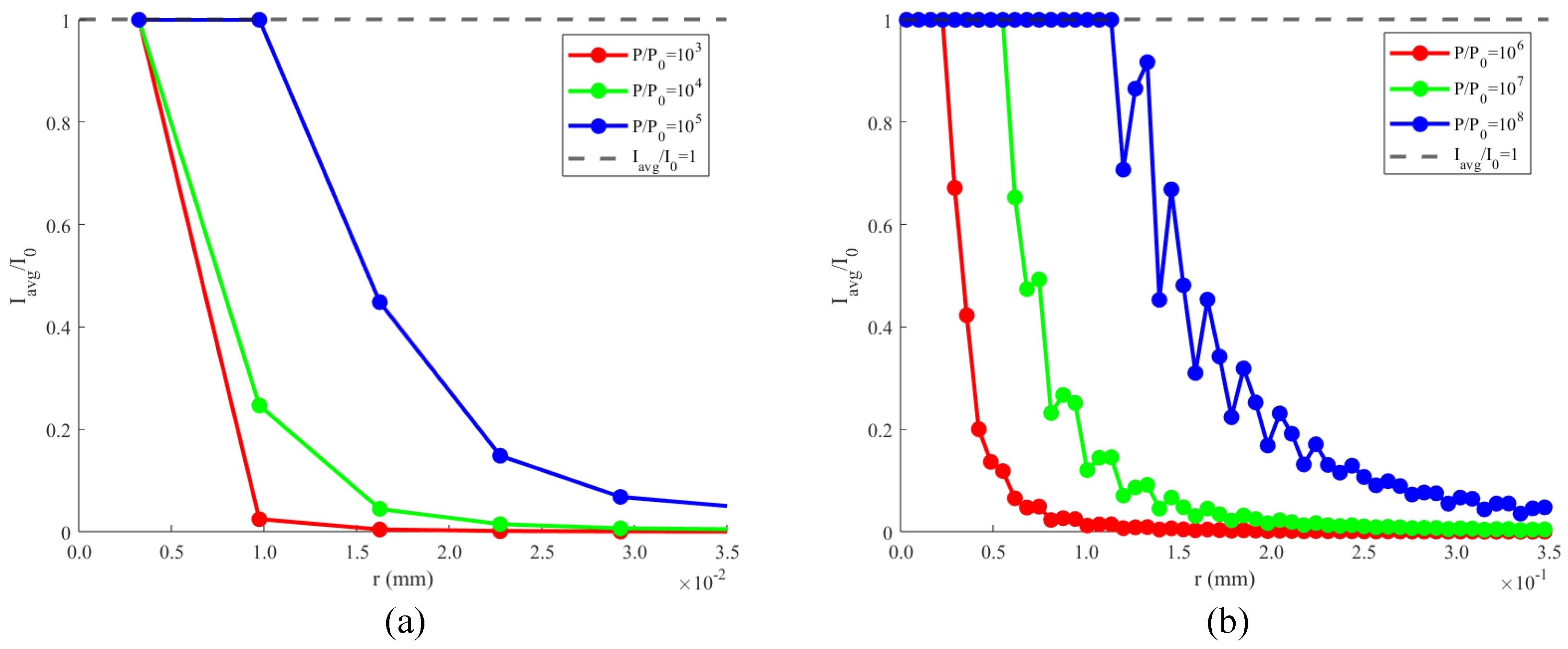
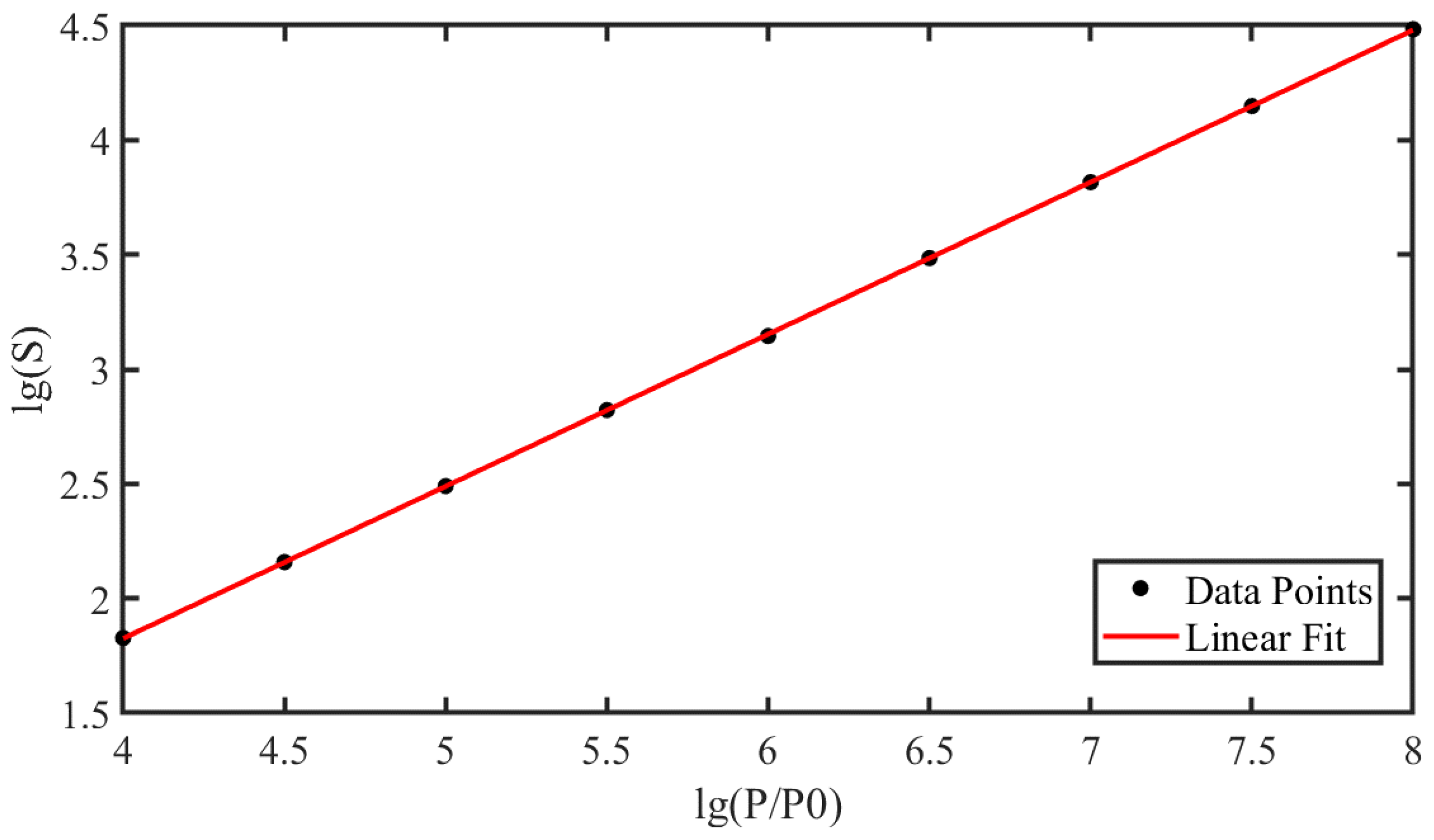
| Laser Parameters | Value | Unit of Parameters |
|---|---|---|
| Wavelength | 532 ± 1 | nm |
| Spectral Line Width | <1 | nm |
| Output Power | 0–2500 | mW |
| Transverse Mode | TEM00 | / |
| Beam Quality (M2 factor) | <1.5 | / |
| Polarization | Line Polarization | / |
| Polarization Ratio | >100:1 | / |
| Beam Diameter at Aperture | 3 | mm |
| Beam Divergence (full angle) | <1.5 | mrad |
| Power Supply | 90–240 VAC@50 Hz | / |
| Operation Temperature | 10–35 | °C |
| Sensor Type | Focal Plane Size | Resolution | Pixel Size | Bit Depth |
|---|---|---|---|---|
| FSI CMOS | 13.3 mm × 13.3 mm | 2048 × 2048 | 6.5 μm × 6.5 μm | 16 |
| BSI CMOS | 13.3 mm × 13.3 mm | 2048 × 2048 | 6.5 μm × 6.5 μm | 16 |
| Wavelength | Lens Focal Length | Circular Aperture Diameter | Power Range |
|---|---|---|---|
| 532 nm | 35 mm | 25 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Xu, Z.; Zhong, H.; Cheng, X.; Xing, Z.; Zhang, J. Fresnel Diffraction Model for Laser Dazzling Spots of Complementary Metal Oxide Semiconductor Cameras. Sensors 2024, 24, 5781. https://doi.org/10.3390/s24175781
Wang X, Xu Z, Zhong H, Cheng X, Xing Z, Zhang J. Fresnel Diffraction Model for Laser Dazzling Spots of Complementary Metal Oxide Semiconductor Cameras. Sensors. 2024; 24(17):5781. https://doi.org/10.3390/s24175781
Chicago/Turabian StyleWang, Xinyu, Zhongjie Xu, Hairong Zhong, Xiang’ai Cheng, Zhongyang Xing, and Jiangbin Zhang. 2024. "Fresnel Diffraction Model for Laser Dazzling Spots of Complementary Metal Oxide Semiconductor Cameras" Sensors 24, no. 17: 5781. https://doi.org/10.3390/s24175781
APA StyleWang, X., Xu, Z., Zhong, H., Cheng, X., Xing, Z., & Zhang, J. (2024). Fresnel Diffraction Model for Laser Dazzling Spots of Complementary Metal Oxide Semiconductor Cameras. Sensors, 24(17), 5781. https://doi.org/10.3390/s24175781






