Low-Cost Dynamometer for Measuring and Regulating Wrist Extension and Flexion Motor Tasks in Electroencephalography Experiments
Abstract
1. Introduction
| Reference | Largest MVC (N) | Smallest MVC (N) | ||
|---|---|---|---|---|
| WE | WF | WE | WF | |
| [19] | 68.88 | 88.27 | 27.37 | 35.20 |
| [7] | 28.57 | 56.12 | 18.37 | 25.51 |
| [20] | 40.82 | 61.22 | 27.93 | 33.52 |
| [21] | 63 | 73 | 45 | 54 |
| [22] | 214 | - | - | - |
| Motor Task for Which Force/Torque Was Measured | Type of Transducer | Used with EEG Recording | Visual Feedback | Reference |
|---|---|---|---|---|
| Isometric WE and WF torque performed at 15% of MVC | Strain gauge and commercial strain gauge amplifier | Yes | Yes | [16] |
| Peak isometric torque of WE and WF | Torque sensor (Scaime DF30-25 Nm) | No | Yes | [19] |
| WE and WF | Wristalyzer with strain gauge torque sensor | Yes | Yes | [17,23] |
| Peak isometric torque of WE and WF | Torque sensor (UTMII-20 Nm) | No | No | [7] |
| Grip force and isokinetic wrist torque | Miniature load cells (Honeywell Sensotec, 13/2244-06-10) | No | No | [20] |
| Isometric WE and WF in different positions | Le Bow load cells (136 kg capacity, Model No. 3397) | No | No | [21] |
| WE; flexion and extension of knee, elbow, neck and foot; shoulder and hip abduction; hip flexion. | Handheld dyno containing a modified Wika pressure gauge (0–300 N) | No | No | [22] |
2. Materials and Methods
2.1. Design Specifications
2.2. Mechanical Design and Construction
2.3. Electronic Measurement System Design and Construction
- A participant performed WF with their RH. The hand tried to move anticlockwise about the wrist joint but was held in place by the wrist supports, forearm supports and left steel cylindrical rod. The palm of the hand pushed the left steel cylindrical force rod medially and perpendicular to the palm and metacarpals.
- The force rod in turn pushed the left steel pin medially in its aluminium casing.
- The left steel pin pushed onto the left load cell, which converted the force of the WF into a voltage.
- This analogue voltage was then conditioned and converted to a digital force by the force conditioning system.
- An Arduino Uno microprocessor computed the digital force signal and sent it to the computer.
- The computer interpreted the force and computed the percentage of force relative to the stored MVC force value.
- The force percentage was displayed on the force gauge interface on the computer screen.
2.4. Software for Force Signal Processing
- The first routine measured the resting force prior to the performance of the repetitive motor tasks. This resting force is denoted as the zero-force-offset value.
- The second routine measured the MVC prior to the performance of the repetitive motor tasks.
- The third routine measured, recorded and displayed the real-time normalised force data as a participant performed multiple repetitions of the motor tasks. This routine is portrayed in Figure 6. It is dependent on the first and second routines.
2.5. Calibration
2.6. Testing Protocol
- Test 1: The accuracy of the measured raw force values was tested. This test was the starting point of the three signal processing routines.
- Test 2: Once the basic raw force measurement was verified, the calculation and display of the relative forces were tested. This verified that users of the device received sufficiently accurate force feedback.
- Test 3: Subsequently, the device was tested within an EEG recording experiment. The force data during this experiment was logged and analysed to verify that participants did in fact perform MVC-normalised repetitions of WE and WF.
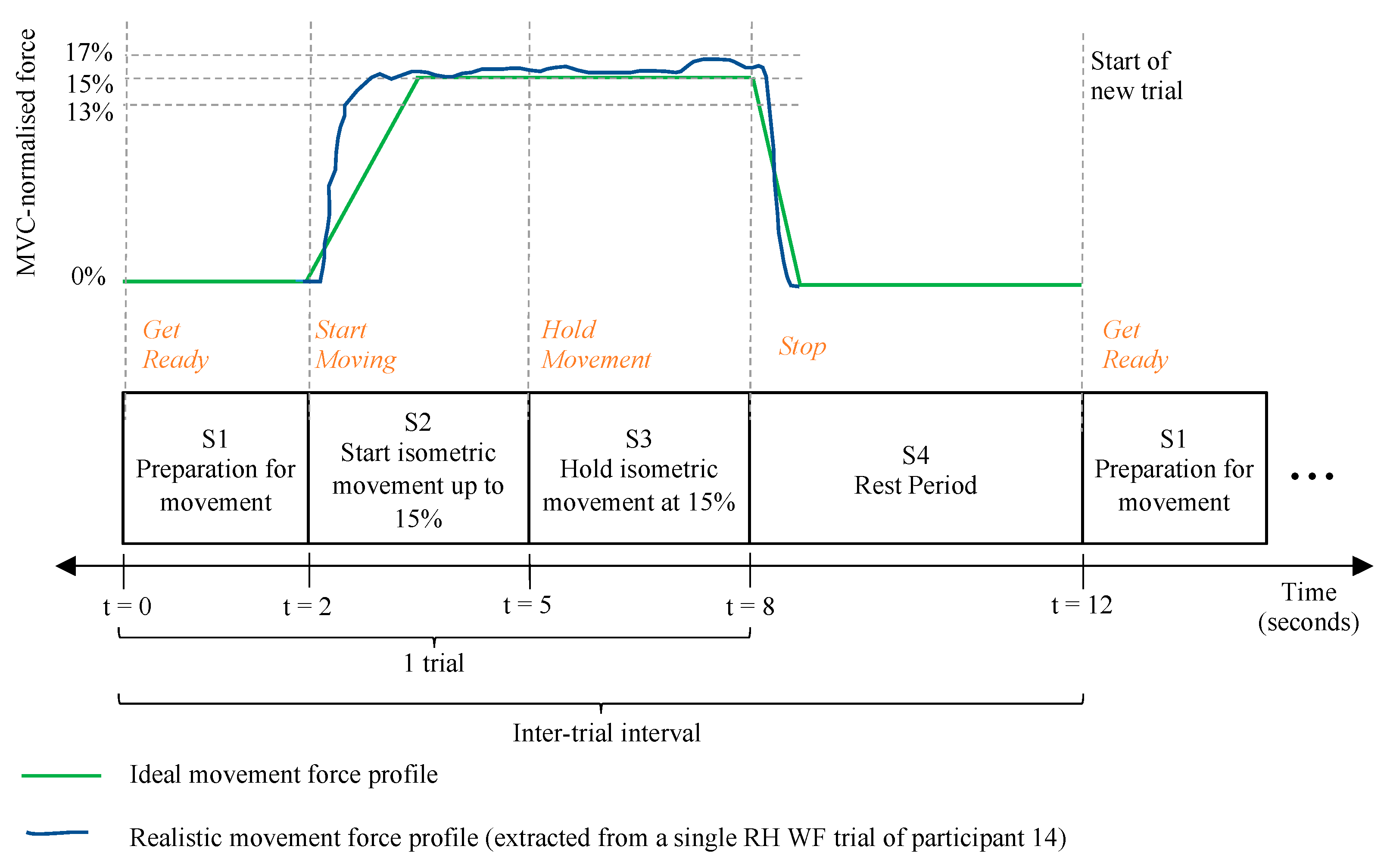
- The participant rested for seven seconds [34]. For the last four seconds of this rest period, a countdown timer prepared the participant for movement.
- Upon instruction to contract, the participant performed and sustained a WE or WF movement with all the strength of their wrist for five seconds [37] until instructed to rest again.
- Steps 1–3 were repeated three times.
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


References
- Rybski, M. Kinesiology for Occupational Therapy; Slack: Thorofare, NJ, USA, 2004; ISBN 1-55642-491-4. [Google Scholar]
- Trombly, C.A.; Radomski, M.V. (Eds.) Occupational Therapy for Physical Dysfunction, 5th ed.; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2002; ISBN 0-7817-2461-9. [Google Scholar]
- Nelson, D.L.; Mitchell, M.A.; Groszewski, P.G.; Pennick, S.L.; Manske, P.R. Wrist Range of Motion in Activities of Daily Living. In Advances in the Biomechanics of the Hand and Wrist; Schuind, F., An, K.N., Cooney, W.P., Garcia-Elias, M., Eds.; Springer US: Boston, MA, USA, 1994; pp. 329–334. ISBN 978-1-4757-9109-9. [Google Scholar]
- Gates, D.H.; Walters, L.S.; Cowley, J.; Wilken, J.M.; Resnik, L. Range of Motion Requirements for Upper-Limb Activities of Daily Living. Am. J. Occup. Ther. 2015, 70, 7001350010p1–7001350010p10. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, A.-K.; Aharonson, V. Four-Class BCI Discrimination of Right and Left Wrist and Finger Movements. IFAC-Pap. 2021, 54, 91–96. [Google Scholar] [CrossRef]
- Forman, G.N.; Forman, D.A.; Avila-Mireles, E.J.; Zenzeri, J.; Holmes, M.W.R. Investigating the Muscular and Kinematic Responses to Sudden Wrist Perturbations during a Dynamic Tracking Task. Sci. Rep. 2020, 10, 4161. [Google Scholar] [CrossRef]
- Yoshii, Y.; Yuine, H.; Kazuki, O.; Tung, W.; Ishii, T. Measurement of Wrist Flexion and Extension Torques in Different Forearm Positions. Biomed. Eng. Online 2015, 14, 115. [Google Scholar] [CrossRef]
- Gu, Y.; Dremstrup, K.; Farina, D. Single-Trial Discrimination of Type and Speed of Wrist Movements from EEG Recordings. Clin. Neurophysiol. 2009, 120, 1596–1600. [Google Scholar] [CrossRef]
- Roy, R.; Sikdar, D.; Mahadevappa, M.; Kumar, C.S. A Fingertip Force Prediction Model for Grasp Patterns Characterised from the Chaotic Behaviour of EEG. Med. Biol. Eng. Comput. 2018, 56, 2095–2107. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, L.; Hao, D.; Rong, Y.; Yang, L.; Zhang, S.; Chen, F.; Zheng, D. Effects of Force Load, Muscle Fatigue and Extremely Low Frequency Magnetic Stimulation on EEG Signals during Side Arm Lateral Raise Task. Physiol. Meas. 2017, 38, 745–758. [Google Scholar] [CrossRef]
- Abiri, R.; Borhani, S.; Sellers, E.W.; Jiang, Y.; Zhao, X. A Comprehensive Review of EEG-Based Brain–Computer Interface Paradigms. J. Neural Eng. 2019, 16, 011001. [Google Scholar] [CrossRef]
- Beck, M.M.; Spedden, M.E.; Dietz, M.J.; Karabanov, A.N.; Christensen, M.S.; Lundbye-Jensen, J. Cortical Signatures of Precision Grip Force Control in Children, Adolescents, and Adults. eLife 2021, 10, e61018. [Google Scholar] [CrossRef]
- Bönstrup, M.; Schulz, R.; Feldheim, J.; Hummel, F.C.; Gerloff, C. Dynamic Causal Modelling of EEG and fMRI to Characterize Network Architectures in a Simple Motor Task. NeuroImage 2016, 124, 498–508. [Google Scholar] [CrossRef]
- Larsen, L.H.; Zibrandtsen, I.C.; Wienecke, T.; Kjaer, T.W.; Langberg, H.; Nielsen, J.B.; Christensen, M.S. Modulation of Task-Related Cortical Connectivity in the Acute and Subacute Phase after Stroke. Eur. J. Neurosci. 2018, 47, 1024–1032. [Google Scholar] [CrossRef] [PubMed]
- Wilkins, K.B.; Yao, J. Coordination of Multiple Joints Increases Bilateral Connectivity with Ipsilateral Sensorimotor Cortices. NeuroImage 2020, 207, 116344. [Google Scholar] [CrossRef]
- Divekar, N.V.; John, L.R. Neurophysiological, Behavioural and Perceptual Differences between Wrist Flexion and Extension Related to Sensorimotor Monitoring as Shown by Corticomuscular Coherence. Clin. Neurophysiol. 2013, 124, 136–147. [Google Scholar] [CrossRef]
- Yang, Y.; Guliyev, B.; Schouten, A.C. Dynamic Causal Modeling of the Cortical Responses to Wrist Perturbations. Front. Neurosci. 2017, 11, 518. [Google Scholar] [CrossRef]
- Jochumsen, M.; Rovsing, C.; Rovsing, H.; Niazi, I.K.; Dremstrup, K.; Kamavuako, E.N. Classification of Hand Grasp Kinetics and Types Using Movement-Related Cortical Potentials and EEG Rhythms. Comput. Intell. Neurosci. 2017, 2017, 7470864. [Google Scholar] [CrossRef]
- Decostre, V.; Canal, A.; Ollivier, G.; Ledoux, I.; Moraux, A.; Doppler, V.; Payan, C.A.M.; Hogrel, J.-Y. Wrist Flexion and Extension Torques Measured by Highly Sensitive Dynamometer in Healthy Subjects from 5 to 80 Years. BMC Musculoskelet. Disord. 2015, 16, 4. [Google Scholar] [CrossRef][Green Version]
- Morse, J.L.; Jung, M.-C.; Bashford, G.R.; Hallbeck, M.S. Maximal Dynamic Grip Force and Wrist Torque: The Effects of Gender, Exertion Direction, Angular Velocity, and Wrist Angle. Appl. Ergon. 2006, 37, 737–742. [Google Scholar] [CrossRef] [PubMed]
- Hallbeck, M.S. Flexion and Extension Forces Generated by Wrist-Dedicated Muscles over the Range of Motion. Appl. Ergon. 1994, 25, 379–385. [Google Scholar] [CrossRef] [PubMed]
- van der Ploeg, R.J.; Fidler, V.; Oosterhuis, H.J. Hand-Held Myometry: Reference Values. J. Neurol. Neurosurg. Psychiatry 1991, 54, 244–247. [Google Scholar] [CrossRef]
- Grimaldi, G.; Lammertse, P.; Braber, N.; Meuleman, J.; Manto, M. A New Myohaptic Device to Assess Wrist Function in the Lab and in the Clinic—The Wristalyzer. In Proceedings of the 6th International Conference on Haptics: Perception, Devices and Scenarios, Madrid, Spain, 11–13 June 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 33–42. [Google Scholar]
- Herz, D.M.; Siebner, H.R.; Hulme, O.J.; Florin, E.; Christensen, M.S.; Timmermann, L. Levodopa Reinstates Connectivity from Prefrontal to Premotor Cortex during Externally Paced Movement in Parkinson’s Disease. NeuroImage 2014, 90, 15–23. [Google Scholar] [CrossRef]
- Loehrer, P.A.; Nettersheim, F.S.; Oehrn, C.R.; Homberg, F.; Tittgemeyer, M.; Timmermann, L.; Weber, I. Increased Prefrontal Top-down Control in Older Adults Predicts Motor Performance and Age-Group Association. NeuroImage 2021, 240, 118383. [Google Scholar] [CrossRef] [PubMed]
- Loehrer, P.A.; Nettersheim, F.S.; Jung, F.; Weber, I.; Huber, C.; Dembek, T.A.; Pelzer, E.A.; Fink, G.R.; Tittgemeyer, M.; Timmermann, L. Ageing Changes Effective Connectivity of Motor Networks during Bimanual Finger Coordination. NeuroImage 2016, 143, 325–342. [Google Scholar] [CrossRef]
- Wilkins, K.B.; Dewald, J.P.A.; Yao, J. Intervention-Induced Changes in Neural Connectivity during Motor Preparation May Affect Cortical Activity at Motor Execution. Sci. Rep. 2020, 10, 7326. [Google Scholar] [CrossRef]
- Boudrias, M.-H.; Gonçalves, C.S.; Penny, W.D.; Park, C.; Rossiter, H.E.; Talelli, P.; Ward, N.S. Age-Related Changes in Causal Interactions between Cortical Motor Regions during Hand Grip. NeuroImage 2012, 59, 3398–3405. [Google Scholar] [CrossRef]
- Kim, H.J.; Lee, J.H.; Kang, N.; Cauraugh, J.H. Visual Feedback Improves Bimanual Force Control Performances at Planning and Execution Levels. Sci. Rep. 2021, 11, 21149. [Google Scholar] [CrossRef] [PubMed]
- Aboul-Hagag, K.E.; Mohamed, S.A.; Hilal, M.A.; Mohamed, E.A. Determination of Sex from Hand Dimensions and Index/Ring Finger Length Ratio in Upper Egyptians. Egypt. J. Forensic Sci. 2011, 1, 80–86. [Google Scholar] [CrossRef]
- Wang, C.; Cai, D. Hand Tool Handle Design Based on Hand Measurements. MATEC Web Conf. 2017, 119, 01044. [Google Scholar] [CrossRef]
- Yu, A.; Yick, K.L.; Ng, S.P.; Yip, J. 2D and 3D Anatomical Analyses of Hand Dimensions for Custom-Made Gloves. Appl. Ergon. 2013, 44, 381–392. [Google Scholar] [CrossRef]
- Jee, S.-C.; Bahn, S.; Yun, M.H. Determination of Sex from Various Hand Dimensions of Koreans. Forensic Sci. Int. 2015, 257, 521.e1–521.e10. [Google Scholar] [CrossRef]
- Reckelhoff, K.E.; Li, J.; Kaeser, M.A.; Haun, D.W.; Kettner, N.W. Ultrasound Evaluation of the Normal Ulnar Nerve in Guyon’s Tunnel: Cross-Sectional Area and Anthropometric Measurements. J. Med. Ultrasound 2015, 23, 171–176. [Google Scholar] [CrossRef]
- Bains, K.N.S.; Lappin, S.L. Anatomy, Shoulder and Upper Limb, Elbow Cubital Fossa. In StatPearls; StatPearls Publishing: Treasure Island, FL, USA, 2020. [Google Scholar]
- Bentley, J.P. Principles of Measurement Systems, 4th ed.; Pearson Prentice Hall: Harlow, UK; New York, NY, USA, 2005; ISBN 978-0-13-043028-1. [Google Scholar]
- Rudisch, J.; Müller, K.; Kutz, D.F.; Brich, L.; Sleimen-Malkoun, R.; Voelcker-Rehage, C. How Age, Cognitive Function and Gender Affect Bimanual Force Control. Front. Physiol. 2020, 11, 245. [Google Scholar] [CrossRef]
- Components 101 HX711–24 Bit Analog to Digital Converter (ADC). Available online: https://components101.com/ics/hx711-24-bit-analog-digital-converter-adc (accessed on 4 May 2020).
- Peirce, J.W. PsychoPy—Psychophysics Software in Python. J. Neurosci. Methods 2007, 162, 8–13. [Google Scholar] [CrossRef] [PubMed]
- Brown, C.E. Coefficient of Variation. In Applied Multivariate Statistics in Geohydrology and Related Sciences; Brown, C.E., Ed.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 155–157. ISBN 978-3-642-80328-4. [Google Scholar]
- Oldfield, R.C. The Assessment and Analysis of Handedness: The Edinburgh Inventory. Neuropsychologia 1971, 9, 97–113. [Google Scholar] [CrossRef] [PubMed]
- Cohen, M. Handedness Questionnaire. Available online: http://www.brainmapping.org/shared/Edinburgh.php (accessed on 30 December 2020).
- Kay, D.; St Clair Gibson, A.; Mitchell, M.J.; Lambert, M.I.; Noakes, T.D. Different Neuromuscular Recruitment Patterns during Eccentric, Concentric and Isometric Contractions. J. Electromyogr. Kinesiol. 2000, 10, 425–431. [Google Scholar] [CrossRef]
- MAT Muscle Meter Handheld Dynamometer—Push, Pull & Grip Strength Testing. Available online: https://www.matassessment.com/musclemeter (accessed on 17 July 2024).
- Jochumsen, M.; Khan Niazi, I.; Taylor, D.; Farina, D.; Dremstrup, K. Detecting and Classifying Movement-Related Cortical Potentials Associated with Hand Movements in Healthy Subjects and Stroke Patients from Single-Electrode, Single-Trial EEG. J. Neural Eng. 2015, 12, 056013. [Google Scholar] [CrossRef]
- Jochumsen, M.; Niazi, I.K.; Dremstrup, K.; Kamavuako, E.N. Detecting and Classifying Three Different Hand Movement Types through Electroencephalography Recordings for Neurorehabilitation. Med. Biol. Eng. Comput. 2016, 54, 1491–1501. [Google Scholar] [CrossRef]
- Moulton, E.; Galléa, C.; Kemlin, C.; Valabregue, R.; Maier, M.A.; Lindberg, P.; Rosso, C. Cerebello-Cortical Differences in Effective Connectivity of the Dominant and Non-Dominant Hand during a Visuomotor Paradigm of Grip Force Control. Front. Hum. Neurosci. 2017, 11, 511. [Google Scholar] [CrossRef]
- Wierzgała, P.; Zapała, D.; Wojcik, G.M.; Masiak, J. Most Popular Signal Processing Methods in Motor-Imagery BCI: A Review and Meta-Analysis. Front. Neuroinform. 2018, 12, 78. [Google Scholar] [CrossRef] [PubMed]
- Cantillo-Negrete, J.; Carino-Escobar, R.I.; Carrillo-Mora, P.; Rodriguez-Barragan, M.A.; Hernandez-Arenas, C.; Quinzaños-Fresnedo, J.; Hernandez-Sanchez, I.R.; Galicia-Alvarado, M.A.; Miguel-Puga, A.; Arias-Carrion, O. Brain-Computer Interface Coupled to a Robotic Hand Orthosis for Stroke Patients’ Neurorehabilitation: A Crossover Feasibility Study. Front. Hum. Neurosci. 2021, 15, 656975. [Google Scholar] [CrossRef]
- Mohamed, A.K.; Marwala, T.; John, L.R. Single-Trial EEG Discrimination between Wrist and Finger Movement Imagery and Execution in a Sensorimotor BCI. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August 2011–3 September 2011; pp. 6289–6293. [Google Scholar]
- Mohamed, A.K.; John, L.R. Single-Trial EEG Discrimination between Five Hand Movement Imagery and Execution: Towards the Control of a Prosthetic/Orthotic Hand Using a Brain-Computer Interface. In Proceedings of the 2014 PRASA, RobMech and AfLaT International Joint Symposium, Cape Town, South Africa, 27–28 November 2014; pp. 25–30. [Google Scholar]
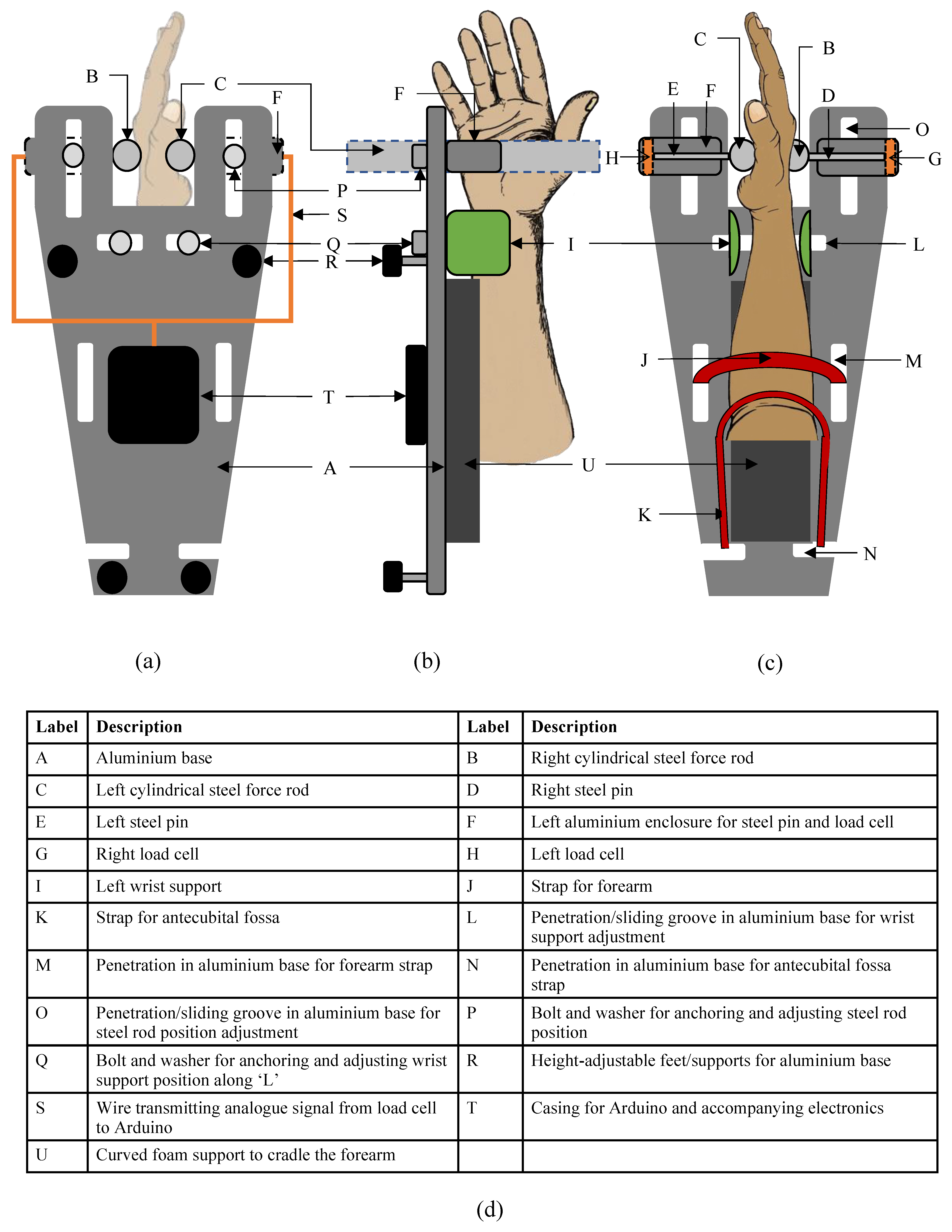

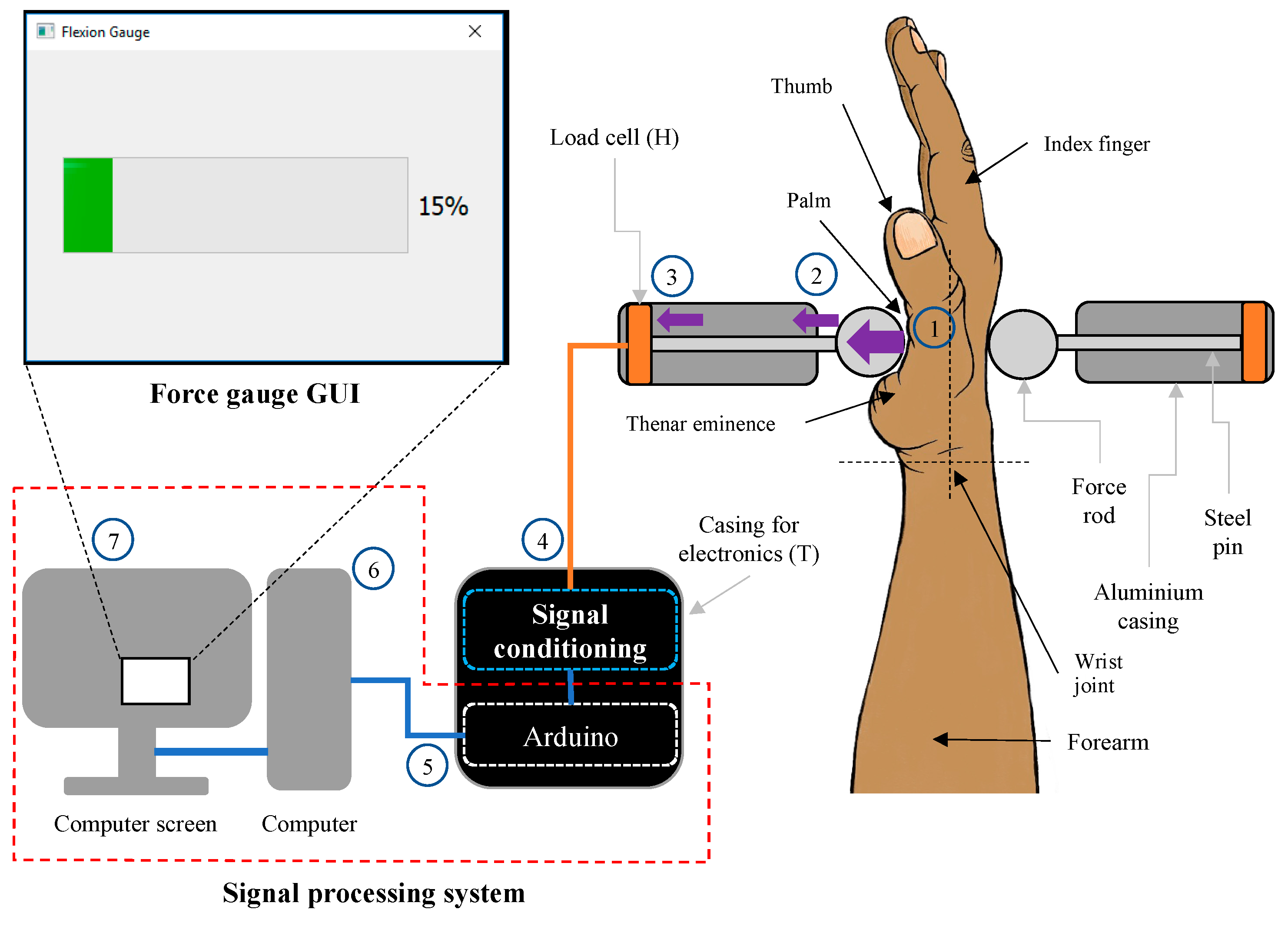
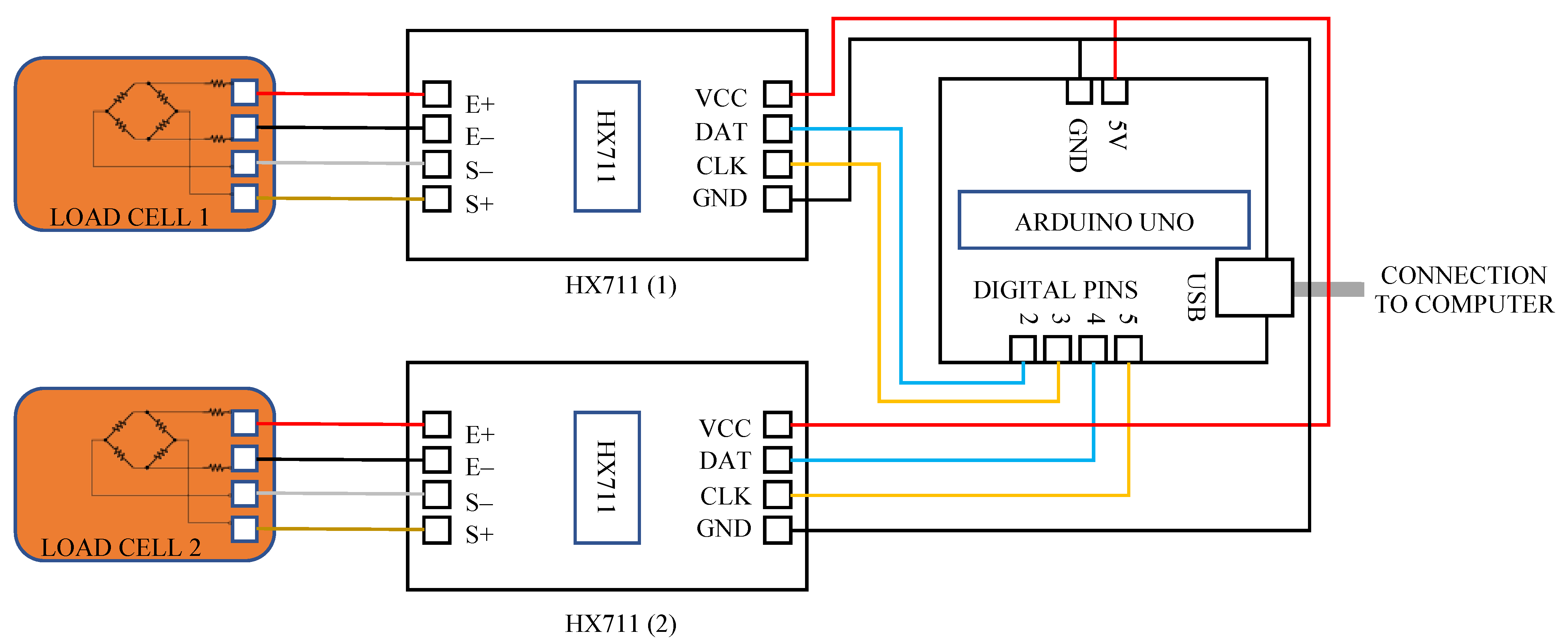
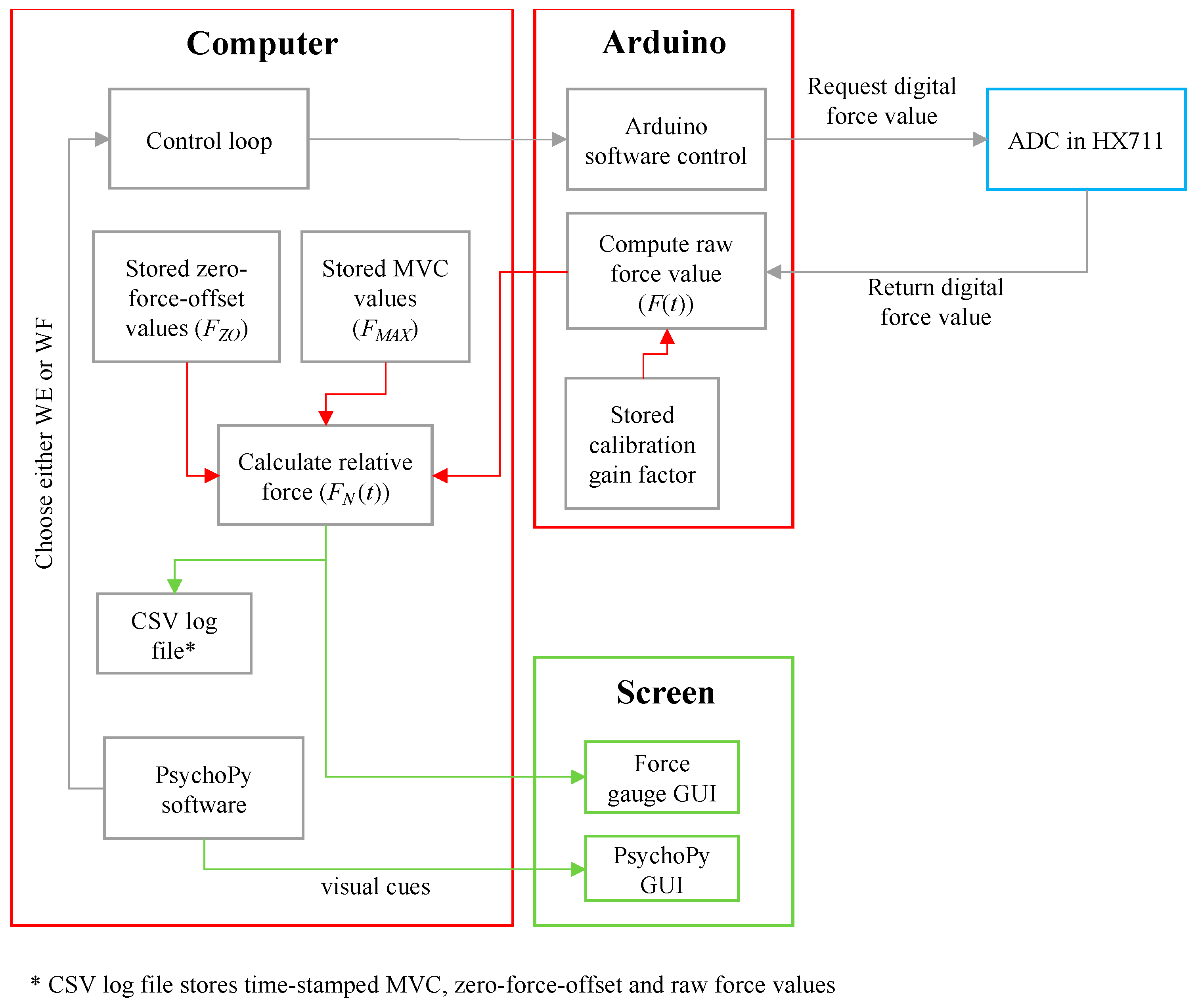
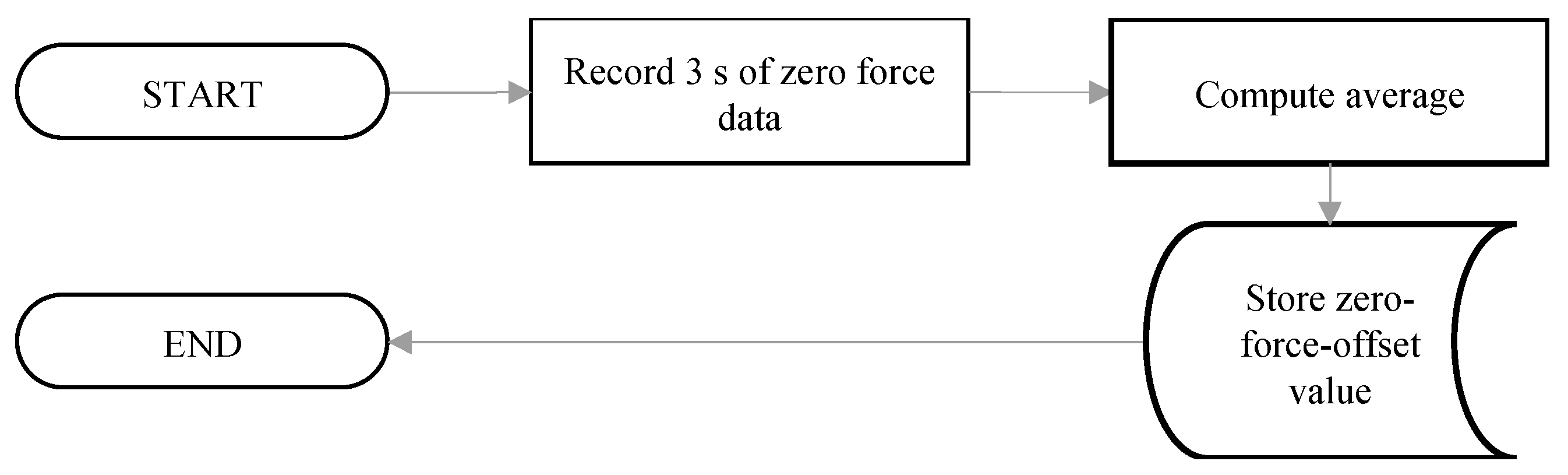
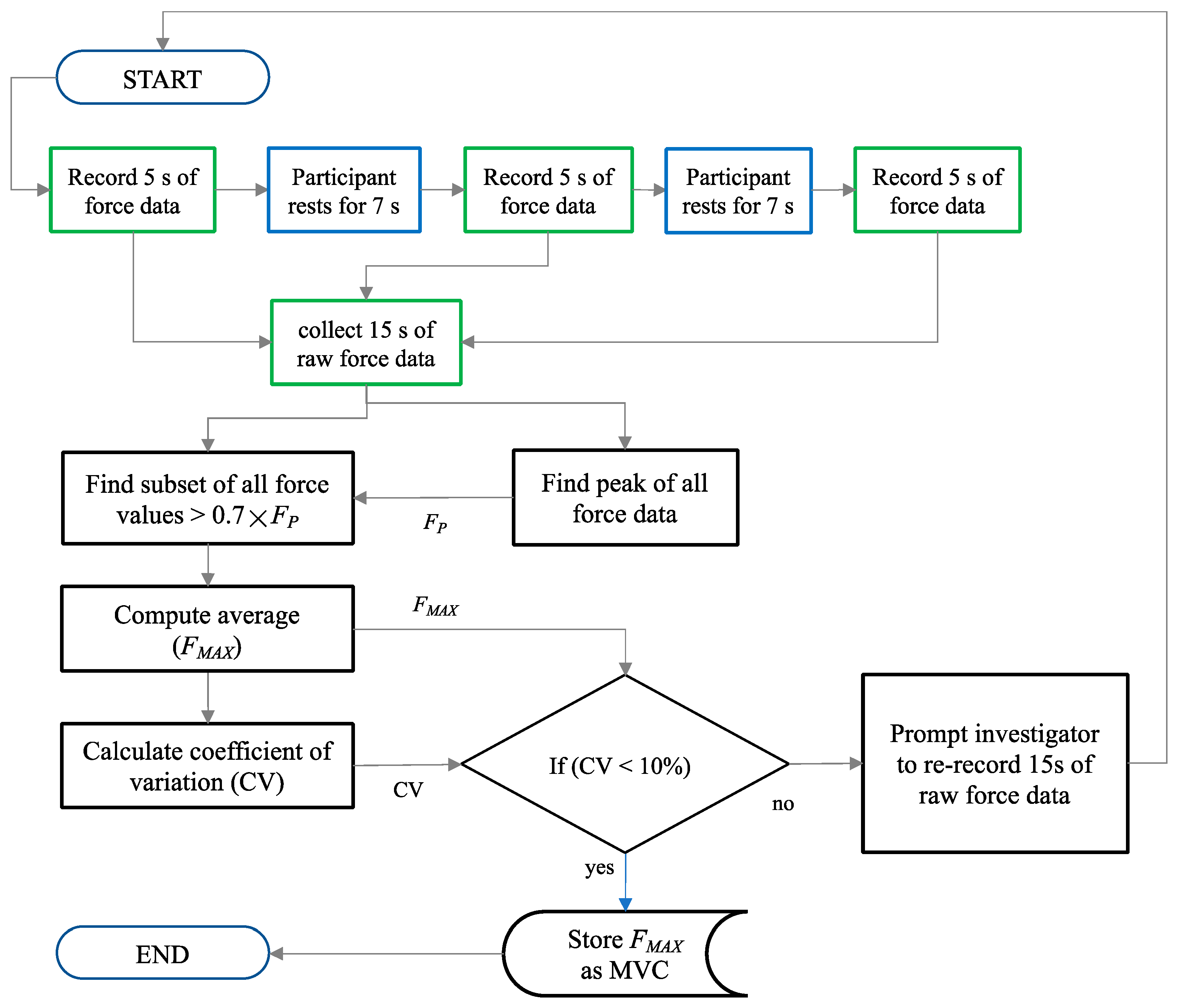
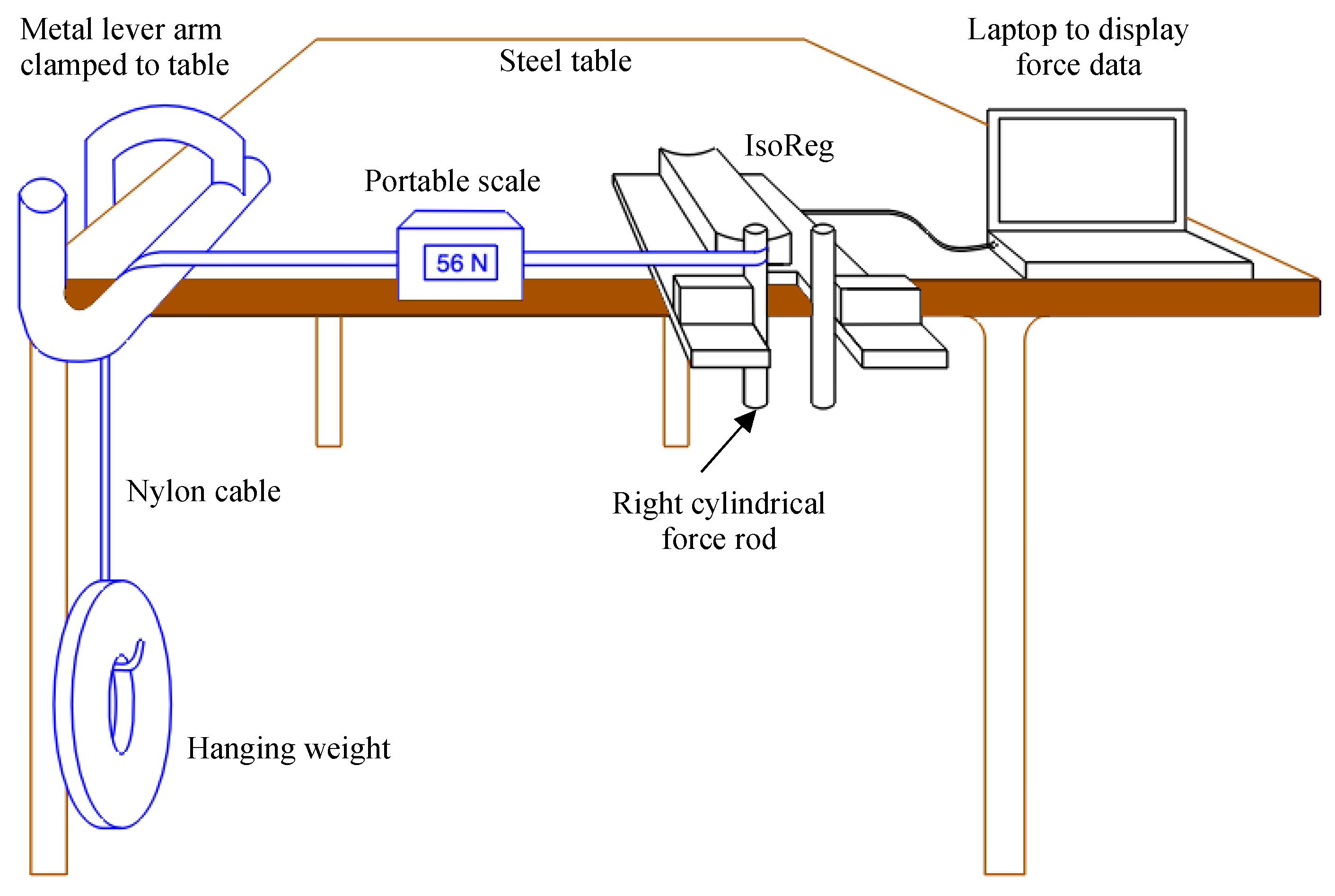
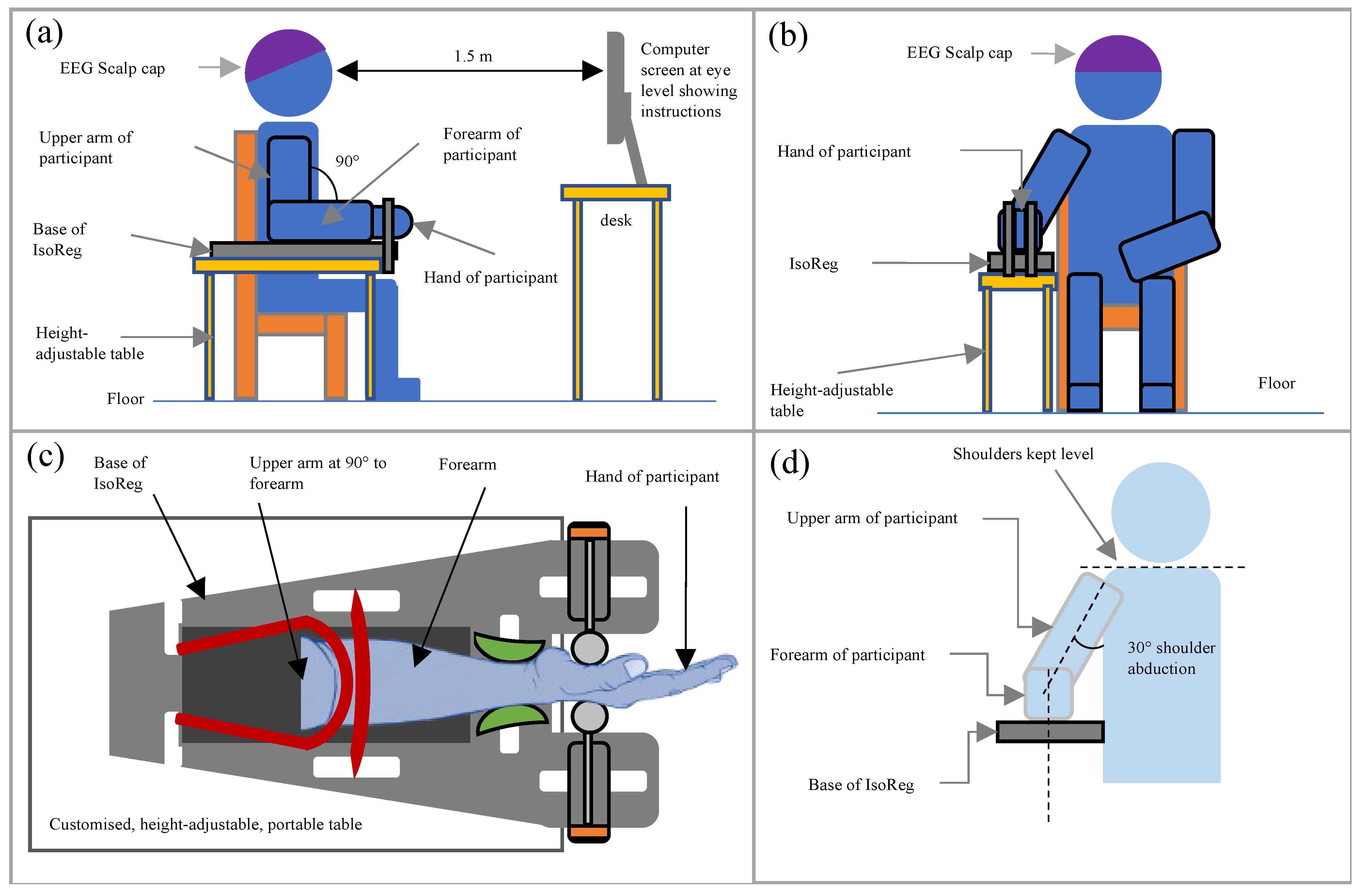


| Design Consideration | Specification |
|---|---|
| Construction | Adjust to accommodate typical dimension of human hands, forearms and wrists for both right and left hands. Comfortable usage for up to four hours. |
| Maximum mass | 3 kg (for portability) |
| Dimensions | <600 mm (length); <350 mm (width) |
| Force range | 0–214 N (from Table 1) |
| Resolution | 1% of minimum MVC from Table 1 = 0.28 N |
| Frequency range of input signals to handle | 0–100 Hz |
| Accuracy | >96% |
| Output display | Force gauge on computer screen with a range of 0–100% relative to MVC |
| Output data logging | Time-stamped forces saved in CSV file |
| Dimensions of supporting table | <600 mm (length); <350 mm (width), 500–800 mm (adjustable height); easy assembly for portability |
| Maximum mass of supporting table | 10 kg for portability |
| Expected force range applied to supporting table | 0–214 N (from Table 1) |
| Cost | <$140 USD |
| Test 1 | Test 2 | |||||
|---|---|---|---|---|---|---|
| AF (N) | F (N) | Error1 for F (%) | FZO (N) | FN on Gauge (N) | AFN (N) | Error2 for FN (%) |
| 24.80 | 24.28 | 2.10 | 0.06 | 24 | 24.22 | 0.91 |
| 25.63 | 26.24 | 2.38 | 0.06 | 26 | 26.18 | 0.68 |
| 27 | 26.97 | 0.11 | 0.06 | 26 | 26.91 | 3.38 |
| 41.10 | 39.85 | 3.04 | −0.07 | 39 | 39.92 | 2.30 |
| 38.30 | 39.04 | 1.93 | −0.07 | 39 | 39.11 | 0.28 |
| 38.17 | 38.81 | 1.67 | −0.07 | 38 | 38.88 | 2.26 |
| 65.31 | 67.02 | 2.62 | 0.16 | 67 | 66.86 | 0.21 |
| 76.83 | 77.27 | 0.57 | 0.16 | 76 | 77.11 | 1.44 |
| 86.53 | 85.44 | 1.26 | 0.16 | 85 | 85.28 | 0.33 |
| 84.88 | 86.43 | 1.83 | 0.16 | 86 | 86.27 | 0.32 |
| 80 | 81.57 | 1.96 | 0.16 | 81 | 81.41 | 0.51 |
| 83.49 | 83.11 | 0.45 | 0.16 | 83 | 82.96 | 0.05 |
| 84.28 | 84.56 | 0.33 | −0.05 | 84 | 84.61 | 0.72 |
| 90.06 | 91.04 | 1.08 | −0.05 | 91 | 91.09 | 0.10 |
| 81.34 | 79.55 | 2.20 | −0.05 | 79 | 79.60 | 0.75 |
| 99.30 | 98.97 | 0.33 | −0.28 | 99 | 99.25 | 0.26 |
| 108.30 | 105.85 | 2.26 | −0.28 | 99 | 106.13 | N/A |
| 95.40 | 95.03 | 0.39 | −0.28 | 95 | 95.31 | 0.33 |
| 156 | 161 | 3.21 | 0.45 | 99 | 160.55 | N/A |
| 155.14 | 160.70 | 3.58 | 0.45 | 99 | 160.25 | N/A |
| 155.10 | 159.90 | 3.09 | 0.45 | 99 | 159.45 | N/A |
| Mean | 1.73 | 0.87 | ||||
| Test 1 | Test 2 | |||||
|---|---|---|---|---|---|---|
| AF (N) | F (N) | Error1 for F (%) | FZO (N) | FN on Gauge (N) | AFN (N) | Error2 for FN (%) |
| 39.25 | 38.18 | 2.74 | 0.17 | 38 | 38.01 | 0.02 |
| 39.35 | 38.38 | 2.48 | 0.17 | 38 | 38.21 | 0.54 |
| 39.83 | 38.65 | 2.96 | 0.17 | 38 | 38.48 | 1.26 |
| 24.45 | 23.66 | 3.22 | 1.20 | 22 | 22.46 | 2.06 |
| 24.30 | 23.67 | 2.58 | 1.20 | 22 | 22.47 | 2.10 |
| 24.84 | 24.04 | 3.20 | 1.20 | 22 | 22.84 | 3.69 |
| 73.20 | 71.12 | 2.84 | 1.73 | 69 | 69.39 | 0.56 |
| 74.90 | 72.49 | 3.21 | 1.73 | 69 | 70.76 | 2.49 |
| 69.70 | 71.12 | 2.04 | 1.73 | 70 | 69.39 | 0.88 |
| 88.50 | 86.56 | 2.19 | 1.75 | 84 | 84.81 | 0.96 |
| 92.60 | 90.35 | 2.43 | 1.75 | 88 | 88.6 | 0.68 |
| 85.50 | 82.39 | 3.64 | 1.75 | 80 | 80.64 | 0.79 |
| Mean | 2.79 | 1.34 | ||||
| Participant Number | Accuracy of Force Normalisation for WE (%) | Accuracy of Force Normalisation for WF (%) | DNF (%) |
|---|---|---|---|
| 1 | 92.37 | 89.21 | 3.16 |
| 2 | 97.83 | 95.93 | 1.9 |
| 3 | 95.08 | 99.81 | 4.73 |
| 4 | 53.54 | 65.09 | 11.55 |
| 5 | 96.23 | 97.27 | 1.04 |
| 6 | 82.86 | 72.38 | 10.48 |
| 7 | 96.5 | 92.76 | 3.74 |
| 8 | 88.10 | 92.57 | 4.47 |
| 9 | 98.67 | 99.35 | 0.68 |
| 10 | 86.97 | 85.35 | 1.62 |
| 11 | 96.31 | 97.64 | 1.34 |
| 12 | 95.14 | 96.21 | 1.07 |
| 13 | N/A | N/A | N/A |
| 14 | N/A | N/A | N/A |
| Mean (SD) | 89.97 (12.46) | 90.3 (11.02) | 3.81 (3.64) |
| Participant Number | Accuracy of Force Normalisation for WE (%) | Accuracy of Force Normalisation for WF | DNF (%) |
|---|---|---|---|
| 1 | 93.35 | 94.33 | 0.98 |
| 2 | 89.86 | 95.83 | 5.97 |
| 3 | 89.96 | 94.75 | 4.79 |
| 4 | 81.92 | 81.58 | 0.33 |
| 5 | 83.83 | 88.47 | 4.64 |
| 6 | 92.86 | 88.38 | 4.48 |
| 7 | 93 | 94.81 | 1.81 |
| 8 | 83.38 | 70.47 | 12.91 |
| 9 | 94.92 | 98.96 | 4.04 |
| 10 | 81.47 | 92.65 | 11.18 |
| 11 | 91.72 | 94.94 | 3.22 |
| 12 | 88.74 | 91.81 | 3.06 |
| 13 | N/A | N/A | N/A |
| 14 | N/A | N/A | N/A |
| Mean (SD) | 88.75 (4.85) | 90.58 (7.79) | 4.79 (3.78) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, A.-K.; Aswat, M.; Aharonson, V. Low-Cost Dynamometer for Measuring and Regulating Wrist Extension and Flexion Motor Tasks in Electroencephalography Experiments. Sensors 2024, 24, 5801. https://doi.org/10.3390/s24175801
Mohamed A-K, Aswat M, Aharonson V. Low-Cost Dynamometer for Measuring and Regulating Wrist Extension and Flexion Motor Tasks in Electroencephalography Experiments. Sensors. 2024; 24(17):5801. https://doi.org/10.3390/s24175801
Chicago/Turabian StyleMohamed, Abdul-Khaaliq, Muhammed Aswat, and Vered Aharonson. 2024. "Low-Cost Dynamometer for Measuring and Regulating Wrist Extension and Flexion Motor Tasks in Electroencephalography Experiments" Sensors 24, no. 17: 5801. https://doi.org/10.3390/s24175801
APA StyleMohamed, A.-K., Aswat, M., & Aharonson, V. (2024). Low-Cost Dynamometer for Measuring and Regulating Wrist Extension and Flexion Motor Tasks in Electroencephalography Experiments. Sensors, 24(17), 5801. https://doi.org/10.3390/s24175801






